1 Introduction

Credit risk assessment has become an increasingly important research topic for financial institutions in recent years. With the increasing number of customers who default on loans, many financial institutions have suffered serious losses over several years. However, it is not reasonable for financial institutions to turn down all applications to avoid any credit risk. For this reason, proper classification of applicants is crucial [1–3]; that is, applicants with good credit scores and those with bad ones. Financial institutions can grant credit to applicants with good credit scores and reject applicants with bad ones. Thus, the accuracy of credit scoring is very important. Even a small improvement in the accuracy of credit risk assessment can greatly reduce financial institution losses.

Recently, many studies on credit risk assessment have been carried out classified mainly into two categories: statistical and intelligent techniques. Techniques such as linear discriminant analysis [4, 5], logistic regression analysis [6, 7], and multivariate adaptive regression splines [8], amongst others, are classified as statistical techniques. However, when applying statistical techniques to credit scoring, a problem arises in that some assumptions, for example, the multivariate normality assumptions for independent variables, are frequently violated in the practice of credit scoring making these techniques theoretically ineffective for finite samples [9]. Intelligent techniques, like artificial neural networks (ANNs) [6, 10] decision trees (DTs) [11, 12], case-based reasoning [13, 14], and support vector machines (SVMs) [15–17], can be used as alternative approaches for credit scoring. In contrast to statistical techniques, intelligent techniques do not need to assume certain data distributions. These techniques voluntarily extract knowledge from training instances. According to previous research, intelligent techniques perform better than statistical techniques in credit scoring tasks, especially for nonlinear pattern classifications [9].

Each of the two categories has its own characteristics and the same approach can have significantly different performance on different credit datasets. Therefore, we cannot state conclusively which technique is the best. Recent research has focused on combinations of multiple classifiers, i.e., ensemble learning. Moreover, many experiments have shown that ensemble learning is an effective strategy for achieving high classification performance, especially with a number of varying structures in the base models, which make the prediction error independent [18–22]. For comparison with multiple classifiers and varying diversity, the performance of single classifiers was investigated by Tsai and Wu [23], with a neural network used as the base learner. Experimental results indicate that the ensemble method is better than single classifiers. Yu, Wang and Lai [24] proposed a method using a combination of multiple neural network models to predict credit risk. From a comparison with single classifiers, they conclude that the ensemble learning model achieves a more promising solution. In [25], Nanni and Lumini carried out an experiment to investigate the performance of several systems based on ensemble learning. The results show that ensemble learning methods can improve the performance of single classifiers for credit risk analysis. Hung and Chen [26] proposed a selective ensemble based on the expected probabilities method for credit risk assessment. This method uses three classifiers: a DT, ANN and SVM. The benefits of the proposed ensemble method are that the advantages and disadvantages of different classification methods are inherited and avoided, respectively. However, the operating principle of ensemble learning is based on multiple classifiers, which requires more computational time and storage space. Moreover, classifiers with both high and low predictive performances are included in the ensemble, and therefore the prediction results of the entire ensemble are negatively affected by classifiers with low performance.

To overcome the existing limitations of ensemble learning, the paradigm of ensemble selection has been proposed, which is also referred to as ensemble pruning, ensemble thinning, or selective ensemble [27]. The purpose of ensemble selection is to select a proper subset from the entire set of original base classifiers. High efficiency and better classification performance are the two most important advantages of ensemble selection. On the one hand, owing to a reduction in ensemble size, execution time is shortened, while at the same time saving storage space. On the other hand, the selected ensemble performs better than the original ensemble in terms of classification, as verified by many previous studies [27–34].

Thus far, very little research has been conducted on applying ensemble selection approaches to credit scoring. Nevertheless, it is expected that the performance of credit risk assessment using the ensemble selection approach will be better than that of its competitors. Since credit risk assessment could be regarded as a special case of the classification problem, according to the description of Zhou et al. in [35], it can be expected that, a properly selected subensemble will perform better than the original ensemble in classification tasks, and more specifically, in credit scoring tasks.

Broadly speaking, ensemble selection can be considered as a combinatorial optimization problem. In recent years, various ensemble selection approaches based on a greedy searching strategy have been proposed [27, 30, 32, 36, 37]. There are three main elements in greedy ensemble selection approaches: the selection direction, the evaluation dataset, and the evaluation measure. In previous research on the greedy ensemble selection approach, researchers have focused on the design of better evaluation measures, while the serious problem of local optima caused by improper starting points or searching methods is often ignored.

Motivated by the above ideas, in this work, we propose a novel ensemble selection algorithm for credit risk assessment, called ELMsGraspEnS, which is based on the extreme learning machine (ELM) and greedy randomized adaptive search procedure (GRASP). Generally, in ELMsGraspEnS, the ELM is used as the base model in the original ensemble, and ensemble selection is implemented using the GRASP algorithm.

The ELM is an efficient learning approach for single hidden layer feedforward neural networks (SLFNs) [38]. Unlike the extensively applied conventional feedforward neural network learning algorithm, i.e., the gradient-based learning algorithm, the ELM can randomly initialize the SLFN weights and bias, while its input weights and biases do not need to be adjusted. With the ELM, it is possible to determine analytically the hidden layer output matrix and the output weights of the SLFNs. The network is obtained with very few computational steps and very low computational cost. Owing to this feature, multiple ELMs can very easily be produced to build an ensemble. In addition, the learning speed of the ELM can be thousands of times faster than the traditional gradient-based learning algorithm, while its generalization performance is better than that of the latter algorithm in quite a few classification applications. Moreover, there are several issues with the traditional gradient-based learning algorithm, for example, local minima, improper learning rate, and overfitting. The ELM can avoid these problems efficiently [38].

Many applications of the ELM algorithm have been proposed in the literature. In [39], the ELM is applied to solve multi-category classification problems using a single ELM classifier and a series of ELM binary classifiers, this work provides a promising solution. Duan, Huang and Wang [40] proposed an ELM method for classification of bank clients, and compared the performance of the ELM with other existing learning methods, i.e., DT, NN and SVM. Their results show that the ELM method is superior to the other three methods. In [41], Huang et al. proved that for typical regression and multi-class classification problems, the ELM outperforms the traditional SVM method. The ELM is used as a classifier for a two-category data classification problem in [42], with the experimental results showing that the ELM method achieves better prediction performance than traditional methods in reduced time. In [43], using a hybrid grouping harmony search and the ELM approach to evaluate the internationalization success of a company, the authors clearly show that the performance of the ELM algorithm is better than other typical classifiers.

In [31], we proposed a novel ensemble selection algorithm based on GRASP (GraspEnS). GRASP is a metaheuristic multi-start algorithm for combinatorial optimization problems introduced by Feo and Resende [44]. It is an iterative procedure [45, 46], where each iterative process includes a construction phase and a local search phase. A feasible solution is generated in the construction phase, and is refined in the local search phase. The two phases are iterated a number of times until the termination criterion is reached, that is, either the maximum number of iterations is reached or the target value of the objective function is satisfied. At the end of the procedure, the final solution output is the best solution obtained from the entire iterative process [44, 45]. GRASP has been applied widely in scheduling, routing, logic, partitioning, location and layout, amongst others. Our proposed GraspEnS is an application of GRASP to the problem of ensemble selection.

The GraspEnS algorithm has some similar characteristics to the classical greedy ensemble selection method. However, it differs significantly from the latter method. GraspEnS has four main advantages [31]. (1) The algorithm can escape from local optima by incorporating random factors in the construction phase. (2) In the local search phase, each feasible solution obtained in the previous construction phase is regarded as a starting point, thereby allowing the GraspEnS algorithm to realize a multi-start search. (3) By searching the neighbors of a feasible solution constructed in the first phase, the solution is further improved, because it is iteratively replaced by a better solution; that is the neighbor of the current solution, with the process continuing until no better solution is found. (4) The generalization performance of GraspEnS is superior to that of the classical greedy ensemble selection approach, i.e., directed hill climbing ensemble pruning (DHCEP) algorithm.

This paper combines the ELM and GraspEnS, and proposes a novel ELMsGraspEnS algorithm, which fully uses not only the convenience of calculation of the ELM, but also the superior generalization performance of GraspEnS. Moreover, ELMsGraspEnS has been successfully applied to credit risk assessment and achieves very good performance. Generally speaking, it can be said that ELMsGraspEnS simultaneously exhibits relatively high efficiency and effectiveness. The contributions of this paper are as follows:

First, the ELMsGraspEnS algorithm intuitively inherits the inherent characteristics of the ELM, such as its fast learning speed, better generalization performance, avoidance of overfitting and local minima, and easy implementation.

Second, ensemble systems can usually be constructed using homogeneous or heterogeneous models. ELMsGraspEnS is constructed with multiple homogeneous ELMs. The ELM randomly sets the initial weights and bias of an SLFN, incorporating random factors into ELMsGraspEnS. Moreover, the SLFN is easy to construct.

Third, using ELMsGraspEnS, the ensemble selection technique is applied to credit scoring. At present, there is very little research on the application of ensemble selection techniques to credit risk assessment. By using the ensemble selection technique in our proposed ELMsGraspEnS, we can improve the performance of credit risk assessment.

Fourth, with ELMsGraspEnS our previously proposed GraspEnS is used as the ensemble selection approach. ELMsGraspEnS makes full use of the advantages of the GraspEnS method. Therefore, the proposed ELMsGraspEnS algorithm not only can escape local optima, but also realizes a multi-start search, making it superior to the classical greedy ensemble selection approach in generalization performance.

Last, to verify the efficacy of the ELMsGraspEnS algorithm, we carried out experiments to compare the credit risk assessment performance of the ELMsGraspEnS algorithm with several state-of-the-art ensemble selection approaches on three benchmark credit datasets. We also compared ELMsGraspEnS with an SVM and multi-layer perceptron (MLP) to illustrate its efficiency. The experimental results indicate that our proposed ELMsGraspEnS algorithm significantly outperforms its competitors on all three datasets.

The remainder of the paper is organized as follows. Section 2 introduces some background knowledge of the ELM. Section 3 briefly reviews the ensemble methods and the classical greedy ensemble selection methods. Section 4 first introduces the GraspEnS algorithm based on GRASP, and then presents the proposed ELMsGraspEnS algorithm. Section 5 presents and discusses the experimental results. Finally, Section 6 summarizes the paper and suggests directions for future work.

2 Background knowledge of the ELM

Guang-Bin Huang et al. [38] originally proposed the ELM, which is an effective and efficient learning algorithm for SLFNs. The outstanding feature of the ELM is that the algorithm randomly initializes the input weights and hidden layer bias of an SLFN. Furthermore, in the ELM, the input weights and hidden layer bias do not need to be tuned. It is easy to calculate the hidden layer output matrix and the output weights explicitly once the random values have been assigned to these two groups of parameters.

Suppose there are N arbitrary distinct samples (x i ,t i ), where x i =[x i1,x i2,…,x i n ]T∈R n and t i =[t i1,t i2,…,t i m ]T∈R m. Then, a standard SLFN with \(\tilde {{N}}\) hidden nodes and an activation function g(x) can be modeled as:

$$ \sum\limits_{i=1}^{\tilde{{N}}} {\beta_{i} } g_{i} (\mathbf{x}_{j} )=\sum\limits_{i=1}^{\tilde{{N}}} {\beta_{i} } g\left( {\mathbf{w}_{i} \cdot \mathbf{x}_{j} +b_{i} } \right)=\mathbf{t}_{j} ,j=1,\mathellipsis ,N,. $$
(1)

These N equations can be written compactly as:

$$ \mathbf{H}\boldsymbol{\upbeta}=\mathbf{T}, $$
(2)

where

$$\begin{array}{@{}rcl@{}} &&\mathbf{H}(\mathbf{w}_{1} ,{\cdots} ,\mathbf{w}_{\tilde{{N}}} ,b_{1} ,{\cdots} ,b_{\tilde{{N}}} ,\mathbf{x}_{1} ,{\cdots} ,\mathbf{x}_{N} )\\&&=\left[ \begin{array}{lll} {g\left( {\mathbf{w}_{1} \cdot \mathbf{x}_{1} +b_{1} } \right)} & {\cdots} & {g\left( {\mathbf{w}_{\tilde{{N}}} \cdot \mathbf{x}_{1} +b_{\tilde{{N}}} } \right)} \\ {\vdots} & {\cdots} & {\vdots} \\ {g\left( {\mathbf{w}_{1} \cdot \mathbf{x}_{N} +b_{1} } \right)} & {\cdots} & {g\left( {\mathbf{w}_{\tilde{{N}}} \cdot \mathbf{x}_{N} +b_{\tilde{{N}}} } \right)} \end{array} \right]_{N\times \tilde{{N}}} , \end{array} $$
$$\mathbf{\upbeta }=\left[ {{\begin{array}{ll} {{\beta_{1}^{T}} } \\ {\vdots} \\ {\beta_{\tilde{{N}}}^{T} } \end{array} }} \right]_{\tilde{{N}}\times m} , \text{and} \mathbf{T}=\left[ {{\begin{array}{ll} {{t_{1}^{T}} }\\ \vdots\\ {{t_{N}^{T}} } \end{array} }} \right]_{N\times m}. $$

Here, w i is the weight vector connecting the i−th hidden node and the input nodes, β i is the weight vector connecting the i−th hidden node and the output nodes, b i is the bias of the i−th hidden node, and w i ⋅x j represents the inner product of w i and x j . As named in Huang et al. [47, 48], H is called the hidden layer output matrix of the neural network; the i−th column of H is the i−th hidden node output with respect to inputs x 1,x 2,⋯,x N .

In traditional feedforward neural network learning methods, one may wish to find specific \(\hat {\mathbf {{w}}}_{i} ,b_{i} ,\hat {\mathbf {\upbeta }}(i=1,{\cdots } ,\tilde {N})\) to minimize ∥Hβ−T∥. Specifically,

$$\begin{array}{@{}rcl@{}} &&\left\| {\mathbf{H}(\hat{\mathbf{{w}}}_{1} ,\cdots ,\hat{\mathbf{{w}}}_{\tilde{{N}}} ,\hat{{b}}_{1} ,\cdots ,\hat{{b}}_{\tilde{{N}}} )\hat{\upbeta}-\mathbf{T}} \right\|\\&&=\min\limits_{\mathbf{w}_{i} ,b_{i} ,\upbeta} \left\| {\mathbf{H}(\mathbf{w}_{1} ,{\cdots} ,\mathbf{w}_{\tilde{{N}}} ,b_{1} ,{\cdots} ,b_{\tilde{{N}}} )\upbeta -\mathbf{T}} \right\|, \end{array} $$
(3)

which is equivalent to minimizing the cost function

$$ Q=\sum\limits_{j=1}^{N} {\left(\sum\limits_{i=1}^{\tilde{{N}}} \beta_{i} g(\mathbf{w}_{i} .\mathbf{x}_{j} +b_{i} )-\mathrm{t}_{j} \right)}^{2}. $$
(4)

Vector W, consisting of a set of weights (w i ,β i ) and bias (b i ) parameters, is updated using gradient-based algorithms in the above minimization procedure as:

$$ \mathbf{W}_{k} =\mathbf{W}_{k-1} -\eta \frac{\partial Q(\mathbf{W})}{\partial \mathbf{W}}, $$
(5)

where η is the learning rate. The backpropagation (BP) algorithm is a powerful supervised learning algorithm for training feedforward neural networks (FNNs). However, there are many shortcomings with the BP algorithm [38]. First, the performance of BP is easily affected by local optima. Second, there exists the problem of overfitting in BP, which can very easily result in very poor prediction performance. Third, BP is a time-consuming algorithm in many cases, and finally, it is difficult to determine the value of η.

These problems of the BP learning algorithm can be resolved by the ELM. Since the input weights and hidden layer bias do not need to be tuned, the hidden layer output matrix H can be calculated once random values have been assigned to them. Then, (3) is equivalent to finding a least-squares solution \(\hat {\upbeta }\) of the linear system Hβ=T:

$$\begin{array}{@{}rcl@{}} &&\left\| {\mathbf{H}(\mathbf{w}_{1} ,{\cdots} ,\mathbf{w}_{\tilde{{N}}} ,b_{1} ,{\cdots} ,b_{\tilde{{N}}} )\hat{\upbeta}-\mathbf{T}} \right\|\\ &&=\min\limits_{\beta } \left\| {\mathbf{H}(\mathbf{w}_{1} ,\cdots ,\mathbf{w}_{\tilde{{N}}} ,b_{1} ,{\cdots} ,b_{\tilde{{N}}} )\upbeta -\mathbf{T}} \right\|. \end{array} $$
(6)

If the number \(\tilde {{N}}\) of hidden nodes is equal to the number N of distinct training samples, \(\tilde {{N}}=N\), matrix H is square and invertible if the input weight vectors w i and the hidden biases b i are randomly chosen, and these training samples can be approximated with zero error. However, in most cases the number of hidden nodes is much smaller than the number of distinct training samples, i.e., \(\tilde {{N}}<<N\). Then, H is a nonsquare matrix and there may not exist \(\mathbf {w}_{i} ,b_{i} ,\upbeta \quad (i=1,\cdots ,\tilde {{N}})\) such that Hβ=T. The ELM algorithm learns the output weights β using a Moore–Penrose generalized inverse of matrix H, denoted as H + . [38]. Then, the smallest norm least squares solution of the above linear system is:

$$ \hat{\upbeta}=\mathbf{H}^{+}\mathbf{T}. $$
(7)

The solution \(\hat {\upbeta }\) defined in (7) has the minimum norm over all the least squares solutions of the linear system defined in (2). Therefore, \(\hat {\upbeta }\) has the best generalization performance over all the other least squares solutions [36].

Thus, the ELM algorithm can be described as follows:

figure d

Compared with the traditional gradient-based learning algorithms for SLFNs, the ELM has several favorable and significant features: the learning speed of the ELM is extremely fast, the generalization performance of the ELM is superior to that of the gradient-based learning algorithms, and the ELM learning algorithm tends to yield solutions straightforwardly without facing several issues like local minima or overfitting, as is the case with the traditional gradient-based learning algorithms [38].

From Algorithm 1, we can see that the size of the hidden node layer \(\tilde {{N}}\) must first be set. From the discussion above, we know that the required number of hidden nodes \(\tilde {{N}}\) cannot exceed the number of distinct training samples. However, it is unreasonable to set too small a number of hidden nodes. Selection of the appropriate number of hidden nodes is discussed further in Section 5.

3 Ensemble learning methods and classical greedy ensemble selection algorithms

3.1 Ensemble learning methods

There are two important phases in ensemble learning methods: generation of multiple predictive models and the combination of these.

3.1.1 Producing the models

In the production of multiple predictive models for an ensemble, the ensemble can be composed of either homogeneous or heterogeneous models. Homogeneous models can be obtained by running the same learning algorithm in different ways. To ensure diversity of the constituent models, many approaches have been followed, including using different parameter values for the learning algorithm, incorporating random factors into the learning algorithm, or manipulating the input attributes and outputs of the models [49]. Bagging [50] and boosting [51] are the two best known classical approaches for generating ensembles with homogeneous constituent models.

Heterogeneous models are generated by applying different learning algorithms to the same dataset. Because the prediction performance of different learning algorithms can vary, diversity among heterogeneous constituent models is relatively easy to ensure.

3.1.2 Combining the models

Various approaches have been employed to combine classification models. The simplest and most frequently used approach is unweighted majority voting. Both homogeneous and heterogeneous models can be combined using this approach. For unweighted majority voting, each model outputs a class value (or ranking or probability distribution), and the final result is the class with the most votes (or the highest average ranking or largest average probability) [27].

Let x represent an instance; then, the following mathematical equation expresses the output of unweighted majority voting method F E (x) for instance x from the original ensemble \(E=\{h_{i} (\mathbf {x})\}_{i}^{k} \), where k is the size of the original ensemble:

$$ F_{E} (\mathbf{x})=\arg \max\limits_{y} \sum\limits_{i= 1}^{k} {I(h_{i} } (\mathbf{x})=y),y\in Y, $$
(8)

where I(⋅) is an indicator function (I(t r u e)=1,I(f a l s e)=0), h i (x) denotes the classification decision of the i−th model, whose value is a class label, and Y={1,2,⋯,C} is the set of all possible class labels.

3.2 Classical greedy ensemble selection methods

Greedy ensemble selection methods greedily select the next state, which is the neighborhood of the current state, to visit. States refer to the different subsets of the initial ensemble \(E=\{h_{i} (\mathbf {x})\}_{i}^{k} \), where k is the size of the original ensemble. The neighborhood of a subset of models S⊆E contains those subsets that can be constructed by expanding one element into S or deleting one element from S [27]. As for classical greedy ensemble selection methods, the selection direction, evaluation dataset, and evaluation measure are the three main factors.

3.2.1 Search direction

As depicted in Fig. 1, there are two main search directions for classical greedy ensemble selection strategies: forward and backward searching [27].

Fig. 1
figure 1

Search space map for the greedy ensemble selection algorithm with an ensemble of four models

Full size image

In forward searching, subset S is initialized as an empty set. The algorithm proceeds by iteratively adding into S model h i ∈E∖S (where “ ∖” denotes subtraction of the two sets) based on a specific evaluation measure [27]. However, in a backward search, subset S is initialized as the entire original set, and the algorithm proceeds by repeatedly deleting from S model h i ∈S according to a specific evaluation measure [27].

For both search directions, \(\frac {k(k+1)}{2}\) subsets must be evaluated by the greedy ensemble selection method, with time complexity of O(k 2 f(k,N p r )), where f(k,N p r ) represents the computational complexity of the evaluation function [25], and N p r denotes the size of the pruning dataset.

3.2.2 Evaluation dataset

The evaluation dataset can refer to the pruning dataset, which can be generated by the training set [32, 37], a separate validation set [36], or even an artificial production. The advantage of using the training set for evaluation is that there is sufficient data for training and evaluation. However, this approach can easily suffer from overfitting. In contrast, using a separate validation set as the pruning dataset is less prone to overfitting; however, using a separate pruning set significantly reduces the amount of training data. A better approach based on k-fold cross-validation was proposed in [33]. In each iteration, one fold is used as the pruning dataset, while the remaining folds are used as the training dataset. Finally, the evaluations are averaged across all folds. This approach is less susceptible to overfitting, and at the same time, makes full use of the training data.

3.2.3 Evaluation measures

Evaluation measures, which play an important role in the classical greedy ensemble selection method, can be roughly classified into two major categories: performance-based and diversity-based measures. The design and implementation of evaluation measures are based on the prediction accuracy of classifiers on the pruning dataset, defined as Pr={(x i ,y i ),i=1,2,⋯,N p r }, where x i represents a feature vector, y i denotes an unknown target value, and N p r is the size of the pruning dataset.

Performance-based evaluation measures

Many effective performance-based evaluation measures have been proposed, for example, accuracy (ACC), receiver operating characteristic (ROC) area, and average precision [27]. All these measures have the same intention, that is, to find a classifier that optimizes the performance of the ensemble generated by expanding (deleting) a candidate element into (from) the current ensemble. Their calculation is affected by the strategy for ensemble combination. The prediction result of the ensemble on the entire pruning dataset is required to calculate performance-based measures.

Among the performance-based evaluation measures, ACC is introduced in detail below. The ACC of model h with respect to ensemble S and pruning set Pr is defined as:

$$ ACC_{\Pr } (h,S)=\sum\limits_{i=1}^{N_{pr} } {I(F_{S\cup h} (\mathbf{x}_{i} )=} y_{i} ),y_{i} \in Y $$
(9)

where N p r is the size of the pruning dataset. F S∪h (x i ) represents the result of unweighted majority voting for instance x i from a new subensemble, generated by adding candidate classifier h into the current subensemble S, while the definition of function F E (x) has been given out in (8). The ACC measure prefers to select classifiers with the best accuracy at each step [31].

Diversity-based evaluation measures

To achieve high generalization performance, great importance must be attached to the diversity among classifiers in an ensemble. Many well-known diversity-based measures have been proposed, including concurrency (CON), complementariness (COM), margin distance minimization (MAR), and uncertainty weighted accuracy (UWA) [27]. The similarities and differences between COM, CON, and UWA are analyzed below.

Before discussing these three measures in detail, it is necessary to present some additional notations. First, we must be able to distinguish the four events in the prediction results of candidate model h and subensemble S with respect to an instance (x i ,y i ) [27].

$$e_{00} (h,S,\mathbf{x}_{i} ,y_{i} ):h(\mathbf{x}_{i} )\ne y_{i} \wedge S(\mathbf{x}_{i} )\ne y_{i} $$
$$e_{01} (h,S,\mathbf{x}_{i} ,y_{i} ):h(\mathbf{x}_{i} )\ne y_{i} \wedge S(\mathbf{x}_{i} )=y_{i} $$
$$e_{10} (h,S,\mathbf{x}_{i} ,y_{i} ):h(\mathbf{x}_{i} )=y_{i} \wedge S(\mathbf{x}_{i} )\ne y_{i} $$
$$ e_{11} (h,S,\mathbf{x}_{i} ,y_{i} ):h(\mathbf{x}_{i} )=y_{i} \wedge S(\mathbf{x}_{i} )=y_{i} $$
(10)

The measures of COM, CON, and UWA are defined, respectively, as follows [27]:

$$ COM(h,S)=\sum\limits_{(x_{i} ,y_{i} )\in \Pr } {I(e_{10} (h,S,\mathbf{x}_{i} ,y_{i} ))} , $$
(11)
$$\begin{array}{@{}rcl@{}} CON(h,S)&=&\sum\limits_{(x_{i} ,y_{i} )\in \Pr } {(2I(e_{10} (h,S,\mathbf{x}_{i} ,y_{i} } ))\\&&+I(e_{11} (h,S,\mathbf{x}_{i} ,y_{i} ))\\&&-2I(e_{00} (h,S,\mathbf{x}_{i} ,y_{i} ))), \end{array} $$
(12)
$$\begin{array}{@{}rcl@{}} UWA(h,S)&=&\sum\limits_{(x_{i} ,y_{i} )\in \Pr } (I(e_{10} (h,S,\mathbf{x}_{i} ,y_{i} ))NT_{i} \\&&-I(e_{01} (h,S,\mathbf{x}_{i} ,y_{i} ))NF_{i} \end{array} $$
(13)

and ,

$$ +I(e(h,S,\mathbf{x}_{i} ,y_{i} ))NF_{i} -I(e(h,S,\mathbf{x}_{i} ,y_{i} ))NT_{i} ) $$

where N T i represents the proportion of member nets in the current subensemble S that correctly classify instance (x i ,y i ), N F i =1−N T i represents the proportion of nets in S that misclassify the instance, and I(⋅) is an indicator function (I(t r u e)=1 and I(f a l s e)=0).

As shown in their definitions, the evaluations of the three measures all depend on the decision of the current subensemble S and the candidate net h. COM focuses on an individual model that can help the current subset that obtains an incorrect result to evaluate the instance correctly. CON is similar to COM, but differs in that two extra events with their corresponding weights are added to CON. The UWA measure ameliorates the drawback of CON and COM by taking into account the uncertainty of the ensemble’s decision. A series of experiments were conducted by Partalas et al. [27, 34], the results of which indicate that UWA achieves better performance under the same condition.

3.2.4 Amount of pruning

The final, but by no means the least significant factor of the classical greedy ensemble selection algorithm is the amount of pruning. Once the other factors have been determined, the prediction performance of the selected ensemble is affected by the amount of pruning. In most cases, the error rate of the selected ensemble decreases with a decrease in its size at the beginning. However, after the minimum error rate has been obtained, the smaller the final amount of pruning is, the larger the error rate becomes.

The DHCEP algorithm, a popular greedy ensemble selection method proposed in previous research [27], automatically determines the pruning rate. In our work, DHCEP represents a general greedy ensemble selection approach, and is compared with the proposed ELMsGraspEnS algorithm, because of its automatic determination of pruning rate.

4 ELMs’ ensemble selection with GRASP for credit scoring

Credit scoring has become a hot topic in financial institutions. Both intelligent and statistical techniques have been developed to solve this problem. However, no conclusion has been reached on which type of technique is the best. Recent studies have tended to combine multiple classifiers, known as ensemble learning, to predict the credit score of an applicant. Many experimental results indicate that ensemble learning has better generalization performance. However, to obtain better generalization performance, quite a few constituent classifiers are needed for the ensemble, resulting in fairly large execution time and storage space requirements. In addition, the performance of the entire ensemble is affected by classifiers with low generalization performance. Therefore, it is necessary to select an appropriate subset of the original ensemble. In this work, we propose ELMsGraspEnS, which uses the ELM as the base learner for the ensemble. Overall, the novelty of the ELMsGraspEnS algorithm can be summarized as the application of the GraspEnS algorithm to search for a good subset of ELM ensemble classifiers.

In this section, we first discuss the GraspEnS algorithm in detail, and thereafter, the proposed ELMsGraspEnS algorithm for credit risk assessment is presented.

4.1 Ensemble selection algorithm based on GRASP

In one of our previously published works, we proposed the GraspEnS algorithm [31]. GRASP is an iterative two-phased metaheuristic procedure consisting of a greedy randomized construction phase and a local search phase. These two phases are repeated until the termination criterion is reached, for example, where the maximum number of iterations or the target value of an objective function is satisfied. The final solution is the best solution obtained from all the iterations [52].

Generally, an appropriate randomized greedy solution is obtained from the greedy randomized construction phase. Specifically, in each iteration of the construction phase, a restricted candidate list (RCL) is generated. Its size and elements are specified, respectively, by the greedy function and an invariable parameter α, where α∈[0, 1]. Parameter α is important in GRASP, because it determines the greediness versus the randomness of GRASP. If α= 0, the construction phase evolves into a greedy algorithm, whereas if α=1, the construction phase reduces to a random construction. An element is randomly selected from the RCL, and is then expanded into the current partial solution. Thereafter, the RCL is updated. The process terminates when a feasible solution of the required size is obtained.

In the local search phase, the solution obtained from the construction phase is refined. To improve the current solution, the neighbors thereof are searched. If a better neighbor is found, the current solution is replaced by this neighbor. The process is repeated a given number of times until no better solution is found.

Our previously proposed GraspEnS algorithm inherits the peculiarities of the GRASP framework, which improves the classical greedy ensemble selection approaches by incorporating random factors [31]. The classical greedy ensemble selection approaches are sensitive to the problem of local optima. However, GraspEnS allows a feasible solution to escape the local optima. The results of different iterations differ from one another owing to the incorporation of random factors. Because each feasible solution can be considered a new starting point, the GraspEnS algorithm effectively realizes a multi-start search. Moreover, in the local search phase, the feasible solution constructed in the construction phase is refined by searching its neighbors[31]. The pseudo code for the GraspEnS algorithm [31], which is similar to GRASP, is given below.

figure e

4.1.1 Greedy randomized construction phase of GraspEnS

During the construction phase of the GraspEnS algorithm, a feasible solution is constructed. First, like the traditional greedy ensemble selection approaches, according to the predictive accuracy of the base classifiers on the pruning dataset, the classifier with the best accuracy is selected and added to the initial feasible solution. Then, the algorithm enters a loop, and the remaining classifiers are ranked according to the values of the greedy function G(h i ,S). Next, the best α candidate classifiers are placed in the RCL. Finally, a classifier is randomly selected from the RCL and expanded into the feasible solution. The process is repeated until the size of the feasible solution is greater than or equal to the required size. The pseudo code for the greedy randomized construction phase of GraspEnS is given below [31].

figure f

It is clear that this phase is similar to the forward search procedure of the classical greedy ensemble selection approaches, but differs in that random factors are incorporated into this phase. The feasible solutions obtained from each iteration are not the same as one another because of the incorporated random factors. Moreover, each different feasible solution could be regarded as a new starting point for the local search phase, thereby allowing GraspEnS to realize a multi-start search.

The greedy function G(h i ,S), the required size of the feasible solution M, and the constant parameter α play important roles in the GraspEnS algorithm, and need to be appropriately set and tuned. Since the greedy function G(h i ,S) is directly related to the construction of the RCL, proper adoption thereof is particularly important. Any of the evaluation measures introduced in Section 3 can be used as the greedy function G(h i ,S) for GraspEnS, including ACC, COM, CON, and UWA. The effect of the different values of parameters M and α and the different choices of greedy function G(h i ,S) on our proposed ELMsGraspEnS algorithm is analyzed in Section 5.

4.1.2 Local search phase of GraspEnS

The solution obtained from the construction phase may not be the optimal solution. Generally, the solution is refined during the local search phase. Several factors could influence the successful realization of the local search phase, such as the structure of the neighborhood, the starting solution itself, and the neighborhood search method. For ELMsGraspEnS, the choice of neighbors is an important factor. In constructing the neighbors of the current feasible solution, if the classifier is included in the solution, it should be removed from it; otherwise the classifier should be extended into it [31]. For instance, consider the original ensemble S={h 1, h 2,h 3,h 4} and feasible solution S 1={h 2,h 3,h 4}. The neighborhood of S 1 is {{h 1,h 2,h 3,h 4},{h 3,h 4},{h 2,h 4},{h 2,h 3}}. Algorithm 4 gives the pseudo code of the local search phase of GraspEnS [31].

As shown in Algorithm 4, the current feasible solution is updated once a better performing solution is found. The size of the final solution is indirectly affected by parameter M in the construction phase. The loop iterates k times, and a part of the entire neighborhood of the current subensemble is investigated.

4.2 ELMs’ ensemble selection algorithm based on GRASP for credit scoring

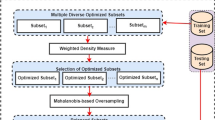
For the ELMsGraspEnS algorithm, first the whole dataset is randomly divided into a training subset, a pruning subset, and a test subset and the ELM is used as the base learner for ELMsGraspEnS. Multiple ELM classifiers can be produced by implementing the ELM multiple times. The generated ELMs are inherently different from one another, thereby guaranteeing the diversity of the original ensemble. Next, an appropriate subset is selected from the original ensemble by the GraspEnS algorithm according to the prediction performance of the base ELM classifiers on the pruning dataset. Finally, the unweighted majority voting method is used to combine the selected subset of ELM classifiers, so as to make predictions for the test data. The entire framework of ELMsGraspEnS is illustrated in Fig. 2, while Algorithm 5 gives the pseudo code for the proposed ELMsGraspEnS algorithm.

figure g
Fig. 2
figure 2

Framework of the ELMsGraspEnS algorithm for enterprise credit risk assessment

Full size image

The main advantages of the proposed ELMsGraspEnS algorithm are the following. First, the learning speed of the ELM is extremely high, and it is seldom that the ELM suffers from overfitting or the local minima problem. Moreover, the ELM algorithm is easy to implement. The input weights and bias of the ELM are initially randomly assigned, and these do not need to be adjusted. Furthermore, its hidden layer output matrix and hence, the output weights can be calculated explicitly. The network can be obtained with very little computational cost in only a few steps. Besides, the generalization performance of the ELM is better than the traditional feedforward neural network learning algorithm in several classification applications. Our proposed ELMsGraspEnS algorithm intuitively inherits the inherent advantages of the ELM, because the ELM is used as the base learner in the original ensemble.

Second, homogeneous ELM models constitute the original ensemble investigated in this work. The ELM randomly sets the initial weights and bias of an SLFN, incorporating random factors into the ELMsGraspEnS, while the construction thereof is easy to implement.

figure h

Third, application research on credit risk assessment with ensemble selection approaches is limited. The popular ensemble learning method needs a large storage space and a vast amount of execution time, while its generalization performance is often impacted by constituent models with low prediction performance. To address these problems, the ensemble selection approach is applied in our ELMsGraspEnS algorithm.

Fourth, the ELMsGraspEnS algorithm uses GraspEnS as its ensemble selection method, as discussed in Section 4.1 Therefore, it is obvious that the proposed ELMsGraspEnS algorithm naturally inherits the inherent characteristics of the GraspEnS method. ELMsGraspEnS is capable of escaping from local optima and realizing a multi-start search, and has superior generalization performance compared with the classical greedy ensemble selection approaches.

Last, ELMsGraspEnS achieves better classification performance than the classical greedy ensemble methods, like the DHCEP algorithm and three other methods, namely, the BSM, ALL and Adaboost.M1 methods. Moreover, the performance of ELMsGraspEnS is obviously superior to that of SVM and MLP. A detailed discussion of the performance comparison follows in the next section.

5 Experiments

5.1 Experimental datasets

Three real-world credit datasets from the UCI Machine Learning repository [53] were used to evaluate the performance of the proposed algorithm: the Australian credit dataset, German credit dataset, and Japanese credit dataset. There were, however, some missing attribute values in the Japanese credit dataset. After removing these missing values from the original dataset, we were left with 653 data. In addition, because an m-class attribute must be replaced by m-1 binary attributes, attributes A6 and A7 of the Japanese credit dataset were found to have too many categories, greatly increasing the input space. Therefore, these two attributes were deleted from the dataset [24].

Each dataset was divided into three parts: a training set, pruning set, and test set, consisting of 60 %, 20 %, and 20 % of the full dataset, respectively. Table 1 gives detailed information about the three datasets used in our experiments, including the number of attributes, classes, and the sizes of the whole dataset, training set, pruning set, and test set. In this work, we used a separate pruning set to reduce the risk of overfitting. Besides, the three adopted datasets were sufficiently large, so adequate data were available for simultaneously creating training, pruning, and test datasets from each.

Table 1 Datasets used for credit risk assessment tasks
Full size table

5.2 Experimental setup

As mentioned in the previous sections, we executed the ELM algorithm many times to generate the original ensemble with multiple ELMs. Specifically, an original ensemble with 100 ELM classifiers was constructed in this work. To demonstrate the effectiveness and efficiency of the proposed ELMsGraspEnS algorithm, we compared it with the classical DHCEP algorithm. In addition, two baseline methods corresponding to two extreme pruning scenarios were implemented, i.e., the best single model (BSM) and ALL. The former selects the best single model from the original ensemble according to the performance of the classifiers on the pruning set, while the latter retains all the models in the original ensemble. In addition, Adaboost.M1 was also used as a comparative ensemble selection method to investigate whether the proposed ELMsGraspEnS algorithm has better classification and generalization performance. Finally, to illustrate the efficiency of our proposed method, an SVM and multi-layer perceptron (MLP) were also compared with the ELMsGraspEnS algorithm. For the SVM method, we used the radial kernel with gamma set to one; the cost parameter of the SVM was set to 0.5. The nodes in the hidden layer and the learning rate of MLP were set to 16 and 0.6, respectively.

To minimize the effect of the changes in the training, pruning, and test data, the experiments reported in this section were performed 50 times for each classification task using a different randomized ordering of its examples. All reported results are averages over these 50 repetitions.

5.3 Experimental results and discussion

From the discussion in Sections 2 and 4, it is clear that five important parameters must be properly set and tuned; that is, the number of hidden nodes \(\tilde {{N}}\), greedy function G(h i ,S), the required number of feasible solutions M, constant parameter α, and the number of Max_iterations. First we discuss the number of Max_iterations, which determines the running times of ELMsGraspEnS. Too small a number of Max_iterations causes the classification performance to be far from the expected result, while too large a number may require much longer running time, and hence, reduce the practicability of the algorithm. In this work, the number of Max_iterations was set to 500, a generally appropriate number.

Next, we analyzed the number of hidden nodes \(\tilde {{N}}\). We chose the CON and UWA evaluation measures as the greedy function, and set M to 30 and α to 0.4. It is clear that \(\tilde {{N}}\) directly affects the performance of the ELM. If \(\tilde {{N}}\) is too small or too large, the final result will be far from the expected one. Consequently, \(\tilde {{N}}\) was varied in the set {10,20,30,40,50,60,70,80,90} . Figures 3 and 4 show the average error rates of the base ELMs with different numbers of hidden nodes using the ELMsGraspEnS algorithm with CON and UWA as the greedy function G(h i ,S) on the three datasets.

Fig. 3
figure 3

Average error rates obtained with varying numbers of hidden nodes \(\tilde {{N}}\) using ELMsGraspEnS with CON as the greedy function G(h i ,S) on three benchmark credit risk assessment datasets

Full size image
Fig. 4
figure 4

Average error rates obtained with varying numbers of hidden nodes \(\tilde {{N}}\) using ELMsGraspEnS with UWA as greedy function G(h i ,S) on three benchmark credit risk assessment datasets

Full size image

From these two figures, we can see that by increasing the number of hidden nodes \(\tilde {{N}}\), the average error rate changes only slightly, especially for the Australian and Japanese credit datasets. In other words, \(\tilde {{N}}\) has no clear effect on the prediction error rates in a certain range. Thus, in the remaining experiments, \(\tilde {{N}}\) was set to 70.

Next, we discuss parameters M and α. In [31], 15 datasets were used to verify the effect of these two parameters on the classification performance of GraspEnS. The conclusion reached was that there was no significant effect for most of the datasets. According to the experimental results in [31], parameters M and α were set to 30 and 0.4, respectively, in this work.

The final and most significant parameter is the greedy function G(h i ,S). Table 2 gives the performance of DHCEP and ELMsGraspEnS using ACC, COM, CON, and UWA as the evaluation measures on the three benchmark credit risk assessment datasets.

Table 2 Average error rates obtained with different evaluation measures using DHCEP and ELMsGraspEnS algorithms on the three benchmark credit risk assessment datasets over 50 runs
Full size table

It is evident from Table 2 that ELMsGraspEnS achieves better performance. On all three datasets, ELMsGraspEnS has lower average error rates compared with DHCEP when using all four evaluation measures, i.e., ACC, COM, CON, and UWA. Moreover, the lowest average error rates for each dataset were obtained using ELMsGraspEnS.

Figures 5, 6, 7, 8, 9, and 10 show the detailed error rates obtained by different evaluation measures using the DHCEP and ELMsGraspEnS algorithms over 50 repeated experimental runs on the German, Japanese, and Australian credit datasets. It should be noted that the mnemonic ACC-G appearing in these figures refers to the corresponding experimental results that were obtained using the proposed ELMsGraspEnS algorithm with the ACC measure, while ACC-D means that the corresponding results were obtained using the DHCEP method with the ACC measure. Using the same analogy, the meaning of the remaining mnemonics used in these figures should be clear.

Fig. 5
figure 5

Error rates obtained with the ACC and CON evaluation measures using DHCEP and ELMsGraspEnS on the German credit dataset

Full size image
Fig. 6
figure 6

Error rates obtained with the COM and UWA evaluation measures using DHCEP and ELMsGraspEnS on the German credit dataset

Full size image
Fig. 7
figure 7

Error rates obtained with the ACC and CON evaluation measures using DHCEP and ELMsGraspEnS on the Japanese credit dataset

Full size image
Fig. 8
figure 8

Error rates obtained with the COM and UWA evaluation measures using DHCEP and ELMsGraspEnS on the Japanese credit dataset

Full size image
Fig. 9
figure 9

Error rates obtained with the ACC and CON evaluation measures using DHCEP and ELMsGraspEnS on the Australian credit dataset

Full size image
Fig. 10
figure 10

Error rates obtained with the COM and UWA evaluation measures using DHCEP and ELMsGraspEnS on the Australian credit dataset

Full size image

It is obvious from the results shown in the six figures above and Table 2 that the error rates obtained by DHCEP are clearly higher than those by ELMsGraspEnS. Furthermore, in most cases, the highest error rate is obtained by DHCEP. Therefore, from Figs. 5–10 and Table 2, it can be concluded that the ELMsGraspEnS algorithm achieves better performance than DHCEP on the three credit datasets.

Next, to ascertain whether ELMsGraspEnS is significantly superior to DHCEP, t-tests were applied to the results of the DHCEP and ELMsGraspEnS algorithms using the four measures on the three datasets. The null hypothesis H 0 indicates that there is no significant difference between Model A and Model B. The detailed p-values are shown in Table 3. Items marked with an asterisk (*) denote that Model A is significantly better than Model B at the 5% significance level. The “Improvement” columns indicate the relative improvement of Model A over Model B in terms of average error rate.

Table 3 Results of t-tests applied to the average error rates of the ELMsGraspEnS and DHCEP algorithms on the three datasets
Full size table

From Table 3, it is clearly seen that ELMsGraspEnS yields better prediction results in all cases. For the German and Australian credit datasets, the classification performance of ELMsGraspEnS is significantly better than that of the classical DHCEP method with COM and UWA as the evaluation measures; these measures belong to the diversity-based evaluation measures. In other words, for diversity-based evaluation measures, there are only 1/3 cases where the ELMsGraspEnS method does not significantly improve the classification performance obtained by the DHCEP algorithm. That is a normal result, because it is well known that the DHCEP method achieves excellent classification performance, and it is a stateoftheart ensemble pruning algorithm Regarding the performance-based evaluation measure ACC, the differences between the two algorithms are not significant. The reason for this may be that ACC focuses on accuracy and ignores diversity, whereas the property of diversity is important in ensemble learning. The results obtained for the Japanese credit dataset differ from those of the other two datasets partly because some values in the dataset were missing and two attributes were deleted, as mentioned in Section 5.1.

Finally, ELMsGraspEnS was compared with the other five algorithms mentioned previously, i.e., ALL, BSM, Adaboost.M1, SVM, and MLP. Table 4 shows the results obtained by ELMsGraspEnS with each of the four evaluation measures as the greedy function G(h i ,S) and the other five algorithms on the three benchmark credit risk assessment datasets.

Table 4 Average error rates using the ELMsGraspEnS algorithm with the four different evaluation measures and five other methods on the three benchmark datasets
Full size table

Table 4 clearly shows that the average error rates obtained by ELMsGraspEnS with the four corresponding measures are distinctly lower than those by the other five algorithms, except for ELMsGraspEnS with the CON measure on the Japanese credit dataset. On the German credit dataset, UWA-G performs the best; COM-G achieves the best generalization performance on the Japanese credit dataset; and both ACC-G and UWA-G have the lowest average classification error rates on the Australian credit dataset.

Figures 11, 12, and 13 show the detailed error rates averaged over 50 experimental runs obtained by ELMsGraspEnS with the four corresponding evaluation measures and the five other algorithms, i.e., Adaboost.M1, ALL, BSM, SVM, and MLP, on the three benchmark credit datasets. These figures show that on all three datasets, the classification performance of the proposed ELMsGraspEnS algorithm is better than that of Adaboost.M1, ALL, BSM, SVM, and MLP. Figure 11 shows that in most cases on the German credit dataset, fewer test samples are misclassified by ELMsGraspEnS with the four corresponding evaluation measures than by BSM, SVM, and MLP. Although the classification error rates of Adaboost.M1, ALL, and ELMsGraspEnS are close to each other, the classification performance of ELMsGraspEnS is still better than that of the other two algorithms. From Fig. 12 and Table 4, it can be seen that COM-G achieves the best generalization performance on the Japanese credit dataset. The classification error rates of UWA-G and ACC-G are similar and are ranked second. Adaboost.M1 and ALL achieve similar average classification performances and are ranked third. CON-G performs a little worse than Adaboost.M1 and ALL, and is ranked fourth. BSM and SVM are ranked fifth and sixth, respectively. The highest average error rate is obtained by MLP. It can be seen from Fig. 13 and Table 4 that the generalization performances of ACC-G and UWA-G are the best on the Australian credit dataset. The performances of COM-G and CON-G are ranked second. The performances of Adaboost.M1, ALL and BSM are close to each other, and are inferior to the other four algorithms, i.e., ACC-G, COM-G, CON-G and UWA-G. And the performance of SVM and MLP is obviously lower than that of our proposed ELMsGraspEnS algorithm.

Fig. 11
figure 11

Error rates obtained by ELMsGraspEnS with the four corresponding evaluation measures and the other five algorithms, i.e., Adaboost.M1, ALL, BSM, SVM, and MLP on the German credit dataset

Full size image
Fig. 12
figure 12

Error rates obtained by ELMsGraspEnS with the four corresponding evaluation measures and the other five algorithms, i.e., Adaboost.M1, ALL, BSM, SVM, and MLP on the Japanese credit dataset

Full size image
Fig. 13
figure 13

Error rates obtained by ELMsGraspEnS with the four corresponding evaluation measures and the other five algorithms, i.e., Adaboost.M1, ALL, BSM, SVM, and MLP on the Australian credit dataset

Full size image

The results of t-tests comparing the proposed ELMsGraspEnS algorithm with the other five algorithms, i.e., BSM, ALL, Adaboost.M1, SVM, and MLP, are shown in Table 5. These results clearly show that for all credit datasets, our proposed method is significantly better than the state-of-the-art algorithms, i.e., SVM and MLP. With the exception of the Japanese credit dataset, ELMsGraspEnS shows performance improvements compared with the other three algorithms, i.e., Adaboost.M1, ALL and BSM, on the other two datasets. On the German and Australian credit dataset, for 10 out of all the 24 comparative cases, the proposed method ELMsGraspEnS did not significantly improve the prediction performance obtained by Adaboost.M1 or ALL. There were no cases where the difference between ELMsGraspEnS and the BSM method was not significant. In other words, our proposed method is significantly better than the BSM algorithm in all cases. Compared with the ALL method, there are only three cases where the new ELMsGraspEnS method is not significantly better. This result is not surprising, since no method exists that performs the best in all cases. There are seven cases where the difference between the typical Adaboost.M1 algorithm and the ELMsGraspEnS method is not significant; on the German credit dataset, however, ELMsGraspEnS with the UWA measure is significantly better than Adaboost.M1. This could lead us to conclude that the size and attribute information of the dataset, and the selection of the evaluation measure influence classification performance of the ELMsGraspEnS method. However, there are no significant differences between ELMsGraspEnS and the other three methods, i.e., BSM, ALL, Adaboost.M1, in most cases on the Japanese credit dataset. The reason for this may be the same as given above, i.e., it is partly because some values in the dataset were missing and two attributes were deleted.

Table 5 Results of t-tests comparing ELMsGraspEnS with the other five algorithms on the three benchmark credit datasets
Full size table

In summary, the proposed ELMsGraspEnS algorithm achieves better generalization performance than the typical DHCEP ensemble selection method and the other five competitors mentioned in this paper.

6 Conclusion and future works

Credit risk assessment has become a main concern in the financial and banking sector, since these institutions need to decide whether to grant loans to applicants. Even a slight improvement in the assessment accuracy could greatly reduce the losses of financial institutions. In this study, we combined the ELM with our previously proposed GraspEnS algorithm to create the novel ELMsGraspEnS algorithm for credit risk assessment of enterprises. ELMsGraspEnS not only inherits the inherent advantages of the ELM and GraspEnS, but also effectively fuses their advantages: the learning speed of the new method is extremely fast, the local optima problem is ameliorated, and multi-start is realized by our proposed algorithm, etc. At the same time, we employed the ensemble selection paradigm in this new method; the disadvantages of the original ensemble method are partly avoided by our proposed ELMsGraspEnS.

The ELMsGraspEnS algorithm was applied to three real world credit datasets, i.e., the Australian, Japanese, and German credit datasets, drawn from the UCI machine learning repository. The experimental results show that in most cases, application of ELMsGraspEnS substantially improves the performance of credit risk assessment compared with several other state-of-the-art algorithms; this is especially true for the ELMsGraspEnS algorithm using the UWA measure as its greedy function. It can be concluded that ELMsGraspEnS simultaneously exhibits high efficiency and effectiveness.

In our future work, we intend to investigate a feasible approach for assigning the number of hidden nodes of the constituent ELMs in the ensemble. Another possible research direction concerns the exploration of a better neighborhood structure or a better neighborhood search method to further improve the performance of our algorithm.