Locating network trees by a bilevel scheme

Abstract

In this paper we investigate how to choose an optimal position of a specific facility that is constrained to a network tree connecting some given demand points in a given area. A bilevel formulation is provided and existence results are given together with some properties when a density describes the construction cost of the networks in the area. This includes the presence of an obstacle or of free regions. To prove existence of a solution of the bilevel problem, that is framed in Euclidean spaces, a lower semicontinuity property is required. This is obtained proving an extension of Goła̧b’s theorem in the general setting of metric spaces, which allows for considering a density function.

1 Introduction

In this paper we investigate a constrained facility location problem: to find an optimal position of a specific location under the constraint that some given demand points must be connected by means of a minimal network. As an example, the location of a water tower requires a minimal path to reach the places of drought that need water as quickly as possible. In addition, each chosen position of the water tower has a construction cost. Mathematically, we deal with a two stage optimization problem: a suitable cost function will be optimized constrained to a network formation that links all the demand points and consists of another optimization problem. Several questions from operation research require the location of some facilities constrained to additional requirements. Relevant examples are irrigation (locate the water tower and find the optimal connection), mining (locate the excavation place and find the optimal connection), and others.

In these examples, the network with the lowest length is desirable: the optimization problem that is the constraint of the bilevel scheme is formulated by solving a Steiner-type problem. The Steiner Tree Problem (Hwang et al., 1992) is to find a connected finite graph (network) containing n given points (terminal points) in the plane and having minimal length. The graph turns out to be a tree (a network containing no loops) and having some other important properties (Ambrosio and Tilli, 2004; Fampa et al., 2016; Ivanov and Tuzhilin, 1994). Existence of solutions for the Steiner problem relies on Goła̧b’s semicontinuity theorem for compact connected sets. A general version of Goła̧b’s theorem has been proved in Euclidean spaces by Dal Maso and Toader (2002). It has also been generalized to metric spaces, see Ambrosio and Tilli (2004); Giacomini (2002); Paolini and Stepanov (2013).

The bilevel optimization has a natural interpretation in the context of game theory (see Başar and Olsder (1999)) where one of two agents, called leader, optimizes his criterium knowing the solutions of the optimization problem solved by the other agent, called follower. Usually the leader’s problem is called upper level problem, the follower’s problem is called the lower level problem. Bilevel problems have a long history that dates back to von Stackelberg (1934) and have been intensively studied from a theoretical point of view as well as in applications to many domains. In case the follower’s problem has several solutions, we see that there is some ambiguity even in the definition of the leader’s problem: we distinguish two extreme situations depending on the leader’s behavior (Carlier and Mallozzi, 2022; Dempe et al., 2007; Dempe and Zemkoho, 2020). The optimistic (or strong) Stackelberg solution assumes a cooperative like behavior between the agents: the leader expects the follower to choose solutions leading to the best outcome for him. On the contrary, in the pessimistic (or weak) Stackelberg solution, as a security strategy for him, the leader assumes that the follower always breaks ties by choosing the worst action for the leader. We will consider in this paper the strong approach and we look for the existence of the solution for the bilevel problem.

Our problem considers a region in an Euclidean space where a density distribution is given. First, a Goła̧b type result is proved under very general assumptions, then an existence result for the bilevel optimization problem is given in the case where demand points form a finite set (concentrated resources case). The generalized Goła̧b’s theorem provides a lower semicontinuity result that allows to solve the bilevel problem. We discuss a possible application of the model: an example of the construction of a bridge under the assumption that, in a second stage, a network connecting some villages with the bridge will be constructed with the constraint to be of minimal length. In this paper we limit to Euclidean spaces, even though some of our results hold in more general metric spaces. However, every time we highlight metric properties we shall actually use.

The paper is structured as follows: after the preliminaries Sect. 2, in Section  3 we introduce the model and prove the results. Finally, some concluding remarks are in Sect. 4.

2 Preliminaries

Let us fix some notation we will use in the following. A set $X\subset {\mathbb {R}}^N$ ($N\in {\mathbb {N}}$) is called a region if it is the closure of an open connected subset. Throughout this paper X is a bounded region and d the Euclidean distance. Given $x\in X$, $A, B\subseteq X$ non empty subsets we denote:

• $B_r(x)=\{y\in X: d(x,y)< r\}$ the open ball with center x and radius $r>0$;

• $\text {diam}\,(A)$ the diameter of A, i.e. sup$\{d(x, x'): x, x'\in A\}$;

• $\text {dist}\,(x, A)$ the distance between x and A, i.e. inf$\{d(x, x'), x'\in A\}$;

• $d_H(A,B)$ the Hausdorff distance between A and B, i.e. the infimum of $r\in {} ]0,+\infty ]$ such that dist$(x,A)\le r$ for any $x\in B$ and $\text {dist}\,(x,B)\le r$ for any $x\in A$; $d_H$ is actually a metric on the family ${{{\mathcal {C}}}}_X$ of nonempty closed subsets of X;

• Lip(f) the Lipschitz constant of a function f;

• $A^c$ the complementary set of A in X.

For any $A\subset X$, the one-dimensional Hausdorff measure of A is defined as

$$\begin{aligned} {\mathcal {H}}^1(A):= \sup _{\delta >0} {\mathcal {H}}^1_{\delta }(A)= \lim _{\delta \rightarrow 0} {\mathcal {H}}^1_{\delta }(A) \end{aligned}$$

where ${\mathcal {H}}^1_{\delta }(A):= \inf \{ \sum _i \text {diam}\,(A_i) \}$ for any $\delta >0$ and the infimum is over all countable families $(A_i)$ of subsets of X which cover A and with $\text {diam}\,(A_i) \le \delta$. It is well known that ${\mathcal {H}}^1$ is actually a measure (i.e. it is countably additive) on the family of Borel subsets.

We recall some well known results for set valued functions. Let X, Y be nonempty sets, a set valued function $M:X\rightrightarrows Y$ is a correspondence which maps an element of X to a subset of Y. In this paper we deal with set valued mappings such that $M(x)\ne \emptyset$ for each x.

Definition 2.1

Let X, Y be metric spaces. The correspondence $M:X\rightrightarrows Y$ has the closed graph property at $x_0\in X$ if the following holds:

for every sequence $\{x_n\}$ in X converging to $x_0$ and for every sequence $\{y_n\}$ in Y such that $y_n\in M(x_n)$ for each n and converging to $y_0\in Y$, then $y_0\in M(x_0)$.

Theorem 2.1

(Berge’s Theorem Aubin and Frankowska (1990); Hu and Papageorgiou (1997)) Given $f :X\times Y \rightarrow {\mathbb {R}}$ and $M :X\rightrightarrows Y$ a real and a set valued function, respectively, let us define

$$\begin{aligned} w(x)= \inf _{y\in M(x)} f(x,y), \quad x\in X. \end{aligned}$$

If f is a lower semicontinuous (l.s.c.) function on $X\times Y$ and M satisfies the closed graph property at each point of X, then w is a lower semicontinuous function on X.

2.1 The Steiner problem

s The Steiner problem (see Fampa et al. 2016; Hwang et al. 1992), as introduced in the 20th century, has the following statement.

Given the set of points $A=\{a_1, \dots , a_n\}$, $n\in {\mathbb {N}}$, in the Euclidean plane, find the shortest graph $\Sigma$ among all connected graphs containing all the given points.

The statement of the Steiner problem only needs the basic concepts of length and connectedness. We can reformulate the Steiner problem in a given metric space X, considering as length the Hausdorff measure and the larger class of compact sets $S\subset X$ instead of finite graphs. We have

Theorem 2.2

Let X be a compact, connected metric space and let $C \subset X$ be a compact set. Then there exists a set S which has minimal ${\mathcal {H}}^1$ measure among all compact connected sets containing C.

The proof is straightforward and based on the compactness with respect to the Hausdorff metric (Blaschke theorem) and the lower semicontinuity of the ${\mathcal {H}}^1$-measure (Goła̧b theorem). We recall these tools here Ambrosio and Tilli (2004); Paolini and Stepanov (2013).

Theorem 2.3

(Goła̧b) If $\Sigma _n$ is a sequence of connected closed subsets of a complete metric space which Hausdorff converges to a set $\Sigma$, then

$$\begin{aligned} {\mathcal {H}}^1(\Sigma )\le \liminf _{n\rightarrow +\infty }{\mathcal {H}}^1(\Sigma _n). \end{aligned}$$

This result on lower semicontinuity of the one-dimensional Hausdorff measure ${\mathcal {H}}^1$ still holds if we assume that the number of connected components of $\Sigma _n$ is bounded by a fixed constant. The conclusion is easly shown to be false if the connectness assumption is completely removed.

Theorem 2.4

(Blaschke) The space of non empty closed subsets of a compact set endowed by the Hausdorff metric is a compact metric space.

When the given set C has infinite ${\mathcal {H}}^1$ measure the formulation of Theorem 2.2 has no sense. A formulation of the concept of connecting a set is to require that $S \cup C$ become connected (and we do not require S to be connected). In this framework the Steiner problem reads as: given a compact set $C\subset X$ find a set S in X such that $C\cup S$ is connected and has minimal length (i.e. minimizing ${\mathcal {H}}^1(S)$).

Although it seems necessary to require S to be connected (which leads to an undesirable behavior, see Paolini and Stepanov (2013)) to apply Goła̧b’s theorem and the compactness of S in view of Blaschke theorem, it is surprising that this is not the case. Indeed the existence of minimizers for this very general formulation of the Steiner problem was proved by Paolini and Stepanov.

We recall that a metric space X is called proper (or having the Heine-Borel property) if every closed ball is compact.

Theorem 2.5

If X is a proper connected metric space and $C \subset X$ is compact, then the Steiner problem admits a solution.

Moreover some quite natural topological properties of solutions to the Steiner problem are summarized as follows: every solution S having finite length ${\mathcal {H}}^1(S) < +\infty$ has the properties:

• a) $S\cup C$ is compact;

• b) $S\setminus C$ has at most countably many connected components, and each of the latter has strictly positive length;

• c) ${\overline{S}}$ contains no closed loops;

• d) if C has a finite number of connected components, then $S \setminus C$ has finitely many connected components, the closure of each of which is a finite geodesic embedded graph with endpoints on C, and with at most one endpoint on each connected component of C.

2.2 On the bilevel approach

Given $f, g :X\times Y \rightarrow {\mathbb {R}}$ two functions, if f expresses the cost of some activities, and g another criterium that must be optimized, one usually tries to minimize the total cost as follows: find $({\check{x}}, {\check{y}})\in X\times Y$ such that

$$\begin{aligned} T:= [f+g] ({\check{x}}, {\check{y}})= \displaystyle \min _{(x,y)\in X\times Y} [f+g] (x,y). \end{aligned}$$

(T)

On the other hand, in some situation it is more natural reasoning in a bilevel formulation, minimizing the cost f with respect to the x variable, under the constraint that g achieves the minimum with respect to the y variable, for any x, and define the bilevel optimization problem as follows Başar and Olsder (1999); Carlier and Mallozzi (2022); Dempe and Zemkoho (2020). We assume that for any $x\in X$ there exists a unique ${\tilde{y}}(x)\in Y$ such that

$$\begin{aligned} g(x,{\tilde{y}}(x))= \displaystyle \min _{y\in Y} g(x,y) \end{aligned}$$

and the bilevel optimization problem consists in finding ${\hat{x}}\in X$ such that

$$\begin{aligned} BL:= f({\hat{x}}, {\tilde{y}}({\hat{x}}))= \displaystyle \min _{x\in X} f (x, {\tilde{y}}(x)) \end{aligned}$$

(BL)

where the map $x \rightarrow {\tilde{y}}(x)$ has been defined above. A solution of (BL) will be the pair $({\hat{x}}, {\tilde{y}}({\hat{x}}))$. In this case the total cost is given by $BL +g({\hat{x}}, {\tilde{y}}({\hat{x}}))$ that clearly is higher than T. However, as it happens in applicative contexts, not always the choice of optimal values of the strategies is made by a decision maker able to control both variables x and y.

An example is given by the mining problem, where the aim is to plan the extraction activity searching for the optimal starting point for extraction (also called ora), minimizing the installation cost together with the transportation cost of the underground material. This transport is supposed to take place along a given network of tunnels. So, the problem turns out to be constrained to a choice of this network of tunnels and this aspect of the project planning can be contracted out.

In a general view, in this paper the bilevel optimization problem corresponds to a situation where the best position of a specific facility that is constrained to a network tree connecting some given demand points is chosen, and where the facility construction and the network construction are managed separately.

A further application in air traffic management can be formalized in a bilevel scheme as well: for example, a group of UAVs (Unmanned Aerial Vehicle) may need to fly in a certain formation to reduce their fuel expenditure and keep active communication links among them. The bilevel problem studied in Zhang and Hu (2008), for example, gives the coordinated motions with the minimum energy cost that can move a group of agents from given initial position to given destination within a certain time horizon under a tree formation constraints. The problem consists in a bilevel optimization problem having a Steiner problem in the lower level.

3 The bilevel problem for concentrated resources

3.1 The model

As mentioned, in this paper we work in Euclidean spaces. Nevertheless every time we will try to highlight the metric properties really necessary.

Let us consider X a bounded region of ${\mathbb {R}}^N$ and $H\subset X$ a compact subset of X. A set $C=\{v_1,\ldots ,v_n\}$ ($n\in {\mathbb {N}}$) is given, where $v_1,\ldots ,v_n \in X$ represent demand points that must be connected by a network between themselves and also with a new facility x that will be installed in H. A function $F:H\rightarrow {\mathbb {R}}^+$ that describes the installation cost of the new facility $x\in H$ is also given.

We suppose that the cost of construction of the network depends on the characteristic of the area X. More precisely, we consider a density distribution $\varphi :X\rightarrow [0,+\infty ]$ that is a lower semicontinuous nonnegative function on X describing the construction costs in X. Then we consider the network installation cost as in the following definition:

Definition 3.1

Given a network S in a region X with l.s.c. density $\varphi$, we define the network installation cost as

$$\begin{aligned} {{\mathcal {K}}}[S]=\int _S \varphi \,{\mathrm d}{\mathcal {H}}^1, \end{aligned}$$

(3.1)

where ${\mathcal {H}}^1$ is the one-dimensional Hausdorff measure.

Given the compact set $C\subset X$, a set S connecting elements of C is an element of the set:

$$\begin{aligned} St(C)=\{ S\subseteq X :\, C\cup S \text { is compact and connected}\}. \end{aligned}$$

Moreover we suppose that the cost of using a network S that has been built depends on its total length, i.e. the one-dimensional Hausdorff measure ${\mathcal {H}}^1(S)$.

The problem: the aim of our study is to find the optimal position $\bar{x}\in H$ and the optimal network $\bar{S}$ that connects the points in C and $\bar{x}$, minimizing all the costs.

As an example, the logistic problem corresponding to this situation is given by a planar region where a river separates the city center from n villages in the countryside and a road network must be planned to connect all the villages and also a bridge has to be built in a suitable location of the river (see example 3.1).

Mathematically, we formulate the problem in the bilevel optimization scheme.

The bilevel problem (U)-(L). Find ${\bar{x}}\in H$ solution of the the upper level problem:

$$\begin{aligned} \inf \left\{ F(x)+ G(x),\,\, x\in H\right\} \end{aligned}$$

(U)

where, for each $x\in H$, G(x) is given by

$$\begin{aligned} G(x)=\inf \left\{ {\mathcal {H}}^1(S), \, S\in {\mathcal {M}}_\varphi (x,C) \right\} \end{aligned}$$

and

$$\begin{aligned} {\mathcal {M}}_\varphi (x,C)=\left\{ S\in St (C\cup \{x\}) :\, {{\mathcal {K}}}[S]\le {{\mathcal {K}}}[S^\prime ], \forall S^\prime \in St (C\cup \{x\}) \right\} \end{aligned}$$

is the set of solutions of the lower level problem

$$\begin{aligned} \inf \left\{ {{\mathcal {K}}}[S],\,\, S\in St (C\cup \{x\})\right\} . \end{aligned}$$

(L)

Any ${\bar{x}}\in H$ solving the problem (U) will be called an optimal solution of the bilevel problem described in (U)-(L). In the upper level problem we are minimizing the total cost incurred in building the facility in x and in using the network connecting x and C, with the constraint that the considered network is an optimal one considering the installation cost derived by the properties of X.

Let us note that the installation cost in (L) covers some special cases such as

• when $\varphi \equiv 1$ the lower level problem corresponds to the classical Euclidean Steiner problem. In this case the costs of construction and usage are equals and the choice of the optimal set S depends only on the installation of x and the length of S;

• when $\varphi$ assume the value $+\infty$ on a subset of X the lower level problem corresponds to a minimal cost problem in presence of obstacles;

• when $\varphi \equiv 0$ on a subset of X the lower level problem takes into account the presence of “free" regions, i.e. regions in which construction costs vanish.

In order to prove the existence of solutions to the lower level problem (L), we need a semicontinuity result for the functional ${{\mathcal {K}}}$ introduced in (3.1).

Remark 3.1

The problem (U)-(L) can be written also in the following way, showing the optimistic nature of the bilevel problem.

The bilevel problem (U)-(L). Find ${\bar{x}}\in H$ solution of the the upper level problem:

$$\begin{aligned} \inf _{x\in H} \inf _{S\in {\mathcal {M}}_\varphi (x,C)} F(x)+ {\mathcal {H}}^1(S) \end{aligned}$$

(U)

where, for each $x\in H$, ${\mathcal {M}}_\varphi (x,C)$ is the set of solutions of the lower level problem

$$\begin{aligned} \inf _{S\in St (C\cup \{x\})} \int _S \varphi \,{\mathrm d}{\mathcal {H}}^1. \end{aligned}$$

(L)

Let us remark that for a given $x\in H$, it is not guaranteed that the set ${\mathcal {M}}_\varphi (x,C)$ is a singleton; however all the Steiner trees in the set have the same minimal length.

3.2 Goła̧b Theorem with density

In this section we prove the following Goła̧b type theorem in the general setting of metric spaces to have the semicontinuity result for the functional ${{\mathcal {K}}}$ introduced in (3.1).

Theorem 3.1

Let X be a complete metric space and let $\varphi :X\rightarrow [0,+\infty ]$ be a lower semicontinuous function. For every Borel subset C of X, we define

$$\begin{aligned} {{\mathcal {K}}}[C]=\int _C\varphi \,{\mathrm d}{\mathcal {H}}^1\end{aligned}$$

Let $C_n$ be compact connected subsets of X, converging to the compact subset C with respect to the Hausdorff metric. Then C is connected and

$$\begin{aligned} {{\mathcal {K}}}[C]\le \liminf _n{{\mathcal {K}}}[C_n]. \end{aligned}$$

(3.2)

Proof

Since Hausdorff convergence preserves connectedness, we know that C is connected, see Ambrosio and Tilli (2004); Paolini and Stepanov (2013). Clearly, we may assume $\varphi \not \equiv 0$ and that the right-hand side of (3.2) is finite. Then, there are at most countably many levels $l>0$ for which the measure

$$\begin{aligned} {\mathcal {H}}^1(\{x\in C:\varphi (x)=l\}) \end{aligned}$$

(3.3)

is strictly positive. Indeed, the set of such levels is

$$\begin{aligned} \bigcup _{k\in {\mathbb {N}}}\left\{ l>\frac{1}{k}:{\mathcal {H}}^1(\{x\in C:\varphi (x)=l\})>\frac{1}{k}\right\} . \end{aligned}$$

We show that this is a countable union of finite sets. Fixed $\lambda >0$ and defined

$$\begin{aligned} E_\lambda =\{x\in X:\varphi (x)\le \lambda \}, \end{aligned}$$

(3.4)

we have

$$\begin{aligned} +\infty >\frac{1}{\lambda }\liminf _n {{\mathcal {K}}}[C_n\setminus E_\lambda ]\ge \liminf _n{\mathcal {H}}^1(C_n\setminus E_\lambda )\ge {\mathcal {H}}^1(C\setminus E_\lambda ), \end{aligned}$$

last inequality being a consequence of [Paolini and Stepanov (2013), Theorem 3.3]. As the subsets considered in (3.3) are pair-wise disjoint, the number of levels $l>\lambda$ for which also the measure in (3.3) is larger than $\lambda$ is finite.

We have

$$\begin{aligned} \lim _{\lambda \downarrow 0}\varphi (x)\chi _{E_\lambda ^c}(x)=\varphi (x) \end{aligned}$$

for all $x\in X$. The equality is trivial if $\varphi (x)=0$. In case $\varphi (x)>0$, for $\lambda <\varphi (x)$ we have $\chi _{E_\lambda ^c}(x)=1$. Hence, we can use monotone convergence theorem to infer

$$\begin{aligned} {{\mathcal {K}}}[C]=\int _C\varphi \,{\mathrm d}{\mathcal {H}}^1=\lim _{\lambda \downarrow 0}\int _{C\setminus E_\lambda }\varphi \,{\mathrm d}{\mathcal {H}}^1\end{aligned}$$

(3.5)

To prove (3.2), we show that, for any fixed $T\in {\mathbb {R}}$ verifying $T<{{\mathcal {K}}}[C]$, we actually have

$$\begin{aligned} T<\liminf _n{{\mathcal {K}}}[C_n]. \end{aligned}$$

(3.6)

To this end, we first assume $\varphi$ continuous and bounded. By (3.5), we find $\lambda$, $0<\lambda <\sup _X\varphi$, such that

$$\begin{aligned} T<{{\mathcal {K}}}[C\setminus E_\lambda ]=\int _{C\setminus E_\lambda }\varphi \,{\mathrm d}{\mathcal {H}}^1. \end{aligned}$$

(3.7)

For any $\varepsilon >0$, we can find positive levels $l_i$, $i=0,\ldots ,k+1$, such that $0<l_{i+1}-l_i<\varepsilon$ for $i\le k$,

$$\begin{aligned} 0<l_0<\lambda<\sup _X\varphi <l_{k+1} \end{aligned}$$

and

$$\begin{aligned} {\mathcal {H}}^1(\{x\in C:\varphi (x)=l_i\})=0,\quad \text {for }i=0,\ldots ,k+1. \end{aligned}$$

(3.8)

We consider the closed subsets

$$\begin{aligned} J_i=\{x\in X:\varphi (x)\le l_i\text { or }\varphi (x)\ge l_{i+1}\},\quad \text {for }i=0,\ldots ,k. \end{aligned}$$

Note that $J_i^c$ are pair-wise disjoint and that $J_i^c \cap (C_n{\setminus } E_\lambda )= C_n{\setminus } (J_i \cup E_\lambda )$. Then

$$\begin{aligned} {{\mathcal {K}}}[C_n]\ge {{\mathcal {K}}}[C_n\setminus E_\lambda ]\ge \sum _{i=0}^k{{\mathcal {K}}}[C_n\setminus (J_i\cup E_\lambda )]\ge \sum _{i=0}^k l_i\,{\mathcal {H}}^1(C_n\setminus (J_i\cup E_\lambda )) \end{aligned}$$

Hence, using again ((Paolini and Stepanov, 2013), Theorem 3.3) we get

$$\begin{aligned} \begin{array}{rl} \displaystyle \liminf _n{{\mathcal {K}}}[C_n] &{}\displaystyle \ge \sum _{i=0}^k l_i\liminf _n{\mathcal {H}}^1(C_n\setminus (J_i\cup E_\lambda ))\ge \sum _{i=0}^k l_i {\mathcal {H}}^1(C\setminus (J_i\cup E_\lambda ))\\ &{}\displaystyle \ge \int _{C\setminus E_\lambda }\varphi \,{\mathrm d}{\mathcal {H}}^1-\varepsilon \,{\mathcal {H}}^1(C\setminus E_\lambda ). \end{array} \end{aligned}$$

Above we used that the subsets $J_i^c$ verify

$$\begin{aligned} {\mathcal {H}}^1((C\setminus E_\lambda )\setminus \cup _i J_i^c)=0 \end{aligned}$$

as a consequence of (3.8). By (3.7), for small $\varepsilon$ we get (3.6).

The extension to the case $\varphi$ lower semicontinuous is straightforward, since $\varphi$ is the limit of an increasing sequence of nonnegative continuous bounded functions $\varphi _h$, and by monotone convergence theorem for any Borel subset C

$$\begin{aligned} \int _C\varphi \,{\mathrm d}{\mathcal {H}}^1=\lim _h\int _C\varphi _h\,{\mathrm d}{\mathcal {H}}^1=\sup _h\int _C\varphi _h\,{\mathrm d}{\mathcal {H}}^1. \end{aligned}$$

$\square$

Remark 3.2

If $K\subset X$ is closed, $\varphi \,\chi _{K^c}$ is lower semicontinuous. Applying Theorem 3.1 with this function in place of $\varphi$, more generally than (3.2) we also have

$$\begin{aligned} {{\mathcal {K}}}[C\setminus K]\le \liminf _n{{\mathcal {K}}}[C_n\setminus K]. \end{aligned}$$

(3.9)

Actually, our proof can easily be modified to show that if, in addition to the assumptions of Theorem 3.1, the sequence $K_n$ of closed subsets converges to the closed subset K with respect to the Hausdorff metric, then

$$\begin{aligned} {{\mathcal {K}}}[C\setminus K]\le \liminf _n{{\mathcal {K}}}[C_n\setminus K_n], \end{aligned}$$

(3.10)

thus reaching a complete analogy with [Paolini and Stepanov (2013), Theorem 3.3]. Indeed, defining $E_\lambda$ as in (3.4), clearly $K_n\cup E_\lambda$ converges to $K\cup E_\lambda$ with respect to the Hausdorff metric, as $n\rightarrow +\infty$. Hence, we can repeat the above argument with $C\setminus K$ and $C_n\setminus K_n$ in place of C and $C_n$, respectively, and see that (3.10) holds if the density $\varphi$ is continuous and bounded. Finally, if the lower semicontinuous function $\varphi$ is the limit of an increasing sequence of nonnegative continuous bounded functions $\varphi _h$, denoting by ${{\mathcal {K}}}_h$ the functional with density $\varphi _h$, for all $h\in {\mathbb {N}}$ we have

$$\begin{aligned} {{\mathcal {K}}}_h[C\setminus K]\le \liminf _n{{\mathcal {K}}}_h[C_n\setminus K_n] \end{aligned}$$

so that

$$\begin{aligned} {{\mathcal {K}}}_h[C\setminus K]\le \liminf _n{{\mathcal {K}}}[C_n\setminus K_n] \end{aligned}$$

and conclude with (3.10) letting $h\rightarrow +\infty$.

Let us recall that we are dealing with the case of n points in which some resources are concentrated, i.e. $C=\{v_1,\ldots ,v_n\}$; then we have the following result.

Theorem 3.2

Let X be a connected compact metric space and let $\varphi :X\rightarrow [0,+\infty ]$ be a lower semicontinuous function on X. The lower level problem (L) admits a solution.

Proof

We observe first that the set $St(C\cup \{x\})\ne \emptyset$ because, since X is assumed to be connected, it belongs to $St(C\cup \{x\})$. Considering a minimizing sequence $S_n$, $n\in {\mathbb {N}}$, for the functional ${{\mathcal {K}}}$, define $\Sigma _n=S_n\cup C\cup \{x\}$. We assume that ${{\mathcal {K}}}[S_n]<+\infty$ because if every $S\in St(C\cup \{x\})$ has ${{\mathcal {K}}}[S]=+\infty$ then every S attains the minimum. Then according to Blaschke Theorem, $\Sigma _n$ converges to a still closed and connected set $\Sigma$ in the sense of Hausdorff metric, up to passing to a subsequence. Remark 3.2 gives

$$\begin{aligned} {{\mathcal {K}}}[\Sigma \setminus C]\le \liminf _n {{\mathcal {K}}}[\Sigma _n\setminus C]=\liminf _n {{\mathcal {K}}}[S_n]. \end{aligned}$$

Hence $\Sigma \setminus C$ is a solution to (L). $\square$

3.3 Existence results for the bilevel problem

In the following we limit to Euclidean spaces and deal with the bilevel problem (U)-(L). We give conditions that ensure the existence of solutions.

We define

$$\begin{aligned} L(x)=\inf \left\{ {{\mathcal {K}}}[S]:S\in St (C\cup \{x\})\right\} \text {,\quad for }x\in H. \end{aligned}$$

(3.11)

Remark 3.3

Note that we may have $L\equiv +\infty$ on H. This can be expected, if $\varphi$ takes the value $+\infty$, or even if it is unbounded. For example, in the region X an obstacle is present which separates H from the points of C.

However, $L\equiv +\infty$ may also happen for $\varphi$ bounded, e.g. $\varphi \equiv 1$, that is ${{\mathcal {K}}}={\mathcal {H}}^1$. Indeed, for some X and a finite subset C, we may have ${\mathcal {H}}^1(S)=+\infty$, for all $S\in St(C)$. On the other hand, assuming for X the segment property (see Adams (1975), pg. 54]) prevents this problem, because then for all $x,y\in X$ there exists a polygonal contained in X connecting x and y.

Now we prove the following existence result.

Theorem 3.3

Let $X\subset {\mathbb {R}}^N$ be a compact region and $\emptyset \ne C\subset X$ be a finite set. Suppose that $\emptyset \ne H\subseteq X$ is a closed subset of X contained in a convex subset $Z\subseteq X$, $\varphi :X\rightarrow [0,+\infty ]$ is l.s.c. and bounded from above on Z and $F:H\rightarrow [0,+\infty [$ is a l.s.c. function on H. Then there exists an optimal solution of the bilevel problem (L)-(U).

Proof

Existence of a solution for the lower level problem (L) is guaranteed by Theorem 3.2 and then the set ${\mathcal {M}}_\varphi (x,C)$ is non empty, for any given $x\in H$.

In order to prove that

$$\begin{aligned} x\rightarrow F(x)+ \inf _{S\in {\mathcal {M}}_\varphi (x,C)} {\mathcal {H}}^1(S) \end{aligned}$$

(3.12)

is l.s.c. on H, we use Berge’s Theorem 2.1. Given $S\in {\mathcal {M}}_\varphi (x,C)$, we set

$$\begin{aligned} \Sigma =S\cup C \cup \{x\}. \end{aligned}$$

Clearly, ${\mathcal {H}}^1(\Sigma )={\mathcal {H}}^1(S)$. Next, we define the following set-valued map

$$\begin{aligned} M :x\in X \rightrightarrows M(x)= \{ \Sigma : S\in {\mathcal {M}}_\varphi (x,C)\}, \end{aligned}$$

(3.13)

taking values in the family ${{{\mathcal {C}}}}_X$ of nonempty closed subsets of X, in which we use Hausdorff metric.

We observe that the function

$$\begin{aligned} f(x, \Sigma )=F(x)+ {\mathcal {H}}^1(\Sigma ) \end{aligned}$$

is l.s.c. on $H\times {{{\mathcal {C}}}}_X$. Now, we show that the mapping M defined at (3.13) has the closed graph property at each point of H, that is, if $x_n\rightarrow x$, $\Sigma _n\in M(x_n)$ for all n, and $\Sigma _n\rightarrow \Sigma$ in the Hausdorff metric, then $\Sigma \in M(x)$. To this end, first we prove that

$$\begin{aligned} \Sigma \in St(C\cup \{x\}). \end{aligned}$$

To show that x belongs to the closed set $\Sigma$, it suffices to prove that x is a limit point for it. Given $\varepsilon >0$, we have $d_H(\Sigma , \Sigma _n) < \varepsilon$ for large n, so that, choosing in the definition of Hausdorff distance $A=\Sigma$, $B=\Sigma _n$, we have $\text {dist}\,(x_n, \Sigma ) < \varepsilon$ and find $y\in \Sigma$ such that $d(x_n, y)< \varepsilon$. Hence, we conclude

$$\begin{aligned} d(x,y) \le d(x, x_n)+ d(x_n, y) < 2 \varepsilon . \end{aligned}$$

Similarly, $C\subset \Sigma$. Moreover $\Sigma$ is connected since $\Sigma _n$ are connected sets.

Now we prove minimality of $\Sigma$, that is, we have

$$\begin{aligned} {{\mathcal {K}}}[\Sigma ]\le {{\mathcal {K}}}[S^\prime ] \end{aligned}$$

for all $S'\in St(C\cup \{x\})$. Consider $[x,x_n]$ the segment connecting x and $x_n$. We have $S^\prime \cup [x,x_n]\in St(C\cup \{x_n\})$ and

$$\begin{aligned} {{\mathcal {K}}}[\Sigma _n]\le {{\mathcal {K}}}[S^\prime \cup [x,x_n]] \le {{\mathcal {K}}}[S^\prime ]+ \int _{[x,x_n]}\varphi \,{\mathrm d}{\mathcal {H}}^1. \end{aligned}$$

(3.14)

Moreover, since $[x,x_n]\subset Z$,

$$\begin{aligned} \int _{[x,x_n]}\varphi \,{\mathrm d}{\mathcal {H}}^1\le \left( \sup _Z\varphi \right) d(x,x_n) \end{aligned}$$

converges to 0 as $n\rightarrow +\infty$. Therefore, we can pass to the limit in (3.14), using lower semicontinuity of ${{\mathcal {K}}}$ in the left-hand side, and get

$$\begin{aligned} {{\mathcal {K}}}(\Sigma ) \le \displaystyle \liminf _{n} {{\mathcal {K}}}(\Sigma _n) \le {{\mathcal {K}}}(S^\prime ). \end{aligned}$$

It is now clear that the upper level problem (U) admits a solution. $\square$

Remark 3.4

Let us observe that in Theorem 3.3 we can relax conditions on H and $\varphi$. Indeed, an inspection of the proof shows that, instead of assuming H contained in a convex set Z, and that $\varphi$ is bounded on it, we may assume that there exists a constant $\Phi$ with the following property: for each point $x\in H$, there exists a ball $B_r(x)$ centered at x such that $X\cap B_r(x)$ is star-shaped with respect to x, and $\varphi (y)\le \Phi$, for all $y\in X\cap B_r(x)$.

Moreover, concerning the possibility $L\equiv +\infty$ discussed in Remark 3.3, we note that, also in the case where $\varphi$ takes the value $+\infty$, under the above assumptions, if $L(x_0)<+\infty$ for a point $x_0\in H$, then $L(x)<+\infty$, for all $x\in H$.

Example 3.1

Two villages and a river. We want to connect two villages in the countryside with a bridge that we build on a river. Let us consider the region $X= [0,1]\times [0,1]\subset {\mathbb {R}}^2$, and two villages located at $O=(0,0)$ and $U=(1,0)$, a river described by $H=X\cap \{y=1 \}$. Problem (L) gives the Steiner tree connecting vertices $B=(x,1)$, O and U. We consider the uniform density $\varphi \equiv 1$ in X and in this case $C=\{O, U\}$ and $L=G$, where G is defined as in the bilevel problem (U)-(L). For any $x\in [0,1]$ the tree in Fig. 1 is the minimal length tree, i.e. the Steiner tree.

Fig. 1

Example 3.1

Let us note that V as in Fig. 1 is the Fermat point of the triangle (Fampa et al., 2016; Hwang et al., 1992) with vertices O, U, B. By means of geometric properties, it is possible to compute the coordinates of V, in particular the abscissa is

$$\begin{aligned} x_V= \frac{ (1+\sqrt{3} x)(1+\sqrt{3} +x)}{ \sqrt{3} [ (1+\sqrt{3})^2 -2x+2x^2]} \end{aligned}$$

that is a continuous function of $x\in [0,1]$. For example, if $x=0.5$ we find $x_V=0.5$.

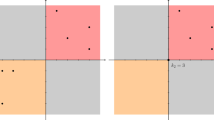
By using classical numerical computation, it is possible to compute the solution of the problem (U): we consider here two cases (Fig. 2):

- (a) If $F(x)=x^2$, we compute $V=(0.314, 0.258), {\bar{x}}=0.191$;

- (b) If $F(x)=(1-x)^2$, we compute $V=(0.697, 0.254), {\bar{x}}=0.828$.

Fig. 2

The Euclidean Steiner tree in cases (a) and (b) of Example 3.1

Remark 3.5

The situation illustrated in the previous example could be also modellized by using the barycenter of the triangle with vertices B, O, U (Drezner, 2022) that is simpler from a computational point of view. However, this leads to a network connecting the points B, O, U with the barycenter that is clearly longer that the one obtained connecting the points B, O, U with the Fermat point V. This confirm that the Steiner tree type choice is optimal, even if computational costly (see Fampa et al. (2016); Ivanov and Tuzhilin (1994); Ras et al. (2017)).

4 Concluding remarks

In this paper we investigated a bilevel optimization problem that arises when a social planner wants to locate a specific facility in a region equipped with a density distribution, under the constraint that this facility will be connected with another facility of a Steiner tree type. The density we considered allows to include particular cases such as obstacle presence.

To prove the existence of a solution of the bilevel problem, that is framed in Euclidean spaces, a lower semicontinuity property has been obtained: this has been reached by proving an extension of Goła̧b’s theorem in the general setting of metric spaces, which allows for considering a density function.

As mentioned above, the bilevel problem studied in this paper has an important impact on applications and then the computational aspect of it is of interest. That is why some important properties must be investigated. For example, under suitable conditions, we can prove that L is a Lipschitz continuous function, then the regularity of the lower level value (L function) makes the upper level optimization problem a smooth one. This is often vital for the computational aspect in bilevel optimization (Başar and Olsder, 1999; Dempe et al., 2007; Dempe and Zemkoho, 2020). In this paper we just mention that algorithmic discussions concerning the Steiner trees have been provided in Hwang et al. (1992); Paolini et al. (2015); Ras et al. (2017).

Proposition 4.1

Let $X\subset {\mathbb {R}}^N$ be a bounded connected Euclidean region, with the segment property; let $\emptyset \ne H\subseteq X$ be contained in a convex subset Z of X and let $\emptyset \ne C\subset X$ be a finite set. Suppose $\varphi :X\rightarrow [0,+\infty [$ is l.s.c. and bounded from above on X. Then the function $L:H\rightarrow [0,+\infty [$ defined by (3.11) is (finite) Lipschitz continuous.

Proof

Clearly, $L(x) \le \big ( \sup \varphi \big ) {\mathcal {H}}^1(S)$, for all $S\in St(C\cup \{x\})$. Then L is finite valued everywhere. Let us fix $x, x_1\in H$ and denote by $[x,x_1]$ the segment joining x and $x_1$. Given $\varepsilon >0$, by the definition of L, there exists $S\in St(C\cup \{x\})$ such that

$$\begin{aligned} \int _{S}\varphi \,{\mathrm d}{\mathcal {H}}^1< L(x)+ \varepsilon \end{aligned}$$

Moreover $S\cup [x,x_1]\in St(C\cup \{x_1\})$, hence

$$\begin{aligned} L(x_1)\le \int _{S\cup [x_1,x]}\varphi \,{\mathrm d}{\mathcal {H}}^1\le \int _{[x_1,x]}\varphi \,{\mathrm d}{\mathcal {H}}^1+ \int _{S }\varphi \,{\mathrm d}{\mathcal {H}}^1\end{aligned}$$

which implies

$$\begin{aligned} L(x_1)- L(x) < \varepsilon + c \, d(x,x_1) \end{aligned}$$

with $c= \sup _X \varphi$. Letting $\varepsilon \downarrow 0$,

$$\begin{aligned} L(x_1)- L(x) \le c \, d(x,x_1) \end{aligned}$$

and we conclude the proof by exchanging the role of x and $x_1$. $\square$

In example 3.1, the set H is assumed to be a hyperplane in the Euclidean space. On the other hand, this assumption is unrealistic, particularly in the case of the above example where it represents a river. Therefore we note that the Lipschitz continuity of the function L, proved in Proposition 4.1, still holds when we replace the convexity assumption by the following more general property:

(P) there exists a constant $c_H>0$ such that for every $x,y\in H$ we can find a path (i.e. continuous immage of the interval $[0,1]\subset {\mathbb {R}}$) $\gamma$ in X connecting x and y such that ${\mathcal {H}}^1(\gamma )\le c_H\,d(x,y)$.

For example, property (P) holds if the set H is a Lipschitz hypersurface.

Moreover, we can vary also the points $v_i\in C$, and arguing as above we can show that the quantity L is Lipschitz continuous also with respect to them.