Computations of volumes and Ehrhart series in four candidates elections

Abstract

We describe several analytical results obtained in four candidates social choice elections under the assumption of the Impartial Anonymous Culture. These include the Condorcet and Borda paradoxes, as well as the Condorcet efficiency of plurality voting with runoff. The computations are done by Normaliz. It finds precise probabilities as volumes of polytopes and counting functions encoded as Ehrhart series of polytopes.

1 Introduction

Lepelley et al. (2008, p. 382) state:

Consequently, it is not possible to analyze four candidate elections, where the total number of variables (possible preference rankings) is 24. We hope that further developments of these algorithms will enable the overcoming of this difficulty.

Normaliz (Bruns et al. 2018) is a software tool that (in particular) may be used for the computation of volumes and Ehrhart series of rational polytopes. In the 20 years of its existence it has found numerous applications. For these, as well for its connections to several computer algebra systems see Bruns et al. (2018). One of the driving forces for the improvements of Normaliz in the past years was the desire to solve the problems raised by Schürmann (2013), that is to compute the volumes and Ehrhart series of certain polytopes related to social choice.

We believe that the recent development in the algorithms of Normaliz have (partially) solved the problem raised by Lepelley, Louichi and Smaoui. Brandt et al. (2016, p. 388) write:

To the best of our knowledge, Normaliz is the only program which is able to compute polytopes corresponding to elections with up to four alternatives.

This remark applies to the computation of Ehrhart series. For volume computations one has other choices; see Remark 4. For a very recent preprint in the same spirit as Brandt et al. (2016), see Brandt et al. (2019).

The model underlying all the election schemes discussed in this paper assumes that every voter has a linear ranking of the candidates. For n candidates there are $N=n!$ such orders. The election profile is the collection of the N numbers $(v_1,\dots ,v_N)$ where $v_i$ is the number of voters that have decided for the i-th ranking. The election scheme then ranks the candidates based on the profile. The first person in this ranking is declared winner and the last is the loser of the election.

In this paper we present several results of our own computational experiments with four candidates elections under the assumption of the Impartial Anonymous Culture (IAC) (Gehrlein and Fishburn 1976) [the (IAC) assumes that all election profiles have the same probability for a fixed number of voters]. The background of these experiments, motivated by social choice theory and its connection with the polytope theory, may be found in Gehrlein and Lepelley (2011, 2017), Lepelley et al. (2008), Schürmann (2013) or Wilson and Pritchard (2007). For discrete convex geometry we refer the reader to Bruns and Gubeladze (2009).

The Condorcet winner is a candidate who is preferred by a majority of voters in all pairwise comparisons with the other candidates. Condorcet observed that a Condorcet winner need not exist: pairwise comparison is not transitive. This phenomenon is called the Condorcet paradox. As an introductory example we discuss this paradox whose (IAC) probability of $331/2048\approx 16.2\%$ for four candidates has been known for quite a while (Gehrlein 2001). This probability and almost every other we present is actually the limit of the probabilities for a finite number k of voters as k goes to infinity.

If the ideal result of an election is the Condorcet winner, provided such exists, then the conditional probability with which the Condorcet winner is selected as the winner of an election is a strong quality measure for the election scheme. This probability is called the Condorcet efficiency. In Gehrlein and Lepelley (2011), it has been studied extensively by Gehrlein and Lepelley. Therefore we continue with the Condorcet efficiency of plurality voting (see Schürmann 2013) and complement it by the Condorcet efficiency of plurality elections with runoff. While plurality voting has Condorcet efficiency $74.3\%$, a runoff ballot of two candidates increases it to $91.2\%$. The gain is substantial and justifies runoff ballots that are part of many voting procedures (in this introduction we content ourselves with approximate probabilities; precise rational numbers will be given later on).

Another problem discussed in Schürmann (2013) is “plurality versus runoff”, namely the probability of $75.5\%$ that the plurality winner also wins the runoff.

Next follows a discussion of the four types of antisymmetric relations between four candidates that can arise from comparisons in majority, and their probabilities. As we will see, the case (i) of a linear order is the most likely one by far. The other three cases, namely that (ii) there exists a Condorcet winner, but not a loser, (iii) a loser, but not a winner, and (iv) neither a winner, nor a loser, have small probabilities $< 10\%$.

We conclude the list of voting outcomes with the Borda paradoxes. The strict Borda paradox occurs if the outcome of the pairwise majority comparison is a linear order and the plurality outcome completely reverses it. For four candidates its conditional probability is approximately $0.156\%$. The strong Borda paradox [also known as the Condorcet loser paradox (Brandt et al. 2016)] has two variants, namely (i) that the Condorcet loser wins the plurality, and (ii) that the Condorcet winner is the last in plurality. As to be expected, their conditional probabilities are considerably larger, namely about $2.268\%$ and $2.379\%$. Though one would intuitively expect that these probabilities agree, they are not equal.

All these events are discussed together with their defining inequalities in Sect. 2. We would like to point out that Normaliz not only computes the volumes of the polytopes in all cases, but also their Ehrhart series, and therefore precise numbers of election profiles that represent the events under discussion, depending on the number of voters. We give the complete numerics only for the Condordet paradox, but all data can be obtained by request from the authors.

Ehrhart series (see Sect. 3) are more easily to compute for closed polytopes than for the ones that arise if one excludes ties. However, in many cases the Ehrhart series of the semiopen polytope can be computed from that of its closure (and conversely). The crucial condition is that all inequalities, except the sign conditions, defining the semiopen polytope are strict, and they are satisfied with equality by the election profile in which every preference order has the same number of voters; see Theorem 5. This follows from a variant of Ehrhart reciprocity [for example, see Bruns and Gubeladze (2009, Th. 6.51)]. From the Ehrhart series of the semiopen polytope one can also read the minimal number of voters that can realize the event under consideration; see Remark 8.

Normaliz can do all computations in dimension 24 (the number of preference orders for four candidates), but the the computation times range from seconds (for the Condorcet paradox) to a few days (for the Condorcet efficiency of the runoff scheme) on a fast machine that allows 32 parallel threads (see Sect. 5.3 for the technical details). Schürmann (2013) made the elegant observation that many computations can be enormously accelerated if one uses the symmetry that is inherent in many polytopes. Only two of the polytopes discussed in this paper do not allow this approach, namely linear order and (consequently) the strict Borda paradox. Symmetrization, which requires the computation of weighted Ehrhart series, shrinks computation times from days to hours, minutes, or even tenths of seconds, depending on the example. Symmetrization is discussed in Sect. 4, and all relevant computation data are listed in Sect. 5.

The reader who is interested in a deeper understanding of the mathematics and algorithms of Normaliz is refereed to the articles by Bruns and Koch (2001), Bruns and Ichim (2010), Bruns et al. (2011, 2016, 2017) and Bruns and Söger (2015).

2 Polytopes in four candidates elections and their volumes

2.1 Voting schemes and volumes of rational polytopes

We briefly sketch the connection between rational polytopes and social choice, referring the reader to Gehrlein and Lepelley (2011), Lepelley et al. (2008), Schürmann (2013) or Wilson and Pritchard (2007) for details and a more extensive treatment. As an introductory example we first consider the well-known Condorcet paradox. The polytopes ${{\mathscr {P}}}$ associated to it and to other voting events are semiopen: ${{\mathscr {P}}}$ is the bounded set of solutions of a system of linear equations and inequalities in which some of the inequalities may be strict.

Consider an election in which each of the k voters fixes a linear preference order of n candidates. In other words, voter i chooses a linear order $j_1\succ _i\dots \succ _i j_n$ of the candidates $1,\dots ,n$. There are $N=n!$ such linear orders that we list lexicographically. The election profile is the N-tuple $(v_1,\dots ,v_N)$ in which $v_p$ is the number of voters that have chosen the preference order p. Then $v_1+\dots +v_N=k$, and $(v_1,\dots ,v_N)$ can be considered as a lattice point in the positive orthant ${{\mathbb {R}}}_+^N$ of ${{\mathbb {R}}}^B$, more precisely, as a lattice point in the simplex

$$\begin{aligned} {{\mathscr {U}}}_k^{(n)}={{\mathbb {R}}}_+^N\cap A_k=k\bigl ({{\mathbb {R}}}_+^N\cap A_1\bigr )=k{{\mathscr {U}}}^{(n)} \end{aligned}$$

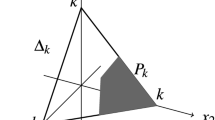
where $A_k$ is the hyperplane defined by $v_1+\dots +v_N=k$, and ${{\mathscr {U}}}^{(n)}={{\mathscr {U}}}_1^{(n)}$ is the unit simplex of dimension $N-1$ naturally embedded in N-space (${{\mathscr {U}}}^{(n)}$ is the convex hull of the unit vectors; see Fig. 1).

Fig. 1

The unit simplex in ${{\mathbb {R}}}^3$

As mentioned in the introduction, the further discussion is based on the Impartial Anonymous Culture (IAC). It assumes that all lattice points in the simplex ${{\mathscr {U}}}_k^{(n)}$ have equal probability of being the outcome of the election.

We fix a specific outcome $v=(v_1,\dots ,v_N)$. By the majority rule candidate j beats candidate $j'$ in the election with profile v if

$$\begin{aligned} \#\{i:j \succ _i j':i=1,\dots ,k\} > \#\{i:j' \succ _i j:i=1,\dots ,k\}. \end{aligned}$$

(2.1)

As the Marquis de Condorcet (1785) observed, the relation “beats” is nontransitive in general, and one must ask for the probability of Condorcet’s paradox, namely an outcome without a Condorcet winner, where candidate j is a Condorcet winner if j beats all other candidates $j'$. The Condorcet winner will sometimes be denoted $CW$ in the following. Given the number k of voters, let $p_{CW }^{(n,j)}(k)$ denote the probability that candidate j is the Condorcet winner, and $p_{CW }^{(n)}(k)$ the probability that there is a Condorcet winner at all. By symmetry and by mutual exclusion, $p_{CW }^{(n)}(k)=n\cdot p_{CW }^{(n,j)}(k)$.

Now, if we assume that the number k of voters is very large, then we are mainly interested in the limit

$$\begin{aligned} p_{CW }^{(n)}=\lim _{k\rightarrow \infty } p_{CW }^{(n)}(k)= n\lim _{k\rightarrow \infty } p_{CW }^{(n,j)}(k)=n\cdot p_{CW }^{(n,j)}. \end{aligned}$$

Let us fix candidate 1. It is not hard to see that the $n-1$ inequalities (2.1) for $j=1$ and $j'=2,\dots ,n$ constitute homogeneous linear inequalities in the variables $v_1,\dots ,v_N$. Together with the sign conditions $v_i\ge 0$ they define a semi-open subpolytope ${{\mathscr {C}}}^{(n)}_k$ of ${{\mathscr {U}}}_k^{(n)}$. Then

$$\begin{aligned} p_{CW }^{(n,1)}=\lim _{k\rightarrow \infty }\frac{\#({{\mathscr {C}}}_k^{(n)}\cap {{\mathbb {Z}}}^N)}{\#({{\mathscr {U}}}_k^{(n)}\cap {{\mathbb {Z}}}^N)}= \frac{{\text {vol}}{{\mathscr {C}}}_1^{(n)}}{{\text {vol}}{{\mathscr {U}}}_1^{(n)}}={\text {vol}}{\overline{{{\mathscr {C}}}}}^{(n)} \end{aligned}$$

(2.2)

where $\overline{\phantom {C}}$ denotes closure and ${{\mathscr {C}}}^{(n)}={{\mathscr {C}}}_1^{(n)}$. For the validity of (2.2) note that we work with the lattice normalized volume in which the unit simplex has volume 1.

In the case of two candidates, Concordet’s paradox cannot occur (if one excludes draws), and for three candidates the relevant volume is not hard to compute, even without a computer (see Gehrlein and Fishburn 1976).

The situation changes significantly for four candidates since ${{\mathscr {C}}}^{(4)}$ has dimension 23 and 234 vertices. From now on we will simplify our notation and omit often the superscript (4) when dealing with four candidates. As a subpolytope of ${{\mathscr {U}}}$, ${{\mathscr {C}}}$ is cut out by the inequalities $\lambda _i(v)>0$, $i=1,2,3$ whose coefficients are in the first 3 rows displayed in Table 1. For the assignment of indices the preference orders are listed lexicographically, starting with $1\succ 2 \succ 3\succ 4$ and ending with $4\succ 3 \succ 2\succ 1$.

Table 1 Inequalities for ${{\mathscr {C}}}$ and ${{\mathscr {E}}}$

Normaliz computes

$$\begin{aligned} {\text {vol}}{{\mathscr {C}}}=\frac{1717}{8192} \end{aligned}$$

in less than a second (the combinatorial data of all polytopes discussed and the computation times are listed in Sect. 5). It follows that $p_CW =1717/2048\approx 0.8384$. This value was first determined by Gehrlein (2001).

2.2 Plurality rule and runoff

A very simple way out of the dilemma that there may not exist a Condorcet winner is plurality voting: candidate j is the plurality winner if j has more first places in the preference orders of the voters than any of the other $n-1$ candidates. A problem discussed in Schürmann (2013) is plurality voting versus plurality runoff. It goes as follows. In the first round of the election the two top candidates in plurality are selected, and in the second round the preference orders are restricted to these two candidates. In order to model this situation by inequalities one must fix an outcome of the first round of plurality voting, for example we may assume that candidate 1 is the winner of the first round and candidate 2 is placed second after the first round. The chosen outcome gives rise to $n-1$ inequalities. Then the n-th inequality expresses that 1 is also the winner of the second round. The volume of the corresponding polytope gives the probability of this event. By mutual exclusion and symmetry, we must multiply the volume by $n(n-1)$ in order to obtain the probability for the event that the winner of the first plurality round wins after runoff.

As a subpolytope of ${{\mathscr {U}}}$, the polytope ${{\mathscr {Q}}}$ is defined by the inequalities in Table 2.

Table 2 Inequalities for ${{\mathscr {Q}}}$

The volume is

$$\begin{aligned} {\text {vol}}{{\mathscr {Q}}}=\frac{9185069468583833}{146081389744226304}. \end{aligned}$$

The total probability of the event that the winner of the first plurality round wins after runoff is

$$\begin{aligned} 12\cdot {\text {vol}}{{\mathscr {Q}}}=\frac{9185069468583833}{12173449145352192} \approx 0.7545. \end{aligned}$$

Therefore, the probability of the failure of the winner of the first round to win the runoff is

$$\begin{aligned} 1-\frac{9185069468583833}{12173449145352192} \approx 0.2455, \end{aligned}$$

in accordance with the results of Schürmann (2013) for a similar model. This computation was first performed by De Loera et al. (2013), where LattE Integrale (Baldoni et al. 2013) was used for the volume computation.

2.3 Condorcet efficiency

The last problem discussed in Schürmann (2013) is the Condorcet efficiency of plurality voting. It is the conditional probability that the Condorcet winner, provided that such exists, is elected by plurality voting, as $k\rightarrow \infty$ (similarly one defines the Condorcet efficiency of other voting schemes). Therefore one must compute the probability of the event that candidate j is both the Condorcet winner and the plurality winner. By symmetry, one can assume $j=1$. The semi-open polytope ${{\mathscr {E}}}_k^{(n)}$, whose lattice points represent this expected outcome, is cut out from ${{\mathscr {C}}}_k^{(n)}$ by $n-1$ further inequalities saying that 1 has more first places than any of the other $n-1$ candidates. Thus one obtains

$$\begin{aligned} \frac{n{\text {vol}}{{\mathscr {E}}}^{(n)}}{p_{CW }^{(n)}} \end{aligned}$$

as the Condorcet efficiency of plurality voting where ${{\mathscr {E}}}^{(n)}={{\mathscr {E}}}_1^{(n)}$.

The extra three inequalities $\lambda _i(v)>0$, $i=4,5,6$, given in the last three lines of Table 1 increase the complexity of the polytope ${{\mathscr {E}}}$ enormously in comparison to ${{\mathscr {C}}}$. Nevertheless, Normaliz computes the volume in moderate time. We have obtained

$$\begin{aligned} {\text {vol}}{{\mathscr {E}}}=\frac{10658098255011916449318509}{68475651442606080000000000}, \end{aligned}$$

so that the Condorcet efficiency of plurality voting turns out to be

$$\begin{aligned} \frac{4{\text {vol}}{{\mathscr {E}}}}{p_CW }= \frac{10658098255011916449318509}{14352135440302080000000000} \approx 0.7426, \end{aligned}$$

in perfect accordance with Schürmann (2013).

Remark 1

Schürmann (2013) used variants of the polytopes ${{\mathscr {Q}}}$ and ${{\mathscr {E}}}$. Our choices (which are demanding slightly more computational resources) avoid inclusion–exclusion calculations that would come up in Sect. 3.

It is interesting to compare the Condorcet efficiency of plurality voting to the the Condorcet efficiency of the runoff voting scheme. In other words, given that there exists a Condorcet winner, what is the probability that she or he is at least second in plurality?

As above, let us assume that candidate 1 is the Condorcet winner. Then there are n possible cases. The first case is when candidate 1 is the plurality winner as well, and this case was studied above. The other $n-1$ cases are associated to the event that candidate j wins or ties candidate 1 in plurality (where $j\ne 1$), while candidate 1 wins the plurality voting against all other candidates. By symmetry, these $n-1$ cases are identical and yield the same volume. The n cases are mutually disjoint and exhaust all the possibilities (disjointness is important in Sect. 3 for avoiding complicated inclusion–exclusion calculations). The semi-open polytope ${{\mathscr {F}}}_{1,j}^{(n)}$, whose lattice points represent the outcome of the cases $j=2,\ldots ,n$, is cut out from ${{\mathscr {C}}}_k^{(n)}$ by the closed condition that candidate j wins against or ties with candidate 1 in plurality and by $n-2$ inequalities saying that 1 has more first places than the remaining $n-2$ candidates. Thus one obtains

$$\begin{aligned} \frac{n{\text {vol}}{{\mathscr {E}}}^{(n)}+n(n-1){\text {vol}}{{\mathscr {F}}}^{(n)}}{p_{CW }^{(n)}} \end{aligned}$$

as the Condorcet efficiency of the runoff, where ${{\mathscr {F}}}^{(n)}={{\mathscr {F}}}_{1,2}^{(n)}$. In fact, there are n choices for the candidate that is simultaneously the Condorcet and the plurality winner, and there are $n(n-1)$ choices for the pair of candidates (A, B) in which A is the plurality winner and B is the CW, but only second in plurality.

As a subpolytope of ${{\mathscr {U}}}$, the polytope ${{\mathscr {F}}}$ is defined by the inequalities in Table 3, where the last line should be interpreted as $\overline{-\lambda _4}(v)\ge 0$, expressing the condition that candidate 1 does not beat candidate 2 in plurality.

Table 3 Inequalities for ${{\mathscr {F}}}$

The volume is

$$\begin{aligned} {\text {vol}}{{\mathscr {F}}}=\frac{7280153240719060220104571}{616280862983454720000000000}. \end{aligned}$$

Finally, the Condorcet efficiency of the runoff is

$$\begin{aligned} \frac{4{\text {vol}}{{\mathscr {E}}}+12{\text {vol}}{{\mathscr {F}}}}{p_CW }= \frac{19627224002877404784030049}{21528203160453120000000000} \approx 0.9117. \end{aligned}$$

2.4 Condorcet classification

In this subsection we classify the asymmetric relations between four candidates given by the majority rule. To the best of our knowledge the computations of the probabilities of the classes is new.

Let us first outline a duality argument that will be used several times below. Consider an election profile $v=(v_1,\dots ,v_N)$ for n candidates, where $N=n!$, the N preference orders $\pi _1,\dots ,\pi _N$ are listed in some order, and $v_i$ is the number of voters of $\pi _i$. Each preference order has an inverse $c(\pi )$ that ranks the candidates in inverse order relative to $\pi$: the inverse order to $1 \succ 2 \succ 3\succ 4$ is $4\succ 3 \succ 2\succ 1$ etc. The assignment $\pi \rightarrow c(\pi )$ defines a permutation of the sequence $1,\dots ,N$, sending i to the index of $c(\pi _i)$. The induced permutation of the coordinates of ${{\mathbb {R}}}^N$ is called inversion of preference orders. It inverts all comparisons in majority. In particular it turns a Condorcet winner into a Condorcet loser, and conversely.

The results of the n candidates elections may be classified in two main categories:

• (A) There exists a Condorcet winner. As seen above, in the case of four candidates elections the results fall into this category with probability

  $$\begin{aligned}P(\exists \text { Condorcet Winner})=1717/2048\approx 0.8384.\end{aligned}$$

• (B) There exists no Condorcet winner. For four candidates elections the results fall into this category with probability

  $$\begin{aligned}P(\not \exists \text { Condorcet Winner})=1-1717/2048=331/2048\approx 0.1616.\end{aligned}$$

We refer the reader to Gehrlein and Lepelley (2011, Section 3.2.1) or Gehrlein and Lepelley (2010) for a discussion of the three candidates situation. Note that in the three candidates scenario the event that there exists a linear order on the result of the majority voting is the same as the event that there exists a Condorcet winner, since the other two candidates are automatically ordered. This no longer true for four or more candidates. Even if a Condorcet winner exists, the remaining candidates need not to be linearly ordered. Therefore, we need to further refine our classification. Precise results for small numbers of voters would have to take into account ties between the candidates. For simplicity we neglect ties in our classification that applies only if the number of voters goes to infinity.

We discuss the case of four candidates in detail:

• (A) Assume that a Condorcet winner (CW) does exist. This situation must be split into two subcategories:

  • (1) The result of the majority voting defines a linear order of the candidates. This further implies (independently of the number of candidates n) that there also exists a Condorcet loser (CL).

  • (2) There exist no linear order on the result of the majority voting. In the (particular) case of four candidates elections this is equivalent to saying that there exists a cycle of length three among the lower candidates (i.e., the three candidates Condorcet Paradox) or that there exists no Condorcet loser.

• (B) Now assume the case that a Condorcet winner does not exist. This situation must also be split into two subcategories:

  • (1) There exists a cycle of order three among the candidates and a Condorcet loser. Inversion of preference orders turns this case into (A2). In particular they have the same probability.

  • (2) There exists a cycle of length four among the candidates or (equivalently) there exists no Condorcet loser. This condition defines only 4 of the 6 relations between the candidates, but it easy to check that all 4 possibilities for the remaining 2 relations are equivalent up to a renaming of the candidates.

Fig. 2

Oriented graphs representing the Condorcet classes of four candidates with respect to the relation given by the majority rule

Table 4 Inequalities for ${{\mathscr {T}}}$

The four cases of the classification are illustrated by their directed graphs in Fig. 2. In order to compute the probabilities of the 4 classes, we consider the polytope ${{\mathscr {T}}}$ which corresponds to the event that candidate 1 beats candidates 2, 3, 4, candidate 2 beats candidates 3, 4 and candidate 3 beats candidate 4. In other words, ${{\mathscr {T}}}$ represents the linear order. As a subpolytope of ${{\mathscr {U}}}$, the polytope ${{\mathscr {T}}}$ is defined by the inequalities in Table 4 (note that $\beta _i=\lambda _i$ for $i=1,2,3$). We have obtained

$$\begin{aligned} {\text {vol}}{{\mathscr {T}}}=\frac{5507086513}{173946175488}, \end{aligned}$$

Since a set of 4 elements admits 24 possible linear orders, the probability to have a linear order on the result of the majority voting is

$$\begin{aligned} P(\exists \text { CW},\exists \text { CL})=\frac{5507086513}{7247757312}\approx 0.7598. \end{aligned}$$

It follows that the probability that a Condorcet winner does exists, and still there exist no linear order on the result of the majority voting is

$$\begin{aligned} P(\exists \text { CW},\not \exists \text { CL})=\frac{ 1717}{2048}-\frac{5507086513}{7247757312}=\frac{569280335}{7247757312}\approx 0.07855. \end{aligned}$$

By the duality argument observed in the case (B1) the probability that a Condorcet loser does exists, but no Condorcet winner, is

$$\begin{aligned} P(\not \exists \text { CW},\exists \text { CL})=\frac{569280335}{7247757312}\approx 0.07855 \end{aligned}$$

as well. The probability of the remaining class (B2), the existence of a 4-cycle, is

$$\begin{aligned} P(\not \exists \text { CW},\not \exists \text { CL})=1-\frac{5507086513}{7247757312}-2*\frac{569280335}{7247757312}=\frac{602110129}{7247757312}\approx 0.0831. \end{aligned}$$

As a test for the correctness of the algorithm, we have nevertheless computed the probability of a 4-cycle directly. To this end, we consider the polytope ${{\mathscr {K}}}$ corresponding to the event that candidate 1 beats candidate 2, candidate 2 beats candidate 3, candidate 3 beats candidate 4 and candidate 4 beats candidate 1. As a subpolytope of ${{\mathscr {U}}}$, the polytope ${{\mathscr {K}}}$ is defined by the inequalities in Table 5.

Table 5 Inequalities for ${{\mathscr {K}}}$

We have obtained

$$\begin{aligned} {\text {vol}}{{\mathscr {K}}}=\frac{602110129}{43486543872}, \end{aligned}$$

Since a set of 4 elements admits 6 possible cycles of length four among the elements (if we fix one element there are 6 possible linear orders among the remaining three elements), one obtains exactly the same probability for the class (B2) that was computed indirectly above.

2.5 Borda paradoxes

In this subsection we study a family of voting paradoxes, first introduced by Chevalier de Borda (1781). To the best of our knowledge all volume computations in this subsection are new.

The strict Borda paradox appears in a voting situation when there is a complete reversal of the ranking of candidates given by the majority voting and plurality voting. In order to model this situation by inequalities one must first assume that there exists a linear order on the result of the majority voting that involves all n candidates, say $1,\dots ,n$ in this order (there are n! possible outcomes). The chosen outcome gives rise to

$$\begin{aligned} \frac{n(n-1)}{2} \end{aligned}$$

inequalities. Then one must add $n-1$ inequalities expressing that the order was completely reversed by the plurality voting. The volume of the corresponding polytope gives the probability of this event. By mutual exclusion and symmetry, we must multiply the volume by n! and then take the conditional probability under the hypothesis that such a linear order exists.

As a subpolytope of ${{\mathscr {U}}}$, the polytope ${{\mathscr {B}}}_{{St }}$ is defined by the inequalities in Table 6. Note that the first six inequalities describe the event that the result of the majority voting yields a linear order. We have obtained

$$\begin{aligned} {\text {vol}}{{\mathscr {B}}}_{{St }}=\frac{1281727528386311499990911876166511}{25940255058441281524973174784000000000}. \end{aligned}$$

Table 6 Inequalities for ${{\mathscr {B}}}_{{St }}$

Finally, conditioned by the assumption that there exists a linear order on the result of the majority voting, we get the probability of the strict Borda paradox for large numbers of voters,

$$\begin{aligned} B_{{St }}= \frac{24\cdot {\text {vol}}{{\mathscr {B}}}_{{St }}}{24\cdot {\text {vol}}{{\mathscr {T}}}}= \frac{1281727528386311499990911876166511}{821261107784328041072841984000000000}\approx 0.00156. \end{aligned}$$

Remark 2

(a) The inequalities defining the strict Borda paradox have an obvious property, which we only state since it does not hold in the case of the strong Borda paradox discussed below: it does not matter if one considers the inequalities in Table 6 or the inequalities defined by the same linear forms multiplied by $-$ 1. In fact, the multiplication by $-$ 1 reverses the linear order on the candidates both for majority and plurality, and thus amounts to a renaming of the candidates.

(b) One may ask, as in Gehrlein and Lepelley (2010), what happens if the negative plurality rule is used instead of the plurality rule. The negative plurality rule requires the voters to cast a vote against their least preferred candidate. It is not difficult to see that inversion of the preference orders as discussed in Sect. 2.4 above, maps an event representing the strict Borda paradox for plurality to an event representing the strict Borda paradox for negative plurality. Therefore no new computation is necessary.

(c) With the notation used in Gehrlein and Lepelley (2010, Formula 19), we have

$$\begin{aligned} B_{{St }}=P_{StBR }^{PR } (4,k,IAC )=P_{StBR }^{NPR } (4,k,IAC ) \quad \text { for } k\rightarrow \infty . \end{aligned}$$

We note that the probability of observing the strict Borda paradox in four candidates elections (under the Impartial Anonymous Culture hypothesis) is significantly smaller than the probability of observing the strict Borda paradox in three candidates elections, which was computed in Gehrlein and Lepelley (2010, Formula 19) and is $1/90\approx 0.0111$.

The strong Borda paradox is the voting situation in which there is an inversion between the winner or the loser from the majority voting to plurality voting. Under the name Condorcet loser paradox it is intensively studied in Brandt et al. (2016). It appears that de Borda was primarily concerned with the outcome that plurality voting might elect the majority voting loser (Chevalier de Borda 1781). In the following we say that the strong Borda paradox occurs if the Condorcet loser is the winner of the plurality voting. Let us assume that candidate 1 is the Condorcet loser. Next, by assuming that 1 wins the plurality we obtain $n-1$ new inequalities. Each candidate may fulfill these conditions, so by symmetry the result must be multiplied by n. Finally, the conditional probability has to be computed.

As a subpolytope of ${{\mathscr {U}}}$, the polytope ${{\mathscr {B}}}_{{Sg }}$ is defined by the inequalities in Table 7.

Table 7 Inequalities for ${{\mathscr {B}}}_{{Sg }}$

One gets

$$\begin{aligned} {\text {vol}}{{\mathscr {B}}}_{{Sg }}=\frac{325451674835828550681491}{68475651442606080000000000}. \end{aligned}$$

Combined with the previous computations, we obtain the probability of the strong Borda paradox for large numbers of voters:

$$\begin{aligned} B_{{Sg }}= \frac{4\cdot {\text {vol}}{{\mathscr {B}}}_{{Sg }}}{p_CW }= \frac{325451674835828550681491}{14352135440302080000000000}\approx 0.02268. \end{aligned}$$

(we have used that the probability that there exists a Condorcet loser equals the probability that there exists a Condorcet winner).

The situation when the Condorcet winner is the loser of the plurality voting presents also interest, in which case we say that the reverse strong Borda paradox appears. This situation is easy to model: we simply have to multiply the linear forms of Table 7 by $-$ 1. In other words, as a subpolytope of ${{\mathscr {U}}}$, the polytope ${{\mathscr {B}}}_{{SgRev }}$ is defined by the inequalities $\ \beta _1,\beta _2,\beta _4,-\beta _{10},-\beta _{11},-\beta _{12}$. Its volume is given by

$$\begin{aligned} {\text {vol}}{{\mathscr {B}}}_{{SgRev }}=\frac{104898234852130241}{21035720123168587776}. \end{aligned}$$

Combined with the previous computations, we get the probability of the reverse strong Borda paradox for large numbers of voters

$$\begin{aligned} B_{{SgRev }}= \frac{4\cdot {\text {vol}}{{\mathscr {B}}}_{{SgRev }}}{p_CW }= \frac{104898234852130241}{4408976007260798976}\approx 0.02379. \end{aligned}$$

The difference between the two forms of the strong Borda paradox may seem surprising, but there is less symmetry than one might assume naively: preference reversal turns the Condorcet winner into the Condorcet loser and conversely, but such exchange does not exist between the plurality winner and the plurality loser. Already the minimal number of voters that can realize the paradoxa differ; see Remark 8(d).

Remark 3

(a) Again one may ask what happens if the negative plurality rule (NPR) is used for the strong Borda paradox (BP) and its reverse variant. In total we then have 4 variants. But the 2 new variants are isomorphic to those considered above via the inversion of preference orders:

$$\begin{aligned} \hbox {reverse BP with NPR} \cong \hbox {BP},\qquad \hbox {BP with NPR} \cong \hbox {reverse BP.} \end{aligned}$$

(2.3)

In fact, the inversion of preference orders turns an event representing the strong Borda paradox for plurality into an event for the reverse strong Borda paradox with negative plurality. Similarly it exchanges the events within the other pair.

(b) With the notation used in Gehrlein and Lepelley (2010, Formula 20), we have

$$\begin{aligned} B_{{Sg }}&=P_{SgBR }^{PR } (4,k,IAC )\quad \text {and} \\ B_{{SgRev }}&=P_{SgBR }^NPR (4,k,IAC ) \quad \text { for } k\rightarrow \infty . \end{aligned}$$

We note that the probability of observing the strong Borda paradox in four candidates elections under the plurality rule (respectively the negative plurality rule) is smaller, but still of the same magnitude, with the probability of observing the strong Borda paradox in three candidates elections under the plurality rule (respectively the negative plurality rule), which was computed in Gehrlein and Lepelley (2010, Formula 20) and is $4/135 \approx 0.0296$ (respectively $17/540 \approx 0.0315$).

Remark 4

After the initial submission of this paper, Lepelley informed us by e-mail that several volume computations in El Ouafdi et al. (2018) can also be done by a combination of the software packages LattE (Baldoni et al. 2013) and lrs (Avis 2018). The authors obtained precisely the same results as we. This is a good test for the correctness of all algorithms involved.

In addition to LattE and lrs the El Ouafdi et al. (2018) also used the descent algorithm of Normaliz (Bruns and Ichim 2018) that was developed after the submission of this paper.

3 Computations of Ehrhart series and quasipolynomials arising in four candidates elections

While the probability for very large numbers of voters of a certain type of election result, for example the Condorcet paradox, can be computed as the volume of a polytope (or the sum of such volumes), one can use the polyhedral method also to find the exact number of election profiles of the given type for a specific number k of voters. For example, if ${{\mathscr {C}}}$ is the semiopen polytope defined by the condition that candidate 1 is the Condorcet winner, then the number of election profiles for k voters with Condorcet winner 1 is

$$\begin{aligned} E({{\mathscr {C}}},k)=\#( k{{\mathscr {C}}}\cap {{\mathbb {Z}}}_+^N). \end{aligned}$$

The function $E({{\mathscr {C}}},k)$ is called the Ehrhart function of ${{\mathscr {C}}}$. The best approach to its computations uses the generating function

$$\begin{aligned} E_{{\mathscr {P}}}(t)=\sum _{k=0}^{\infty } E({{\mathscr {C}}},k)t^k. \end{aligned}$$

This Ehrhart series is the power series expansion of a rational function at the origin. It is computed as a rational function, and in the following we will always represent Ehrhart series in the form numerator/denominator. The numerator is a polynomial with integer coefficients. The denominator can always be written as a product of d terms $1-t^g$, $d=\dim {{\mathscr {P}}}+1$:

$$\begin{aligned} E_{{\mathscr {P}}}(t)=\frac{h_0+h_1t+\dots +h_st^s}{(1-t^{g_1})\cdots (1-t^{g_d})},\qquad h_i\in {{\mathbb {Z}}}. \end{aligned}$$

Note that in general there exists no canonical representation in this form; see Bruns et al. (2016, Section 4) for a brief discussion of this problem. If ${{\mathscr {P}}}$ is closed, then $h_0=1$, and the denominator can be chosen in such a way that all $h_i$ are nonnegative. In the semiopen case such a representation may not exist. The theory of Ehrhart series is developed in several books, for example in Bruns and Gubeladze (2009). For a treatment under the aspect of social choice we refer the reader to Lepelley et al. (2008).

For closed polytopes ${{\mathscr {P}}}$, the Ehrhart function $E({{\mathscr {P}}},k)$ itself is given by a quasipolynomial $q_{{\mathscr {P}}}$ for all $k\ge 0$. Roughly speaking, this means that $q_{{\mathscr {P}}}(k)$ is a polynomial whose coefficients depend periodically on k. The period is a divisor of the least common multiple of the exponents g in the factors $1-t^g$ in the denominator. In the Normaliz output the period is always exactly the least common multiple. In the semiopen case one has $E({{\mathscr {P}}},k)=q_{{\mathscr {P}}}(k)$ only for sufficiently large k. More precisely, if r is the degree of $E_{{\mathscr {P}}}(t)$ as a rational function, then $E({{\mathscr {P}}},r)\ne q_{{\mathscr {P}}}(r)$, but $E({{\mathscr {P}}},k)= q_{{\mathscr {P}}}(k)$ for all $k>r$.

For $n=4$ the Ehrhart series of ${{\mathscr {C}}}$ has the numerator

$$\begin{aligned}&\phantom {+}6 t^{1} + 15 t^{2} + 481 t^{3} + 890 t^{4} + 12346 t^{5} + 17845 t^{6}\\&\quad + 152891 t^{7} + 180850 t^{8} + 1113216 t^{9} + 1111974 t^{10} +5320122 t^{11}\\&\quad + 4580485 t^{12} + 17837843 t^{13} + 13415068 t^{14} + 43770180 t^{15} + 28993857 t^{16}\\&\quad + 80758791 t^{17} + 47336170 t^{18} + 113925878 t^{19} + 59177761 t^{20} + 123966919 t^{21}\\&\quad + 56990048 t^{22} + 104272000 t^{23} + 42243510 t^{24} + 67509138 t^{25} + 23917200 t^{26}\\&\quad + 33268048 t^{27} + 10182887 t^{28} + 12235441 t^{29} + 3176870 t^{30} +3255226 t^{31}\\&\quad + 697232 t^{32} + 596834 t^{33} + 100915 t^{34} + 69821 t^{35} + 8655 t^{36}\\&\quad + 4581 t^{37} + 363 t^{38} + 133 t^{39} + 5 t^{40} + t^{41}.\\ \end{aligned}$$

The Ehrhart series of ${\overline{{{\mathscr {C}}}}}$ has the numerator

$$\begin{aligned}&\phantom {+}1+5t^{1}+133t^{2}+363t^{3}+4581t^{4}\\&\quad +8655t^{5}+69821t^{6}+100915t^{7}+596834t^{8}+697232t^{9}\\&\quad +3255226t^{10}+3176870t^{11}+12235441t^{12}+10182887t^{13}+33268048t^{14}\\&\quad +23917200t^{15}+67509138t^{16}+42243510t^{17}+104272000t^{18}+56990048t^{19}\\&\quad +123966919t^{20}+59177761t^{21}+113925878t^{22}+47336170t^{23}+80758791t^{24}\\&\quad +28993857t^{25}+43770180t^{26}+13415068t^{27}+17837843t^{28}+4580485t^{29}\\&\quad +5320122t^{30}+1111974t^{31}+1113216t^{32}+180850t^{33}+152891t^{34}\\&\quad +17845t^{35}+12346t^{36}+890t^{37}+481t^{38}+15t^{39}+6t^{40}. \end{aligned}$$

Both have the same denominator

$$\begin{aligned} (1-t)(1-t^2)^{14}(1-t^4)^{9}. \end{aligned}$$

Numerator and denominator are coprime, but in general one cannot find a coprime representation if one insists on a denominator that is a product of terms $1-t^g$.

If we write the numerator of ${\overline{{{\mathscr {C}}}}}$ as $\sum _{i=0}^{40} a_it^i$, then the numerator of ${{\mathscr {C}}}$ is $\sum _{i=0}^{40} a_{40-i}t^{i+1}$: up to a shift in degree, they are palindromes of each other. This rather unexpected relationship is not an accident, and is explained by the following theorem.

Theorem 5

Let $\lambda _1,\dots ,\lambda _m$ be linear forms on ${{\mathbb {R}}}^d$, and let ${\mathbf {1}}\in {{\mathbb {R}}}^d$ be the vector with the entry 1 at all coordinates. Suppose that $\lambda _i({\mathbf {1}})=0$ for all $i=1,\dots ,m$. Set $C=\{x\in {{\mathbb {R}}}^d_+: \lambda _i(x)\ge 0,i=1\dots ,m\}$, and

$$\begin{aligned} D=\{x\in {{\mathbb {R}}}^d_+: \lambda _i(x)>0,i=1\dots ,m\}. \end{aligned}$$

Define the he semiopen polytope ${{\mathscr {P}}}$ by

$$\begin{aligned} {{\mathscr {P}}}=\left\{ x\in D: \sum x_i=1\right\} . \end{aligned}$$

If $\dim {{\mathscr {P}}}=d-1$ (the maximal dimension), then the following hold:

• (1) $J=I-{\mathbf {1}}$, where J is the set of lattice points in D and I is the set of interior lattice points of C.

• (2)
  $$\begin{aligned} E_{{{\mathscr {P}}}}(t)=(-1)^d\,t^{-d}E_{{{\overline{{{\mathscr {P}}}}}}}(t^{-1}). \end{aligned}$$

• (3) Suppose that

  $$\begin{aligned} E_{{{\overline{{{\mathscr {P}}}}}}}(t)=\frac{h_0+h_1t\dots +h_st^s}{(1-t^{g_1})\cdots (1-t^{g_d})}. \end{aligned}$$

  Then the Ehrhart series of ${{\mathscr {P}}}$ has the numerator polynomial

  $$\begin{aligned} h_st^w+\dots +h_0t^{w+s} ,\qquad w=\sum _{i=1}^d g_i-d-s, \end{aligned}$$

  over the same denominator.

Proof

The crucial observation is (1). Since $\dim {{\mathscr {P}}}=d-1$, the interior of C is

$$\begin{aligned} \{x: x_i>0,i=1,\dots ,d,\lambda _j(x)>0,j=1,\dots ,m\}. \end{aligned}$$

For lattice points $x\in {{\mathbb {Z}}}^d$ these inequalities amount to $x_i\ge 1$ and $\lambda _j(x)\ge 1$. Thus x belongs to the interior of C if and only if $x-{\mathbf {1}}$ satisfies the inequalities $x_i\ge 0$ for $i=1,\dots ,d$, and $\lambda _j(x)>0$ for $j=1,\dots ,m$. This proves $J=I-{\mathbf {1}}$.

By Ehrhart reciprocity (for example, see Bruns and Gubeladze 2009, Th. 6.51) the Ehrhart series of the interior of ${{\overline{{{\mathscr {P}}}}}}$ is $(-1)^dE_{{{\overline{{{\mathscr {P}}}}}}}(t^{-1})$. In view of (1) we have to multiply this series by $t^{-d}$ to obtain the Ehrhart series of ${{\mathscr {P}}}$. This gives (2).

Part (3) is now an elementary transformation. $\square$

Remark 6

(a) The condition $\lambda _i({\mathbf {1}})=0$ in Theorem 5 is equivalent to the natural assumption that it only depends on the differences $v_i-v_j$ whether a voting profile $(v_1,\dots ,v_d)$ belongs to the event defined by the inequalities.

(b) We have formulated Theorem 5 for the grading by total degree. It can easily be generalized to other gradings.

In the case of our polytopes we have $d=24$. So, for ${{\mathscr {C}}}$ we obtain $\sum _{i=1}^d g_i-d-s=65-24-40=1$, as observed. Theorem 5 is applicable to all polytopes in Sect. 2 with the exception of ${{\mathscr {F}}}$. Nevertheless we have computed both Ehrhart series in each case since the comparison is an excellent test of the Normaliz algorithm. For ${{\mathscr {F}}}$ the formula in Theorem 5 does indeed not hold.

The Ehrhart quasipolynomials of ${{\mathscr {C}}}$ and ${\overline{{{\mathscr {C}}}}}$ have period 4. Moreover, they are equal for an odd number of voters k and have the same expression

$$\begin{aligned} \#({{\mathscr {C}}}_k\cap {{\mathbb {Z}}}^N)=\#({\overline{{{\mathscr {C}}}}}_k\cap {{\mathbb {Z}}}^N)= \frac{R_{1,3}(k)*(12 + k)*\prod _{i=1, i \text { odd }}^{23} (i+k) }{23!*131072} \end{aligned}$$

(for $k\equiv 1,3 \text { mod }4$), where

$$\begin{aligned} R_{1,3}(k)&=261812975764725 +308449567353120 k + 165347938576012 k^2 \\&\quad + 50600971266720 k^3 + 9607752151310 k^4+ 1183838427360 k^5\\&\quad + 96296973756 k^6+5130593760 k^7 + 172122725 k^8 + 3296640 k^9 + 27472 k^{10}. \end{aligned}$$

Let us reformulate this result in terms of probabilities. With the notation introduced at the beginning of Sect. 2, we have

$$\begin{aligned} p_{CW }^{(4)}(k)=4p_{CW }^{(4,1)}(k), \end{aligned}$$

where

$$\begin{aligned} p_{CW }^{(4,1)}k(k)=\frac{\#({{\mathscr {C}}}_k\cap {{\mathbb {Z}}}^N)}{\#({{\mathscr {U}}}_k\cap {{\mathbb {Z}}}^N)}. \end{aligned}$$

Since

$$\begin{aligned} \#({{\mathscr {U}}}_k\cap {{\mathbb {Z}}}^N)=\frac{\prod _{i=1}^{23} (i+k) }{23!} \end{aligned}$$

we get

$$\begin{aligned} p_{CW }^{(4)}(k)=\frac{R_{1,3}(k)*(12 + k)}{32768*\prod _{i=1, i \text { even }}^{23} (i+k)} \quad \text { if }k\equiv 1,3 \text { mod }4. \end{aligned}$$

This is exactly the same formula as the one computed first by Gehrlein Gehrlein (2001). For the case of even k we set

$$\begin{aligned} R_{0}(k)&=4981367114669230129152000 + 11069309139290261311979520 k \\&\quad +11286725167650172468985856 k^2 + 6970525765323041332002816 k^3 \\&\quad + 2896901556002851225731072 k^4 + 857336679021412589010944 k^5 \\&\quad + 187293111169997407690752 k^6 + 30935327102400429176832 k^7 \\&\quad +3923664152075008433664 k^8 + 385511913998009006208 k^9 \\&\quad + 29422431828810359328 k^{10} +1738486466127164288 k^{11} +\\&\quad +78715287099505056 k^{12} + 2678620940814672 k^{13} + 66260942646564 k^{14} \\&\quad + 1124326347564 k^{15}+ 11698573833 k^{16} + 56262656 k^{17} \end{aligned}$$

and

$$\begin{aligned} R_{2}(k)&=9794451243189989376000 + 921057250987916963020800 k \\&\quad +1705900639387417842032640 k^2 + 1489106767895973053595648 k^3 \\&\quad + 792353026020511342854144 k^4 + 284373446368099671547904 k^5 \\&\quad + 72772788665361422238720 k^6 + 13747699097527641501696 k^7 \\&\quad +1960073323091557035648 k^8 + 213683286033339310848 k^9 \\&\quad + 17913763440866689440 k^{10} + 1153396601212907264 k^{11}\\&\quad + 56538334354261872 k^{12} + 2071748534241792 k^{13} + 54936786331200 k^{14} \\&\quad + 995421043392 k^{15} + 11023421961 k^{16} + 56262656 k^{17}, \end{aligned}$$

then we get

$$\begin{aligned} p_{CW }^{(4)}(k)= {\left\{ \begin{array}{ll} \frac{R_{0}(k)*k}{67108864*\prod _{i=0}^{5} (1+4*i+k)(2+4*i+k)(3+4*i+k)} \quad \text { if }k\equiv 0 \text { mod }4;\\ \frac{R_{2}(k)*k}{67108864*\prod _{i=0}^{5} (4*i+k)(1+4*i+k)(3+4*i+k)} \quad \quad \text { if }k\equiv 2 \text { mod }4.\\ \end{array}\right. } \end{aligned}$$

To the best of our knowledge the above formula for an even number of voters has not been computed before our computations with Normaliz.

In Fig. 3 we present the graph of $p_{CW }^{(4)}(k)$ and in Fig. 4 we present the graph of $p_{CW }^{(4)}(k^2)$ for $k=0,\ldots ,48$. The difference between the values of $p_{CW }^{(4)}$ for even and odd numbers of voters is due to the fact that in the case of an even number of voters ties do occur. The graphs are drawn using the software package R, see R Core Team (2013).

Fig. 3

Probabilities for a small number of voters

Fig. 4

Probabilities for a large number of voters

Remark 7

With the notation used in Gehrlein and Lepelley (2011, Formula 1.27 and 1.29), we have

$$\begin{aligned} p_{CW }^{(4)}(k)=P_{PMRW }^S(4,k,IAC ) \quad \text { for all } k\in {{\mathbb {Z}}}_{+}. \end{aligned}$$

For the other eight polytopes, since the numerators of the Ehrhart series are very long, we only list the denominators for a representation similar to the one given above for ${{\mathscr {C}}}$ and ${\overline{{{\mathscr {C}}}}}$ (with non-coprime numerators):

$$\begin{aligned} {{\mathscr {Q}}},{\overline{{{\mathscr {Q}}}}}:&\;(1-t)(1-t^2)^2(1-t^4)^5(1-t^{12})^{16},\\ {{\mathscr {E}}},{\overline{{{\mathscr {E}}}}}, {{\mathscr {F}}},{\overline{{{\mathscr {F}}}}}, {{\mathscr {B}}}_{{Sg }},\overline{{{\mathscr {B}}}_{{Sg }}}:&\;(1-t)(1-t^2)^2(1-t^4)^5(1-t^{12})^4(1-t^{24})(1-t^{120})^{11},\\ {{\mathscr {T}}},{\overline{{{\mathscr {T}}}}}:&\;(1-t)(1-t^2)^{14}(1-t^4)^5(1-t^{12})^{3}(1-t^{24}),\\{} {{\mathscr {K}}},{\overline{{{\mathscr {K}}}}}:&\;(1-t)(1-t^2)^{14}(1-t^4)^5(1-t^{12})^{4},\\ {{\mathscr {B}}}_{{St }},\overline{{{\mathscr {B}}}_{{St }}}:&\;(1-t)(1-t^2)^2(1-t^{4})^5(1-t^{12})^4(1-t^{24})(1-t^{120})^4\\&(1-t^{840})^2(1-t^{2520})^2(1-t^{27720})^{2}(1-t^{55440}),\\ {{\mathscr {B}}}_{{SgRev }},\overline{{{\mathscr {B}}}_{{SgRev }}}:&\;(1-t)(1-t^2)^{2}(1-t^4)^6(1-t^{12})^{3}(1-t^{24})^{12}. \end{aligned}$$

The denominators have 24 factors. All computed data is available and will be provided by the authors on request.

The reciprocity between $E_{{\mathscr {P}}}(t)$ and $E_{{{\overline{{{\mathscr {P}}}}}}}(t)$ in Theorem 5 can be recast into a relation between the Ehrhart quasipolynomials. In terms of quasipolynomials, Ehrhart reciprocity says $q_{{relint }{{\overline{{{\mathscr {P}}}}}}}(k)=(-1)^{d-1}q_{{{\overline{{{\mathscr {P}}}}}}}(-k)$ for all $k\ge 1$ (for example, see Bruns and Gubeladze 2009, Th. 6.51), and in view of Theorem 5 this implies

$$\begin{aligned} q_{{\mathscr {P}}}(\ell )=(-1)^{d-1}(-\ell -d). \end{aligned}$$

It follows that under the conditions of Theorem 5 one has $E({{\mathscr {P}}},k)=q_{{\mathscr {P}}}(k)$ for all $k>-d$, and therefore for all $k>0$.

Remark 8

(a) In Table 8 we summarize the essential data of the numerators of the Ehrhart series of the polytopes (with the exception of ${{\mathscr {F}}}$), according to the notations introduced in Theorem 5. The last column represents the period of the associated Ehrhart quasipolynomials.

Table 8 Data for the numerators of the Ehrhart series and quasipolynomials

(b) The numerator of ${\overline{{{\mathscr {F}}}}}$ is a polynomial of degree 1386 whereas the numerator of ${{\mathscr {F}}}$ has degree 1389. They are not related by Theorem 5, so the Ehrhart series must be computed separately by Normaliz. The Ehrhart quasipolynomials of ${{\mathscr {F}}}$ and ${\overline{{{\mathscr {F}}}}}$ have period 120.

(c) The number w in Table 8 is the smallest number of voters that can realize the respective election outcome since it is the initial degree of the Ehrhart series, i.e., the lowest exponent of t that appears in the Ehrhart series (when written as a power series). It is also the coefficient of the smallest power of t in the numerator polynomial of the Ehrhart series when written as a rational function. In fact, one obtains the series expansion by multiplying the numerator polynomial with the power series expansion of 1 / q(t) where q is the polynomial in the denominator, and this power series has constant coefficient 1.

Future versions of Normaliz may contain a function that allows the computation of the initial degree without the computation of the full Ehrhart series. The latter is much more difficult.

(d) The values of w can be checked by elementary arguments, independently from the Ehrhart series computation. We explain it for the strong Borda paradox. Let candidate A be the plurality winner. Then he has got more first places, say m, than any of the three other candidates. On the other hand, he is the Condorcet loser, and therefore must be behind any of the other candidates in at least $m+1$ preference orders. Another candidate, for example B, gets first place in at least one of these $m+1$ preference orders. Then $m>1$, so $m\ge 2$. For the total number of voters k it follows that $k \ge 2m+1\ge 5$. The strong Borda paradox can indeed be realized with 5 voters; see Table 9 where the numbers in the last lines indicate the number of voters that have the preference ranking above them. Note that the same argument works for any number of candidates, with the exception of the three candidates situation where the minimal number of voters is 7. Similarly one can see that, for four candidates elections, the strict Borda paradox needs 9 voters, whereas the reverse strong Borda paradox requires only 3 of them, as shown in Table 9.

Table 9 Minimal profiles realizing some paradoxa

4 The exploitation of symmetry

The elegant approach of Schürmann Schürmann (2013) for the computation of the volumes of ${{\mathscr {C}}}$ and variants of ${{\mathscr {Q}}}$ and ${{\mathscr {E}}}$ uses the high degree of symmetries of these polytopes. Suppose that a polytope $P\subset {{\mathbb {R}}}^d$ is defined by the sign inequalities $x_i\ge 0$, $i=1,\dots ,d$, and further inequalities $\lambda _i(x)\ge 0$ (or $>0$). If certain variables $x_{i_1},\dots ,x_{i_u}$ occur in all of the linear forms $\lambda _i$ with the same coefficient (that may depend on i), then any permutation of them acts as a symmetry on the corresponding polytope, and the variables $x_{i_1},\dots ,x_{i_u}$ can be replaced by their sum $y_j=x_{i_1}+\dots +x_{i_u}$ in the $\lambda _i$ (the polytopes may have further symmetries). The substitution can be used for a projection into a space of much lower dimension, mapping the polytope P to a polytope Q (this requires that the grading affine hyperplane $A_1$ is mapped onto an affine hyperplane by the projection). Instead of counting the lattice points in kP one counts the lattice points in kQ weighted with their number of preimage lattice points in kP. This amounts to the consideration of a weighted Ehrhart function

$$\begin{aligned} k\mapsto \sum _{y\in kQ\cap {{\mathbb {Z}}}^d} f(y). \end{aligned}$$

The polynomial f is easily determined by elementary combinatorics: if $y_j$, $j=1,\dots ,m$, is the sum of $u_j$ variables $x_i$, then

$$\begin{aligned} f(y)=\left( {\begin{array}{c}u_1+y_1-1\\ u_1-1\end{array}}\right) \cdots \left( {\begin{array}{c}u_m+y_m-1\\ u_m-1\end{array}}\right) . \end{aligned}$$

The theory of weighted Ehrhart functions has recently been developed in several papers; see Baldoni et al. (2011, 2012) and Bruns and Söger (2015). In Schürmann (2013), only the leading form of the polynomial f is used. Integration of the leading form with respect to Lesbesgue measure yields the volume.

In the case of the Condorcet polytope ${{\mathscr {C}}}$ for four candidates the symmetrization yields a polytope of dimension 7: there are two groups of 6 variables each that can be replaced by their sums, and 6 groups of two variables each. We leave it to the reader to spot them. Fortunately Normaliz finds them automatically. The polynomial f, also computed automatically, is

$$\begin{aligned} f(y)=\left( {\begin{array}{c}y_1+5\\ 5\end{array}}\right) (y_2+1)(y_3+1)(y_4+1)(y_5+1)(y_6+1)(y_7+1)\left( {\begin{array}{c}y_8+5\\ 5\end{array}}\right) \end{aligned}$$

in this case. Among our polytopes, only ${{\mathscr {T}}}$ and ${{\mathscr {B}}}_{{St }}$ do not allow any symmetrization.

Before Version 3.2.0 of Normaliz called its offspring NmzIntegrate behind the scenes for the symmetrized computation of volumes and weighted Ehrhart series. From version version 3.3.0 on, NmzIntgerate is included in Normaliz itself and no longer exist as a separate program. The algorithmic approach of NmzIntegrate is developed in Bruns and Söger (2015). For polynomial arithmetic Normaliz uses CoCoALib by Abbott et al. (2018).

5 Computational report

In this section we want to document the use of Normaliz and computations performed with it during the preparation of this work.

5.1 Use of Normaliz

Normaliz is distributed as open source under the GPL. In addition to the source code, the distribution contains executables for the major platforms Linux, Mac and Windows. We include some details on the use of Normaliz in order to show that the input files have a transparent structure and that the syntax of the execution command is likewise simple.

The polytope ${{\mathscr {C}}}$ has the following input file:

The first line amb_space 24 sets the ambient space to

${{\mathbb {R}}}^{24}$. The 3 excluded_faces represent the strict inequalities $\lambda _i>0$, $i=1,2,3$ of Table 1 (the input type of non-strict inequalities is inequalities). The keyword nonnegative indicates that all 24 coordinates are to be taken nonnegative, whereas total_degree defines the grading in which each coordinate has weight 1. HilbertSeries indicates that we want to compute the Hilbert series. The last two lines NoExtRaysOutput and NoSuppHypsOutput suppress output data that do not interest us for the Hilbert series. Let us suppose the file is called Condorcet.in.

In Normaliz the simplest command for the computation is

Depending on the installation, it may be necessary to prefix normaliz or Condorcet by a path. Often one adds the option -c to get terminal output showing the progress of the computation. If one is only interested in the volume, one replaces HilbertSeries by Multiplicity or Volume (without any explicit computation goal, Normaliz would compute both the Hilbert series and Hilbert basis by default). The number of parallel threads can be limited by adding the option -x$=<$N> to the command line where <N> stands for the number of threads.

The computation results are contained in Condorcet.out. We display the relevant part:

The volume we are interested in is called multiplicity because of its algebraic interpretation. Hilbert series is followed by the numerator polynomial of the rational function. The denominator is $(1{-}t)(1{-}t^2)^{14}(1{-}t^4)^9$. The Hilbert quasi-polynomial is printed by residue classes modulo the period. All coefficients must be divided by the common denominator.

As will be apparent from the terminal output (obtained with -c on the command line or Verbose in the input file), Normaliz successfully tries symmetrization. One should note that Normaliz does automatic symmetrization only if the cone D defined by image ${{\mathscr {Q}}}$ has dimension $\le 2\dim (C)/3$ where C is the cone over the polytope ${{\mathscr {P}}}$ to be computed. The bound has been introduced since one cannot expect a saving in computation time if the dimension does not drop enough. However, the user can force Normaliz to use symmetrization.

Remark 9

(a) Normaliz has an input type strict_inequalities. While it seems a natural choice and will yield the same results as excluded_faces, its use for the computations of this paper is not advisable since the algorithmic approach does not (yet) allow symmetrization, and even for cases without symmetrization it is usually significantly slower than excluded_faces.

(b) A graphical interface called jNormaliz (Almendra and Ichim 2018) is also available in the Normaliz package. For its use Java must be installed on the system.

5.2 Overview of the examples

The columns of Table 10 contain the values of characteristic numerical data of the examples studied, namely: $\#$vertices is the number of the vertices of the polytope, and $\#$supp the number of its support hyperplanes. $\#$Hilb is the size of the Hilbert basis of the Ehrhart cone over the polytope [see Bruns and Ichim (2010) for more details]. These data are invariants of the polytope.

Table 10 Numerical data of test examples

The last two columns list the number of simplicial cones in the triangulation and the number of components of the Stanley decomposition [see Bruns et al. (2016) for details on these numbers]. These data are not invariants of the polytope. The information is included to show the complexity of the computations if symmetrization is not used. Normaliz can do all computations without symmetrization, but then some of them will take days, even those with a high degree of symmetry. The size of the lexicographic triangulation depends on the order in which the extreme rays are processed. The polytopes in the table above are defined by their support hyperplanes, and therefore Normaliz first computes the extreme rays from them. Moreover, bottom decomposition, see Bruns et al. (2017), is used automatically if the ratio of the largest degree among the generators and the smallest is $\ge 10$. This further influences the data contained in the last two columns.

Of all our polytopes, only ${{\mathscr {T}}}$ and ${{\mathscr {B}}}_{{St }}$ cannot be symmetrized. The combinatorial data of the symmetrized polytopes are contained in Table 11.

Table 11 Numerical data of symmetrized polytopes

We remark that, for Hilbert basis computations, the dual algorithm of Normaliz (see Bruns and Ichim 2010) is much faster than the primal algorithm for the examples of this paper, and all computations run in a few seconds. This is by no means always the case (see Bruns et al. 2016).

5.3 Hardware characteristics

Almost all computations were run on a compute server with operating system CentOS 7.3, 4 Intel Xeon E5-2660 at 2.20 GHz (a total of 32 cores) and 192 GB of RAM. With the exception of ${{\mathscr {B}}}_{{St }}$, all computations were also done on a standard laptop with operating system Ubuntu 16.04, an Intel i5-4200M CPU at 2.5 GHz and 12 GB RAM. In parallelized computations we have limited the number of threads used to 30. In Tables 12 and 14, 4x and 30x indicates parallelization with 4 and 30 threads, respectively. As the large examples below show, the parallelization scales efficiently; see also Table 13. The version that we have used exchanges data via files. The laptop has an SSD, but the server has only hard disks, and it is not a local hard disk of the machine, but the files must go through the NFS, the network file system.

Normaliz needs relatively little memory. All computations mentioned in this paper run stably with $< 0.5$ GB of RAM for each thread used.

Table 12 Computation times for volumes

Table 13 Efficiency of parallelization in volume computations

5.4 Volumes

Table 12 contains the computation times for the volumes of the studied polytopes, as obtained with version 3.2.1. Since version 3.5.2 Normaliz has a second algorithm for the computation of volumes that is very often significantly faster. It was developed after the submission of this paper; see Bruns and Ichim (2018).

The input for all these examples is given in the form of inequalities. When one runs Normaliz on such examples, it first computes the extreme rays of the cone and uses them as generators. This small extra time is also included in the reported times below (it is also apparent and not surprising that small examples profit from a small number of parallel threads).

In order to measure the parallelization we have run the volume computation of ${{\mathscr {E}}}$ with varying number of threads. Table 13 shows that Normaliz is very efficiently parallelized.

Remark 10

The volume of the polytope ${{\mathscr {C}}}$ was first computed by Gehrlein (2001). The volumes of variants of the polytopes ${{\mathscr {Q}}}$ and ${{\mathscr {E}}}$ had been computed by Schürmann (2013) with LattE integrale (Baldoni et al. 2013). This information was very useful for checking the correctness of Normaliz.

5.5 Ehrhart series and quasipolynomials

The experimental times obtained for computation of Ehrhart series and quasipolynomials are contained in Table 14. As above, the presented times include the time used by Normaliz for computing the extreme rays of the cone. Moreover, the Ehrhart quasipolynomials are computed from the Ehrhart series (see Bruns and Ichim 2010). This requires for some examples like ${{\mathscr {B}}}_{{St }}$ a significant extra time, which has likewise been included. We have also measured the parallelization for the Ehrhart series computation of ${{\mathscr {B}}}_{{St }}$; see Table 15. Somewhat surprisingly, the efficiency is $>100\%$ for certain numbers of threads, an effect that can only be explained by the memory management of the system.

Table 14 Computation times for Ehrhart series and quasipolynomials

Table 15 Efficiency of parallelization in Ehrhart series computations