An exact solution approach for risk-averse mixed-integer multi-stage stochastic programming problems

Abstract

Risk-averse mixed-integer multi-stage stochastic programming problems are challenging, large scale and non-convex optimization problems. In this study, we propose an exact solution algorithm for a type of these problems with an objective of dynamic mean-CVaR risk measure and binary first stage decision variables. The proposed algorithm is based on an evaluate-and-cut procedure and uses lower bounds obtained from a scenario tree decomposition method called as group subproblem approach. We also show that, under the assumption that the first stage integer variables are bounded, our algorithm solves problems with mixed-integer variables in all stages. Computational experiments on risk-averse multi-stage stochastic server location and generation expansion problems reveal that the proposed algorithm is able to solve problem instances with more than one million binary variables within a reasonable time under a modest computational setting.

1 Introduction and literature review

In their seminal work, Artzner et al. (1999) establish the theory of coherent risk measures in order to reflect risk-averse preferences in stochastic optimization problems. Later, Ruszczyński and Shapiro (2006b, c) provide theoretical properties of risk-averse stochastic optimization problems where the objective function is a coherent measure of risk. The theory of coherent risk measures is also extended to multi-stage problems where dynamic risk measures are used to quantify the risk of a cost sequence. Risk-averse multi-stage stochastic optimization problems are discussed by Shapiro et al. (2009) with theoretical results and example models.

Risk-averse multi-stage stochastic models require higher computational effort compared to their risk-neutral counterparts where the objective is to minimize expected cost. Scenario-wise (Carøe and Schultz 1999) and stage-wise (Pereira and Pinto 1991; Shapiro 2011) decomposition methods are available for risk-neutral multi-stage stochastic programming problems. Although these methods are not applicable to risk-averse multi-stage problems directly, recent works extend decomposition methods to these problems as well. Collado et al. (2012) use dual representation of coherent risk measures in order to employ a scenario decomposition algorithm for risk-averse multi-stage problems. Shapiro et al. (2013) and Philpott et al. (2013) extend a stage-wise decomposition approach, namely stochastic dual dynamic programming, to risk-averse multi-stage problems with dynamic coherent risk measures. Convergence of the aforementioned methods relies on some assumptions. One of these assumptions is convexity, that is, the problems are convex. In mixed-integer case, where some of the variables are assumed to be integer valued, these methods can be extended to serve as heuristics. Schultz (2003) also points out that, in risk-averse multi-stage problems, the complex structure of non-anticipativity constraints prohibits efficient solution methods for these problems. Therefore, risk-averse mixed-integer multi-stage stochastic programming problems are in a class of challenging problems for which, to the best of our knowledge, no exact solution method is available.

Another stream of research focuses on group subproblem approach to obtain bounds for risk-neutral (Sandıkı et al. 2013; Maggioni et al. 2014, 2016; Sandıkı and Özaltın 2017) and risk-averse (see Maggioni and Pflug 2016; Mahmutoulları et al. 2018) mixed-integer multi-stage stochastic programming problems. The method is based on solving the problem for subsets of scenarios instead of the original set of scenarios in order to obtain bounds on the optimal value of the problem. Computational experiments on group subproblem approach show that the obtained bounds are reasonably tight even for large scale instances.

Recent studies reveal that it is possible to come up with exact solution methods for risk-neutral and risk-averse two-stage mixed-integer stochastic programming problems by exploiting the nature of binary variables. Ahmed (2013) uses no-good cuts in an evaluate-and-cut procedure for risk-neutral two-stage mixed-integer models with binary first stage decisions. The proposed procedure is a scenario decomposition algorithm which iteratively evaluates the objective value for a set of binary first stage solutions and cuts these solutions from the feasible set. Deng et al. (2017) extend the procedure to risk-averse two-stage problems with binary first stage variables. They consider three different exact solution algorithms using dual representations of coherent risk measures, scenario decomposition, cutting planes, subgradient method and no-good cuts. The computational experiments presented by Ahmed (2013) and Deng et al. (2017) reveal that risk-neutral and risk-averse two-stage stochastic programing problems with binary first stage variables can be solved optimally within reasonable computation times. On the other hand, no exact solution method is available for the risk-averse mixed-integer multi-stage stochastic programming problems since these problems form a class of large scale and non-convex optimization problems. In this study, we show that a combination of an evaluate-and-cut procedure and group subproblem approach yields an easily implementable solution algorithm for these problems.

The contribution of this study is as follows: In this paper, we propose an exact solution algorithm for risk-averse mixed-integer multi-stage stochastic programming problems with an objective of dynamic mean-CVaR risk measure and binary first stage variables. The proposed method is based on an evaluate-and-cut procedure where the lower bounds are obtained from group subproblems. Moreover, we show that, under the assumption that the first stage integer variables are bounded, the problem with mixed-integer variables in all stages can be solved with the proposed algorithm. In order to observe the performance of the proposed algorithm, we conduct a set of computational experiments on risk-averse mixed-integer multi-stage problems. In our experiments, we consider large instances of risk-averse multi-stage stochastic server location and generation expansion problems. We also investigate some implementation details of the algorithm such as scenario partitioning choices and group sizes and then analyze their effects on the performance of the algorithm. As the computational experiments reveal, under modest computational settings, the proposed algorithm is able to solve large problem instances with over one million binary variables within a reasonable time.

The organization of the rest of the paper is as follows: In Sect. 2, we define risk-averse mixed-integer multi-stage stochastic programing problems. In Sect. 3, we present the bounds obtained by scenario grouping. The proposed algorithm is presented in Sect. 4. In Sect. 5, we show that our algorithm can also be used for the problems with mixed-integer variables in all stages. The computational experiments are given in Sect. 6. The concluding remarks are presented Sect. 7.

2 Risk-averse mixed-integer multi-stage stochastic programming

We consider a T-stage decision environment, where decisions at each stage result in a random cost for which smaller realizations are preferable. Let $(\varOmega ,{\mathscr {F}},P)$ be a probability space where $\varOmega$ is a sample space, ${\mathscr {F}}$ is the set of all events defined on $\varOmega$, and P is the reference probability distribution. Also, let $\{\emptyset ,\varOmega \} = {\mathscr {F}}_{1} \subset \dots \subset {\mathscr {F}}_{T} = {\mathscr {F}}$ be a filtration representing increasing information through stages 1 to T and ${\mathscr {Z}}_{t} := {\mathscr {L}}_{p}(\varOmega ,{\mathscr {F}}_{t},P)$, $t \in \{1,\dots ,T\}$ be the space of ${\mathscr {F}}_{t}$-measurable and p-integrable random variables for $p\ge 1$. The collection of problem parameters at stage t is denoted by $\xi _t$, which is random and adopted to the filtration, i.e. $\xi _t \in {\mathscr {Z}}_{t}$ for $t \in \{1,\dots ,T\}$. Since ${\mathscr {F}}_{1}$ is trivial, $\xi _1$ is deterministic. An element $\omega$ of $\varOmega$ is called as a scenario. A scenario $\omega \in \varOmega$ corresponds to a realization $\xi _1, \xi _2(\omega ),\ldots ,\xi _T(\omega )$ of random problem parameters.

Decisions at stage $t \in \{1,\ldots ,T\}$ are made based on the available information up to stage t. This requirement is called as non-anticipativity. Moreover, for any state of the system at stage t, optimal decisions should not involve possible future realizations that cannot happen. This principle is called as time consistency (see Shapiro 2009). Let $x_t$ represent the collection of all decisions at stage $t \in \{1,\ldots ,T\}$. Then, the decision process in a multi-stage stochastic problem is given in Fig. 1.

Fig. 1

Decision process in a multi-stage stochastic programming problem

Since $\xi _1$ is deterministic, $x_1$ is deterministic as well. The decision $x_t$ is, however, ${\mathscr {F}}_{t}$-measurable for $t \in \{2,\ldots ,T\}$. Our interest is to minimize the risk of the cost sequence $f_1(x_1),f_2(x_2,\xi _2),\ldots ,f_T(x_T,\xi _T)$ through stages 1 to T where $f_1(\cdot )$ is a deterministic cost function and $f_t(\cdot ,\xi _t)$ is an ${\mathscr {F}}_{t}$-measurable cost function for $t \in \{2,\ldots ,T\}$. Due to time consistency requirement [see Shapiro (2009) for a detailed discussion], we can write risk-averse mixed-integer multi-stage stochastic programming problem as

$$\begin{aligned}&\underset{x_1 \in {\mathscr {X}}_1}{\min } f_1(x_1) + \rho _{{\mathscr {F}}_2|{\mathscr {F}}_1} \left( \underset{x_2 \in {\mathscr {X}}_2(x_1,\xi _2)}{\min } f_2(x_2,\xi _2) + \cdots \right. \nonumber \\&\quad \left. + \rho _{{\mathscr {F}}_{T}|{\mathscr {F}}_{T-1}} \left( \underset{x_T \in {\mathscr {X}}_T(x_{T-1},\xi _{T})}{\min } f_T(x_T,\xi _T)\right) \cdots \right) , \end{aligned}$$

(1)

where ${\mathscr {X}}_1 \subseteq {\mathbb {R}}_+^{K_{1}} \times {\mathbb {Z}}_+^{L_{1}} \times \{0,1\}^{M_{1}}$ is a mixed-integer deterministic set and ${\mathscr {X}}_t: {\mathbb {R}}_+^{K_{t-1}} \times {\mathbb {Z}}_+^{L_{t-1}} \times \{0,1\}^{M_{t-1}} \times \varOmega \rightrightarrows {\mathbb {R}}_+^{K_{t}} \times {\mathbb {Z}}_+^{L_{t}} \times \{0,1\}^{M_{t}}$ is the point-to-set mapping representing mixed-integer ${\mathscr {F}}_{t}$-measurable decisions at stage $t \in \left\{ 2,\ldots ,T\right\}$.

The function $\rho _{{\mathscr {F}}_{t+1}|{\mathscr {F}}_{t}}: {\mathscr {Z}}_{t+1} \rightarrow {\mathscr {Z}}_{t}$ is a conditional coherent measure of risk which quantifies the risk at stage $t+1$ based on the available information at stage $t \in \{1,\ldots ,T-1\}$. As presented by Shapiro et al. (2009) and Ruszczyński and Shapiro (2006a), a conditional coherent measure of risk $\rho _{{\mathscr {F}}_{t+1}|{\mathscr {F}}_{t}}(\cdot )$ satisfies the following axioms:

• (A1) Convexity: $\rho _{{\mathscr {F}}_{t+1}|{\mathscr {F}}_{t}}(\alpha Z + (1-\alpha )W) \preceq \alpha \rho _{{\mathscr {F}}_{t+1}|{\mathscr {F}}_{t}} (Z) + (1-\alpha )\rho _{{\mathscr {F}}_{t+1}|{\mathscr {F}}_{t}}(W) \text { for all } Z,W \in {\mathscr {Z}}_{t+1} \text { and } \alpha \in [0,1]$,

• (A2) Monotonicity: $Z \preceq W \text { implies } \rho _{{\mathscr {F}}_{t+1}|{\mathscr {F}}_{t}}(Z) \preceq \rho _{{\mathscr {F}}_{t+1}|{\mathscr {F}}_{t}}(W) \text { for all } Z,W \in {\mathscr {Z}}_{t+1}$,

• (A3) Translational Equivariance: $\rho _{{\mathscr {F}}_{t+1}|{\mathscr {F}}_{t}}(Z + W) = \rho _{{\mathscr {F}}_{t+1}|{\mathscr {F}}_{t}}(Z) + W \text { for all } W \in {\mathscr {Z}}_{t} \text { and } Z \in {\mathscr {Z}}_{t+1}$,

• (A4) Positive Homogeneity: $\rho _{{\mathscr {F}}_{t+1}|{\mathscr {F}}_{t}}(tZ) = t\rho _{{\mathscr {F}}_{t+1}|{\mathscr {F}}_{t}}(Z) \text { for all } t > 0 \text { and } Z \in {\mathscr {Z}}_{t+1}$,

where $\preceq$ is the partial ordering defined on the corresponding space of random variables. The axioms (A1)–(A4) are first proposed by Artzner et al. (1999) for coherent measures of risk and later extended to conditional coherent measures of risk (see, for example, Ruszczyński and Shapiro (2006a) and references therein). As discussed by Ruszczyński and Shapiro (2006a), in order to quantify the risk involved in a cost sequence, a dynamic coherent risk measure$\rho _{1,T}: {\mathscr {Z}}_1 \times {\mathscr {Z}}_2 \times \cdots \times {\mathscr {Z}}_T \rightarrow {\mathbb {R}}$ is defined as

$$\begin{aligned} \rho _{1,T}(Z_1,Z_2,\ldots ,Z_T) := Z_1 + \rho _{{\mathscr {F}}_2|{\mathscr {F}}_1} \left( Z_2 + \cdots + \rho _{{\mathscr {F}}_T|{\mathscr {F}}_{T-1}} (Z_T) \cdots \right) , \end{aligned}$$

(2)

and hence the problem defined in (1) can be written as

$$\begin{aligned} \min \;&\rho _{1,T}(f_1(x_1),f_2(x_2,\xi _2),\dots ,f_T(x_T,\xi _T)) \nonumber \\ \text {s.t.} \;&x_1 \in {\mathscr {X}}_1, \nonumber \\&x_t \in {\mathscr {X}}_t(x_{t-1},\xi _t), \; \forall t \in \left\{ 2,\ldots ,T\right\} . \end{aligned}$$

(3)

In this paper, we focus on the case where $\rho _{{\mathscr {F}}_{t+1}|{\mathscr {F}}_{t}}$ is a conditional mean-CVaR risk measure for $t \in \{1,\ldots ,T-1\}$. The conditional mean-CVaR is defined as

$$\begin{aligned} \rho _{{\mathscr {F}}_{t+1}|{\mathscr {F}}_{t}}(Z_{t+1}) = (1-\varepsilon ){\mathbb {E}}[Z_{t+1}|{\mathscr {F}}_t] + \varepsilon \text{ CVaR }_\alpha (Z_{t+1}|{\mathscr {F}}_t), \end{aligned}$$

(4)

where

$$\begin{aligned} \text{ CVaR }_\alpha (Z_{t+1}|{\mathscr {F}}_t) = \inf _{\eta \in {\mathscr {Z}}_{t}}\left\{ \eta + \frac{1}{1-\alpha }{\mathbb {E}}[(Z_{t+1}-\eta )_+|{\mathscr {F}}_t]\right\} , \end{aligned}$$

is conditional CVaR defined with parameter $\alpha \in [0,1)$ and $\epsilon \in [0,1]$. In (4), mean-CVaR value of a random variable $Z_{t+1} \in {\mathscr {Z}}_{t+1}$ can be interpreted as a convex combination of its conditional expectation and conditional CVaR values. CVaR is first defined in Rockafellar and Uryasev (2000). A detailed discussion on mean-CVaR risk measure can be found in Ruszczyński and Shapiro (2006c).

If the sequence $\xi _1,\ldots ,\xi _T$ evolves as a discrete time stochastic process with finite support, then the whole process can be represented by a scenario tree with T stages. Let ${\mathscr {N}}$ and ${\mathscr {E}}$ be the set of nodes and edges of the scenario tree, respectively. Nodes at stage $t \in \{1,\ldots ,T\}$ correspond to possible realizations of the history until that stage. Let $\varOmega _t$ be the set of nodes at stage $t \in \{1,\ldots ,T\}$ and hence ${\mathscr {N}} = \bigcup _{t \in \{1,\ldots ,T\}} \varOmega _t$. At the first stage, there is only one node r called as the root node.

A scenario can also be defined as a unique path from the root node to a node in $\varOmega _T$. Let $p_{\omega }$ be the probability of scenario $\omega \in \varOmega$. Then, probability associated with node $n \in {\mathscr {N}}$ is $p_n = \sum _{\omega \in {\mathscr {P}}_n}p_\omega$ where ${\mathscr {P}}_n$ is the set of scenarios passing through node $n \in {\mathscr {N}}$. For the root node, we naturally have $p_r = 1$.

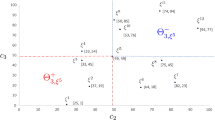
In the scenario tree representation, the sigma algebra ${\mathscr {F}}_T$ consists of all subsets of $\varOmega _T$. For every node $n \in {\mathscr {N}} \setminus \{r\}$ at stage t, there exists a unique ancestor node${\mathscr {A}}(n) \in \varOmega _{t-1}$ such that the edge $({\mathscr {A}}(n),n)$ is in ${\mathscr {E}}$. For each node $n \in {\mathscr {N}} \setminus \varOmega _T$, there exists a set of children nodes${\mathscr {C}}(n) = \{m \in \varOmega _{t+1}: {\mathscr {A}}(m) = n\}$ such that $\varOmega _{t+1} = \bigcup _{n \in \varOmega _t} {\mathscr {C}}(n)$. For $t \in \{1,\ldots ,T-1\}$, let ${\mathscr {F}}_t$ be the subalgebra of ${\mathscr {F}}_{t+1}$ generated by sets ${\mathscr {C}}(n)$ for all $n \in \varOmega _t$. Hence, there is a one-to-one correspondence between elementary events of ${\mathscr {F}}_{t}$ and nodes in the set $\varOmega _t$, for $t \in \{1,\ldots ,T\}$. By construction, we get the filtration ${\mathscr {F}}_1 \subset {\mathscr {F}}_2 \cdots \subset {\mathscr {F}}_T$. The aforementioned notation is depicted on an example of four-stage scenario tree in Fig. 2.

Fig. 2

A four-stage scenario tree

The number of decision variables in Problem (3) is proportional to the number of nodes $|{\mathscr {N}}|$ in the scenario tree. Since $|{\mathscr {N}}|$ grows exponentially with the number of stages for any non-trivial scenario tree, solving Problem (3) is computationally demanding for even small number of stages.

3 Lower bounds via scenario grouping

In this section, we present a lower bound for our problem by using scenario grouping. The scenario grouping idea is previously considered by Sandıkı and Özaltın (2017) and Mahmutoulları et al. (2018) in mixed-integer multi-stage stochastic problems. The proposed lower bound is used in the algorithm presented in the next section.

Recall the probability space $(\varOmega ,{\mathscr {F}},P)$ where $\varOmega$ is the sample space. A subset of scenarios $S \subseteq \varOmega$ is called as a group. Let ${\mathscr {S}} = \{S_j\}_{j=1}^J$ be a collection of groups that forms a partition of $\varOmega$, that is, $\bigcup _{j=1}^J S_j = \varOmega$ and $S_j \bigcap S{j'} = \emptyset$ for all $j,j' \in \{1,2,\ldots ,J\}$ such that $j \ne j'$. The empty intersection requirement can be relaxed (see, Sandıkı and Özaltın (2017), for example).

The total probability of scenarios in group $S_j$ is $p_j = \sum _{\omega \in S_j}p_{\omega }$ for $j \in \{1,\ldots ,J\}$. We also define conditional probability of scenario $\omega$ given that $\omega \in S_j$ as ${\widetilde{p}}_\omega = p_\omega / p_j$ and ${\widetilde{P}}$ as the probability distribution defined by these conditional probabilities on the sample space $S_j$.

We define jth group subproblem as problem (3) which is defined on the probability space $(S_j,\widetilde{{\mathscr {F}}},{\widetilde{P}})$ where $\widetilde{{\mathscr {F}}}$ is the sigma algebra generated by $S_j$.

Proposition 1

Let $z_j$ be the optimal value of jth group subproblem. Then, $\sum _{j=1}^J p_jz_j$ is a lower bound for the optimal value of (3).

Proof

See Theorem 1 in Mahmutoulları et al. (2018).$\square$

In this paper, we develop another lower bound obtained from scenario grouping.

Proposition 2

Let ${\tilde{z}}_j$ be the optimal value of jth group subproblem in which integrality requirements for the decision variables at stages $t \in \{2,3,\ldots ,T\}$ are relaxed. Then $\sum _{j=1}^J p_j{\tilde{z}}_j$ is a lower bound for the optimal value z of (3).

Proof

Due to Proposition 1, we have $z \ge \sum _{j=1}^J p_jz_j$. Since, $z_j \ge {\tilde{z}}_j$ for all $j \in \{1,2,\ldots ,J\}$, we get $z \ge \sum _{j=1}^J p_jz_j \ge \sum _{j=1}^J p_j{\tilde{z}}_j$. $\square$

Note that the lower bound in Proposition 2 is no stronger than the lower bound in Proposition 1. However, calculating the lower bound in Proposition 2 is computationally easier since it requires solving group problems without integrality requirements for the decision variables at stages $t \in \{2,3,\ldots ,T\}$. Hence, the latter lower bound is used in the proposed algorithm.

Scenario grouping significantly reduces the computational effort required to solve the risk-averse mixed-integer multi-stage programming problem (3). Figure 3 illustrates the scenario trees of group subproblems obtained via scenario grouping. The scenarios of the original problem are placed in groups $S_1, S_2$ and $S_3$ and indicated by colors red, green and blue, respectively.

Fig. 3

A four-stage scenario tree and the new scenario trees used in group subproblems

4 An exact solution algorithm for the problems with binary first stage variables

In this section, extending the idea in Ahmed (2013), we propose an exact solution algorithm for the risk-averse mixed-integer multi-stage stochastic programming problem (3) with binary first stage variables, that is, ${\mathscr {X}}_1 \subseteq \{0,1\}^{M_1}$ and $K_1 = L_1 = 0$.

The proposed algorithm stores a set ${\mathscr {D}} \subseteq {\mathscr {X}}_1$ of candidate first stage solutions and an incumbent first stage solution $x^*_1 \in {\mathscr {D}}$ through execution. If a candidate first stage solution $x'_1 \in {\mathscr {D}}$ is a feasible first stage solution for problem (3), then solving (3) with constraint $x_1 = x'_1$ gives an upper bound for the optimal value of (3). The incumbent solution $x^*_1$ is the first stage solution which yields the smallest upper bound value among all candidate solutions in ${\mathscr {D}}$.

For a given scenario partition, a socalled lower bound is obtained on the optimal value of (3) by applying scenario grouping for (3) with first stage feasibility set ${\mathscr {X}}_1 \setminus {\mathscr {D}}$. Note that, this is not necessarily a lower bound for the original problem (3) since some feasible first stage solutions are eliminated from ${\mathscr {X}}_1$. At each iteration, if this lower bound is smaller than the objective value given by $x_1^*$, then the algorithm adds the new candidate solutions to set ${\mathscr {D}}$; otherwise, the algorithm terminates.

Since we assume that all first stage decision variables are binary, extraction of the candidate first stage solutions in ${\mathscr {D}}$ from ${\mathscr {X}}_1$, that is obtaining the set ${\mathscr {X}}_1 \setminus {\mathscr {D}}$, can be done by using no-good cuts. A no-good cut separates a specific binary vector from a set. Specifically, a no-good cut for binary vector $x'_{1}$ is of the form

$$\begin{aligned} \sum _{i:x'_{1i}=1}(1-{x_1}_i) + \sum _{i:x'_{1i} = 0}{x_1}_i \ge 1, \end{aligned}$$

where $x_{1i}$ and $x'_{1i}$ correspond to the ith component of vectors $x_1$ and $x'_1$, respectively (see, for example, DAmbrosio et al. 2010). Then we have,

$$\begin{aligned} {\mathscr {X}}_1 \setminus {\mathscr {D}} = \left\{ x_1 \in {\mathscr {X}}_1: \sum _{i:x'_{1i}=1}(1-{x_1}_i) + \sum _{i:x'_{1i} = 0}{x_1}_i \ge 1, ~\forall x'_1 \in {\mathscr {D}} \right\} . \end{aligned}$$

The overall scheme of the proposed algorithm is an evaluate-and-cut procedure presented in Algorithm 1.

Proposition 3

Algorithm 1 terminates after a finite number of iterations finding an optimal solution if problem (3) is feasible and has finite optimal value or with declaration of infeasibility if (3) is infeasible.

Proof

At the lower bounding phase of each iteration of the algorithm, at least one first stage solution is removed from ${\mathscr {X}}_1$ and added to ${\mathscr {D}}$ or the algorithm terminates directly. Also since ${\mathscr {X}}_1 \subseteq \{0,1\}^{M_1}$, the cardinality of ${\mathscr {X}}_1$ is finite. Therefore, the algorithm terminates after a finite number of iterations. Consider the following two cases:

• (a) Problem (3) is feasible and has finite optimal value: Let $z^*({\mathscr {X}}_1)$ be the optimal value of problem (3) as a function of the first stage feasibility set ${\mathscr {X}}_1$. Since, the cardinality of ${\mathscr {X}}_1$ is finite, we have

  $$\begin{aligned} z^*({\mathscr {X}}_1) = \min \left\{ z^*({\mathscr {D}}), z^*({\mathscr {X}}_1 \setminus {\mathscr {D}}) \right\} \end{aligned}$$

  (5)

  at any iteration of the algorithm. For an incumbent solution $x^*_1 \in {\mathscr {D}}$, we also have $UB = z^*(\{x_1^*\}) = z^*({\mathscr {D}})$ and $LB \le z^*({\mathscr {X}}_1 \setminus {\mathscr {D}})$ due to definitions of upper and lower bounds used in the algorithm. When the algorithm terminates with $UB \le LB$, the incumbent first stage solution guarantees $z^*(\{x_1^*\}) = z^*({\mathscr {D}}) = UB \le LB \le z^*({\mathscr {X}}_1 \setminus {\mathscr {D}})$. Hence, using (5), we get $z^*({\mathscr {X}}_1) = z^*(\{x_1^*\})$ and therefore $x_1^*$ is an optimal first stage solution of problem (3).

• (b) Problem (3) is infeasible: If the problem is infeasible, UB never takes a finite value since none of the problems in upper bounding phase is feasible. Then, at the end of the algorithm, the incumbent is null and UB is positive infinity.

$\square$

If each group includes only one scenario, the proposed algorithm is a scenario decomposition algorithm where the non-anticipativity in all stages is completely relaxed. However, the proposed algorithm allows to obtain stronger lower bounds by partially maintaining non-anticipativity due to scenario grouping.

Another important property of Algorithm 1 is decomposition of the problem in the upper bounding phase. When the first stage decisions are fixed to $x'_1$ in the original problem, the resulting problem decomposes into $|\varOmega _2|$ smaller problems. These smaller problems are risk-averse mixed-integer multi-stage problems with $T-1$ stages. Therefore, we benefit from decomposition of the original problem in both lower and upper bounding phases of Algorithm 1.

In the next section, we show that the proposed algorithm can be used to solve the risk-averse mixed-integer multi-stage stochastic programming problems where the first stage decisions are mixed-integer as well.

5 Extension to the general risk-averse mixed-integer multi-stage stochastic programming problems

Although the proposed algorithm guarantees an exact solution for risk-averse mixed-integer multi-stage stochastic programming problems with a dynamic mean-CVaR objective function and binary first stage variables, it can be used for the general case, where the first stage decision variables are not necessarily pure binary. Let $Q(x_1)$ be the risk adjusted cost-to-go function depending on the first stage solution $x_1$, that is,

$$\begin{aligned} Q(x_1):= & {} \rho _{{\mathscr {F}}_2|{\mathscr {F}}_1} \left( \underset{x_2 \in {\mathscr {X}}_2(x_1,\xi _2)}{\min } f_2(x_2,\xi _2) + \cdots \right. \nonumber \\&\left. + \rho _{{\mathscr {F}}_{T}|{\mathscr {F}}_{T-1}}\left( \underset{x_T \in {\mathscr {X}}_T(x_{T-1},\xi _{T})}{\min } f_T(x_T,\xi _T)\right) \cdots \right) . \end{aligned}$$

(6)

Then, the general risk-averse mixed-integer multi-stage stochastic programming problem can be written as

$$\begin{aligned} \min \;&f_1(x_1) + Q(x_1) \nonumber \\ \text {s.t.} \;&x_1 = (r_1 ; y_1; b_1) \in {\mathscr {X}}_1, \nonumber \\&r_1 = (r_{11},r_{12},\ldots ,r_{1K_1}) \in {\varvec{R}} \subseteq {\mathbb {R}}_+^{K_1}, \nonumber \\&y_1 = (y_{11},y_{12},\ldots ,y_{1L_1}) \in {\varvec{Z}} \subseteq {\mathbb {Z}}_+^{L_1}, \nonumber \\&b_1 = (b_{11},b_{12},\ldots ,b_{1M_1}) \in {\varvec{B}} \subseteq \{0,1\}^{M_1}, \end{aligned}$$

(7)

where $r_1, y_1,$ and $b_1$ represent continuous, integer and binary decision vectors in the first stage, respectively and $x_1$ represents the concatenate vector of first stage variables. Recall that we have already assumed the decisions at stages $2,3,\ldots ,T$ are mixed-integer.

Recently, Zou et al. (2017) show that, under some reasonable assumptions, any risk-neutral mixed-integer stochastic problems with mixed-integer state variables can be approximated by binarizing the state variables. In our context, we only consider binarizing the first stage integer variables. Following the similar arguments presented by Glover (1975) and Zou et al. (2017), we can solve the general mixed-integer problem (7) by using binary representation of the integer first stage variables $y_1$.

Assumption 1

The first stage integer variables in the general mixed-integer problem (7) are bounded.

Assumption 1 holds for the most real life problems and ensures that there exists a non-negative real number U such that $y_{1l} \le U$ for all $l\in \{1,2,\ldots ,L_1\}$. For each $l \in \{1,2,\ldots ,L_1\}$, $y_{1l} = \sum _{i=0}^{\tau } 2^i \gamma _{1li}$ is an exact representation of $y_{1l}$ with binary variables $\gamma _{1li}$, $i \in \{0,1,\ldots ,\tau \}$ and $\tau = \left\lfloor \log _2 U \right\rfloor$. Thus, the general mixed-integer problem (7) can be written as

$$\begin{aligned} \min \;&f_1(x_1) + Q(x_1) \nonumber \\ \text {s.t.} \;&x_1 = (r_1 ; A (\varGamma ); b_1) \in {\mathscr {X}}_1, \nonumber \\&r_1 \in {\varvec{R}}, A (\varGamma ) \in {\varvec{Z}}, \varGamma \in \{0,1\}^{L_1 \times (\tau +1)}, b_1 \in {\varvec{B}}, \end{aligned}$$

(8)

where $A: \{0,1\}^{L_1 \times (\tau +1)} \rightarrow {\mathbb {Z}}_+^{L_1}$ is a linear mapping that restores $y_{1}$ from binary variables $\varGamma$.

We can employ Algorithm 1 to solve (8) where the evaluate-and-cut procedure is applied only to the first stage binary variables. Unlike the case where the first stage variables are pure binary, the continuous variables in the first stage prohibit decomposition in the upper bounding phase of the algorithm. However, the computational results in Sect. 6.2 reveal that the proposed algorithm efficiently solves the general mixed-integer problem though decomposition is possible only in the lower bounding phase.

6 Computational experiments

In this section, we present the results of the computational experiments conducted on risk-averse multi-stage stochastic server location problem (SSLP) and generation expansion problem (GEP). In risk-averse multi-stage SSLP, the first stage decision variables are pure binary. Therefore, Algorithm 1 is directly applied to the problem. However, in risk-averse GEP, the first stage variables are mixed-integer and hence we use the extension presented in Sect. 5 to solve these problems.

In our experiments, we use different degrees of risk aversion (DRA) by changing the values of the parameters of conditional mean-CVaR risk measure (4). These values are presented in Table 1.

Table 1 The degrees of risk aversion used in computational experiments

The computational experiments are performed on an Intel(R) Core(TM) i7-4790 CPU@3.60 GHz computer with 8.00 GB of RAM. The algorithm is implemented on Java 1.8.0.31 where IBM ILOG CPLEX version 12.6 with default settings is used to solve optimization problems. For each test problem, five instances are generated randomly and average values are reported. The performance of the proposed algorithm is compared to deterministic equivalent problem (DEP) of same instances.

6.1 Stochastic server location problem

SSLP is a popular two-stage risk-neutral stochastic programming problem in the literature. The motivation and detailed discussion on SSLP can be found in Ntaimo and Sen (2005). An instance of SSLP is available in SIPLIB library at http://www2.isye.gatech.edu/~sahmed/siplib. In our experiments, we use a risk-averse and multi-stage version of SSLP.

The statement of risk-averse multi-stage SSLP is as follows: In a T-stage decision horizon, the objective is to determine the location of servers on a set of potential nodes of a given network so as to minimize the dynamic coherent risk defined in (2) where we use conditional mean-CVaR risk measure with parameters $\epsilon$ and $\alpha$ at each stage.

Servers can be located on M different potential server location nodes. There is a fixed cost $c_m$ of locating a server at node $m \in \{1,2,\ldots ,M\}$. There are V different clients, whose demands at stage $t \in \{2,3,\ldots ,T\}$ should be satisfied by one of the located servers. Let $d_{vm}^t$ be the demand of client v if it is served by the server located at m at stage t. One unit of profit is obtained for each unit of served demand. The service capacity of a server is u. If the capacity is not enough to serve all demands, a unit of demand can be served by the server located at m by an overcapacity serving cost $q_{m}^t$ at stage t. A client may or may not appear under each scenario independently from other clients. Under each scenario, a client may appear at a stage with probability 0.5. Let $h_{v}^t(\omega ) = 1$ if client v appears at stage t under scenario $\omega$, and 0, otherwise. Let $h^t$ be an ${\mathscr {F}}_t$-measurable random vector whose components are $h_{v}^t$ with $P\{h_{v}^t = 1\} = P\{h_{v}^t = 0\} =0.5$.

Location decisions are made at the first stage. Therefore, fixed cost due to server location decisions is incurred in the first stage. The allocation decisions are made at subsequent stages $t \in \{2,3,\ldots ,T\}$. At stage t, the random cost is the total service cost at stage t. The DEP of risk-averse multi-stage SSLP can be modeled by using parameters and decision variables for each node of the scenario tree. Moreover, linearization of mean-CVaR risk measure is possible by defining additional auxiliary variables and constraints (see, for example, Mahmutoulları et al. 2018).

As an example, the DEP of the risk-averse three-stage SSLP is given below which can be extended for larger number of stages easily. In the below model, a superscript n or $n'$ indicates that the corresponding parameter or decision variable is defined for node $n \in \varOmega _2$ or $n' \in \varOmega _3$ of the scenario tree, respectively.

$$\begin{aligned} \min \;&\sum _{m=1}^{M}c_m z_m + (1-\varepsilon ) \sum _{n \in \varOmega _2}p_n\widetilde{Z}^n_2 \nonumber \\&+ \varepsilon \left( \eta _1 +\frac{1}{1-\alpha }\sum _{n \in \varOmega _2}p_n\varphi ^n_2\right) , \end{aligned}$$

(9)

$$\begin{aligned} \text {s.t.} \;&\widetilde{Z}^n_2 = \sum _{m=1}^M \left( \sum _{v=1}^V -d_{vm}^{2n}y_{vm}^{2n} + q_m^{2n}o_m^{2n}\right) + (1-\varepsilon ) \sum _{n' \in \mathscr {C}(n)}\frac{p_{n'}}{p_n}\widetilde{Z}^{n'}_3 \nonumber \\&\quad \qquad +\varepsilon \left( \eta _2^n + \frac{1}{1-\alpha }\sum _{n' \in \mathscr {C}(n)}\frac{p_{n'}}{p_n}\varphi ^{n'}_3\right) , \quad \forall n \in \varOmega _2, \end{aligned}$$

(10)

$$\begin{aligned}&\widetilde{Z}^{n'}_3 = \sum _{m=1}^M \left( \sum _{v=1}^V -d_{vm}^{3n'}y_{vm}^{3n'} + q_m^{3n'}o_m^{3n'}\right) , \quad \forall n' \in \varOmega _3, \end{aligned}$$

(11)

$$\begin{aligned}&\varphi ^{n}_2 \ge \widetilde{Z}^{n}_2 - \eta _1, \quad \forall n \in \varOmega _2, \end{aligned}$$

(12)

$$\begin{aligned}&\varphi ^{n'}_3 \ge \widetilde{Z}^{n'}_3 - \eta _2^n, \quad \forall n \in \varOmega _2, n' \in \mathscr {C}(n), \end{aligned}$$

(13)

$$\begin{aligned}&\sum _{v=1}^{V} d^{tn}_{vm} y^{tn}_{vm} \le u z_m + o^{tn}_m, \quad \forall m \in \{1,2,\ldots ,M\}, n \in \varOmega _t, t \in \{2,3\}, \end{aligned}$$

(14)

$$\begin{aligned}&\sum _{m=1}^{M} y^{tn}_{vm} = h_v^{tn}, \quad \forall v \in \{1,2,\ldots ,V\}, n \in \varOmega _t, t \in \{2,3\}, \end{aligned}$$

(15)

$$\begin{aligned}&z_m\in \{0,1\}, y^{tn}_{vm} \in \{0,1\} , o^{tn}_{m}\ge 0, \nonumber \\&\quad \forall m \in \{1,2,\ldots ,M\}, v \in \{1,2,\ldots ,V\}, n \in \varOmega _t, t \in \{2,3\}, \end{aligned}$$

(16)

$$\begin{aligned}&\widetilde{Z}_t^{n}, \varphi _t^{n}\ge 0, \quad \forall n \in \varOmega _t, t \in \{2,3\}, \end{aligned}$$

(17)

$$\begin{aligned}&\eta _1, \eta _2^n \in \mathbb {R}, \quad \forall n \in \varOmega _2, \end{aligned}$$

(18)

where $z_m$ takes value 1 if a server is located on node m and 0 otherwise, $y^{tn}_{vm}$ takes value 1 if client v is served by a server located on node m for $n \in \varOmega _t$ at stage t and 0 otherwise, and $o^{tn}_m$ is the over capacity used by server m for the node $n \in \varOmega _t$ at stage t.

Table 2 Problem statistics for risk-averse multi-stage SSLP instances

The objective function (9) and constraints (10)–(13) linearize the dynamic coherent risk measure (2) defined by mean-CVaR at each stage. The constraints (14) and (15) are capacity and allocation constraints, respectively. The variables in (16) are the original problem variables. The auxiliary variables in (17) are used to linearize the mean-CVaR risk measure. Finally, variables in (18) are due to definition of mean-CVaR.

A test problem of risk-averse multi-stage SSLP is represented as T-SSLP-M-V-b where T is the number of stages, M is the number of potential server location nodes, V is the number of clients and b is the number of different values that the random vector $h^t$ can take at stage t. Therefore, the number of scenarios in T-SSLP-M-V-b is $b^{T-1}$. Similar to Ntaimo and Sen (2005), the problem parameters are selected as $c_m \sim {\mathscr {U}}[40,80], d_{vm}^t \sim {\mathscr {U}}[0,25], u = 2\frac{\sum _{v=1}^{V} \max _{m,n,t} d_{vm}^{tn}}{M}$, and $q_{m}^t=1000$. Here, $~{\mathscr {U}}[a,b]$ indicates that the respective value is sampled form the uniform distribution with range [a, b]. Problem statistics for risk-averse multi-stage SSLP instances used in the experiments are presented in Table 2.

In the proposed algorithm, for each instance of all problems presented in Table 2, we consider a partition with two groups with equal cardinalities, that is, ${\mathscr {S}} = \{S_1,S_2\}$ with $|S_1| = |S_2|$. The partitions are constructed in three different ways by using the scenario tree structure or randomly. In similar partition, the groups are generated by placing the scenarios with large number of common nodes in the scenario tree into the same group. However, in different partition, we place the scenarios with small number of common nodes into the same group. Finally, in random partition, the scenarios are assigned to the groups randomly. Note that for two-stage problems, all partitioning strategies are equivalent since the locations of nodes in the second stage of the scenario tree are interchangeable. For a deeper discussion on the construction of partitions and their impact on the quality of bounds, we refer to Bakır et al. (2016) and Mahmutoulları et al. (2018) where various extensions on scenario grouping are considered. However, as seen in the results of our computational experiments, using a simple scenario grouping strategy is adequate for the proposed algorithm. Figure 4 depicts the three different scenario partitions we consider on a three-stage scenario tree.

Fig. 4

The partitions similar, different and random (from left to right, respectively) for a three-stage scenario tree where each color represents a group

In Table 3, we report the number of instances solved optimally (# opt out of five), average optimality gap (Gap) and solution time in seconds (Time) for DEP. Two hours of time limit is imposed when solving DEP of each instance. We also report the average number of iterations (# iter) and running time in seconds (Time) for the proposed algorithm with the three different partitions we consider. Note that, all reported values are averages for five instances of each problem.

Table 3 Computational study results for risk-averse multi-stage SSLP

The computational experiments reveal that as problem size grows, CPLEX fails to solve DEPs of the problem instances. For example, the problems 2-SSLP-10-50-2000 and 3-SSLP-10-50-50 have over one million binary variables, none of the DEPs are solved optimally within two hours of time limit for any value of DRA. Especially, 3-SSLP-10-50-50 instances terminate with large optimality gap values (59.11%, 85.64% and 27.91%, for DRA I, II, and III, respectively). However, the proposed algorithm solves all of these instances optimally in less than two hours with at least one of the three partitions we consider.

In Table 3, the bold entries are the smallest running times among the three different partitions for each problem. Moreover, in the last row of the table, for each partitioning strategy, we present the percentage of test problems in which this strategy performs better than the other ones. When the three partitioning strategies are compared in the two-stage problems, no significant difference is observed as expected. However, for three- and four-stage problems, the similar partition performs better than different and random partitions. Since each group subproblems obtained by the similar partition includes scenarios with many common nodes of the scenario tree, these group subproblems have less complicated structure than the ones obtained by other partitions. Hence, in the lower bounding phase of the proposed algorithm, the similar partition yields group subproblems that are easier to solve. On the other hand, the lower bounds and candidate solutions provided by different partition are expected to be better than the ones given by similar partition. Overall, similar is the best scenario partition choice among all partitions in 47.06% of all instances. This value is 37.25% and 15.69% for different and random partitions, respectively.

When we analyze the test problem 4-SSLP-5-25-20 at DRA I, it is observed that CPLEX could only solve 2 out of 5 DEP instances optimally within the time limit and the average optimality gap is 10.36%. On the other hand, our algorithm could solve all of the five instances optimally and the average computation time of our proposed algorithm is 1830.9, 2539.3 and 2795.1 s for the similar, different and random partitions, respectively. We observe similar results for the test problem 4-SSLP-5-25-20 at DRA II as well. CPLEX could only solve 3 out of 5 DEP optimally within the time limit of 7200 s. The average gap is 3.37% for those instances. We again could solve all of the five instances optimally and the average computation time of our proposed algorithm is 1205.5, 1849.1 and 1957.0 s for the similar, different and random partitions, respectively.

Although the proposed algorithm with the simplest choice of the number of groups $J=2$ enables us to solve the large scale instances efficiently, we also investigate the performance of the algorithm by changing the value of J. As the number of groups J increases, the number of scenarios per group subproblem decreases. In that case, it can be expected that the group subproblems are easier to solve and hence the running time of Algorithm 1 decreases with the number of groups J.

In Fig. 5, we present the average running time of the proposed algorithm in seconds with respect to different number of groups $J \in \{2,4,8,16,32,64,128,256\}$ for five instances of 3-SSLP-5-25-16 problem with different degrees of risk-aversion and partitions.

Fig. 5

Average running time (in seconds) of the proposed algorithm with respect to different number of groups for five instances of 3-SSLP-5-25-16 problem with different degrees of risk-aversion and partitions

Since the total number of scenarios in 3-SSLP-5-25-16 instances is 256, the number of scenarios in a group subproblem is 128, 64, 32, 16, 8, 4, 2 and 1 for the respective values 2, 4, 8, 16, 32, 64, 128 and 256 of J. Although it may be expected that the running time of Algorithm 1 decreases with increasing number of groups J, we observe the contrary in the results of our experiments in general. There can be two reasons of this. First, in the upper bounding phase, the algorithm requires evaluation of each candidate solution in ${\mathscr {D}}$. When the number of group subproblems is large, we can expect the cardinality of the set ${\mathscr {D}}$ to be large as well. Therefore, large values of J may yield evaluation of upper bound values for large number of candidate solutions. The second reason is that a larger number of groups J yields looser lower bounds and therefore the running time of the algorithm increases. In the extreme case of $J=256$, the performance of the proposed algorithm is the worst compared to the other values of J. Note that this result motivates to use scenario grouping instead of pure scenario decomposition. Nonetheless, increasing the J value can still be beneficial for some instances as shown in Fig. 5. For example, for the instances with DRA I and different partition, the running time decreases as J increases from 2 through 8.

6.2 Generation expansion problem

The generation expansion problem (GEP) is an optimization problem that appears in power systems. The objective of GEP is to minimize the total cost due to construction and generation decisions for different types of generators over a fixed-length decision horizon. We use the mathematical model used in Zou et al. (2017) where the problem data are adopted from Jin et al. (2011).

In the deterministic version of the problem, the power demand at stage $t \in \{1,\ldots ,T\}$ is given as $d_t$ and it is assumed that I types of power generators are available.The fixed construction and unit production costs of a type $i \in \{1,\ldots ,I\}$ generator are $a_{i}$ and $b_{i}$, respectively. There is a limit $u_i$ on the total number of type i generators constructed over the decision horizon. Moreover, the production amount of a type i generator cannot exceed $U_i$. The deterministic GEP is given as

$$\begin{aligned} \min \;&\sum _{t=1}^{T}\sum _{i=1}^{I} \left( a_{i}z_{ti} + b_{i}y_{ti}\right) , \end{aligned}$$

(19)

$$\begin{aligned} \text {s.t.} \;&y_{ti} \le \left( \sum _{\tau =1}^{t} z_{\tau i}\right) U_i, \quad \forall i \in \{1,\ldots ,I\}, t \in \{1,\ldots ,T\}, \end{aligned}$$

(20)

$$\begin{aligned}&\sum _{t=1}^{T} z_{ti} \le u_i , \quad \forall i \in \{1,\ldots ,I\}, \end{aligned}$$

(21)

$$\begin{aligned}&\sum _{i=1}^{I} y_{ti} \ge d_t , \quad \forall i \in \{1,\ldots ,I\}, \end{aligned}$$

(22)

$$\begin{aligned}&y_{ti} \ge 0, \quad z_{ti} \in \mathbb {Z}_+, \quad \forall i \in \{1,\ldots ,I\}, t \in \{1,\ldots ,T\}, \end{aligned}$$

(23)

where $z_{ti}$ is the number of generators of type $i \in \{1,\ldots ,I\}$ constructed at stage $t \in \{1,\ldots ,T\}$ and $y_{ti}$ is the total production amount of type i generators at stage t. The objective function (19) is the sum of construction and production costs over T stages. Constraints (20) and (21) ensure that the production schedule is feasible. The demand satisfaction is ensured in constraint (22). Domain restrictions are given in constraint (23).

We consider a risk-averse version of GEP where the demand at stages $t=2,\ldots ,T$ is random. The objective of risk-averse GEP is to determine the number of generators to be constructed and production amounts for each type of generators so as to minimize the dynamic coherent risk defined in (2) with conditional mean-CVaR at each stage. The DEP of risk-averse GEP can be obtained easily by defining additional variables and constraints similar to DEP (9)–(18) of SSLP.

A test problem of risk-averse GEP is represented as T-GEP-b where T is the number of stages and b is the number of different values that the random demand $d_t$ can take at each stage $t \in \{2,\ldots ,T\}$. Problem statistics for the risk-averse GEP instances used in the experiments are given in Table 4.

Table 4 Problem statistics for risk-averse GEP instances

The deterministic problem parameters are given in Table 5. We assume that the first stage demand is $d_1 = D/2$ and the demand at stages $t \in \{2,\ldots ,T\}$ is $d_t \sim U[D/4,3D/4]$ where D is the total production capacity, that is, $D = \sum _{i=1}^I U_i u_i$.

Table 5 Parameters of GEP instances

Since both integer and continuous variables appear in all stages of GEP, we can use the extension of the proposed method presented in Sect. 5 to solve risk-averse GEP. Therefore, we binarize the integer variables in the first stage of GEP and perform the evaluate-and-cut procedure in Algorithm 1 for only these variables. In this case, the problem in the upper bounding phase of the algorithm does not enjoy decomposition.

In computational experiments on GEP instances, we consider similar partition with $J=2$ and 4 where cardinalities of the groups of a partition are the same. In Table 6, we report the number of instances solved optimally (# opt out of five) and solution time in seconds (Time) for DEP. Four hours of time limit is imposed when solving DEP of each instance. We also report the average number of iterations (# iter) and running time in seconds (Time) of the proposed algorithm for $J=2$ and 4. As before, all reported values are averages of five instances of each test problem.

Table 6 Computational study results for risk-averse GEP

For small instances such as 3-GEP-10, 3-GEP-20, 3-GEP-40, 4-GEP-10 and 4-GEP-20 solution time of DEP is less than the running time of the algorithm for all degrees of risk aversion. For a moderate instance 3-GEP-100, the algorithm with $J=2$ outperforms solving DEP for DRA I and II. For the largest instance, namely 4-GEP-50, CPLEX either does not report any feasible solution of DEP within the time limit or terminates with memory error before four hours. The algorithm with $J=2$ also does not terminate for these instances in four hours. However, the algorithm with $J=4$ solves all 4-GEP-50 instances in 11,089.7, 11,188.5 and 12,850.2 s for DRA I, II and III, respectively. Although $J=2$ is a better choice for small and moderate instances, for larger instances $J=4$ yields better results.

The results of the computational experiments on risk-averse multi-stage SSLP and GEP demonstrate the effectiveness of our proposed algorithm. They also verify our initial claim that it is an easily implementable exact solution algorithm for risk-averse mixed-integer multi-stage stochastic problems with an objective of dynamic mean-CVaR and binary first stage decisions. Although, in GEP, we partially binarize the first stage variables and do not benefit decomposition in the upper bounding phase, the algorithm is able to solve large instances of this problem.

7 Conclusion and possible future extensions

Risk-averse mixed-integer multi-stage stochastic programming problems form a class of challenging large scale and non-convex optimization problems. Moreover, no exact solution algorithm is available for these problems in the literature. In this paper, we propose an exact solution algorithm for risk-averse mixed-integer multi-stage stochastic programming problems with an objective of dynamic mean-CVaR risk measure and binary first stage decisions. Later, we prove that the algorithm can be used to solve the general risk-averse mixed-integer multi-stage stochastic programming problems.

The proposed algorithm is based on an evaluate-and-cut procedure and a simple scenario tree decomposition method. The computational experiments on large instances of risk-averse multi-stage SSLP reveal that the proposed algorithm requires significantly less computational effort than solving the deterministic equivalent problem with CPLEX. Moreover, an extension of the proposed method is used to solve large instances of risk-averse GEP where mixed-integer decisions appear in all stages. We also discuss the effect of implementation details, such as partitioning strategy and number of groups in a partition, on the performance of the algorithm.

Since we did not make any structural assumptions on the problem structure such as complete or relative recourse, stage-wise independency, convexity, and linearity of feasibility constraints, our proposed algorithm could be applied to a wide range of problems.

A parallel implementation of the proposed algorithm may decrease computation time significantly. In lower bounding phase of the algorithm, group subproblems can be solved in parallel since they share no information. Similarly, candidate first stage solutions can be evaluated in the upper bounding phase in parallel. Therefore, it can be possible to solve existing instances in smaller computation time or larger instances can be solved.