1 Introduction

Anecdotal and empirical evidence indicates that global warming is directly related to emissions of carbon and other greenhouse gases (Zhang and Xu 2013; Zhang and Hao 2017; Li et al. 2017). Many countries have tried to control carbon emissions through the cap-and-trade system, such as the Chinese centralized carbon trading system.Footnote 1 In practice, this system has generally been regarded as one of the most effective tools for controlling emissions (Betsill and Hoffmann 2011; Dormady 2014; Tang et al. 2015). The China Beijing Environment ExchangeFootnote 2 (CBEE), one of the earliest established environment exchanges in China, has adopted the cap-and-trade system since 2015 to control emissions. Under the cap-and-trade system, a certain number of emission permits are allocated by the CBEE to each emitter via an allocation mechanism. This process is called the initial allocation of emission permits (AEP) (Chen et al. 2016). After their initial allocation, emission permits are viewed as the wealth of enterprises since they can be traded on the market as valuable commodities. Real cases can be found in the carbon emission permits trading of the CBEE,Footnote 3 the U.S. sulfur dioxide trade system (Schmalensee et al. 1998), and the European Union Emissions Trading Scheme (Ellerman and Buchner 2007). More specifically, if a firm fails to achieve its emission reduction targets and the assigned emission permits are insufficient, it can buy extra permits in the CBEE via the emission trading mechanism for further production. If a firm over-meets its emission reduction targets and ends up with extra emission permits, it can also sell these redundant permits in the CBEE through the emission trading mechanism. This emission trading process is referred to as the re-allocation of emission permits (RAEP) (Sun et al. 2014).

In practice, the CBEE applied the simple methods for RAEP, such as pricing transaction and bidding methods. In the pricing transaction method, a buyer (or seller) proposes a price for an emission permit, and then a buyer and sellers (or a seller and buyers) trade the emission permits in accordance with this proposed price. Sun (2014) pointed out that it was very difficult to set a reasonable price for emission rights. A high trading price would greatly increase production cost of firms, and further reduce the number of firms involved in emissions trading. In contrast, a low trading price would lead to a loss of control over pollution emissions. In the bidding method, a seller (or buyer) usually discloses his bid price as well as maximizing the possible emissions trading volume. Then, buyers (or sellers) participate in the bidding. Finally, the exchange determines the winners based on their bid prices. In fact, this bidding method is a one-sided auction method. In one-sided auctions, one party (one buyer or one seller) holds the information advantage (e.g. knowledge of the bidding information of other participants), while the other parties are merely passive receivers. This may result in fewer final traders and consequently lower trading efficiencies (Pesendorfer 2000; Guan et al. 2001). With regard to the above analysis, it has been noted that the RAEP methods applied by the CBEE are controversial and suffer from the lack of a universally acknowledged RAEP scheme.

Extensive studies have been conducted on the initial AEP process. The initial AEP has been successfully applied to the SO2 trading system in the USA (Ackerman and Moomaw 1997), the US NOx trade system (Cason and Gangadharan 2003), and the European Union Emissions Trading Scheme (EU ETS) (Boutabba and Lardic 2017). The existing methods for AEP can be classified into two categories. One is free allocation. Free allocation methods mainly include grandfathering, output-based allocation and data envelopment analysis (DEA) (Sun et al. 2014). These free allocation methods are widely utilized for AEP on account of their feasibility and simplicity of implementation. Nevertheless, there exist some deficiencies in free allocation methods. For example, Hu et al. (2016) mentioned that the outcomes of AEP are dependent on the private information that each participant provides, such as historical emissions (Böhringer and Lange 2005; Wei et al. 2014). However, the authenticity and reliability of such private information cannot be guaranteed, thus limiting the utilization of free allocation. Furthermore, free allocation methods may result in the occurrence of corruption and embezzlement (Wang et al. 2016).

The other type of AEP is the auctioning method. Compared to the free allocation method, auctioning carries several significant advantages. First, Goeree et al. (2010) experimentally proved that auctioning may result in slightly lower product prices and higher consumer welfare, which was more favorable to low emitters. They also concluded that the main role of auctioning is that the windfall profits of enterprises with higher emissions be transferred to the government. In addition, auctioning can effectively avoid the occurrence of corruption and embezzlement since it is a market-driven approach (Dormady 2014).

Compared to AEP methods, so far, few theoretical models have been developed for RAEP (which is also called emission permits trading); therefore, a strong demand for further research exists, especially for a feasible design of an effective re-allocation mechanism for emission permits (Sun et al. 2014; Ji et al. 2017a, b). The purpose of this paper is to design a workable RAEP mechanism based on auction method for the CBEE. In the process of RAEP, there are multiple emission buyers and multiple emission sellers. Therefore, the double auction method would be appropriate. Specifically, this paper firstly proposes an optimization method for helping firms to determine their supply/demand volume of emission permits. Then, the double auction model for RAEP is designed based on the principle of maximizing the total social welfare utility. We consider three scenarios in the double auction based on the balance between supply and demand of the emission permits. For each scenario, the matching trading rule is proposed. Finally, the validity and practicability of the proposed double auction model and matching trading rules are verified by a CBEE case.

The main theoretical contributions of this paper can be summarized as follows: First, the double auction method is employed and specifically extended for RAEP. Compared to AEP methods (Böhringer and Lange 2005), the extended double auction method does not require private information of participants (e.g. historical emissions, outputs, and inputs). Therefore, the auctioneer can be free of worry about the authority of such private information. Second, this paper expands the application scenario of the auction model in RAEP from the perspective of a bilateral market. Compared to auction models in a one-sided market (Malik 2002; Cason et al. 2003), the extended auction model presented in this paper can effectively reduce the monopoly status of the firm. Third, to further explain the auction model, three matching rules are proposed. Each rule can meet both the incentive compatibility and emission permits balance of supply and demand.

Beyond the theoretical contributions, several valuable results are also derived via computational analysis of the CBEE case as follows: First, the results of the CBEE case show the validity and practicability of this extended method. Second, compared to the auction method actually used in the CBEE, the auction method presented in this paper can effectively increase the number of traded participants, improve the auction transaction efficiency, and increase the utilities of trading participants. Third, the results of a variety of randomly generated data indicate that the method described in this paper is applicable regardless of the size of the permit market. In addition, the trading rate of buyers/sellers remains relatively stable, regardless of how many participants are involved. Last, the impact of the degree of truthful biding of buyer/seller on the performance of the auction was also analyzed. The results show that if buyers/sellers submit untrue biddings, their actual social welfare utility will decrease, and final trading rates will also decrease. This further illustrates that our method effectively realizes the incentive compatibility.

The remainder of this paper is structured as follows. Section 2 reviews the relevant literature on the allocation of emission permits. The description of the research problem relating to RAEP is discussed in Sect. 3. The double auction model and matching trading rules are suggested in Sect. 4. Section 5 proposes the properties of the auction trading mechanism developed in this paper, and Sect. 6 provides a CBEE case to illustrate the RAEP mechanism. Conclusions and possibilities for future research are presented in Sect. 7.

2 Literature review

Three main streams of relevant literature are related to this study: (1) traditional free allocation methods for emission permits (2) the double auction method, and (3) auctions for emission permit allocation.

2.1 Traditional free allocation methods for emission permits

The conventional free allocation methods for emission permits mainly include grandfathering, output-based allocation (OBA), and date envelopment analysis (DEA) methods. Emission permits are assigned on the basis of an enterprise’s historical emissions or production levels, according to the grandfathering method (Goeree et al. 2010). Due to the feasibility and simplicity of this method, grandfathering has been commonly utilized for AEP. Cases using grandfathering to allocate emission permits can be found in Cason et al. (2003) and Huang and Nagasaka (2011). However, some scholars have cast doubts on the validity of the grandfathering method. For example, Goeree et al. (2010) pointed out that grandfathering may have more influence over the product prices than auctioning when utilized for the initial allocation of emission permits. Sijm et al. (2002) considered that grandfathering probably results in unfair allocation results among participants. More specifically, some enterprises can be allocated too many permits, while others are allocated too few, when grandfathering is applied for AEP. Böhringer and Lange (2005) studied grandfathering schemes from a dynamic point of view, finding that grandfathering results in an open trading system and closed trading system are different. Rosendahl and Storrøsten (2008) further extended Böhringer and Lange’s (2005) research by considering the firms’ movement into and out of trading system.

Apart from grandfathering, there exist other free allocation methods, such as output-based allocation (OBA). OBA allocates emission permits in proportion to enterprises’ current outputs (Takeda et al. 2014). In comparing three AEP methods (auctioning, grandfathering and OBA), Fischer and Fox (2007) find OBA is an efficient method for reducing carbon leakage, and also is favored by energy-intensive firms. However, other authors have pointed out that OBA may simultaneously stimulate both enterprises’ outputs and emissions. Subsequently, the former authors further expanded their research by combining auctioning and OBA (Fischer and Fox. 2010). They found that combining auctioning and OBA is more cost-effective than auctioning alone for energy-intensive firms in the USA. Since then, Fischer and Fox’s (2007, 2010) studies have been extended in order to address the problem of carbon leakage in Japan (Takeda et al. 2014).

Date envelopment analysis (DEA) is an effective approach for assessing the relative efficiency of decision making units (DMUs). Since DEA was first introduced by Charnes et al. (1978), it has been found to be highly effective and has been widely applied in various areas (Ji et al. 2017a, b), of which AEP is a typical example. For instance, Lozano et al. (2009) proposed a DEA method for the reallocation of emission permits from a centralized perspective. The proposed method did not require information on the prices of inputs and outputs. Different from the work of Lozano et al. (2009), Sun et al. (2014) proposed two DEA–AEP models from centralized and individual perspectives, respectively. By comparing two models, they concluded that the effect of a centralized DEA–AEP model was better than an individual DEA–AEP model. The unit with the least efficiency usually decides the overall efficiency of a system (Guan et al. 2016). The centralized DEA–AEP model proposed by Sun et al. (2014) can improve this least efficient unit in the process of permit allocation. Feng et al. (2015) proposed a DEA model for coordinating contradiction between overall and individual interests. Their model includes two steps. In the first step, the total emission permits are allocated to all participants from the centralized perspective. In the second step, an improved allocated scheme is proposed based on participants’ emission reduction contributions (including their optimal efficiencies), while aiming to maintain the optimal overall efficiency. Wu et al. (2016) first proposed a two-stage AEP target setting approach to determine the total emission permits for all participants. Then, another DEA allocation model was proposed for allocating the permits to each participant.

2.2 Double auction method

The double auction method is employed and specifically extended for RAEP; therefore, a literature review of the double auction method is proposed in this section. In a double auction, there is a third-party auctioneer (e.g. market clearing broker), buyers, and sellers. The important characteristic of the double auction is that both buyers and sellers are allowed to bid simultaneously (Myerson and Satterthwaite 1983; McAfee 1992; Krishna 2009). So far, several double auction methods have been proposed by scholars. For example, McAfee (1992) proposed a double auction mechanism based on the dominant strategy, which allowed each participant to only buy/sell one unit of goods. McAfee’s auction mechanism is usually called McAfee or single-unit trade reduction auction. Wurman et al. (1998) proposed the M price sealed auction and the M + 1 price sealed auction under the electronic commerce environment. However, Wurman’s mechanism cannot satisfy the incentive compatibility for the case of multi-unit bidding, nor can it meet the incentive compatibility of both buyer and seller simultaneously. Yokoo et al. (2005) indicated that the McAfee mechanism would not meet the incentive compatibility if the participants did not bid the true price. The authors revised the McAfee mechanism, and proposed the threshold price double auction. They also showed that the newly proposed mechanism was still incentive compatible if an untrue price was bid by seller/buyer. Aimed at the case where each participant can only trade one unit of an item, Chu and Shen (2006) developed the agent competition double auction (AC-DA) mechanism. They further showed that the proposed mechanism satisfied the incentive compatibility, individual rationality, and weak budget balance. Because the auction would generate a specific transaction cost, Chu and Shen (2008) designed two multi-stage double auction mechanisms that considered transaction costs. The authors also showed that the developed mechanisms were asymptotically efficient. Sometimes, a buyer/seller would like to purchase/sell a bundle of different types of goods. Aimed at this case, Chu (2009) proposed two double auction mechanisms from the perspective of buyer’s demand. For the problem of transport service procurement, it may be possible that carriers (sellers) cooperate in the transportation network. Xu et al. (2016) constructed three bundle double auction methods for realizing potential carrier collaboration. Their computational study showed that all proposed methods could effectively realize cost savings if carrier collaboration were considered.

2.3 Auctions for emission permit allocation

A substantial number of studies have been conducted from the perspective of free allocation. However, these methods all allocate emission permits according to private information (e.g. outputs, inputs, and emission of entities). Neither the authenticity nor reliability of such private information can be guaranteed, thus limiting the utilization of free allocation. More importantly, during the re-allocation of emission permits (the emissions trading process), the main problem is how to trade the emission permits between firms (i.e., buyers and sellers). These free allocation methods including grandfathering, OBA and DEA are obviously ineffective in that context.

According to market structure differences, the auction can be divided into a one-side auction and a two-side auction (double auction). In the one-side auction market, only one buyer interacts with more than one seller (or correspondingly, only one seller interacts with more than one buyer). Using one-side auction for allocating emission permits attracted the attention of several scholars. For example, Cramton and Kerr (2002) pointed out that auctioning is more suitable for AEP than grandfathering, given its propensity to reduce tax distortions and stimulate innovation. Burtraw et al. (2009) studied the issue of collusion in emission permit auctions. They concluded that collusion in auctions may lead to a lower price of goods and lower income of the seller, thus having a negative impact on market efficiency. They also concluded that the auction mechanism design for emission permits should consider stimulating competition between bidders. Wang et al. (2011, 2017) mentioned that not all auction mechanisms can be utilized for allocating emission permits. They compared and analyzed the English auction and the sequential ascending auction methods. They concluded that the straightforward bidding strategy is an optimal bidding strategy in the English auction, while the truth-telling strategy is bidders’ most favorable strategy in the sequential ascending auction method. Later, they extended their research and proposed an improved auction mechanism (Wang et al. 2014). These authors also proved that the auction results converge to the Pareto equilibrium.

In the context of an emission permits auction, there may be one leader firm and other follower firms. Alvarez and André (2016) designed an auction mechanism according to this situation. Through this mechanism, they yielded similar results to a previous study they had undertaken (see Alvarez and André 2015). Namely, if the auction mechanism could eliminate the leader’s market power, the auction results would be more cost-effective than grandfathering. Hu et al. (2016) studied the issue of AEP in which the marginal cost is dependent on the participant’s private information. The authors suggested an auction mechanism that would regard emission permits as divisible goods, and accordingly analyzed the participants’ bidding strategies and the government’s emission permits supply strategies. Wang and Wang (2016) suggested a multi-unit auction mechanism for initial AEP, in which the emitters (i.e., the emission permit buyers) were considered to be interdependent, and the emission permits were considered as divisible goods. They concluded that the proposed auction mechanism could induce emitters to reveal truthful marginal costs, and thus achieve fair and effective initial AEP results.

In contrast to one-side auction, the double auction considers multiple buyers and sellers within the market. However, most of the research on emission permit trading using the double auction remained at the experimental level. For example, Hizen and Saijo (2001) conducted two experiments to investigate the efficiency of the double auction in the context of AEP. They found that the efficiency of both auction institutions was high, in spite of publishing or non-publishing the contracted price, and that the marginal abatement costs of both would equalize as time went by. They also concluded that the contracted price obtained via the double auction would be approximate to the competitive price. Muller et al. (2002) conducted a double auction laboratory experiment, assuming the existence of participants with market monopoly power. They found that if the double auction trading market is monopolist (or monopsonist), the transaction price would shift from a competitive equilibrium price in the direction of the monopolist (or monopsonist). Sturm (2008) undertook a double auction experiment by employing numerous observations. He found that emissions trading systems employing the double auction method could achieve high trade efficiency, and that the factor of price discrimination should be considered when designing a double auction for the initial AEP.

2.4 Summary of the literature review

The limitations of this existing research on the allocation of emission permits using auctions lie in the following aspects: First, in a one-side auction market, there is always one side (the unique buyer or seller), which holds the scarce resources of the market and the monopoly of resources. Due to this advantage, the side with resource superiority can prioritize to select trading modes and establish trading rules. This is unfair to the side with resource inferiority. Second, one-side auction assumes that there exist only one buyer and multiple sellers (or one seller and multiple buyers). In the RAEP, there may be multiple sellers and multiple buyers. Therefore, the one-side auction is not suitable for REAP. Third, some scholars have studied the application of the double auction in the emission permits allocation from the perspective of experiments, while few studies have involved the construction of a double auction mechanism on RAEP. Aiming to address these problems, the double auction model is employed and specifically extended for RAEP, and corresponding matching rules are proposed. The extended double auction method is proved to satisfy incentive compatibility. This paper also suggests an optimization method for each firm to estimate the demand/supply emission permit volume.

3 Problem description

According to the rules of the CBEE case, we consider an RAEP mechanism that contains m + n homogeneous firms which emit the same pollutant, and a governing body (e.g. CBEE). The pollution abatement costs of m firms are high, while n firms have low pollution abatement costs. Through the initial allocation, each firm is able to obtain a certain number of initial emission permits. Since a firm with a high pollution abatement cost emits more pollutants than its initial allocation emission permits, it needs to buy emission permits on the market to meet its production requirements. In order to yield greater profits, a firm with a low pollution abatement cost will sell its redundant permits in the trading market. Therefore, how to design an effective multi-unit emission permits double auction mechanism is the main research problem of this paper.

In the context of the multi-unit emission permits double auction mechanism, the organizer (e.g. CBEE) is responsible for organizing the auction and trading. Firms with high pollution treatment costs are emission permit buyers, and firms with low pollution treatment costs are emission permit sellers. The information possessed by the buyer/seller is asymmetric; that is, each buyer/seller does not know the bid information of other buyers/sellers. The organizer, however, has insight into all the buyers’ and sellers’ information. In view of the complexity of the double auction mechanism of emission permits, this paper employs the periodical double auction method to simplify the research problem without losing generality. This method determined that, over a fixed period of time, the organizer collects bid information from both buyers and the sellers, and then determines the winners, the winners’ trading volume, and the transaction price (also called the market clearing price). Finally, the transaction is carried out in accordance with the trading rules. The process of the double auction of emission permits is shown in Fig. 1.

Fig. 1
figure 1

The process of the double auction trading mechanism for emission permits

Full size image

To facilitate model formulation, the notations used in this study are summarized in Table 1.

Table 1 Model notations
Full size table

4 Estimation of demand and supply volume for emission permits

4.1 Estimation of buyers’ demand volume

Let \( y_{i}^{B} \) (i = 1,2,…,m) denote the productivity of buyer i (firm i with a high pollution abatement cost), \( \alpha_{i}^{B} \) denote the rate of pollutant generation, and \( E_{i}^{B} \) denote total initial emission permits. We consider that the pollution emissions of firms with high pollution abatement costs are far greater than the initial emission permit volume set. The price of the products produced by all participating firms is denoted by \( p^{p} \). Since the price of the product is determined by the whole market, it will not be affected if the productivity of the firm participating in the auction changes. That is, \( p^{p} \) is an invariant constant. The total volume of emission permits demanded by firm i is denoted by \( q_{i}^{B} \). This paper adopts the double auction uniform price mode, whereby the final auction price of a unit emission permit is pre-supposed as \( p_{a} \). The unit pollution abatement cost function of firm i is denoted by \( \varphi_{i}^{B} \), and the unit product cost function of firm i is denoted by \( f_{i}^{B} \). After the purchase of \( q_{i}^{B} \) emission permits, the amount of pollutants that firm i needs to treat is \( \alpha_{i}^{B} y_{i}^{B} - E_{i}^{B} - q_{i}^{B} \).

Given that the amount of pollution emitted by the firm with a high pollution abatement cost exceeds its initial allocation of emission permits (\( \alpha_{i}^{B} y_{i}^{B} - E_{i}^{B} > 0 \)), the firm needs to buy emission permits from the market. The amount of pollution emitted and the pollution abatement cost of each firm may differ. Therefore, the way in which to determine the optimal productivity and demand volume of emission permits of firm i can be considered an optimization problem, as follows:

$$ \hbox{max} {\kern 1pt} {\kern 1pt} {\kern 1pt} p^{p} y_{i}^{B} - \varphi_{i}^{B} \times \left( {\alpha_{i}^{B} y_{i}^{B} - E_{i}^{B} - q_{i}^{B} } \right) - p_{a} q_{i}^{B} - f_{i}^{B} y_{i}^{B} $$
(1)

In formula (1), \( y_{i}^{B} \) and \( q_{i}^{B} \) are variables. Then, through the first derivative of formula (1) with respect to \( y_{i}^{B} \) and \( q_{i}^{B} \), we have

$$ {\kern 1pt} p^{p} - \frac{{\partial \varphi_{i}^{B} }}{{\partial y_{i}^{B} }} \times (\alpha_{i}^{B} y_{i}^{B} - E_{i}^{B} - q_{i}^{B} ) - \alpha_{i}^{B} \varphi_{i}^{B} - \frac{{\partial f_{i}^{B} }}{{\partial y_{i}^{B} }}y_{i}^{B} - f_{i}^{B} = 0 $$
(2)
$$ - \frac{{\partial \varphi_{i}^{B} }}{{\partial q_{i}^{B} }} \times (\alpha_{i}^{B} y_{i}^{B} - E_{i}^{B} - q_{i}^{B} ) + \varphi_{i}^{B} - p_{a} = 0 $$
(3)

Formulas (2) and (3) form the simultaneous equations, from which we can obtain the results of \( y_{i}^{B} \) and \( q_{i}^{B} \), shown as (4) and (5).

$$ {\kern 1pt} y_{i}^{B} = \frac{{\frac{{\partial \varphi_{i}^{B} }}{{\partial y_{i}^{B} }}p_{a} - \frac{{\partial \varphi_{i}^{B} }}{{\partial y_{i}^{B} }}\varphi_{i}^{B} + \frac{{\partial \varphi_{i}^{B} }}{{\partial q_{i}^{B} }}p^{p} - \frac{{\partial \varphi_{i}^{B} }}{{\partial q_{i}^{B} }}\varphi_{i}^{B} \alpha_{i}^{B} - \frac{{\partial \varphi_{i}^{B} }}{{\partial q_{i}^{B} }}f_{i}^{B} }}{{\frac{{\partial f_{i}^{B} }}{{\partial y_{i}^{B} }} \times \frac{{\partial \varphi_{i}^{B} }}{{\partial q_{i}^{B} }}}} $$
(4)
$$ {\kern 1pt} q_{i}^{B} = \frac{{p_{a} \alpha_{i}^{B} - \varphi_{i}^{B} (\alpha_{i}^{B} )^{2} - f_{i}^{B} \alpha_{i}^{B} }}{{\frac{{\partial f_{i}^{B} }}{{\partial y_{i}^{B} }}}} + \frac{{\frac{{\partial \varphi_{i}^{B} }}{{\partial y_{i}^{B} }}p_{a} \alpha_{i}^{B} - \frac{{\partial \varphi_{i}^{B} }}{{\partial y_{i}^{B} }}\varphi_{i}^{B} \alpha_{i}^{B} }}{{\frac{{\partial f_{i}^{B} }}{{\partial y_{i}^{B} }}\frac{{\partial \varphi_{i}^{B} }}{{\partial q_{i}^{B} }}}} + \frac{{p_{a} - \varphi_{i}^{B} }}{{\frac{{\partial \varphi_{i}^{B} }}{{\partial q_{i}^{B} }}}} - E_{i}^{B} $$
(5)

Formulas (4) and (5) represent the optimal product productivity and permit demand volume of firm i in the context of emission trading.

4.2 Estimation of sellers’ supply volume

Let \( y_{j}^{S} \) (j = 1, 2,…,n) denote the productivity of seller j (firm j with low pollution abatement costs), \( \alpha_{j}^{S} \) denote the rate of pollutant generation, and \( E_{j}^{S} \) denote the total initial emission permits. The total amount of emission permits supplied by firm j is denoted by \( q_{j}^{S} \). The unit pollution abatement cost function of firm j is denoted by \( \varphi_{j}^{S} \), and the unit product cost function of firm j is denoted by \( f_{j}^{S} \). After selling a certain number of emission permits, the amount of pollutants that firm j needs to treat is \( \alpha_{j}^{S} y_{j}^{S} - E_{j}^{S} + q_{j}^{S} \). Therefore, the way in which to determine the optimal productivity and supply volume of emission permits of firm j can be considered an optimization problem, as follows:

$$ \hbox{max} {\kern 1pt} {\kern 1pt} {\kern 1pt} p^{p} y_{j}^{S} - \varphi_{j}^{S} \times (\alpha_{j}^{S} y_{j}^{S} - E_{j}^{S} + q_{j}^{S} ) + p_{a} q_{j}^{S} - f_{j}^{S} y_{j}^{S} $$
(6)

In formula (6), \( y_{j}^{S} \) and \( q_{j}^{S} \) are variables. Then, through the first derivative of formula (6) with respect to \( y_{j}^{S} \) and \( q_{j}^{S} \), we have

$$ {\kern 1pt} p^{p} - \frac{{\partial \varphi_{j}^{S} }}{{\partial y_{j}^{S} }} \times (\alpha_{j}^{S} y_{j}^{S} - E_{j}^{S} + q_{j}^{S} ) - \alpha_{j}^{S} \varphi_{j}^{S} - \frac{{\partial f_{j}^{S} }}{{\partial y_{j}^{S} }}y_{j}^{S} - f_{j}^{S} = 0 $$
(7)
$$ - \frac{{\partial \varphi_{j}^{S} }}{{\partial q_{j}^{S} }} \times (\alpha_{j}^{S} y_{j}^{S} - E_{j}^{S} + q_{j}^{S} ) - \varphi_{j}^{S} + p_{a} = 0 $$
(8)

Formulas (7) and (8) form the simultaneous equations, from which we can obtain the results of \( y_{j}^{S} \) and \( q_{j}^{S} \), shown as (9) and (10).

$$ {\kern 1pt} y_{j}^{S} = \frac{{\frac{{\partial \varphi_{j}^{S} }}{{\partial y_{j}^{S} }}\varphi_{j}^{S} - \frac{{\partial \varphi_{j}^{S} }}{{\partial y_{j}^{S} }}p_{a} - \frac{{\partial \varphi_{j}^{S} }}{{\partial q_{j}^{S} }}f_{j} - \frac{{\partial \varphi_{j}^{S} }}{{\partial q_{j}^{S} }}\varphi_{j}^{S} \alpha_{j}^{S} + \frac{{\partial \varphi_{j}^{S} }}{{\partial q_{j}^{S} }}p^{p} }}{{\frac{{\partial f_{j}^{S} }}{{\partial y_{j}^{S} }} \times \frac{{\partial \varphi_{j} }}{{\partial q_{j}^{S} }}}} $$
(9)
$$ {\kern 1pt} q_{j}^{S} = - \frac{{p^{p} \alpha_{j}^{S} - f_{j}^{S} \alpha_{j}^{S} - \varphi_{j}^{S} (\alpha_{j}^{S} )^{2} }}{{\frac{{\partial f_{j}^{S} }}{{\partial y_{j}^{S} }}}} + \frac{{p_{a} - \varphi_{j}^{S} }}{{\frac{{\partial \varphi_{j}^{S} }}{{\partial q_{j}^{S} }}}} - \frac{{\frac{{\partial \varphi_{j}^{S} }}{{\partial y_{j}^{S} }}p_{a} \alpha_{j}^{S} - \frac{{\partial \varphi_{j}^{S} }}{{\partial y_{j}^{S} }}\varphi_{j}^{S} \alpha_{j}^{S} }}{{\frac{{\partial f_{j}^{S} }}{{\partial y_{j}^{S} }} \times \frac{{\partial \varphi_{j}^{S} }}{{\partial q_{j}^{S} }}}} + E_{j}^{S} $$
(10)

Formulas (9) and (10) represent the optimal product productivity and permit supply volume of firm j in the context of emission trading.

5 Mechanism design of double auction for emission permits

In a multi-unit double auction market, there are m buyers and n sellers. We assume that each buyer/seller can only submit information pertaining to their demand/supply bid and has only one bid chance. The unit price of an emission permit and buyer i’s demand are denoted by \( \left( {p_{i}^{B} ,q_{i}^{B} } \right) \)(i = 1, 2,…,m), and the unit price of an emission permit and seller j’s supply are denoted by \( (p_{j}^{S} ,q_{j}^{S} ) \) (j = 1, 2,…,n), where \( p_{i}^{B} \), \( q_{i}^{B} \), \( p_{j}^{S} \) and \( q_{j}^{S} \) are the positive real numbers. Without loss of generality, we assume that

$$ p_{1}^{B} \ge p_{2}^{B} \ge \cdots \ge p_{m}^{B} \, $$
(11)
$$ p_{1}^{S} \le p_{2}^{S} \le \cdots \le p_{n}^{S} \, $$
(12)
$$ p_{1}^{B} \ge p_{1}^{S} $$
(13)

The Eq. (13) ensures that transactions between buyers and sellers can always be executed. If we consider that r buyers and s sellers have successfully traded, then r and s satisfy the following constraints:

$$ \, p_{1}^{B} \ge p_{2}^{B} \ge \cdots \ge p_{r}^{B} \ge p_{s}^{S} \ge p_{s - 1}^{S} \ge \cdots \ge p_{1}^{S} $$
(14)
$$ p_{m}^{B} \le p_{m - 1}^{B} \le \cdots \le p_{r + 1}^{B} \le p_{s + 1}^{S} \le p_{s + 2}^{S} \le \cdots \le p_{n}^{S} $$
(15)
$$ 0 \le \sum\limits_{j = 1}^{n} {x_{ij} } \le q_{i}^{B} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (i \in M) $$
(16)
$$ 0 \le \sum\limits_{i = 1}^{m} {x_{ij} } \le q_{j}^{S} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (j \in N) $$
(17)

In the Eqs. (16) and (17), \( x_{ij} \) denotes the emission permit quantity that firm i buys from firm j. Equation (16) states that a buyer will buy no more than needed, while Eq. (17) indicates that a seller will not sell more than is possessed. In order to verify the uniqueness of the auction model proposed in this section, we establish the following two principles.

Principle 1

If any two buyers submit two bids at the same price, such as \( (p^{B} ,q_{1}^{B} ) \) and \( (p^{B} ,q_{2}^{B} ) \), then we can consider the two buyers as a single buyer submitting a bid \( (p^{B} ,q_{1}^{B} + q_{2}^{B} ) \). If the single buyer finally gets the \( q^{B*} \) emission permits, then the two buyers can obtain \( q_{1}^{B*} = round\left(\frac{{q^{B*} q_{1}^{B} }}{{q_{1}^{B} + q_{2}^{B} }}\right) \), and \( q_{2}^{B*} = round\left(\frac{{q^{B*} q_{2}^{B} }}{{q_{1}^{B} + q_{2}^{B} }}\right) \) or \( q_{2}^{B*} = q^{B*} - q_{1}^{B*} \). For any two sellers who submit bids at the same price, the above method dealing with buyers can also be used.

Principle 2

Based on Principle 1, it can be considered that the bid prices submitted by any two buyers are different, and that the bid prices submitted by any two sellers are also different.

Under Principles 1 and 2, (11), (12), (14) and (15) are equivalent to

$$ p_{1}^{B} > p_{2}^{B} { > } \cdots { > }p_{m}^{B} \, $$
(18)
$$ p_{1}^{S} { < }p_{2}^{S} { < } \cdots { < }p_{n}^{S} $$
(19)
$$ \, p_{1}^{B} > p_{2}^{B} > \cdots > p_{r}^{B} \ge p_{s}^{S} > p_{s - 1}^{S} > \cdots > p_{1}^{S} $$
(20)
$$ p_{m}^{B} < p_{m - 1}^{B} < \cdots < p_{r + 1}^{B} < p_{s + 1}^{S} < p_{s + 2}^{S} < \cdots < p_{n}^{S} $$
(21)

Based on Principles 1 and 2, the double auction model of emission permits and its matching mechanism are proposed in Sects. 5.1 and 5.2.

5.1 Double auction model of emission permits

We assume that the final auction price of a unit emission is \( p_{o} \). After the transaction, the social welfare utility of buyer i is

$$ U_{i} = p_{i}^{B} \sum\limits_{j = 1}^{n} {x_{ij}^{{}} } - p_{o} \sum\limits_{j = 1}^{n} {x_{ij}^{{}} } , $$
(22)

and the social welfare utility of seller j is

$$ U_{j}^{{}} = p_{o} \sum\limits_{i = 1}^{m} {x_{ij}^{{}} } - p_{j}^{S} \sum\limits_{i = 1}^{m} {x_{ij}^{{}} } . $$
(23)

Then, the total social welfare utility of all buyers and sellers is

$$ U = \sum\limits_{i = 1}^{m} {U_{i}^{{}} } + \sum\limits_{j = 1}^{n} {U_{j}^{{}} } = \sum\limits_{i = 1}^{m} {\left( {p_{i}^{B} \sum\limits_{j = 1}^{n} {x_{ij}^{{}} } } \right) - \sum\limits_{j = 1}^{n} {\left( {p_{j}^{S} \sum\limits_{i = 1}^{m} {x_{ij}^{{}} } } \right)} } . $$
(24)

According to the maximization of the total social welfare utility, the double auction model is proposed as follows.

$$ \begin{aligned}\begin{gathered} \hbox{max} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} U = \sum\limits_{i = 1}^{m} {\left( {p_{i}^{B} \sum\limits_{j = 1}^{n} {x_{ij} } } \right) - \sum\limits_{j = 1}^{n} {\left( {p_{j}^{S} \sum\limits_{i = 1}^{m} {x_{ij} } } \right)} } \hfill \\\kern-6pc s.t.{\kern 1pt} {\kern 1pt} \sum\limits_{j = 1}^{n} {x_{ij} } \le q_{i}^{B} ,i = 1, \ldots ,m \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{i = 1}^{m} {x_{ij} } \le q_{j}^{S} ,j = 1 \ldots ,n \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} x_{ij} \ge 0,\forall i,j. \hfill \\ \end{gathered}\end{aligned} $$
(25)

While the final trading price does not show up in model (25), this price will affect each buyer/seller’s utility. If all information is made public, the maximum degree of social welfare can easily be obtained. However, this solution is usually not available because trading rules do not allow buyers or sellers to disclose information.

5.2 Matching mechanism design of double auction of emission permits

To induce each buyer/seller to submit truthful bids, this section presents the design of a multi-unit double auction mechanism for model (25). All buyers’ bids are ranked as \( p_{1}^{B} > p_{2}^{B} { > } \cdots { > }p_{m}^{B} \, \), and all sellers’ bids are ranked as \( p_{1}^{S} { < }p_{2}^{S} { < } \cdots { < }p_{n}^{S} \). If there are r buyers and s sellers wining in the auction, the supply and demand between buyers and sellers may be balanced or unbalanced. This paper discusses three different cases of the balance of supply and demand in detail. In each case, the matching rule for r buyers and s sellers is different, which is shown as follows.

$$ \begin{aligned} (I) \, \sum\limits_{i = 1}^{r} {q_{i}^{B} } < \sum\limits_{j = 1}^{s} {q_{j}^{S} } \hfill \\ (II) \, \sum\limits_{i = 1}^{r} {q_{i}^{B} } > \sum\limits_{j = 1}^{s} {q_{j}^{S} } \hfill \\ (III) \, \sum\limits_{i = 1}^{r} {q_{i}^{B} } = \sum\limits_{j = 1}^{s} {q_{j}^{S} } \hfill \\ \end{aligned} $$

In case (I), if \( \sum\nolimits_{i = 1}^{r} {q_{i}^{B} } = \sum\nolimits_{j = 1}^{s} {q_{j}^{S} } \), then the matching rule between buyers and sellers is as follows:

$$ \sum\limits_{j = 1}^{s} {x_{ij}^{{}} } = q_{i}^{B} ,\sum\limits_{i = 1}^{r} {x_{ij}^{{}} } = q_{j}^{S} ,\quad (i = 1,2, \ldots r;j = 1,2, \ldots s), $$
$$ \sum\limits_{j = s + 1}^{n} {x_{ij}^{{}} } = \sum\limits_{i = r + 1}^{m} {x_{ij}^{{}} } = 0\quad (i = r + 1,r + 2, \ldots ,m;j = s + 1, \ldots ,n) $$

In case (II), if \( \sum\nolimits_{i = 1}^{r} {q_{i}^{B} } > \sum\nolimits_{j = 1}^{s} {q_{j}^{S} } \), the following rule between buyers and sellers is adopted.

Step 1\( \sum\nolimits_{i = 1}^{r} {q_{i}^{B} } > \sum\nolimits_{j = 1}^{s} {q_{j}^{S} } \) indicates that buyers’ demand exceeds sellers’ supply. This may then lead to the demand of the rth buyer not being fully satisfied. Therefore, buyer r* denotes buyer r (Here, “r*”only indicates that demand of this buyer can be satisfied, but not that it can be fully satisfied)

Step 2 Seller s’ emission permit supply and emission permit of the sellers whose price is lower than seller s can be traded, and the trading volume is \( \sum\nolimits_{i = 1}^{m} {x_{ij} } = q_{j}^{S} \)\( (j = 1,2, \ldots s) \). Sellers whose price is higher than seller s cannot trade any emission permits; that is, \( \sum\nolimits_{i = 1}^{m} {x_{ij}^{{}} } = 0\quad (j = s + 1,\;2,\; \ldots n) \)

Step 3 The emission permit demand of buyers whose price is higher than buyer r*’s can all be satisfied; that is, \( \sum\nolimits_{j = 1}^{n} {x_{ij}^{{}} } = q_{i}^{B} \)\( (i = 1,2, \ldots r* - 1) \). For buyer i\( (i = r* + 1,r* + 2, \ldots m) \), the bid price is lower than for buyer r*. Thus, buyer i cannot buy any emissions permits; that is, \( \sum\nolimits_{j = 1}^{n} {x_{ij} } = 0 \)

Step 4 For buyer r*, we have \( \sum\nolimits_{i = 1}^{r - 1} {q_{i}^{B} } < \sum\nolimits_{j = 1}^{s} {q_{j}^{S} } = \sum\nolimits_{i = 1}^{r*} {q_{i}^{B} } \), thus its final transaction volume is \( \sum\nolimits_{j = 1}^{n} {x_{r*j} } = \sum\nolimits_{j = 1}^{s} {q_{j}^{S} - } \sum\nolimits_{i = 1}^{r - 1} {q_{i}^{B} } \)

In case (III), if \( \sum\nolimits_{i = 1}^{r} {q_{i}^{B} } < \sum\nolimits_{j = 1}^{s} {q_{j}^{S} } \), the following rule between buyers and sellers is adopted.

Step1\( \sum\nolimits_{i = 1}^{r} {q_{i}^{B} } < \sum\nolimits_{j = 1}^{s} {q_{j}^{S} } \) indicates that the buyers’ demand is lower than sellers’ supply. This may then lead to the supply of the sth seller not being fully traded. Let s* denote seller s. (Here, “s*” only indicates that supply of this seller can be traded, but not that it can be fully traded).

Step 2 For buyer r and buyers whose price is higher than that of buyer r, the number of emission permits is adequate. Therefore, the buyers’ demand can be satisfactorily completed; that is, \( \sum\nolimits_{j = 1}^{n} {x_{ij} } = q_{i}^{B} \)\( (i = 1,2, \ldots r) \). Buyers whose prices are lower than those of buyer r cannot buy any emission permits; that is, \( \sum\nolimits_{i = 1}^{n} {x_{ij} } = 0\quad (i - r + 1,\;2\; \ldots m) \).

Step 3 The emission permit supply of sellers whose price is lower than that of seller s* can all be traded; that is, \( \sum\nolimits_{i = 1}^{m} {x_{ij} } = q_{j}^{S} \)\( (j = 1,2, \ldots s* - 1) \). As the sellers’ bid price is higher than that of seller s*, and also higher than the auction transaction price \( p_{o}^{{}} \), they thus cannot sell any emissions permits; that is, \( \sum\nolimits_{i = 1}^{m} {x_{ij} } = 0 \)\( (j = s* + 1,s* + 2, \ldots n) \).

Step 4 For seller s*, we have \( \sum\nolimits_{j = 1}^{s - 1} {q_{j}^{S} } < \sum\nolimits_{i = 1}^{r} {q_{i}^{B} = } \sum\nolimits_{j = 1}^{s*} {q_{j}^{S} } \), thus the final transaction volume of seller s is \( \sum\nolimits_{i = 1}^{m} {x_{is*}^{{}} } = \sum\nolimits_{i = 1}^{r} {q_{i}^{B} } - \sum\nolimits_{j = 1}^{s - 1} {q_{j}^{S} } \).

From the above three cases, it can be seen that in any case, the final emissions trading volume \( Q* = \hbox{min} \left\{ {\sum\nolimits_{i = 1}^{r} {q_{i}^{B} ,\sum\nolimits_{j = 1}^{s} {q_{j}^{S} } } } \right\} = \sum\nolimits_{j = 1}^{s*} {\sum\nolimits_{i = 1}^{r} {x_{ij} = \sum\nolimits_{i = 1}^{r*} {\sum\nolimits_{j = 1}^{s} {x_{ij} } } } } \).

5.3 Properties of the auction trading mechanism

This section discusses the properties of the auction trading mechanism in the form of theorems.

Theorem 1

In model (25), assuming that there are r buyers and s sellers that can trade, if\( \sum\nolimits_{i = 1}^{r} {q_{i}^{B} } = \sum\nolimits_{j = 1}^{s} {q_{j}^{S} } \), we have

$$ p_{r + 1}^{B} < p_{s}^{S} $$
(26)

or

$$ p_{s}^{S} \le {\text{p}}_{r + 1}^{B} < p_{s + 1}^{S} $$
(27)

Proof

If \( \sum\nolimits_{i = 1}^{r} {q_{i}^{B} } = \sum\nolimits_{j = 1}^{s} {q_{j}^{S} } \) and r buyers and s sellers are trading, we have \( p_{r + 1}^{B} < p_{s}^{S} \) or \( p_{r + 1}^{B} \ge p_{s}^{S} \), but \( \left( {p_{r + 1}^{B} < p_{s}^{S} } \right) \cap \left( {p_{r + 1}^{B} \ge p_{s}^{S} } \right) \) = ∅. If \( p_{r + 1}^{B} < p_{s}^{S} \), then (26) is established. Therefore, we only need to prove that if \( p_{r + 1}^{B} \ge p_{s}^{S} \), we get \( p_{s}^{S} \le {\text{p}}_{r + 1}^{B} < p_{s + 1}^{S} \). Using the anti-hypothesis method, we assume that \( p_{r + 1}^{B} \ge p_{s + 1}^{S} \). In that case, there are r + 1 buyers and s + 1 sellers that can trade. This is contrary to the original assumption of Theorem 1. Hence, if \( p_{r + 1}^{B} \ge p_{s}^{S} \), we get \( p_{r + 1}^{B} < p_{s + 1}^{S} \). Then \( p_{s}^{S} \le {\text{p}}_{r + 1}^{B} < p_{s + 1}^{S} \) is established.

Theorem 2

In model (25), assuming that there are r buyers and s sellers that can trade, if\( \sum\nolimits_{i = 1}^{r} {q_{i}^{B} } < \sum\nolimits_{j = 1}^{s} {q_{j}^{S} } \)(that is\( \sum\nolimits_{i = 1}^{r} {q_{i}^{B} } = \sum\nolimits_{j = 1}^{s*} {q_{j}^{S} } \)), we have

$$ p_{r + 1}^{B} < p_{s*}^{S} $$
(28)

or

$$ p_{s*}^{S} \le {\text{p}}_{r + 1}^{B} < p_{s + 1}^{S} $$
(29)

Proof

If \( \sum\nolimits_{i = 1}^{r} {q_{i}^{B} } = \sum\nolimits_{j = 1}^{s*} {q_{j}^{S} } \) and r buyers and s* sellers are trading, we have \( p_{r + 1}^{B} < p_{s*}^{S} \) or \( p_{r + 1}^{B} \ge p_{s*}^{S} \), but \( \left( {p_{r + 1}^{B} < p_{s}^{S} } \right) \cap \left( {p_{r + 1}^{B} \ge p_{s*}^{S} } \right) \) = ∅. If \( p_{r + 1}^{B} < p_{s*}^{S} \), then (28) is established. Therefore, we only need to prove that if \( p_{r + 1}^{B} \ge p_{s*}^{S} \), we get \( p_{s*}^{S} \le {\text{p}}_{r + 1}^{B} < p_{s + 1}^{S} \). Using the anti-hypothesis method, we assume that \( p_{r + 1}^{B} \ge p_{s + 1}^{S} \). In that case, there are r + 1 buyers and s + 1 sellers that can trade. This is contrary to the original assumption of Theorem 2. Hence, if \( p_{r + 1}^{B} \ge p_{s*}^{S} \), we get \( p_{r + 1}^{B} < p_{s + 1}^{S} \). Then \( p_{s*}^{S} \le {\text{p}}_{r + 1}^{B} < p_{s + 1}^{S} \) is established.

Theorem 3

In model (25), assuming that there are r buyers and s sellers that can trade, if\( \sum\nolimits_{i = 1}^{r} {q_{i}^{B} } > \sum\nolimits_{j = 1}^{s} {q_{j}^{S} } \)(that is\( \sum\nolimits_{i = 1}^{r*} {q_{i}^{B} } = \sum\nolimits_{j = 1}^{s} {q_{j}^{S} } \)), we have

$$ p_{r* + 1}^{B} < p_{s}^{S} $$
(30)

or

$$ p_{s}^{S} \le {\text{p}}_{r + 1}^{B} < p_{s + 1}^{S} $$
(31)

Proof

If \( \sum\nolimits_{i = 1}^{r*} {q_{i}^{B} } = \sum\nolimits_{j = 1}^{s} {q_{j}^{S} } \) and r* buyers and s sellers are trading, we have \( p_{r* + 1}^{B} < p_{s}^{S} \) or \( p_{r* + 1}^{B} \ge p_{s}^{S} \), \( \left( {p_{r* + 1}^{B} < p_{s}^{S} } \right) \cap \left( {p_{r* + 1}^{B} \ge p_{s}^{S} } \right) \) = ∅. If \( p_{r* + 1}^{B} < p_{s}^{S} \), then (30) is established. Therefore, only need to prove that if \( p_{r* + 1}^{B} \ge p_{s}^{S} \), we get \( p_{s}^{S} \le {\text{p}}_{r* + 1}^{B} < p_{s + 1}^{S} \). Using the anti-hypothesis method, we assume that \( p_{r* + 1}^{B} \ge p_{s + 1}^{S} \). Then there are r* + 1 buyers and s + 1 sellers that can trade. This is contrary to the original assumption of Theorem 3. Hence, if \( p_{r* + 1}^{B} \ge p_{s}^{S} \), we get \( p_{r* + 1}^{B} < p_{s + 1}^{S} \). Then \( p_{s}^{S} \le {\text{p}}_{r* + 1}^{B} < p_{s + 1}^{S} \) is established.

Theorems 1, 2 and 3 further explain the effects of buyers’ and sellers’ bid prices on the auction. If there are r buyers and s sellers who win in the auction, the bid price must satisfy (\( p_{s}^{S} < p_{r}^{B} \) and \( p_{r + 1}^{B} < p_{s}^{S} \)) or (\( p_{s}^{S} < p_{r}^{B} \) and \( p_{s}^{S} \le {\text{p}}_{r + 1}^{B} < p_{s + 1}^{S} \)).

Theorem 4

The matching rule is the optimal solution of model (25).

Proof

The proof here consists of two parts. The first part is to prove that the matching mechanism scheme is the solution of model (25), as follows.

In case (I), the matching schemes are \( \sum\nolimits_{j = 1}^{s} {x_{ij} } = q_{i}^{B} \) and \( \sum\nolimits_{i = 1}^{r} {x_{ij} } = q_{j}^{S} \), \( (i = 1,2, \ldots r;j = 1,2, \ldots s), \) which satisfy the constraints of model (25); therefore, the matching scheme of case (I) is the feasible solution of model (25).

In case (II), the matching scheme is \( \sum\nolimits_{i = 1}^{m} {x_{ij} } = q_{j}^{S} \)\( (j = 1,2, \ldots s), \)\( \sum\nolimits_{j = 1}^{n} {x_{ij} } = q_{i}^{B} \)\( (i = 1,2, \ldots r* - 1) \) and \( \sum\nolimits_{j = 1}^{n} {x_{r*j} } = \sum\nolimits_{j = 1}^{s} {q_{j}^{S} } - \sum\nolimits_{i = 1}^{r* - 1} {q_{i}^{B} } \le q_{r}^{B} \), which satisfy the constraints of model (25); therefore, the matching scheme of case (II) is the feasible solution of model (25).

The proof required for case (III) is similar to case (II).

The second part is to prove that the matching mechanism scheme is the optimal solution of model (25), as follows.

The objective function of model (25) is equivalent to \( U = \sum\nolimits_{i = 1}^{m} {\left[ {(p_{i}^{B} - p_{o} )\sum\nolimits_{j = 1}^{n} {x_{ij} } } \right]} + \sum\nolimits_{j = 1}^{n} {\left[ {(p_{o} - p_{j}^{S} )\sum\nolimits_{i = 1}^{m} {x_{ij} } } \right]} \). Assuming that there are r buyers and s sellers that can trade, we have \( p_{r}^{B} \ge p_{o}^{{}} > p_{r + 1}^{B} \) or \( p_{s}^{S} \le p_{o} < p_{s + 1}^{S} \).

In case (I), the utility value according to rule (I) is denoted as \( U(r,s) \). If \( \sum\nolimits_{j = 1}^{n} {x_{ij}^{{}} } \le q_{i} {\kern 1pt} {\kern 1pt} (i = 1, \ldots r) \) or \( \sum\nolimits_{i = 1}^{m} {x_{ij}^{{}} } \le q_{j}^{{}} {\kern 1pt} {\kern 1pt} (j = 1, \ldots ,s) \), the utility value is denoted as \( U'(r,s) \), then we have \( U'(r,s) \le U(r,s) \). If buyer r + 1 or seller s + 1 can trade, then \( (p_{r + 1}^{B} - p_{o}^{{}} )\sum\nolimits_{j = 1}^{n} {x_{r + 1,j}^{{}} } < 0 \) or \( (p_{o}^{{}} - p_{s + 1}^{S} )\sum\nolimits_{i = 1}^{m} {x_{i,s + 1}^{{}} } < 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} . \) Thus, \( U(r + 1,s) \le U(r,s) \) or \( U(r,s + 1) \le U(r,s) \). Therefore, the matching mechanism scheme of case (I) is the optimal solution of model (25).

In case (II), the utility value according to rule (II) is denoted as \( U(r*,s) \). If \( \sum\nolimits_{j = 1}^{n} {x_{r*j}^{{}} } \le q_{r}^{*} \), \( \sum\nolimits_{j = 1}^{n} {x_{ij}^{{}} } \le q_{i} {\kern 1pt} {\kern 1pt} (i = 1, \ldots r - 1), \) or \( \sum\nolimits_{i = 1}^{m} {x_{ij}^{{}} } \le q_{j}^{{}} {\kern 1pt} {\kern 1pt} (j = 1, \ldots ,s) \), the utility value is denoted as \( U'(r*,s) \), then we have \( U'(r*,s) \le U(r*,s) \). If the demand of buyer r can be satisfactorily completed, seller \( s'{\kern 1pt} {\kern 1pt} (s' > s) \) will sell (\( q_{r}^{{}} - q_{r}^{*} \)) to buyer s. The utility value of r sellers and s’ sellers is denoted as \( U(r,s') \). Then, the utility value is \( U(r,s') = \sum\nolimits_{i = 1}^{r - 1} {\left[ {(p_{i}^{B} - p_{o}^{{}} )\sum\nolimits_{j = 1}^{n} {x_{ij}^{{}} } } \right]} + (p_{r}^{B} - p_{o}^{{}} )q_{r}^{*} + (p_{r}^{B} - p_{o}^{{}} )(q_{r}^{{}} - q_{r}^{*} )+ \sum\nolimits_{j = 1}^{s} {\left[ {(p_{o}^{{}} - p_{j}^{S} )\sum\nolimits_{i = 1}^{m} {x_{ij}^{{}} } } \right]} + (p_{o}^{{}} - p_{s'}^{{}} )(q_{r}^{{}} - q_{r}^{*} ) = U(r*,s) + (p_{r}^{B} - p_{s'}^{{}} )(q_{r}^{{}} - q_{r}^{*} ) \). Since \( p_{r}^{B} \le p_{o}^{{}} < p_{s + 1}^{S} \), we can obtain \( p_{r}^{B} \le p_{o}^{{}} < p_{s'}^{S} \), and then \( (p_{r}^{B} - p_{s'}^{{}} )(q_{r}^{{}} - q_{r}^{*} ) < 0 \). Therefore, we calculate that \( U(r,s') < U(r*,s) \). If buyer r + 1 or seller s + 1 can trade, then \( (p_{r + 1}^{B} - p_{o}^{{}} )\sum\nolimits_{j = 1}^{n} {x_{r + 1,j}^{{}} } < 0 \) or \( (p_{o}^{{}} - p_{s + 1}^{S} )\sum\nolimits_{i = 1}^{m} {x_{i,s + 1}^{{}} } < 0 \). Thus, \( U(r + 1,s) < U(r*,s) \) or \( U(r,s + 1) < U(r*,s) \).

The proof required for case (III) is similar to case (II).

Theorem 5

The double auction mechanism designed in this paper satisfies the incentive compatibility.

Proof

The proof of incentive compatibility is similar to Vickrey’s argument for single object auctions (Vickrey 1961). Suppose that seller j with reservation value \( {}^{r}p_{j}^{S} \) submits a sealed bid \( p_{j}^{S} \), and other sellers submit their real valuations.

If \( {}^{r}p_{j}^{S} \le p_{o} \), there are three possible scenarios. Scenario (I), \( p_{j}^{S} \le {}^{r}p_{j}^{S} \le p_{o} \). Seller j wins the bidding, but due to underbidding. The unit’s expected utility is \( (p_{o} - {}^{r}p_{j}^{S} ) \ge 0 \), which is equivalent to the unit’s expected utility when seller j bids for at the reservation price \( {}^{r}p_{j}^{S} \). Scenario (II), \( {}^{r}p_{j}^{S} \le p_{o} \le p_{j}^{S} \), seller j loses the bidding, and the unit’s expected utility is zero. Scenario (III), \( {}^{r}p_{j}^{S} \le p_{j}^{S} \le p_{o} \), Seller j wins the bidding, but due to the buyer’s overbidding. The unit’s expected utility is also \( (p_{o} - {}^{r}p_{j}^{S} ) \ge 0 \), which is equivalent to the unit’s expected utility when seller j bids at the reservation price \( {}^{r}p_{j}^{S} \).

If \( {}^{r}p_{j}^{S} > p_{o} \), there also exist three possible scenarios. Scenario (IV), \( p_{j}^{S} \le p_{o} \le {}^{r}p_{j}^{S} \). Seller j wins the bidding, but due to underbidding. The unit’s expected utility is \( (p_{o} - {}^{r}p_{j}^{S} ) < 0 \). Scenario (V), \( p_{o} < p_{j}^{S} < {}^{r}p_{j}^{S} \), seller j loses the bidding, and the unit’s expected utility is zero. Scenario (VI), \( p_{o} \le {}^{r}p_{j}^{S} \le p_{j}^{S} \), seller j loses the bidding, and the unit’s expected utility is zero.

Examining the above six scenarios, it was found that if a seller bids not in accordance with the true reservation value, the unit’s expected utility may be negative, zero or the same compared to if the seller were to bid truthfully. The proof for buyers is similar. Thus, the mechanism designed in this paper does hold incentive compatibility for all the participants.

Theorem 6

The double auction mechanism developed in this paper satisfies the weak budget balance.

Proof

From the formula (20), we have \( p_{r}^{B} \ge p_{s}^{S} \). If there are r buyers and s sellers that can trade, we obtain \( {\kern 1pt} {\kern 1pt} U = \sum\nolimits_{i = 1}^{m} {\left( {p_{i}^{B} \sum\nolimits_{j = 1}^{n} {x_{ij}^{{}} } } \right) - \sum\nolimits_{j = 1}^{n} {\left( {p_{j}^{S} \sum\nolimits_{i = 1}^{m} {x_{ij}^{{}} } } \right)} } \ge 0 \). This indicates that the proposed mechanism has always a non-negative social welfare utility and hence it satisfies the weak budget balance.

Theorem 7

The double auction mechanism developed in this paper satisfies the individually rational.

Proof

The rules of three cases in Sect. 5.2 indicate that each buyer/seller obtains a non-negative social welfare utility and hence, the individually rational is satisfied.

6 Computational analysis of real cases

To facilitate carbon emissions trading and effectively control carbon emissions in Beijing, the China Beijing Environment Exchange (CBEE) was established in 2008. By the end of 2017, the total carbon emissions trading volume in the CBEE has exceeded 40 million tonnes. The CBEE currently employs the real carbon emissions trading mechanism based on the one-sided auction method, which may result in fewer final traders and consequently lower trading efficiencies. In this section, we will compare the proposed mechanism with the real mechanism used by the CBEE, and analyze the advantages of the proposed trading mechanism. Specifically, we will simulate bidding data for buyers and sellers based on the CBEE transaction price data and simulation schemes of Xu (2014) in Sect. 6.1. In Sects. 6.2 and 6.3, the trading results obtained by the proposed mechanism are presented and analyzed. In Sect. 6.4, the real carbon emissions trading mechanism of CBEE is introduced. Afterwards, we compare the proposed mechanism with the real mechanism of CBEE, and analyze the advantages of the trading mechanism proposed in this paper in terms of transaction efficiency, transaction utility, and number of winners. In Sect. 6.5, we use a variety of randomly generated data to further validate the performance of the proposed mechanism.

6.1 Data collection

To further verify the effectiveness and practicability of our double auction mechanism for emission permits, we considered 15 buyers and 12 sellers according to the rules of CBEE, as shown in Table 2. Without loss of generality, there are more buyers than sellers in a carbon trading market. Formally, we assumed that \( q_{i}^{B} \) follows the discrete uniform distribution in the interval [100, 200], and that \( q_{j}^{S} \) follows the discrete uniform distribution in the interval [100, 150]. To overlap the buyer/seller’s bids, we assumed that \( p_{i}^{B} \) follows the continuous uniform distribution in the interval [28, 40], and that \( p_{j}^{S} \) follows the continuous uniform distribution in the interval [28, 35]. All the data were randomly generated by Matlab software (2010b version), based on the carbon emissions trading rules issued by the China Beijing Environment Exchange.

Table 2 Buyers’ and sellers’ bidding information
Full size table

6.2 Auction results and analysis

From Table 3, it is evident that the total permits demand of all buyers is 2140 t, and that the total permits supply is 1564 t. The total demand is thus higher than the total supply, but this does not mean that each seller’s carbon permits can be traded given that the market organizer has to match the supply and demand based on buyers’ and sellers’ bid prices. From Table 3, it can also be noted that the bid price of buyer I is larger than the bid price of seller k, and that the bid price of buyer J is lower than the bid price of seller k. Hence, the transaction set of buyers is \( \{ A,B, \ldots ,I\} \), and the transaction set of sellers is \( \{ a,b, \ldots ,k\} \). The final double auction transaction price is a value in the interval [32.89, 33.59].

Table 3 Buyers’ and sellers’ bidding ranking information
Full size table

Table 3 provides the matching results for all buyers and sellers, which are illustrated in graph form in Fig. 2. In the latter, the top stepped line reflects each buyer’s bid price and emission permit demand, and the bottom stepped line provides each seller’s bid price and emission permit supply. From this, it can be seen that the intersection of the two stepped lines occurs with buyer I and seller k. From Table 3, we can deduce that the total emission permit demand from buyer A to buyer I is 1356 t, and that the total emission permit supply from buyer a to buyer k is 1421 t. This indicates that not every seller here can completely trade their permit supply. Given that \( \sum\nolimits_{i = A}^{I} {q_{i}^{B} } < \sum\nolimits_{i = a}^{k} {q_{j}^{S} } \), rule (III) is adopted. The bidding and matching results are shown in Table 4. The trade volume of seller k is obtained by \( \sum\nolimits_{i = A}^{I} {q_{i}^{B} } < \sum\nolimits_{i = a}^{k - 1} {q_{j}^{S} } \), according to rule (III).

Fig. 2
figure 2

Matching results for all buyers and sellers

Full size image
Table 4 Buyers’ and sellers’ bidding and matching results
Full size table

Both buyers’ and sellers’ prices were generated by MATLAB, and each price was different. This section discusses how the principles proposed in this paper can be used for dealing with the case where two buyers/sellers bid at the same price. For winning buyers, if two buyers bid at the same price, their trade results will not be affected. For example, if buyers H and I bid at the same price, which is supposed to be the price given by buyer I, these two buyers also could obtain their maximum demands. This is due to the fact that the price of buyer I (or H) is higher than the final transaction price. If buyers J and K provide the same price as the price of buyer J, they will also lose the bidding in the auction.

However, if two winning sellers bid at the same price, a different situation will occur. For instance, if seller j and k bid at the same price, there will occur two possible scenarios, as shown in Fig. 3. In Fig. 3a, the bid prices of seller j and k are supposed to be 32.89 RMB (the price of seller k). According to Principle 1 designed in this paper, seller j and k are considered as a “single” seller j’. According to rule (III), the permit supply of seller j’ cannot be completely traded, and the permit trading volume is \( \sum\nolimits_{i = A}^{I} {q_{i}^{B} } - \sum\nolimits_{j = a}^{j' - 1} {q_{j}^{S} } \) = 164 t. Based on Principle 1, the permit trading volume of seller j is \( q_{j}^{{}} = round\left( {\frac{{q^{*} q_{j} }}{{q_{j} + q_{k} }}} \right) \) = 88 ton, and the permit trading volume of seller k is \( q_{k}^{{}} = round\left( {\frac{{q^{*} q_{k} }}{{q_{j} + q_{k} }}} \right) \) = 76 ton. From Fig. 3b, the bid prices of seller j and k are supposed to be 32.18 RMB (the price of seller j). It is found that the intersection of the two stepped lines in Fig. 3 will change, as instigated by buyer J and seller k. This means that buyer \( (A,B, \ldots ,I,J) \) and seller \( (a,b, \ldots ,k) \) can trade within the mechanism. Since \( \sum\nolimits_{i = A}^{J} {q_{i}^{{}} } > \sum\nolimits_{i = a}^{k} {q_{j}^{{}} } \), the permit demand of buyer J cannot be completely satisfied, and the permit volume obtained will be \( \sum\nolimits_{j = a}^{k} {q_{i}^{S} } - \sum\nolimits_{i = A}^{I} {q_{i}^{B} } \) = 82 t.

Fig. 3
figure 3

Two sellers bid at the same price

Full size image

6.3 Incentive compatibility analysis

This section analyzes the incentive compatibility of the double carbon auction mechanism from the perspectives of both buyer and seller. For any buyer, the best decision is to bid at the real reservation price. For buyer J, 32.54 RMB per ton is its real reservation price. Figure 2 shows that buyer J cannot buy any permits when bidding at this price (32.54 RMB per ton). If buyer J’s bid price is higher than the real reservation price, e.g. 33.79 RMB per ton. After reordering the price, buyer J and seller k will be able to trade. Here, Although buyer J can win in the auction, the unit’s expected utility is negative, that is \( 32.54 - p_{o}^{{}} < 0 \). If buyer J’s bid price is lower than the real reservation price, it still cannot buy any permits in the auction. In another example, the real reserve price can enable buyer I to obtain the carbon permits. However, the real reserve price can only guarantee that the permits can be traded, not that they will be traded at an ideal price. Changing the biding price may thus have no effect on this buyer, or reduce the unit’s utility; this buyer may even be kicked out of the trade set. If buyer I bids at 32.79 RMB per ton, they are still in the trade set but their total demand cannot be completely satisfied. If buyer I bids at 32.24 RMB per ton, they will lose in the auction and buyer J will enter into the trade set. Therefore, for any buyer, biding at the real reserve price is arguably the optimum strategy.

For any seller, bidding at the real reservation price is also the most favorable decision. For example, if seller j decreases their bidding price, this will have no effect on the trading set and the final auction price. However, if seller j bids at a high price, they will be kicked out of the trading set, ultimately losing in the auction. Another example can be seen in the case of seller l. If he bid at a higher price, they still cannot trade their permits in the auction. If, however, they bid at the price of 32.79 RMB, they will win in the auction but the unit’s expected utility will be negative.

It is also useful to examine the special case of seller k, who is ranked last in the seller trading set. If their bidding price is higher than 33.59 RMB, they will lose in the auction. If the bidding price of seller k lies between 32.89 RMB and 33.59 RMB, they can still trade in the auction and obtain more auction revenue, but this would infer a higher risk. Since all price information is sealed, seller k does not know they rank last in the trade set. If they were to decrease the bidding price to lower than 32.89 RMB, they would also stay in the trade set. However, the final auction transaction price would be lower, meaning that seller k’s auction revenue would be reduced. Therefore, the outcomes of this special case also confirm that biding at the real reserve price is an optimum strategy for any seller.

6.4 Comparison with the actual auction method of the CBEE case

To standardize the trading of carbon emissions and to maintain the order of the carbon emissions trading market, several local Chinese governments have formulated carbon emission trading rules. For example, the CBEE of China allows traders to trade carbon permits via auctions. Specifically, buyers or sellers report their information (price and purchase or sale quantity) to the trading platform. The information becomes publicly available on the trading platform. If a buyer is interested in the offer of a particular seller z, he can place a bid to this particular seller z. The bid price of the buyer cannot be below the price of the seller. If other buyers are also interested in the offer of seller z, they can place their bids. When the trading time has run out, the trading platform determines the winners on the basis of the buyer’s price. In this paper, a scenario with a seller and several buyers (or a buyer) is defined as sell auction. Similarly, if a seller were interested in the demand of a particular buyer Y, he could place a bid to this buyer Y. Other sellers could also place bids to buyer Y if they were interested in the demand of buyer Y. The scene with a buyer and several sellers (or one seller) has been defined as a buy auction in this paper. For specific trading rules, interested readers can refer to the Beijing Environment Exchange (http://www.cbeex.com.cn).

We first discuss the sell auction scenario: Suppose the buyers A, B, and C bid to seller a. Buyers’ bid prices (39.18, 38.15, and 38.06) are all larger than the price of seller a (29.06); therefore, the bids of all buyers are valid. However, the supply volume of seller a is only 117. Based on the ranking of bidding prices, only buyer A can trade emission permits with seller a. This means that only buyer A can buy 117 permits from seller a. Similarly, suppose buyers G, H, and K bid to the seller j. The bid price of buyer K is lower than the price of seller j; therefore, the bid of buyer K is invalid. The bid price of buyer G is higher than that of buyer H; therefore, buyer G has the priority to buy emission permits from seller j. The results are that buyer G can obtain 114 permits, and buyer H can obtain the remaining 18 permits.

In a buy auction scenario, suppose the sellers g, h, and k bid to buyer J. Since the bid price of seller k (32.89) is higher than the price of buyer J, seller k’s bid is invalid. Seller g’s bid price is lower than that of seller h; therefore, seller g has the priority to sell emission permits to buyer J. The results indicate that seller g sells 130 permits to buyer J, while seller h sells 62 permits to buyer J.

In the above example, we merely generated random buy/sell auction scenarios. To better verify the superiority of the method proposed in this paper, we randomly generated 10, 100, and 10,000 buy/sell auction scenarios. The specific comparison results are shown in Tables 5 and 6. These tables use the following five indicators: (1) Average number of traded buyers (ANTB) and average number of traded Sellers (ANTS). If we generated a random sell auction scenario i, there would be \( d_{i}^{B} \) buyers who can obtain permits from the seller. When we randomly generate n sell auction scenarios, ANTB = \( {{\sum\nolimits_{i = 1}^{n} {d_{i}^{B} } } \mathord{\left/ {\vphantom {{\sum\nolimits_{i = 1}^{n} {d_{i}^{B} } } n}} \right. \kern-0pt} n} \). Similarly, If we generated a random buy auction scenario i’, there would be \( d_{i'}^{S} \) sellers who can sell permits to the buyer. Then, we can obtain ANTS = \( {{\sum\nolimits_{i' = 1}^{n} {d_{i'}^{S} } } \mathord{\left/ {\vphantom {{\sum\nolimits_{i' = 1}^{n} {d_{i'}^{S} } } n}} \right. \kern-0pt} n} \). (2) Average auction transaction efficiency (AATE). In a randomly generated sell auction scenario i, ATEi = (buyers’ transaction volume + seller’s transaction volume)/(all buyers’ demand volume + all sellers’ supply volume). If we randomly generated n sell auction scenarios, AATE = \( {{\sum\nolimits_{i = 1}^{n} {ATE_{i} } } \mathord{\left/ {\vphantom {{\sum\nolimits_{i = 1}^{n} {ATE_{i} } } n}} \right. \kern-0pt} n} \). (3) Average seller utility (AST) and average buyer utility (ABT). In a randomly generated sell auction scenario i, suppose J buyers buy permits from seller z. Then, STi =  \( \sum\nolimits_{j = 1}^{J} {(p_{j}^{B} } - p_{z}^{S} )*Buyer{\kern 1pt} j's \, transaction \, volume \). If we randomly generated n sell auction scenarios, AST = \( {{\sum\nolimits_{i = 1}^{n} {ST_{i} } } \mathord{\left/ {\vphantom {{\sum\nolimits_{i = 1}^{n} {ST_{i} } } n}} \right. \kern-0pt} n} \). Similarly, for a randomly generated buy auction scenario i’, suppose J’ sellers sell permits to buyer z’. BTi’ = \( \sum\nolimits_{j' = 1}^{J'} {(p_{z'}^{B} } - p_{j'}^{S} )*{\kern 1pt} {\kern 1pt} the{\kern 1pt} {\kern 1pt} {\kern 1pt} transaction \, volume{\kern 1pt} {\kern 1pt} {\kern 1pt} of{\kern 1pt} {\kern 1pt} seller{\kern 1pt} j' \, \). If we randomly generated n buy auction scenarios, ABT = \( {{\sum\nolimits_{i' = 1}^{n} {BT_{i'} } } \mathord{\left/ {\vphantom {{\sum\nolimits_{i' = 1}^{n} {BT_{i'} } } n}} \right. \kern-0pt} n} \).

Table 5 Performance comparison between one-side sell auction and double auction
Full size table
Table 6 Performance comparison between one-side buy auction and double auction
Full size table

According to the ANBT results of Table 5, the number of buyers who win in the one-side auction is very small, and an average below two buyers can buy permits from a seller. However, in our proposed double auction method, nine buyers are winners. The AATE results show that the market efficiency of one–side auction is relatively low. This indicates that many auction participants lose in a one-side auction. The AATE score of the proposed double auction is 0.73, which means that 73% of the trading requirements of the auction participants can be satisfied. The AST results also show that the seller utility of our proposed method is higher than that in the one-side auction. That is because there is only one seller in the one-side auction, while multiple sellers exist in our method. Table 6 provides the same result, showing that the results obtained via our method are better than those via one-side auction.

Compared to the proposed auction method in this paper, the auction method used in the Beijing Environment Exchange has at least three major deficiencies: First, few buyers/sellers can win an auction. In one-side auction, one seller and less than two buyers exist (or one buyer and less than two sellers). However, in our proposed method, there are nine buyers and eleven sellers, which can trade permits. This has also been validated by Cheng et al. (2016) who concluded that double auction could attract more participants to bid and expand the market size. Second, the efficiency of the transaction was low. For instance, in the sell/buy auction scenario, the efficiency was about 0.3. The transaction efficiency in our method was 0.73, indicating that the efficiency of the double auction is higher than that of one-side auction (Muller et al. 2002; Xu 2014). Third, the utilities of the buyer or seller are reduced. For example, in the seller auction, only one seller exists, while eleven sellers exist in our method. Thus, the seller utility obtained with our method is higher and has a better performance.

6.5 Performances of the proposed mechanisms

This section validates the performance of the proposed model and mechanism, using a variety of randomly generated data. In the following tables, “SU” represents the social welfare utility acquired by solving the model (25); “SUTB” represents the actual social welfare utility of the transaction buyers; “SUTS” represents the actual social welfare utility of the transaction sellers; “TAB” represents the trading rate of buyers, which is equal to the ratio of the transaction volume of buyers to the total demand of buyers; “TAS” represents trading rate of sellers, which is equal to the ratio of the transaction volume of sellers to the total supply of buyers.

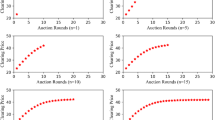
The main findings can be summarized as follows: First, while the market size increases (e.g. an increase in the buyers/sellers of the auction), the total social welfare utility increases as well. Second, the SUTB and SUTS increase with market size. In addition, in each line of Table 7, the sum of SUTB and SUTS is equivalent to SU, which is consistent with formulas (22), (23), and (24). These findings indicate that the proposed method is applicable in both a large size permit market and a small size permit market. Third, TAB ranges between 0.558 and 0.652, and TAS ranges between 0.666 and 0.732. This indicates that the trading rate of buyers/sellers is relatively stable, regardless of the number of involved participants.

Table 7 Performance of the proposed method
Full size table

To further verify that the method proposed in this paper is incentive compatible, we conducted a computational experiment to study the impact of the degree of truthful biding of buyer/seller on the performance of the auction. This degree of the truthful biding of one buyer/seller equals the ratio of his bid to the true valuation. For a buyer, the actual bid price may be lower than the true valuation, because he/she wants to obtain more carbon permits at less cost. Therefore, the degree of truthful biding for the buyer is below 1. For a seller, the actual bid price may be higher than the true valuation, because he/she wants to sells his/her carbon permits at a higher price so that he/she can increase profits. Therefore, the degree of truthful biding for the seller is above 1. In this experiment, the number of buyers/sellers is set from 30 to 50. The corresponding results are listed in Table 7.

As shown in Table 8, the total social welfare utility and the actual social welfare utility of transaction buyers and sellers all show downward trends with decreasing degree of truthful biding of the buyer. In the case of 30 Buyers and Sellers, and while the degree of buyers’ truthful biding decreases from 0.98 to 0.90, the SU decreases from 16221 to 6317, the SUTB decreases from 11867 to 5140, and the SUTS decreases from 4353 to 1177. In addition, the trading rates of buyers and sellers decrease. In the case of 30 Buyers and 30 Sellers, TAB and TAS also show downward trends as the degree of truthful biding of the buyer reduces. For sellers, the results are similar. SU, SUTB, SUTS, TAB, and TAS all decrease when the ratio of the bid to the true valuation increases. These findings indicate that our method can effectively realize incentive compatibility. If buyers/sellers submit untrue biddings, their actual social welfare utility will decrease, and final trading rates will also decrease.

Table 8 Impact of the degree of truthful biding
Full size table

7 Conclusion

The practical use of auction theory and methods is increasing in the allocation of emission permits, which imposes great impacts on production decisions between manufacturing companies. However, most existing studies on emission permit auctions focus on a single buyer and multiple sellers, or a single seller and multiple buyers. Fewer studies pay close attention to multiple sellers and buyers simultaneously. In order to address this gap, we propose an allocation mechanism of emission permits based on a multi-unit double auction. This began with estimating the emission demand and supply of each enterprise in cases where there are multiple firms with high pollution abatement costs (buyers), and multiple firms with low pollution abatement costs (sellers). Second, based on the principle of maximizing the total social welfare utility, the paper extends the double auction model for emission permits. Third, the auction mechanism was divided into three cases according to the balance between permit supply and demand. For each type of cases, we designed a transaction matching rule. This paper then proved that the double auction mechanism designed satisfied incentive compatibility, whereby it was found that each rational buyer/seller is best off bidding at a true reserve price under the double auction mechanism. Finally, the computational analysis of a real CBEE case was conducted to validate the validity and practicability of the mechanism. The results showed that the extended auction method presented in this paper could effectively increase the number of traded participants, improve the auction transaction efficiency, and increase the utilities of traded participants; regardless of the size of the permit trading market, the mechanism presented in this paper is always applicable; the method could effectively realize the incentive compatibility, thus encouraging each buyer/seller to submit the true bidding.

With regard to future research, this work can be extended in several directions. Although the double auction mechanism is designed for emission permit allocation, it can also be used in other limited resource allocation scenarios. In addition, game theory can be considered and integrated into the double auction mechanism. This integration would treat seller/buyers in the group as individual decision makers with different levels of cooperation and coordination.