Physarum solver: a bio-inspired method for sustainable supply chain network design problem

Abstract

A supplier of products and services aims to minimize the capacity investment cost and the operational cost incurred by unwanted byproducts, e.g. carbon dioxide emission. In this paper, we consider a sustainable supply chain network design problem, where the capacity and the product flow along each link are design variables. We formulate it as a multi-criteria optimization problem. A bio-inspired algorithm is developed to tackle this problem. We illustrate how to design a sustainable supply chain network in three steps. First, we develop a generalized model inspired by the foraging behaviour of slime mould Physarum polycephalum to handle the network optimization with multiple sinks. Second, we propose a strategy to update the link cost iteratively, thus making the Physarum model to converge to a user equilibrium. Third, we perform an equivalent operation to transform a system optimum problem into a corresponding user equilibrium problem so that it is solvable in the Physarum model. The efficiency of the proposed algorithm is illustrated with numerical examples.

1 Introduction

Supply chain network is a vital component of production, storage, and distribution of products to customers. With the rapid development of e-commerce, customers are more than ever concerned with the on-time delivery of goods. An optimal supply chain network not only helps the company to decrease the cost, but also speeds up the on-time delivery of products. As a result, the optimal supply chain network design is of upmost importance concerned by many researchers (Esmaeilikia et al. 2016; Philpott and Everett 2001; Ramezani et al. 2014; Xiao et al. 2005).

In recent years, the sustainability of supply chains has received more and more attention from operational researchers not only due to a need to reduce the transportation cost involved, but also to minimize the impact of transportation on the climate (Dong et al. 2016; Hugo and Pistikopoulos 2005; Nagurney et al. 2007). A range of approaches has been developed to achieve environmental sustainability. For example, Hugo and Pistikopoulos (2005) mapped the environmental issues with traditional economic criteria to a multi-objective optimisation problem. A mathematical programming was developed to optimize the selection, allocation and capacity extension of processing technologies and assignment of transportation links. Krikke et al. (2003) formulated a quantitative model to facilitate the decision-making related to product designs and logistic networks, where they quantified the environmental impact of a close-loop supply chain for refrigerators using a linear-energy and waste function. Tsai and Hung (2009) developed a fuzzy-goal programming approach that integrated activity-based costing and performance evaluation in a value-chain structure to choose the optimal supplier.

In the abundant literature, one of the commonly used means to measure the sustainability of a supply chain is to consider the amount of carbon dioxide emissions generated in this process. For example, Becken and Patterson (2006) employed the amount of national carbon dioxide emissions from tourism as an indicator to quantify the sustainability of tourism industry. Lopez-Ruiz and Crozet (2010) analyzed the sustainability of transport in France and proposed an approach that combined technology and public policy to achieve the reduction in CO$_2$ emission. Nagurney et al. (2007) defined a function to quantify the cost resulted from the CO$_2$ emission at each operation phase and formulated a mathematical model to characterize the multi-criteria sustainable supply chain network design problem. They modeled the problem in the framework of variational inequality and developed a modified projection method to find out the optimal solution to the sustainable supply chain network design problem.

However, there is still space to improve the method developed by Nagurney et al. (2007). Each link a can be associated with two design variables: the flow of the product through the link ($f_a$), and the design capacity of the link ($u_a$). We will demonstrate the equivalence between the design capacity and the product flow. In addition, the projection method for solving the supply chain network problem Nagurney and Nagurney (2010) requires to enumerate all the possible paths connecting the suppliers with the demand markets. With the increase of network size, the enumeration process consumes more and more time. Last but not least, the method proposed by Nagurney and Nagurney (2010) requires a substantial number of iterations for the solution to converge. Specifically, for a supply chain network design problem with 11 nodes and 17 links, it takes 497 iterations for the proposed approach to converge to a stale solution (Nagurney 2010).

Engineers are always looking into behaviour, mechanics, physiology of living systems to uncover novel principles of distributed sensing, information processing and decision making that could be adopted in development of future and emergent computing paradigms, architectures and implementations (Deng et al. 2015; Du et al. 2015, 2016; Zhang et al. 2013a). For example, Lei and Guo (2013) developed a modified artificial bee colony (MABC) algorithm to solve the job shop scheduling problem with lot streaming and transportation. They illustrated that the method was efficient in identifying the near-optimal solutions but without exploring the search space exhaustively. To overcome the premature convergence of Particle Swarm Optimization (PSO), Wang et al. (2013) developed a hybrid PSO algorithm using a diversity enhancing mechanism. The performance of the proposed method was demonstrated on a set of benchmark functions, including rotated multi-modal and shifted high-dimensional problems. Besides, some available theories, e.g. evidence theory, probabilistic graphs, have been leveraged to address the uncertainty arising in various optimization problems (Jensen and Nielsen 2013; Jiang et al. 2016a, b; Ning et al. 2016; Yao et al. 2013).

Nowadays, one of the popular living computing substrates is a slime mould Physarum Polycephalum. Plasmodium is a vegetative stage of acellular slime mould P. polycephalum, a single cell with many nuclei, which feeds on microscopic particles (Stephenson et al. 1994). When foraging the plasmodium propagates towards sources of food, surrounds them, secretes enzymes and digests the food; it may form a congregation of protoplasm covering the food source. When several sources of nutrients are scattered in the plasmodium’s environment, the plasmodium forms a network of protoplasmic tubes connecting the masses of protoplasm at the food sources. The network is optimal because it minimises transportation time of metabolites. The fact that Physarum optimises its protoplasmic network inspired researchers to interpret the slime mould’s behaviour in terms of computation and to develop experimental laboratory prototypes and computer and mathematical models of Physarum-based algorithms and computing devices. In laboratory experiments and theoretical studies, it is shown that the slime mould can solve many graph theoretical problems, such as finding the shortest path (Nakagaki et al. 2000; Zhang et al. 2013b, c), connecting different arrays of food sources in an efficient manner (Adamatzky 2014; Jones and Adamatzky 2014; Nakagaki et al. 2007), and network design (Adamatzky and Martinez 2013; Masi and Vasile 2014; Tero et al. 2010; Zhang et al. 2015a).

In this paper, we are motivated to develop a approach that overcomes the deficiencies existing in Nagurney’s method. We explore the principles of Physarum’s protoplasmic network optimisation, including a continuity of cytoplasm flow during the iterative process of the optimization and dynamic reconfiguration of the network, to design an optimal supply chain networks with minimal cost associated with the capacity investment and environment emissions. In order to get the optimal solution, we need to perform the following modifications to the original Physarum solver. First, we extend the Physarum model to resolve the network optimization problem where multiple sinks exist. Second, we develop a novel strategy to update the link cost iteratively, thus making the Physarum model converge to the user equilibrium (UE). Third, we perform an equivalent operation to transform the system optimum (SO) problem into a corresponding user equilibrium problem, which is solvable by the Physarum model. In addition, we prove an important optimality condition: for any link, its design capacity $u_a$ should be equal to the product flow $f_a$ in the optimal solution. Such proposition simplifies the model greatly through reducing a number of design variables and eliminating the need to enumerate all possible paths in the network. Since the Physarum model allows to travel all the alternate paths between the origins and the destinations, such mechanism is very useful in solving the supply chain network design problem.

The remainder of this paper is organised as follows. In Sect. 2, we describe the sustainable supply network design problem. In Sect. 3, we illustrate the method proposed by Nagurney and Nagurney (2010) and the deficiencies. In Sect. 4, we develop a Physarum-based method for designing the sustainable supply chain network. In Sect. 5, numerical examples are used to demonstrate the practicality and flexibility of the proposed approach; we also compare our approach with the method developed in (Nagurney and Nagurney 2010). In Sect. 6, we summarize our results and discuss future research directions.

2 Preliminaries

In this section, the supply chain network design model and the Physarum model are introduced.

Fig. 1

The supply chain network topology

2.1 The multicriteria sustainable supply chain network design model (Nagurney and Nagurney 2010)

Table 1 Notation and parameters in the multicriteria sustainable supply chain network design model

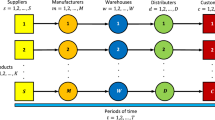
Let us consider the supply chain network shown in Fig. 1, a firm at the top level (origin) aims at delivering the goods or products to the nodes corresponding to the retail outlets (destinations) at the bottom level. The links connecting the source node 1 with the destination nodes represent the activities of production, storage and transportation of good or services. Different network topologies correspond to different supply chain network problems. We assume that there exists at least one path linking node 1 with each destination node, which can guarantee that the demand at each retail outlet will be satisfied. The notations used for the model are shown in Table 1.

As shown in Fig. 1, the firm takes into consideration $n_M$ manufacturers, $n_D$ distribution centers when $n_R$ retailers with demands ${d_{{R_1}}},{d_{{R_2}}}, \ldots ,{d_{{R_{{n_R}}}}}$ must be served. Node 1 in the first layer is linked with the possible $n_M$ manufacturers, which are represented as ${M_1},{M_2}, \ldots ,{M_{{n_M}}}$. These edges in the manufacturing level are associated with the possible distribution center nodes, which are expressed by ${D_{1,1}},{D_{2,1}}, \ldots ,{D_{{n_D},1}}$. These links mean the possible shipment between the manufacturers and the distribution centers. The links connecting ${D_{1,1}},{D_{2,1}}, \ldots ,{D_{{n_D},1}}$ with ${D_{1,2}},{D_{2,2}}, \ldots ,{D_{{n_D},2}}$ reflect the possible storage links. The links between ${D_{1,2}},{D_{2,2}}, \ldots ,{D_{{n_D},2}}$ and ${R_1},{R_1}, \ldots ,{R_{{n_R}}}$ denote the possible shipment links connecting the storage centers with the retail outlets.

Let the supply chain network be represented by a graph G(N, L), where N is a set of nodes and L is a set of links. Each link in the network is associated with a cost function and the cost reflects the total cost of all the specific activities in the supply chain network, such as the transport of the product, the delivery of the product, etc. The cost associated with link a is expressed by ${{\widehat{c}}_a}$. A path p connecting node 1 with a retail node shown in Fig. 1 denotes the whole activities related with manufacturing the products, storing them and transporting them, etc. Assume $w_k$ denotes the set of source and destination nodes $(1, R_k)$ and $P_{w_k}$ represents the set of alternative associated possible supply chain network processes joining $(1,R_k)$. We assume P is a set of all paths joining $(1,R_k)$ and $x_p$ is the flow of the product on path p. The following Eq. (1) holds:

$$\begin{aligned} \sum \limits _{p \in {P_{{w_k}}}} {{x_p}} = {d_{{w_k}}},\quad k = 1, \ldots ,{n_R}. \end{aligned}$$

(1)

Let $f_a$ represent the flow on link a, then the following conservation flow must be met:

$$\begin{aligned} {f_a} = \sum \limits _{p \in P} {{x_p}{\delta _{ap}}} ,\quad \forall \,a \in L. \end{aligned}$$

(2)

Equation (2) means that the inflow is equal to the outflow on link a.

These flows can be grouped into the vector f. The flow on each link must be a nonnegative number, i. e. the following Eq. (5) must be satisfied:

$$\begin{aligned} {x_p} \ge 0,\quad \forall \,a \in L. \end{aligned}$$

(3)

Suppose the maximum capacity on link a is expressed by $u_a, \forall a \in L$. The actual flow through the link a cannot exceed the maximum capacity on this link:

$$\begin{aligned} \begin{array}{l} {f_a} \le {u_a},\quad \forall \,a \in L, \\ 0 \le {u_a},\quad \forall \,a \in L. \\ \end{array} \end{aligned}$$

(4)

The total cost on each link, for simplicity, is represented as a function of the flow of the product on all the links (Nagurney 2006, 2009; Nagurney and Woolley 2010; Nagurney et al. 2002):

$$\begin{aligned} {{\widehat{c}}_a} = {{\widehat{c}}_a}\left( f_a \right) ,\quad \forall \,a \in L. \end{aligned}$$

(5)

The total investment cost of increasing capacity $u_a$ of link a can be expressed as follows:

$$\begin{aligned} {{\widehat{\pi }} _a} = {{\widehat{\pi }} _a}\left( {{u_a}} \right) ,\quad \forall \,a \in L. \end{aligned}$$

(6)

Summarily, the supply chain network design optimization problem aims to satisfy the demand of each retail outlet and minimize the total cost, including the total cost of operating the various links and the capacity investments:

$$\begin{aligned} Minimize\;\;\sum \limits _{a \in L} {{{{\widehat{c}}}_a}\left( f_a \right) } + \sum \limits _{a \in L} {{{{\widehat{\pi }} }_a}\left( {{u_a}} \right) } \end{aligned}$$

(7)

subject to constraints (1)–(4).

We also take into account the cost associated with the total amount of carbon dioxide emissions generated both in the capital investment phase and operation phase. Suppose we are going to invest in a power plant. In the investment phase, we estimate the production and transportation of various raw materials, such as steel, concrete, and copper. The production and shipment of these materials contribute to the emissions of carbon dioxide. In the operation phase, the operation of a power plant consumes a certain quantity of resources, e.g. coal, water. The combustion of coal, however, adds a significant amount of carbon dioxide to the emission per unit of heat energy. Thus, it is necessary to account for the cost related with the carbon dioxide emissions generated both in the capital investment phase and operation phase.

Suppose $e_a(f_a)$ represents the emission-generation function on link a in the operation phase, proportional to the flow on this link. Let ${{\widehat{e}}_a}\left( {{u_a}} \right)$ denotes the emission-generation function on link a in the capital investment period. This is the function of the product flow on that link. Thus minimisation of the emission can be expressed in the following form:

$$\begin{aligned} Minimize\quad \sum \limits _{a \in L} {{e_a}\left( {{f_a}} \right) + {{{\widehat{e}}}_a}\left( {{u_a}} \right) } \end{aligned}$$

(8)

Combining two objectives shown in Eqs. (7) and (8), we can construct the following objective function:

$$\begin{aligned} \begin{array}{l} Minimize\quad \sum \limits _{a \in L} {{\hat{c}}_a\left( {{f_a}} \right) + {{{\widehat{\pi }} }_a}\left( {{u_a}} \right) } + \omega \left( {\sum \limits _{a \in L} {{e_a}\left( {{f_a}} \right) + {{{\widehat{e}}}_a}\left( {{u_a}} \right) } } \right) \\ s.t.\; \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad {f_a} \le {u_a} \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad {0} \le {u_a} \\ \end{array} \end{aligned}$$

(9)

where $\omega$ is a nonnegative constant assigned to the emission-generation attribute. It reflects how much the firm is willing to pay per unit of emission; alternatively, it can be thought of as the tax imposed by the government (Wu et al. 2006).

Our objective is to determine the optimal product flow $f_a$ and the link design capacity $u_a$ on any link $a \in L$, so that the total cost of the supply chain network, defined by Eq. (9), can be minimized.

2.2 Physarum solver

Physarum Polycephalum is a large, single-celled amoeboid organism forming a dynamic tubular network connecting the discovered food sources during foraging. The mechanism of tube formation can be described as follows. Tubes thicken in a given direction when shuttle streaming of the protoplasm persists in that direction for a certain time. There is a positive feedback between the flux and the tube thickness, as the conductance of the sol is greater in a thicker channel. With this mechanism in mind, a mathematical model illustrating the shortest path finding has been constructed by Tero et al. (2007).

Suppose the shape of the network formed by the Physarum is represented by a graph, in which a plasmodial tube refers to an edge of the graph and a junction between tubes refers to a node. Two special nodes labeled as $N_1$, $N_2$ act as the starting node and ending node respectively. The other nodes are labeled as $N_3,N_4,N_5,N_6$ etc. The edge between nodes $N_i$ and $N_j$ is $M_{ij}$. The parameter $Q_{ij}$ denotes the flux through tube $M_{ij}$ from node $N_i$ to $N_j$. Assume the flow along the tube is approximated by Poiseuille flow, then the flux ${Q_{ij}}$ can be expressed as:

$$\begin{aligned} {Q_{ij}} = \frac{{{D_{ij}}}}{{{L_{ij}}}}({p_i} - {p_j}) \end{aligned}$$

(10)

where ${p_i}$ is the pressure at node ${N_i}$, ${D_{ij}}$ is the conductivity of the tube ${M_{ij}}$, and $L_{ij}$ is its length.

By assuming that the inflow and outflow must be balanced, we have:

$$\begin{aligned} \sum {{Q_{ij}}} = 0\quad (j \ne 1,2) \end{aligned}$$

(11)

For the source node ${N_1}$ and the sink node ${N_2}$, the following equation holds:

$$\begin{aligned} \begin{array}{l} \sum \limits _i {{Q_{i1}} + {I_0} = 0} ,\\ \sum \limits _i {{Q_{i2}} - {I_0} = 0} . \end{array} \end{aligned}$$

(12)

where ${I_0}$ is the flux flowing from the source node, and ${I_0}$ is a constant value here.

In order to describe such an adaptation of tubular thickness we assume that the conductivity ${D_{ij}}$ changes over time according to the flux ${Q_{ij}}$. An evolution of ${D_{ij}(t)}$ can be described by the following equation:

$$\begin{aligned} \frac{d}{{dt}}{D_{ij}} = f(|{Q_{ij}}|) - \gamma {D_{ij}} \end{aligned}$$

(13)

where $\gamma$ is a decay rate of the tube. The equation implies that a conductivity becomes nil if there is no flux along the edge. The conductivity increases with the flux. The f is monotonically increasing continuous function satisfying $f(0) =0$.

Then the network Poisson equation for the pressure can be obtained from Eq. (10–12) as follows:

$$\begin{aligned} \sum \limits _i {\frac{{{D_{ij}}}}{{{L_{ij}}}}({p_i} - {p_j})} = \left\{ { \begin{array}{ll} { + 1} &{}\quad {for} \; {i = 1,} \\ { - 1} &{}\quad {for} \; {j = 2,} \\ 0 &{}\quad {otherwise.} \\ \end{array}} \right. \end{aligned}$$

(14)

By setting ${p_2}$=0 as a basic pressure level, all ${p_i}$ can be determined by solving Eq. (14) and each ${Q_{ij}} = \frac{{{D_{ij}}}}{{{L_{ij}}}}({p_i} - {p_j})$ is also obtained.

We assume $f(Q) = |Q|$ because $f\left( {\left| {{Q_{ij}}} \right| } \right) = \left| Q \right| ,\gamma = 1$, the Physarum converges to the shortest path with a high rate (Tero et al. 2007). With the flux calculated, the conductivity can be derived, where Eq. (15) is used instead of Eq. (13), adopting the functional form $f(Q) = |Q|$.

$$\begin{aligned} \frac{{D_{ij}^{n + 1} - D_{ij}^n}}{{\delta t}} = |Q| - D_{ij}^{n + 1} \end{aligned}$$

(15)

where $\delta t$ is a time mesh size, and the upper index n indicates a time step. For details, please refer to Tero et al. (2007).

3 Nagurney’s method

In Nagurney’s method, the supply chain network design problem is formulated as following: determine $(f^*, u^*, \beta ^*)$, where $f^*$ denotes the link flow, $u^*$ denotes the design capacity, and $\beta ^*$ denotes the optimal Lagrange multipliers associated with constraint (4), such that the following equation holds:

$$\begin{aligned}&\sum \limits _{a \in L} {\left[ {\frac{{\delta {{{\widehat{c}}}_a}\left( {f_a^*} \right) }}{{\delta {f_a}}} + \omega \frac{{\delta {e_a}\left( {f_a^*} \right) }}{{\delta {f_a}}} + \beta _a^*} \right] } \times \left[ {{f_a} - f_a^*} \right] + \sum \limits _{a \in L} {\left[ {\frac{{\delta {{{\widehat{\pi }} }_a}\left( {u_a^*} \right) }}{{\delta {u_a}}} + \omega \frac{{\delta {{{\widehat{e}}}_a}\left( {u_a^*} \right) }}{{\delta {u_a}}} - \beta _a^*} \right] } \times \left[ {{u_a} - u_a^*} \right] \nonumber \\&\quad + \sum \limits _{a \in L} {\left[ {u_a^* - f_a^*} \right] } \times \left[ {{\beta _a} - \beta _a^*} \right] \ge 0,\;\forall \left( {f,u,\beta } \right) \in K. \end{aligned}$$

(16)

where $K \equiv \left\{ {\left. {\left( {f,u,\beta } \right) } \right| \exists x \ge 0, {\;} and{\;} (1)-(3) {\;}and {\;}(9){\;} hold {\;}and{\;} \beta >0} \right\}$, where f is the vector of link flows, u is the vector of link capacities and x is the vector of path flows.

The variational inequality problem (VIP) represented by Eq. (16) can be put in the following standard form: determine $X^* \in K$, such that

$$\begin{aligned} \left\langle {F{{\left( {{X^*}} \right) }^T},X - {X^*}} \right\rangle \ge 0,\;\forall \,X \in K. \end{aligned}$$

(17)

where $\left\langle { \cdot , \cdot } \right\rangle$ denotes the inner product in the corresponding Euclidean space, and $F\left( X \right) \equiv \left( {{F_1}\left( X \right) ,{F_2}\left( X \right) ,{F_3}\left( X \right) } \right)$, such that:

$$\begin{aligned} \begin{array}{l} {F_1}\left( X \right) = \left[ {\frac{{\delta {{{\widehat{c}}}_a}\left( {{f_a}} \right) }}{{\delta {f_a}}} + \omega \frac{{\delta {e_a}\left( {{f_a}} \right) }}{{\delta {f_a}}} + {\beta _a};\;a \in L} \right] ,\\ {F_2}\left( X \right) = \left[ {\frac{{\delta {{{\widehat{\pi }} }_a}\left( {{u_a}} \right) }}{{\delta {u_a}}} + \omega \frac{{\delta {{{\widehat{e}}}_a}\left( {{u_a}} \right) }}{{\delta {u_a}}} - {\beta _a};\;a \in L} \right] ,\\ {F_3}\left( X \right) = \left[ {{u_a} - {f_a};\;a \in L} \right] . \end{array} \end{aligned}$$

(18)

The VIP formulated in Eq. (16) can be solved by the modified projection method. The general problem-solving procedures can be summarized in Algorithm 1:

However, there are some issues in the method developed by Nagurney. As indicated in Eq. (16), there are three design variables in X, namely: the link flow, the path flow, and the link capacity. To obtain the product flow along each path, a precondition is to enumerate all the alternate paths connecting the firm with the demand markets. The enumeration process is time consuming. With the increase of network size and the complexity of network topology, it is not realistic to enumerate all the possible paths. This deficiency in turn hinders the application of Nagurney’s method into real-world scenarios. Another issue is that the modified projection method takes many iterations before convergence. To be specific, in Nagurney (2010), in a supply chain network with only 11 nodes, the modified projection method consumes 497 iterations for convergence. Last but not least, as shown in Algorithm 1, the modified projection method needs to solve two variational inequality sub-problems. As a result, we need to implement different optimization techniques to determine the value of ${{\overline{X}} ^{k - 1}}$ and $X^k$ at each iteration.

4 Proposed method

In this section, we employ the Physarum model to solve the supply chain network design problem. There are two sub-problems to address:

• In the shortest path finding model, there is only one source node and one ending node. However, in the sustainable supply chain network design problem, there are more than one retail outlets.

• In the sustainable supply network design problem, the objective is to minimize the total cost, including the operation cost, the capacity investment cost, and the emission-generation cost. We need to modify the classical Physarum model to achieve this objective.

4.1 One source multiple-sinks Physarum model

In the original model constructed by Tero et al. (2007), there is one starting node and one ending node. In the sustainable supply chain network design problem, as shown in Fig. 1, there are ${n_R}$ retail outlets in demand of the goods or products. From the left to the right, from the top to the bottom, we can label these nodes one by one. In order to solve the one source multi-sinks’ model in the supply chain network design, the following Eq. (19) is derived:

$$\begin{aligned} \sum \limits _{i} { {\frac{{{D_{ij}}}}{{{L_{ij}}}}} \left( {{p_i} - {p_j}} \right) } = \left\{ \begin{array}{l@{\quad }l} + \sum \nolimits _{i = 1}^{n_R} {{d_{{R_i}}}} &{}for\;j = 1 \\ - d_{R_j} &{}for\;j = {1},{2}, \ldots {{{n_R}}} \\ 0&{}otherwise \\ \end{array} \right. \end{aligned}$$

(19)

where $j=1$ means that $\sum \nolimits _{i = 1}^{n_R} {{d_{{R_i}}}}$ units of goods are distributed from the firm to the other manufacturing facilities, $j ={{n_R}}$ denotes $n_R$ retail outlets are in need of $d_{R_{j}}$ units of goods, respectively.

4.2 Physarum-inspired model for designing sustainable supply chain network

In the sustainable supply chain design problem, it is required that the flow is less than its actual capacity. In our view, in the optimal solution to such problem, its capacity $u_a$ is equal to its actual flow $f_a$.

Lemma 1

Optimality condition: For each link a, $\forall a \in {L}$, its design capacity $u_a$ should be equal to the corresponding link flow $f_a$ in the optimal solution.

Fig. 2

The relationship between $\pi _a$ and $u_a$

Proof

According to Eq. (4), the flow $f_a$ passing through link a cannot exceed its design capacity $u_a$. Hence, we have ${f_a} \le {u_a}$. Suppose ${u_a} > {f_a}$, let ${\Delta _a} = {u_a} - {f_a}$ denote the remaining capacity. Since $\Delta _a > 0$, some capacity on link a is not used. As ${\hat{\pi }}_a$ is monotonically increasing, as can be observed from Fig. 2, we have ${{\widehat{\pi }} _a}\left( {{f_a} + {\Delta _a}} \right) > {{\widehat{\pi }} _a}\left( {{f_a}} \right)$.

In contrast, if $u_a = f_a$, on one hand, the constraint defined in Eq. (6) can be satisfied. On the other hand, the cost of designing a link with capacity $f_a$ is ${{\widehat{\pi }} _a}\left( {{f_a}} \right)$, which is less than ${{\widehat{\pi }} _a}\left( {{f_a} + {\Delta _a}} \right)$. As a consequence, in the optimal solution, for each firm, $u_a = f_a$. In other words, ${u_a} = \sum \limits _{p \in P} {{x_p}{\delta _{ap}}} ,\forall a \in L.$ $\square$

According to Lemma 1, for any link $a \in L$, its link capacity $u_a$ is equal to $f_a$ in the optimal solution. As a result, we can replace $u_a$ with $f_a$ and the objective function defined in Eq. (9) can be simplified as follows:

$$\begin{aligned} {Minimize\quad \sum \limits _{a \in L} {{{{\hat{c}}}_a}\left( {{f_a}} \right) + {{{\hat{\pi }} }_a}\left( {{f_a}} \right) } + \omega \left( {\sum \limits _{a \in L} {{e_a}\left( {{f_a}} \right) + {{{\hat{e}}}_a}\left( {{f_a}} \right) } } \right) } \end{aligned}$$

(20)

By replacing $u_a$ with $f_a$, we can benefit from the following aspects:

• The design variable $u_a$ is eliminated from our method. Nagurney’s approach has $n_{P}+2*n_{L}$ design variables whereas our method only has $n_{L}$ design variables, where $n_P$ and $n_L$ denote the number of paths and links in the network, respectively.

• As $u_a = f_a$, the constraint defined in Eq. (6) is not in need any more. In Nagurney’s paper, in order to guarantee that the link flow does not exceed the capacity, they bing another variable—Lagrange multipliers $\beta$ as shown in Eq. (16), which in turn increases the complexity of solving the problem in terms of the number of constraints and design variables.

Another issue is how to modify Physarum model so that it can be used for solving the sustainable supply chain network design problem. The sustainable supply chain network design problem is a system optimum (SO) problem from the point view of flow theory in the field of transportation science, which aims at minimizing the total cost. There is an equivalent conversion between system optimum problem and user equilibrium optimization problem. To date, Physarum has been successfully implemented to handle the user equilibrium (UE) problem in the transportation networks, e.g. see Zhang et al. (2014, 2015b). The idea is to update the cost of each link according to the cost functions at each iteration. Algorithm 2 illustrates the detailed procedures for solving UE in the sustainable supply chain network.

However, different from UE solution, in the sustainable supply chain network, we aim at determine a system optimum solution of minimizing the total cost. For the purpose of using Physarum model to address this issue, we transform the SO state into the corresponding UE state based on the following Eq. (21) (Bell and Iida 1997; Bingfeng and Ziyou 2013).

$$\begin{aligned} {{\widetilde{t}}_a}\left( {{x_a}} \right) = {t_a}\left( {{x_a}} \right) + {x_a}\frac{{d{t_a}\left( {{x_a}} \right) }}{{d{x_a}}},\;\forall \,a \in L \end{aligned}$$

(21)

where $x_a$ represents the flow on link a, $t_a(x_a)$ is the cost function per unit of flow on link a while ${{\widetilde{t}}_a}\left( {{x_a}} \right)$ denotes the transformed cost function per unit of flow.

In the sustainable supply chain network, $L_{a}$ is the cost when the flow is $Q_{a}$. Hence, the following Eq. (22) is derived to express the cost for per unit of flow:

$$\begin{aligned} L{F_{a}} = \frac{{{{{\hat{c}}}_a}\left( {{Q_{a}}} \right) + {{{\hat{\pi }} }_a}\left( {{Q_{a}}} \right) + \omega \left( {{e_a}\left( {{Q_{a}}} \right) + {{{\hat{f}}}_a}\left( {{Q_{a}}} \right) } \right) }}{{{Q_{a}}}} \end{aligned}$$

(22)

By combining with Eq. (21), we update the cost along link a as follows:

$$\begin{aligned} {L_a} = \frac{{{{{\hat{c}}}_a}\left( {{Q_a}} \right) + {{{\hat{\pi }} }_a}\left( {{Q_a}} \right) + \omega \left( {{e_a}\left( {{Q_a}} \right) + {{{\hat{f}}}_a}\left( {{Q_a}} \right) } \right) }}{{{Q_a}}} + {Q_a} * {\frac{{d\left( {\frac{{{{{\hat{c}}}_a}\left( {{x_a}} \right) + {{{\hat{\pi }} }_a}\left( {{x_a}} \right) + \omega \left( {{e_a}\left( {{x_a}} \right) + {{{\hat{f}}}_a}\left( {{x_a}} \right) } \right) }}{{{x_a}}}} \right) }}{{d{x_a}}}_{\left| {{x_a}} \right. = {Q_a}}}\nonumber \\ \end{aligned}$$

(23)

According to the proposed method, the general flow for solving the optimal sustainable supply chain network can be summarized in Algorithm 3. The most time consuming part in the proposed approach is to solve the linear equations defined in Eq. (19). The upper bound of computational effort solving linear equations with n unknown variables is $O(n^3)$.

There are several possible solutions to decide when to stop execution of Algorithm 3, e.g. the maximum number of iterations is achieved or a flux through each tube remains unchanged for some period of time. In the examples illustrated in the next section we use the following termination criterion. In numerical experiments discussed in next section the algorithm halts when the $\sum \nolimits _{i,j = 1,2, \ldots ,n} {\left( {\left| {D_{ij}^{count + 1} - D_{ij}^{count}} \right| } \right) } \le 0.001$, where $D_{ij}^{count + 1}, D_{ij}^{count}$ is the conductivity associated with the edge $L_{ij}$ during the ${n+1}_{th}$ and$n_{th}$ iterations respectively, and n is the number of nodes in the network.

In summary, the proposed algorithm has the following advantages:

• 1. There is no need to enumerate all possible paths from a firm to demand markets. The underlying mechanism in Physarum model produces the traversal of all the paths and the optimal product flow allocation through each path.

• 2. The modified projection method needs to employ different optimization techniques to perform the update at each iteration to obtain the value of ${{\overline{X}} ^{k - 1}}$ and $X^k$. Whereas, the proposed algorithm does not require to implement any optimization technique. Instead, we only need to solve linear equations defined in Eq. (19).

• 3. The proposed algorithm converges faster than the modified projection approach (this will be illustrated in the next section).

5 Numerical examples

We demonstrate efficiency of our algorithm in several numerical examples. The algorithm is implemented using Matlab on an Intel Pentium Dual-Core E4600 processor (2.40 GHz) with 2GB of RAM under Windows Seven. The baseline for all the examples are shown in Fig. 3. In this figure, the numbers along the links represent the sequence. There are three alternative manufacturing plants and each of them has two possible technologies. Each manufacturer is in association with two possible distribution centers. Similarly, each distribution center is associated with two possible storage centers. The firm has to satisfy the demand from three possible retail outlets. The basic data for the following examples is shown in Table 2.

Fig. 3

Adopted from Nagurney and Nagurney (2010)

The baseline supply chain network topology for all the examples.

Table 2 Total cost and emission functions for the numerical examples.

Example 1

In this example, the demands for each retail outlet is

$$\begin{aligned} {d_{{R_1}}} = 45,\quad {d_{{R_3}}} = 35,\quad {d_{{R_3}}} = 5 \end{aligned}$$

The cost functions and emission functions are shown in Table 2. In this example, we assume that the firm does not care about the emission generated in its supply chain. Therefore, $\omega =0$. Figure 4 shows us the flux changing trend during the iterative process. It can be seen that Physarum model converges to the optimal solution after 25 iterations whereas Nagurney’s solution consumes 497 iterations for the same supply chain network.

Table 3 indicates the specific flow on each link. As expected, the flow associated with each link is equal to its capacity. According to Eq. (9), we can see that the overall cost is 10716.33, which is consistent with that in Nagurney and Nagurney (2010). From Table 3, we can see that link 14 has zero capacity and zero flow. Hence, in the optimal sustainable supply chain network, link 14 will be removed.

Fig. 4

The flux variation during the iterative process in the Example 1

Table 3 The optimal solution of Example 1

Example 2

Here we modify data from Example 1 by adopting the parameter $\omega =5$, which shows a degree of the firm’s concern about the environment. The optimal solution to this example is given in Table 4. Fig. 5 demonstrates how the flow along each link converges to a stable value. As can be seen, the Physarum solver finds the optimal solution within 25 iterations. The total cost as shown in Eq. (7) for this example is 11288.27 while it is 11285.04 in Nagurney’s solution. The total emission cost is 7735.71. Our solution is approximately the same as Nagurney’s solution in terms of product flow and link design capacity along each link.

In Nagurney’s solution, they rounded the solution to the second decimal, but this caused one problem, such as the violation of flow conservation law. Specifically, for the node $M_1$, its inflow is the sum of the flow on link 18 and link 1: 33.22 (19.32 $+$ 13.90). Its outflow consists of two separate flows on link 4 and link 5, which is 33.23 (19.43 $+$ 13.80). The inflow is not equal to the outflow. Similarly, it is also observed that such kind of phenomenon can be found in the node $D_{2,1}$. The rounding error is also the reason resulting in the negligible difference between our objective function value and Nagurney’s objective function value.

The Physarum model converges to the optimal solution after 22 iterations. In the optimal solution, all the links have positive capacity and flows. In addition, the flows are equal to the capacity on all the links. In Example 1, links 1 and 18 have the same flow. However, in Example 2, the flow on link 1 is increased by 50% while the flow on link 18 only increases by about 10%. This is because the emission cost on link 1 is less than that on link 18. Such kind of behavior, can also be found on links 2 and 19.

Table 4 The optimal solution to Example 2

Fig. 5

The flux variation during the iterative process in the Example 2

Example 3

Example 3 has the same data as Example 2 except that the firm cares more about the environment: $\omega =10$. The optimal solution is given in Table 5. Figure 6 shows the changing trend of each link during the iterative process. In this example, the total cost is 11418.44 while it is 11414.07 in Nagurney’s solution. But the rounding error in Example 2 is also found in the solution of Nagurney and Nagurney (2010). Specifically, for node $M_1$, its inflow is equal to 26.35 (15.80 $+$ 10.55) while its outflow is 26.36 (14.37 $+$ 11.99). As for node $M_3$, its inflow is 24.32 (13.10 $+$ 11.22) while its outflow is 24.33 (15.45 $+$ 8.88). In a similar way, for node $D_{1,1}$, its inflow is 49.48 (19.66 $+$ 14.37 $+$ 15.45) while its outflow is 49.47 (24.30 $+$ 25.17). The rounding error also results in the tiny difference on the objective function values.

In the proposed Physarum model, it takes 0.018 seconds and 21 iterations to converges to the optimal solution. As illustrated in Example 2, all the links have positive flows and capacity.

Table 5 The optimal solution to Example 3

Fig. 6

The flux variation during the iterative process in the Example 3

6 Conclusions

We used Physarum solver to propose a biologically inspired solution to the sustainable supply chain network design problem, where both the product flow and link capacity are design variables. Our contributions are four-fold. First, we prove an important optimality condition: the product flow must be equal to the link capacity in the optimal solution. Second, we generalize the original Physarum model such that it can be used to deal with network optimization problem with multiple sinks. Third, we develop a novel strategy with straightforward update procedures at each iteration to obtain the cost along each link, which results in that the Physarum model converges to the user equilibrium (UE) state. Last but not least, an equivalent transformation between the system optimum (SO) problem and the user equilibrium problem is carried out to make the sustainable supply chain network design problem solvable by the modified Physarum model.

Future research will progress as follows. Since the Physarum model can solve the user equilibrium problem, which is formulated as a variational inequality problem, we will enrich the model to solve other generalized variational inequality problems, such as the multi-class, multi-criteria traffic network equilibrium problem, and user equilibrium problem with elastic demand. The flux is continuous in the Physarum algorithm during the iterations, this characteristic makes the algorithm capable to accommodate dynamical changes in the network structure. We can make full use of this feature to extend Physarum model and hybridise it with other available techniques to solve a wide range of optimization problem in dynamic environment.