Bayesian forecasting of multivariate time series: scalability, structure uncertainty and decisions

Abstract

I discuss recent research advances in Bayesian state-space modeling of multivariate time series. A main focus is on the “decouple/recouple” concept that enables application of state-space models to increasingly large-scale data, applying to continuous or discrete time series outcomes. Applied motivations come from areas such as financial and commercial forecasting and dynamic network studies. Explicit forecasting and decision goals are often paramount and should factor into model assessment and comparison, a perspective that is highlighted. The Akaike Memorial Lecture is a context to reflect on the contributions of Hirotugu Akaike and to promote new areas of research. In this spirit, this paper aims to promote new research on foundations of statistics and decision analysis, as well as on further modeling, algorithmic and computational innovation in dynamic models for increasingly complex and challenging problems in multivariate time series analysis and forecasting.

1 Introduction

Hirotugu Akaike was a seminal contributor to statistical science in its core conceptual bases, in methodology and in applications. I overview some recent developments in two areas in which Akaike was an innovator: statistical time series modeling and statistical model assessment (e.g., Akaike 1974, 1978, 1979, 1981; Parzen et al. 1998). These continue to be challenging areas in basic statistical research as well as in expanding applications. I highlight recent developments that address statistical and computational scalability of multivariate dynamic models, and questions of evaluating and comparing models in the contexts of explicit forecasting and decision goals. The content is selective, focused on Bayesian methodology emerging in response to challenges in core and growing areas of time series applications.

Several classes of models are noted. In each, advances have used variants of the “decouple/recouple” concept to: (a) define flexible dynamic models for individual, univariate series; (b) ensure flexibility and relevance of cross-series structures to define coherent multivariate dynamic models; (c) maximally exploit simple, analytic computations for sequential model fitting (forward filtering) and forecasting; and (d) enable scalability of resulting algorithms and computations for model fitting, forecasting and use. Model classes include dynamic dependency network models (Sect. 3) and the more general simultaneous dynamic graphical models (Sect. 4). These define flexibility and scalability for conditionally linear dynamic models and address, in particular, concerns for improved multivariate volatility modeling. Further classes of models are scalable, structured multivariate and multi-scale approaches for forecasting discrete/count time series (Sect. 5), and new classes of dynamic models for complicated and interacting flows of traffic in networks of various kinds (Sect. 6). In each of these areas of recent modeling innovation, specific problems defining applied motivation are noted. These include problems of time series monitoring in areas including studies of dynamic flows on Internet networks, problems of forecasting with decision goals such as in commercial sales and macroeconomic policy contexts, and problems of financial time series forecasting for portfolio decisions.

Following discussion of background and multivariate Bayesian time series literature in Sect. 2, Sects. 3–6 each contact one of the noted model classes, with comments on conceptual innovation linked to decouple/recouple strategies to address the challenges of scalability and modeling flexibility. Contact is also made with questions of model comparisons and evaluation in the contexts of specific applications, with the example areas noted representing ranges of applied fields for which the models and methods are increasingly relevant as time series data scales increase. Each section ends with some comments on open questions, challenges and hints for future research directions linked to the specific models and applied contexts of the section.

2 Background and perspectives

2.1 Multivariate time series and dynamic models

Multivariate dynamic linear models (DLMs) with conditionally Gaussian structures remain at the heart of many applications (West and Harrison 1997, chap. 16; Prado and West 2010, chaps. 8–10; West 2013). In such contexts, denote by $\mathbf {y}_t$ a q-vector time series over equally spaced discrete time t where each element $y_{j,t}$ follows a univariate DLM: $y_{j,t} = \mathbf {F}_{j,t}'\varvec{\theta }_{j,t} + \nu _{j,t}$ with known dynamic regression vector $\mathbf {F}_{j,t},$ latent state vector $\varvec{\theta }_{j,t}$ and zero-mean, conditionally normal observation errors $\nu _{j,t}$ with, generally, time-varying variances. The state vector evolves via a conditionally linear, Gaussian evolution equation $\varvec{\theta }_{j,t} = \mathbf {G}_{j,t} \varvec{\theta }_{j,t-1} + \varvec{\omega }_{j,t}$ with known transition matrix $\mathbf {G}_{j,t}$ and zero-mean, Gaussian evolution errors (innovations) $\varvec{\omega }_{j,t}.$ The usual assumptions include mutual independence of the error series and their conditional independence on past and current states. Discount factors are standard in structuring variance matrices of the evolution errors and dynamics in variances of observation errors, a.k.a. volatilities. See Chapter 4 in  West and Harrison 1997; Prado and West 2010 for complete details. In general, $\mathbf {F}_{j,t}$ may contain constants, predictor variables, lagged values of the time series and latent factors that are also modeled. In the latter case, resulting dynamic latent factor models are not amenable to analytic forward filtering and forecasting computations; computationally intensive methods including Markov chain Monte Carlo (MCMC) are needed.

Some multivariate models central to applied work just couple together this set of univariate DLMs. Consider special cases when $\mathbf {F}_{j,t}=\mathbf {F}_t$ and $\mathbf {G}_{j,t}=\mathbf {G}_t$ for all $j=1\,{:}\,q,$ so the DLMs share common regression vectors and evolution matrices. This defines the class of common components, or exchangeable time series models (Prado and West 2010, chap. 10) with $\mathbf {y}_t = \mathbf {F}_t'\varvec{\Theta }_t + \varvec{\nu }_t$ where $\varvec{\Theta }_t = [\varvec{\theta }_{1,t},\ldots ,\varvec{\theta }_{q,t}]$ and where $\varvec{\nu }_t$ is the q-vector of the observation errors. The state evolution becomes a matrix system for $\varvec{\Theta }_t$ with conditional matrix-normal structure. Special cases include traditional time-varying vector autoregressions (TV-VAR) when $\mathbf {F}_t$ includes lagged values of the $y_{j,t}$ (Kitagawa and Gersch 1996; Prado and West 2010, chap. 9). A critical feature is that these models allow coupling via a volatility matrix $V(\varvec{\nu }_t) = \varvec{\Sigma }_t$ to represent dynamics in cross-series relationships through a role in the matrix-normal evolution of $\varvec{\Theta }_t$ as well as in individual volatilities. The standard multivariate discount volatility model underlies the class of dynamic inverse Wishart models for $\varvec{\Sigma }_t$, akin to random walks on the implied precision matrices $\varvec{\Omega }_t = \varvec{\Sigma }_t^{-1}.$ Importantly, the resulting analysis for forward filtering and forecasting is easy. Prior and posterior distributions for $\varvec{\Sigma }_t$ as it changes over time are inverse Wishart, enabling efficient sequential analysis, and retrospective analysis exploits this for simple posterior sampling over historical periods. Alternative multivariate volatility models—such as various multivariate GARCH and others—are, in contrast, often difficult to interpret and challenging to fit and obviate analytic sequential learning and analysis. Though the dynamic Wishart/common components model comes with constraints (noted below), it remains a central workhorse model for monitoring, adapting to and—in short-term forecasting—exploiting time variation in multivariate relationships in relatively low-dimensional series.

2.2 Parameter sparsity and dynamic graphical model structuring

Interest develops in scaling to higher dimensions q, particularly in areas such as financial time series. A main concern with multivariate volatility models is/was that of over-parametrization of variance matrices $\varvec{\Sigma }_t = \varvec{\Omega }_t^{-1}$, whether time varying or not. One natural development to address this was the adaptation of ideas of Bayesian graphical modeling (Jones et al. 2005; Jones and West 2005). A conditional normal model in which each $\varvec{\Omega }_t$ has zeros in some off-diagonal elements reflects conditional independence structures among the series visualized in an undirected graph: pairs of variables (nodes) are conditionally dependent given all other variables if, and only if, they have edges between them in the graph. The binary adjacency matrix of the graph is a visual of this. Consider the $q=30$ series of monthly returns on a set of Vanguard mutual funds in Fig. 1 as an example; viewing the image in Fig. 2 as if it were purely white/black, it represents the adjacency matrix of a graph corresponding to off-diagonal zeros in $\varvec{\Omega }_t$. The image indicates strong sparsity representing a small number of nonzero elements; this means significant conditional independence structure and constraints leading to parameter dimension reduction in $\varvec{\Sigma }_t.$

Fig. 1

Time series of monthly % financial returns on a set of $q=30$ Vanguard mutual funds over a period of years indicated. The series represent 18 actively managed funds and 12 index funds that are, in principle, less expensive for an investor. High dependence across returns series is clear, suggesting that model parameter dimension reduction—such as offered by graphical model structuring of precision matrices $\varvec{\Omega }_t$—is worth exploring

Fig. 2

Image of posterior probabilities of pairwise edge inclusion in the adjacency matrix of the graph underlying the dynamic precision structure of a multivariate volatility model for 30 monthly Vanguard fund return times series. The scale runs from 0 (white) to 1 (black) with increasing intermediate gray shades. The horizontal and vertical lines separate the funds into the set of 18 managed funds (above/left) and index funds (below/right). Funds are ordered within each category so that most of the high probability edges cluster near the diagonal. The figure indicates very concentrated posterior probabilities with multiple edges clearly in and many others excluded, and a strong level of sparsity

Advances in dynamic modeling extending theory of hyper-inverse Wishart distributions for (decomposable) graphical models (Jones et al. 2005) represented the first practical use of graphical models for parameter dimension reduction. One of the key features of such extensions is that the analytically tractable forward filtering, forecasting and retrospective posterior sampling methodology is maintained for these models conditional on any specified set of conditional independence relationships, i.e., on any specified graph $\mathcal {G}$ (Carvalho and West 2007a, b; Carvalho et al. 2007). Examples in these papers prove the principle and highlight practical advances in methodology. First, sparsity is often supported by time series data, and forecast accuracy is often improved as a result when using graphs $\mathcal {G}$ that are sparse and that the data support. Second, decisions based on data-relevant sparse models are often superior—in terms of realized outcomes—to those of the over-parametrized traditional full models, i.e., models with a complete graph and no zeros in $\varvec{\Omega }_t.$ The statistical intuition that complicated patterns of covariances across series—and their changes over time—can be parsimoniously represented with often far fewer parameters than the full model allows is repeatedly borne out in empirical studies in financial portfolio analyses, econometric and other applications (e.g., Carvalho and West 2007b; Reeson et al. 2009; Wang and West 2009; Wang 2010; Wang et al. 2011). More recent extensions—that integrate these models into larger Bayesian analyses with MCMC-based variable selection ideas and others (e.g.,Ahelegbey et al. 2016a, b; Bianchi et al. 2019)—continue to show the benefits of sparse dynamic graphical model structuring.

2.3 Model evaluation, comparison, selection and combination

Graphically structured extensions of multivariate state-space models come with significant computational challenges unless q is rather small. Since $\mathcal {G}$ becomes a choice, there is a need to evaluate and explore models indexed by $\mathcal {G}$. Some of the above references use MCMC methods in which $\mathcal {G}$ is an effective parameter, but these are simply not attractive beyond rather low dimensions. As detailed and exemplified in Jones et al. (2005), for example, MCMC can be effective in models with $q\sim 20$ or less with decomposable graphical models, but simply infeasible computationally—in terms of convergence—as q increases further. The MCMC approach is simply very poorly developed in any serious applied sense in more general, non-decomposable graphical models, to date; examples in Jones et al. (2005) showcase the issues arising with MCMC in even low dimensions ($q\sim 15$ or less) for the general case. One response to these latter issues has been the development of alternative computational strategies using stochastic search to more swiftly find and evaluate large numbers of models/graphs $\mathcal {G}.$ The most effective, to date, builds on shotgun stochastic search concepts (e.g., Jones et al. 2005; Hans et al. 2007a, b; Scott and Carvalho 2008; Wang 2015). This approach uses a defined score to evaluate a specific model based on one graph $\mathcal {G}$ and then explore sets of “similar” graphs that differ in terms of a small number of edges in/out. This process is sequentially repeated to move around the space of models/graphs, guided by the model scores, and can exploit parallelization to enable swift exploration of large numbers of more highly scoring graphs.

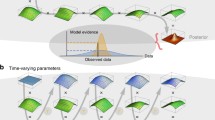
Write $\mathcal {D}_t$ for all observed data at time t and all other information—including values of all predictors, discount factors, interventions or changes to model structure, future values of exogenous predictors—relevant to forecasting. The canonical statistical score of $\mathcal {G}$ based on data over $t=1\,{:}\,n$ is the marginal likelihood value $p(\mathbf {y}_{1\,{:}\,n}|\mathcal {G}, \mathcal {D}_0) = \prod _{t=1\,{:}\,n} p(\mathbf {y}_t|\mathcal {G}, \mathcal {D}_{t-1} )$. At time n, evaluating this score across graphs $\mathcal {G}_1,\ldots ,\mathcal {G}_k$ with specified prior probabilities leads—by Bayes’ theorem—to posterior model probabilities over these k graphs at this time t. With this score, stochastic search methods evaluate the posterior over graphs conditional on those found in the search. Inferences and predictions can be defined by model averaging across the graphs in the traditional way (West and Harrison 1997, chap. 12; Prado and West 2010, chaps. 12). The image in Fig. 2 shows partial results of this from one analysis of the Vanguard funds. This simple model used constitutes a local level with discount-based volatility on any graph $\mathcal {G}$ (precisely as in other examples in (Prado and West 2010, sects. 10.4 & 10.5). The figure shows a high level of implied sparsity in $\varvec{\Omega }_t$ with strong signals about nonzero/zero entries.

Traditional model scoring via AIC, BIC and variants (Akaike 1974, 1978, 1979, 1981; Konishi and Kitagawa 2007, and references therein Prado and West 2010, sect. 2.3.4) define approximations to log marginal likelihoods. As with full Bayesian analysis based on implied model probabilities, these statistical metrics score models based on one-step ahead forecasting accuracy: The overall score from n observations is the product of realized values of one-step forecast densities. This clearly demarks the applied relevance of this score. If the view is that a specific “true” data generating process is within the span of a set of selected models $\mathcal {G}_1,\ldots ,\mathcal {G}_k,$ posterior model probabilities will indicate which are “nearest” to the data; for large n, they will concentrate on one “Kullback-Leibler” nearest model (West and Harrison 1997, sect. 12.2). This is relevant in contexts where the graphical structure is regarded as of inherent interest and one goal is to identify data-supported graphs (e.g., Tank et al. 2015, and references therein).

However, more often than not in applications, the role of $\mathcal {G}$ is as a nuisance parameter and a route to potentially improve accuracy and robustness in forecasting and resulting decisions. That posterior model probabilities ultimately degenerate is a negative in many contexts and is contrary to the state-space perspective that changes are expected over time—changes in relevant model structures as well as state vectors and volatility matrices within any model structure. Further, models scoring highly in one-step forecasting may be poor for longer-term forecasting and decisions reliant on forecasts. While these points have been recognized in recent literature, formal adoption of model evaluation based on other metrics is not yet mainstream. In an extended class of multivariate dynamic models, Nakajima and West (2013a) and Nakajima and West (2013b) focused on comparing models based on h-step ahead forecast accuracy using horizon-specific model scores: time aggregates of evaluated predictive densities $p(\mathbf {y}_{t+h-1}|\mathcal {G}, \mathcal {D}_{t-1})$. It is natural to consider extensions to score full path forecasts over times $t\,{:}\,t+h-1$ based on time aggregates of $p(\mathbf {y}_{t\,{:}\,t+h-1}|\mathcal {G}, \mathcal {D}_{t-1})$ (Lavine et al. 2019). Similar ideas underlie model comparisons for multi-step forecasting in different contexts in McAlinn and West (2019) and McAlinn et al. (2019), where models rebuilt for specific forecast horizons are shown to be superior to using one model for all horizons, whatever the model selection/assessment method.

Fig. 3

Image formatted as in Fig. 2. Now, the 0–1 (white–gray–black) scale indicates frequency of pairwise edge inclusion across 1000 graphical models identified in stochastic search over graphs guided by a chosen portfolio allocation decision analysis. These 1000 graphs were those—out of many millions evaluated—generating the highest returns over a test time period. Funds are reordered within each of the two categories so that most of the high probability edges cluster near the diagonal. The figure indicates somewhat different structure and a higher level of sparsity than that in Fig. 2

Extending this point, models scoring highly on statistical metrics may or may not be optimal for specific decisions reliant on forecasts. While it is typical to proceed this traditional way, increasing attention is needed on decision-guided model selection. An empirical example in sequential portfolio analysis of the Vanguard mutual fund series highlights this. Using the same model as underlies the statistical summaries on sparse structure in $\varvec{\Omega }_t$ in Fig. 2, stochastic search analysis over graphs $\mathcal {G}$ was rerun guided by a portfolio metric rather than the conditional posterior model probabilities. For one standard target portfolio loss function, portfolios were optimized and returns realized over the time period, and the score used is simply the overall realized return. Comparing sets of high probability models with sets of high portfolio return models leads to general findings consistent with expectations. Models with higher posterior probability are sparse, with typically 20–30% of edges representing nonzero off-diagonal (and of course time-varying) precision elements; these models tend to generate ranges of realized returns at low-to-medium portfolio risk levels. Models with higher realized returns are also sparse and generally somewhat sparser, and some of the highest return models have rather low risk.

Figure 3 shows relative frequencies of edge inclusion across a large number of high scoring portfolio graphs. This appears sparser than in Fig. 2 and has a distinct feature in that one series (US Growth listed last in the first group of managed funds) has a large number of edges to other funds; this series is a “hub” in these top-scoring graphs. Model search on posterior model probabilities identifies graphs that represent the complex patterns of collinearities among the series over time in different ways. Typically, “small” dependencies can be represented in multiple ways; hence, the posterior over graphs will tend to identify more candidate edges for inclusion. In contrast, the portfolio decision-guided analysis finds value in sparser graphs with this hub-like structure that is able to generate even weak dependencies among funds other than the hub fund via the one degree of separation feature. One notable result is that the conditional dependence structure among the index funds (lower right in the figures) appears much sparser under decision-guided analysis than under statistical analysis. Across top graphs in terms of portfolios, the US Growth hub fund is a dominant parental predictor for index funds; Fig. 3 shows that the set of index funds are rendered almost completely mutually independent conditional on the US Growth fund. This is quite different to the structure across most highly probably models exhibited in Fig. 2.

While in this applied context the structure of relevant graphs is not of primary interest compared to finding good models for portfolio outcomes, this rationalization of differences is illuminating. The example underscores the point that—whether in time series or other contexts—forecasting and/or decision goals should play central roles in model evaluation and comparison.

2.4 Challenges and opportunities

Graphical modeling to introduce sparsity—hence parsimony and potential improved forecasting and decisions—is seeing increased use in time series as referenced earlier. However, several issues in existing model classes limit modeling flexibility and scalability. With studies in 10s to several 100s of series in areas of finance and macroeconomics becoming routine, some specific issues are noted.

Common components models—including the key class of models with TV-VAR components—are constrained by the common $\mathbf {F}_t,\mathbf {G}_t$ structure and hence increasingly inflexible in higher dimensions. Then, parameter dimension is a challenge. A TV-VAR(p) component implies $\mathbf {F}_t$ includes pq lagged values $\mathbf {y}_{t-1\,{:}\,t-p}$, indicating the issue. Dimension is a key issue with respect to the use of hyper-inverse Wishart (and Wishart) models, due to their inherent inflexibility beyond low dimensions. The single degree-of-freedom parameter of such models applies to all elements of the volatility matrix, obviating customization of practical importance. Larger values of q make search over graphical models increasingly computationally challenging.

Some of these problems are addressed using more complex models with MCMC and related methods for model fitting. Models with dynamic latent factors, Bayesian model selection priors for elements of state vectors (e.g., subset TV-VAR components), and involving “dynamic sparsity” are examples (e.g., Aguilar et al. 1999; Aguilar and West 2000; Prado et al. 2006; Lopes and Carvalho 2007; Del Negro and Otrok 2008; Koop and Korobilis 2010; Carvalho et al. 2011; Koop and Korobilis 2013; Nakajima and West 2013a, b; Zhou et al. 2014; Nakajima and West 2015; Ahelegbey et al. 2016a, b; Kastner et al. 2017; Nakajima and West 2017; Bianchi et al. 2019; McAlinn and West 2019; McAlinn et al. 2019, and many others). However, one of our earlier noted desiderata is to enable scaling and modeling flexibility in a sequential analysis format, which conflicts with increasingly large-scale MCMC methods: Such methods are often inherently challenging to tune and run, and application in a sequential context requires repeat MCMC analysis each time point.

3 Dynamic dependence network models

3.1 Background

Dynamic dependence network models (DDNMs) as in Zhao et al. (2016) nucleated the concept of decouple/recouple that has since been more broadly developed. DDNMs define coherent multivariate dynamic models via coupling of sets of customized univariate DLMs. While the DDNM terminology is new, the basic ideas and strategy are much older and have their bases in traditional recursive systems of structural (and/or simultaneous) equation models in econometrics (e.g.,Bodkin et al. 1991, and references therein). At one level, DDNMs extend this traditional thinking to time-varying parameter/state-space models within the Bayesian framework. Connecting to more recent studies, DDNM structure has a core acyclic directed graphical component that links across series at each time t to define an overall multivariate (volatility) model, indirectly generating a full class of dynamic models for $\varvec{\Omega }_t$ in the above notation. DDNMs thus extend earlier multiregression dynamic models that involve acyclic directed graphical components (Queen and Smith 1993; Queen 1994; Queen et al. 2008; Anacleto et al. 2013; Costa et al. 2015).

Series ordering means that these are Cholesky-style volatility models (e.g., Smith and Kohn 2002; Primiceri 2005; Shirota et al. 2017; Lopes et al. 2018). The resulting triangular system of univariate models can be decoupled for forward filtering and then recoupled using theory and direct simulation for coherent forecasting and decisions. In elaborate extensions of DDNMs to incorporate dynamic latent factors and other components, the utility has been evidenced in a range of applications (e.g., Nakajima and West 2013a, b, 2015, 2017; Zhou et al. 2014; Irie and West 2019).

3.2 DDNM structure

As in Sect. 2.1, take univariate DLMs $y_{j,t} = \mathbf {F}_{j,t}'\varvec{\theta }_{j,t} + \nu _{j,t}$ under the usual assumptions. In a DDNM, the regression vectors and state vectors are conformably partitioned as $\mathbf {F}_{j,t}' = (\mathbf {x}_{j,t}',\mathbf {y}_{pa(j),t}')$ and $\varvec{\theta }_{j,t}'= ( \varvec{\phi }_{j,t}', \varvec{\gamma }_{j,t}')$. Here, $\mathbf {x}_{j,t}$ has elements such as constants, predictor variables relevant to series j,  lagged values of any of the q series, and so forth; $\varvec{\phi }_{j,t}$ is the corresponding state vector of dynamic coefficients on these predictors. Choices are customizable to series j and, while each model will tend to have a small number of predictors in $\mathbf {F}_{j,t},$ there is full flexibility to vary choices across series. Then, $pa(j)\subseteq \{ j+1\,{:}\,q \}$ is an index set selecting some (typically, a few) of the concurrent values of other series as parental predictors of $y_{j,t}.$ The series order is important; only series h with $h>j$ can be parental predictors. In graph-theoretic terminology, any series $h \in pa(j)$ is a parent of j, while j is a child of h. The modeling point is clear: If I could know the values of other series at future time t, I would presumably choose some of them to use to aid in predicting $y_{j,t}$; while this is a theoretical construct, it reduces to a practicable model as noted below. Then, $\varvec{\gamma }_{j,t}$ is the state vector of coefficients on parental predictors of $\mathbf {y}_{j,t}.$ Third, the random error terms $\nu _{j,t}$ are assumed independent over j and t, with $\nu _{j,t}\sim N(0,1/\lambda _{j,t})$ with time-varying precision $\lambda _{j,t}.$ Figure 4 shows an illustration of the structure.

Fig. 4

DDNM for daily prices of international currencies (FX) relative to the US dollar. In order from top-down: The univariate DLM for the Singapore dollar (SGD) relies on SGD-specific predictors $\mathbf {x}_{1,t}$ and volatility $\lambda _{1,t},$ along with parental predictors given by the contemporaneous values of prices of the Swiss franc (CHF) and the British pound (GBP); that for the Swiss franc has specific predictors $\mathbf {x}_{2,t}$ and the Japanese yen, British pound and Euro as parents. Further down the list, the potential parental predictors are more and more restricted, with the final series $j=q$, here the EURO, having no parents

For each series $y_{j,t} = \mu _{j,t} + \mathbf {y}_{pa(j),t}'\varvec{\gamma }_{j,t} + \nu _{j,t}$ where $\mu _{j,t} = \mathbf {x}_{j,t}'\varvec{\phi }_{j,t}$. With $\varvec{\mu }_t = (\mu _{1,t},\ldots ,\mu _{q,t})'$ and $\varvec{\nu }_t=(\nu _{1,t},\ldots ,\nu _{q,t})'$, the multivariate model has structural form $\mathbf {y}_t = \varvec{\mu }_t + \varvec{\Gamma }_t\mathbf {y}_t + \varvec{\nu }_t$ where $\varvec{\Gamma }_t$ is the strict upper triangular matrix with above diagonal rows extending the $\varvec{\gamma }_{j,t}'$ padded with zeros; that is, row j of $\varvec{\Gamma }_t$ has nonzero elements taken from $\varvec{\gamma }_{j,t}$ in the columns corresponding to indices in pa(j). With increasing dimension q,  models will involve relatively small parental sets so that $\varvec{\Gamma }_t$ is sparse. The reduced form of the model is $\mathbf {y}_t =\varvec{\alpha }_t + N(\mathbf {A}_t\varvec{\mu }_t, \varvec{\Sigma }_t)$ where $\mathbf {A}_t = (\mathbf {I}-\varvec{\Gamma }_t)^{-1}$ so that the mean and precision of $\mathbf {y}_t$ are

$$\begin{aligned} \mathbf {A}_t \varvec{\mu }_t= & {} \varvec{\mu }_t + \varvec{\Gamma }_t \varvec{\mu }_t + \varvec{\Gamma }_t^2 \varvec{\mu }_t + \cdots + \varvec{\Gamma }_t^{q-1} \varvec{\mu }_t, \nonumber \\ \varvec{\Omega }_t= & {} \varvec{\Sigma }_t^{-1} = (\mathbf {I}-\varvec{\Gamma }_t)'\varvec{\Lambda }_t (\mathbf {I}-\varvec{\Gamma }_t) = \varvec{\Lambda }_t - \{ \varvec{\Gamma }_t'\varvec{\Lambda }_t + \varvec{\Lambda }_t\varvec{\Gamma }_t\} + \varvec{\Gamma }_t'\varvec{\Lambda }\varvec{\Gamma }_t \end{aligned}$$

(1)

where $\varvec{\Lambda }_t = \text {diag}(\lambda _{1,t},\ldots ,\lambda _{q,t}).$ The mean vector $\mathbf {A}_t \varvec{\mu }_t$ shows cross talk through the $\mathbf {A}_t$ matrix: Series-specific forecast components $\mu _{j,t}$ can have filtered impact on series earlier in the ordering based on parental sets. In Fig. 4, series-specific predictions of CHF and GBP impact predictions of SGD directly through the terms from the first row of $\varvec{\Gamma }_t\varvec{\mu }_t;$ parental predictors have a first-order effect. Then, series-specific predictions of EURO also impact predictions of SGD through the $\varvec{\Gamma }_t^2\varvec{\mu }_t$ term—EURO is a grandparental predictor of SGD though not a parent. Typically, higher powers of $\varvec{\Gamma }_t$ decay to zero quickly (and $\varvec{\Gamma }_t^q=\mathbf {0}$ always) so that higher-order inheritances become negligible; low-order terms can be very practically important. For the precision matrix $\varvec{\Omega }_t,$ Eq. (1) shows first that nonzero off-diagonal elements are contributed by the term $\varvec{\Gamma }_t'\varvec{\Lambda }_t + \varvec{\Lambda }_t\varvec{\Gamma }_t;$ element $\varvec{\Omega }_{j,h,t}=\varvec{\Omega }_{h,j,t} \ne 0$ if either $j\in pa(h)$ or $h\in pa(j).$ Second, the term $\varvec{\Gamma }_t'\varvec{\Lambda }\varvec{\Gamma }_t$ contributes nonzero values to elements $\varvec{\Omega }_{j,h,t}$ if series j, h are each elements of pa(k) for some other series k;  this relates to moralization of directed graphs, adding edges between cases in which j, h are neither parents of the other but share a relationship through common child series in the DDNM.

3.3 Filtering and forecasting: decouple/recouple in DDNMs

In addition to the ability to customize individual DLMs, DDNMs allow sequential analysis to be decoupled—enabling fast, parallel processing—and then recoupled for forecasting and decisions. The recoupled model gives joint p.d.f. for $\mathbf {y}_t$ in compositional form $\prod _{j=1\,{:}\,q} p(y_{j,t}|\mathbf {y}_{pa(j),t},\varvec{\theta }_{j,t},\lambda _{j,t} ,\mathcal {D}_{t-1})$ which is just the product of normals $\prod _{j=1\,{:}\,q} N(y_{j,t}|\mathbf {F}_{j,t}'\varvec{\theta }_{j,t},1/\lambda _{j,t})$ where $N(\cdot |\cdot ,\cdot )$ is the normal p.d.f. For sequential updating, this gives the time t likelihood function for $\varvec{\theta }_{1\,{:}\,q,t},\lambda _{1\,{:}\,q,t};$ independent conjugate priors across series are conjugate and lead to independent posteriors. Using discount factor DLMs, standard forward filtering analysis propagates prior and posterior distributions for $(\varvec{\theta }_{j,t},\lambda _{j,t})$ over time using standard normal/inverse gamma distribution theory (Prado and West 2010, chap. 4) independently across series. Sequential filtering is analytic and scales linearly in q.

Forecasting involves recoupling and, due to the roles of parental predictors and that practicable models often involve lagged elements of $\mathbf {y}_*$ in $\mathbf {x}_{j,t}$, is effectively accessed via direct simulation. Zhao et al. (2016) discuss recursive analytic computation of k-step ahead mean vectors and variance matrices—as well as precision matrices—but full inferences and decisions will often require going beyond these partial and marginal summaries, so simulation is preferred. The ordered structure of a DDNM means that simulations are performed recursively using the implicit compositional representation. At time t,  the normal/inverse gamma posterior $p(\varvec{\theta }_{q,t},\lambda _{q,t}|\mathcal {D}_t)$ is trivially sampled to generate samples from $p(\varvec{\theta }_{q,t+1},\lambda _{q,t+1}|\mathcal {D}_t)$ and then $p(y_{q,t+1}|\mathcal {D}_t).$ Simulated $y_{q,t+1}$ values are then passed up to the models for other series $j<q$ for which they are required as parental predictors. Moving to series $q-1,$ the process is repeated to generate $y_{q-1,t}$ values and, as a result, samples from $p(y_{q-1\,{:}\,q,t+1}|\mathcal {D}_t).$ Recursing leads to full Monte Carlo samples drawn directly from $p(\mathbf {y}_{t+1}|\mathcal {D}_t).$ Moving two steps ahead, on each Monte Carlo sampled vector $\mathbf {y}_{t+1}$ this process is repeated with posteriors for DLM states and volatilities conditioned on those values and time index incremented by 1. This results in sampled $\mathbf {y}_{t+2}$ vectors jointly with the conditioning vales at $t+1,$ hence samples from $p(\mathbf {y}_{t+1\,{:}\,t+2}|\mathcal {D}_t).$ Continue this process to k-steps ahead to generate full Monte Carlo samples of the path of the series into the future, i.e., generating from $p(\mathbf {y}_{t+1\,{:}\,t+k}|\mathcal {D}_t).$ Importantly, the analysis is as scalable as theoretically possible; the computational burden scales as the product of q and the chosen Monte Carlo sample size and can exploit partial parallelization.

3.4 Perspectives on model structure uncertainty

Examples in Zhao et al. (2016) with $q=13$ financial time series illustrate the analysis, with foci on one-step and five-step forecasting and resulting portfolio analyses. There the univariate DLM for series j has a local level and some lagged values of series j only, representing custom time-varying autoregressive (TVAR) predictors for each series. The model specification relies on a number of parameters and hence there are model structure uncertainty questions. Write $\mathcal {M}_j$ for a set of $|\mathcal {M}_j|$ candidate models for series j,  with elements $\mathcal {M}_j^r$ indexed by specific models $r\in \{ 1\,{:}\,|\mathcal {M}_j|\}.$ In Zhao et al. (2016), each $\mathcal {M}_j^r$ involved one choice of the TVAR order for series j,  one value of each of a set of discount factors (one for each of $\varvec{\phi }_{j,t}, \varvec{\gamma }_{j,t}, \lambda _{j,t}$) from a finite grid of values, and one choice of the parental set pa(j) from all possibilities. Importantly, each of these is series specific and the model evaluation and comparison questions can thus be decoupled and addressed using training data to explore, compare and score models. Critically for scalability, decoupling means that this involves a total of $\sum _{j=1\,{:}\,q} |\mathcal {M}_j|$ models for the full vector series, whereas a direct multivariate analysis would involve a much more substantial set of $\prod _{j=1\,{:}\,q} |\mathcal {M}_j|$ models; for even relatively small q and practical models, this is a major computational advance.

A main interest in Zhao et al. (2016) was on forecasting for portfolios, and the benefits of use of DDNMs are illustrated there. Scoring models on portfolio outcomes is key, but that paper also considers comparisons with traditional Bayesian model scoring via posterior model probabilities. One interest was to evaluate discount-weighted marginal likelihoods and resulting modified model probabilities that, at each time point, are based implicitly on exponentially down-weighting contributions from past data. This acts to avoid model probabilities degenerating and has the flavor of representing stochastic changes over time in model space. Specifically, a model power discount factor $\alpha \in (0,1]$ modifies the time n marginal likelihood on $\mathcal {M}$ to give log score $\sum _{t=1\,{:}\,n} \alpha ^{n-t} \log (p(\mathbf {y}_t|\mathcal {M}, \mathcal {D}_{t-1})).$ In terms of model probabilities at time t,  the implication is that $Pr(\mathcal {M}|\mathcal {D}_t) \propto Pr(\mathcal {M}|\mathcal {D}_{t-1})^\alpha p(\mathbf {y}_t|\mathcal {M}, \mathcal {D}_{t-1})$, i.e., a modified form of Bayes’ theorem that “flattens” the prior probabilities over models using the $\alpha$ power prior to updating via the current marginal likelihood contribution. At $\alpha =1$, this is the usual marginal likelihood. Otherwise, smaller values of $\alpha$ discount history in weighting models currently and allow for adaptation over time in model space if the data suggest that different models are more relevant over different periods of time. Examples in Zhao et al. (2016) highlight this; in more volatile periods of time (including the great recessionary years 2008–2010), models with lower discount factors on state vectors and volatilities tend to be preferred for some series, while preference for higher values and, in some cases, higher TVAR order increases in more stable periods. That study also highlights the implications for identifying relevant parental sets for each series and how that changes through time.

Zhao et al. (2016) show this modified model weighting can yield major benefits. Short- and longer-term forecast accuracy is generally improved with $\alpha <1,$ but the analysis becomes over-adaptive as $\alpha$ is reduced further. In comparison, portfolio outcomes—in terms of both realized returns and risk measures—are significantly improved with $\alpha$ just slightly less than 1—but clearly lower than 1—but deteriorate for lower values. The power discounting idea (Xie 2012; Zhao et al. 2016) was used historically in Bayesian forecasting ( West and Harrison 1989a, p.445) and has more recently received attention linking to parallel historical literature where discount factors are called “forgetting” factors (Raftery et al. 2010; Koop and Korobilis 2013). The basic idea and implementation are simple; in terms of a marginal broadening of perspectives on model structure uncertainty and model weighting, this power discounting is a trivial technical step and can yield substantial practical benefits.

3.5 Challenges and opportunities

Scaling DDNMs to increasingly large problems exacerbates the issue of model structure uncertainty. An holistic view necessitates demanding computation for search over spaces of models. DDNMs contribute a major advance in reducing the dimension of model space and open the opportunity for methods such as variants of stochastic search to be applied in parallel to sets of decoupled univariate DLMs. Nevertheless, scaling to 00s or 000s of series challenges any such approach.

DDNMs require a specified order of the q series. This is a decision made to structure the model, but is otherwise typically not of primary interest. It is not typically a choice to be regarded as a “parameter” and, in some applications, should be regarded as part of the substantive specification. For example, with lower-dimensional series in macroeconomic and financial applications, the ordering may reflect economic reasoning and theory, as I (with others) have emphasized in related work (e.g., Primiceri 2005; Nakajima and West 2013a, b; Zhou et al. 2014).

Theoretically, series order is irrelevant to predictions as they rely only on the resulting precision matrices (and regression components) that are order-free. Practically, of course, the specification of priors and specific computational methods rely on the chosen ordering and so prediction results will vary under different orders. There are then questions of more formal approaches to defining ordering(s) for evaluation, and a need to consider approaches to relaxing the requirement for ordering to begin.

4 Simultaneous graphical dynamic linear models

4.1 SGDLM context and structure

As introduced in Gruber and West (2016), SGDLMs generalize DDNMs by allowing any series to be a contemporaneous predictor of any other. To reflect this, the parental set for series j is now termed a set of simultaneous parents, denoted by $sp(j) \subseteq \{ 1\,{:}\,q\backslash j \},$ with the same DLM model forms, i.e., $y_{j,t} = \mathbf {F}_{j,t}' \varvec{\theta }_{j,t} + \nu _{j,t} = \mathbf {x}_{j,t}' \varvec{\phi }_{j,t} + \mathbf {y}_{sp(j),t}'\varvec{\gamma }_{j,t} + \nu _{j,t}$ and other assumptions unchanged. Figure 5 shows an example to compare with Fig. 4; directed edges can point down as well as up the list of series—model structure is series order independent and the directed graphical structure is no longer necessarily acyclic as a result. The implied joint distributions are as in DDNMs but now $\varvec{\Gamma }_t$—while generally still sparse and with diagonal zeros—does not need to be upper triangular. This resolves the main constraint on DDNMs while leaving the overall structural form of the model unchanged. DDNMs are special cases when $sp(j)=pa(j)$ and $\varvec{\Gamma }_t$ is upper triangular. The reduced form of the full multivariate model is $\mathbf {y}_t =\varvec{\alpha }_t + N(\mathbf {A}_t\varvec{\mu }_t, \varvec{\Sigma }_t)$ with prediction cross talk matrix $\mathbf {A}_t = (\mathbf {I}-\varvec{\Gamma }_t)^{-1}$; the mean vector and precision matrix are as in eqn. (1), but now the equation for $\mathbf {A}_t \varvec{\mu }_t$ is extended to including sums of terms $\varvec{\Gamma }_t^k \varvec{\mu }_t$ for $k\ge q.$ In general, sparse $\varvec{\Gamma }_t$ implies that this infinite series converges as the higher-order terms quickly become negligible. Cross talk is induced among series as in DDNMs, as is graphical model structure of $\varvec{\Omega }_t$ in cases of high enough levels of sparsity of parental sets sp(j) and hence of $\varvec{\Gamma }_t$; see Fig. 6 for illustration.

Fig. 5

Schematic of SGDLM for FX time series to compare with the DDNM in Fig. 4

Fig. 6

Left: Indicator of simultaneous parents in an example SGDLM with $q=100;$ nonzero elements in each row of $\varvec{\Gamma }_t$ are shaded. Center: Implied nonzero/zero pattern in precision matrix $\varvec{\Omega }_t.$Right: Implied nonzero/zero pattern in prediction cross talk matrix $\mathbf {A}_t = (\mathbf {I}-\varvec{\Gamma }_t)^{-1}$

4.2 Recoupling for forecasting in SGDLMs

Prediction of future states and volatilities uses simulation in the decoupled DLMs; these are then recoupled to full joint forecast distributions to simulate the multivariate outcomes. At time $t-1,$ the SGDLM analysis (Gruber and West 2016, 2017) constrains the prior $p(\varvec{\theta }_{1\,{:}\,q,t},\lambda _{1\,{:}\,q,t} |\mathcal {D}_{t-1})$ as a product of conjugate normal/inverse gamma forms for the $\{ \varvec{\theta }_{j,t},\lambda _{j,t} \}$ across series. These are exact in DDNM special cases and (typically highly) accurate approximations in sparse SGDLMs otherwise. These priors are easily simulated (in parallel) to compute Monte Carlo samples of the implied $\mathbf {A}_t\varvec{\mu }_t,\varvec{\Omega }_t$; sampling the full one-step predictive distribution to generate synthetic $\mathbf {y}_t$ follows trivially. Each sampled set of states and volatilities underlies conditional sampling of those at the next time point, hence samples of $\mathbf {y}_{t+1}$. This process is recursed into the future to generate Monte Carlo samples from predictive distributions over multi-steps ahead; see Fig. 7. This involves only direct simulation, so is efficient and scales linearly in q as in simpler DDNMs.

Fig. 7

Decoupled DLM simulations followed by recoupling for forecasting in SGDLMs

4.3 Decouple/recouple for filtering in SGDLMs

The recoupled SGLM no longer defines a compositional representation of the conditional p.d.f. for $\mathbf {y}_t$ given all model quantities (unless $\varvec{\Gamma }_t$ is diagonal). The p.d.f. is now $|\mathbf {I}-\varvec{\Gamma }_t|_+\ \prod _{j=1\,{:}\,q} N(y_{j,t}|\mathbf {F}_{j,t}'\varvec{\theta }_{j,t},1/\lambda _{j,t})$ where $|*|_+$ is the absolute value of the determinant of the matrix argument $*$. Independent normal/inverse gamma priors for the $\{ \varvec{\theta }_{j,t},\lambda _{j,t} \}$ imply a joint posterior proportional to $|\mathbf {I}-\varvec{\Gamma }_t|_+ \ \prod _{j=1\,{:}\,q} g_j(\varvec{\theta }_{j,t},\lambda _{j,t}|\mathcal {D}_t)$ where the $g_j(\cdot |\cdot )$ are the normal/inverse gamma posteriors from each of the decoupled DLMs. The one-step filtering update is only partly decoupled; the determinant factor recouples across series, involving (only) state elements related to parental sets. For sequential filtering to lead to decoupled conjugate forms at the next time point, this posterior must be approximated by a product of normal/inverse gammas. In practical contexts with larger q, the sp(j) will be small sets and so $\varvec{\Gamma }_t$ will be rather sparse; increasing sparsity means that $|\mathbf {I}-\varvec{\Gamma }_t|_+$ will be closer to 1. Hence, the posterior will be almost decoupled and close to a product of conjugate forms. This insight underlies an analysis strategy (Gruber and West 2016, 2017) that uses importance sampling for Monte Carlo evaluation of the joint (recoupled) time t posterior, followed by a variational Bayes’ mapping to decoupled conjugate forms.

The posterior proportional to $|\mathbf {I}-\varvec{\Gamma }_t|_+\ \prod _{j=1\,{:}\,q} g_j(\varvec{\theta }_{j,t},\lambda _{j,t}|\mathcal {D}_t)$ defines a perfect context for importance sampling (IS) Monte Carlo when—as is typical in practice—the determinant term is expected to be relatively modest in its contribution. Taking the product of the $g_j(\cdot |\cdot )$ terms as the importance sampler yields normalized IS weights proportional to $|\mathbf {I}-\varvec{\Gamma }_t|_+$ at sampled values of $\varvec{\Gamma }_t.$ In sparse cases, these weights will vary around 1, but tend to be close to 1; in special cases of DDNMs, they are exactly 1 and IS is exact random sampling. Hence, posterior inference at time t can be efficiently based on IS sample and weights and monitored through standard metrics such as the effective sample size $ESS = 1/\sum _{i=1\,{:}\,I} w_{i,t}^2$ where $w_{i,t}$ represents the IS weight on each Monte Carlo sample $i=1\,{:}\,I$. To complete the time t update and define decoupled conjugate form posteriors across the series requires an approximation step. This is done via a variational Bayes (VB) method that approximates the posterior IS sample by a product of normal/inverse gamma forms—a mean field approximation—by minimizing the Kullback–Leibler (KL) divergence of the approximation from the IS-based posterior; see Fig. 8. This is a context where the optimization is easily computed and, again in cases of sparse $\varvec{\Gamma }_t,$ will tend to be very effective and only a modest modification of the product of the $g_j(\cdot |\cdot )$ terms. Examples in Gruber and West (2016) and Gruber and West (2017) bear this out in studies with up to $q=401$ series in financial forecasting and portfolio analysis.

Fig. 8

Filtering updates in SGDLMs. The coupled joint posterior $p(\varvec{\theta }_{1:q,t},\lambda _{1:q,t}|\mathcal {D}_t)$ is evaluated by importance sampling and then decoupled using variational Bayes to define decoupled conjugate form posteriors for the states and volatilities in each univariate model

4.4 Entropy-based model assessment and monitoring

Examples referenced above demonstrate scalability and efficiency of SGDLM analysis (with parallel implementations— Gruber 2019) and improvements in forecasting and decisions relative to standard models. Examples include $q=401$ series of daily stock prices on companies in the S&P index along with the index itself. The ability to customize individual DLMs improves characterization of short-term changes and series-specific volatility, and selection of the sp(j) defines adaptation to dynamics in structure across subsets of series that improves portfolio outcomes across a range of models and portfolio utility functions.

Those examples also highlight sequential monitoring to assess efficacy of the IS/VB analysis. At each time t, denote by $E_t$ the evaluated ESS for IS recoupling and by $K_t$ the minimized KL divergence in VB decoupling. These are inversely related: IS weights closer to uniform lead to high $E_t$ and low $K_t;$  Gruber and West (2016) discuss theoretical relationships and emphasize monitoring. If a period of low $K_t$ breaks down to higher values, then recent data indicate changes that may be due to increased volatility in some series or changes in cross-series relationships. This calls for intervention to modify the model through changes to current posteriors, discount factors and/or parental sets. Simply running the analysis on one model class but with no such intervention (Gruber and West 2017, as in) gives a benchmark analysis; over a long period of days, the resulting $K_t$ series is shown in Fig. 9.

Figure 9 shows context and comparison with a major financial risk index—the St. Louis Federal Reserve Bank Financial Stress Index (Kliesen and Smith 2010)—widely regarded as local predictor of risk in the global financial systems. Comparison with the $K_t$ “Entropy Index” is striking. As a purely statistical index based on stock price data rather than the macroeconomic and FX data of the St. Loius index, $K_t$ mirrors the St. Louis index but shows the ability to lead, increasing more rapidly in periods of growing financial stress. This is partly responding to changes in relationships across subsets of series that are substantial enough to impact the IS/VB quality and signal caution, and that $K_t$ is a daily measure while the St. Louis index is weekly. Routine use of the entropy index as a monitor on model adequacy is recommended.

Fig. 9

Trajectories of the daily entropy index $K_t$ in SGDLM analysis of $q=401$ S&P series, and the weekly St. Louis Federal Reserve Bank Financial Stress Index, over 2005–2013 with four key periods indicated. A: Aug 2007 events including the UK government intervention on Northern Rock bank, generating major news related to the subprime loan crisis; B: Oct 2008 US loans “buy-back” events and the National Economic Stimulus Act; C: Mar 2010 initial responses by the European Central Bank to the “Eurozone crisis”; D: Aug 2011 US credit downgraded by S&P

4.5 Evaluation and highlight of the role of recoupling

Questions arise as to whether the IS/VB analysis can be dropped without loss when $\varvec{\Gamma }_t$ is very sparse. In the S&P analysis (Gruber and West 2017), the 401-dimensional model is very sparse; $|sp(j)|=20$ for each j so that 95% of entries in $\varvec{\Gamma }_t$ are zero. Thus, the decoupled analysis can be expected to be close to that of a DDNM. One assessment of whether this is tenable is based on one-step forecast accuracy. In any model, for each series j and time t, let $u_{j,t} = P(y_{j,t}|\mathcal {D}_{t-1})$ be the realized value of the one-step-ahead forecast c.d.f. The more adequate the model, the closer the $u_{j,t}$ to resembling U(0, 1) samples; if the model generates the data, the $u_{j,t}$ will be theoretically U(0, 1). From the SGDLM analysis noted, Fig. 10 shows histograms of the $u_{j,t}$ over the several years for three chosen series. The figure also shows such histograms based on analysis that simply ignores the IS/VB decouple/recouple steps. This indicates improvements in that the c.d.f. “residuals” are closer to uniform with recoupling. These examples are quite typical of the 401 series; evidently, recoupling is practically critical even in very sparse (non-triangular) models.

Fig. 10

Realized one-step forecast c.d.f. values for three stocks. Left: without recoupling; Right: with recoupling. Recoupling induces a more uniform distribution consistent with model adequacy

4.6 Perspectives on model structure uncertainty in prediction

SGDLM analysis faces the same challenges of parameter and parental set specification as in the special case of DDNMs. Scaling presses the questions of how to assess and modify the sp(j) over time, in particular. Viewing these as parameters for extended model uncertainty analysis leads to enormous model spaces and is simply untenable computationally. More importantly, inference on parental set membership—i.e., model structure “identification”—is rarely a goal. As Gruber and West (2016) and Gruber and West (2017) exemplify, a more rational view is that parental sets are choices to be made based on forecast accuracy and decision outcomes. Often I am not at all interested in “learning” these aspects of model structure—I want good choices in terms of forecast and decision outcomes. With q even moderately large, each series j may be adequately and equally well predicted using one of many possible small parental sets, especially in contexts such as ours of high levels of (dynamic) interdependencies. Any one such choice is preferable to weighting and aggregating a large number since small differences across them simply contribute noise; hence, I focus on “representative” parental sets to use as a routine, with sequential monitoring over time to continually assess adequacy and respond to changes by intervention to modify the parental sets.

Gruber and West (2017) developed a Bayesian decision analysis-inspired approach in which sp(j) has three subsets: a “core set,” a “warm-up” set and a “cool-down” set. A simple Wishart discount model is run alongside the SGDLM to identify series not currently in sp(j) for potential inclusion in the warm-up set. Based on posterior summaries in the Wishart model at each time t, one such series is added to the warm-up subset of sp(j). Also at each t, one series in the current cool-down subset is moved out of sp(j) and series in the warm-up subset is considered to be moved to the core subset based on current posterior assessment of predictive relationships with series j. Evolving the model over time allows for learning on state elements related to new parental series added, and adaptation for the existing parents removed. This nicely enables smooth changes in structure over time via the warm-up and cool-down periods for potential parental predictors, avoiding the need for abrupt changes and model refitting with updated parental sets.

Fig. 11

Parental inclusion for 3M SGDLM. Dark shading predictor stocks included as core simultaneous parents; Light shading: stocks in warm-up and cool-down sets; White stocks not included

Figure 11 shows an illustration with series j the stock price of company 3M; analysis used $|pa(j)|=20$. Several series are in sp(j) over the entire period. Others come in/out once or twice but are clearly relevant over time; some enter for short periods, replacing others. Relatively few of the 400 possible parental series are involved across the years. The names of series shown in the figure are of no primary interest. Viewing the names indicates how challenging it would be to create a serious contextual interpretation; but, we have little interest in that, as the parents simply aid in predicting 3M price changes while contributing to quantifying multivariate structure in $\varvec{\Omega }_t$, its dynamics and implications for portfolio decisions, per analysis goals.

4.7 Challenges and opportunities

As discussed in Sect. 4.6, the very major challenge is that of addressing the huge model structure uncertainty problem consistent with the desiderata of (i) scalability with q, and (b) maintaining tractability and efficiency of the sequential filtering and forecasting analysis. Routine model averaging is untenable computationally and, in any case, addresses what is often a non-problem. Outcomes in specific forecasting and/or decision analyses should guide thinking about new ways to address this. The specific Bayesian hot-spot technique exemplified is a step in that direction, though somewhat ad hoc in its current implementation. Research questions relate to broader issues of model evaluation, combination and selection and may be addressed based on related developments in other areas such as Bayesian predictive synthesis (McAlinn and West 2019; McAlinn et al. 2019) and other methods emerging based on decision perspectives (e.g., Walker et al. 2001; Clyde and Iversen 2013; McAlinn et al. 2018; Yao et al. 2018). Opportunities for theoretical research are clear, but the challenges of effective and scalable computation remain major.

A perhaps subtle aspect of evaluation of the full multivariate dynamic model is that, while some progress can be made at the level of each univariate series (e.g., training data to select discount factors) much assessment of forecast and decision outcomes can only be done with the recoupled multivariate model. This should be an additional guiding concern for new approaches.

SGDLMs involve flexible and adaptive models for stochastic volatility at the level of each univariate time series. Explaining (and, in the short term, predicting) volatility of a single series through the simultaneous parental concept is of inherent interest in itself. Then, the ability to coherently adapt the selection of parental predictors—via the Bayesian hot spot as reviewed in Sect. 4.6 or perhaps other methods—opens up new opportunities for univariate model advancement.

There is potential for more aggressive development of the IS/VB-based ESS/KL measures of model adequacy with practical import. As exemplified, the $K_t$ entropy index relates to the entire model—all states and volatilities across the q series. KL divergence on any subset of this large space can be easily computed and, in fact, relates to opportunities to improve the IS accuracy on reduced dimensions. This opens up the potential to explore ranges of entropy indices for subsets of series, e.g., the set of industrial stocks, the set of financial/banking stocks, etc., separately. Changes observed in the overall $K_t$ may be reflected in states and volatilities for just some but not all stocks or sectors, impacting the overall measure and obscuring the fact that some or many components of the model may be stable. At such times, intervention to adapt models may then be focused and restricted to only the relevant subsets of the multivariate series.

5 Count time series: scalable multi-scale forecasting

5.1 Context and univariate dynamic models of nonnegative counts

Across various areas of application, challenges arise in problems of monitoring and forecasting discrete time series, and notably many related time series of counts. These are increasingly common in areas such as consumer behavior in a range of socioeconomic contexts, various natural and biological systems, and commercial and economic problems of analysis and forecasting of discrete outcomes (e.g., Cargnoni et al. 1997; Yelland 2009; Terui and Ban 2014; Chen and Lee 2017; Aktekin et al. 2018; Glynn et al. 2019). Often, there are questions of modeling simultaneously at different scales as well as of integrating information across series and scales (West and Harrison 1997; Ferreira et al. 2006, chapter 16 of). The recent, general state-space models of Berry and West (2019) and Berry et al. (2019) focus on such contexts under our desiderata: defining flexible, customizable models for decoupled univariate series, ensuring relevant and coherent cross-series relationships when recoupled, and maintaining scalability and computational efficiency in sequential analysis and forecasting. The theory and methodology of such models are applicable in many fields and define new research directions and opportunities in addressing large-scale, complex and dynamic discrete data-generating systems.

New classes of dynamic generalized linear models (DGLMs, West et al. 1985; West and Harrison 1997, chapter 14) include dynamic count mixture models (DCMM,  Berry and West 2019) and extensions to dynamic binary cascade models (DBCM,  Berry et al. 2019). These exploit coupled dynamic models for binary and Poisson outcomes in structured ways. Critical advances for univariate count time series modeling include the use of time-specific random effects to capture over-dispersion, and customized “binary cascade” ideas for predicting clustered count outcomes and extremes. These developments are exemplified in forecasting customer demand and sales time series in these papers, but are of course of much broader import. I focus here on the multi-scale structure and use simple conditional Poisson DGLMs as examples. Each time series $y_{j,t} \sim Po(\mu _{j,t})$ with log link $\log (\mu _{t}) = \mathbf {F}_{j,t}'\varvec{\theta }_{j,t}$ where state vectors $\varvec{\theta }_{j,t}$ follow linear Markov evolution models—independently across j—as in DLMs. Decoupled, we use the traditional sequential filtering and forecasting analysis exploiting (highly accurate and efficient) coupled variational Bayes/linear Bayes computations (West et al. 1985; West and Harrison 1997; Triantafyllopoulos 2009). Conditional on the $\mathbf {F}_{j,t}$, analyses are decoupled across series.

5.2 Common dynamic latent factors and multi-scale decouple/recouple

Many multivariate series share common patterns for which hierarchical or traditional dynamic latent factor models would be first considerations. Integrating hierarchical structure into dynamic modeling has seen some development (e.g., Gamerman and Migon 1993; Cargnoni et al. 1997; Ferreira et al. 1997), but application quickly requires intense computation such as MCMC and obviates efficient sequential analysis and scaling to higher dimensions with more structure across series. The same issues arise with dynamic latent factor models, Gaussian or otherwise (e.g., Lopes and Carvalho 2007; Carvalho et al. 2011; Nakajima and West 2013b; Kastner et al. 2017; Nakajima and West 2017; McAlinn et al. 2019). The new multi-scale approach of Berry and West (2019) resolves this with novel Bayesian model structures that define latent factor models but maintain fast sequential analysis and scalability. The ideas are general and apply to all dynamic models, but are highlighted here in the conditional Poisson DGLMs. Suppose that series j has $\mathbf {F}_{j,t}' = (\mathbf {x}_{j,t}',\varvec{\phi }_t')$ where $\mathbf {x}_{j,t}$ include series j-specific predictors and $\varvec{\phi }_t$ represents a vector of dynamic latent factors impacting all series. The state vectors are conformably partitioned: $\varvec{\theta }_{j,t}'=(\varvec{\gamma }_{j,t}',\varvec{\beta }_{j,t}')$ where $\varvec{\beta }_{j,t}$ allows for diversity of the impact of the latent factors across series.

Denote by $\mathcal {M}_j$ the DGLM for series j. With independent priors on states across series and conditional on latent factors $\varvec{\phi }_{t\,{:}\,t+h}$ over h steps ahead, analyses are decoupled: forward filtering and forecasting for the $\mathcal {M}_j$ are parallel and efficient. The multi-scale concept involves an external or “higher level/aggregate” model $\mathcal {M}_0$ to infer and predict the latent factor process, based on “top-down” philosophy (West and Harrison 1997, section 16.3). That is, $\mathcal {M}_0$ defines a current posterior predictive distribution for $\varvec{\phi }_{t\,{:}\,t+h}$ that feeds each of the $\mathcal {M}_j$ with values for their individual forecasting and updating. Technically, this uses forward simulation: $\mathcal {M}_0$ generates Monte Carlo samples of latent factors, and for every such sample, each of the decoupled $\mathcal {M}_j$ directly updates and forecasts. In this way, informed predictions of latent factor processes from $\mathcal {M}_0$ lead to fully probabilistic inferences at the micro/decoupled series level, and within each there is an explicit accounting for uncertainties about the common features $\varvec{\phi }_{t\,{:}\,t+h}$ in the resulting series-specific analyses.

5.3 Application contexts, model comparison and forecast evaluation

Supermarket sales forecasting examples (Berry and West 2019; Berry et al. 2019) involve thousands of individual items across many stores, emphasizing needs for efficiency and scalability of analyses. The focus is on daily transactions and sales data in each store: for each item, and over multiple days ahead to inform diverse end-user decisions in supply chain management and at the store management level. Models involve item-level price and promotion predictors, as well as critical day-of-week seasonal effects. The new univariate models allow for diverse levels of sales, over-dispersion via dynamic random effects, sporadic sales patterns of items via dynamic zero-inflation components and rare sales events at higher levels. Daily seasonal patterns are a main focus for the new multi-scale approach. In any store, the “traffic” of, for example, the overall number of customers buying some kind of pasta product is a key predictor of sales of any specific pasta item; hence, an aggregate-level $\mathcal {M}_0$ of total sales—across all pasta items—is expected to define more accurate evaluation and prediction of the seasonal effects for any one specific item than would be achievable using only day on that item. Figure 12 displays two example sales series; these illustrate commonalities as well as noisy, series-specific day-of-week structure and other effects (e.g., of prices and promotions). Given very noisy data per series but inherently common day-of-week traffic patterns, this is an ideal context for the top-down, multi-scale decouple/recouple strategy.

Fig. 12

Sales data on two pasta items in one store over 365 days, taken from a large case study in Berry et al. (2019). Daily data are +; black lines indicate item-specific day-of-week seasonal structure, while the gray line is that from an aggregate model $\mathcal {M}_0.$ Item-specific effects appear as stochastic variations on the latter, underscoring interest in information sharing via a multi-scale analysis. Diverse levels and patterns of stochastic variation apparent are typical across many items; item A is at high levels, item B lower with multiple zeros. This requires customized components in each of the decoupled univariate dynamic models, while improved forecasts are achieved via multi-scale recoupling

Results in Berry et al. (2019) demonstrate advances in statistical model assessments and in terms of measures of practical relevance in the consumer demand and sales context. A key point here is that the very extensive evaluations reported target both statistical and contextual concerns: (a) broad statistical evaluations include assessments of frequency calibration (for binary and discrete count outcomes) and coverage (of Bayesian predictive distributions), and their comparisons across models; (b) broad contextual evaluations explore ranges of metrics to evaluate specific models and compare across models—metrics based on loss functions such as mean absolute deviation, mean absolute percentage error and others that are industry/application-specific and bear on practical end-user decisions. These studies represent a focused context for advancing the main theme that model evaluation should be arbitrated in the contexts of specific and explicit forecast and decision goals in the use of the models. Purely statistical evaluations are required as sanity checks on statistical model adequacy, but only as precursors to the defining concerns in applying models.

5.4 Challenges and opportunities

The DCMM and DBCM frameworks define opportunities for applications in numerous areas—such of monitoring and forecasting in marketing and consumer behavior contexts, epidemiological studies and others where counts arise from underlying complex, compound and time-varying processes. In future applications, the shared latent factor processes will be multivariate, with dimensions reflecting different ways in which series are conceptually related. The new multi-scale modeling concept and its decouple/recouple analysis open up potential to apply to many areas in which there are tangible aggregate-level or other external information sources that generate information relative to aspects of the common patterns/shared structure in multiple series. One of the challenges is that, in a given applied context, there may be multiple such aggregate/higher-level abstractions, so that technical model developments will be of interest to extend the analysis to integrate inferences (in terms of “top-down projections”) from two or more external models. A further challenge and opportunity relates to the question of maintaining faith with the desiderata of fast and scalable computation; the approaches to date involve extensive—though direct—simulation in $\mathcal {M}_0$ of the latent factors $\varvec{\phi }_t$ for projection to the micro-level models $\mathcal {M}_j.$ In extensions with multiple higher-level models, and with increasing numbers q of the univariate series within each of which concomitant simulations will be needed, this will become a computational challenge and limitation. New theory and methodology to address these coupled issues in scalability are of interest.

6 Multivariate count series: network flow monitoring

6.1 Dynamic network context and DGLMs for flows

Related areas of large-scale count time series concern flows of “traffic” in various kinds of networks. This topic is significantly expanding with increasingly large-scale data in Internet and social network contexts, and with regard to physical network flow problems. Bayesian models have been developed for network tomography and physical traffic flow forecasting (e.g., Tebaldi and West 1998; Congdon 2000; Tebaldi et al. 2002; Anacleto et al. 2013; Jandarov et al. 2014; Hazelton 2015), but increasingly large dynamic network flow problems require new modeling approaches. I contact recent innovations that address: (a) scaling of flexible and adaptive models for analysis of large networks to characterize the inherent variability and stochastic structure in flows between nodes, and into/out of networks; (b) evaluation of formal statistical metrics to monitor dynamic network flows and signal/allow for informed interventions to adapt models in times of signaled change or anomalies; and (c) evaluation of inferences on subtle aspects of dynamics in network structure related to node-specific and node-node interactions over time that also scale with network dimension. These goals interact with the core desiderata detailed earlier of statistical and computational efficiency, and scalability of Bayesian analysis, with the extension of doubly-indexed count time series: Now, $y_{i,j,t}$ labels the count of traffic (cars, commuters, IP addresses or other units) “flowing” from a node i to a node j in a defined network on I nodes in time interval $t-1\rightarrow t$; node index 0 represents “outside” the network as in Fig. 13.

Fig. 13

Network schematic and notation for flows at time t

In dynamic network studies of various kinds, forecasting may be of interest but is often not the primary objective. More typically, the goals are to characterize normal patterns of stochastic variation in flows, monitor and adapt models to respond to changes over time, and inform decisions based on signals about patterns of changes. Networks are increasingly large; Internet and social networks can involve hundreds or thousands of nodes and are effectively unbounded in any practical sense from the viewpoint of statistical modeling. The conceptual and technical innovations in Chen et al. (2018) and Chen et al. (2019) define flexible multivariate models exploiting two developments of the decouple/recouple concept—these advance the ability to address the above concerns in a scalable Bayesian framework.

6.2 Decouple/recouple for dynamic network flows

Dynamic models in Chen et al. (2018) and Chen et al. (2019) use flexible, efficient Poisson DGLMs for in-flows to the network $y_{0,i,t}$ independently across nodes $i=1\,{:}\,I.$ Within-network flows are inherently conditionally multinomial, i.e., $y_{i,0\,{:}\,I,t}$ is multinomial based on the current “occupancy” $n_{i,t-1}$ of node i at time t . The first use of decoupling is to break the multinomial into a set of I Poissons, taking $y_{i,j,t} \sim Po(m_{i,t}\phi _{i,j,t})$ where $\log (\phi _{i,j,t}) = \mathbf {F}_{i,j,t} \varvec{\theta }_{i,j,t}$ defines a Poisson DGLM with state vector $\varvec{\theta }_{i,j,t}.$ The term $m_{i,t} = n_{i,t-1}/n_{i,t-2}$ is an offset to adjust for varying occupancy levels. With independence across nodes, this yields a set of $I+1$ Poisson DGLMs per node that are decoupled for online learning about underlying state vectors. Thus, fast, parallel analysis yields posterior inferences on the $\phi _{i,j,t}$; Fig. 14a comes from an example discussed further in Section 6.4. Via decoupled posterior simulation, these are trivially mapped to implied transition probabilities in the node- and time-specific multinomials implied, i.e., for each node i, the probabilities $\phi _{i,j,t}/\sum _{j=0\,{:}\,I}\phi _{i,j,t}$ on $j=0\,{:}\,I.$

6.3 Recoupling for Bayesian model emulation

The second use of recoupling defines an approach Bayesian to “model emulation” (e.g., Liu and West 2009; Irie and West 2019) in the dynamic context. While the decoupled DGLMs run independently, they are able to map relationships across sets of nodes as they change over time. Using posterior samples of trajectories of the full sets of $\phi _{i,j,t}$, we are able to emulate inferences in a more structured model that explicitly involves node–node dependencies. Specifically, the so-called dynamic gravity models (DGMs) of Chen et al. (2018) and Chen et al. (2019) extend prior ideas of two-way modeling in networks and other areas (e.g., West 1994; Sen and Smith 1995; Congdon 2000) to a rich class of dynamic interaction structures. The set of modified Poisson rates are mapped to a DGM via $\phi _{i,j,t} = \mu _t\alpha _{i,t} \beta _{j,t} \gamma _{i,j,t}$ where: (i) $\mu _t$ is an overall network flow intensity process over time, (ii) $\alpha _{i,t}$ is a node i-specific “origin (outflow)” process, (iii) $\beta _{j,t}$ is a node j-specific “destination (inflow)” process, and (iv) $\gamma _{i,j,t}$ is a node $i\rightarrow j$ affinity (interaction)” process. Subject to trivial aliasing constraints (fixing geometric means of main and interaction effects at 1), this is an invertible map between the flexible decoupled system of models and the DGM effect processes.

6.4 Application context and online model monitoring for intervention

In Chen et al. (2019), flow data record visitors (IP addresses) to nodes (web “domains”) of the Fox News Web site. A network of $I=237$ nodes illustrates analysis scalability (over 56, 000 node–node series). Counts are for five-minute intervals, and key examples use data on September 17, 2015; see Fig. 14 looking at flows from node $i=$“Games/Online Games” and $j=$“Games/Computer & Video Games,” with raw flow counts in frame (a). There are no relevant additional covariates available, so the univariate Poisson DGLMs are taken as local linear trend models, with two-dimensional state vectors representing local level and gradient at each time (West and Harrison 1997, chapt. 7). While this is a flexible model for adapting to changes in the $\phi _{i,j,t}$ over time as governed by model discount factors, it is critical to continuously monitor model adequacy over time in view of the potential for periods when flows represent departure from the model, e.g., sudden unpredicted bursts of traffic or unusual decreases of traffic over a short period based on news or other external events not available to the model. This aspect of model evaluation is routine in many other areas of Bayesian time series, and there are a range of technical approaches.

Effective, tractable and computationally simple methods of Bayesian model monitoring and adaptation are based on sequential Bayes’ factors as tracking signals in a decision analysis context (West and Harrison 1986, 1997 chapt. 11). Each DGLM is subject to such automatic monitoring and the ability to adapt the model via flagging outliers and using temporarily decreased discount factors to more radically adapt to structural changes. In Fig. 14, it can be seen that this is key in terms of two periods of abrupt changes in gradient of the local linear trend around the 16 and 22 hour marks, and then again for a few short periods later in the day when flows are at high levels but exhibit swings up/down.

Fig. 14

Posterior summaries for aspects of flows involving two web domain nodes in the Fox News Web site on September 17, 2015. Nodes $i=$ Games/Online Games and $j=$ Games/Computer & Video Games. a Posterior trajectory for Poisson levels $\phi _{i,j,t}$ for flows $i\rightarrow j$; b Posterior trajectory for the origin (outflow) process $\alpha _{i,t}$; c Posterior trajectory for the destination (inflow) process $\beta _{j,t}$; d Posterior trajectory for the affinity process $\gamma _{i,j,t}$. Trajectories are approximate posterior means and $95\%$ credible interval, and the + symbols indicate empirical values from the raw data

Figure 14 also shows trajectories of imputed DGM processes from recoupling-based emulation. Here, it becomes clear that both the node i origin and node j destination effect processes vary through the day, with the latter increasing modestly through the afternoon and evening, and then they each decay at later hours. Since these processes are multipliers in the Poisson means and centered at 1, both origin and destination processes represent flow effects above the norm across the network. The figure also shows the trajectory of the affinity effect process $\gamma _{i,j,t}$ for these two nodes. Now, it becomes quite clear that the very major temporal pattern is idiosyncratic to these two nodes; the interaction process boosts very substantially at around the 16-hour mark, reflecting domain-specific visitors at the online games node aggressively flowing to the computer and video games node in the evening hours.

6.5 Challenges and opportunities

The summary example above and more in Chen et al. (2019) highlight the utility of the new models and the decouple/recouple strategies. Critically, DGMs themselves are simply not amenable to fast and scalable analysis; the recouple/emulation method enables scalability (at the optimal rate ${\sim }I^2$) of inferences on what may be very complex patterns of interactions in flows among nodes as well as in their origin and destination main effects. For future applications, the model is open to use of node-specific and node–node pair covariates in underlying univariate DGLMs when such information is available. Analysis is also open to the use of feed-forward intervention information (West and Harrison 1989b, 1997, chapt. 11) that may be available to anticipate upcoming changes that would otherwise have to be signaled by automatic monitoring. Canonical Poisson DGLMs can be extended to richer and more flexible forms; without loss in terms of maintaining faith with the key desiderata of analytic tractability and computational efficiency, the models in Sect. 5.1 offer potential to improve characterization of patterns in network flows via inclusion of dynamic includes random effects for over-dispersion as well as flexible models for very low or sporadic flows between certain node pairs. Finally, these models and emulation methods will be of interest in applications in areas beyond network flow studies.