Abstract
A time-domain test for the assumption of second-order stationarity of a functional time series is proposed. The test is based on combining individual cumulative sum tests which are designed to be sensitive to changes in the mean, variance and autocovariance operators, respectively. The combination of their dependent p values relies on a joint-dependent block multiplier bootstrap of the individual test statistics. Conditions under which the proposed combined testing procedure is asymptotically valid under stationarity are provided. A procedure is proposed to automatically choose the block length parameter needed for the construction of the bootstrap. The finite-sample behavior of the proposed test is investigated in Monte Carlo experiments, and an illustration on a real data set is provided.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Within the last decades, statistical analysis for functional time series has become a very active area of research [see the monographs Bosq (2000), Ferraty and Vieu (2006), Horváth and Kokoszka (2012) and Hsing and Eubank (2015), among others]. Many authors impose the assumption of stationarity, which allows for developing advanced statistical theory. For instance, Bosq (2002) and Dehling and Sharipov (2005) investigate stationary functional processes with a linear representation and Hörmann and Kokoszka (2010) provide a general framework to model functional observations from stationary processes. Frequency domain analysis of stationary functional time series has been considered by Panaretos and Tavakoli (2013), while van Delft and Eichler (2018) propose a new concept of local stationarity for functional data. The assumption of second-order stationarity is also of particular importance for prediction problems [see Antoniadis and Sapatinas (2003), Aue et al. (2015), Hyndman and Shang (2009) among others] and for dynamic principal component analysis (Hörmann et al. 2015).
Ideally, the assumption of stationarity should be checked before applying any statistical methodology. Several authors have considered this problem, in particular within the context of change point analysis where the null hypothesis of stationarity is tested against the alternative of a structural change in certain parameters of the process; see Aue et al. (2009), Berkes et al. (2009), Horvath et al. (2010), Aston and Kirch (2012) among others. Tests that are designed to be powerful against more general alternatives are often based on an analysis in the frequency domain. For example, Aue and van Delft (2017) generalize the approach of Dwivedi and Subba Rao (2011) and Jentsch and Subba Rao (2015) to functional time series. More precisely, they begin by showing that the functional discrete Fourier transform (fDFT) is asymptotically uncorrelated at distinct Fourier frequencies if and only if the process is weakly stationary. The corresponding test is then based on a quadratic form based on a finite-dimensional projection of the empirical covariance operator of the fDFT’s. Consequently, the properties of the test depend on the number of lagged fDFT’s included. As an alternative, van Delft et al. (2017) construct a test using an estimate of a minimal distance between the spectral density operator of a non-stationary process and its best approximation by a spectral density operator corresponding to a stationary process (see also Dette et al. 2011 for a discussion of this approach in the univariate context). The test statistic consists of sums of Hilbert–Schmidt inner products of periodogram operators (evaluated at different frequencies) and is asymptotically normal distributed.
In the present paper, we propose an alternative time-domain test for second-order stationarity of a functional time series. More precisely, we suggest to address the problem of detecting non-stationarity by individually checking the hypothesis that the mean and the autocovariance operators at a given lag, say h, of a collection (indexed by time) of approximating stationary functional time series are in fact time independent. As explained in the next paragraph, the individual tests are then combined to yield a joint test including autocovariances up to a given maximal lag H. Thus, the approach investigated here is similar in spirit to the classical Portmanteau tests for serial correlation of a univariate time series, where the hypothesis of white noise is checked by investigating whether correlations up to a given lag vanish (see Box and Pierce 1970; Ljung and Box 1978). For the problem of checking stationarity in real-valued time series, similar approaches have been taken by Jin et al. (2015) and Bücher et al. (2018).
To combine the individual tests for stationarity of the mean and the autocovariance operators at a given lag h, we use appropriate extensions of well-known p value combination methods dating back to Fisher (1932). Each individual test is relying on a block multiplier approach making necessary the choice of a joint block length parameter m. Following ideas put forward in Politis and White (2004), a procedure is proposed to automatically select that parameter data adaptively in such a way that, asymptotically, a certain MSE criterion is optimized.
The remaining part of this article is organized as follows: In Sect. 2, we collect necessary mathematical preliminaries. In Sect. 3, we first propose individual tests for the hypothesis of second-order stationarity which are particularly sensitive to deviations in the mean, variance and a given lag h autocovariance, respectively. The tests are then combined to a joint test for second-order stationarity which is sensitive to deviations in the mean, variance and the first H autocovariances. In Sect. 4, we discuss an exemplary locally stationary time series model in great theoretical detail, while finite-sample results and a case study are presented in Sect. 5. The central proofs are collected in Sect. 6, while less central proofs and auxiliary results are provided in a supplementary material.
2 Mathematical preliminaries
2.1 Random elements in \(L^p\)-spaces
For some separable measurable space \((S, \mathcal {S},\nu )\) with a \(\sigma \)-finite measure \(\nu \) and \(p>1\), let \(\mathcal {L}^p(S, \nu )\) denote the set of measurable functions \(f:S \rightarrow \mathbb {R}\) such that \(\Vert f\Vert _p = (\int |f|^p {\,\mathrm {d}}\nu )^{1/p}<\infty \). For \(f\in \mathcal {L}^p(S, \nu )\), let [f] be the set of all functions g such that \(f=g\), \(\nu \)-almost surely. The space \(L^p(S, \nu )\) of all equivalence classes [f] then becomes a separable Banach space, and standard weak convergence theory is applicable. If S is a subset of \(\mathbb {R}^d\) and \(\nu \) is the Lebesgue measure, we occasionally write \(\mathcal {L}^p(S)\) and \(L^p(S)\).
Let \((\Omega , \mathcal {A}, \mathbb {P})\) denote a probability space and let \(X: S\times \Omega \rightarrow \mathbb {R}\) be \((\mathcal {S}\otimes \mathcal {A})\)-measurable such that \(X(\cdot , \omega ) \in \mathcal {L}^p(S, \mu )\) for \(\mathbb {P}\)-almost every \(\omega \). It follows from Lemma 6.1 in Janson and Kaijser (2015) that \(\omega \mapsto [X(\cdot , \omega )]\) is a random variable in \(L^p(S, \mu )\) (equipped with the Borel \(\sigma \)-field). Conversely, note that for any random variable [Y] in \(L^p(S, \mu )\), we can choose a \((\mu \otimes \mathbb {P})\)-a.s. unique \((\mathcal {S}\otimes \mathcal {A})\)-measurable mapping \(Y': S \times \Omega \rightarrow \mathbb {R}\) such that \(Y'(\cdot , \omega ) \in [Y](\omega )\) for \(\mathbb {P}\)-almost every \(\omega \). We can hence (a.s.) identify random variables in \(L^p(S, \mu )\) with measurable functions on \(S\times \Omega \) which are p-integrable in the first argument (\(\mathbb {P}\)-a.s.); slightly abusing notation, we also write X for the equivalence class [X].
A random variable X in \(L^2([0,1]^d)\) is called integrable if \(\mathbb {E}\Vert X\Vert _2 < \infty \). In that case, it follows from the Riesz representation theorem that there exists a unique element \(\mu _X =\mathbb {E}X \in L^2([0,1]^d)\) such that \(\mathbb {E}\langle X,f\rangle = \langle \mu _X,f\rangle \) for all \(f\in L^2([0,1]^d)\), where \(\langle f,g\rangle =\int _{\scriptscriptstyle [0,1]^d} fg {\,\mathrm {d}}\lambda _d\). If X is even square integrable, that is, \(\mathbb {E}\Vert X\Vert _2^2 < \infty \), the covariance operator of X is defined as the operator \(C_X: L^2([0,1]^d) \rightarrow L^2([0,1]^d)\) given by \(C_X(f)=\mathbb {E}[\langle f,X-\mu _X \rangle (X-\mu _X)]\). \(C_X\) is nuclear and hence a Hilbert–Schmidt operator (Bosq 2000, Sect. 1.5), whence, by Theorem 6.11 in Weidmann (1980), there exists a kernel \(c_X \in L^2([0,1]^d \times [0,1]^d)\) such that
for almost every \(\tau \in [0,1]^d\) and every \(f\in L^2([0,1]^d)\). Similarly, for square integrable random elements \(X,Y\in L^2([0,1]^d)\) we define the cross-covariance operator \(C_{X,Y}: L^2([0,1]^d) \rightarrow L^2([0,1]^d)\) by \(C_{X,Y}(f) = \mathbb {E}[\langle X- \mu _X, f\rangle (Y-\mu _Y)]\). By the same reasoning as above, there exists a kernel \(c_{X,Y}\in L^2([0,1]^d \times [0,1]^d)\) such that
If X is in fact a \((\mathcal {B}([0,1]^d) \otimes \mathcal {A})\)-measurable function from \([0,1]^d \times \Omega \) to \(\mathbb {R}\) with \(X(\cdot , \omega ) \in \mathcal {L}^2([0,1]^d)\) a.s., then it can be shown that, in the respective \(L^2\)-spaces,
By the preceding paragraph, this notation also makes sense for equivalence classes \(X,Y\in L^{2}([0,1]^d)\).
2.2 Functional time series in \(L^2([0,1])\)
For each \(t\in \mathbb {Z}\), let \(X_{t}: [0,1] \times \Omega \rightarrow \mathbb {R}\) denote a \((\mathcal {B}|_{[0,1]} \otimes \mathcal {A})\)-measurable function with \(X_{t}(\cdot , \omega ) \in \mathcal {L}^2([0,1])\). By the preceding section, we can regard \([X_{t}]\) as a random variable in \(L^2([0,1])\), which we also write as \(X_{t}\). The sequence \( (X_{t})_{t\in \mathbb {Z}} \) will be referred to as a functional time series in \(L^2([0,1])\).
The functional time series will be called stationary if, for all \(q\in \mathbb {Z}\) and all \(h,t_1,\dots ,t_q\in \mathbb {Z}\)
in \(L^2([0,1])^{q}\).
Let \(\rho >0\). A sequence of functional time series \((X_{t,T})_{t\in \mathbb {Z}}\), indexed by \(T\in \mathbb {N}\), is called locally stationary (of order\(\rho \)) if, for any \(u\in [0,1]\), there exists a strictly stationary functional time series \(\{X_t^{\scriptscriptstyle (u)} \mid t\in \mathbb {Z}\}\) in \(L^2([0,1])\) and an array of real-valued random variables \(\{P_{\scriptscriptstyle t,T}^{\scriptscriptstyle (u)} \mid t=1,\dots ,T\}_{T\in \mathbb {N}}\) with \(\mathbb {E}|P_{t,T}^{\scriptscriptstyle (u)}|^\rho <\infty \), uniformly in \(1\le t\le T, T\in \mathbb {N}\) and \(u\in [0,1]\), such that
for all \(t=1,\dots ,T,T\in \mathbb {N}\) and \(u\in [0,1]\). This concept of local stationarity was first introduced by Vogt (2012) for p-dimensional time series (\(p\in \mathbb {N}\)). By the arguments in the preceding section, we may assume that \(X_t^{\scriptscriptstyle (u)}\) is in fact a \((\mathcal {B}([0,1])\times \mathcal {A})\)-measurable function from \([0,1]\times \Omega \) to \(\mathbb {R}\) such that \(X_t^{\scriptscriptstyle (u)}(\cdot , \omega ) \in \mathcal {L}^2([0,1])\) for \(\mathbb {P}\)-almost every \(\omega \). In the subsequent sections, we will usually assume that \(\rho \ge 2\) and that \(\mathbb {E}[ \Vert X_t^{(u)}\Vert _2^2]< \infty \) for all \(u\in [0,1]\). Despite the fact that \(\{(X_{t,T})_{t\in \mathbb {Z}}: T\in \mathbb {N}\}\) is a sequence of time series, we will occasionally simply call \((X_{t,T})_{t\in \mathbb {Z}}\) a locally stationary time series.
2.3 Further notation
In the following, we will deal with different norms on the spaces \(L^p([0,1]^d)\), for \(p\ge 1,d\in \mathbb {N}\). To avoid confusion, we denote the corresponding norms by \(\Vert \cdot \Vert _{p,d}\). As a special case, we will write \(\Vert \cdot \Vert _p\) instead of \(\Vert \cdot \Vert _{p,1}\). Further, we introduce the notation \(\Vert \cdot \Vert _{p,\Omega \times [0,1]^d}\) for the p-norm on the space \(L^p(\Omega \times [0,1]^d,\mathbb {P}\otimes \lambda ^d)\). Finally, we define \((f\otimes g)(x,y)=f(x)g(y)\) for functions \(f,g\in L^p([0,1])\).
3 Detecting deviations from second-order stationarity
3.1 Second-order stationarity in locally stationary time series
Before we can propose suitable test statistics for detecting deviations from second-order stationarity in a locally stationary functional time series, we need to clarify what is meant by second-order stationarity. Loosely speaking, we want to test the null hypothesis that the mean and/or the (auto)covariances do not vary too much over time. Meaningful asymptotic results will be obtained by formulating these null hypotheses in terms of the approximating sequences \(\{X_{t}^{\scriptscriptstyle (u)}: t \in \mathbb {Z}\}\) defined in Sect. 2.2. More precisely, we will subsequently assume that \(\mathbb {E}[ \Vert X_t^{(u)}\Vert _2^2]< \infty \) for all \(u\in [0,1]\) and consider the hypotheses
and, for some lag \(h\ge 0\),
Note that the intersection
corresponds to the case where the approximating sequences \(\{X_{t}^{\scriptscriptstyle (u)}: t \in \mathbb {Z}\}\), indexed by \(u\in [0,1]\), all share the same first- and second-order characteristics. We will therefore call the sequence of time series \((X_{t,T})_{t\in \mathbb {Z}}\), indexed by \(T\in \mathbb {N}\), second-order stationary if the global hypothesis \(H_0\) is met. The test statistics we are going to propose will be particularly sensitive to deviations from (weak) stationarity in the mean, the variance, and the first H autocovariances, which leads us to define
where \(H \in \mathbb {N}_0\) is fixed and denotes the maximum number of lags under consideration.
Remark 1
The hypotheses \(H_0^{\scriptscriptstyle (m)}\) and \(H_0^{\scriptscriptstyle (c,h)}\) are independent of the choice of the approximating family \(\{X_t^{\scriptscriptstyle (u)}: t\in \mathbb {Z}\}_{u\in [0,1]}\). Indeed, suppose there were two approximating families \(\{X_t^{\scriptscriptstyle (u)}: t\in \mathbb {Z}\}_{u\in [0,1]}\) and \(\{Y_t^{\scriptscriptstyle (u)}: t\in \mathbb {Z}\}_{u\in [0,1]}\) satisfying (1). By stationarity and the triangle inequality, we have, for any \(t,T\in \mathbb {N}\),
This implies \(\mathbb {E}\Vert X_t^{\scriptscriptstyle (u)}-Y_t^{\scriptscriptstyle (u)}\Vert _2=0\) and hence \(\Vert X_t^{\scriptscriptstyle (u)}-Y_t^{\scriptscriptstyle (u)}\Vert _2=0\) almost surely. \(\square \)
The following lemma provides two interesting equivalent formulations of each of the above hypotheses. Introduce the notations \(M:[0,1]^2\rightarrow \mathbb {R}, M_h:[0,1]^3\rightarrow \mathbb {R}\), where
Lemma 1
Let \(\{(X_{t,T})_{t\in \mathbb {Z}}: T\in \mathbb {N}\}\) denote a locally stationary functional time series of order \(\rho \ge 4\) with approximating sequences \((X_{t}^{\scriptscriptstyle (u)})_{t \in \mathbb {Z}}\) satisfying \(\mathbb {E}[\Vert X_{0}^{\scriptscriptstyle (u)} \Vert _2^4]<\infty \) for all \(u\in [0,1]\). Then, the hypothesis \(H_0^{\scriptscriptstyle (m)}\) in (2) is met if and only if
Likewise, for any \(h\in \mathbb {N}_0\), \(H_0^{\scriptscriptstyle (c,h)}\) in (3) is met if and only if
Moreover, the hypothesis \(H_0^{\scriptscriptstyle (m)}\) is equivalent to
and \(H_0^{\scriptscriptstyle (c,h)}\) is equivalent to
The lemma is proven in Sect. 6.2. We will heavily rely on conditions (7) and (8) when constructing the test statistics in the next section. Assertions (9) and (10) are interesting in their own rights, as they provide a sub-asymptotic formulation of the hypothesis of second-order stationarity. They are used in the next section for showing that the tests are consistent and will also be crucial when extending consistency results to the case of piecewise locally stationary processes in Sect. 3.5.
3.2 Test statistics
In the subsequent sections, we assume to observe, for some \(T\in \mathbb {N}\), an excerpt \(X_{1,T}, \dots , X_{T,T}\) from a locally stationary time series \(\{(X_{t,T})_{t\in \mathbb {Z}}:T\in \mathbb {N}\}\). We are interested in testing the hypotheses \(H_0^{\scriptscriptstyle (m)}\) and \(H_0^{\scriptscriptstyle (c,h)}\) formulated in the preceding section, which can be done individually by a CUSUM-type procedure. More precisely, for \(u,\tau \in [0,1]\), let
denote the CUSUM process for the mean, and, for \(u,\tau _1, \tau _2\in [0,1]\) and \(h \in \mathbb {N}_0\), let
denote the CUSUM process for the (auto)cross-moments at lagh. Under the null hypothesis \(H_0^{\scriptscriptstyle (m)}\), \(T^{-1/2} {U}_T(u,\tau )\) can be regarded as an estimator of the quantity \(M(u,\tau )\) defined in (5), and a similar statement holds for \(T^{-1/2} {U}_{T,h}\), which estimates the \(M_h\) in (6). Hence, by Lemma 1, it seems reasonable to reject \(H_0^{\scriptscriptstyle (m)}\) or \(H_0^{\scriptscriptstyle (c,h)}\) for large values of
respectively.
Alternatively, one could use the \(L^2\)-norm in \(\tau \) and \((\tau _1,\tau _2)\), respectively, and the supremum in u, as proposed in Sharipov et al. (2016). However, preliminary simulation results suggested that a test based on the \(L^2\)-norm in u performs better in applications with small sample sizes.
In Sect. 3.4, we will propose a procedure that allows to combine the previous tests statistics to obtain a joint test for the combined hypothesis \(H_0^{\scriptscriptstyle (H)}\), with maximal lag \(H\in \mathbb {N}_0\) fixed. For that purpose, we will first need (asymptotic) critical values for the individual test statistics \(\mathcal {S}_T^{(m)}\) and \(\mathcal {S}_T^{(c,h)}\), which in turn can be deduced from the joint asymptotic distribution of the CUSUM processes in (11) and (12). The basic tools are the following partial sum processes
where \(u,\tau ,\tau _1, \tau _2 \in [0,1]\) and \(h\in \mathbb {N}_0\). The expected values within the sums will be denoted by
The following assumptions are sufficient to guarantee weak convergence of these processes.
Condition 1
(Assumptions on the functional time series)
- (A1)
Local stationarity The observations \(X_{1,T}, \dots X_{T,T}\) are an excerpt from a locally stationary functional time series \(\{(X_{t,T})_{t\in \mathbb {Z}}:T\in \mathbb {N}\}\) of order \(\rho =4\) in \(L^2([0,1],\mathbb {R})\).
- (A2)
Moment condition For any \(k\in \mathbb {N}\), there exists a constant \(C_k<\infty \) such that \(\mathbb {E}\Vert X_{t,T}\Vert _2^k\le C_k\) and \(\mathbb {E}\Vert X_0^{\scriptscriptstyle (u)}\Vert _2^k\le C_k\) uniformly in \(t\in \mathbb {Z},T\in \mathbb {N}\) and \(u\in [0,1]\).
- (A3)
Cumulant condition For any \(j\in \mathbb {N}\), there is a constant \(C_j <\infty \) such that
$$\begin{aligned} \sum _{t_1,\dots ,t_{j-1}=-\infty }^{\infty } \big \Vert {{\,\mathrm{cum}\,}}(X_{t_1,T},\dots ,X_{t_j,T})\big \Vert _{2,j} \le C_j<\infty , \end{aligned}$$(14)for any \(t_j\in \mathbb {Z}\) (for \(j=1\), the condition is to be interpreted as \(\Vert \mathbb {E}X_{t_1,T}\Vert _2\le C_1\) for all \(t_1 \in \mathbb {Z}\)). Further, for \(k\in \{2,3,4\}\), there exist functions \(\eta _k:\mathbb {Z}^{k-1}\rightarrow \mathbb {R}\) satisfying
$$\begin{aligned} \sum _{t_1,\dots ,t_{k-1}=-\infty }^{\infty } (1+|t_1|+\dots +|t_{k-1}|)\eta _k(t_1,\dots ,t_{k-1}) < \infty \end{aligned}$$such that, for any \(T\in \mathbb {N}, 1 \le t_1 , \dots , t_k \le T, v, u_1, \dots , u_k \in [0,1],h_1,h_2\in \mathbb {Z}\), \(Z_{t,T}^{\scriptscriptstyle (u)}\in \{X_{\scriptscriptstyle t, T},X_{t}^{\scriptscriptstyle (u)}\}\), and any \(Y_{t,h,T}(\tau _1,\tau _2)\in \{ X_{t,T}(\tau _1), X_{t,T}(\tau _1)X_{t+h,T}(\tau _2) \}\), we have
- (i)
\(\Vert {{\,\mathrm{cum}\,}}(X_{t_1,T}-X_{t_1}^{(t_1/T)},Z_{t_2,T}^{(u_2)},\ldots ,Z_{t_k,T}^{(u_k)})\Vert _{2,k} \le \frac{1}{T} \eta _k(t_2-t_1,\dots ,t_k-t_1)\),
- (ii)
\(\Vert {{\,\mathrm{cum}\,}}(X_{t_1}^{(u_1)}-X_{t_1}^{(v)},Z_{t_2,T}^{(u_2)},\ldots ,Z_{t_k,T}^{(u_k)})\Vert _{2,k} \le |u_1-v| \eta _k(t_2-t_1,\dots ,t_k-t_1)\),
- (iii)
\(\Vert {{\,\mathrm{cum}\,}}(X_{t_1,T},\dots ,X_{t_k,T})\Vert _{2,k} \le \eta _k(t_2-t_1,\ldots ,t_k-t_1)\),
- (iv)
\(\int _{[0,1]^{2}} |{{\,\mathrm{cum}\,}}\big (Y_{t_1,h_1,T}(\tau ),Y_{t_2,h_2,T}(\tau ) \big )|{\,\mathrm {d}}\tau \le \eta _2(t_2-t_1)\).
- (i)
Assumption (A2) is needed to ensure existence of all cumulants. The cumulant condition (A3) is a (partially) weakened version of the assumptions made by Lee and Subba Rao (2017) and Aue and van Delft (2017) and has its origins in classical multivariate time series analysis (see Brillinger (1981), Assumption 2.6.2). Lemma 2 shows that the cumulant conditions in (A3) hold, provided (A1), (A2), a further moment condition and a strong mixing condition are satisfied. In particular, they are met for the models employed in Sect. 5 within our simulation study (see in particular Lemma 4).
The following theorem, proven in Sect. 6.2, shows that \(\tilde{B}_{T}\) and \(\tilde{B}_{T,h}\) jointly converge weakly with respect to the \(L^2\)-metric. For \(H \in \mathbb {N}_0\), let the Cartesian product
be equipped with the sum of the individual scalar products, such that \(\mathcal {H}_{H+2}\) is a Hilbert space itself.
Theorem 1
Suppose that Assumptions (A1)–(A3) are met. Then, the vector \(\mathbb {B}_T=(\tilde{B}_T,\tilde{B}_{T,0},\dots ,\tilde{B}_{T,H})\) converges weakly to a centered Gaussian variable \(\mathbb {B}=(\tilde{B},\tilde{B}_0,\dots ,\tilde{B}_H)\) in \(\mathcal {H}_{H+2}\) with covariance operator \(C_\mathbb {B}:\mathcal {H}_{H+2} \rightarrow \mathcal {H}_{H+2}\) defined as
Here, the kernel functions \(r^{(m)}, r^{(c)}_{h,h'}\) and \(r^{(m,c)}_h\) are given by
with
for any \(0\le h,h'\le H\). In particular, the infinite sums and integrals converge.
The following corollary on joint weak convergence of the CUSUM processes defined in (11) and (12) is essentially a mere consequence of the continuous mapping theorem. Let
and, similarly,
Corollary 1
Suppose that Assumptions (A1)–(A3) are satisfied. If \(H_0^{\scriptscriptstyle (m)}\) holds, then
If \(H_0^{\scriptscriptstyle (c,h)}\) holds, then
As a consequence, if the hypothesis \(H_0^{\scriptscriptstyle (H)}\) in (4) holds, then,
On the other hand, if \(H_0^{\scriptscriptstyle (m)}\) or \(H_0^{\scriptscriptstyle (c,h)}\) does not hold, then \(\mathcal {S}_T^{(m)}\rightarrow \infty \) or \(\mathcal {S}_T^{(c,h)} \rightarrow \infty \) in probability, respectively.
The corollary suggests to reject \(H_0^{\scriptscriptstyle (m)}\) or \(H_0^{\scriptscriptstyle (c,h)}\) for large values of \(\mathcal {S}_T^{(m)}\) or \(\mathcal {S}_T^{(c,h)}\), respectively. However, the corresponding null-limiting distributions \(\Vert \tilde{G} \Vert _{2,2}\) and \(\Vert \tilde{G}_h \Vert _{2,3}\) depend in a complicated way on the functions \(c_{k,j}\) defined in Theorem 1 and cannot be easily transformed into a pivotal distribution. We therefore propose to derive critical values by a suitable block multiplier bootstrap approximation worked out in detail in Sect. 3.4.
3.3 Strong mixing and cumulants
In this section, we will demonstrate that under the assumption of a strong mixing locally stationary functional time series, Assumption (A3) is met. To be precise, let \(\mathcal {F}\) and \(\mathcal {G}\) be \(\sigma \)-fields in \((\Omega , \mathcal {A})\) and define
A functional time series \(\{(X_{t,T})_{t\in \mathbb {Z}}: T\in \mathbb {N}\}\) in \(L^2([0,1])\) is called \(\alpha \)- or strongly mixing if the mixing coefficients
vanish as k tends to infinity. Analogously, we define
as mixing coefficients of the family of approximating stationary processes. Further, we define \(\alpha (k)=\max \{\alpha '(k),\alpha ''(k)\}\). A locally stationary, functional time series is called strongly mixing, if \(\alpha (k)\) vanishes, as k tends to infinity and exponentially strongly mixing if \(\alpha (k) \le c a^k \) for some constants \(c >0 \) and \(a \in (0,1)\). Note that we can define the mixing coefficients in terms of a function in \(\mathcal {L}^2([0,1])\) rather than an element of the space \(L^2([0,1])\) of equivalence classes by Lemma 6.1 in Janson and Kaijser (2015). The main result of this section provides sufficient conditions for the theory developed so far for strong mixing processes.
Lemma 2
Let \(\{(X_{t,T})_{t\in \mathbb {Z}}: T\in \mathbb {N}\}\) be a strongly mixing locally stationary functional time series in \(L^2([0,1],\mathbb {R})\) such that Assumptions (A1), (A2) and the condition
are satisfied for any integer \(r> 2\). If \(\{(X_{t,T})_{t\in \mathbb {Z}}: T\in \mathbb {N}\}\) is exponentially strongly mixing, then it also satisfies the summability conditions for the cumulants in Assumption (A3).
3.4 Bootstrap approximation
The bootstrap approximation will be based on two smoothing parameters: a block length sequence \(m=m_T\) needed to asymptotically catch the serial dependence within the time series, and a bandwidth sequence \(n=n_T\) needed to estimate expected values locally in time. We will impose the following condition.
Condition 2
(Assumptions on the bootstrap scheme)
- (B1)
Let \(m=m(T) \le T\) be an integer-valued sequence, to be understood as the block length within a block bootstrap procedure. Assume that m tends to infinity and m / T vanishes, as \(T\rightarrow \infty \).
- (B2)
Let \(n=n(T) \le T/2\) be an integer-valued sequence such that both m / n and \(mn^2/T^2\) converge to zero, as T tends to infinity.
- (B3)
Let \(\{R_i^{\scriptscriptstyle (k)}\}_{i,k\in \mathbb {N}}\) denote independent standard normally distributed random variables, independent of the stochastic process \(\{(X_{t,T})_{t\in \mathbb {Z}}:T\in \mathbb {N}\}\).
Under this set of notations, we define
as a bootstrap approximation for \(\tilde{B}_T(u, \tau )\), where
denotes an estimator for \(\mu _{t,T}(\tau )\) relying on the bandwidth sequence n via
for \(0\le h\le H\). Similarly, for any \(0\le h\le H\), bootstrap approximations for \(\tilde{B}_{T,h}(u, \tau _1, \tau _2)\) are defined as
where
Finally, for fixed \(k\in \mathbb {N}\), collect the bootstrap approximations in the vector
The following theorem shows that the bootstrap replicates can be regarded as asymptotically independent copies of the original process \(\mathbb {B}_T\) from Theorem 1.
Theorem 2
Suppose that Assumptions (A1)–(A3) and (B1)–(B3) are met. Then, for any fixed \(K\in \mathbb {N}\) and as \(T \rightarrow \infty \),
in \(\{ L^2([0,1]^2)\times (L^2([0,1]^3))^{H+1}\}^{K+1}\), where \(\mathbb {B}^{\scriptscriptstyle (k)}\) (\(k=1,\dots ,K\)) are independent copies of the centered Gaussian variable \(\mathbb {B}\) from Theorem 1. Equivalently (Bücher and Kojadinovic 2017, Lemma 2.2),
where \(d_{\mathrm {BL}}\) denotes the bounded Lipschitz metric between probability distributions on \(L^2([0,1]^2)\times (L^2([0,1]^3))^{H+1}\).
The proof is given in Sect. 6.2. The preceding theorem, together with Corollary 1, suggests to define the following bootstrap approximation for the CUSUM processes defined in (11) and (12):
Theorem 2, Corollary 1 and the continuous mapping theorem then imply that, under the hypothesis \(H_0^{\scriptscriptstyle (H)}\) in (4),
where \(\Phi (G_{-1},G_0, \dots , G_{H}) = (\Vert G_{-1} \Vert _{2,2}, \Vert G_{0}\Vert _{2,3}, \dots , \Vert G_H\Vert _{2,3})\) and where \(\mathbb {G}^{\scriptscriptstyle (1)},\dots ,\mathbb {G}^{\scriptscriptstyle (K)}\) are independent copies of \(\mathbb {G}\). Individual bootstrap-based tests for, e.g., \(H_{0}^{\scriptscriptstyle (c,h)}\) are then naturally defined by the p value
where \(S_{T,h}^{\scriptscriptstyle (k)}\) and \(S_{T,h}\) denote the \((h+2)\)nd coordinate of \(\varvec{S}_{T}^{\scriptscriptstyle (k)}\) and \(\varvec{S}_T\), respectively; in particular, \(S_{T,-1}=\mathcal {S}_T^{\scriptscriptstyle (m)}\) and \(S_{T,h}=\mathcal {S}_T^{\scriptscriptstyle (c,h)}\) as defined in (13). Indeed, we can show the following result for each individual test.
Proposition 1
Suppose that Assumptions (A1)–(A3) and (B1)–(B3) are met. Then, for all \(h \in \mathbb {Z}_{\ge -1}\), provided \(K=K_T \rightarrow \infty \), and with \(H_0^{(c,-1)}=H_0^{(m)}\), we have
Moreover, we can rely on an extension of Fisher’s p value combination method (Fisher 1932) as described in Sect. 2 in Bücher et al. (2018) to obtain a combined test for the joint hypothesis \(H_0^{\scriptscriptstyle (H)}\) in (4). More precisely, let \(\psi :(0,1)^{H+2} \rightarrow \mathbb {R}\) be a continuous function that is decreasing in each argument (throughout the simulations, we employ \(\psi (p_{-1},\dots ,p_H)=\sum _{i=-1}^{H}w_i\Phi ^{-1}(1-p_i)\) with weights \(w_{-1}=w_{0}=1/3\) and \(w_1=\cdots =w_H= (3H)^{-1}\).) The combined test is defined by its p value calculated based on the following algorithm.
Algorithm 1
(Combined Bootstrap test for\(H_0^{\scriptscriptstyle (H)}\))
- (1)
Let \(\varvec{S}_T^{\scriptscriptstyle (0)} = \varvec{S}_{T}\).
- (2)
Given a large integer K, compute the sample of K bootstrap replicates \(\varvec{S}_T^{\scriptscriptstyle (1)},\dots ,\varvec{S}_T^{\scriptscriptstyle (K)}\) of the vector \(\varvec{S}_T^{\scriptscriptstyle (0)}\).
- (3)
Then, for all \(i \in \{0,1,\dots ,K\}\) and \(h \in \{-1,\dots ,H\}\), compute
$$\begin{aligned} p_{T,K}(S_{T,h}^{(i)}) = \frac{1}{K+1} \bigg \{\frac{1}{2} + \sum _{k=1}^K \varvec{1} \left( S_{T,h}^{(k)} \ge S_{T,h}^{(i)} \right) \bigg \}. \end{aligned}$$ - (4)
Next, for all \(i \in \{0,1,\dots ,K\}\), compute
$$\begin{aligned} W_{T,K}^{(i)} = \psi \{ p_{T,K}(S_{T,0}^{(i)}),\dots ,p_{T,K}(S_{T,H}^{(i)}) \}. \end{aligned}$$ - (5)
The global statistic is \(W_{T,K}^{\scriptscriptstyle (0)}\), and the corresponding p value is given by
$$\begin{aligned} p_{T,K}(W_{T,K}^{(0)}) =\frac{1}{K} \sum _{k=1}^K \varvec{1} \left( W_{T,K}^{(k)} \ge W_{T,K}^{(0)} \right) . \end{aligned}$$
Consistency of this procedure is a mere consequence of Proposition 2.1 in Bücher et al. (2018); details are omitted for the sake of brevity.
3.5 Consistency against AMOC-piecewise locally stationary alternatives
In the previous section, the proposed tests were shown to be consistent against locally stationary alternatives. In classical change point settings, the underlying CUSUM principle is also known to be consistent against piecewise (locally) stationary alternatives, notably against those that involve a single change in the signal of interest (AMOC = at most one change). We are going to derive such results within the present setting.
For the sake of brevity, we only consider AMOC alternatives in the mean. More precisely, we assume that \(\{(X_{t,T})_{t \in \mathbb {Z}}:T\in \mathbb {N}\}\) follows the data-generating process
for some \(\lambda \in (0,1), \mu _1, \mu _2 \in \mathcal {L}^2([0,1])\) and \(\{(Y_{t,T})_{t \in \mathbb {Z}}:T\in \mathbb {N}\}\) a locally stationary time series satisfying Condition 1. In the literature on classic change point detection, one would be interested in testing for the null hypothesis that \(\Vert \mu _1 - \mu _2 \Vert _2 =0\), against the alternative that this \(L^2\)-norm is positive.
Now, if \(\Vert \mu _1 - \mu _2 \Vert _2 =0\), we are back in the situation of the preceding sections. However, one can show (by contradiction) that if \(\Vert \mu _1 - \mu _2 \Vert _2 > 0\), \(\{(X_{t,T})_{t \in \mathbb {Z}}:T\in \mathbb {N}\}\) is not locally stationary, whence additional theory must be developed to show consistency of the test statistic \(\mathcal {S}_{T}^{\scriptscriptstyle (H)}\). Note that even the formulation of \(H_0^{\scriptscriptstyle (H)}\) relying on (2) and (3) is not possible anymore, so that we need to rely on their equivalent sub-asymptotic counterparts (9) and (10) in Lemma 1.
Proposition 2
Let \(\{(X_{t,T})_{t \in \mathbb {Z}}:T\in \mathbb {N}\}\) be a sequence of functional time series as defined in (17), with \(\mu _1 \ne \mu _2\) in \(L^2([0,1])\) and with \(\{(Y_{t,T})_{t \in \mathbb {Z}}:T\in \mathbb {N}\}\) satisfying Conditions (A1)–(A3). Then, the test statistic \(\mathcal {S}_T^{\scriptscriptstyle (m)}=S_{T,-1}\) based on observations \(X_{1,T}, \dots , X_{T,T}\) diverges to infinity, in probability. If, additionally, (B1)–(B3) are met, then the bootstrap variables \(\hat{S}_{T,-1}^{\scriptscriptstyle (k)}\) are stochastically bounded. As a consequence, the proposed test is consistent.
Remark 2
A careful inspection of the proof of Proposition 2 shows that the testing procedure is also consistent against local alternatives of the form \(\mu _2 = \mu _1 + d_T\), for any sequence \(d_T\) with \(d_T \sqrt{T}\rightarrow \infty \).
3.6 Data-driven choice of the block length parameter m
The bootstrap procedure depends on the choice of the width of the local mean estimator, n, and the length of the bootstrap blocks, m. Preliminary simulation studies suggested that the performance of the procedure crucially depends on the choice of m, while it is less sensitive to the choice of n (which may also be chosen by other standard criteria in specific applications, like adaptations of Silverman’s rule of thumb, cross-validation or visual investigation of respective plots). In this section, we propose a data-driven procedure for choosing the block length m based on a certain optimality criterion.
Recall that the limiting null distributions of the proposed test statistics depend in a complicated way on the covariances \(\text {Cov}\{\tilde{B}(u,\tau ),\tilde{B}(v,\varphi )\}, \text {Cov}\big \{ \tilde{B}_h(u,\tau _1,\tau _2),\tilde{B}_{h'}(v,\varphi _1,\varphi _2)\}\) and \(\text {Cov}\{\tilde{B}(u,\tau ),\tilde{B}_{h}(v,\varphi _1,\varphi _2)\}\). Following Sect. 5 in Bücher and Kojadinovic (2016), the procedure we propose essentially chooses m in such a way that the bootstrap approximation for \(\sigma _c(\tau , \varphi )=\text {Cov}\{\tilde{B}(1,\tau ),\tilde{B}(1,\varphi )\}\) is optimal, with respect to m, in a certain asymptotic sense. More precisely, we propose to first minimize the integrated mean squared of the “bootstrap estimator”
considered as an estimator for \(\sigma _c(\tau , \varphi )\), with respect to m theoretically (see Lemma 3), and then use a simple plug-in approach to obtain a formula that solely depends on observable quantities. Observe that \(\tilde{\sigma }_T(\tau ,\varphi )\) can be rewritten as
whence \(\tilde{\sigma }_T(\tau ,\varphi )\) is not a proper estimator as it depends on the unknown expectation \(\mu _{t,T}\). The asymptotic integrated bias and integrated variance satisfy the following expansions. For simplicity, we replace Condition (A3) by a strong mixing condition as in Sect. 3.3.
Lemma 3
Let \(m=m(T)\) be an integer-valued sequence, such that m tends to infinity and \(m^2/T\) vanishes, as T tends to infinity. If conditions (A1) and (A2) are met and \(\{(X_{t,T})_{t\in \mathbb {Z}}: T\in \mathbb {N}\}\) is exponentially strongly mixing, then, as \(T\rightarrow \infty \),
where
and
As a consequence of this lemma, we obtain the expansion
which can next be minimized with respect to m to get a natural choice for the block length. More precisely, the dominating function \(\Lambda (m)=\tfrac{m}{T} \Gamma + \tfrac{1}{m^2} \Delta \) is differentiable in m with \(\Lambda '(m)=\tfrac{\Gamma }{T} - \tfrac{2\Delta }{m^3}\) and \(\Lambda ''(m)=\tfrac{6\Delta }{m^4}\), whence \(m=\big (\tfrac{2\Delta T}{\Gamma }\big )^{1/3}\) is the unique minimizer of \(\Lambda \). In practice, both \(\Gamma \) and \(\Delta \) are unknown and must be estimated in terms of the observed data. This leads us to define
where, for some constant \(L\in \mathbb {N}\) specified below,
and
Here \(\hat{\gamma }_{i,k,T}\) is defined by
and \(\bar{n}_{t,h},\underline{n}_t\) and \(\tilde{n}_{t,h}\) are given in (16). Note that the above estimators depend on the choice of the integer L. Following Bücher and Kojadinovic (2016) and Politis and White (2004), we select L to be the smallest integer, such that
is negligible for any \(k>L\); more precisely, L is chosen as the smallest integer such that \(\hat{\rho }_{L+k,T} \le 2 \sqrt{\log (T)/T}\), for any \(k=1,\ldots , K_T\), with \(K_T= \max \{5, \sqrt{\log T}\}\).
4 Time-varying random operator functional AR processes
We consider an exemplary class of functional locally stationary processes and specify the approximating family of stationary processes. The results in this section are similar to Theorem 3.1 of Bosq (2000).
Let \(\mathcal {L}=\mathcal {L}\big (L^2([0,1]),L^2([0,1])\big )\) be the space of bounded linear operators on \(L^2([0,1])\). Further, denote by \(\Vert \cdot \Vert _\mathcal {L}\) and \(\Vert \cdot \Vert _\mathcal {S}\) the standard operator norm and the Hilbert–Schmidt norm, respectively, i. e.,
for \(\ell \in \mathcal {L}\) with eigenvalues \(\lambda _1\ge \lambda _2\ge \dots \). By Eq. (1.55) in Bosq (2000), we have \(\Vert \cdot \Vert _\mathcal {L} \le \Vert \cdot \Vert _\mathcal {S}\). For any \(T\in \mathbb {N}\), consider the recursive functional equation
where \(({\varepsilon }_{t,T})_{t\in \mathbb {Z}}\) is a sequence of independent zero mean innovations in \(L^2([0,1])\) and where \(A_{t,T}:L^2([0,1]) \rightarrow L^2([0,1])\) denotes a possibly random and time-varying bounded linear operator. The equation defines what might be called a (time-varying) random operator functional autoregressive process of order one, denoted by \(\mathrm{tvrFAR}(1)\) (see also van Delft et al. (2017), Sect. 4.1) for the non-random case with \({\varepsilon }_{t,T}\) not depending on T.
In the following, we will only consider the case where \(\mu \) is the null function. In the more general case of \(\mu \) being Lipschitz, if there exists a locally stationary solution \(Y_{t,T}\) of the equation on the right-hand side of (18) with approximating family \(\{Y_t^{\scriptscriptstyle (u)}|t\in \mathbb {Z}\}_{u\in [0,1]}\), then \(X_{t,T} = Y_{t,T} + \mu (t/T)\) is obviously locally stationary with approximating family \(X_t^{\scriptscriptstyle (u)}=Y_t+\mu (u)\).
To be precise, we restrict ourselves to the following specific parameterization
where a and \(\sigma >0\) are measurable functions on [0, 1]. The following lemma provides sufficient conditions for ensuring local stationarity of the model and provides an explicit expression for the approximating family of stationary processes. For a related result in the case where \(A_{t/T}\) is non-random and \({\varepsilon }_{t,T}\) does not depend on T, see Theorem 3.1 in van Delft and Eichler (2018).
For a sequence of operators \((B_i)_i\) in \(\mathcal {L}\), we will write \(\prod _{i=0}^{n} B_i = B_0 \circ \dots \circ B_n\) for \(n\in \mathbb {N}\). The empty product will be identified with the identity on \(L^2([0,1])\), that is, \(\prod _{i=0}^{-1} B_i = {{\,\mathrm{id}\,}}_{L^2([0,1])}\).
Lemma 4
Let \((\tilde{{\varepsilon }}_t)_{t\in \mathbb {Z}}\) be strong white noise in \(L^2([0,1])\). Further, let a and \(\sigma \) be measurable functions on \((-\infty ,1]\) such that \(\sigma >0\), \(a(u) = a(0)\) and \(\sigma (u)=\sigma (0)\) for all \(u\le 0\). Finally, let \({\varepsilon }_{t,T}=\sigma (t/T)\tilde{\varepsilon }_t\), \({\varepsilon }_t^{(u)} = \sigma (u) \tilde{\varepsilon }_t\) and \(A_u=a(u) \tilde{A}\), where \(\tilde{A}\) denotes a random operator in \(\mathcal {L}\) that is independent from \((\tilde{\varepsilon }_t)_{t\in \mathbb {Z}}\) and satisfies \(\sup _{u \in [0,1]} \Vert A_u\Vert _\mathcal {S}\le q<1\) with probability one. Then:
- (i)
For any \(u\in [0,1]\), there exists a unique stationary solution \((Y_t^{\scriptscriptstyle (u)})_{t \in \mathbb {Z}}\) of the recursive equation
$$\begin{aligned} Y_t^{(u)}=A_u(Y_{t-1}^{(u)})+{\varepsilon }_{t}^{(u)}, \qquad t \in \mathbb {Z}, \end{aligned}$$namely
$$\begin{aligned} Y_t^{(u)}=\sum _{j=0}^{\infty } A_u^j({\varepsilon }_{u,t-j}), \end{aligned}$$where the latter series converges in \(L^2(\Omega \times [0,1], \mathbb {P}\otimes \lambda )\) and almost surely in \(L^2([0,1])\).
- (ii)
If \(\sigma \) and a are Lipschitz continuous, then there exists a unique locally stationary solution \((Y_{t,T})\) of order \(\rho =2\) satisfying \(\sup _{t\in \mathbb {Z}, T\in \mathbb {N}} \mathbb {E}[\Vert Y_{t,T}\Vert _2^2]<\infty \) of the recursive equation
$$\begin{aligned} Y_{t,T}=A_{t/T}(Y_{t-1,T})+{\varepsilon }_{t,T}, \qquad t \in \mathbb {Z}, T\in \mathbb {N}, \end{aligned}$$namely
$$\begin{aligned} Y_{t,T}=\sum _{j=0}^{\infty } \left( \prod _{i=0}^{j-1} A_{\tfrac{t-i}{T}} \right) ({\varepsilon }_{t-j,T}), \end{aligned}$$the series again being convergent in \(L^2(\Omega \times [0,1], \mathbb {P}\otimes \lambda )\) and almost surely in \(L^2([0,1])\). The locally stationary process has approximating family \(\{(Y_t^{(u)})_{t\in \mathbb {Z}}: u \in [0,1] \}\).
Remark 3
The previous lemma provides sufficient conditions for local stationarity of the random operator FAR model. In the simulation study of the following section, we use specific models for the parameter curves and the functional white noise and show that those models satisfy the cumulant condition in Assumption (A3) as well.
5 Finite-sample results
5.1 Monte Carlo simulations
A large-scale Monte Carlo simulation study was performed to analyze the finite-sample behavior of the proposed tests. The major goals of the study were to analyze the level approximation and the power of the various tests, with a particular view on investigating various different forms of alternatives, notably models from \(H_1^{\scriptscriptstyle (m)}, H_1^{\scriptscriptstyle (c,0)}\) and \(H_1^{\scriptscriptstyle (c,1)}\). All stated results related to testing the joint hypothesis \(H_0^{\scriptscriptstyle (H)}\) are for the combined test described in Algorithm 1, with \(\psi (p_{-1},\dots ,p_H)=\sum _{i=-1}^{H}w_i\Phi ^{-1}(1-p_i)\) with weights \(w_1=w_0=1/2\) for \(H=0\) and \(w_{-1}=w_{0}=1/3\) and \(w_1=\cdots =w_H= (3H)^{-1}\) for \(H\ge 1\).
For the data-generating processes, we employed 10 different choices for the parameters in (18), which will be described next. Let \((\psi _i)_{i\in \mathbb {N}_0}\) denote the Fourier basis of \(L^2([0,1])\), that is, for \(n\in \mathbb {N}\),
Let \((\tilde{\varepsilon }_t)_{t\in \mathbb {Z}}\) denote an i.i.d. sequence of mean zero random variables in \(L^2([0,1])\), defined by \(\tilde{\varepsilon }_t = \sum _{i=0}^{16} u_{t,i} \psi _i\), where \(u_{t,i}\) are independent and normally distributed with mean zero and variance \(\text {Var}(u_{i,t}) = \exp (-i/10)\). Independent of \((\tilde{\varepsilon }_t)_{t\in \mathbb {Z}}\), let \(\varvec{G}=(G_{i,j})_{i,j=0, \dots , 16}\) denote a matrix with independent normally distributed entries with \(\text {Var}(G_{i,j})=\exp (-i-j)\). Let \(\tilde{A} :L^2([0,1]) \rightarrow L^2([0,1])\) denote the (random) integral operator defined by
where \({\left| \left| \left| \varvec{G}\right| \right| \right| }_F\) denotes the Frobenius norm (note that the Hilbert–Schmidt norm of \(\tilde{A}\) is equal to 1 / 3, see Horváth and Kokoszka 2012, Sect. 2.2). Finally, let
for \(u\in [0,1]\) and let \(a_j(u)=a_j(0)\) for \(u\le 0\) and \(a_j(u)=a_j(1)\) for \(u\ge 1\). The following ten data-generating processes are considered:
Stationary case. Let
$$\begin{aligned} \mu \equiv 0, \qquad A_{t/T} = \tilde{A}, \qquad {\varepsilon }_{t,T} = \tilde{\varepsilon }_t. \end{aligned}$$(19)Models deviating from\(H_0^{\scriptscriptstyle (m)}\). For \(j=1,\dots , 3\), consider the choices
$$\begin{aligned} \mu (\tau ) = a_j(\tau ), \qquad A_{t/T} = \tilde{A}, \qquad {\varepsilon }_{t,T} = \tilde{\varepsilon }_t. \end{aligned}$$(20)Models deviating from\(H_0^{\scriptscriptstyle (c,0)}\). For \(j=1,\dots , 3\), consider the choices
$$\begin{aligned} \mu \equiv 0, \qquad A_{t/T} = \tilde{A}, \qquad {\varepsilon }_{t,T} = a_j(t/T) \tilde{\varepsilon }_t. \end{aligned}$$(21)Models deviating from\(H_0^{\scriptscriptstyle (c,1)}\). For \(j=1,\dots , 3\), consider the choices
$$\begin{aligned} \mu \equiv 0, \qquad A_{t/T} = a_j(t/T) \tilde{A}, \qquad {\varepsilon }_{t,T} = \tilde{\varepsilon }_t. \end{aligned}$$(22)
Remark 4
The models defined in (19)–(22) satisfy condition (A3) if the functions a and \(\sigma \) are Lipschitz continuous. To see this, we exemplarily derive (14), as the other parts follow by similar arguments. Observe that in all models, the mean function \(\mu \) is in \(L^2\); thus, (14) is trivial for \(j=1\). For \(j\ge 2\), consider first the case that \(\tilde{A}\) is non-random first. Then, by Lemma 4 (ii), the definition of \(A_{t/T}\) and \({\varepsilon }_{t,T}\), and linearity of both (powers of) the operator \(\tilde{A}\) and the cumulants,
By independence of the random variables \(u_{t,\ell }\), the cumulants on the right-hand side of the previous display are zero if there is an index \(\nu \in \{2,\ldots ,j\}\) such that \(\ell _1\ne \ell _\nu \) or \(t_1-k_1\ne t_\nu -k_\nu \). Further, the random variables \(u_{t,\ell }\) are normally distributed and the higher cumulants, for \(j>2\), are zero. Thus, (14) is trivial for \(j>2\). Now, let \(j=2\) and consider \(t_2\ge t_1\) without loss of generality. Then, by the previous considerations,
which can be bounded by
since \(\Vert \tilde{A}\Vert _\mathcal {S}= \tfrac{1}{3}\), \(\text {Var}(u_{t,\ell })=\exp (-\ell /10)\), and both a and \(\sigma \) can be bounded from above by 3 / 2. Thus,
which proves (14) in case \(\tilde{A}\) is non-random. The random case follows since the upper bound does not depend on \(\tilde{A}\) and since \(\tilde{A}\) is assumed to be independent of \(\tilde{\varepsilon }_t\).
Subsequently, the respective models will be denoted by \((\mathcal {M}_0)\) and \((\mathcal {M}_{m,j}), (\mathcal {M}_{v,j})\) and \((\mathcal {M}_{a,j})\) for \(j=1, \dots , 3\). Note that the model descriptions are non-exclusive: For instance, the models in (20) exhibiting deviations from \(H_0^{\scriptscriptstyle (m)}\) also deviate from \(H_0^{\scriptscriptstyle (c,0)}\).
Preliminary simulation studies showed that the data-driven choice of m, as introduced in Sect. 3.6, yields similar results as a manual choice of m and should be favored. Further parameters of the simulation design are as follows: The number of bootstrap replicates is set to \(K=200\). Two sample sizes were considered, namely \(T=256\) and \(T=512\). Observe though that, unlike many frequency domain-based methods for functional time series, the proposed testing procedure does not require the sample sizes to be a power of two to work effectively. The hyperparameter n for estimating local means is set to \(n=45,60,75,90,T\). Finally, the maximum number of lags considered was set to \(H=4\). Empirical rejection rates are based on \(N=500\) simulation runs each and are summarized in Tables 1 and 2.
From the previous results, it can be seen that different choices of n do not lead to crucially different results. For \(T=256\), the tests for the hypotheses \(H_0^{\scriptscriptstyle (m)}\) and \(H_0^{\scriptscriptstyle (c,0)}\) already have good power against the alternatives \((\mathcal {M}_{m,1}),(\mathcal {M}_{m,3})\) and \((\mathcal {M}_{v,1}),(\mathcal {M}_{v,2}),(\mathcal {M}_{v,3})\), respectively. When combining \(H_0^{\scriptscriptstyle (m)}\) and \(H_0^{\scriptscriptstyle (c,0)}\) and taking even more autocovariances into account, the test does not loose significant power. For \(T=512\), the power further increases such that all tests have good power against the alternatives \((\mathcal {M}_{m,i})\) and \((\mathcal {M}_{v,i})\), \(i=1,2,3\). Detecting non-stationarities in models \((\mathcal {M}_{a,i}),i=1,2,3\) turns out to be more difficult. Even though the power increases with T, for small values of T, the results are not too convincing. These findings can be explained by the fact that the measures of non-stationarity\(\Vert M\Vert _{2,2}\) and \(\Vert M_h\Vert _{2,3}\), as introduced in (5) and (6), are comparably small for models \((\mathcal {M}_{a,i}),i=1,2,3\). This can be deduced from Table 3, where these measures of non-stationarity are approximated by their natural estimators \(\Vert M_T\Vert _{2,2}=\Vert U_T\Vert _{2,2}/\sqrt{T}\) and \(\Vert M_{T,h}\Vert _{2,3}=\Vert U_{T,h}\Vert _{2,3}/\sqrt{T}\), based on 2000 Monte Carlo repetitions and for various choices of T. It is noticeable that the values for models \((\mathcal {M}_{a,1})\) and \((\mathcal {M}_{a,2})\) are close to those for \((\mathcal {M}_{0})\), which perfectly explains the results of the simulation study.
As pointed out by a reviewer, it is of interest to investigate the sensitivity of the test with respect to the number of components included in the procedure. For this purpose, we highlight in Table 4 the rejection probabilities of the tests for the different hypotheses in the models \((\mathcal {M}_{m,1})\) and \((\mathcal {M}_{v,1})\), which correspond to a change in the mean (and as a consequence in all second-order moments) and changes in all second-order moments (with no change in the mean), respectively.
We observe that the impact of the number of components on the power of the tests shows no clear pattern. For example, the power is almost constant under model \((\mathcal {M}_{m,1})\) if additional components are included in the test statistic. Conversely, under model \((\mathcal {M}_{v,1})\), the power decreases with the number of components.
We also list results for the functional moving average model

with \(\sigma (u)=\mathbb {1}(u\le 0.5)-\mathbb {1}(u>0.5)\) and \(\tilde{\varepsilon }_t\) as for the autoregressive model. This model has constant mean and covariances, except of the covariance with lag 2, and consequently only the tests for hypotheses \(H_0^{(H)}\) (\(H\ge 2\)) should reject the null since all moments besides \(\mathbb {E}[X_{t,T}X_{t+2,T}]\) are constant. This effect is clearly visible in the last rows of Table 4, where we observe the largest rejection probabilities by the test constructed for the hypotheses \(H_0^{(2)}\). The power decreases for the hypotheses \(H_0^{(3)}\) and \(H_0^{(4)}\), which can be explained by the fact that in this case the statistics combines stationary and non-stationary parts of the serial dependence. Compared to the other cases, the test has less power in model \(\mathcal {M}_\mathrm{{MA}}\). An intuitive explanation for this observation consists of the fact that the weights of the p values, as introduced in Sect. 3.4, favor changes in the mean and the second moment (the corresponding weights in the test statistic are larger), which makes it more difficult to detect changes in models that are only non-stationary in the second-order moments at higher lags. On the other hand, it is worthwhile to mention that the null hypothesis \(H_0^{(c,2)}\) is rejected in nearly \(100\%\) of the cases in the \(\mathcal {M}_\mathrm{{MA}}\) model (these results are not displayed).
5.2 Case study
Functional time series naturally arise in the field of meteorology. For instance, the daily minimal temperature at one place over time can be naturally divided into yearly functional data.
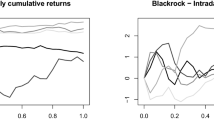
To illustrate the proposed methodology, we consider the daily minimum temperature recorded at eight different locations across Australia. Exemplary, the temperature curves of Melbourne and Sydney are displayed in Fig. 1. The results of our testing procedure can be found in Table 5, where we employed \(K=1000\) bootstrap replicates, considered up to \(H=4\) lags and chose \(n=25\), based on visual exploration of the respective plots. The null hypotheses of stationarity can be rejected, at level \(\alpha =0.05\), for all measuring stations except of Gunnedah Pool, for which the p values exceed \(\alpha \) by a small amount.
6 Proofs
Throughout the proofs, C denotes a generic constant whose value may change from line to line. If not specified otherwise, all convergences are for \(T\rightarrow \infty \).
6.1 A fundamental approximation lemma in Hilbert spaces
Lemma 5
Fix \(p\in \mathbb {N}\). For \(i=1, \dots , p\) and \(T\in \mathbb {N}\), let \(X_{i,T}\) and \(X_i\) denote random variables in a separable Hilbert space \((H_i, \langle \cdot , \cdot \rangle _i)\). Futher, let \((\psi _k^{\scriptscriptstyle (i)})_{k\in \mathbb {N}}\) be an orthonormal basis of \(H_i\) and for brevity write \(\langle \cdot , \cdot \rangle = \langle \cdot , \cdot \rangle _i\). Suppose that
Then, using the notation \(\Vert (x_k)_{k\in \mathbb {N}}\Vert _2=\sum _{k=1}^\infty x_k^2\),
and, as a consequence,
Proof of Lemma 1
To prove the first part, we employ Theorem 2 of Dehling et al. (2009). Expand the random variables \(Y_T^n\) and \(Y_n\) in \(\mathbb {R}^{pn}\) to
in \((\ell ^2(\mathbb {N}), \Vert \cdot \Vert _2)^p\), where \(a_{T,k}^{\scriptscriptstyle (i)}=\langle X_{i,T},\psi _k^{\scriptscriptstyle (i)}\rangle \) and \(a_{k}^{\scriptscriptstyle (i)}=\langle X_i,\psi _k^{\scriptscriptstyle (i)}\rangle \), for any \(1\le k\le n\), and \(a_{T,k}^{\scriptscriptstyle (i)}=a_k^{\scriptscriptstyle (i)}=0\), for any \(k>n\), \(i=1,\dots ,p\). By the continuous mapping theorem, \(\tilde{Y}_{T,n}^\infty \) converges weakly to \(\tilde{Y}_n^\infty \) in \((\ell ^2(\mathbb {N}), \Vert \cdot \Vert _2)^p\), for any \(n\in \mathbb {N}\) and as T tends to infinity.
By assumption (2) and since the space \((\ell ^2(\mathbb {N}), \Vert \cdot \Vert _2)^p\) is separable and complete, there is a random variable \(\tilde{Y}^\infty \in (\ell ^2(\mathbb {N}), \Vert \cdot \Vert _2)^p\) such that \(Y_T^\infty \rightsquigarrow \tilde{Y}^\infty \), as T tends to infinity, and \(\tilde{Y}_n^\infty \rightsquigarrow \tilde{Y}^\infty \), as n tends to infinity, by Theorem 2 of Dehling et al. (2009). Due to the latter convergence, the finite-dimensional distributions of \(\tilde{Y}^\infty \) and \(Y^\infty \) are the same. Thus, by Theorem 1.3 of Billingsley (1999) and Lemma 1.5.3 of van der Vaart and Wellner (1996), \(\tilde{Y}^\infty \) and \(Y^\infty \) have the same distribution in \( (\ell ^2(\mathbb {N}), \Vert \cdot \Vert _2)^p\).
Next, observe that, for an arbitrary Hilbert space H, the function
\(\Phi :=\Bigg \{\begin{array}{llc}\ell ^2(\mathbb {N})&{}\rightarrow &{}H \\ (y_k)_{k\in \mathbb {N}}&{}\mapsto &{}\sum _{k=1}^\infty y_k \psi _k\end{array}\)
is continuous, provided \((\psi _k)_{k\in \mathbb {N}}\) is an orthonormal basis of H. Indeed,
Thus, the mapping
is continuous too, and the continuous mapping theorem implies that
as T tends to infinity. \(\square \)
6.2 Proofs for Sects. 3.1, 3.2, 3.3 and 3.4
Proof of Lemma 2
We only prove the equivalence concerning \(H_0^{\scriptscriptstyle (h)}\); the equivalences regarding \(H_0^{\scriptscriptstyle (m)}\) follow along similar lines.
Step 1: Equivalence between (3) and (8). Suppose that (8) is met. To prove (3), it is sufficient to show that
for any \(u\in [0,1]\).
Fix \(u\in [0,1)\) and let \(\delta >0\) be sufficiently small such that \(u+\delta <1\). By the reverse triangle inequality, we obtain that
By continuity of integrals in the upper integration limit, it follows from (8) that both summands on the right-hand side of this display are equal to zero. As a consequence,
By Jensen’s inequality, we can bound the right-hand side of this display from above by
By employing Jensen’s inequality again, we can bound the integrand by
Thus, by Fubini’s theorem, (25) is less than or equal to
This term is of the order \(O(\delta ^{1/2})\) due to the inequality
where the final bound follows from Lemma C.2 in the supplementary material. Since \(\delta \) was chosen arbitrarily, we obtain that the right-hand side of (24) is equal to zero. This proves (23) for \(u\in [0,1)\), and the case \(u=1\) follows from (26), which is also valid for \(u=1\).
Conversely, if (3) holds true, we have by a change of variables, linearity of the integral, Jensen’s inequality and Fubini’s theorem,
Step 2: Equivalence between (3) and (10). Note that, irrespective of whether (3) or (10) is met, local stationarity of \(X_{t,T}\) of order \(\rho \ge 4\) and stationarity of \((X_t^{\scriptscriptstyle (u)})_{t\in \mathbb {Z}}\) with \(\mathbb {E}\Vert X_t^{\scriptscriptstyle (u)}\Vert _2^4 < \infty \) implies that
for any \(u\in [0,1]\) and \(T\in \mathbb {N}\) and for some universal constant \(C>0\).
Now, suppose that (3) is met. Then, the previous display implies that
for any \(u\in [0,1]\) and \(T\in \mathbb {N}\), that is, (10) is met.
Conversely, if (10) is met, then, by (27) and (1), for any \(u,v\in [0,1]\) and \(T\in \mathbb {N}\),
Since T was arbitrary, the left-hand side of this display must be zero, whence (3). \(\square \)
Proof of Theorem 1
This theorem is an immediate consequence of Theorem C.3 of the supplementary material. \(\square \)
Proof of Corollary 1
Suppose that \(H_0^{\scriptscriptstyle (c,h)}\) is met. Then, by the triangle inequality and a slight abuse of notation (note that u is a variable of integration in the norm \(\Vert \cdot \Vert _{2,3}\)), for \(h\le T\),
This expression is of the order \(O(T^{-1/2})\) by (10) and Assumption (A2). Hence, \(\Vert U_{T,h}-\tilde{G}_{T,h}\Vert _{2,3}=o_\mathbb {P}(1)\), and the assertion for \(U_{T}\) follows along similar lines.
Now, consider the assertion regarding the alternative \(H_1^{\scriptscriptstyle (H)} = H_1^{\scriptscriptstyle (m)} \cup H_1^{\scriptscriptstyle (c,0)} \cup \dots \cup H_1^{\scriptscriptstyle (c,H)}\). We only treat the case where \(H_1^{\scriptscriptstyle (c,h)}\) is met for some \(h\in \{0, \dots , H\}\) and the case \(H_1^{\scriptscriptstyle (m)}\) is similar. It is to be shown that \(\Vert U_{T,h}\Vert _{2,3}\rightarrow \infty \) in probability.
By the reverse triangle inequality, we have
The term \(\Vert \tilde{G}_{T,h}\Vert _{2,3}\) converges weakly to \(\Vert \tilde{G}_h\Vert _{2,3}\). Thus, it suffices to show that the second term \(\Vert \mathbb {E}U_{T,h}\Vert _{2,3}\) diverges to infinity. For that purpose, note that another application of the reverse triangle inequality implies that
where
and
In the following, we will show that \(S_{1,T}\) vanishes as T increases and that \(S_{2,T}\) diverges to infinity. We have
which is of order \(O(T^{-1/2})\) since \(\Vert \mathbb {E}[X_{t,T}\otimes X_{t+h,T}]-\mathbb {E}[X_t^{\scriptscriptstyle (t/T)}\otimes X_{t+h}^{\scriptscriptstyle (t/T)}] \Vert _{2,2}\le C/T\) by (1). For the second term \(S_{2,T}\), we have, by stationarity
where the norm converges to
by the dominated convergence theorem and the moment condition (A2). The expression in the latter display is strictly positive since (8) is not satisfied and by the continuity of
in \(u\in [0,1]\). Thus, \(S_{2,T}\rightarrow \infty \), which implies the assertion. \(\square \)
Proof of Lemma 3
We will only give a proof of (14). Parts (i)–(iv) of the cumulant condition (A3) follow by similar arguments, which are omitted for the sake of brevity. According to Theorem 3 in Statulevicius and Jakimavicius (1988), we have
for any increasing sequence \(t_1\le t_2\le \dots \le t_k\). Straightforward calculations combined with Hölder’s and Jensen’s inequality lead to
Thus, combining the previous results leads to
for any \(i=1,\dots ,k-1\), where the constant \(C_{k,4}>0\) depends on k only. Hence,
Analogously, for arbitrary, not necessarily increasing \(t_1,\dots ,t_k\), we may obtain that
where \(\big (t_{(1)},\dots ,t_{(k)}\big )\) denotes the order statistic of \((t_1,\dots ,t_k)\). The latter expression is symmetric in its arguments, and thus, we have, for any \(t_k\in \mathbb {Z}\),
By assumption, \(\{(X_{t,T})_{t\in \mathbb {Z}}: T\in \mathbb {N}\}\) is exponentially strong mixing, and the inner sum is finite and can be bounded by some constant \(C_{k,2}\). Thus,
Repeating this argument successively, we obtain finally (14) as asserted. \(\square \)
Proof of Theorem 2
By Slutsky’s lemma and Theorem C.3 of the supplementary material, it is sufficient to prove that
in \(\{ L^2([0,1]^2)\times \{L^2([0,1]^3)\}^{H+1}\}^{K}\), as T tends to infinity. This in turn is equivalent to
in \(\mathbb {R}^{K(H+2)}\). The last convergence holds true if and only if the coordinates converge, i.e., if \(\Vert \hat{B}_{T}^{\scriptscriptstyle (k)}-\tilde{B}_{T}^{\scriptscriptstyle (k)}\Vert _{2,3}=o_\mathbb {P}(1)\) and \(\Vert \hat{B}_{T,h}^{\scriptscriptstyle (k)}-\tilde{B}_{T,h}^{\scriptscriptstyle (k)}\Vert _{2,3}=o_\mathbb {P}(1)\), for all \(k=1,\dots ,K\) and \(h=0,\dots ,H\). We only consider the latter assertion (the former can be treated similarly), and in fact, we will show convergence in \(L^2(\Omega , \mathbb {P})\), which is even stronger. For this purpose, observe that by Fubini’s theorem and the independence of the family \((R_i^{\scriptscriptstyle (k)})_{i\in \mathbb {N}}\)
where
and
Since \(A_{t,1}\) is deterministic and since \(A_{t,2}\) is centered, we can rewrite the expectation in the previous integral as
In the following, we bound both parts separately. For the term \(A_{t,1}\), first note that, by stationarity of \((X_t^{\scriptscriptstyle (u)})_{t\in \mathbb {Z}}\),
in \(L^2([0,1]^2)\). Thus, by Jensen’s inequality and Fubini’s theorem, we have
The norm on the right-hand side of the previous inequality be bounded by the triangle inequality by
and the inner summands can be bounded due to the local stationarity of \((X_{t,T})\): first,
and similarly
Assembling bounds, we obtain that
which converges to zero by Assumption (B2).
For the term \(A_{t,2}\), first observe that, by Jensen’s inequality for convex functions,
By the same arguments as in the proof of Proposition C.7 of the supplementary material and Assumption (A3), one can see that the right-hand side of the inequality
is of order \(\mathcal {O}(m/n)\). The assertion follows since \(m/n=o(1)\) by Assumption (B2).
\(\square \)
Proof of Proposition 1
The cumulative distribution function of the \((h+2)\)nd coordinate of \(\varvec{S}\) is continuous by Theorem 7.5 of Davydov and Lifshits (1985). The assertion under the null hypothesis follows from Lemma 4.1 in Bücher and Kojadinovic (2017). Consistency follows from the fact that the bootstrap quantiles are stochastically bounded by Theorem 2, whereas the test statistic diverges by Corollary 1. \(\square \)
References
Antoniadis, A., Sapatinas, T. (2003). Wavelet methods for continuous time prediction using hilbert-valued autoregressive processes. Journal of Multivariate Analysis, 87, 133–158.
Aston, J. A. D., Kirch, C. (2012). Detecting and estimating changes in dependent functional data. Journal of Multivariate Analysis, 109(Supplement C), 204–220.
Aue, A., van Delft, A. (2017). Testing for stationarity of functional time series in the frequency domain. ArXiv e-prints.
Aue, A., Gabrys, R., Horváth, L., Kokoszka, P. (2009). Estimation of a change-point in the mean function of functional data. Journal of Multivariate Analysis, 100, 2254–2269.
Aue, A., Dubart Nourinho, D., Hörmann, S. (2015). On the prediction of stationary functional time series. Journal of the American Statistical Association, 110, 378–392.
Berkes, I., Gabrys, R., Horvath, L., Kokoszka, P. (2009). Detecting changes in the mean of functional observations. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 71(5), 927–946.
Billingsley, P. (1999). Convergence of probability measures. New York: Wiley.
Bosq, D. (2000). Linear processes in function spaces, Vol. 149., Lecture notes in statistics New York: Springer.
Bosq, D. (2002). Estimation of mean and covariance operator of autoregressive processes in Banach spaces. Statistical inference for Stochastic Processes, 5, 287–306.
Box, G. E. P., Pierce, D. A. (1970). Distribution of residual autocorrelations in autoregressive-integrated moving average time series models. Journal of the American Statistical Association, 65(332), 1509–1526.
Brillinger, D. (1981). Time series: Data analysis and theory. San Francisco: Holden Day Inc.
Bücher, A., Kojadinovic, I. (2016). A dependent multiplier bootstrap for the sequential empirical copula process under strong mixing. Bernoulli, 22(2), 927–968.
Bücher, A., Kojadinovic, I. (2017). A note on conditional versus joint unconditional weak convergence in bootstrap consistency results. Journal of Theoretical Probability, 1–21.
Bücher, A., Fermanian, J.-D., Kojadinovic, I. (2018). Combining cumulative sum change-point detection tests for assessing the stationarity of univariate time series. ArXiv e-prints.
Davydov, Y. A., Lifshits, M. A. (1985). Fibering method in some probabilistic problems. Journal of Soviet Mathematics, 31(2), 2796–2858.
Dehling, H., Sharipov, O. (2005). Estimation of mean and covariance operator for banach space valued autoregressive processes with independent innovations. Statistical Inference for Stochastic Processes, 8, 137–149.
Dehling, H., Durieu, O., Volny, D. (2009). New techniques for empirical processes of dependent data. Stochastic Processes and their Applications, 119(10), 3699–3718.
Dette, H., Preuß, P., Vetter, M. (2011). A measure of stationarity in locally stationary processes with applications to testing. Journal of the American Statistical Association, 106(495), 1113–1124.
Dwivedi, Y., Subba Rao, S. (2011). A test for second-order stationarity of a time series based on the discrete fourier transform. Journal of Time Series Analysis, 32, 68–91.
Ferraty, F., Vieu, P. (2006). Nonparametric functional data analysis: Theory and practice. New York: Springer.
Fisher, R. (1932). Statistical methods for research workers. London: Olivier and Boyd.
Hörmann, S., Kokoszka, P. (2010). Weakly dependent functional data. Annals of Statistics, 38(3), 1845–1884.
Hörmann, S., Kidziński, Ł., Hallin, M. (2015). Dynamic functional principal components. Journal of the Royal Statistical Society: Series B, 77(2), 319–348.
Horváth, L., Kokoszka, P. (2012). Inference for functional data with applications. New York: Springer.
Horvath, L., Huskova, M., Kokoszka, P. (2010). Testing the stability of the functional autoregressive process. Journal of Multivariate Analysis, 101(2), 352–367.
Hsing, T., Eubank, R. (2015). Theoretical foundations of functional data analysis, with an introduction to linear operators. New York: Wiley.
Hyndman, R. J., Shang, H. L. (2009). Forecasting functional time series. Journal of the Korean Statistical Society, 38(3), 199–211.
Janson, S., Kaijser, S. (2015). Higher moments of Banach space valued random variables. Memoirs of the American Mathematical Society, 238(1127), vii+110.
Jentsch, C., Subba Rao, S. (2015). A test for second order stationarity of a multivariate time series. Journal of Econometrics, 185, 124–161.
Jin, L., Wang, S., Wang, H. (2015). A new non-parametric stationarity test of time series in the time domain. Royal Statistical Society, 77, 893–922.
Lee, J., Subba Rao, S. (2017). A note on general quadratic forms of nonstationary stochastic processes. Statistics, 51(5), 949–968.
Ljung, G. M., Box, G. E. P. (1978). On a measure of lack of fit in time series models. Biometrika, 65(2), 297–303.
Panaretos, V. M., Tavakoli, S. (2013). Fourier analysis of stationary time series in function space. Annals of Statistics, 41(2), 568–603.
Politis, D. N., White, H. (2004). Automatic block-length selection for the dependent bootstrap. Econometric Reviews, 23(1), 53–70.
Sharipov, O., Tewes, J., Wendler, M. (2016). Sequential block bootstrap in a hilbert space with application to change point analysis. Canadian Journal of Statistics, 44(3), 300–322.
Statulevicius, V., Jakimavicius, D. (1988). Estimates of semiinvariants and centered moments of stochastic processes with mixing. I. Lithuanian Mathematical Journal, 28, 226–238.
van Delft, A., Eichler, M. (2018). Locally stationary functional time series. Electronic Journal of Statistics, 12(1), 107–170.
van Delft, A., Bagchi, P., Characiejus, V., Dette, H. (2017). A nonparametric test for stationarity in functional time series. ArXiv e-prints.
van der Vaart, A., Wellner, J. (1996). Weak convergence and empirical processes, Vol. 1., Springer series in statistics New York: Springer.
Vogt, M. (2012). Nonparametric regression for locally stationary time series. The Annals of Statistics, 40, 2601–2633.
Weidmann, J. (1980). Linear operators in Hilbert spaces, Vol. 68., Graduate texts in mathematics New York: Springer.
Acknowledgements
Financial support by the Collaborative Research Center “Statistical modeling of non-linear dynamic processes” (SFB 823, Teilprojekt A1, A7 and C1) of the German Research Foundation, by the Ruhr University Research School PLUS, funded by Germany’s Excellence Initiative [DFG GSC 98/3], by the DAAD (German Academic Exchange Service) and the National Institute of General Medical Sciences of the National Institutes of Health (Award Number R01GM107639) is gratefully acknowledged. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. Parts of this paper were written when Axel Bücher was a postdoctoral researcher at Ruhr-Universität Bochum and while Florian Heinrichs was visiting the Universidad Autónoma de Madrid. The authors would like to thank the institute, and in particular Antonio Cuevas, for its hospitality.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
About this article
Cite this article
Bücher, A., Dette, H. & Heinrichs, F. Detecting deviations from second-order stationarity in locally stationary functional time series. Ann Inst Stat Math 72, 1055–1094 (2020). https://doi.org/10.1007/s10463-019-00721-7
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10463-019-00721-7