1 Introduction

Variable selection is an important aspect of high dimensional statistical modelling, particularly in regression and classification. In the regularization framework, various penalty functions are used to perform variable selection by putting relatively large penalties on small coefficients. The best subset selection, namely, the \(L_0\) penalty, along with the traditional model selection criteria such as AIC, BIC and RIC (Akaike 1973; Schwarz 1978; Foster and George 1994) is attractive for variable selection since it directly penalizes the number of nonzero coefficients. However, one drawback of \(L_0\) penalized least squares (PLS) procedure is instability of the resulting estimators (Breiman 1996). This results from the fact that the \(L_0\) penalty is not continuous at 0. Another perhaps more significant drawback of the \(L_0\) penalty is that implementing \(L_0\) PLS procedures is NP-hard and may involve an exhaustive search over all possible models. Thus, implementing these procedures is computationally infeasible when the number of potential predictors is even moderately large, let along the high dimensional data.

Such computational difficulty motivated various continuous relaxations. For example, the bridge regression (Frank and Friedman 1993) uses the \(L_q\) penalty, \(0 < q \le 2\). In particular, the use of the \(L_2\) penalty is called the ridge regression. The nonnegative garrote was introduced by Breiman (1995) for variable selection and shrinkage estimation. The \(L_1\) PLS method was termed LASSO by Tibshirani (1996), which is also collectively referred to as the \(L_1\) penalization methods in other contexts. However, LASSO may not consistently select the correct model and is not necessarily asymptotically normal (Knight and Fu 2000; Zou 2006). Other commonly used penalty functions include the SCAD (Fan and Li 2001), MCP (Zhang 2010), SICA (Lv and Fan 2009), Elastic net (Zou and Hastie 2005), SELO (Dicker et al. 2013) and so on.

In this paper, we propose a exponential type penalty function named EXP penalty which very closely approximates the \(L_0\) penalty. EXP penalty is continuous, so the EXP estimators may be more stable than those obtained through \(L_0\) penalized methods. Furthermore, the EXP penalty is a smooth function on \([0,\infty )\) and we use a coordinate descent (CD) algorithm (Friedman et al. 2010; Fan and Lv 2011). Also, we formally establish the model selection oracle property enjoyed by EXP estimators. In particular, the asymptotic normality of the EXP is formally established. Our asymptotic framework allows the number of predictors \(p\rightarrow \infty \), along with the number of observations n, provided \(p/n \rightarrow 0\).

The practical performance of PLS procedures depends heavily on the choice of a tuning parameter. In our study, we propose a modified BIC (MBIC) tuning parameter selector that accounts for lost degrees of freedom and performs very well when used in conjunction with EXP penalty. Furthermore, we also prove that this EXP/MBIC procedure consistently identifies the correct model, if \(p/n \rightarrow 0\) and other regularity conditions are met.

This paper is organized in the following way: In Sect. 2, we introduce PLS estimators and give a brief overview of existing nonconvex penalty terms, and a new nonconvex penalty function is presented. Then, we discuss some of its theoretical properties in Sect. 3. In Sect. 4, we propose an MBIC tuning parameter selection method for EXP. In Sect. 5, we describe a simple and efficient algorithm for obtaining the EXP estimator. Simulation studies and an application of the proposed methodology are presented in Sect. 6. The proofs are relegated to the Appendix.

2 Variable selection and estimation with EXP penalty

2.1 Linear models and penalized least squares

We start with the linear regression model

$$\begin{aligned} \mathbf y =\mathbf{X }\beta ^*+\varepsilon , \end{aligned}$$
(1)

where \(\mathbf{X }={(x_1,x_2,\ldots ,x_n)}^\mathrm{T}\) is an \(n \times p\) design matrix, \(\mathbf y ={(y_1,y_2,\ldots , y_n)}^\mathrm{T}\) is an n-dimensional response vector, and \(\varepsilon \) are the iid random errors with mean 0 and variance \(\sigma ^2\) n-dimensional noise vector, \(\beta ^*={(\beta ^*_{1},\ldots , \beta ^*_{p})}^\mathrm{T}\) are the regression parameter.

The problem of interest involves estimating a vector of coefficients \(\beta \) defined by minimizing an objective function \(Q(\beta )\) composed of a loss function combined with a penalty that encourages sparsity and prevents overfitting:

$$\begin{aligned} Q(\beta )=\frac{1}{2n}{\Vert \mathbf y -\mathbf{X }\beta \Vert }^2+\sum _{j=1}^pp_\lambda (|\beta _j|), \end{aligned}$$
(2)

where \({\Vert \cdot \Vert }^2\) denotes the \(L_2\) norm, and \(p_\lambda (\cdot )\) is a penalty function indexed by the regularization parameter \(\lambda \ge 0\). By regularizing the conventional least-squares estimation, we hope to simultaneously select important variables and estimate their regression coefficients with sparse estimates.

Various penalty functions have been used in the variable selection literature for linear regression models. Tibshirani (1996) proposed the LASSO. However, LASSO estimates may be biased and inconsistent for model selection (Fan and Li 2001; Zou 2006). This implies that the LASSO does not have the oracle property. The adaptive LASSO is a weighted version of LASSO which has the oracle property (Zou 2006). Other commonly used penalty functions include the SCAD and MCP. The SCAD penalty is the continuous function, whose derivative is given by

$$\begin{aligned} p'_\lambda (t)=\lambda \left\{ I(t \le \lambda )+\frac{{(a\lambda - t)}_+}{(a-1)\lambda }I(t >\lambda )\right\} , \end{aligned}$$
(3)

where \(a>2\). Fan and Li (2001) recommended taking \(a = 3.7\) and we follow this recommendation throughout. A closely related minimax concave penalty (MCP) was proposed by Zhang (2010), the MCP is the continuous function defined by

$$\begin{aligned} p'_\lambda (t)= \frac{{(a\lambda -t)}_+}{a}, \end{aligned}$$
(4)

where the parameter \(a > 0\) determines the concavity of \(p_\lambda (\cdot )\). Zhang (2010) proved that the MCP procedure may select the correct model with probability tending to 1 and that MCP estimators have good properties in terms of \(L_q\)-loss, provided \(\lambda \) and a satisfy certain conditions. Zhang’s results in fact allow for \(p \gg n\).

2.2 EXP penalty

The EXP penalty is defined by

$$\begin{aligned} p_{\lambda ,a}(|\theta |)=\lambda \left\{ 1-\mathrm{e}^{-\frac{|\theta |}{a}}\right\} , \end{aligned}$$
(5)

The EXP penalty has a tuning parameter \(a >0\), in addition to \(\lambda \), and when a is small, \(p_\lambda (|\theta |)\approx \lambda I(\theta \ne 0)\). In fact, we have

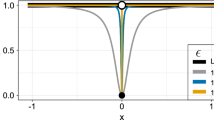
$$\begin{aligned} \lim _{a \rightarrow 0} p_{\lambda ,a}(|\theta |)=\left\{ \begin{array}{ll} \lambda , &{}\quad \text {if } |\theta | \ne 0,\\ 0, &{}\quad \text {if } |\theta | =0.\end{array}\right. \ \end{aligned}$$

It is clearly that the EXP penalty is a continuous approximation to the \(L_0\) penalty. Since the EXP penalty is continuous, the associated PLS procedure is more stable than \(L_0\) procedure. The EXP penalty function (\(a=0.5\)) is plotted in Fig. 1, along with the SCAD, LASSO, MCP and \(L_0\) penalties. Notice that the EXP penalty mimics the \(L_0\) penalty much more closely than the \(L_1\), MCP or SCAD penalties.

Fig. 1
figure 1

Plots of the penalties (including \(L_0\), LASSO, SCAD, MCP and EXP)

Full size image

Also, we can see MCP and EXP penalty begin by applying the same rate of penalization as the LASSO, but continuously relax that penalization. MCP relaxes the rate of penalization linearly, and thus results in \(p'(|\theta |)=0\) for all \( |\theta |> a\lambda \), where a is an additional tuning parameter of MCP playing a role similar to a in (5). The EXP penalty, on the other hand, allows the penalty to decay exponentially, approaching \(p'_{\lambda ,a}(|\theta |) = 0\) asymptotically but never reaching it. The diminishing rate of penalization is an attractive property; as discussed in Fan and Li (2001), it leads to the estimator \(\hat{\theta }\) being nearly unbiased given a large enough sample size.

It is worth mentioning that Douglas (2011) also proposed a continuous function which very closely resembles the \(L_0\) penalty. The penalty function is of the form:

$$\begin{aligned} p_{\lambda }(|\theta |)=\lambda \left\{ 1-\mathrm{e}^{-\frac{\theta ^2}{a^2}}\right\} . \end{aligned}$$

Similar to the EXP penalty proposed by us, the penalty function is continuous and can have arbitrarily steep slope in a neighborhood near zero, thus mimicking the \(L_0\) penalty. However the function is not singular at zero, \(\theta \) will have no zero-valued components, although some will have been shrunk arbitrarily close thereto. The EXP function we proposed is singular at zero and satisfies the condition of sparsity (Fan and Li 2001). Also, we noticed that the EXP penalty is similar to that proposed by Breheny (2015)

$$\begin{aligned} p_{\lambda ,a}(|\theta |)=\frac{\lambda ^2}{a}\left\{ 1-\mathrm{e}^{-\frac{a|\theta |}{\lambda }}\right\} . \end{aligned}$$
(6)

Despite the penalties in Eqs. (5) and (6) have the different forms, but they have similar properties. The two penalties allow the penalty to decay exponentially, approaching \(p'_{\lambda ,a}(|\theta |) = 0\) asymptotically but never reaching it. The EXP penalty in (5) is infinitely differentiable with a smooth derivative that decays exponentially at a rate regulated by the parameter a, while the exponential penalty in (6) is controlled by the parameter a and \(\lambda \). For example, the EXP penalty in (5) approaches the \(L_0\) penalty as \(a\rightarrow 0\), the parameter a controlled the degree of approximation, while the the exponential penalty in (6) approaches the \(L_0\) penalty as \(\frac{\lambda }{a}\rightarrow 0\). Furthermore, Breheny (2015) only focus on using the exponential penalty for grouped regularization, and detailed study of the properties of the estimator for the ungrouped case is not be done.

Like the exponential penalty in (6), the EXP penalty in (5) is not convex, neither the coordinate descent algorithms nor the LLA algorithm are guaranteed to converge to a global minimum in general. However, it is possible for the objective function to be convex with respect to \(\beta \) even though it contains a nonconvex penalty component. These conditions are presented in the following proposition. Let

$$\begin{aligned} Q_n(\beta )=\frac{1}{2n}{\Vert \mathbf y -\mathbf{X }\beta \Vert }^2+\sum _{j=1}^p p_{\lambda ,a}(|\beta _j|), \end{aligned}$$
(7)

be the objective function, and \(p_{\lambda ,a}(|\beta _j|)\) is the EXP penalty function.

Proposition 1

Let \(\lambda _\mathrm{min}(\frac{1}{n}{\mathbf {X}}^\mathrm{T}{\mathbf {X}})\) denote the minimum eigenvalue of \(\frac{1}{n}{\mathbf {X}}^\mathrm{T}{\mathbf {X}}\), Then objective function (7) is strictly convex if \(\lambda _\mathrm{min}(\frac{1}{n}{\mathbf {X}}^\mathrm{T}{\mathbf {X}})>\frac{\lambda }{a^2}\).

Remark 1

Proposition 1 indicates that if \(Q_n(\beta _j)\) denote (7) considered as a function only of \(\beta _j\), with all other coefficients fixed. Then \(Q_n(\beta _j)\) is strictly convex if \(\lambda <a^2\). However, the conclusion is different with Breheny (2015) which required \(a<1\). In fact, the \(\frac{\lambda }{a^2}\) in EXP penalty (5) is equal to a in the exponential penalty (6). The proof is similar, so we omit it here.

Remark 2

Since the penalty function is separable and the objective function is convex in each coordinate dimension, we may apply a coordinate descent approach to solve for \(\beta \) and the approach is guaranteed to converge to the minimum.

Remark 3

In high dimensions (\(p > n\)), the minimum eigenvalue \(\lambda _\mathrm{min}(\frac{1}{n}\mathbf{X }^\mathrm{T}\mathbf{X })\) will be zero, so the strict global convexity is not possible. However, local convexity may still apply.

3 Theoretical properties of the EXP estimator

In this section we study the theoretical properties of the EXP estimator proposed in Sect. 2 in the situation where the number of parameters p tends to \(\infty \) with increasing sample size n. When discussing variable selection, it is convenient to have concise notation. Denote the columns of \(\mathbf{X }\) by \(\mathbf x _1, \ldots ,\mathbf x _p \in R^n\) and the rows of \(\mathbf{X }\) by \(x_1,\ldots , x_n \in R^p\). Let \(A = \{j; \beta ^*_j \ne 0\}\) be the true model and suppose that \(p_0\) is the size of the true model. That is, suppose that \(|A| = p_0\), where |A| denotes the cardinality of A. In addition, for \(S \subseteq \{1,2,\ldots ,p\}\), let \(\beta _S = {(\beta _j)}_{j \in S}\) be the |S|-dimensional sub-vector of \(\beta \) containing entries indexed by S and let \(\mathbf{X }_S\) be the \(n \times |S|\) matrix obtained from \(\mathbf{X }\) by extracting columns corresponding to S. Given a \(p\times p\) matrix C and subsets \(S_1, S_2 \subseteq \{1,2,\ldots ,p\}\), let \(C_{S_1,S_2}\) be the \(|S_1|\times |S_2|\) sub-matrix of C with rows determined by \(S_1\) and columns determined by \(S_2\).

3.1 Regularity conditions

We need to place the following conditions:

  1. (A)

    \(n\rightarrow \infty \) and \(p\sigma ^2/n\rightarrow 0\).

  2. (B)

    \(\rho \sqrt{n/{(p\sigma ^2)}}\rightarrow \infty \), where \(\rho =\min _{j\in A}|\beta ^*_j|\).

  3. (C)

    \(\lambda =O(n^{-\gamma })\), \(\lambda \sqrt{n/{(p\sigma ^2)}}\rightarrow \infty \), \(a =O(p^{1/2}\sigma n^{-\gamma /2})\) for some positive constant \(0<\gamma <1\).

  4. (D)

    There exist constants \(C_1, C_2 \in R\) such that \(C_1< \lambda _\mathrm{min}(\frac{1}{n}\mathbf{X }^\mathrm{T}\mathbf{X })< \lambda _\mathrm{max}(\frac{1}{n}\mathbf{X }^\mathrm{T}\mathbf{X }) < C_2\), where \(\lambda _\mathrm{min}(\frac{1}{n}\mathbf{X }^\mathrm{T}\mathbf{X })\) and \(\lambda _\mathrm{max}(\frac{1}{n}\mathbf{X }^\mathrm{T}\mathbf{X })\) are the smallest and largest eigenvalues of \(\frac{1}{n}\mathbf{X }^\mathrm{T}\mathbf{X }\), respectively.

  5. (E)

    \(\lim _{n\rightarrow \infty }n^{-1}\max _{1\le i \le n}\sum _{j=1}^p x_{ij}^2=0\).

  6. (F)

    \(E({|\varepsilon _i/\sigma |}^{2+\delta })< M\) for some \(\delta \) and \(M< \infty \).

Since p may vary with n, it is implicit that \(\beta ^*\) may vary with n. Additionally, we allow the model A and the distribution of \(\varepsilon \) (in particular, \(\sigma ^2\)) to change with n. Condition (A) limits how p and \(\sigma ^2\) may grow with n. This condition is the same as that required in Dicker et al. (2013) and substantially weaker than that required in Fan and Peng (2004), who require \(p^5/n\rightarrow 0\), and slightly weaker than that required in Zou and Zhang (2009), who require \(\log (p)/\log (n)\rightarrow \nu \in [0, 1)\). As mentioned in Sect. 1, other authors have studied PLS methods in settings where \(p > n\), i.e. their growth condition on p is weaker than Condition (A). However, if Condition (A) is relaxed, additional stronger conditions are typically required in order to obtain desirable theoretical properties. For instance, Kim et al. (2008) require a stronger moment condition on \(\varepsilon _i\) and an additional condition on \(p_0\). Fan and Lv (2011) require stronger conditions on \(n^{-1}\mathbf{X }^\mathrm{T}\mathbf{X }\). Condition (B) gives a lower bound on the size of the smallest nonzero entry of \(\beta ^*\). Notice that the smallest non-zero entry of \(\beta ^*\) is allowed to vanish asymptotically, provided it does not do so faster than \(\sqrt{p\sigma ^2/n}\). Similar conditions are found in Fan and Peng (2004) and Zou and Zhang (2009). Condition (C) restricts the rates of the tuning parameters \(\lambda \) and a. Note that condition (C) does not constrain the minimum size of a. Indeed, no such constraint is required for our asymptotic results about the EXP estimator. Since the EXP penalty approaches the \(L_0\) penalty as \(a \rightarrow 0\), this suggests that the EXP and \(L_0\)-penalized least squares estimator have similar asymptotic properties. On the other hand, in practice, we have found that one should not take a too small, in order to preserve stability of the EXP estimator. Condition (D) is an identifiability condition. Conditions (E) and (F) are used to prove asymptotic normality of EXP estimators and are related to the Lindeberg condition of the Lindeberg–Feller central limit theorem. As we will see in Theorem 2, which is stated below, Conditions (A)–(F) imply that EXP has the oracle property and may correctly identify the model A.

3.2 Oracle properties

Theorem 1

Suppose that conditions (A)–(D) hold, then for every \(r \in (0, 1)\), there exists a constant \(C_0 > 0\) such that

$$\begin{aligned} \mathop {\lim \inf }\limits _{n\rightarrow \infty }P\left[ \mathop {\arg \min }\limits _{\beta }Q_n(\beta )\subseteq \left\{ \beta \in R^p \Vert \beta -\beta ^*\Vert \le C \sqrt{{p\sigma ^2}/n} \right\} \right] >1-r. \end{aligned}$$
(8)

whenever \(C \ge C_0\). Consequently, there exists a sequence of local minimizers of \(Q_n(\beta )\), \({\hat{\beta }}\), such that \(\Vert {\hat{\beta }}-\beta ^*\Vert =O_P(\sqrt{{p\sigma ^2}/n})\).

Theorem 2

(Oracle properties) Suppose that (A)–(F) hold, then there exists a sequence of \(\sqrt{n/{{p\sigma ^2}}}\)-consistent local minima of EXP, \({\hat{\beta }}\), such that:

  1. (i)

    (Model selection consistency)

    $$\begin{aligned} \lim _{n\rightarrow \infty }P(\{j; {\hat{\beta }}_j\ne 0\} = A) = 1. \end{aligned}$$
  2. (ii)

    (Asymptotic normality)

    $$\begin{aligned} \sqrt{n}B_n{(n^{-1}X_A^\mathrm{T}X_A/\sigma ^2)}^{1/2}({\hat{\beta }}_A-\beta _A^*)\rightarrow N(0, G), \end{aligned}$$

in distribution, where \(B_n\) is any arbitrary \(q\times |A|\) matrix such that \(B_nB^\mathrm{T}_ n\rightarrow G\), and G is a \(q\times q\) nonnegative symmetric matrix.

It is worth pointing out that we do not make any assumptions about the sparsity level of \(\beta ^*\) in Theorem 2. In other words, we do not make any assumptions about \(p_0\), other than those implied by our assumptions about p. In any implementation of EXP, concrete values of the tuning parameters \(\lambda \) and a must be selected. In Sect. 4 we propose an MBIC tuning parameter selection procedure and prove that when EXP is implemented with MBIC tuning parameter selection, the resulting estimator consistently selects the correct model.

4 Regularity parameter selection

Tuning parameter selection is an important issue in most PLS procedures. There are relatively few studies on the choice of penalty parameters. Traditional model selection criteria, such as AIC (Akaike 1973) and BIC (Schwarz 1978), suffer from a number of limitations. Their major drawback arises because parameter estimation and model selection are two different processes, which can result in instability (Breiman 1996) and complicated stochastic properties. To overcome the deficiency of traditional methods, Fan and Li (2001) proposed the SCAD method, which estimates parameters while simultaneously selecting important variables. They selected tuning parameter by minimizing the generalized cross-validation criterion (Breiman 1995; Tibshirani 1996; Fan and Li 2001).

However, it is well known that GCV and AIC-based methods are not consistent for model selection in the sense that, as \(n\rightarrow \infty \), they may select irrelevant predictors with non-vanishing probability (Shao 1993; Wang et al. 2007). On the other hand, BIC-based tuning parameter selection roughly corresponds to maximizing the posterior probability of selecting the true model in an appropriate Bayesian formulation and has been shown to be consistent for model selection in several settings (Wang et al. 2007; Wang and Leng 2007; Zou and Hastie 2007; Lee et al. 2014). The BIC tuning parameter selector is defined by

$$\begin{aligned} \mathrm{BIC}=\log \left( \frac{{\Vert \mathbf y -\mathbf{X }{\hat{\beta }}\Vert }^2}{n}\right) +\widehat{DF}\frac{\log (n)}{n}. \end{aligned}$$
(9)

where \(\widehat{DF}\) is the generalized degrees of freedom given by

$$\begin{aligned} {\widehat{DF}}= \mathrm{tr} \left\{ \mathbf{X }{({\mathbf{X }}^\mathrm{T}+n\Sigma _\lambda )}^\mathrm{T} {\mathbf{X }}^\mathrm{T} \right\} , \end{aligned}$$

and \(\Sigma _\lambda = \mathrm{diag} \{p'_\lambda (|{\hat{\beta }}_1|)/{|{\hat{\beta }}_1|},\ldots , p'_\lambda (|{\hat{\beta }}_p|)/{|{\hat{\beta }}_p|}\}\). The diagonal elements of \(\Sigma _\lambda \) are coefficients of quadratic terms in the local quadratic approximation to the SCAD penalty function \(p_\lambda (\cdot )\) (Fan and Li 2001). Dicker et al. (2013) pointed out that the consistency results for BIC tuning parameter selection assume that the number of predictors is fixed, they proposed a BIC-like procedures which implemented by minimizing

$$\begin{aligned} \mathrm{BIC}_0=\log \left( \frac{{\Vert \mathbf y -\mathbf{X }{\hat{\beta }}\Vert }^2}{n-\hat{p}_0}\right) +\frac{\log (n)}{n}\hat{p}_0. \end{aligned}$$

They proposed estimating the degrees of freedom by the number of selected coefficients: \(\widehat{DF}=\hat{p}_0\), where \(\hat{p}_0=|\{j: {\hat{\beta }}_j \ne 0\}|\). To estimate the residual variance, they use \(\hat{\sigma }^2={(n-\hat{p}_0)}^{-1}{\Vert \mathbf y -\mathbf{X }{\hat{\beta }}\Vert }^2\). This differs from other estimates of the residual variance used in PLS methods, where the denominator \(n-\hat{p}_0\) is replaced by n (Wang et al. 2007); here, \(n-\hat{p}_0\) is used to account for degrees of freedom lost to estimation.

In this section, motivated by Zou and Hastie (2007) and Dicker et al. (2013), we propose an MBIC tuning parameter selector for the EXP procedure and show that the EXP/MBIC procedure is consistent for model selection, provided \(p\sigma ^2/n\rightarrow 0\) and other regularity conditions hold. On the basis of the above notation, we defined an MBIC as

$$\begin{aligned} \mathrm{MBIC} =\log \left( \frac{{\Vert \mathbf y -\mathbf{X }{\hat{\beta }}\Vert }^2}{n-\hat{p}_0}\right) +\frac{\log (n)\hat{p}_0}{n}C_n, \end{aligned}$$
(10)

where \(C_n\) is some positive constant to be discussed more carefully. If \(C_n=1\), the modified BIC (10) reduces to the BIC\(_0\). Moreover, p is allowed to diverge to \(\infty \) as \(n \rightarrow \infty \). Slightly stronger conditions on p and \(\rho =\min _{j\in A}|\beta ^*_j|\) than those required for Theorem 2 are needed for the next theorem, which implies that the EXP/MBIC procedure is consistent for model selection.

(A\('\)) \(n \rightarrow \infty \) and \(C_n\sigma ^2p\log (n)/n\rightarrow 0\).

(B\('\)) \(\rho \sqrt{n/C_n\sigma ^2p\log (n)}\rightarrow \infty \), where \(\rho =\min _{j\in A}|\beta ^*_j|\).

Theorem 3

Suppose that conditions (A\('\)–B\(')\), (C) and (E–F) hold and \(C_n\rightarrow \infty \). Suppose further that \(\Omega \subseteq R^2\) is a subset which contains a sequence \((\lambda , a) = (\lambda ^*_n, a^*_n)\) such that condition (C) holds. Let \({\hat{\beta }}^*={\hat{\beta }}(\lambda ^*_n, a^*_n)\) be the local minima of EXP described in Theorem 2 and let \(\mathrm {MBIC}^{-}= \inf \{\mathrm {MBIC}\) \(\{{\hat{\beta }}(\lambda , a)\}; (\lambda , a) \in \Omega , {\hat{A}} \ne A\}\). Then

$$\begin{aligned} \lim _{n\rightarrow \infty }P\left\{ \mathrm {MBIC}\{{\hat{\beta }}(\lambda ^*_n, a^*_n)\} < \mathrm {MBIC}^{-}\right\} =1, \end{aligned}$$

where \({\hat{A}}=\{j; {\hat{\beta }}_j\ne 0\}\).

Theorem 3 implies that if \({\hat{\beta }}(\hat{\lambda }, \hat{a})\) is chosen to minimize MBIC, then \({\hat{\beta }}(\hat{\lambda }, \hat{a})\) is consistent for model selection. In other words, if \(\mathrm {MBIC}\{{\hat{\beta }}(\hat{\lambda }, \hat{a})\}= \mathrm {MBIC}^{-}\), then \(\lim _{n\rightarrow \infty }P\{\{j; {\hat{\beta }}_j(\hat{\lambda }, \hat{a})\ne 0\}=A\}=1\).

Although in theory we require \(C_n\rightarrow \infty \), its rate of divergence can be arbitrarily slow. For example, \(C_n=\log (\log (p))\) is used for all our numerical experiments and the simulation results are quite encouraging.

5 Implementation: algorithm

Finding the estimator of \(\beta \) that minimizes the objective function (7) poses a number of interesting challenges because the penalized functions are nondifferentiable at the origin and nonconcave with respect to \(\beta \) (Breheny 2015).

Coordinate optimization has been widely used to solve regularization problems. For example, for the PLS problem, Fu (1998), Daubechies et al. (2004) and Wu and Lange (2008) proposed a coordinate descent (CD) algorithm that iteratively optimizes Eq. (7) one component at a time. The algorithm was also recently proposed for a very general class of penalized likelihood methods by Fan and Lv (2011), who refer to the algorithm as “iterative coordinate ascent” (ICA). Coordinate descent algorithms for fitting LASSO-penalized models have also been described by Friedman et al. (2007, 2010) and Breheny and Huang (2011). Recently, Peng and Wang (2014) proposed a new iterative coordinate descent algorithm (QICD) for solving nonconvex penalized quantile regression in high dimension. In this section, we consider the CD algorithm for obtaining EXP estimators for a range of tuning parameter values. The EXP tuning parameter selection procedure is described above.

Next we describe CD algorithms for least squares regression penalized by EXP. For \(\beta >0\), the derivative of the EXP penalty is

$$\begin{aligned} p'_{\lambda ,a}=\frac{\lambda }{a}\mathrm{e}^{-\frac{\beta }{a}}, \end{aligned}$$

for \(\lambda>0,a>0\). The rationale behind the penalty can be understood by considering its derivative: EXP penalty allows the penalty to decay exponentially, approaching 0 asymptotically but never reaching it.

The rationale behind the EXP can also be understood by considering its univariate solution. Consider the simple linear regression of y upon x, with unpenalized least squares solution \(z = n^{-1}x^\mathrm{T}y\) (recall that x has been standardized so that \(x^\mathrm{T}x = n\)). In fact, for this simple linear regression problem, it is easy to show that the EXP estimator has the following closed form:

$$\begin{aligned} {\hat{\beta }}=\left\{ \begin{array}{ll} \mathrm{sign}(z)\beta _s, &{}\quad \text {if } |z| >\frac{\lambda }{a},\\ 0, &{}\quad \text {if } |z| \le \frac{\lambda }{a}.\end{array}\right. \ \end{aligned}$$
(11)

where \(\beta _s\) is the solution of equation \(\beta -|z|+\mathrm{sign}(\beta )\frac{\lambda }{a}\mathrm{e}^{-\frac{|\beta |}{a}}=0\), which may be done very rapidly using Newton iterative formula or some other procedure.

The idea of the CD algorithm is to find local optima of a multivariate optimization problem by solving a sequence of univariate optimization problems. Consider a penalized residual sum squares as (7). Without loss of generality, let us assume that the predictors are standardized: \(\sum _{i=1}^nx_{ij}=0\), \(\frac{1}{n}\sum _{i=1}^n x_{ij}^2=1\). For each fixed \(\lambda , a\), cyclic coordinate descent can be easily implemented for solving the EXP. Let \(r_i = y_i-x_i^\mathrm{T}\tilde{\beta }\) be the current residual. To update the estimate for \(\beta _j\) we need to solve a univariate EXP problem

$$\begin{aligned} {\hat{\beta }}_j=\arg \min _{\beta _j}Q_n(\beta _j|\tilde{\beta }), \end{aligned}$$

where

$$\begin{aligned} Q_n(\beta _j|\tilde{\beta })= \frac{1}{2}{(\beta _j-\tilde{\beta }_j)}^2-\frac{1}{n}\sum _{i=1}^nr_ix_{ij}(\beta _j-\tilde{\beta }_j)+\lambda p_{\lambda ,a}(\beta _j). \end{aligned}$$

Indeed, one observes that the solution can be obtained by Eq. (11).

The CD algorithm is implemented by minimizing \(Q_n(\beta _j|\tilde{\beta })\) and using the solution to update \(\beta \); we next set \(\tilde{\beta }_j = {\hat{\beta }}_j\) as the new estimate. In this way, we cycle through the indices \(j = 1,\ldots ,p\). The operation is sequentially conducted on each coordinate \(\beta _j\) till convergence.

The CD algorithm returns the minimum of the EXP PLS, for a fixed pair of tuning parameters, \((\lambda , a)\). To obtain a EXP solution path, we repeatedly implement CD algorithm for a range of value \((\lambda , a)\). The details are given in Algorithm 1. In practice, we have found that if the columns of \(\mathbf{X }\) are standardized so that \({\Vert \mathbf x _j\Vert }^2=n\), for \(j = 1, \ldots , p\), then taking \(a=0.01\) or selecting a from a relatively small range of possible values works well.

figure a

6 Simulation studies and a data example

The standard errors for the estimated parameters can be obtained directly because we are estimating parameters and selecting variables at the same time. Let \({\hat{\beta }}={\hat{\beta }}(\lambda , a)\) be a local minimizer of EXP. Following Fan and Li (2001) and Fan and Peng (2004), standard errors of \({\hat{\beta }}\) may be estimated by using quadratic approximations to EXP. Indeed, the approximation

$$\begin{aligned} p_{\lambda ,a}(|\beta _j|)\approx p_{\lambda ,a}(|\beta _{j0}|) +\frac{1}{2|\beta _{j0}|}p'_{\lambda ,a}(|\beta _{j0}|)(\beta _j^2-\beta _{j0}^2), \quad \text {for } \beta _j\approx \beta _{j0} \end{aligned}$$
(12)

suggests that EXP may be replaced by the quadratic minimization problem

$$\begin{aligned} \min \left\{ \frac{1}{n}{\Vert \mathbf y -\mathbf{X }\beta \Vert }^2+\sum _{j=1}^p \frac{p'_{\lambda ,a}(|\beta _{j0}|)}{|\beta _{j0}|}\beta _j^2\right\} , \end{aligned}$$
(13)

at least for the purposes of obtaining standard errors. Using this expression, we obtain a sandwich formula for the estimated standard error of \({\hat{\beta }}_{{\hat{A}}}\),

$$\begin{aligned} {\widehat{\mathrm{cov}}} ({{\hat{\beta }}}_{{\hat{A}}})= {\hat{\sigma }}^2\{\mathbf{X }_{{\hat{A}}}^\mathrm{T} {\mathbf{X }}_{{\hat{A}}}+n\Delta _{{\hat{A}},{\hat{A}}}({{\hat{\beta }}}) \}^{-1}{\mathbf{X }}_{{\hat{A}}}^\mathrm{T} {\mathbf{X }}_{{\hat{A}}}\{ {\mathbf{X }}_{{\hat{A}}}^\mathrm{T} {\mathbf{X }}_{{\hat{A}}}+n\Delta _{{\hat{A}},{\hat{A}}}({{\hat{\beta }}}) \} \end{aligned}$$
(14)

where \({\hat{A}} = \{j; {\hat{\beta }}_j\ne 0\}\), \(\Delta (\beta ) = \mathrm{diag}\{p'_{\lambda ,a}(|\beta _1|)/{|\beta _1|},\ldots ,p'_{\lambda ,a}(|\beta _p|)/{|\beta _p|}\}\), \(\hat{\sigma }^2={(n-\hat{p}_0)}^{-1}{\Vert \mathbf y -\mathbf{X }{\hat{\beta }}\Vert }^2\), and \(\hat{p}_0=|{\hat{A}}|\) is the number of elements in \(|{\hat{A}}|\).

6.1 Simulation studies I

In this example, simulation data are generated from the linear regression model,

$$\begin{aligned} y=\mathbf x ^\mathrm{T}\beta +\sigma \varepsilon , \end{aligned}$$

where \(\beta = {(3, 1.5, 0, 0, 2, 0, 0, 0, 0, 0, 0, 0)}^\mathrm{T}\), \(\varepsilon \sim N(0, 1)\) and \(\mathbf x \) is multivariate normal distribution with zero mean and covariance between the ith and jth elements being \(\rho ^{|i-j|}\) with \(\rho = 0.5\). In our simulation, the sample size n is set to be 100 and 200, \(\sigma =3\). For each case, we repeated the simulation 1000 times.

In addition to EXP, we consider the LASSO, adaptive LASSO (ALASSO) (with weights \(\omega _j ={|{\hat{\beta }}^{(0)}|}^{-1}\), where \({\hat{\beta }}^{(0)}\) is the OLS estimator), SCAD and MCP procedures. Covariates were standardized to have \(\Vert \mathbf x _j\Vert =n,~j=1,\ldots , p\), prior to obtaining estimates; however, all summary statistics discussed below pertain to estimators transformed to the original scale. In our simulations, EXP, LASSO, ALASSO, MCP and SCAD solution paths are all computed using CD algorithms. The tuning parameter selection is all performed with MBIC as (10). For EXP tuning parameter selection, we find that \(a=0.01\) works well.

The model error for \(\hat{\mu } = \mathbf x ^\mathrm{T}{\hat{\beta }}\) is \(ME(\hat{\mu }) = {({\hat{\beta }}- \beta )}^\mathrm{T}E(\mathbf x {} \mathbf x ^\mathrm{T})({\hat{\beta }}- \beta )\) for linear model. Simulation results are summarized in Table 1, in which MRME stands for median of ratios of ME of a selected model to that of the un-penalized minimum square estimate under the full model. Both the columns of “C” and “IC” are measures of model complexity. Column “C” shows the average number of nonzero coefficients correctly estimated to be nonzero, and column “IC” presents the average number of zero coefficients incorrectly estimated to be nonzero. In the column labeled “Under-fit”, we present the proportion of excluding any nonzero coefficients in 1000 replications. Likewise, we report the probability of selecting the exact subset model and the probability of including all three significant variables and some noise variables in the columns “Correct-fit” and “Over-fit”, respectively.

Table 1 Simulation results for linear regression models of simulation I
Full size table

As can be seen from Table 1, all variable selection procedures dramatically reduce model error. EXP has the smaller model error among all competitors, followed by the MCP and SCAD. In terms of sparsity, EXP also has the higher probability of correct fit. The EXP penalty performs better than the other penalties. Also, EXP has some advantages when the dimensionality p is high which can be seen in simulation III.

We now test the accuracy of our standard error formula (14). The median absolute deviation divided by 0.6745, denoted by SD in Table 2, of 1000 estimated coefficients in the 1000 simulations can be regarded as the true standard error. The median of the 1000 estimated SD’s, denoted by SD\(_m\), and the median absolute deviation error of the 1000 estimated standard errors divided by 0.6745, denoted by SD\(_\mathrm{mad}\), gauge the overall performance of the standard error formula (13). Table 2 presents the results for nonzero coefficients when the sample size \(n=200\). The results for the other case with \(n=100\) are similar. Table 2 suggests that the sandwich formula performs surprisingly well.

Table 2 Standard deviations of estimators for the linear regression model (\(n=200\))
Full size table

The simulation results described above give an indication of the performance of the proposed EXP methods, in comparison with current recommended implementations of other PLS methods. In particular, we focus on MBIC criterion (10) implementations when implementing the alternative PLS methods. Table 1 summarizes the results of a simulation study where the same MBIC criterion for (7) was used for each PLS method.

Then, when the common BIC criterion (9) is utilized, the results indicate that EXP performs well when compared to the alternative methods. The details can be seen in Table 3. Compare Tables 1 with 3, we can see: (1) EXP/MBIC perform better than EXP/BIC which indicate that MBIC criteria is more suitable for EXP estimator; (2) LASSO, ALASSO, SCAD estimation method have the smaller model error under the BIC criterion; (3) MCP estimator perform better with MBIC than with BIC, the reason need to be further explained; (4) When \(n\rightarrow \infty \), all kinds of variable selection methods can identify the correct model consistently and reduce the model error.

Table 3 Simulation results for linear regression models of simulation I with common BIC
Full size table

6.2 Simulation study II

The example is from Wang et al. (2009). In this example, we consider the situation where the dimension of the full model and the dimension of the true model are all diverging. More specifically, we take \(p =[7n^{1/4}]\) and the dimension of the true model to be \(p_0 =[p/3]\), [t] stands for the largest integer no larger than t. To summarize the simulation results, we computed the median of the relative model error MRME, the average model size (i.e. the number of non-zero coefficients), MS, and also the percentage of the correctly identified true models CM. Intuitively, a better model selection procedure should produce more accurate prediction results (i.e. smaller MRME-value), more correct model sizes (i.e. \(\mathrm {MS} \approx p_0\)) and better model selection capability (i.e. larger CM-value). For a more detailed explanation of MRME, MS and CM, we refer to Fan and Li (2001) and Wang and Leng (2007). The detailed results are reported in Fig. 2. As one can see that the CM-value of EXP/MBIC approaches 100 % quickly, which clearly confirms the consistency of the MBIC proposed. As a direct consequence, the MRME-values are consistently smaller and the MS-values approximately equal \(p_0\).

Fig. 2
figure 2

Detailed simulation results with normal \(\varepsilon \): MRME (left); MS (middle); CM (right)

Full size image

6.3 Simulation study III

In this simulation study presented here, we examined the performance of the various PLS methods for p substantially larger than in the previous studies. In particular, we took \(p = 339, n = 500, \sigma ^2 = 5\), and \(\beta ^* = (2I^\mathrm{T}_{37},-3I^\mathrm{T}_{37},I^\mathrm{T}_{37},0^\mathrm{T}_{228})\), where \(I^k \in R^k\) is the vector with all entries equal to 1. Thus, \(p_0= 111\). We simulated 200 independent datasets \(\{(y_1, x_1^\mathrm{T}),\ldots , (y_n, x_n^\mathrm{T})\}\) in this study and, for each dataset, we computed estimates of \(\beta ^*\). Results from this simulation study are found in Table 4.

Perhaps the most striking aspect of the results presented in Table 4 is that hardly no method ever selected the correct model in this simulation study. However, given that \(p, p_0\), and \(\beta ^*\) are substantially larger in this study than in the previous simulation studies, this may not be too surprising. Notice that on average, EXP selects the most parsimonious models of all methods and has the smaller model error. EXP’s nearest competitor in terms of model error is ALASSO. This implementation of ALASSO has mean model error 0.2783, but its average selected model size is 103.5250 larger than EXP’s. Since \(p_0 = 111\), it is clear that EXP underfits in some instances. In fact, all of the methods in this study underfit to some extent. This may be due to the fact that many of the non-zero entries in \(\beta ^*\) are small relative to the noise level \(\sigma ^2=5\).

Table 4 Simulation results for linear regression models of Example 3
Full size table

6.4 Application

In this section, we apply the EXP regularization scheme to a prostate cancer example. The dataset in this example is derived from a study of prostate cancer by Stamey et al. (1989). The dataset consists of the medical records of 97 patients who were about to receive a radical prostatectomy. The predictors are eight clinical measures: log (cancer volume) (lcavol), log (prostate weight) (lweight), age, the logarithm of the amount of benign prostatic hyperplasia (lbph), seminal vesicle invasion (svi), log (capsular penetration) (lcp), Gleason score (Gleason) and percentage Gleason score 4 or 5 (pgg45). The response is the logarithm of prostate-specific antigen (lpsa). One of the main aims here is to identify which predictors are more important in predicting the response.

The LASSO, ALASSO, SCAD, MCP and EXP are all applied to the data. The BIC and MBIC are used to select tuning parameters. We also compute the OLS estimate of the prostate cancer data. Results are summarized in Table 5. The OLS estimator does not perform variable selection. LASSO selects five variables in the final model, SCAD and MCP select lcavol, lweight lbph and svi in the final model. While ALASSO and EXP select lcavol, lweight and svi. Thus, EXP selects a substantially simpler model than LASSO, SCAD and MCP. Furthermore, as indicated by the columns labeled \(R^2\) (\(R^2\) is equal to one minus the residual sum of squares divided the total sum of squares) and \(R^2/{R^2_\mathrm{OLS}}\) in Table 5, the EXP estimator describes more variability in the data than LASSO and ALASSO, and nearly as much as OLS estimator.

Table 5 Prostate cancer data: comparing different methods
Full size table

7 Conclusion

In this paper, a new EXP penalty which very closely resembles the \(L_0\) penalty is proposed. The model selection oracle property is investigated and the EXP is implemented by using CD algorithm. Moreover, an MBIC tuning parameter selection method for EXP is proposed and it is shown that it consistently identifies the correct model. Numerical studies further endorse our theoretical results and the advantage of our new methods for model selection.

It would be interesting to extend the results to regularization methods for the generalized linear models (GLMs) and more general models and loss functions. Also, motivated by the elastic net (Zou and Hastie 2005) and the adaptive elastic net (Zou and Zhang 2009), one could consider a mixed penalty involving EXP and an \(L_2\)-norm penalty. In this paper, we do not address the situation where \(p \gg n\), in fact, the proposed EXP method can be easily extended for variable selection in the situation \(p \gg n\). These problems are beyond the scope of this paper and will be interesting topics for future research.