1 Introduction

Finite mixture of regression models, also known as switching regression models in econometrics, have been widely applied in various fields, see, for example, in econometrics (Wedel and DeSarbo 1993; Frühwirth-Schnatter 2001), and in epidemiology (Green and Richardson 2002). Since Goldfeld and Quandt (1973) first introduced the mixture regression model, many efforts have been made to extend the traditional parametric mixture of linear regression models. For example, Young and Hunter (2010), and Huang and Yao (2012) studied models which allow the mixing proportions to depend on the covariates nonparametrically; Huang et al. (2013) proposed a fully nonparametric mixture of regression models by assuming the mixing proportions, the regression functions, and the variance functions to be nonparametric functions of a covariate; Cao and Yao (2012) suggested a semiparametric mixture of binomial regression models for binary data.

In this article, we propose a new semiparametric mixture of regression models, where the mixing proportions and variances are constants, but the component regression functions are nonparametric functions of a covariate. Compared to traditional finite mixture of linear regression models, the newly proposed model relaxes the parametric assumption on the regression functions, and allows the regression function in each component to be an unknown but smooth function of covariates. Compared to the fully nonparametric mixture of regression models proposed by Huang et al. (2013), our new model improves the efficiency of the estimates of the mean functions by assuming the mixing proportions and variances to be constants, which are also presumed by the traditional mixture of linear regressions. The new model is more challenging to estimate due to the existence of both global parameters and local parameters. The comparison of our paper to Huang et al. (2013) is similar to the comparison between semiparametric regression and fully nonparametric regression. Although the parametric parts of our model have stronger assumption than the nonparametric parts of Huang et al. (2013), they can provide more homogeneous model and more efficient estimate. Therefore, the proposed semiparametric model can combine the good properties of both parametric models and nonparametric models.

Our new model is motivated by a US house price index data, which is also used by Huang et al. (2013). The data set contains the monthly change of S&P/Case-Shiller House Price Index (HPI) and monthly growth rate of United States Gross Domestic Product (GDP) from January 1990 to December 2002, see Fig. 3a for a scatter plot. Based on the plot, it can be seen that there are two homogeneous groups and the relationship between HPI and GDP are different in different groups. In addition, it is clear that the relationship in each group is not linear. Therefore, the traditional mixture of linear regression models can not be applied. In Fig. 3b, we added the two fitted component regression curves based on our new model, and it is clear that the new model successfully recovered the two-component regression curves. In addition, the observations were classified into two groups corresponding to two different macroeconomic cycles, which possibly explains that the impact of GDP growth rate on HPI change may be different in different macroeconomic cycles.

We will show the identifiability of the proposed model under some regularity conditions. To estimate the unknown smoothing functions, we propose both a regression spline based estimator and a local likelihood estimator using the kernel regression technique. To achieve the optimal convergence rate for both the global parameters and the nonparametric functions, we propose a one-step backfitting estimation procedure. The asymptotic properties of the one-step backfitting estimate are investigated. In addition, we propose two EM-type algorithms to compute the proposed estimates and prove their asymptotic ascent properties. A generalized likelihood ratio test is proposed for testing whether the mixing proportions and variances are indeed constants. We investigate the asymptotic behavior of the test and prove that its limiting null distribution follows a \(\chi ^2\)-distribution independent of the nuisance parameters. A simulation study and two real data applications are used to demonstrate the effectiveness of the new model.

The rest of the paper is organized as follows. In Sect. 2, we introduce the new semiparametric mixture of regression models and the estimation procedure. In particular, we propose a regression spline estimate and a one-step backfitting estimate. A generalized likelihood ratio test is also introduced for some semiparametric inferences. In Sect. 3, we use a Monte Carlo study and two real data examples to demonstrate the finite sample performance of the proposed model and estimates. We conclude the paper with a brief discussion in Sect. 4 and defer the proofs to the Appendix.

2 Estimation procedure and asymptotic properties

2.1 The semiparametric mixture of regression models

Assume \(\{(X_i,Y_i),\,i=1,\ldots ,n\}\) are a random sample from the population (X, Y). Let Z be a latent variable with \(P(Z=j)=\pi _j\) for \(j=1,\ldots ,k\). Suppose \(E(Y|X=x,Z=j)=m_j(x)\) and conditioning on \(Z=j\) and \(X=x\), Y follows a normal distribution with mean \(m_j(x)\) and variance \(\sigma _j^2\). Then, without observing Z, the conditional distribution of Y given \(X=x\) can be written as

$$\begin{aligned} Y|_{X=x}\sim \sum _{j=1}^k \pi _j\phi (Y|m_j(x),\sigma _j^2), \end{aligned}$$
(1)

where \(\phi (y|\mu ,\sigma ^2)\) is the normal density with mean \(\mu \) and variance \(\sigma ^2\). In this paper, we only considered the case when X is univariate. The estimation methodology and theoretical results discussed can be readily extended to multivariate X, but due to the “curse of dimensionality”, the extension is less applicable and thus omitted here. Throughout the paper, we assume that k is fixed, and therefore, refer to (1) as a finite semiparametric mixture of regression models, since \(m_j(x)\) is a nonparametric function of x, while \(\pi _j\) and \(\sigma _j\) are global parameters. If \(m_j(x)\) is indeed linear in x, model (1) boils down to a regular finite mixture of linear regression models. When \(k=1\), then model (1) is a nonparametric regression model. Therefore, model (1) is a natural extension of the finite mixture of linear regression models and the nonparametric regression model.

Huang et al. (2013) studied a nonparametric mixture of regression models (NMR),

$$\begin{aligned} Y|_{X=x}\sim \sum _{j=1}^k\pi _j(x)\phi (Y|m_j(x),\sigma _j^2(x)), \end{aligned}$$
(2)

where \(\pi _j(\cdot )\), \(m_j(\cdot )\), and \(\sigma _j^2(\cdot )\) are unknown but smooth functions. Compared to model (2), model (1) improves the efficiency of the estimates of \(\pi _j\), \(\sigma _j\) and \(m_j(x)\) by assuming the mixing proportions and variances to be constants, which are also presumed by the traditional mixture of linear regressions. We will demonstrate such improvement in Sect. 3. However, the new model (1) is more challenging to estimate than model (2) due to the existence of both global parameters and local parameters. In fact, we will demonstrate later that the model estimate of (2) is an intermediate result of the proposed one-step backfitting estimate. In this article, we will also develop a generalized likelihood ratio test to compare the proposed model with model (2) and illustrate its use in Sect. 3.

Identifiability is a critical issue in many mixture models. Some well known results of identifiability of finite mixture models include: mixture of univariate normals is identifiable (Titterington et al. 1985), and finite mixture of linear regression models is identifiable provided that covariates have a certain level of variability (Hennig 2000). Based on Theorem 1 in Huang et al. (2013) and Theorem 3.2 in Wang et al. (2014), we can get the following result on the identifiability of model (1).

Proposition 1

Assume that

  1. (1)

    \(m_j(x)\) are differentiable functions, \(j=1,\ldots ,k\).

  2. (2)

    One of the following conditions holds:

    1. (a)

      For any \(i\ne j\), \(\sigma _i\ne \sigma _j\);

    2. (b)

      If there exists \(i\ne j\) such that \(\sigma _i=\sigma _j\), then \(\Vert m_i(x)-m_j(x)\Vert +\Vert m_i'(x)-m_j'(x)\Vert \ne 0\) for any x.

  3. (3)

    The domain \(\mathscr {X}\) of x is an interval in \(\mathbb {R}\).

Then, model (1) is identifiable.

2.2 Estimation procedure and asymptotic properties

2.2.1 Regression spline based estimator

We first introduce a regression spline based estimator, which uses the regression spline (Hastie et al 2003; de Boor 2001) to transfer the semiparametric mixture model to a parametric mixture model. A cubic spline approximation for \(m_j(x)\) can be expressed as

$$\begin{aligned} m_j(x)\approx \sum _{q=1}^{Q+4}\beta _{jq}B_q(x),\quad j=1,\ldots ,k, \end{aligned}$$
(3)

where \(B_1(x),...,B_{Q+4}(x)\) is a cubic spline basis and Q is the number of internal knots. Many spline bases can be used here, such as a truncated power spline basis or a B-spline basis. In this paper, we mainly focus on the B-spline basis.

Based on the approximation (3), model (1) becomes

$$\begin{aligned} Y|_{X=x}\sim \sum _{j=1}^k \pi _j\phi \left( Y\big |\sum _{q=1}^{Q+4}\beta _{jq}B_q(x),\sigma _j^2\right) . \end{aligned}$$

The log likelihood of the collected data \(\{(X_i,Y_i),i=1,..,n\}\) is

$$\begin{aligned} \ell ({{\varvec{\pi }}},{{\varvec{\beta }}},{{\varvec{\sigma }}}^2)=\sum _{i=1}^n\log \left\{ \sum _{j=1}^k\pi _j\phi (Y_i|\sum _{q=1}^{Q+4}\beta _{jq}B_q(X_i),\sigma _j^2)\right\} , \end{aligned}$$

where \({{\varvec{\pi }}}=\{\pi _1,\ldots ,\pi _{k-1}\}^T\), \({{\varvec{\beta }}}=\{{{\varvec{\beta }}}_1,\ldots ,{{\varvec{\beta }}}_k\}^T\), \({{\varvec{\beta }}}_j=\left( \beta _{j1},\ldots ,\beta _{j,Q+4}\right) ^T\), and \({{\varvec{\sigma }}}^2=\{\sigma _1^2,\dots ,\sigma _k^2\}^T\). The parameters \(({{\varvec{\pi }}},{{\varvec{\beta }}},{{\varvec{\sigma }}}^2)\) can be estimated by the traditional EM algorithm for mixtures of linear regression models.

The estimation method based on the regression spline approximation is easy to implement, and therefore, will be used as an initial value for our other estimation procedures.

2.2.2 One-step backfitting estimation procedure

In this section, we propose a one-step backfitting estimation procedure to achieve the optimal convergence rates for both the global parameters and the nonparametric component regression functions.

Let \(\ell ^*({{\varvec{\pi }}},{{\varvec{m}}}(\cdot ),{{\varvec{\sigma }}}^2)\) be the log-likelihood of the collected data \(\{(X_i,Y_i),i=1,..,n\}\). That is,

$$\begin{aligned} \ell ^*({{\varvec{\pi }}},{{\varvec{m}}}(\cdot ),{{\varvec{\sigma }}}^2)=\sum _{i=1}^n\log \left\{ \sum _{j=1}^k\pi _j\phi (Y_i|m_j(X_i),\sigma _j^2)\right\} , \end{aligned}$$
(4)

where \({{\varvec{\pi }}}=\{\pi _1,...,\pi _{k-1}\}^T\), \({{\varvec{m}}}(\cdot )=\{m_1(\cdot ),...,m_k(\cdot )\}^T\), and \({{\varvec{\sigma }}}^2=\{\sigma _1^2,...,\sigma _k^2\}^T\). Since \({{\varvec{m}}}(\cdot )\) consists of nonparametric functions, (4) is not ready for maximization. Next, we propose a one-step backfitting procedure. First, we estimate \({{\varvec{\pi }}}\), \({{\varvec{m}}}\) and \({{\varvec{\sigma }}}^2\) locally by maximizing the following local log-likelihood function:

$$\begin{aligned} \ell _1({{\varvec{\pi }}}(x),{{\varvec{m}}}(x),{{\varvec{\sigma }}}^2(x))=\sum _{i=1}^n\log \left\{ \sum _{j=1}^k\pi _j\phi (Y_i|m_j,\sigma _j^2)\right\} K_h(X_i-x), \end{aligned}$$
(5)

where \(K_h(t)=h^{-1}K(t/h)\), \(K(\cdot )\) is a kernel density function, and h is a tuning parameter.

Let \(\tilde{{{\varvec{\pi }}}}(x)\), \(\tilde{{{\varvec{m}}}}(x)\), and \(\tilde{{{\varvec{\sigma }}}}^2(x)\) be the maximizer of (5), which are in fact the model estimates of (2) proposed by Huang et al. (2013). Note that, in (5), the global parameters \({{\varvec{\pi }}}\) and \({{\varvec{\sigma }}}^2\) are estimated locally. To improve the efficiency, we propose to update the estimates of \({{\varvec{\pi }}}\) and \({{\varvec{\sigma }}}^2\) by maximizing the following log-likelihood function:

$$\begin{aligned} \ell _2({{\varvec{\pi }}},{{\varvec{\sigma }}}^2)=\sum _{i=1}^n\log \left\{ \sum _{j=1}^k\pi _j\phi (Y_i|\tilde{m}_j(X_i),\sigma _j^2)\right\} , \end{aligned}$$
(6)

which, compared to (4), replaces \(m_j(\cdot )\) by \(\tilde{m}_j(\cdot )\).

Denote by \(\hat{{{\varvec{\pi }}}}\) and \(\hat{{{\varvec{\sigma }}}}^2\) the solution of maximizing (6). We can then further improve the estimate of \({{\varvec{m}}}(\cdot )\) by maximizing the following local log-likelihood function:

$$\begin{aligned} \ell _3({{\varvec{m}}}(x))=\sum _{i=1}^n\log \left\{ \sum _{j=1}^k\hat{\pi }_j\phi (Y_i|m_j,\hat{\sigma }_j^2)\right\} K_h(X_i-x). \end{aligned}$$
(7)

which, compared to (5), replaces \(\pi _j\) and \(\sigma _j^2\) by \(\hat{\pi }_j\) and \(\hat{\sigma }_j^2\), respectively.

Let \(\hat{{{\varvec{m}}}}(x)\) be the solution of (7), and we refer to \(\hat{{{\varvec{\pi }}}}\), \(\hat{{{\varvec{m}}}}(x)\), and \(\hat{{{\varvec{\sigma }}}}^2\) as the one-step backfitting estimates. In Sect. 2.2.4, we show that the one-step backfitting estimates achieve the optimal convergence rate for both the global parameters, and the nonparametric mean functions. In (7), since \(\hat{\pi }_j\) and \(\hat{\sigma }_j^2\) have root n convergence rate, unlike \(\tilde{{{\varvec{m}}}}(x)\), \(\hat{{{\varvec{m}}}}(x)\) does not need to adjust the uncertainty of estimating \(\pi _j\) and \(\sigma _j^2\). Therefore, \(\hat{{{\varvec{m}}}}(x)\) can have better estimation accuracy than \(\tilde{{{\varvec{m}}}}(x)\) proposed by Huang et al. (2013).

2.2.3 Computing algorithms

In this section, we propose a local EM-type algorithm (LEM) and a global EM-type algorithm (GEM) to perform the one-step backfitting.

Local EM-type algorithm (LEM)

In practice, we usually want to evaluate unknown functions at a set of grid points, which in this case, requires us to maximize local log-likelihood functions at a set of grid points. If we simply employ an EM algorithm separately for different grid points, the labels in the found estimators may change at different grid points, and we may not be able to get smoothed estimated curves (Huang and Yao 2012). Next, we propose a modified EM-type algorithm, which estimates the nonparametric functions simultaneously at a set of grid points. Let \(\{u_t,t=1,\ldots ,N\}\) be a set of grid points where some unknown functions are evaluated, and N be the number of grid points.

Step 1: modified EM-type algorithm to maximize \(\varvec{\ell _1}\) in (5)

In Step 1, we use the modified EM-type algorithm of Huang et al. (2013) to maximize \(\ell _1\) and obtain the estimates \(\tilde{{{\varvec{\pi }}}}(\cdot )\), \(\tilde{{{\varvec{m}}}}(\cdot ),\) and \(\tilde{{{\varvec{\sigma }}}}^2(\cdot )\). Specifically, at the \((l+1)\mathrm{th}\) iteration,

E-step Calculate the expectations of component labels based on estimates from the lth iteration:

$$\begin{aligned} p_{ij}^{(l+1)}=\frac{\pi _j^{(l)}(X_i)\phi (Y_i|m_j^{(l)}(X_i),\sigma _j^{2(l)}(X_i))}{\sum _{j=1}^k\pi _j^{(l)}(X_i)\phi (Y_i|m_j^{(l)}(X_i),\sigma _j^{2(l)}(X_i))}, \quad i=1,\ldots ,n, j=1,\ldots ,k. \end{aligned}$$

M-step Update the estimates

$$\begin{aligned}&\pi _j^{(l+1)}(x)=\frac{\sum _{i=1}^np_{ij}^{(l+1)}K_h(X_i-x)}{\sum _{i=1}^nK_h(X_i-x)},\end{aligned}$$
(8)
$$\begin{aligned}&m_j^{(l+1)}(x)=\frac{\sum _{i=1}^np_{ij}^{(l+1)}Y_iK_h(X_i-x)}{\sum _{i=1}^np_{ij}^{(l+1)}K_h(X_i-x)},\end{aligned}$$
(9)
$$\begin{aligned}&\sigma _j^{2(l+1)}(x)=\frac{\sum _{i=1}^np_{ij}^{(l+1)}(Y_i-m_j^{(l+1)}(x))^2K_h(X_i-x)}{\sum _{i=1}^np_{ij}^{(l+1)}K_h(X_i-x)}, \end{aligned}$$
(10)

for \(x\in \{u_t,t=1,\ldots ,N\}\). We then update \(\pi _j^{(l+1)}(X_i)\), \(m_j^{(l+1)}(X_i),\) and \(\sigma _j^{2(l+1)}(X_i)\), \(i=1,\ldots ,n\), by linear interpolating \(\pi _j^{(l+1)}(u_t)\), \(m_j^{(l+1)}(u_t),\) and \(\sigma _j^{2(l+1)}(u_t)\), \(t=1,\ldots ,N\), respectively.

Note that in the M-step, the nonparametric functions are estimated simultaneously at a set of grid points, and therefore, the classification probabilities in the the E-step can be estimated globally to avoid the label switching problem (Celeux et al. 2000; Stephens 2000; Yao 2012, 2015; Yao and Lindsay 2009).

Step 2: EM algorithm to maximize \(\varvec{\ell _2}\) in (6)

In Step 2, given \(\tilde{m}_j(x)\) from Step 1, a regular EM algorithm can be used to maximize \(\ell _2\) and update the estimates of \({{\varvec{\pi }}}\) and \({{\varvec{\sigma }}}^2\) as \(\hat{{{\varvec{\pi }}}}\) and \(\hat{{{\varvec{\sigma }}}}^2\). At the \((l+1)\)th iteration,

E-step Calculate the expectations of component labels based on the estimates from the lth iteration:

$$\begin{aligned} p_{ij}^{(l+1)}=\frac{\pi _j^{(l)}\phi (Y_i|\tilde{m}_j(X_i),\sigma _j^{2(l)})}{\sum _{j=1}^k\pi _j^{(l)}\phi (Y_i|\tilde{m}_j(X_i),\sigma _j^{2(l)})}, i=1,\ldots ,n, j=1,\ldots ,k. \end{aligned}$$

M-step Update the estimates

$$\begin{aligned}&\pi _j^{(l+1)}=\frac{\sum _{i=1}^np_{ij}^{(l+1)}}{n},\\&\sigma _j^{2(l+1)}=\frac{\sum _{i=1}^np_{ij}^{(l+1)}(Y_i-\tilde{m}_j(X_i))^2}{\sum _{i=1}^np_{ij}^{(l+1)}}. \end{aligned}$$

The ascent property of the above algorithm follows from the theory of the ordinary EM algorithm.

Step 3: Modified EM-type algorithm to maximize \(\varvec{\ell _3}\) in (7)

In Step 3, given \(\hat{{{\varvec{\pi }}}}\) and \(\hat{{{\varvec{\sigma }}}}^2\) from Step 2, we would then maximize \(\ell _3\) to find the estimates \(\hat{{{\varvec{m}}}}(x)\). At the \((l+1)\)th iteration,

E-step Calculate the expectations of component labels based on estimates from the lth iteration:

$$\begin{aligned} p_{ij}^{(l+1)}=\frac{\hat{\pi }_j\phi (Y_i|m_j^{(l)}(X_i),\hat{\sigma }_j^2)}{\sum _{j=1}^k\hat{\pi }_j\phi (Y_i|m_j^{(l)}(X_i),\hat{\sigma }_j^2)},\quad i=1,\ldots ,n, j=1,\ldots ,k. \end{aligned}$$
(11)

M-step Update the estimate

$$\begin{aligned} m_j^{(l+1)}(x)=\frac{\sum _{i=1}^np_{ij}^{(l+1)}Y_iK_h(X_i-x)}{\sum _{i=1}^np_{ij}^{(l+1)}K_h(X_i-x)}, \end{aligned}$$

for \(x\in \{u_t,t=1,...,N\}\). Similar to Step 1, we update the estimates at a set of grid points first, and then update \(m_j^{(l+1)}(X_i)\), \(i=1,\ldots ,n\), by linear interpolating \(m_j^{(l+1)}(u_t)\), \(t=1,\ldots ,N\).

Global EM-type algorithm (GEM)

To improve the estimation efficiency, one might further iterate Step 1 to Step 3 until convergence. Next, we propose a global EM-type algorithm (GEM) to approximate such iteration, but with much less computation. At the \((l+1)\)th iteration,

E-step Calculate the expectations of component labels based on estimates from the lth iteration:

$$\begin{aligned} p_{ij}^{(l+1)}=\frac{\pi _j^{(l)}\phi \left( Y_i|m_j^{(l)}(X_i),\sigma _j^{2(l)}\right) }{\sum _{j=1}^k\pi _j^{(l)}\phi \left( Y_i|m_j^{(l)}(X_i),\sigma _j^{2(l)}\right) }, i=1,\ldots ,n, j=1,\ldots ,k. \end{aligned}$$

M-step Simultaneously update the estimates

$$\begin{aligned} \pi _j^{(l+1)}&=\frac{\sum _{i=1}^np_{ij}^{(l+1)}}{n},\\ m_j^{(l+1)}(x)&=\frac{\sum _{i=1}^np_{ij}^{(l+1)}Y_iK_h(X_i-x)}{\sum _{i=1}^np_{ij}^{(l+1)}K_h(X_i-x)},\\ \sigma _j^{2(l+1)}&=\frac{\sum _{i=1}^np_{ij}^{(l+1)}(Y_i-m_j^{(l+1)}(X_i))^2}{\sum _{i=1}^np_{ij}^{(l+1)}}, \end{aligned}$$

for \(x\in \{u_t,j=1,\ldots ,N\}\). We then update \(m_j^{(l+1)}(X_i)\), \(i=1,...,n\) by linear interpolating \(m_j^{(l+1)}(u_t)\), \(t=1,\ldots ,N\).

2.2.4 Asymptotic properties

Next, we investigate the asymptotic properties of the proposed one-step backfitting estimates and the asymptotic ascent properties of the two proposed EM-type algorithms.

Let \({{\varvec{\theta }}}=({{\varvec{m}}}^T,{{\varvec{\pi }}}^T,({{\varvec{\sigma }}}^2)^T)^T\), \({{\varvec{\beta }}}=({{\varvec{\pi }}}^T,({{\varvec{\sigma }}}^2)^T)^T\), then \({{\varvec{\theta }}}=({{\varvec{m}}}^T,{{\varvec{\beta }}}^T)^T\). Define

$$\begin{aligned} \ell ({{\varvec{\theta }}},y)=\log \sum _{j=1}^k\pi _j\phi (y|m_j,\sigma _j^2), \end{aligned}$$
(12)

and let

$$\begin{aligned}&I_\theta (x)=-E\left[ \frac{\partial ^2\ell ({{\varvec{\theta }}},y)}{\partial {{\varvec{\theta }}}\partial {{\varvec{\theta }}}^T}|X=x\right] , \quad I_\beta (x)=-E\left[ \frac{\partial ^2\ell ({{\varvec{\theta }}},y)}{\partial {{\varvec{\beta }}}\partial {{\varvec{\beta }}}^T}|X=x\right] ,\\&I_m(x)=-E\left[ \frac{\partial ^2\ell ({{\varvec{\theta }}},y)}{\partial {{\varvec{m}}}\partial {{\varvec{m}}}^T}|X=x\right] ,\\&I_{\beta m}(x)=-E\left[ \frac{\partial ^2\ell ({{\varvec{\theta }}},y)}{\partial {{\varvec{\beta }}}\partial {{\varvec{m}}}^T}|X=x\right] , \Lambda (u|x)=E\left[ \frac{\partial \ell ({{\varvec{\theta }}}(x),y)}{\partial {{\varvec{m}}}}|X=u\right] . \end{aligned}$$

Define

$$\begin{aligned} \kappa _l=\int t^lK(t)dt, \quad \nu _l=\int t^lK^2(t)dt. \end{aligned}$$

Under further conditions defined in the Appendix, the consistency and asymptotic normality of \(\hat{{{\varvec{\pi }}}}\) and \(\hat{{{\varvec{\sigma }}}}^2\) are established in the next theorem.

Theorem 1

Suppose that conditions (C1) and (C3)|(C10) in the Appendix are satisfied, then

$$\begin{aligned} \sqrt{n}(\hat{{{\varvec{\beta }}}}-{{\varvec{\beta }}})\overset{D}{\rightarrow }N(0,B^{-1}\Sigma B^{-1}), \end{aligned}$$

where \(B=E\{I_\beta (X)\}\), \(\Sigma =Var\{\partial \ell ({{\varvec{\theta }}}(X),Y)/\partial {{\varvec{\beta }}}-\varpi (X,Y)\}\), \(\varpi (x,y)=I_{\beta m}\varphi (x,y)\), and \(\varphi (x,y)\) is a \(k\times 1\) vector consisting of the first k elements of \(I_\theta ^{-1}(x)\partial \ell ({{\varvec{\theta }}}(x),y)/\partial {{\varvec{\theta }}}\).

Based on the above theorem, we can see that the proposed one-step backfitting estimator of the global parameters have achieved the optimal square root n convergence rate.

The next theorem gives the asymptotic property of \(\hat{{{\varvec{m}}}}(\cdot )\).

Theorem 2

Suppose that conditions (C2)|(C10) in the Appendix are satisfied, then

$$\begin{aligned} \sqrt{nh}(\hat{{{\varvec{m}}}}(x)-{{\varvec{m}}}(x)-\Delta _m(x)+o_p(h^2))\overset{D}{\rightarrow }N(0,f^{-1}(x)I_m^{-1}(x)\nu _0), \end{aligned}$$

where \(f(\cdot )\) is the density of X, \(\Delta _m(x)\) is a \(k\times 1\) vector consisting of the first k elements of \(\Delta (x)\) with

$$\begin{aligned} \Delta (x)=I_m^{-1}(x)\left\{ \frac{1}{2}\Lambda ''(x|x)+f^{-1}(x)f'(x)\Lambda '(x|x)\right\} \kappa _2h^2. \end{aligned}$$

Based on the above theorem, we can see that \(\hat{{{\varvec{m}}}}(x)\) has the same asymptotic properties as if \({{\varvec{\beta }}}\) were known, since \(\hat{{{\varvec{\beta }}}}\) has faster convergence rate than \(\hat{{{\varvec{m}}}}(x)\).

The asymptotic ascent properties of the proposed EM-type algorithms are provided in the following theorem.

Theorem 3

  1. (i)

    For the modified EM-type algorithm (Step 1) to maximize \(\ell _1\), given condition (C2),

    $$\begin{aligned} \liminf _{n\rightarrow \infty }n^{-1}\left[ \ell _1({{\varvec{\theta }}}^{(l+1)}(x))-\ell _1({{\varvec{\theta }}}^{(l)}(x))\right] \ge 0 \end{aligned}$$

    in probability, for any given point \(x\in \mathscr {X}\), where \(\ell _1(\cdot )\) is defined in (5).

  2. (ii)

    For the modified EM-type algorithm (Step 3) to maximize \(\ell _3\), given condition (C2),

    $$\begin{aligned} \liminf _{n\rightarrow \infty }n^{-1}\left[ \ell _3({{\varvec{m}}}^{(l+1)}(x))-\ell _3({{\varvec{m}}}^{(l)}(x))\right] \ge 0 \end{aligned}$$

    in probability, for any given point \(x\in \mathscr {X}\), where \(\ell _3(\cdot )\) is defined in (7).

  3. (iii)

    For the GEM algorithm, we have

    $$\begin{aligned} \liminf _{n\rightarrow \infty }n^{-1}\left[ \ell ^*({{\varvec{m}}}^{(l+1)}(\cdot ),{{\varvec{\pi }}}^{(l+1)},{{\varvec{\sigma }}}^{2(l+1)})-\ell ^*({{\varvec{m}}}^{(l)}(\cdot ),{{\varvec{\pi }}}^{(l)},{{\varvec{\sigma }}}^{2(l)})\right] \ge 0 \end{aligned}$$

    in probability, for any given point \(x\in \mathscr {X}\), where \(\ell ^*(\cdot )\) is defined in (4).

2.3 Hypothesis testing

Huang et al. (2013) proposed a nonparametric mixture of regression models where mixing proportions, means, and variances are all unknown but smooth functions of a covariate. Compared to Huang et al. (2013), our model can be more efficient by assuming the mixing proportions and variances to be constants. Then, a natural question to ask is whether or not the mixing proportions and variances indeed depend on the covariate. This amounts to testing the following hypothesis:

$$\begin{aligned} H_0:&\pi _j(x)\equiv \pi _j,j=1,\ldots ,k-1;\\&\sigma ^2_j(x)\equiv \sigma ^2_j,j=1,\ldots ,k;\\&\pi _j \text { and } \sigma _j^2 \text { are unknown in } (0,1) \text { and } \mathbb {R}^+.\\ H_1:&\pi _j(x)\text { or }\sigma ^2_j(x) \text { is not constant for some } j. \end{aligned}$$

Next, we propose to use the idea of the generalized likelihood ratio test (Fan et al. 2001) to compare model (1) with model (2).

Let \(\ell _n(H_0)\) and \(\ell _n(H_1)\) be the log-likelihood functions computed under the null and alternative hypothesis, respectively. Then, we can construct a likelihood ratio test statistic

$$\begin{aligned} T=\ell _n(H_1)-\ell _n(H_0). \end{aligned}$$
(13)

Note that this likelihood ratio statistic is different from the parametric likelihood ratio statistics, since the null and alternative are both semiparametric models, and the number of parameters under \(H_0\) or \(H_1\) are undefined. The following theorem establishes the Wilks types of results for (13), that is, the asymptotic null distribution is independent of the nuisance parameters \({{\varvec{\pi }}}\) and \({{\varvec{\sigma }}}\), and the nuisance nonparametric mean functions \({{\varvec{m}}}(x)\).

Theorem 4

Suppose that conditions (C9)–(C13) in the Appendix hold and that \(nh^{4}\rightarrow 0\) and \(nh^2\log (1/h)\rightarrow \infty \), then

$$\begin{aligned} r_KT\overset{a}{\sim }\chi ^2_{\delta }, \end{aligned}$$

where \(r_K=[K(0)-0.5\int K^2(t)dt]/\int [K(t)-0.5K*K(t)]^2 dt\), \(\delta =r_K(2k-1)|\mathscr {X}|[K(0)-0.5\int K^2(t)dt]/h\), \(|\mathscr {X}|\) denotes the length of the support of X, and \(K*K\) is the 2nd convolution of \(K(\cdot )\).

Theorem 4 unveils a new Wilks type of phenomenon, and provides a simple and useful method for semiparametric inferences. We will demonstrate its application in Sect. 3.

3 Examples

3.1 Simulation study

In this section, we use a simulation study to investigate the finite sample performance of the proposed regression spline estimate (Spline), the one-step backfitting estimate using local EM-type algorithm (LEM), and the global EM-type algorithm (GEM), and compare them with the traditional mixture of linear regressionss estimate (MLR), and the nonparametric mixture of regression models (NMR, Huang et al. 2013). For the regression spline, we use \(Q=5\), where Q is the number of internal knots. For LEM, GEM and NMR, we use both the true value and the regression spline estimate as initial values, denoted by (T) and (S), respectively.

We conduct a simulation study for a two-component semiparametric mixture of regression models:

$$\begin{aligned}&\pi _1=0.5\, \text {or}\,\, \pi _1=0.7,\\&m_1(x)=4-\sin (2\pi x)\,\, \text {and}\,\, m_2(x)=1.5+\cos (3\pi x),\\&\sigma _1^2=0.09\,\,\text {and} \,\,\sigma _2^2=0.16. \end{aligned}$$

The covariate X is generated from the one-dimensional uniform distribution in [0, 1], and the Gaussian kernel is used in the simulation. The sample sizes \(n=200\) and \(n=400\) are conducted over 500 repetitions.

The performance of the estimates of the mean functions \({{\varvec{m}}}(x)\) is measured by the square root of the average squared errors (RASE),

$$\begin{aligned} \text {RASE}_m^2=N^{-1}\sum _{j=1}^2\sum _{t=1}^N\left[ \hat{m}_j(u_t)-m_j(u_t)\right] ^2, \end{aligned}$$

where \(\{u_t,t=1,\ldots ,N\}\) are a set of grid points at which the unknown functions are evaluated. In our simulation, we set \(N=100\). To compare between model (1) and the nonparametric mixture of regression models proposed by Huang et al. (2013), we also report the RASE of \(\pi \) and \(\sigma ^2\), denoted by RASE\(_\pi \) and RASE\(_{\sigma ^2}\), respectively.

Bandwidth plays an important role in the estimation of \({{\varvec{m}}}(\cdot )\). There are ways to calculate the theoretical optimal bandwidth, but in practice, data driven methods, such as cross-validation (CV), are popularly used. Please see Zhang and Yang (2015) and the reference therein for the application and properties of cross-validation. Let \(\mathscr {D}\) be the full data set, and divide \(\mathscr {D}\) into a training set \(\mathscr {R}_l\) and a test set \(\mathscr {T}_l\). That is, \(\mathscr {R}_l\cup \mathscr {T}_l=\mathscr {D}\) for \(l=1,...,L\). We use the training set \(\mathscr {R}_l\) to obtain the estimates \(\{\hat{{{\varvec{\pi }}}},\hat{{{\varvec{m}}}}(\cdot ),\hat{{{\varvec{\sigma }}}}^2\}\), then consider a likelihood version CV, which is defined by

$$\begin{aligned} \mathrm{CV}(h)=\sum _{l=1}^L\sum _{t\in \mathscr {T}_l}\log \left\{ \sum _{j=1}^k\hat{\pi }_j\phi (y_t|\hat{m}_j(x_t),\hat{\sigma }_j^2)\right\} . \end{aligned}$$

In the simulation, we set \(L=10\) and randomly partition the data. We repeat the procedure 30 times, and take the average of the selected bandwidths as the optimal bandwidth, denoted by \(\hat{h}\). In the simulation, we consider three different bandwidths, \(\hat{h}\times n^{-2/15}\), \(\hat{h}\), and \(1.5\hat{h}\), which correspond to under-smoothing (US), appropriate smoothing (AS), and over-smoothing (OS), respectively.

Tables 1 and 2 report the average of RASE\(_\pi \), RASE\(_m\), and RASE\(_{\sigma ^2}\), for \(\pi _1=0.5\) and \(\pi _1=0.7\), respectively. All the values are multiplied by 100. From Tables 1 and 2, we can see that LEM, GEM, and the regression spline estimates give better results than the mixture of linear regressions estimate. Compared to NMR, model (1) improves the efficiency of the estimation of mixing proportions and variances, and provides slightly better estimates for the mean functions. In addition, both LEM and GEM provide better results for the mean functions than the regression spline estimate when the sample size is small. We further notice that LEM(S) and GEM(S) provide similar results to LEM(T) and GEM(T). Therefore, the spline estimate provides good initial values for other estimates.

From Tables 1 and 2, LEM and GEM have similar performance in terms of model fitting. However, in terms of computation time, GEM has an absolute advantage over LEM. For example, on a personal laptop with an i7-3610QM CPU and 8GB of RAM, the average calculation time (in s) for each repetition when \(n=200\) is 0.072 and 0.017 for LEM and GEM, respectively, and 0.105 and 0.028 when \(n=400\).

Table 1 The average of RASE\(_{\pi }\), RASE\(_{\sigma ^2}\) & RASE\(_{m}\) when \(\pi _1=0.5\) (true values times 100)
Full size table
Table 2 The average of RASE\(_{\pi }\), RASE\(_{\sigma ^2}\) & RASE\(_{m}\) when \(\pi _1=0.7\) (true values times 100)
Full size table

Next, we test the accuracy of the standard error estimation and the confidence interval construction for \(\pi _1\), \(\sigma _1\) and \(\sigma _2\) via a conditional bootstrap procedure. Given the covariate \(X=x\), the response \(Y^*\) can be generated from the estimated distribution \(\sum _{j=1}^k\hat{\pi }_j\phi (Y|\hat{m}_j(x),\hat{\sigma }_j^2)\). For the simplicity of presentation, we only report the results for GEM(T). We apply the proposed estimation procedure to each of the 200 bootstrap samples, and further obtain the confidence intervals.

Table 3 reports the results from the bootstrap procedure. SD contains the standard deviation of 500 replicates, and can be considered as true standard errors. SE and STD contain the mean and standard deviation of the 500 estimated standard errors based on the conditional bootstrap procedure. In addition, the coverage probability of the 95% confidence intervals based on the estimated standard errors are also reported. From Table 3 we can see that the bootstrap procedure estimates the true standard error quite well, since all the differences between the true value and the estimates are less than two standard errors of the estimates. The coverage probabilities are satisfactory for \(\pi _1\), but a bit low for \(\sigma _1\) and \(\sigma _2\), especially for over-smoothing bandwidth.

Table 3 Standard errors and coverage probabilities
Full size table

We also apply the bootstrap procedure to investigate the point-wise coverage probability of the mean functions, at a set of evenly distributed grid points. Table 4 shows the results of the 95% confidence interval for the two-component mean functions. From the table, we can see that the mean function of the first component tends to have higher coverage probability than the second component, especially for over-smoothing bandwidth. In addition, the coverage probability is generally lower than the nominal level for over-smoothing bandwidth.

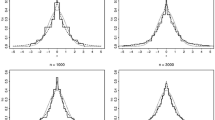
Table 4 Pointwise coverage probabilities
Full size table

Next, we assess the performance of the testing procedure proposed in Sect. 2.3. Under the null hypothesis, the mixing proportion \(\pi _1\) and variances \(\sigma ^2_1\) and \(\sigma ^2_2\) are constants. We compute the distribution of T with \(n=200\) and \(n=400\) via 500 repetitions, and compare it with the \(\chi ^2\)-approximation. The histogram of the null distribution is shown in Fig. 1, where the solid line corresponds to a density of the \(\chi ^2\)-distribution with degrees of freedom \(\delta \) defined in Theorem 4. Figure 2 shows the Q-Q plot for the two cases. From Figs. 1 and 2, the finite sample null distribution is quite close to a \(\chi ^2\)-distribution with degrees of freedom \(\delta \), especially for the case of \(n=400\).

Fig. 1
figure 1

Histogram of \(T_n\) and \(\chi ^2\)-approximation of \(T_n\): a \(n=200\), b \(n=400\)

Full size image
Fig. 2
figure 2

Q–Q plot: a \(n=200\), b \(n=400\)

Full size image

3.2 Real data applications

Example 1 (The US house price index data) In this section, we illustrate the proposed methodologies with an empirical analysis of US house price index data (sample size \(n=141\)) that are introduced in Sect. 1. GDP is a well known measure of the size of a nation’s economy, as it recognizes the total goods and services produced within a nation in a given period, and HPI is known as a measure of a nation’s average housing price in repeat sales. It is believed that the housing price and GDP are correlated, and so it is of interest to study how GDP growth rate helps to predict HPI change.

Fig. 3
figure 3

a Scatterplot of US house price index data; b estimated mean functions with 95% confidence intervals and a clustering result

Full size image

First, a two-component mixture of nonparametric regression models is fitted to the data. For real data sets, we use Monte-Carlo cross-validation (MCCV) (Shao 1993) to select the bandwidths. In MCCV, the data are randomly partitioned into disjoint training subsets with size \(n(1-p)\) and test subsets with size np, where p is the percentage of data used for testing. The procedure is repeated for 100 times, and we take the average as the selected bandwidth. For estimation and testing purpose, we use MCCV with \(p=10\%\), and the selected bandwidth is 0.030. Figure 3b contains the estimated mean functions and their 95% point-wise confidence intervals through the conditional bootstrap procedure, and the 95% confidence interval for \(\pi _1\), \(\sigma _1\) and \(\sigma _2\) are (0.347, 0.518), (0.009, 0.020) and (0.004, 0.008), respectively. Figure 3b also reports the hard-clustering results, denoted by dots and squares, respectively, for the two components. The hard-clustering results are obtained by maximizing classification probabilities \(\{p_{i1},p_{i2}\}\) for all \(i=1,\ldots ,n\). It can be checked that the dots in the lower cluster are mainly from Jan 1990 to Sep 1997, while the squares in the upper cluster are mainly from Oct 1997 to Dec 2002, when the economy experienced an internet boom and bust. In addition, it can be seen that in the first cycle of lower component, GDP growth has an overall positive impact on HPI change. However, in the second cycle of the upper component, GDP growth has a negative impact on HPI change, if GDP growth is smaller than 0.3; when GDP growth is larger than 0.3, it then has a similar positive impact on HPI change as the first cycle.

To examine whether the mixing proportions and variances are indeed constant, we apply the generalized likelihood ratio test developed in Sect. 2.3. The p-value is 0.331, and shows that model (1) is more appropriate for the data. To evaluate the prediction performance of the proposed model and compare it to the NMR model proposed by Huang et al. (2013), in Table 5, we use MCCV with repetition time 500 to report the average and standard deviation of the mean squared prediction error (MSPE) evaluated at the testing sets. It can be seen that the prediction performance of model (1) is slightly better than that of the NMR model (Huang et al. 2013).

Table 5 Average (standard deviation) of MSPE
Full size table
Fig. 4
figure 4

a Scatterplot of NO data; b estimated mean functions with 95% confidence intervals and a clustering result

Full size image

Example 2 (NO data) This data set gives the equivalence ratio, a measure of the richness of the air-ethanol mix in an engine against the concentration of nitrogen oxide emissions in a study using pure ethanol as a spark-ignition engine fuel. The data set contains 99 observations and is presented in Hurvich et al. (1998). Figure 4a shows the scatter plot of the data, which clearly indicates two different nitrous oxide concentration dependencies, with no clear linear trend. As a result, a two-component mixture of nonparametric regression models is fitted to the data.

Similar to the above example, the selected bandwidth is 0.091 based on MCCV with \(p=10\%\). The confidence intervals for parameter estimates are (0.395, 0.608), (0.005, 0.012), (0.025, 0.053) for \(\pi _1\), \(\sigma _1\) and \(\sigma _2\), respectively. Figure 4b contains the estimated mean functions and their 95% point-wise confidence intervals through the bootstrap procedure. The p-value of the generalized likelihood ratio test is 0.219, indicating that model (1) is the preferred model. Table 5 reports the average and standard deviation of MSPE evaluated at the testing sets based on MCCV. Based on Table 5, the new model has better prediction performance than the NMR model.

4 Discussion

Motivated by a US house index data, in this article, we proposed a new class of semiparametric mixture of regression models, where mixing proportions and variances are constants, but the component regression functions are smooth functions of a covariate. The identifiability of the proposed model is established and a one-step backfitting estimation procedure is proposed to achieve the optimal convergence rate for both the global parameters and the nonparametric regression functions. The proposed regression spline estimate is simple to calculate and can be easily extended to some other semiparametric and nonparametric mixture of regression models (Young and Hunter 2010; Huang et al. 2013; Huang and Yao 2012). But it requires more research to derive the asymptotic results for such regression spline based estimators for mixture models. A generalized likelihood ratio test has been proposed for semiparametric inferences.

When the dimension of the predictors is high, due to the curse of dimensionality, it is unpractical to estimate the component regression functions fully nonparametrically. Therefore, it is our interest to further extend the proposed mixture of nonparametric regression models to some other nonparametric or semiparametric models, such as mixture of partial linear regression models, mixture of additive models, and mixture of varying coefficient partial linear models.

In this paper, we assume that the number of components is known. However, in some applications, it might be infeasible to assume a known number of components in advance. Therefore, more research is needed to select the number of components for the proposed semiparametric mixture model. One possible way is to use AIC or BIC to choose the number of components. However, it is not clear how to define the degree of freedom for a semiparametric mixture model. Similar to Huang et al. (2013), one might also fit a mixture of linear regression using local data and choose the number of components based on traditional AIC or BIC. In addition, as one reviewer pointed out that when the number of components, k, is too large, the variance of model parameter estimates may be very large and the asymptotic results might not hold for the finite-sample setting. In this case, one might use a bootstrap procedure to estimate the standard errors of parameter estimates. Furthermore, it will be also interesting to investigate whether there are any minimax properties of the proposed estimation procedure.