Abstract
Multi-dimensional classification is a cutting-edge problem, in which the values of multiple class variables have to be simultaneously assigned to a given example. It is an extension of the well known multi-label subproblem, in which the class variables are all binary. In this article, we review and expand the set of performance evaluation measures suitable for assessing multi-dimensional classifiers. We focus on multi-dimensional Bayesian network classifiers, which directly cope with multi-dimensional classification and consider dependencies among class variables. A comprehensive survey of this state-of-the-art classification model is offered by covering aspects related to their learning and inference process complexities. We also describe algorithms for structural learning, provide real-world applications where they have been used, and compile a collection of related software.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
The multi-dimensional (supervised) classification problem refers to an extension of the traditional one-dimensional classification problem, in which one deals with multiple (usually related) class variables instead of a single one. Multi-dimensional classification can also be seen as a generalization of the better-known multi-label classification problem (Tsoumakas and Katakis 2007; Zhang and Zhou 2014), where all the class variables (called labels) are binary and can be present or absent for any example. Multi-label classification problems come about in numerous application domains, e.g., a person can simultaneously feel multiple emotions (a given emotion is felt, present, or not, absent), a film may belong to multiple genres, a drug may have multiple biological actions, a customer can be the target of multiple related products, music may be performed by multiple instruments (Gibaja and Ventura 2015). However, there are many others real-world problems that need to be approached with multi-dimensional classification, since the class variables may represent other non-binary information, such as:
-
the grade of presence of a label, e.g., a patient presents no problems, some problems or severe problems (Borchani et al. 2012);
-
the score on a discrete scale, e.g., a customer post is negative, neutral or positive (Ortigosa-Hernández et al. 2012); or
-
the type of a category set, e.g., the species of a neuron (Fernandez-Gonzalez et al. 2015).
Multi-dimensional classification is a more difficult problem than its one-dimensional and multi-label counterparts (Bielza et al. 2011). A large number of possible class configurations, \(\left| I\right|\), and a usual sparseness of available data are the main problems in this multi-dimensional context. In quantitative terms, for d class variables of K possible values eachFootnote 1, it holds that \(\left| I\right| = K^d\) in the multi-dimensional problem, compared to \(\left| I\right| =2^{d}\) in the multi-label case, and \(\left| I\right| =K\) in the one-dimensional scenario. Besides the problem of high cardinality, it is also hard to estimate the required parameters to model the joint probability distribution from a (sparse) data set in the d-dimensional space I (Bielza et al. 2011). In addition, multi-dimensional (and multi-label) classification usually involve dependencies between class variables (Read et al. 2013).
According to the popular taxonomy presented by Tsoumakas et al. (2009), there are two main strategies for solving multi-label classification problems: problem transformation methods and algorithm adaptation methods. We argue that this taxonomy can be also extrapolated to more general multi-dimensional classification problems. The former transform a multi-dimensional problem into one or more one-dimensional problems, whereas the latter extend a one-dimensional algorithm to directly handle multi-dimensional data (e.g., Zhang and Zhou 2007 proposed a multi-label extension of the traditional k-nearest neighbor algorithm). Binary relevance and label powerset (Boutell et al. 2004) are two simple, well known problem transformation methods that construct, respectively, one independent classifier per class variable and a single classifier with a compound class variable that models all possible joint configurations of the class variables. Binary relevance methods do not capture interactions among the class variables, and may not return the most likely configuration of class values, but return the most likely class value for each independent classifier. Label powerset methods can implicitly model interclass correlations, although the compound class variable these methods generate usually has too many values, with extremely few training examples for some of them. Moreover, these methods are unable to generalize to any compound class configurations that do not appear in the training set. Both methods have been extended to more sophisticated (but less interpretable) algorithms that overcame some of those limitations, such as chain classifiers (Read et al. 2011), which extended binary relevance, random k-labelsets (Tsoumakas and Vlahavas 2007) and (ensembles of) pruned sets (Read 2008), both of which adapted label powerset, among other algorithms.
Nowadays, interpretable machine learning is in high demand (Rudin 2019). Standard (one-class) Bayesian network classifiers (Friedman et al. 1997; Bielza and Larrañaga 2014) offer an explicit, graphical, and interpretable representation of uncertain knowledge supported by probability theory, and have shown competitive results in traditional classification problems. However, they cannot deal with multi-dimensional problems in a straightforward manner. On the one hand, they could be used (as base classifiers) together with any of the aforementioned problem transformation methods as this approach is algorithm-independent, but the interpretability of the model would be reduced. For example, they have been used together with chain classifiers (Zaragoza et al. 2011b; Sucar et al. 2014; Rivas et al. 2018). On the other hand, an algorithm adaptation method of standard Bayesian networks classifiers has been proposed to directly solve multi-dimensional classification problems. The so-called multi-dimensional Bayesian network classifier (MBC) (van der Gaag and de Waal 2006; Bielza et al. 2011): (1) allows reduction of the number of required parameters that multi-dimensional classification entails by means of a factorization of the joint probability distribution by exploiting conditional independences among variables, (2) takes into account the relationships between the class variables by joining all of them in the same classification task, and (3) offers an inherently interpretable model and many other advantages inherited from standard Bayesian network classifiers (Bielza and Larrañaga 2014).
MBCs have received increasing attention, and several contributions can be found in the literature, in which they have shown competitive results for multi-dimensional classification. This current article offers two main contributions: (1) a comprehensive survey on the family of MBCs including their learning, inference, applications and software, and (2) the extension of three multi-dimensional performance measures, to provide other complementary forms of evaluation of multi-dimensional classification problems.
The remainder of this article is organized as follows. In Sect. 2, formal definitions of the multi-dimensional classification problem and a description of the fundamentals of MBCs are provided. In Sect. 3, some aspects related to the complexity of MBCs in both model learning and inference problems are covered and extended. In Sect. 4, reviews of existing performance evaluation measures suitable for assessing multi-dimensional classifiers are given, along with a proposal for a new set of measures. In Sect. 5, the approaches proposed in the literature for structural learning are presented, while in Sect. 6 real-world applications where MBCs have been used are described, together with a collection of software for learning MBCs and benchmark data sets that are found in the literature to deal with the multi-dimensional problem. Finally, in Sect. 7 a discussion and future work are provided.
2 Fundamentals
2.1 Multi-dimensional classification
A one-dimensional supervised classification problem consists of finding a function \(h_1\) that assigns a single value c to each example given by a vector value \({\mathbf{x}} = (x_1, \ldots , x_m)\) of m feature variables:
We assume that C is a discrete class variable, where \(\Omega _{C}\) denotes its sample space. Analogously, \(\Omega _{X_i}\) is the sample space of the discrete feature variable \(X_i\) for all \(i \in \{1, \ldots , m\}\) (Bielza et al. 2011). These problems are classically binary, i.e., \(\left| \Omega _{C}\right| = 2\). When each example is assigned to a single value within a larger sample space, i.e., \(\left| \Omega _{C}\right| \ge 2\), the problem is called multi-class classification.
In a multi-dimensional classification problem one deals with multiple class variables \(C_1, \ldots , C_d\), such that a vector \({\mathbf{c}} = (c_1, \ldots , c_d)\) of d class values is assigned to each example by a function \(h_d\) (Bielza et al. 2011):
We assume that \(C_j\) is a discrete class variable, for all \(j \in \{1, \ldots , d\}\), where \(\Omega _{C_j}\) denotes its sample space and \(I = \Omega _{C_1} \times \cdots \times \Omega _{C_d}\) is the space of joint configurations of the class variables (Bielza et al. 2011). When all the class variables are binary, i.e., \(| \Omega _{C_j} | = 2\) for all \(j \in \{1, \ldots , d\}\), where each one represents a label that may be assigned or not to a given example, the problem is called multi-label classification (Zhang and Zhou 2014). The positive and negative values of these binary variables represent, respectively, what in the literature is said as \(\ll\)a label is relevant\(\gg\) or \(\ll\)irrelevant\(\gg\) for a given example. We hereby suggest not to use this terminology, as it may be confused with that in the feature subset selection context, in which a feature variable is said to be relevant or irrelevant with respect to a given class variable. Instead, the terms \(\ll\)the label is present\(\gg\) or \(\ll\)absent\(\gg\) will be used, respectively. Multi-label classification is actually a better-known problem, and considerable contributions can be found in the literature. For example, the two recent reviews by Zhang and Zhou (2014) and Gibaja and Ventura (2015) present the main aspects of the multi-label paradigm that have been developed during recent years.
With the aim of avoiding possible confusion, we would like to remark that multi-label classification is usually defined in the literature with other notation, as follows:
such that a labelset Y (i.e., a subset of labels) that comes from a set of d possible labels \(\lambda _1, \ldots , \lambda _d\) is assigned to each example. A (binary) class variable \(C_j\) is viewed as the presence/absence of a label \(\lambda _j\), for all \(j \in \{1, \ldots , d\}\). Nevertheless, this is simply another notation, and multi-label classification can still be reformulated from a multi-dimensional classification point of view as in Eq. (1).
Note that a binary classification problem is a particular setting of multi-class classification with \(\left| \Omega _{C}\right| = 2\), and multi-label classification with \(d=1\). Also, note that these two paradigms, multi-class and multi-label classification, give rise to the more general multi-dimensional classification problem (Fig. 1).
2.2 Multi-dimensional Bayesian network classifiers
A Bayesian network (Pearl 1988; Koller and Friedman 2009) over a set of discrete random variables \(\{Z_1, \ldots , Z_n\}\), \(n \ge 1\), is a pair \({\mathcal {B}} = (G, {\varvec{\Theta }})\). \(G = (V, A)\) is a directed acyclic graph (DAG) whose vertices V correspond to variables \(Z_i\) and whose arcs A represent direct probabilistic dependencies between the variables. \({\varvec{\Theta }}\) is a vector of parameters such that \(\theta _{z_i|{\mathbf{pa}} _G(z_i)}\) = \(p(z_i|{\mathbf{pa}} _G(z_i))\) defines the conditional probability of each possible value \(z_i\) of \(Z_i\) given a vector value \({\mathbf{pa}} _G(z_i)\) of the parents of \(Z_i\) in G. \({\mathcal {B}}\) represents the joint probability distribution \(p_{\mathcal {B}}\) over all random variables factorized according to its structure, G:
Bayesian network classifiers (Friedman et al. 1997; Bielza and Larrañaga 2014) are Bayesian networks of restricted topology tailored to solve one-dimensional classification problems. The finite set of vertices V of a Bayesian network classifier is partitioned into a set, \(V_X = \{X_1,\ldots ,X_m\}\), \(m \ge 1\), of feature variables, and a singleton set \(V_C = \{C\}\) that corresponds to the class variable (i.e., \(n = m + 1\)).
An MBC is a Bayesian network especially designed to solve multi-dimensional classification problems. The graph \(G = (V, A)\) of an MBC has a set V of vertices also partitioned into two sets \(V_C = \{C_1, \ldots , C_d\}\), \(d \ge 1\), of class variables, and \(V_X = \{X_1, \ldots , X_m\}\), \(m \ge 1\), of feature variables (i.e., \(n = m + d\)). Note that Bayesian network classifiers are a particular setting (\(d=1\)) of MBCs (Bielza et al. 2011). The graph has also a restricted topology in which the set of arcs A is partitioned into three sets: \(A_C\), \(A_X\) and \(A_{CX}\). The first time MBCs were proposed by van der Gaag and de Waal (2006), the three sets of arcs were defined as:
-
1.
The set \(A_C \subseteq V_C \times V_C\) is composed of the arcs between the class variables, that form a subgraph \(G_C = (V_C, A_C)\), called the class subgraph, of G induced by \(V_C\);
-
2.
The set \(A_X \subseteq V_X \times V_X\) is composed of the arcs between the feature variables, that form a subgraph \(G_X = (V_X, A_X)\), called the feature subgraph, of G induced by \(V_X\);
-
3.
The set \(A_{CX} \subseteq V_C \times V_X\) is composed of the arcs from the class variables to the feature variables, that form a subgraph \(G_{CX} = (V, A_{CX})\), called the feature selection subgraph, of G induced by V, such that for each \(X_i \in V_X\), there is a \(C_j \in V_C\) with the arc \((C_j, X_i) \in A_{CX}\) and for each \(C_j \in V_C\), there is an \(X_i \in V_X\) with the arc \((C_j, X_i) \in A_{CX}\).
MBCs were later extended by Bielza et al. (2011) such that the two conditions of the set of arcs \(A_{CX}\) were removed, and the resulting subgraph was renamed using another term:
-
3.
The set \(A_{CX} \subseteq V_C \times V_X\) is composed of the arcs from the class variables to the feature variables, that form a subgraph \(G_{CX} = (V, A_{CX})\), called the bridge subgraph, of G induced by V.
This last definition has been more widely adopted in the literature. Figure 2 shows an example of an MBC structure and its three subgraphs. Note that the initial definition of van der Gaag and de Waal (2006) does not recognize this structure as an MBC because for \(X_4 \in V_X\), there is no \(C_j \in V_C\) with \((C_j, X_4) \in A_{CX}\). The extension of Bielza et al. (2011) can be seen as a more general definition.
This introduction subsection to MBCs has been mostly reproduced from the subsection with same name of Gil-Begue et al. (2018).
2.3 Families of MBCs
As van der Gaag and de Waal (2006) detailed, different families of MBCs can be distinguished if one looks at their graphical structures. Later, Bielza et al. (2011) proposed a complete conventional notation based on the fact that, in general, class and feature subgraphs may be empty, trees, forests of trees, polytrees, and general DAGs. Thus, the different families of MBCs in these two subgraphs are named as {class subgraph structure}-{feature subgraph structure} MBC, which can possess any of the five, aforementioned structures. As an example, if both the class and feature subgraphs of an MBC are trees, then it belongs to the tree-tree MBCs family. Other examples of MBC families are shown in Fig. 3.
Bielza et al. (2011) stated that well known Bayesian network classifiers such that naïve Bayes (Minsky 1961), selective naïve Bayes (Langley and Sage 1994), tree-augmented naïve Bayes (Friedman et al. 1997), selective tree-augmented naïve Bayes (Blanco et al. 2005) and k-dependence Bayesian classifiers (Sahami 1996) are special cases of MBCs where \(d = 1\). Some of them have been extended to the multi-dimensional context: multi-dimensional naïve Bayes and tree-augmented naïve Bayes (van der Gaag and de Waal 2006) and multi-dimensional k-dependence Bayesian classifiers (Rodríguez and Lozano 2008).
2.4 CB-decomposable MBCs
Bielza et al. (2011) defined class-bridge decomposable MBCs (CB-MBCs for short) such that:
-
1.
\(G_C \cup G_{CX}\) can be decomposed as \(G_C \cup G_{CX} = \bigcup _{i=1}^{r} (G_{C_{comp_i}} \cup G_{({CX})_{comp_i}})\), \(r \in \{2, \ldots , d\}\), where \(G_{C_{comp_i}} \cup G_{({CX})_{comp_i}}\), with \(i \in \{1, \ldots , r\}\), are its r maximal connected componentsFootnote 2.
-
2.
\({\mathbf{Ch}} (V_{C_{comp_i}}) \cap {\mathbf{Ch}} (V_{C_{comp_j}}) = \emptyset\), with \(i, j \in \{1, \ldots , r\}\) and \(i \ne j\), where \({\mathbf{Ch}} (V_{C_{comp_i}})\) denotes the children of all the variables in \(V_{C_{comp_i}}\), i.e., the subset of class variables in \(G_{C_{comp_i}}\) (non-shared children property).
An example of a CB-MBC structure is found in Fig. 4a, which has \(r=3\) maximal connected components as shown in Fig. 4b. The subgraph to the left of the first dashed vertical line is \(G_{C_{{{comp}}_1}} \cup G_{({CX})_{{{comp}}_1}}\), i.e., the first maximal connected component, such that \(V_{C_{{{comp}}_1}} = \{C_1, C_2\}\) and \({\mathbf{Ch}} (V_{C_{{{comp}}_1}}) = \{X_1, X_2\}\). Analogously, the subgraph between the dashed lines is the second maximal connected component \(G_{C_{{{comp}}_2}} \cup G_{({CX})_{{{comp}}_2}}\), with \(V_{C_{{{comp}}_2}} = \{C_3\}\) and \({\mathbf{Ch}} (V_{C_{{{comp}}_2}}) = \{X_3, X_4\}\). Finally, the subgraph to the right-hand side is the third maximal connected component \(G_{C_{{{comp}}_3}} \cup G_{({CX})_{{{comp}}_3}}\), such that \(V_{C_{{{comp}}_3}} = \{C_4, C_5\}\) and \({\mathbf{Ch}} (V_{C_{{{comp}}_3}}) = \{X_5, X_6\}\). It holds that \({\mathbf{Ch}} (\{C_1, C_2\}) \cap {\mathbf{Ch}} (\{C_3\}) = \emptyset\), \({\mathbf{Ch}} (\{C_1, C_2\}) \cap {\mathbf{Ch}} (\{C_4, C_5\}) = \emptyset\) and \({\mathbf{Ch}} (\{C_3\}) \cap {\mathbf{Ch}} (\{C_4, C_5\}) = \emptyset\) as required. Note that the class subgraph of a CB-decomposable MBC is always a forest structure, but not all MBCs with a forest class subgraph structure are CB-decomposable (i.e., the MBC shown in Fig. 3c is not a CB-MBC as \({\mathbf{Ch}} (\{C_1, C_2\}) \cap {\mathbf{Ch}} (\{C_3, C_4\}) = \{X_3\} \ne \emptyset\)).
We will see later that an inference process over a CB-MBC can be computed independently in each maximal connected component with the implied computational savings.
3 Complexity in MBCs
3.1 Learning problem: the cardinality of an MBC structure space
Bielza et al. (2011) stated that knowledge about the cardinality of an MBC structure space can help us infer the complexity of the learning problem, as many algorithms for learning MBCs from data move within this space (see Sect. 5). Thus, they calculated the number of all possible MBC structures, and highlighted two cases. The first is the general MBC defined by Bielza et al. (2011), while the other is the initial definition of an MBC by van der Gaag and de Waal (2006), which places two constraints on the MBC bridge subgraph: (a) for each \(X_i \in V_X\), there is a \(C_j \in V_C\) with the arc \((C_j, X_i) \in A_{CX}\), and (b) for each \(C_j \in V_C\), there is an \(X_i \in V_X\) with the arc \((C_j, X_i) \in A_{CX}\).
-
1.
The number of all possible MBC structures with d class variables and m feature variables, \({\small MBC}(d,m)\), is (Bielza et al. 2011, Theorem 6):
$$\begin{aligned} MBC(d,m) = S(d) \cdot 2^{dm} \cdot S(m), \end{aligned}$$where
$$\begin{aligned} S(n) = \sum _{i=1}^{n} (-1)^{i+1} \left( {\begin{array}{c}n\\ i\end{array}}\right) 2^{i(n-i)}S(n-i) \end{aligned}$$is Robinson’s formula (Robinson 1973) that counts the number of possible DAG structures of n nodes, which is initialized as \(S(0) = S(1) = 1\). Therefore, S(d) and S(m) count the possible number of DAG structures in the class subgraph and feature subgraph, respectively. \(2^{dm}\) is the number of possible bridge subgraphs.
-
2.
The number of all possible MBC structures with d class variables and m feature variables, \(m \ge d\), that satisfy conditions (a) and (b), MBC\(^{{\mathrm{ab}}}(d,m)\), is (Bielza et al. 2011, Theorems 7, 8):
$$\begin{aligned} {MBC}^{{\mathrm{ab}}}(d,m) = S(d) \cdot BRS(d,m) \cdot S(m), \end{aligned}$$where \({\small BRS}(d,m)\) counts the number of all possible bridge subgraphs of the MBCs that satisfy the two previous conditions:
$$\begin{aligned} BRS(d,m) = \sum _{k=m}^{dm} BRS(d,m,k), \end{aligned}$$which is in turn calculated from all bridge subgraphs with k arcs, \({\small BRS}(d,m,k)\), with \(k \ge m\) so that there is no feature variable with no connection and \(k \le dm\) is the maximum possible number of arcs in a bridge subgraph:
$$\begin{aligned} BRS(d,m,k) = \left( {\begin{array}{c}dm\\ k\end{array}}\right) - \sum _{\begin{array}{c} x \le d,\ y \le m\\ k \le xy \le dm-d \end{array}} \left( {\begin{array}{c}d\\ x\end{array}}\right) \left( {\begin{array}{c}m\\ y\end{array}}\right) BRS(x,y,k). \end{aligned}$$Any invalid subgraph that does not satisfy the two required conditions is subtracted from all possible bridge subgraphs with k arcs, \(\binom{dm}{k}\), knowing that \(k{=}dm{-}d{+}1\) is the minimum number of arcs required for a bridge subgraph to be always valid. The recursion is initialized as \({\small BRS}(1,1,1) = {\small BRS}(1,2,2) = {\small BRS}(2,1,2) = 1\).
Bielza et al. (2011) showed that:
Thus, it holds that \({\small BRS}(d,m) < 2^{dm}\), for all \(d \ge 1\) and \(m \ge 1\), because the bridge subgraphs that do not satisfy the two required conditions are subtracted from the number of all possible bridge subgraphs, i.e., \(2^{dm}\). Therefore, it holds that \({\small MBC}^{{\mathrm{ab}}}(d,m)<\) \({\small MBC}(d,m)\), for all \(d {\ge } 1\) and \(m {\ge } 1\). Knowing that the complexity of Robison’s formula (Robinson 1973) was shown to be super-exponential, i.e., \(O(S(n)) = n^{2^{O(n)}}\), then the complexity of the MBC structure space is (Bielza et al. 2011, Corollary 4):
In this work, we extend the existing knowledge about the cardinality of the MBC structure space by computing the number of all possible CB-MBC structures with d class variables, m feature variables and r maximal connected components that satisfy both constraints, (a) and (b), on the MBC bridge subgraph, CB-MBC\(^{{\mathrm{ab}}}(d,m,r)\), which thus require \(r \le \min \{d,m\}\):
This recursive formula computes for the first maximal connected component all possible combinations that include x class variables, \(\binom{d}{x}\), and y feature variables, \(\binom{m}{y}\), up to a maximum of \(d{-}r{+}1\) and \(m{-}r{+}1\), respectively, so that the following components have also at least one class and feature variable in order to satisfy conditions (a) and (b). Next, all possible non-decomposable structures, i.e., those with just one maximal connected component, are computed for each previous combination of variables. The recursion continues for each combination with the count of structures having \(r{-}1\) components over the remaining \(d{-}x\) class variables and \(m{-}y\) feature variables, and ends with the count of structures for the last maximal connected component. For this, a single component must be forced to be non-decomposable:
which is achieved by subtracting all structures with multiple components from all possible MBC structures. Division by r! is required of all computed structures in order to remove all identical structures because of having to account for the order of the components (note that Eq. (2) only shows a division by r because the factorial is automatically done through the recursion).
Table 1 and Fig. 5 offer a better visualization of this super-exponential complexity by computing the cardinality of the MBC structure space for different numbers of variables and maximal connected components. It is clearly observed that a huge growth in the number of structures occurs when more variables are added to the classification problem, which makes evident the need for learning algorithms that search efficiently within this structure space. We can also observe that the MBC definition of Bielza et al. (2011) is more general and accepts a greater number of valid structures compared to the definition of van der Gaag and de Waal (2006), although this does not make much difference and both remain in the same order of magnitude. The number of all possible DAG structures of a standard Bayesian network over all variables, \(S(d{+}m)\), is larger by a few more orders of magnitude, which is explained by the restriction of arcs from the feature variables to the class variables. Finally, the dimension of the CB-MBC structure space is several orders of magnitude smaller than the general MBC structure space, and it can be further reduced for more maximal connected components.
Number of DAG and MBC structures for different numbers of variables (i.e., n) in a classification problem. The shadowed area is plotted for MBCs instead of a single line because different cardinalities are obtained for different numbers of m feature and d class variables (\(n=m+d\), with \(m\ge 1, d\ge 1\)). The largest structure space is obtained for \(d=1\) or \(m=1\), and the smallest for \(d={\lfloor }{\tfrac{n}{2}}{\rfloor }\) or \(d={\lceil }{\tfrac{n}{2}}{\rceil }\). \({CB \text{-} MBC}^{{\mathrm{ab}}}(d,m)\) is the number of structures with multiple maximal connected components, i.e., \(\sum _{r=2}^{\min \{d,m\}} {CB \text{-} MBC}^{{\mathrm{ab}}}(d,m,r)\)
3.2 Inference problem: The tractability of multi-dimensional classification in MBCs
In this section, we review the existing literature about the complexity of the inference process in MBCs. Multi-dimensional classification needs a loss function \(\lambda ({\mathbf{c '}},{\mathbf{c}} )\) for each pair of vectors \({\mathbf{c '}},{\mathbf{c}} \in I\) that represents the cost of classifying an example as \({\mathbf{c '}}\) when its true value is \({\mathbf{c}}\). Two loss functions have been studied in the literature. The first is the standard 0-1 loss function that assigns a unit loss to any error, i.e., whenever \({\mathbf{c '}} \ne {\mathbf{c}}\), and no loss to a correct classification, i.e., when \({\mathbf{c '}} = {\mathbf{c}}\) (Bielza et al. 2011). The second is the additive CB-decomposable loss function that fits CB-MBC structures.
3.2.1 0-1 loss functions
Let
be the expected loss or conditional risk of classifying a vector of feature values \({\mathbf{x}}\) as the class configuration \({\mathbf{c}} '\). Then, under a 0-1 loss function, the Bayes decision rule that minimizes the expected loss \(R({\mathbf{c '}} | {\mathbf{x}} )\) is equivalent to selecting the class configuration \({\mathbf{c}} _g\) that maximizes the posterior probability \(p({\mathbf{c}} _g | {\mathbf{x}} )\) (Bielza et al. 2011, Theorem 1):
In this way, performing multi-dimensional classification with a 0-1 loss function and assuming that all the feature variables are observed is equivalent to computing the most probable explanation (MPE) of the class variables (Bielza et al. 2011). This problem is a type of maximum a posteriori, i.e., a more general concept where there is no need to observe all the feature variables.
It has been shown that computing the MPE in Bayesian networks is an NP-hard problem (Shimony 1994), likewise approximating it with a constant ratio bound (Abdelbar and Hedetniemi 1998). As Bielza et al. (2011) summarized, algorithms that solve this problem in an exact way include approaches that use junction trees (Dawid 1992; Dechter 1999), variable elimination (Li and D’Ambrosio 1993) and branch-and-bound searches (Kask and Dechter 2001; Marinescu and Dechter 2009). Approximate algorithms cover the use of genetic algorithms (Gelsema 1995; Rojas-Guzman and Kramer 1993), stochastic local search algorithms (Kask and Dechter 1999; Hutter et al. 2005), variable elimination (Dechter and Rish 1997), best-first searches (Shimony and Charniak 1990) and linear programming (Santos 1991).
In order to obtain the MPE, it is necessary to compute the posterior probabilities of all the class configurations in I. Bielza et al. (2011) followed a special ordering when enumerating this I space, which was motivated by the similarity between the posterior probability of two class configurations that have the same class values in all variables but one. For this, the authors proposed an extension of the Gray code adaptation presented by Guan (1998), such that it allows enumerating joint configurations of class variables with different numbers of possible values, where each pair of adjacent configurations differs in a single variable with a difference of just 1 or – 1. The authors showed in their Theorem 2 the savings and an upper bound when comparing the number of factors needed in the posterior probability computations with Gray codes and with standard brute-force.
The same authors exploited the special structure of CB-MBCs and showed in their Theorem 3 that the maximization problem of obtaining the MPE can be decomposed into r-independent maximization problems over smaller spaces, i.e., over each space of joint configurations \(I_j\) of the class variables belonging to the j-th maximal connected component:
where
Bielza et al. (2011) showed that it holds:
The same idea of enumerating all class configurations with an extension of the Gray code was applied in Bielza et al. (2011, Theorem 4) on each maximal connected component of a CB-MBC, which leads to even greater gains in the number of factors needed to calculate the posterior probabilities of all the class configurations in the computation of the MPE.
The remainder of this subsection was reviewed by Benjumeda et al. (2018). Although the problem of obtaining the MPE in a Bayesian network \({\mathcal {B}}\) is usually NP-hard, it can be computed in polynomial time in \({\mathcal {B}}\) if the treewidth, treewidth(G), of its structure G is bounded (Sy 1992). The treewidth of a directed graph is the width of its moralized graph, i.e., the undirected graph that results from connecting the parents of each variable and subsequently eliminating the directions of the arcs (Fig. 6b). Given MBC structural constraints, de Waal and van der Gaag (2007) showed in their Theorem 1 that the MPE can be computed in polynomial time if the treewidth of its feature subgraph \(G_X\) and the number of class variables d are restricted as:
which implies that the connectivity of the class subgraph is not relevant for the tractability of the classification (Bielza et al. 2011). Kwisthout (2011) applied the same idea to CB-MBC structures:
where \(\left| d_{max} \right|\) is the number of class variables of the component with the maximum number of class variables. Thus, multi-dimensional classification over a CB-MBC can be performed in polynomial time if the treewidth of its feature subgraph \(G_X\) and the number of class variables of each component are bounded.
Pastink and van der Gaag (2015) found further bounds on MBCs with an empty feature subgraph:
where \(G_{\bar{F}}\) is the structure of an MBC with an empty feature subgraph and \(G'\) is its pruned graph, i.e., the undirected graph that results from moralizing the structure of an MBC and then removing all the feature variables (Fig. 6c).
Finally, Benjumeda et al. (2018) extended this bound to more general DAG-DAG MBCs motivated by the dependence between a query on a Bayesian network and its inference complexity, as the parameters of the network can be updated with the values of the evidence variables before performing the inference. In this way, the authors showed in their Theorem 1 that an MBC can compute MPEs in polynomial time if the treewidth of its pruned graph and the number of parents of each evidence variable, i.e., of each feature variable in \(V_X\), are bounded.
Although the computational cost of calculating the treewidth of a pruned graph is less than calculating the treewidth of a complete structure, it is still an NP-complete problem (Arnborg et al. 1987). Since
Benjumeda et al. (2018) concluded that an MPE can be computed in polynomial time if the number of class variables d and the number of parents of each feature variable are bounded. The same reasoning was extrapolated to CB-MBCs, such that the number of class variables of each component should be restricted in order to perform multi-dimensional classification in polynomial time.
3.2.2 Additive CB-decomposable loss functions
Bielza et al. (2011) defined the additive CB-decomposable loss functions according to a CB-MBC such that:
where \(\lambda _j\) is a non-negative loss function defined on \(I_j\). The authors used the Hamming distance as an example of the behaviour of these loss functions.
In their Theorem 5, the authors showed that obtaining the class configuration \({\mathbf{c}} '\) that minimizes the expected loss can be decomposed, in a similar way as in Eq. (3), into r-independent minimization problems over smaller spaces, i.e., over each space of joint configurations \(I_j\) of the class variables that belong to the j-th maximal connected component:
where
This sum, which is to be minimized, is the expected loss over the maximal connected component \(\textit{comp}_{j}\) (Bielza et al. 2011).
4 Performance evaluation measures for multi-dimensional classifiers
The evaluation of models in a multi-dimensional context should take into account the simultaneous performance of all class variables. Several performance evaluation measures have been extended to the particular multi-label setting, but only few extensions to the more general multi-dimensional classification problem can be found in the literature. In this work, we also contribute to the extension of some multi-label performance evaluation measures to the multi-dimensional paradigm.
It is well known that all the following measures should be estimated in an honest way, i.e., without testing those examples that have already been used for training a classifier. A special issue arises when using a stratified approach in this multi-dimensional classification scenario, both with holdout and cross-validation methods. In a one-dimensional problem, there is only one class variable to guarantee the same distribution of its values over the data subsets; but here, there are multiple conflicting class variables to assure their stratified distribution. Sechidis et al. (2011) proposed two different stratification perspectives for multi-label data with the goal of maintaining in each sampled data subset the proportion of (1) examples of each joint class configuration and (2) positive valued examples of each binary class variable. For this second perspective, an iterative algorithm was proposed that greedily distributed the examples of the class variable with the fewest remaining examples with a positive value. One can easily think that the first perspective implies the second one; but if we look closely, this does not happen for data sets with large ratios of distinct class configurations to the number of examples (which may happen with a small sample of examples or a large number of class variables), as most class configurations will just have one example. Therefore, the authors surmised that these two stratification methods were better suited, respectively, for (1) small and (2) large ratio scenarios, while both were consistently better than the typical random sampling found in the literature. Further research is hence necessary in the multi-dimensional context.
4.1 Multi-label measures
The most frequently used performance measures for multi-label classification were summarized by Gibaja and Ventura (2015), and compiled here in the column named Multi-label measures in Table 2 following an adaptation of the taxonomy proposed by Tsoumakas et al. (2009), which differentiated between measures to evaluate non-probabilistic classifications (we also add measures for probabilistic classifications) and measures to evaluate rankings. Performance measures that have a multi-dimensional extension are described below, but for some measures we argue that they cannot be extended to the multi-dimensional scenario.
4.1.1 Measures to evaluate classifications
This set of measures compares the predictions made by a classification model with the corresponding true class values. In the multi-label literature, they may be referred to as measures to evaluate the bipartitions of labels into ‘present’ and ‘absent’ for a given example. Measures to evaluate classifications can be categorized into two groups: example-based (also known as instance-based) and label-based (Tsoumakas et al. 2009). “The former are calculated for each test example and then averaged across the test set, while the latter are calculated for each label and then they are averaged across all labels” (Gibaja and Ventura 2015).
-
EXAMPLE-BASED. The 0/1 subset accuracy (Zhu et al. 2005), also called the classification accuracy or exact match ratio, computes the fraction of correctly classified examples, i.e., those whose predicted label set is exactly the same as their corresponding set of true labels. This measure can be seen as an extension of the traditional accuracy to the multi-label problem. It is a very strict evaluation measure, especially when the size of the label space, \(2^d\), is large. Completely incorrect and partially correct predictions are both considered as classification errors.
The Hamming loss (Schapire and Singer 1999) evaluates the fraction of misclassified example–label pairs. This measure considers both prediction errors (i.e., absent labels are predicted), and omission errors (i.e., present labels are missed).
Finally, the set of measures adopted from the information retrieval (IR) area proposed by Godbole and Sarawagi (2004) are also commonly used. However, we argue that these measures are specific to the multi-label paradigm and cannot be extended to the (more general) multi-dimensional problem, since the recovery performance of these labels is measured by their presence or absence. In contrast, a class variable in a multi-dimensional domain will be always present, with either one value or another. The only possible extension would be if each class variable had a not present semantic value in relation to the negative value of a binary class variable or absence of a label. In such a case, the operation of this set of measures on a multi-dimensional problem would be the same as in a multi-label context.
-
LABEL-BASED. Given a confusion matrix, a measure B is computed based on the number of true positives, tp, false positives, fp, true negatives, tn, and false negatives, fn. Commonly, B is the accuracy \(= \frac{tp+tn}{tp+fp+tn+fn}\), precision \(= \frac{tp}{tp+fp}\), recall \(= \frac{tp}{tp+fn}\) or \(F_{\beta } = (1{+}\beta )\frac{{{precision}} \cdot {{recall}}}{\beta \cdot {{precision}} + {{recall}}}\). Note that they are different from those measures with the same name in the IR area. A \(2{\times }2\)-dimensional confusion matrix is obtained for each label, so an average value extended over all labels has to be computed, which can be done in two possible ways: macro and micro.
-
The macro approach computes one measure \(B_j\) for each label and then the values are averaged:
$$\begin{aligned} B_{{macro}} = \frac{1}{d} \sum _{j=1}^{d} B_j = \frac{1}{d} \sum _{j=1}^{d} B\left( tp_j, fp_j, tn_j, fn_j \right) . \end{aligned}$$(7) -
The micro approach aggregates the counters of the confusion matrices of all labels, and then calculates the average measure with the aggregated confusion matrix:
$$\begin{aligned} B_{{micro}} = B\left( \sum _{j=1}^{d} tp_j, \sum _{j=1}^{d} fp_j, \sum _{j=1}^{d} tn_j, \sum _{j=1}^{d} fn_j \right) . \end{aligned}$$(8)
-
In this multi-label domain, it holds that \(accuracy_{macro} = accuracy_{micro} = 1 - \textit{Hamming loss}\).
Gibaja and Ventura (2015) stated that “these two types of averaging are informative and there is no general agreement about using a macro or micro approach”. An equal weight is given by macro-averaged scores to each label, regardless of its frequency (i.e., per-label averaging). This leads to a stronger influence of rare label performance. However, micro-averaged scores give equal weights to each example (i.e., per-example averaging) and tend to be dominated by the performance of the most frequent labels (Yang 1999; Yang and Liu 1999).
4.1.2 Measures to evaluate probabilistic classifications
The aforementioned measures evaluate model performance by only considering the final classification. Probabilistic models such as Bayesian classifiers give us more information, i.e., the estimated a posteriori probability (joint and marginals) of each class value, in addition to the classification itself, which can be derived as the class configuration that maximizes the estimated joint probability under a standard 0-1 loss function. Other classifiers, such as random k-labelsets (Tsoumakas and Vlahavas 2007), also provide a marginal confidence score to each label after its voting scheme. With the aim of generalization, we denote both the probability and these scoring functions with the letter p for the remainder of this section.
Zhang and Zhou (2014) extended the traditional area under the ROC curve (AUC) measure to the multi-label setting in the two averaging ways, i.e., macro and micro.
-
The macro approach computes one measure \(AUC_j\) for each label and then the values are averaged:
$$\begin{aligned} AUC_{{macro}} = \frac{1}{d} \sum _{j=1}^{d} AUC_j = \frac{1}{d} \sum _{j=1}^{d} \frac{| \{ ({\mathbf{x}} , \overline{{\mathbf{x }}})\ |\ p(C_j = c_j | {\mathbf{x}} ) \ge p(C_j = c_j | \overline{{\mathbf{x }}}), {\mathbf{x}} \in D_j, \overline{{\mathbf{x }}} \in \overline{D}_j \} |}{| D_j | | \overline{D}_j |}, \end{aligned}$$(9)where \(D_j = \{ {\mathbf{x}} _i\ |\ c_{ij} = c_j, i \in \{ 1, \ldots , N\} \}\) and \(\overline{D}_j = \{ {\mathbf{x}} _i\ |\ c_{ij} = \overline{c}_j, i \in \{ 1, \ldots , N\} \}\) correspond, respectively, to the data subsets of the test examples with and without the j-th label from a test set of N examples, i.e., the true value of the binary class variable \(C_j\) for the example i, \(c_{ij}\), is positive (present), \(c_j\), and negative (absent), \(\overline{c}_j\).
-
The micro approach considers the probabilistic predictions from all example–label pairs together:
$$\begin{aligned} AUC_{{micro}} = \frac{| \{ ({\mathbf{x}} , \overline{{\mathbf{x }}}, j, k)\ | \ p(C_j = c_j | {\mathbf{x}} ) \ge p(C_k = c_k | \overline{{\mathbf{x }}}), ({\mathbf{x}} , j) \in D, (\overline{{\mathbf{x }}}, k) \in \overline{D} \} |}{| D | | \overline{D} |}, \end{aligned}$$(10)where \(D = \{ ({\mathbf{x}} _i, j)\ |\ c_{ij} = c_j, i \in \{ 1, \ldots , N\} \}\) and \(\overline{D} = \{ ({\mathbf{x}} _i, k)\ |\ c_{ik} = \overline{c}_k, i \in \{ 1, \ldots , N\} \}\), for all \(j, k \in \{ 1, \ldots , d \}\), correspond to the data subsets of the present and absent example–label pairs, respectively.
All the above multi-label measures lie between 0 and 1. For all of them but the Hamming loss, the larger the measure value, the better the performance.
4.1.3 Measures to evaluate rankings
There are multi-label classification models, like the pairwise methods proposed by Hüllermeier et al. (2008) and Fürnkranz et al. (2008), which output a ranking of presence among all the possible labels for a given example. Several measures have been proposed in the multi-label context (see Table 2) that compare the predicted ranking of presence with the corresponding set of true labels. We argue again that this set of measures is specific to the multi-label paradigm and has no extension to the multi-dimensional problem, since ranking the values of all class variables altogether makes no sense. The multi-label meaning of presence or absence of the labels is no longer used. Instead, a ranking among all the multi-dimensional class configurations could be derived, as proposed in Sect. 4.3.
4.2 Multi-dimensional measures found in the literature
4.2.1 Measures to evaluate classifications
The following performance measures proposed by Bielza et al. (2011) extend the two aforementioned multi-label measures.
-
The global or joint accuracy of a d-dimensional class variable extends the multi-label 0/1 subset accuracy by computing the fraction of correctly classified examples, i.e., those whose every predicted class value is exactly the same as its corresponding true value. Again, it is a very strict evaluation measure, especially when the size of the class space, \(\left| I\right|\), is large. Let \({\mathbf{c}} '_i\) be the d-dimensional binary prediction for the example i, \({\mathbf{c}} _i\) its corresponding true value, and \(\delta\) the Kronecker’s delta function, such that \(\delta ({\mathbf{c}} '_i,{\mathbf{c}} _i)=1\) if \({\mathbf{c}} '_i = {\mathbf{c}} _i\), and \(\delta ({\mathbf{c}} '_i,{\mathbf{c}} _i)=0\) if \({\mathbf{c}} '_i \ne {\mathbf{c}} _i\). Then, the global accuracy is defined as:
$$\begin{aligned} Acc = \frac{1}{N} \sum _{i=1}^{N} \delta \left( {\mathbf{c}} '_{i}, {\mathbf{c}} _{i}\right) . \end{aligned}$$(11) -
The mean or average accuracy over the d class variables evaluates the fraction of correctly classified example–class pairs. Let \(c'_{ij}\) be the \(C_j\) class value predicted by the model for the example i in the test data set, \(c_{ij}\) its corresponding true value, \(\delta (c'_{ij},c_{ij})=1\) if \(c'_{ij} = c_{ij}\), and \(\delta (c'_{ij},c_{ij})=0\) if \(c'_{ij} \ne c_{ij}\). Then, the mean accuracy is:
$$\begin{aligned} \overline{Acc}_d = \frac{1}{d} \sum _{j=1}^{d} Acc_j = \frac{1}{d} \sum _{j=1}^{d} \frac{1}{N} \sum _{i=1}^{N} \delta \left( c'_{ij}, c_{ij}\right) . \end{aligned}$$(12)This measure is the complementary to the multi-label Hamming loss measure, i.e., the mean accuracy \(+\) Hamming loss \(=\) 1, but is extended to the multi-dimensional classification problem.
-
Bielza et al. (2011) also extended a similar concept to CB-decomposable MBCs by means of the mean accuracy over the r maximal connected components:
$$\begin{aligned} \overline{Acc}_r = \frac{1}{r} \sum _{j=1}^{r} \frac{1}{N} \sum _{i=1}^{N} \delta \left( {\mathbf{c}} _{i}^{\prime \downarrow V_{C_j}}, {\mathbf{c}} _{i}^{\downarrow V_{C_j}}\right) , \end{aligned}$$(13)where \({\mathbf{c}} _{i}^{\downarrow V_{C_j}}\) represents the projection of vector \({\mathbf{c}} _i\) to the coordinates found in \(V_{C_j}\).
It holds that \(Acc \le \overline{Acc}_r \le \overline{Acc}_d\), since counting correct predictions in a vector of components as a whole is stricter than in a component-wise fashion (Bielza et al. 2011).
This subsection has been mostly reproduced from Gil-Begue et al. (2018).
4.2.2 Measures to evaluate probabilistic classifications
As for the classification measures, the set of probabilistic measures can be categorized into the same two groups: example- and label-based.
-
EXAMPLE-BASED. The Brier score (Brier 1950) measures the calibration of probabilistic models by taking into account the estimated a posteriori probabilities, such that the classifiers that are almost sure when making correct predictions will have lower (better) Brier measures. In a one-dimensional problem where a single class variable C is classified as one of \(\left| \Omega _C \right|\) possible values, \(c_k\) is the k-th class value, \(c_i\) the true value for example i with feature values \({\mathbf{x}} _i\) in the test data set, and the rest of the symbols are defined as before; the corresponding Brier score takes the form:
$$\begin{aligned} Bs = \frac{1}{N} \sum _{i=1}^{N} \sum _{k=1}^{\left| \Omega _C \right| } \left( p\left( C=c_k | {\mathbf{x}} _i\right) - \delta \left( c_k, c_i\right) \right) ^2. \end{aligned}$$(14)The Brier score was generalized by Fernandes et al. (2013) to the multi-dimensional problem (including the one-dimensional and multi-label problems) in the three variants outlined below.
-
Global or joint Brier score:
$$\begin{aligned} Bs = \frac{1}{N} \sum _{i=1}^{N} \sum _{g=1}^{\left| I \right| } \left( p\left( {\mathbf{C}} ={\mathbf{c}} _g | {\mathbf{x}} _i\right) - \delta \left( {\mathbf{c}} _g, {\mathbf{c}} _i\right) \right) ^2, \end{aligned}$$(15)where \({\mathbf{C}} =(C_1, \ldots , C_d)\) is the d-dimensional class variable, \({\mathbf{c}} _g\) is the g-th configuration of I and \({\mathbf{c}} _i\) is the true value of \({\mathbf{C}}\) for \({\mathbf{x}} _i\).
-
Mean or average Brier score:
$$\begin{aligned} \overline{Bs}_d = \frac{1}{d} \sum _{j=1}^{d} Bs_j = \frac{1}{d} \sum _{j=1}^{d} \frac{1}{N} \sum _{i=1}^{N} \sum _{k=1}^{| \Omega _{C_j} |} \left( p\left( C_j=c_{jk} | {\mathbf{x}} _i\right) - \delta \left( c_{jk}, c_{ij}\right) \right) ^2, \end{aligned}$$(16)where \(c_{jk}\) is the k-th class value of the j-th class variable, \(C_j\), and \(c_{ij}\) is the true value of \(C_j\) for \({\mathbf{x}} _i\).
Both Brier score generalizations are in the range [0, 2], as for the one-dimensional version. In the same way, the lower the score, the more calibrated the model, such that a score of zero is obtained when the model predicts the true value with total certainty for all class variables and examples in the test data set. A score of two occurs when the model predicts a class configuration that differs from the true values of all the class variables with total certainty and for all examples in the test data set.
Although both measures consider the estimated probability assigned to each class, the global Brier score rewards only the estimated probability of the class configuration that matches exactly with the true value, and the mean Brier score rewards the class variables separately. For this reason, a third measure was proposed to reward the number of classes correctly classified for each configuration of \({\mathbf{C}}\), such that the score is lower when higher probabilities are assigned to configurations closer to the true value.
-
-
-
Multi-dimensional calibrated Brier scoreFootnote 3:
$$\begin{aligned} CBs = \frac{1}{N d} \sum _{i=1}^{N} \sum _{g=1}^{\left| I \right| } p\left( {\mathbf{C}} ={\mathbf{c}} _g | {\mathbf{x}} _i\right) \sum _{j=1}^{d} 1- \delta \left( c_{gj},c_{ij}\right) , \end{aligned}$$(17)where \(c_{gj}\) is the \(C_j\) class value of the g-th configuration, \({\mathbf{c}} _g\).
-
-
LABEL-BASED. Although no formal definitions were given, Benjumeda et al. (2018) proposed a combination of the multi-class AUC measure defined by Provost and Domingos (2000) with the aforementioned multi-label macro and micro averages (Eqs. (9) and (10), respectively) presented by Zhang and Zhou (2014) in order to extend the AUC measure to the multi-dimensional classification context.
-
The macro approach:
$$\begin{aligned} AUC_{{macro}} = \frac{1}{d} \sum _{j=1}^{d} AUC_j, \end{aligned}$$(18)where
$$\begin{aligned} AUC_j = \left\{ \begin{array}{ll} \sum _{k=1}^{| \Omega _{C_j} |} p(C_j = c_{jk}) \frac{| \{ ({\mathbf{x}} , \overline{{\mathbf{x }}})\ |\ p(C_j = c_{jk} | {\mathbf{x}} ) \ge p(C_j = c_{jk} | \overline{{\mathbf{x }}}), {\mathbf{x}} \in D_{jk}, \overline{{\mathbf{x }}} \in \overline{D}_{jk} \} |}{| D_{jk} | | \overline{D}_{jk} |}, &{} \text {if } | \Omega _{C_j} | > 2 \\ \frac{| \{ ({\mathbf{x}} , \overline{{\mathbf{x }}})\ |\ p(C_j = c_j | {\mathbf{x}} ) \ge p(C_j = c_j | \overline{{\mathbf{x }}}), {\mathbf{x}} \in D_j, \overline{{\mathbf{x }}} \in \overline{D}_j \} |}{| D_j | | \overline{D}_j |}, &{} \text {if } | \Omega _{C_j} | = 2 \end{array}\right. \end{aligned}$$\(D_{jk} = \{ {\mathbf{x}} _i\ |\ c_{ij} = c_{jk}, i \in \{ 1, \ldots , N\} \}\) and \(\overline{D}_{jk} = \{ {\mathbf{x}} _i\ |\ c_{ij} \ne c_{jk}, i \in \{ 1, \ldots , N\} \}\) correspond to the data subsets of test examples whose j-th class variable, \(C_j\), takes its k-th class value, \(c_{jk}\), and a different value of its k-th class value, respectively.
-
The micro approach, when at least one class variable \(C_j\) is not binary, i.e., \(|\Omega _{C_j}| > 2\), is:
$$\begin{aligned} AUC_{{micro}}= & {} \sum _{g=1}^{\left| I_{>2} \right| } p({\mathbf{C}} = {\mathbf{c}} _g) \nonumber \\&\qquad \frac{| \{ ({\mathbf{x}} , \overline{{\mathbf{x }}}, j, k)\ | \ p(C_j = c_{gj} | {\mathbf{x}} ) \ge p(C_k = c_{gk} | \overline{{\mathbf{x }}}), ({\mathbf{x}} , j) \in D_g, (\overline{{\mathbf{x }}}, k) \in \overline{D}_g \} |}{| D_g | | \overline{D}_g |}, \end{aligned}$$(19)where
 is the space of joint configurations of the non-binary class variables, and \(D_g = \{ ({\mathbf{x}} _i, j)\ |\ c_{ij} = c_{gj}, i \in \{ 1, \ldots , N\} \}\) and \(\overline{D}_g = \{ ({\mathbf{x}} _i, k)\ |\ c_{ik} \ne c_{gk}, i \in \{ 1, \ldots , N\} \}\), for all \(j,k \in \{1,\ldots ,d\}\), correspond to the data subsets of example–class pairs with the same (positive values of binary class variables as well) and different (negative values of binary class variables as well) class values as a given class configuration \({\mathbf{c}} _g \in I_{>2}\), respectively. For a binary class variable \(C_j\), we make \(c_{gj} = c_j\), i.e., its positive class value. When all class variables are binary, Eq. (10) should be used.
is the space of joint configurations of the non-binary class variables, and \(D_g = \{ ({\mathbf{x}} _i, j)\ |\ c_{ij} = c_{gj}, i \in \{ 1, \ldots , N\} \}\) and \(\overline{D}_g = \{ ({\mathbf{x}} _i, k)\ |\ c_{ik} \ne c_{gk}, i \in \{ 1, \ldots , N\} \}\), for all \(j,k \in \{1,\ldots ,d\}\), correspond to the data subsets of example–class pairs with the same (positive values of binary class variables as well) and different (negative values of binary class variables as well) class values as a given class configuration \({\mathbf{c}} _g \in I_{>2}\), respectively. For a binary class variable \(C_j\), we make \(c_{gj} = c_j\), i.e., its positive class value. When all class variables are binary, Eq. (10) should be used.
-
4.3 Multi-dimensional measures extended in this work
From the previous section and when compared to those measures of the multi-label setting, we can observe that the set of multi-dimensional measures found in the literature is very limited. In this section, we make three contributions to the performance evaluation measures for models that solve multi-dimensional classification problems. In this way, a better understanding and from different perspectives (i.e., classification, probabilistic and ranking) can be derived from the performance of a given multi-dimensional classifier.
-
1)
The first one follows the same idea as in Eq. (13), but applied to the Brier score of Eq. (16). Let
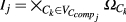 be the space of joint configurations of the class variables that belong to the j-th maximal connected component, \({{comp}}_j\), and \({\mathbf{c}} _{jg}\) the g-th configuration of \(I_j\). Then, the Brier score over the r maximal connected components is defined as:$$\begin{aligned} \overline{Bs}_r = \frac{1}{r} \sum _{j=1}^{r} \frac{1}{N} \sum _{i=1}^{N} \sum _{g=1}^{\left| I_j\right| } \left( p\left( {\mathbf{C}} ^{\downarrow V_{C_{{{comp}}_j}}}={\mathbf{c}} _{jg} | {\mathbf{x}} _i\right) - \delta \left( {\mathbf{c}} _{jg}, {\mathbf{c}} _{i}^{\downarrow V_{C_{{{comp}}_j}}}\right) \right) ^2. \end{aligned}$$(20)
be the space of joint configurations of the class variables that belong to the j-th maximal connected component, \({{comp}}_j\), and \({\mathbf{c}} _{jg}\) the g-th configuration of \(I_j\). Then, the Brier score over the r maximal connected components is defined as:$$\begin{aligned} \overline{Bs}_r = \frac{1}{r} \sum _{j=1}^{r} \frac{1}{N} \sum _{i=1}^{N} \sum _{g=1}^{\left| I_j\right| } \left( p\left( {\mathbf{C}} ^{\downarrow V_{C_{{{comp}}_j}}}={\mathbf{c}} _{jg} | {\mathbf{x}} _i\right) - \delta \left( {\mathbf{c}} _{jg}, {\mathbf{c}} _{i}^{\downarrow V_{C_{{{comp}}_j}}}\right) \right) ^2. \end{aligned}$$(20)This measure also lies in the range [0, 2] and, in contrast to the accuracy measures, it may not hold that \(Bs \ge \overline{Bs}_r \ge \overline{Bs}_d\) (note that the inequality relations are reversed because, unlike the accuracy measures, the lower the Brier score, the better the performance).
-
2)
The second contribution extends the label-based measures that evaluate classifications in the multi-dimensional paradigm. Following the same idea, a \(| \Omega _{C_j} | {\times } | \Omega _{C_j} |\)-dimensional confusion matrix is obtained for each class variable \(C_j\), and an average value is computed in two possible ways.
-
The macro approach computes one measure for each class variable value, and then all the outputs are averaged. If a class variable \(C_j\) is binary, i.e., \(| \Omega _{C_j} | = 2\), only a measure for one of the two classes is computed in order to avoid redundancy (the true positives of a class will be the true negatives of the other one, and the same happens with the false positives and false negatives). Let \(tp_{jk}\) be the true positives of the k-th value of the j-th class variable, \(C_j\), and analogously for the rest of the counters, then:
$$\begin{aligned} B_{{macro}} = \frac{1}{d} \sum _{j=1}^{d} B_j, \quad \text {where } B_j= \left\{ \begin{array}{ll} \frac{1}{| \Omega _{C_j} |} \sum _{k=1}^{| \Omega _{C_j} |} B\left( tp_{jk}, fp_{jk}, tn_{jk}, fn_{jk} \right) , &{} \text {if } | \Omega _{C_j} | > 2 \\ B\left( tp_{j}, fp_{j}, tn_{j}, fn_{j} \right) , &{} \text {if } | \Omega _{C_j} | = 2\\ \end{array}\right. \end{aligned}$$(21) -
The micro approach follows the idea of aggregating the counters of all the confusion matrices. However, a normalization is performed within each class variable so that variables with many possible values do not have more influence on the final output. Again, the aforementioned redundancy is avoided. Thus:
$$\begin{aligned} B_{{micro}} = B\left( \sum _{j=1}^{d} TP_j, \sum _{j=1}^{d} FP_j, \sum _{j=1}^{d} TN_j, \sum _{j=1}^{d} FN_j\right) , \end{aligned}$$(22)where
$$\begin{aligned} \{TP_j, FP_j, TN_j, FN_j\}= \left\{ \begin{array}{ll} \frac{1}{| \Omega _{C_j} |} \sum _{k=1}^{| \Omega _{C_j} |} \{tp_{jk}, fp_{jk}, tn_{jk}, fn_{jk}\}, &{} \text {if } | \Omega _{C_j} | > 2 \\ \{tp_j, fp_j, tn_j, fn_j\}, &{} \text {if } | \Omega _{C_j} | = 2 \end{array}\right. \end{aligned}$$
In this multi-dimensional scenario, it also holds that the \(accuracy_{macro} = accuracy_{micro}\), but in this case it is not equal to the mean accuracy. In addition, the same remarks made in the multi-label domain by Yang (1999) and Yang and Liu (1999) can be also extrapolated to this multi-dimensional paradigm, such that macro-averaged scores will lead to a stronger influence of rare class value performances, whereas micro-averaged scores tend to be dominated by the performance of the most frequent class values.
For all the above multi-dimensional measures except the Brier score generalizations, the larger the measure value, the better the performance, where the optimal value is 1.
-
-
3)
The third contribution offers a different approach to the multi-label measures to evaluate rankings. Here, we do not rank the grade of presence among the different labels, but instead the grade of confidence among the class values \(c_{jk}\) of the same class variable \(C_j\) (or among the joint class values \({\mathbf{c}} _g\) of a vector of class variables \({\mathbf{C}}\)). We denote their rank in a given example \({\mathbf{x}} _i\) based on the descending order induced from the probability or any other scoring function p as \({{rank}}_p\left( C_j = c_{jk} | {\mathbf{x}} _i\right)\) and \({{rank}}_p\left( {\mathbf{C}} = {\mathbf{c}} _g | {\mathbf{x}} _i\right)\), respectively. A rank of 1 means the most confident (joint) class value. Then, we define the following measures:
-
The global or joint posterior rank confidence over the d-dimensional class variable:
$$\begin{aligned} Prc = \frac{1}{N} \sum _{i=1}^{N} \frac{{{rank}}_p\left( {\mathbf{C}} = {\mathbf{c}} _{i} | {\mathbf{x}} _i\right) - 1}{\left| I\right| - 1}. \end{aligned}$$(23) -
The mean or average posterior rank confidence over the d class variables:
$$\begin{aligned} \overline{Prc}_d = \frac{1}{d} \sum _{j=1}^{d} \frac{1}{N} \sum _{i=1}^{N} \frac{{{rank}}_p\left( C_j = c_{ij} | {\mathbf{x}} _i\right) - 1}{|\Omega _{C_j}| - 1}. \end{aligned}$$(24) -
The mean or average posterior rank confidence over the r maximal connected components:
$$\begin{aligned} \overline{Prc}_r = \frac{1}{r} \sum _{j=1}^{r} \frac{1}{N} \sum _{i=1}^{N} \frac{{{rank}}_p\left( {\mathbf{C}} ^{\downarrow V_{C_{{{comp}}_j}}} = {\mathbf{c}} _{i}^{\downarrow V_{C_{{{comp}}_j}}} | {\mathbf{x}} _i\right) - 1}{\left| I_j\right| - 1}. \end{aligned}$$(25)
These three measures lie between 0 and 1, such that the lower they are, the better the performance. They measure the average percentile of the true (joint) class values in the confidence ranking. For example, a global posterior rank confidence that takes a value of 0 means that the true value always corresponds to the most confident joint class value for all examples. Conversely, a value of 1 implies the least confident one. Again, it may not hold that \(Prc \ge \overline{Prc}_r \ge \overline{Prc}_d\).
Note that \(\overline{Prc}_d = \textit{Hamming loss}\) becomes true in a multi-label setting, and \(\overline{Prc}_d \le 1 - \overline{Acc}_d\) in a more general multi-dimensional scenario, when classification is derived as the class value that maximizes the probability, or other scoring function, of each (binary) class variable separately. Similarly, it holds that \(Prc \le 1 - Acc\) when classification is derived as the class configuration that maximizes the estimated joint probability under a standard 0-1 loss function.
-
5 Learning MBCs from data
Several methods have been proposed in the literature to learn MBC structure from a given data set (Table 3). However, none of them have addressed the problem of estimating model parameters, as it is done in standard Bayesian networks (e.g., maximum likelihood or Bayesian estimation of parameters).
There are two main approaches to learn a Bayesian network structure from data (Koller and Friedman 2009, Chapter 18): score-based (also known as score and search methods), which try to find the structure that maximizes a given score (e.g., the likelihood of the data given the structure itself), and constraint-based methods, which try to find a structure that represents all the conditional independencies between triplets of variables.
5.1 Score-based algorithms
5.1.1 MBCs with simple class subgraph structures
The first approach found in the literature for learning MBCs from data was proposed by van der Gaag and de Waal (2006). The authors focused on efficiently learning tree-tree MBC structures such that the class and feature subgraphs can be learned in an optimal and independent way given a bridge subgraph, both in polynomial time, by using a score-and-search learning strategy based on the minimum description length score (Rissanen 1978). The maximum weighted undirected spanning tree (Kruskal 1956) is initially searched to construct the class subgraph, where the weight of an edge that connects two class variables is the mutual information shared between them, and then it is transformed into a directed tree by selecting an arbitrary root node (Chow and Liu 1968). Similarly and for a fixed bridge subgraph, the maximum weighted directed spanning tree (Chu and Liu 1965) is built for the feature subgraph, where the weight of an arc from a feature variable to another is the conditional mutual information between them given the parents (classes) of the second feature. Any initial bridge subgraph may be chosen, but the authors stated that two popular approaches are to start with a fully empty or a complete bridge subgraph. The global algorithm results in a hybrid approach (of filter and wrapper strategies), as the bridge subgraph is greedily changed by a wrapper strategy that tries to improve the global accuracy.
The same authors theoretically extended this study to the optimal recovery of polytree-polytree MBC structures (de Waal and van der Gaag 2007). The class and feature polytrees are separately learned by following the algorithm proposed by Rebane and Pearl (1987), which adds a directionality decision step over the undirected tree that is learned with the aforementioned method of Chow and Liu (1968). However, no information about the learning process of the bridge subgraph is given.
Zaragoza et al. (2011a) presented a hybrid score-based algorithm that consists of a first filter phase that very quickly learns the initial structure with the strongest dependencies, which is then refined in a second wrapper phase with greater computational intensity. During the first phase, the previous method of de Waal and van der Gaag (2007) is adopted such that polytree structures are independently learned for both class and feature subgraphs. Then, the arcs from the class to the feature variables with greater mutual information than a fixed threshold are included in the bridge subgraph. The second phase iteratively includes all arcs of the bridge subgraph that achieve an accuracy improvement.
5.1.2 MBCs with more complex class subgraph structures
Rodríguez and Lozano (2008) proposed a novel algorithm for learning MBCs with kDB structures in both class and feature subgraphs (a special case of DAG-DAG MBCs). The authors used an evolutionary algorithm, where an individual corresponds to an MBC structure coded as a binary vector in relation to the presence/absence of each possible arc. In particular, a multi-objective approach is used by means of the NSGA-II algorithm (Deb et al. 2002), such that the objective functions are the individual accuracies \(Acc_j\) (Eq. (12)) of each class variable \(C_j\). The proposed algorithm returns the Pareto set of efficient structures and their individual accuracies over all the class variables; hence, it is necessary to choose the one that best suits the particular problem.
Bielza et al. (2011) proposed three different methods for learning general DAG-DAG MBCs:
-
1.
A pure wrapper algorithm that greedily tries to add or delete an arc in any position whenever the global accuracy, or any other performance measure, is improved, provided that the MBC constraints are respected. The algorithm stops when no improvement can be obtained with the addition or deletion of any arc to the current structure.
-
2.
A pure filter algorithm that solves the learning problem as two separate problems, analogously to the method proposed by van der Gaag and de Waal (2006), by first searching the best structure for the class subgraph, and then learning the feature subgraph constrained by fixed class parents given in a candidate bridge subgraph. This method assumes an ancestral order among the variables when learning both subgraphs in order to reduce the computation time. The authors used the K2 algorithm of Cooper and Herskovits (1992) as an example to take into account the given order, and also to allow the learning of more general DAG structures. The bridge subgraph is learned by using a best-first search algorithm. A single arc is added at each iteration, which allows the computational burden to be reduced when using a decomposable score by only carrying out local computations over the terms involving the new arc.
-
3.
A hybrid algorithm like the previous one, but the learning of the bridge subgraph is guided by the global accuracy, or any other performance measure, rather than by a filter strategy.
In the work of Hernández-González et al. (2015), a method for learning MBCs from a crowd of non-expert annotators was proposed. Their method estimates a set of reliability weights that determine the degree of expertise of each annotator, and consequently the contribution of their annotated labels to the learning process. First, the weights are initialized as the grade of agreement of each annotator with the others (consensus), and an initial MBC structure is learned in a similar greedy way as the pure wrapper algorithm proposed by Bielza et al. (2011), but using the K2 score. Then, the parameters of the MBC and the reliability weights are iteratively updated until convergence is attained, based on the EM algorithm (Dempster et al. 1977). For this, the weights of each annotator are updated based on their accuracy performance with respect to the current fitted MBC. An external structural learning loop is added based on the structural EM algorithm (Friedman 1997), such that once the parameter learning of the current structure has converged, the inclusion/deletion of the arc that most improves the K2 score is chosen.
5.1.3 Meta-classifiers
An ensemble-based model of MBCs was proposed by Antonucci et al. (2013). In particular, there are as many tree-empty MBCs in the ensemble as class variables (i.e., d). Each individual classifier adopts a different class variable as the root of its tree feature subgraph structure, such that it is the unique parent of all the other class variables (i.e., a superparent node), and no more arcs are present. In this way, all class and feature subgraphs of the ensemble are fixed and only the bridge subgraphs must be learned. In fact, the authors showed that all models of the ensemble have the same bridge subgraph given these structural constraints, which can be computed by maximizing the Bayesian Dirichlet equivalent uniform (BDEu) score (Buntine 1991) on each feature variable independently. The joint distributions encoded by each \({ \hbox {MBC}}_j\) of the ensemble are combined via a geometric average for the multi-dimensional classification task:
The multi-dimensional meta-classifier proposed by Gil-Begue et al. (2018) places general MBCs in the leaf nodes of a classification tree. An internal node of the so-called MBCTree is a feature variable, and it has as many children nodes as the possible values of the associated feature. New examples are classified with the corresponding MBC leaf in relation to the values of the feature variables that make up the internal nodes. The authors also proposed an algorithm for learning MBCTrees from data in a wrapper-like way by greedily choosing internal nodes from top to bottom of the tree as the feature variables that best split the data (i.e., that maximize the global accuracy), until splitting no longer achieves a sufficient accuracy improvement when compared to an MBC learned with all the data reaching the current node. In such a case, this MBC is placed as a leaf node. The wrapper strategy of Bielza et al. (2011) is used for learning general DAG-DAG MBCs.
Arias et al. (2016) presented a meta-classifier for multi-dimensional classification, although its relationship with MBCs is frail and we do not include it in Table 3. In the first stage, a base classifier is learned for each pair of class variables (encoding their joint distribution, in contrast to base classifiers of the multi-label pairwise methods proposed by Hüllermeier et al. (2008) and Fürnkranz et al. (2008) which encode the preference between them). Concretely, the authors used naïve Bayes classifiers to this end. In the second stage, inference is performed in a pairwise Markov random field induced by the outputs of the base classifiers. The authors state that this final classifier plays the role of the class subgraph in the MBC, and the feature and bridge subgraphs are captured by the base classifiers.
5.2 Constraint-based algorithms
Borchani et al. (2012) were motivated by the fact that the classification performance of a class variable is only affected by parts of the structure that lie inside its Markov blanket (MB), i.e., its parents, children and spouses (the parents of its children) in the graph structure. Therefore, the authors extended the HITON algorithm (Aliferis et al. 2010a, b) to a multi-dimensional context to first determine the MB around each class variable, and then easily deduce the subgraphs of the MBC. Unlike the aforementioned methods, this approach is scalable with respect to the data set dimensionality (Borchani et al. 2012), since the MB of each class variable can be learned separately. The proposed algorithm was later extended by Borchani et al. (2016) to deal with the potential concept drifts of multi-dimensional data streams (see more details in Sect. ).
A method that uses independence tests, rather than mutual information, to search for strong dependencies between variables was proposed by Ortigosa-Hernández et al. (2012), as they realized that mutual information is not normalized for different cardinalities of the variables. Knowing that \(2N\cdot MI(Z_i, Z_j)\) asymptotically follows a \(\chi ^2\) distribution with \((|\Omega _{Z_i}|-1)(|\Omega _{Z_j}|-1)\) degrees of freedom if the variables \(Z_i\) and \(Z_j\) are independent (Kullback 1997), where \(MI(Z_i, Z_j)\) is the mutual information between both variables, the proposed method evaluates the independence between each pair of class variables and each pair of a class and a feature variable in order to build the class and bridge subgraphs, respectively. Any arc with a strong enough dependence is iteratively added to the structure as long as the topology of the MBC is respected, such that the arc inclusion follows a special order based on the p-value result of the independence tests. The same idea is used to learn the feature subgraph by knowing that \(2N\cdot MI(Z_i, Z_j | {\mathbf{Z}} )\) asymptotically follows a \(\chi ^2\) distribution with \((|\Omega _{Z_i}|-1)(|\Omega _{Z_j}|-1)\left| {\mathbf{Z}} \right|\) degrees of freedom if the variables \(Z_i\) and \(Z_j\) are conditionally independent given the set of variables \({\mathbf{Z}}\) (Kullback 1997), where \(MI(Z_i, Z_j | {\mathbf{Z}} )\) is the conditional mutual information between the variables \(Z_i\) and \(Z_j\) given the set of variables \({\mathbf{Z}}\). Additionally, the authors extended the learning of MBCs to a semi-supervised framework with an adaptation of the EM algorithm that performs a search in the joint space of structures and parameters, in a similar way to the Bayesian structural EM algorithm proposed by Friedman (1998).
Zhu et al. (2016) suggested that an independence test only affirms whether the variables are (in)dependent, rather than quantifying their degree of dependence. Therefore, the authors defined a dependence coefficient between any two variables \(Z_i\) and \(Z_j\) as:
where \(\chi _{\alpha ,l}\) is the critical value of a \(\chi ^2\) distribution with \(l=(|\Omega _{Z_i}|-1)(|\Omega _{Z_j}|-1)|\Omega _{Z_k}|\) degrees of freedom at the significance level \(\alpha\). If \(c_{ij\alpha } > 0\), then the two variables \(Z_i\) and \(Z_j\) present a statistically significant dependence regardless of the variable \(Z_k\) involved. If \(c_{ij\alpha } < 0\), then this dependence does not appear for at least one way of conditioning a variable \(Z_k\). In this way, the authors proposed a learning algorithm that combines both constraint-based, by using these dependence factors, and score-based strategies, with the goal of maximizing the scoring function
in a feasible set of structures that maintain the restricted topology of an MBC, where \(a_{ij} = 1\) if there is an arc between the variables \(Z_i\) and \(Z_j\), and 0 otherwise. Further restrictions are added to the maximization problem in order to obtain MBCs with kDB structures in both the class and feature subgraphs. We argue that they could be simply removed to learn more general DAG-DAG MBCs.
5.3 Feature subset selection algorithms
The next algorithms do not perform any structural learning process, but instead they conduct feature subset selection. Simply, class and feature subgraphs are empty structures, and a bridge subgraph connects each class variable with all selected feature variables. Note that performing classification over an MBC with an empty class subgraph does not imply the independent classification of each class variable, as they may have other class variables as part of their MB (i.e., in the form of spouses, since multiple class variables may share the same feature variable). Only CB-MBCs with \(r=d\) maximal connected components assume complete independence between the class variables.
Zhang et al. (2009) incorporated a two-stage feature selection strategy in a multi-label setting. In the first stage, feature-extraction techniques based on a principal component analysis (PCA) are employed. In the second stage, subset-selection techniques based on a genetic algorithm (on the space of PCAs) are used to choose the most appropriate subset of features for classification. In particular, the performance of each feature subset (i.e., the fitness function of the genetic algorithm) is evaluated with the arithmetic mean of the Hamming loss and the ranking loss measures. Individuals in the population are coded as binary vectors in relation to the selection/rejection of each feature variable. The proposed multi-label empty-empty MBC allows one to work with continuous feature variables by assuming Gaussianity, such that the density of any feature variable given the class values follows a Gaussian density.
Fernandes et al. (2013) developed a correlation-based feature subset selection method (Hall 2000) in order to obtain the relevant subset of feature variables for classification, and then build a bridge subgraph of an empty-empty MBC. The one-dimensional version of this method scores each feature subset, rewarding the correlation of each feature variable in the subset with the class variable, and penalizing the correlation between pairs of feature variables in the subset. The authors extended this selection method to the multi-dimensional scenario in tree approaches, such that the relevant feature subset for multi-dimensional classification may be:
-
1.
The union of the highest-scoring feature subsets of each class variable separately;
-
2.
The highest-scoring feature subset of the compound class variable that models all possible joint configurations of the class variables;
-
3.
The highest-scoring feature subset of a modified scoring function, such that it rewards the correlation of each feature variable in the subset with each class variable.
The non-parametric Kolmogorov-Smirnov test was used by Qazi et al. (2007) to rank feature variables according to their relevance with each class variable. Unlike the two previous methods that connected each class variable with all the selected feature variables, this approach builds a bridge subgraph by connecting each class variable with its particular top-ranked feature variables. In addition, a DAG structure is learned for the class subgraph, although no further information about the learning process is given.
5.4 Algorithms that address the problem of inference complexity
In contrast to all the aforementioned methods, only a few have been proposed in the literature that consider the inference complexity of an MBC during its learning process (Benjumeda et al. 2018).
5.4.1 Algorithms that do not provide theoretical guarantees on the tractability of the learned MBCs
Corani et al. (2014) extended their previous method (Antonucci et al. 2013) to learn a single forest-empty MBC, also guided by the BDEu score. Despite this arc sparsity in the learned model, the treewidth of the structure may be large enough, which is only bounded by the number of class variables (Eq. (4)). Note that the same happens with the empty-empty MBCs defined in the previous section, since their bridge subgraphs are completely connected.
Borchani et al. (2010) proposed the first method for learning CB-MBCs, based on a wrapper strategy. First, a selective naïve Bayes (Langley and Sage 1994) is learned for each class variable, and all shared children between them are eliminated afterwards. In this way, a first bridge subgraph with as many maximal connected components as class variables is obtained. Second, the feature subgraph is learned by iteratively adding all arcs that achieve an accuracy improvement. This phase can take advantage of the decomposable aspect of the CB-MBC, since the addition of an arc to certain feature variable will only change the local accuracy of the component it belongs to. Finally, the components are iteratively merged in a third phase by adding any arc between class variables that belongs to different components that achieve the highest accuracy improvements, until there is no arc whose inclusion improves the accuracy or there are no more components to merge. After each iteration, the bridge and feature subgraphs of the merged component are updated by the iterative addition of arcs that also improve the accuracy. Fernandez-Gonzalez et al. (2015) adapted this algorithm to handle feature variables with a continuous nature following a Gaussian distribution, so that there is no need to discretize the data.
5.4.2 Algorithms that provide theoretical guarantees on the tractability of the learned MBCs
Although the aforementioned learning algorithms address the problem of inference complexity, neither provides guarantees regarding the tractability of multi-dimensional classification in the learned models (Benjumeda et al. 2018). Pastink and van der Gaag (2015) proposed a method that allows one to perform classification in polynomial time because it searches for a forest-empty MBC that does not exceed a fixed treewidth. First, a forest structure is learned for the class subgraph, which does not change anymore in the learning process. Second, the bridge subgraph is built in a filter way based on the BDEu score, and which follows a branch-and-bound approach in order to not exceed the fixed treewidth. For this, the treewidth of each new candidate structure is computed, and those that exceed the fixed value are rejected. The treewidth is calculated on the pruned graph to reduce the computation time (Eq. (5)). Optionally, in a third phase it is possible to obtain a forest feature subgraph structure by adding arcs that improve the BDEu score but do not exceed the treewidth of the structure.
Finally, Benjumeda et al. (2018) learned more general DAG-DAG MBCs with an adaptation of the order-based search (Bouckaert 1992), such that only those orderings in which the class variables precede the feature variables are considered, thus avoiding any arcs from feature to class variables. A greedy strategy with local changes among the orderings (Teyssier and Koller 2005) is applied along with a tabu list and random restarts to avoid local optima. The Bayesian information criterion (Schwarz 1978) is used as the scoring function to maximize, although any other decomposable score could be used. The authors proposed two strategies to guarantee the tractability of the learned MBCs. The first one, which is more computationally expensive but has greater predictive precision, is also based on rejecting any structures whose pruned graph treewidth exceeds a fixed bound. This differs to the previous method because it does not require an empty feature subgraph (as explained in Sect. 3.2.1). The second strategy, which is much more computationally efficient, is based on learning CB-MBCs that do not have any maximal connected component with more class variables than a fixed size (extrapolation of Eq. (6) to CB-MBCs).
5.5 Learning from multi-dimensional concept-drifting data streams
There are progressively more online applications that, contrary to traditional stationary scenarios, continuously produce data at very high speeds. Such data, known as data streams, usually present a concept-drifting aspect (Widmer and Kubat 1996). Concept drift mainly refers to an online supervised learning scenario where the relationships between the feature variables and the class variable(s) evolve over time (Gama et al. 2014). A data-stream environment has additional requirements related to memory resources (i.e., the stream cannot be fully stored in memory), and time (i.e., the stream should be continuously processed, and the learned classification model should be available at any time to be used for prediction) (Borchani et al. 2016).
Data stream classification problems have been extensively studied in the literature. The main objective of all the proposed approaches consists of coping with the concept drift by following an active learning approach, i.e., by maintaining the classification model up-to-date along the continuous flow of data. A detection method is normally used to monitor the concept drift, and an adaptation method is used to update the classification model over time. However, most of the work within this field has only focused on mining data streams, where each input example has to be assigned to a single class variable. A survey of the concept drift adaptation of such data can be found in the work of Gama et al. (2014). The problem of mining multi-dimensional data streams, where each example has to be simultaneously associated with multiple class variables, remains largely unexplored and only few multi-dimensional streaming methods have been introduced (paragraph mostly reproduced from Borchani et al. (2016)).
In addition, all the proposed methods in the literature are based on a multi-label setting (Qu et al. 2009; Xioufis et al. 2011; Kong and Philip 2011; Read et al. 2012; Wang et al. 2012; Song and Ye 2014; Wang et al. 2017), except the adaptive method based on MBCs proposed by Borchani et al. (2016), who place no constraints on the cardinalities of the class variables. This method extends the stationary learning algorithm of Borchani et al. (2012) to deal with the concept-drifting aspect of data streams. Unlike most of the proposed methods that use ensemble learningFootnote 4 to cope with concept drift, this algorithm monitors concept drift over time with a single base classifier (an MBC) using the likelihood of the most recent data to the current model and the Page-Hinkley test (Page 1954; Hinkley 1971). Then, if the algorithm detects a concept drift, the current MBC is locally adapted around each changed class variable by again extending the HITON algorithm, with no need to re-learn the whole network from scratch. A global adaptation can be also employed, such that the whole network is re-learned to represent the new concept, which may be interesting in the cases of abrupt (Gama and Castillo 2006) or severe (Minku et al. 2010) concept drift.
6 Applications, benchmark data sets and software
To the best of our knowledge, the first application that used an MBC was a medical problem by Qazi et al. (2007), although the authors were not concerned about the existence of a formal definition in the literature of the model they were using (van der Gaag and de Waal 2006). Later a few other applications arose, most of them also related to medical problems. A summary of all the applications of MBCs found in the literature is described below and compiled in Table 4. Also, a collection of data sets that are used in the literature to deal with the multi-dimensional problem is given, together with a collection of public domain MBC software.
6.1 Medical problems
The following applications can be listed:
-
Coronary heart disease diagnosis by the prediction of wall-motion abnormalities for the 16 segments of the left ventricle of the heart (Qazi et al. 2007). Each binary class variable, i.e., each one of the segments, can be predicted as normal or abnormal (a multi-label setting). Actually, the data set was labelled with up to four different types of abnormalities that the authors simplified by indiscriminately pairing them with a single true class value. Contour-detection techniques were used to extract feature variables that characterize cardiac motion from ultrasound images.
-
Estimation of the health-related quality of life of Parkinson’s patients (Borchani et al. 2012). Five class variables, namely mobility, self-care, usual activities, pain/discomfort, and anxiety/depression, have three options of response: no problems, some problems and severe problems. A questionnaire of 39 health-related questions, each being scored on a five-point scale (never, occasionally, sometimes, often and always), defined the set of feature variables.
-
Assistance in the treatment of multiple sclerosis by predicting the disease out of four possible subtypes, and the expected time to reach a severity level indicated whether assistance for walking was required (Rodríguez et al. 2012), which was discretized into four time intervals. The feature variables were composed of DNA and clinical information.
-
Prediction of human immunodeficiency virus type 1 (HIV-1) inhibitors, both with reverse transcriptase (RTIs) and protease inhibitors (PIs) (Borchani et al. 2013). Ten and eight drugs were considered, respectively. This is a multi-label problem that attempted to determine whether a patient was resistant or not to a specific drug. The feature variables were a set of resistance mutations.
-
Classification of neurons (Fernandez-Gonzalez et al. 2015). The aim was to determine the neuron species (rat, human, mouse or elephant), gender (male or female), cell type level one (principal cell or interneuron), cell type level two out of six possible values, development stage (neonate, young, adult or old), and brain region where it was located out of fourteen possible locations. Morphological measures of the neurons made up the set of feature variables.
-
Early detection of classical swine fever in pigs (Bolt and van der Gaag 2017). The class variables denoted the five phases commonly distinguished in the progression of an infection, where each was either present or absent (a multi-label setting). This is a typical medical problem where the feature variables correspond to a set of clinical symptoms. A particularity of this application is that the MBC was built by hand with the help of veterinary experts.
6.2 Other applications
Other fields of applications where MBCs have been used are:
-
Sentiment analysis by characterising the attitude of a customer when writing a post by three related class variables: subjectivity (objective or subjective), sentiment polarity (very negative, negative, neutral, positive or very positive) and will to influence (declarative text, soft, medium or high) (Ortigosa-Hernández et al. 2012). A morphological analyser was used to extract the feature variables from the words and phrases of the posts (e.g., number of verbs in the first person).
-
Fish recruitment forecast (Fernandes et al. 2013). In particular, three (class) species of commercial interest in the Bay of Biscay were studied: anchovy, sardine and hake. The authors divided recruitment into low, medium and high for each species. In order to predict recruitment, environmental and climatic information were used as feature variables.
6.3 Benchmark data sets
Surprisingly, there is a lack in the literature of benchmark data repositories for multi-dimensional classification. Three different approaches have been followed to evaluate and compare the algorithms reviewed in Table 3 for learning an MBC:
-
A popular benchmark multi-label data repositoryFootnote 5 (e.g., see Bielza and Larrañaga (2014) and Corani et al. (2014)). On a positive note, these real-world data sets have been well-studied and allow to compare a multi-dimensional model with other multi-label algorithms. On a negative note, they only represent multi-label settings, so the power of MBCs on more general multi-dimensional scenarios cannot be measured.
-
Sampled synthetic data from a randomly generated MBC (e.g., see Borchani et al. (2010), Ortigosa-Hernández et al. (2012) and Gil-Begue et al. (2018)). Both the structure and parameters are chosen at random, and a data set is simulated by using probabilistic logic sampling (Henrion 1988). This approach allows customization of the cardinality of a multi-dimensional classification problem and the size of the simulated data set, so the algorithm can be consequently evaluated at different scenarios. However, no real-world problem is tackled, and the results lose reproducibility.
-
Sampled synthetic data from an existing Bayesian network, such that a subset of its variables are selected as class variables (see van der Gaag and de Waal (2006) and Benjumeda et al. (2018)). Similar comments to those of the previous approach can be derived.
6.4 Software
Similarly, public domain software in relation to both multi-dimensional classification and MBCs is limited. There is no standardized library that proposes a general multi-dimensional classification framework and integrates multiple methods for learning MBCs. Instead, a few individual contributions can be found, which could benefit from further extensions and integration:
-
Zhang et al. (2009) shared a Matlab implementationFootnote 6 regarding their work of multi-label naïve Bayes classifier.
-
The Java implementationFootnote 7 of the methods proposed by Fernandes et al. (2013) is based on adapting the well-known general purpose platform Weka.
-
Arias et al. (2016) published an implementationFootnote 8 of their multi-dimensional classification method, which is mainly written in Java and Matlab.
-
Benjumeda et al. (2018) offered an extensive Python repositoryFootnote 9 for their proposed tractable MBCs learning methods.
-
The hybrid method of Gil-Begue et al. (2018) is available in R codeFootnote 10.
Multi-label classification, on the contrary, offers a variety of popular software packages, e.g., the Java platforms Mulan (Tsoumakas et al. 2011) and Meka (Read et al. 2016), the R packages mldr (Charte and Charte 2015) and utiml (Rivolli and de Carvalho 2018), and the Python library scikit-multilearn (Szymanski and Kajdanowicz 2019).
7 Discussion
The objective of this survey has been twofold:
-
1.
First, we have dealt with classification problems from the multi-dimensional perspective. A formal definition of the multi-dimensional classification problem has been provided, such that it was differentiated from the more popular multi-label subproblem, with which it is usually confused. We have also compiled a list of performance evaluation measures suitable for assessing multi-dimensional classifiers, including existing measures in the literature and a new set of proposed measures.
-
2.
Second, we have offered a comprehensive survey of the state-of-the-art MBC, which is an inherently interpretable model for multi-dimensional classification problems that allows intrinsic contemplation of the dependencies among the class variables and deals with the complexity entailed by this kind of problem. Unlike other pattern recognition classifiers, MBCs can be clearly organized based on their graphical structure from the simplest empty-empty to the most complex DAG-DAG. These probabilistic classifiers offer high model expressiveness, but at the expense of suffering from a super-exponential structure space in the number of variables. A plethora of structural learning algorithms have been proposed motivated by this fact, some of which also deal with the general NP-hardness of multi-dimensional classification in MBCs. Finally, MBCs have shown competitive results for multi-dimensional classification, and they have been successfully used in several real-world applications.
Given increased attention to multi-dimensional classification with Bayesian networks, it would be interesting to extend other models, such as dynamic (Dean and Kanazawa 1989) or continuous time (Nodelman et al. 2002; Stella and Amer 2012) Bayesian networks, to the multi-dimensional classification problem. Other machine-learning paradigms, such as ordinal classification (Frank and Hall 2001) or label ranking (Cheng et al. 2009), could also benefit from a multi-dimensional point of view (which could be approached with MBCs as well).
In addition, there is still room for research on MBCs. Other alternative approaches for handling continuous feature variables rather than a discretization or a Gaussian assumption could be derived, such as kernel density estimation (John and Langley 1995; Pérez et al. 2009). Simple unsupervised discretization methods have been used at most for the experiments with benchmark data sets and real-world problems, and only the work of Fernandes et al. (2013) has proposed a multi-dimensional extension of the state-of-the-art supervised discretization method of Fayyad and Irani (1993). The study of sensitivity functions for tuning MBCs is already ongoing (Bolt and van der Gaag 2017), and could benefit from further attention. Feature subset selection and stratified performance evaluation for multi-dimensional classifiers are still open problems. Feature weighting methods proposed in the multi-label setting (Yang and Ding 2019) could be extended to the multi-dimensional classification problem, and specially to MBCs. Also, the application of MBCs to more real-world problems would be interesting, especially if they show more challenging settings, such as data-streaming situations or cost-sensitive classification.
To this end, research addressing the current lack of public domain software related to multi-dimensional classification, and concretely to MBCs, is needed. A good starting point could be to extend the prominent software regarding multi-label classification. Similarly, no benchmark multi-dimensional data repositories were found in the literature. Among the strategies followed to evaluate and compare the proposed algorithms for learning an MBC, a benchmark multi-label data repository has been mostly used. Other approaches are based on using sampled synthetic data from a randomly generated MBC, or from an existing Bayesian network with class variables selected at random. As they are functional, but not sufficient, strategies to evaluate and compare multi-dimensional classifiers, we expect and encourage the creation of a benchmark multi-dimensional data repository. Again, the progress made in the multi-label scenario (Charte et al. 2018) could provide a useful starting point.
Notes
This is a simplification taken from Read et al. (2013) to facilitate discussion of the problem complexity. Actually, we will see later that each class variable can take a different number of values.
A graph is said to be maximal connected if there is a path between every pair of vertices in its undirected version (Bielza et al. 2011).
Note that we have modified the term \(r_s = \sum _{j=1}^{d} |\Omega _{C_j}|\) of Fernandes et al. (2013) by d in the denominator of the equation in order to correctly normalize the score to lie between 0 and 1.
The popular approach to handle concept drifts named ensemble learning consists of combining the predictions of a set of individual classifiers, the so-called ensemble, in order to predict new incoming examples. A comprehensive review of ensemble approaches for data stream analysis was conducted by Krawczyk et al. (2017).
References
Abdelbar AM, Hedetniemi SM (1998) Approximating MAPs for belief networks is NP-hard and other theorems. Artif Intell 102(1):21–38
Aliferis CF, Statnikov A, Tsamardinos I, Mani S, Koutsoukos XD (2010a) Local causal and Markov blanket induction for causal discovery and feature selection for classification. Part I: Algorithms and empirical evaluation. J Mach Learn Res 11:171–234
Aliferis CF, Statnikov A, Tsamardinos I, Mani S, Koutsoukos XD (2010b) Local causal and Markov blanket induction for causal discovery and feature selection for classification. Part II: Analysis and extensions. J Mach Learn Res 11:235–284
Antonucci A, Corani G, Mauá D, Gabaglio S (2013) An ensemble of Bayesian networks for multilabel classification. In: Proceedings of the 23rd international joint conference on artificial intelligence, AAAI Press, pp 1220–1225
Arias J, Gámez JA, Nielsen TD, Puerta JM (2016) A scalable pairwise class interaction framework for multidimensional classification. Int J Approx Reason 68:194–210
Arnborg S, Corneil DG, Proskurowski A (1987) Complexity of finding embeddings in a k-tree. SIAM J Alg Discrete Methods 8(2):277–284
Benjumeda M, Bielza C, Larrañaga P (2018) Tractability of most probable explanations in multidimensional Bayesian network classifiers. Int J Approx Reason 93:74–87
Bielza C, Larrañaga P (2014) Discrete Bayesian network classifiers: A survey. ACM Comput Surv 47(1):5
Bielza C, Li G, Larrañaga P (2011) Multi-dimensional classification with Bayesian networks. Int J Approx Reason 52(6):705–727
Blanco R, Inza I, Merino M, Quiroga J, Larrañaga P (2005) Feature selection in Bayesian classifiers for the prognosis of survival of cirrhotic patients treated with TIPS. J Biomed Inform 38(5):376–388
Bolt JH, van der Gaag LC (2017) Balanced sensitivity functions for tuning multi-dimensional Bayesian network classifiers. Int J Approx Reason 80:361–376
Borchani H, Bielza C, Larrañaga P (2010) Learning CB-decomposable multi-dimensional Bayesian network classifiers. In: Proceedings of the 5th European workshop on probabilistic graphical models, pp 25–32
Borchani H, Bielza C, Martínez-Martín P, Larrañaga P (2012) Markov blanket-based approach for learning multi-dimensional Bayesian network classifiers: An application to predict the European Quality of Life-5 Dimensions (EQ-5D) from the 39-item Parkinson’s Disease Questionnaire (PDQ-39). J Biomed Inform 45(6):1175–1184
Borchani H, Bielza C, Toro C, Larrañaga P (2013) Predicting human immunodeficiency virus inhibitors using multi-dimensional Bayesian network classifiers. Artif Intell Med 57(3):219–229
Borchani H, Larrañaga P, Gama J, Bielza C (2016) Mining multi-dimensional concept-drifting data streams using Bayesian network classifiers. Intell Data Anal 20(2):257–280
Bouckaert RR (1992) Optimizing causal orderings for generating DAGs from data. In: Proceedings of the 8th conference on uncertainty in artificial intelligence, Morgan Kaufmann Publishers Inc, pp 9–16
Boutell MR, Luo J, Shen X, Brown CM (2004) Learning multi-label scene classification. Pattern Recogn 37(9):1757–1771
Brier GW (1950) Verification of forecasts expressed in terms of probability. Mon Weather Rev 78(1):1–3
Buntine W (1991) Theory refinement on Bayesian networks. In: Proceedings of the 7th conference on Uncertainty in artificial intelligence, Morgan Kaufmann Publishers Inc, pp 52–60
Charte F, Charte D (2015) Working with multilabel datasets in R: The mldr package. R J 7(2):149–162
Charte F, Rivera AJ, Charte D, del Jesus MJ, Herrera F (2018) Tips, guidelines and tools for managing multi-label datasets: The mldr.datasets R package and the Cometa data repository. Neurocomputing 289:68–85
Cheng W, Hühn J, Hüllermeier E (2009) Decision tree and instance-based learning for label ranking. In: Proceedings of the 26th annual international conference on machine learning, ACM, pp 161–168
Chow C, Liu C (1968) Approximating discrete probability distributions with dependence trees. IEEE Trans Inf Theory 14(3):462–467
Chu YJ, Liu TH (1965) On the shortest arborescence of a directed graph. Sci Sinica 14:1396–1400
Cooper GF, Herskovits E (1992) A Bayesian method for the induction of probabilistic networks from data. Mach Learn 9(4):309–347
Corani G, Antonucci A, Mauá DD, Gabaglio S (2014) Trading off speed and accuracy in multilabel classification. In: Proceedings of the 7th European workshop on probabilistic graphical models, Lecture Notes in Artificial Intelligence, Springer, pp 145–159
Dawid AP (1992) Applications of a general propagation algorithm for probabilistic expert systems. Stat Comput 2(1):25–36
Dean T, Kanazawa K (1989) A model for reasoning about persistence and causation. Comput Intell 5(2):142–150
Deb K, Pratap A, Agarwal S, Meyarivan T (2002) A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans Evol Comput 6(2):182–197
Dechter R (1999) Bucket elimination: A unifying framework for reasoning. Artif Intell 113(1–2):41–85
Dechter R, Rish I (1997) A scheme for approximating probabilistic inference. In: Proceedings of the 13th conference on uncertainty in artificial intelligence, Morgan Kaufmann Publishers Inc, pp 132–141
Dempster AP, Laird NM, Rubin DB (1977) Maximum likelihood from incomplete data via the EM algorithm. J R Stat Soc Ser B (Methodol) 39(1):1–38
Fayyad U, Irani K (1993) Multi-interval discretization of continuous-valued attributes for classification learning. In: Proceedings of the 13th international joint conference on artificial intelligence, pp 1022–1027
Fernandes JA, Lozano JA, Inza I, Irigoien X, Pérez A, Rodríguez JD (2013) Supervised pre-processing approaches in multiple class variables classification for fish recruitment forecasting. Environ Modell Softw 40:245–254
Fernandez-Gonzalez P, Bielza C, Larrañaga P (2015) Multidimensional classifiers for neuroanatomical data. In: ICML Workshop on statistics, machine learning and neuroscience (Stamlins 2015)
Frank E, Hall M (2001) A simple approach to ordinal classification. In: Proceedings of the 12th European conference on machine learning, Lecture Notes in Artificial Intelligence, Springer, pp 145–156
Friedman N (1997) Learning belief networks in the presence of missing values and hidden variables. In: Proceedings of the 14th international conference on machine learning, Morgan Kaufmann Publishers Inc, vol 97, pp 125–133
Friedman N (1998) The Bayesian structural EM algorithm. In: Proceedings of the 14th conference on uncertainty in artificial intelligence, Morgan Kaufmann Publishers Inc, pp 129–138
Friedman N, Geiger D, Goldszmidt M (1997) Bayesian network classifiers. Mach Learn 29(2–3):131–163
Fürnkranz J, Hüllermeier E, Mencía EL, Brinker K (2008) Multilabel classification via calibrated label ranking. Mach Learn 73(2):133–153
van der Gaag LC, de Waal PR (2006) Muti-dimensional Bayesian network classifiers. In: Proceedings of the 3rd European workshop in probabilistic graphical models, pp 107–114
Gama J, Castillo G (2006) Learning with local drift detection. In: Proceedings of the 2nd international conference on advanced data mining and applications, Lecture Notes in Artificial Intelligence, Springer, pp 42–55
Gama J, Zliobaite I, Bifet A, Pechenizkiy M, Bouchachia A (2014) A survey on concept drift adaptation. ACM Comput Surv 46(4):44
Gelsema ES (1995) Abductive reasoning in Bayesian belief networks using a genetic algorithm. Pattern Recogn Lett 16(8):865–871
Gibaja E, Ventura S (2015) A tutorial on multi-label learning. ACM Comput Surv 47(3):52
Gil-Begue S, Larrañaga P, Bielza C (2018) Multi-dimensional Bayesian network classifier trees. In: Proceedings of the 19th international conference on intelligent data engineering and automated learning, Lecture Notes in Computer Science, Springer, pp 354–363
Godbole S, Sarawagi S (2004) Discriminative methods for multi-labeled classification. In: Proceedings of the 8th Pacific-Asia conference on knowledge discovery and data mining, Lecture Notes in Artificial Intelligence, Springer, pp 22–30
Guan DJ (1998) Generalized Gray codes with applications. In: Proceedings of the national science council of the Republic of China, part a: Physical science and engineering, vol 22, No 6, pp 841–848
Hall MA (2000) Correlation-based feature selection for discrete and numeric class machine learning. In: Proceedings of the 17th international conference on machine learning, Morgan Kaufmann Publishers Inc, pp 359–366
Henrion M (1988) Propagating uncertainty in Bayesian networks by probabilistic logic sampling. In: Machine intelligence and pattern recognition, vol 5, Elsevier, pp 149–163
Hernández-González J, Inza I, Lozano JA (2015) Multidimensional learning from crowds: Usefulness and application of expertise detection. Int J Intell Syst 30(3):326–354
Hinkley DV (1971) Inference about the change-point from cumulative sum tests. Biometrika 58(3):509–523
Hüllermeier E, Fürnkranz J, Cheng W, Brinker K (2008) Label ranking by learning pairwise preferences. Artif Intell 172(16–17):1897–1916
Hutter F, Hoos HH, Stützle T (2005) Efficient stochastic local search for MPE solving. In: Proceedings of the 19th international joint conference on artificial intelligence, Morgan Kaufmann Publishers Inc, pp 169–174
John GH, Langley P (1995) Estimating continuous distributions in Bayesian classifiers. In: Proceedings of the 11th conference on uncertainty in artificial intelligence, Morgan Kaufmann Publishers Inc, pp 338–345
Kask K, Dechter R (1999) Mini-bucket heuristics for improved search. In: Proceedings of the 15th conference on uncertainty in artificial intelligence, Morgan Kaufmann Publishers Inc, pp 314–323
Kask K, Dechter R (2001) A general scheme for automatic generation of search heuristics from specification dependencies. Artif Intell 129(1–2):91–131
Koller D, Friedman N (2009) Probabilistic graphical models: Principles and techniques. The MIT Press, London
Kong X, Philip SY (2011) An ensemble-based approach to fast classification of multi-label data streams. In: Proceedings of the 7th international conference on collaborative computing: Networking, applications and worksharing, IEEE, pp 95–104
Krawczyk B, Minku LL, Gama J, Stefanowski J, Woźniak M (2017) Ensemble learning for data stream analysis: A survey. Inf Fusion 37:132–156
Kruskal JB (1956) On the shortest spanning subtree of a graph and the traveling salesman problem. Proc Am Math Soc 7(1):48–50
Kullback S (1997) Information theory and statistics. Courier Corporation
Kwisthout J (2011) Most probable explanations in Bayesian networks: Complexity and tractability. Int J Approx Reason 52(9):1452–1469
Langley P, Sage S (1994) Induction of selective Bayesian classifiers. In: Proceedings of the 10th conference on uncertainty in artificial intelligence, Morgan Kaufmann Publishers Inc, pp 399–406
Li Z, D’Ambrosio B (1993) An efficient approach for finding the MPE in belief networks. In: Proceedings of the 9th conference on uncertainty in artificial intelligence, Morgan Kaufmann Publisher Inc, pp 342–349
Marinescu R, Dechter R (2009) AND/OR branch-and-bound search for combinatorial optimization in graphical models. Artif Intell 173(16–17):1457–1491
Mencía EL, Fürnkranz J (2010) Efficient multilabel classification algorithms for large-scale problems in the legal domain. In: Semantic processing of legal texts, Springer, pp 192–215
Minku LL, White AP, Yao X (2010) The impact of diversity on online ensemble learning in the presence of concept drift. IEEE Trans Knowl Data Eng 22(5):730–742
Minsky M (1961) Steps toward artificial intelligence. Proc Inst Radio Eng 49(1):8–30
Nodelman U, Shelton CR, Koller D (2002) Continuous time Bayesian networks. In: Proceedings of the 18th conference on uncertainty in artificial intelligence, Morgan Kaufmann Publishers Inc, pp 378–387
Ortigosa-Hernández J, Rodríguez JD, Alzate L, Lucania M, Inza I, Lozano JA (2012) Approaching sentiment analysis by using semi-supervised learning of multi-dimensional classifiers. Neurocomputing 92:98–115
Page ES (1954) Continuous inspection schemes. Biometrika 41(1/2):100–115
Park S, Fürnkranz J (2008) Multi-label classification with label constraints. In: Proceedings of the joint European conference on machine learning and principles and practice of knowledge discovery in databases workshop on preference learning, pp 157–171
Pastink A, van der Gaag LC (2015) Multi-classifiers of small treewidth. In: Proceedings of the 13th European conference on symbolic and quantitative approaches to reasoning and uncertainty, Lecture Notes in Artificial Intelligence, Springer, pp 199–209
Pearl J (1988) Probabilistic reasoning in intelligent systems: Networks of plausible inference. Morgan Kaufmann Publishers, New York
Pérez A, Larrañaga P, Inza I (2009) Bayesian classifiers based on kernel density estimation: Flexible classifiers. Int J Approx Reason 50(2):341–362
Provost F, Domingos P (2000) Improving probability estimation trees. Mach Learn 52(3):199–215
Qazi M, Fung G, Krishnan S, Rosales R, Steck H, Rao RB, Poldermans D, Chandrasekaran D (2007) Automated heart wall motion abnormality detection from ultrasound images using Bayesian networks. In: Proceedings of the 20th international joint conference on artificial intelligence, Morgan Kaufmann Publishers Inc, pp 519–525
Qu W, Zhang Y, Zhu J, Qiu Q (2009) Mining multi-label concept-drifting data streams using dynamic classifier ensemble. In: Proceedings of the 1st Asian conference on machine learning, Lecture Notes in Artificial Intelligence, Springer, pp 308–321
Read J (2008) A pruned problem transformation method for multi-label classification. In: Proceedings of the New Zealand computer science research student conference, pp 143–150
Read J, Pfahringer B, Holmes G, Frank E (2011) Classifier chains for multi-label classification. Mach Learn 85(3):333–359
Read J, Bifet A, Holmes G, Pfahringer B (2012) Scalable and efficient multi-label classification for evolving data streams. Mach Learn 88(1–2):243–272
Read J, Bielza C, Larrañaga P (2013) Multi-dimensional classification with super-classes. IEEE Trans Knowl Data Eng 26(7):1720–1733
Read J, Reutemann P, Pfahringer B, Holmes G (2016) MEKA: A multi-label/multi-target extension to WEKA. J Mach Learn Res 17:667–671
Rebane G, Pearl J (1987) The recovery of causal poly-trees from statistical data. In: Proceedings of the 3rd conference on uncertainty in artificial intelligence, AUAI Press, pp 222–228
Rissanen J (1978) Modeling by shortest data description. Automatica 14(5):465–471
Rivas JJ, Orihuela-Espina F, Sucar LE (2018) Circular chain classifiers. In: Proceedings of the 9th international conference on probabilistic graphical models, proceedings of machine learning research, pp 380–391
Rivolli A, de Carvalho ACPLF (2018) The utiml package: Multi-label classification in R. The R J 10(2):24–37
Robinson RW (1973) Counting labeled acyclic digraphs. In: New directions in the theory of graphs, Academic Press, pp 239–273
Rodríguez JD, Lozano JA (2008) Multi-objective learning of multi-dimensional Bayesian classifiers. In: Proceedings of the 8th international conference on hybrid intelligent systems, IEEE Computer Society, pp 501–506
Rodríguez JD, Perez A, Arteta D, Tejedor D, Lozano JA (2012) Using multidimensional Bayesian network classifiers to assist the treatment of multiple sclerosis. IEEE Trans Syst Man Cybern Part C Appl Rev 42(6):1705–1715
Rojas-Guzman C, Kramer MA (1993) GALGO: A genetic algorithm decision support tool for complex uncertain systems modeled with Bayesian belief networks. In: Proceedings of the 9th conference on uncertainty in artificial intelligence, Morgan Kaufmann Publisher Inc, pp 368–375
Rudin C (2019) Stop explaining black box machine learning models for high stakes decisions and use interpretable models instead. Nat Mach Intell 1(5):206–215
Sahami M (1996) Learning limited dependence Bayesian classifiers. In: Proceedings of the 2nd international conference on knowledge discovery and data mining, AAAI Press, 1, pp 335–338
Santos E (1991) On the generation of alternative explanations with implications for belief revision. In: Proceedings of the 7th conference on uncertainty in artificial intelligence, Morgan Kaufmann Publishers Inc, pp 339–347
Schapire RE, Singer Y (1999) Improved boosting algorithms using confidence-rated predictions. Mach Learn 37(3):297–336
Schapire RE, Singer Y (2000) BoosTexter: A boosting-based system for text categorization. Mach Learn 39(2–3):135–168
Schwarz G (1978) Estimating the dimension of a model. Ann Stat 6(2):461–464
Sechidis K, Tsoumakas G, Vlahavas I (2011) On the stratification of multi-label data. In: Proceedings of the joint European conference on machine learning and knowledge discovery in databases, Lecture Notes in Artificial Intelligence, Springer, pp 145–158
Shimony SE (1994) Finding MAPs for belief networks is NP-hard. Artif Intell 68(2):399–410
Shimony SE, Charniak W (1990) A new algorithm for finding MAP assignments to belief networks. In: Proceedings of the 6th annual conference on uncertainty in artificial intelligence, Elsevier, pp 185–196
Song G, Ye Y (2014) A new ensemble method for multi-label data stream classification in non-stationary environment. In: Proceedings of the 2014 international joint conference on neural networks, IEEE, pp 1776–1783
Stella F, Amer Y (2012) Continuous time Bayesian network classifiers. J Biomed Inform 45(6):1108–1119
Sucar LE, Bielza C, Morales EF, Hernandez-Leal P, Zaragoza JH, Larrañaga P (2014) Multi-label classification with Bayesian network-based chain classifiers. Pattern Recogn Lett 41:14–22
Sy BK (1992) Reasoning MPE to multiply connected belief networks using message passing. In: Proceedings of the 10th national conference on artificial intelligence, AAAI Press, pp 570–576
Szymanski P, Kajdanowicz T (2019) Scikit-multilearn: A scikit-based Python environment for performing multi-label classification. J Mach Learn Res 20:209–230
Teyssier M, Koller D (2005) Ordering-based search: A simple and effective algorithm for learning Bayesian networks. In: Proceedings of the 21st conference on uncertainty in artificial intelligence, AUAI Press, pp 584–590
Tsoumakas G, Katakis I (2007) Multi-label classification: An overview. Int J Data Warehouse Min 3(3):1–13
Tsoumakas G, Vlahavas I (2007) Random k-labelsets: An ensemble method for multilabel classification. In: Proceedings of the 18th European conference on machine learning, Lecture Notes in Artificial Intelligence, Springer, pp 406–417
Tsoumakas G, Katakis I, Vlahavas I (2009) Mining multi-label data. In: Data mining and knowledge discovery handbook, Springer, pp 667–685
Tsoumakas G, Spyromitros-Xioufis E, Vilcek J, Vlahavas I (2011) MULAN: A Java library for multi-label learning. J Mach Learn Res 12:2411–2414
de Waal PR, van der Gaag LC (2007) Inference and learning in multi-dimensional Bayesian network classifiers. In: Proceedings of the 9th European conference on symbolic and quantitative approaches to reasoning with uncertainty, Lecture Notes in Artificial Intelligence, Springer, pp 501–511
Wang L, Shen H, Tian H (2017) Weighted ensemble classification of multi-label data streams. In: Proceedings of the 21st Pacific-Asia conference on knowledge discovery and data mining, Lecture Notes in Artificial Intelligence, Springer, pp 551–562
Wang P, Zhang P, Guo L (2012) Mining multi-label data streams using ensemble-based active learning. In: Proceedings of the 2012 SIAM international conference on data mining, SIAM, pp 1131–1140
Widmer G, Kubat M (1996) Learning in the presence of concept drift and hidden contexts. Mach Learn 23(1):69–101
Xioufis ES, Spiliopoulou M, Tsoumakas G, Vlahavas IP (2011) Dealing with concept drift and class imbalance in multi-label stream classification. In: Proceedings of the 22nd international joint conference on artificial intelligence, AAAI Press, pp 1583–1588
Yang Y (1999) An evaluation of statistical approaches to text categorization. Inf Retrieval 1(1–2):69–90
Yang Y, Ding M (2019) Decision function with probability feature weighting based on Bayesian network for multi-label classification. Neural Comput Appl 31(9):4819–4828
Yang Y, Liu X (1999) A re-examination of text categorization methods. In: Proceedings of the 22nd annual international ACM SIGIR conference on research and development in information retrieval, ACM, pp 42–49
Zaragoza JH, Sucar LE, Morales EF (2011a) A two-step method to learn multidimensional Bayesian network classifiers based on mutual information measures. In: Proceedings of the 24th international FLAIRS conference, AAAI Press, pp 644–649
Zaragoza JH, Sucar LE, Morales EF, Bielza C, Larranaga P (2011b) Bayesian chain classifiers for multidimensional classification. In: Proceedings of the 22nd international joint conference on artificial intelligence, AAAI Press, pp 2192–2197
Zhang ML, Zhou ZH (2007) ML-KNN: A lazy learning approach to multi-label learning. Pattern Recogn 40(7):2038–2048
Zhang ML, Zhou ZH (2014) A review on multi-label learning algorithms. IEEE Trans Knowl Data Eng 26(8):1819–1837
Zhang ML, Peña JM, Robles V (2009) Feature selection for multi-label naive Bayes classification. Inf Sci 179(19):3218–3229
Zhu M, Liu S, Jiang J (2016) A hybrid method for learning multi-dimensional Bayesian network classifiers based on an optimization model. Appl Intell 44(1):123–148
Zhu S, Ji X, Xu W, Gong Y (2005) Multi-labelled classification using maximum entropy method. In: Proceedings of the 28th annual international ACM SIGIR conference on research and development in information retrieval, ACM, pp 274–281
Acknowledgements
This work has been partially supported by the Spanish Ministry of Science and Innovation through the PID2019-109247GB-IOO project. Santiago Gil-Begue has been supported by the predoctoral grant FPU17/04341 from the Spanish Ministry of Science, Innovation and Universities.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Gil-Begue, S., Bielza, C. & Larrañaga, P. Multi-dimensional Bayesian network classifiers: A survey. Artif Intell Rev 54, 519–559 (2021). https://doi.org/10.1007/s10462-020-09858-x
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10462-020-09858-x











 is the space of joint configurations of the non-binary class variables, and
is the space of joint configurations of the non-binary class variables, and 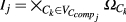 be the space of joint configurations of the class variables that belong to the j-th maximal connected component,
be the space of joint configurations of the class variables that belong to the j-th maximal connected component,