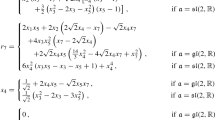Abstract
Fino and Kath determined all possible holonomy groups of seven-dimensional pseudo-Riemannian manifolds contained in the exceptional, non-compact, simple Lie group \(\mathrm {G}_2^*\) via the corresponding Lie algebras. They are distinguished by the dimension of their maximal semi-simple subrepresentation on the tangent space, the socle. An algebra is called of Type I, II or III if the socle has dimension 1, 2 or 3, respectively. This article proves that each possible holonomy group of Type III can indeed be realized by a metric of signature (4, 3). For this purpose, metrics are explicitly constructed, using Cartan’s methods of exterior differential systems, such that the holonomy of the manifold has the desired properties.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Holonomy theory is a very rich field of research between differential geometry and algebra for about a century. When Cartan classified Riemannian symmetric spaces in 1926 [5], he thereby also classified the irreducible holonomy groups of such spaces. Irreducible here means that the natural representation of the holonomy group on the tangent space, the holonomy representation, does not leave invariant any proper subspaces. Thirty years later Berger classified simply connected semi-Riemannian manifolds with irreducible holonomy which are not locally symmetric [3]. The result is the well-known Berger list for Riemannian and pseudo-Riemannian manifolds. In 1987, Bryant finally showed that manifolds with holonomy \(\mathrm {G}_2\) and \(\mathrm {Spin}(7)\) exist [4]. Thus, in the Riemannian case each group on Berger’s list is indeed realizable by a metric, i.e., there exists a Riemannian metric such that its holonomy group is equal to that one on Berger’s list. It follows that the (reduced) holonomy groups of irreducible, not locally symmetric Riemannian manifolds are completely classified.
In the case of pseudo-Riemannian manifolds the situation is more complicate. Since the holonomy representation can have degenerate subspaces, it is not sufficient to classify only irreducible holonomy groups. It is necessary to consider indecomposable ones as well, where indecomposability means that the holonomy representation does not leave invariant any proper, non-degenerate subspace.
While the holonomy of irreducible pseudo-Riemannian manifolds is also classified by Berger’s list, little is known about the holonomy of the indecomposable ones, especially about those with index greater than 2. Holonomy groups of Lorentzian manifolds were classified by Leistner [11, 17], while Galaev classified those of pseudo-Kählerian manifolds of index 2 [12] and Einstein not Ricci-flat pseudo-Riemannian manifolds [13]. Besides these classifications only some results associated with certain special geometries are known (cf. [9, 14, 18]).
This article treats of pseudo-Riemannian manifolds with signature (4, 3) and their holonomy. Throughout this article, manifolds are assumed to be simply connected such that holonomy coincides with reduced holonomy and Berger’s results are applicable. If a manifold with signature (4, 3) has irreducible holonomy, then it is either generic \(\mathrm {SO}(4,3)\) or \(\mathrm {G}_2^{*}\) by Berger’s list. Therefore, it is natural to ask which proper subgroups of \(\mathrm {G}_2^{*}\) are holonomy groups, i.e., have indecomposable holonomy representation. As the manifold is simply connected, the holonomy group is connected and one may equivalently asks which subalgebras of \(\mathfrak {g}_2^{*}\) are holonomy algebras, i.e., the Lie algebra of a holonomy group. Here, \(\mathfrak {g}_2^{*}\) denotes the Lie algebra of \(\mathrm {G}_2^{*}\). There are already some results in this direction, e.g., in [15] indefinite symmetric spaces were classified, and it turns out that their holonomy algebras are two or three dimensional and Abelian.
The article is based upon results of Fino and Kath in [8] and is part of a project whose aim is to classify and realize all proper subgroups of \(\mathrm {G}_2^{*}\) which are holonomy groups. As said before, the classification is due to the holonomy algebras \(\mathfrak {h}\subset \mathfrak {g}_2^{*} \subset \mathfrak {so}(4,3)\) and up to conjugation in \(\mathrm {SO}(4,3)\). Algebraic restrictions on the holonomy algebras arise from indecomposability, i.e., the natural representation of the holonomy algebra \(\mathfrak {h}\subset \mathfrak {g}_2^{*} \subset \mathfrak {so}(4,3)\) on the tangent space \(T_xM \cong \mathbb {R}^{4,3}\) has to leave invariant an isotropic subspace if \(\mathfrak {h}\ne \mathfrak {g}_{2}^{*}\), and the fact that each holonomy algebra has to be a Berger algebra, i.e., satisfies Berger’s first criterion. Possible holonomy algebras are further divided into three different types by their maximal semi-simple subrepresentation, the so-called socle. The algebras are named as of Type I, II or III if the socle has dimension 1, 2 or 3, respectively. In [7] it is shown by Fino and Kath that all possible holonomy algebras of Type I can indeed be realized, i.e., for each algebra there exists a metric g with signature (4, 3) such that the pseudo-Riemannian manifold (M, g) has holonomy according to the particular algebra. In the present article, these investigations are continued and it is shown that the same holds for all algebras of Type III as well. Hence, metrics g will be explicitly constructed such that each Type III algebra is the holonomy algebra of a pseudo-Riemannian manifold (M, g) with signature (4, 3).
In the following section a brief review of the characterization of \(\mathrm {G}_2^{*}\) and the algebras of Type III is given. Also, most of the notation is introduced and some results from [8], which are necessary to state the classification theorem for Type III algebras, are provided. Section 3 outlines the construction approach for local metrics with specific holonomy properties using the concept of H-structures and Cartan’s methods of exterior differential systems. Afterward, the ‘machinery’ developed in this way is used to prove the main theorem of this article:
Theorem 1
Each possible holonomy algebra of Type III can be realized by a pseudo-Riemannian metric of signature (4, 3).
As the proof is constructive, also an example is provided in each case considered. Furthermore, the construction yields (quasi-)normal forms for the metrics. Here, ‘quasi’ refers to some additional conditions imposed on the metrics by certain PDEs. These (quasi-)normal forms can be used to describe the deformation spaces of the metrics. This aspect is not further investigated, as it is beyond the scope of this article.
2 Type III holonomy algebras
The group \(\mathrm {G}_2^{*}\) is strongly related to the exceptional, complex, simple Lie group \(\mathrm {G}_2\), which is well known from classical Lie theory. The complex Lie algebra \(\mathfrak {g}_2\) of \(\mathrm {G}_2\) has two real forms: \(\mathfrak {g}_2^{c}\) and \(\mathfrak {g}_2^{*}\), corresponding to the compact group \(\mathrm {G}_2^{c}\) and the non-compact \(\mathrm {G}_2^{*}\). Each of these groups \(\mathrm {G}_2,\,\mathrm {G}_2^c,\,\mathrm {G}_2^{*}\) appears on Berger’s list, for either Riemannian or pseudo-Riemannian manifolds [3, 4].
There are several ways to characterize the group \(\mathrm {G}_2^{*}\). Here, an approach via an alternating 3-form is used, which traces back to Engel when he first described the complex group \(\mathrm {G}_2\) [6]. He found that \(\mathrm {G}_2\) is the stabilizer of a generic complex 3-form \(\omega ^{\mathbb {C}}\), i.e., \(\omega ^{\mathbb {C}}\) has open \(\mathrm {GL}(7,\mathbb {C})\)-orbit. Passing to the real numbers this orbit splits into two, each of them corresponding to real, generic, \(\mathrm {GL}(7,\mathbb {R})\)-equivalent 3-forms [1, 21]. One can show that the stabilizers of these forms are exactly \(\mathrm {G}_2^{*}\) and \(\mathrm {G}_2^{c}\). For any real vector space V one can thus describe \(\mathrm {G}_2^{*}\) as the stabilizer of a generic real 3-form \(\omega \in \Lambda ^{\!3}V^{*}\) on V.
Before elaborating the details, notice some other characterizations based on stabilizer properties of \(\mathrm {G}_2^{*}\). It is also the stabilizer of a non-isotropic element of the real spinor representation of \(\mathrm {Spin}(4,3)\) or of an specific cross-product on \(\mathbb {R}^{4,3}\). Each of these approaches corresponds to each other, see [15] for a detailed description. Furthermore, \(\mathrm {G}_2^{*}\) is the automorphism group of the split octonion algebra, which is a more classical characterization approach.
Now, let V be a 7-dimensional real vector space on which \(\mathrm {G}_{2}^{*}\) acts as a subgroup of \(\mathrm {GL}(V)\). Identify \(V \cong \mathbb {R}^7\) and choose the canonical basis as the basis \(b_1,\ldots ,b_7\) for V. Then, \(\mathrm {G}_2^{*}\) can be considered as the stabilizer of the real 3-form \(\omega \) given by
where \(b^1,\ldots ,b^7\) denotes the dual basis and \(b^{ijk} = b^i \wedge b^j \wedge b^k\). This 3-form induces an inner product on V by
where \(\iota \) is the interior product. See [4] for details. With respect to this inner product consider \(\mathrm {G}_2^{*}\) as a subgroup of \(\mathrm {SO}(4,3)\), now under the identification \(V \cong \mathbb {R}^{4,3}\). Elements of the Lie algebra \(\mathfrak {g}_2^{*}\) are then given by matrices of the form
with \(s_i \in \mathbb {R}\). The Lie algebra \(\mathfrak {g}_2^{*}\) also exhibits the structure of a |3|-graded Lie algebra. Thus, it exists a direct sum vector space decomposition
such that \(\left[ \mathfrak {g}_i,\mathfrak {g}_j\right] \subset \mathfrak {g}_{i+j}\). The components \(\mathfrak {g}_i\) can simply be computed from the root diagram of \(\mathfrak {g}_{2}^{*}\) (cf. [10]), e.g., \(\mathfrak {g}_0\) corresponds to the subalgebra generated by the longer primitive root vector, its negative and the (canonical) Cartan subalgebra. Since \(\mathfrak {g}_0 \oplus \cdots \oplus \mathfrak {g}_3\) also contains the smaller primitive root vector, it contains a Borel subalgebra of \(\mathfrak {g}_2^{*}\).
Remark 1
The Lie algebra \(\mathfrak {g}_{2}^{*}\) also carries the structure of a |2|-graded Lie algebra. In this case \(\mathfrak {g}_0\) is generated by the shorter primitive root vector, its negative and the Cartan subalgebra. This grading will not be considered here further, but it is the appropriate one when dealing with Type II algebras.
With respect to the metric g, the line \(\mathbb {R}\cdot b_1\) is isotropic. The subalgebra \(\mathfrak {p}_1 \subset \mathfrak {g}_2^{*}\), which is the stabilizer of this isotropic line, is given by
Note that \(\mathfrak {p}_1\) is parabolic.
The algebraic considerations above can be used to describe manifolds with holonomy contained in \(\mathrm {G}_2^{*}\). Let M be smooth manifold with \(\dim M = 7\). The vector space V is now taken to be the tangent space at some \(x \in M\), i.e., \(V = T_xM\). Next, consider the principal frame bundle \(\mathrm {GL}(M)\) over M with structure group \(\mathrm {GL}(7,\mathbb {R})\). A \(\mathrm {G}_{2}^{*}\)-structure on M is a reduction of \(\mathrm {GL}(M)\) along the inclusion \(\mathrm {G}_{2}^{*} \hookrightarrow \mathrm {GL}(7,\mathbb {R})\). By the considerations above, \(\mathrm {G}_{2}^{*}\) defines a metric g on M via the inner product. Thus, \(\mathrm {G}_{2}^{*} \subset \mathrm {SO}(4,3)\) and the reduction can be thought along the inclusion \(\mathrm {G}_{2}^{*} \hookrightarrow \mathrm {SO}(4,3)\hookrightarrow \mathrm {GL}(7,\mathbb {R})\). In this case, it is known (cf. [19]) that the holonomy of M is contained in the structure group \(\mathrm {G}_2^{*}\) if and only if the \(\mathrm {G}_{2}^{*}\)-structure is torsion-free.
Since the objects of investigation are holonomy groups which are proper subgroups of \(\mathrm {G}_2^{*}\), or equivalently subalgebras \(\mathfrak {h}\subset \mathfrak {g}_{2}^{*}\), the holonomy representation has to be indecomposable but not irreducible (which would imply \(\mathfrak {h} = \mathfrak {g}_{2}^{*}\)). Thus, there is at least one \(\mathfrak {h}\)-invariant isotropic subspace of V. Using this fact, it was proven in [8] that Type III algebras are in general of the form
where
with elements \( A = \begin{pmatrix} a_1 &{} a_2 \\ a_3 &{} a_4\end{pmatrix} \in \mathfrak {gl}(2, \mathbb {R}), \; y = (y_1, y_2)^{\top } \in \mathbb {R}^2 , \; v \in \mathbb {R} \). The commutator of two elements \(h(A,v_A,y_A)\) and \(h(B,v_B,y_B)\) is given by
It is appropriate to introduce some further notation at this point, which is adapted from [8]. First, define the Lie algebras
Then, under the identification
consider the algebra \(\mathfrak {h}^{\textit{III}}\) as a semi-direct product
where elements \(A \in \mathfrak {gl}(2,\mathbb {R})\) act on \(\mathfrak {m}\) by
Furthermore, identify \(\mathrm {GL}(2,\mathbb {R})\) with a subgroup of diagonal block matrices in \(\mathrm {G}_2^{*}\) using the map
and note the adjoint action on \(\mathfrak {h}^{\textit{III}}\) given by
Later on, elements of \(\mathfrak {h}\) are conjugated several times with elements of the form \(\exp (h(0,v,y))\). The adjoint action is given by
The classification theorem for Type III algebras was already proven in [7], but it is restated here as it becomes more simple when dealing with Type III algebras alone. First of all, it is a well-known fact that every holonomy algebra is a Berger algebra, i.e., \(\mathfrak {h}\subset \mathfrak {h}^{\textit{III}}\) has to satisfy Berger’s first criterion. Next, consider
the space of algebraic curvature endomorphisms, and define the space
Berger’s first criterion now implies \(\mathfrak {h} = \underline{\mathfrak {h}}\) for \(\mathfrak {h}\) being a holonomy algebra. A parameterization for the space \(\mathscr {K}\!(\mathfrak {h})\) is given in the case of Type I algebras by [8]. Since \( \mathfrak {h}^{\textit{III}} \subset \mathfrak {h}^{ \textit{I}}\), in principle the same parameterization is used for Type III algebras.
Lemma 1
In the case of Type III algebras the space \(\mathscr {K}(\mathfrak {h})\) can be parameterized by \(a_1,a_2\), \(a_3,d_1\), \(d_2 \in \mathbb {R}\), \(c_k,j_k \in \mathbb {R}\) with \(k= 1,\ldots ,4\) and \(v_1,v_2,t \in \mathbb {R}\), where \(R = h(A,v,y)\) is given by the data in Table 1.
Proof
The lemma follows directly from Proposition 2.8 in [8] and the fact that \(\mathfrak {h}^{\textit{III}} \cap \mathfrak {g}_1 = \emptyset \). \(\square \)
Some last piece of notation is necessary before stating the main theorem from [8] for Type III holonomy algebras. Therefore, define the following matrix algebras
Theorem 2
([9], Type III holonomy algebras) If \(\mathfrak {h}\) is of Type III, then there exists a basis of V such that we are in one of the following cases
-
1.
\(\mathfrak {h} = \mathfrak {a} \ltimes \mathfrak {m}(1,2)\) with \(\mathfrak {a} \in \{\mathfrak {gl}(2,\mathbb {R}),\mathfrak {sl}(2,\mathbb {R}),\mathfrak {co}(2),\mathfrak {d}\}\)
-
2.
\(\mathfrak {h} = \mathfrak {a} \ltimes \mathfrak {m}(1,k)\) with \(\mathfrak {a} \in \{\mathbb {R}\cdot \mathrm {diag}(1,0),0\}\), where \(k = 1,2\).
Proof
Let \(b_i\) be the basis chosen as in (2), with dual basis \(b^i\) as in (1). By [8] the three-dimensional socle S of \(\mathfrak {h}\) is spanned by \(b_1,b_2,b_3\), where the line spanned by \(\mathbb {R}\cdot b_1\) is isotropic. The socle splits under the semi-simple action of \(\mathfrak {h}\) into \(S = \mathbb {R}\cdot b_1 \oplus \hat{S}\), where \(\hat{S} = \mathrm {span}\{b_2,b_3\}\) (cf. [8]). Since \(\mathfrak {h}\) acts semi-simply on \(\hat{S}\), \(\mathfrak {a}\) acts semi-simply on \(\mathbb {R}^{2}\). Thus, \(\mathfrak {a} \in \{0,\mathfrak {gl}(2,\mathbb {R}),\mathfrak {sl}(2,\mathbb {R}\})\) or it is conjugated to one of the algebras \(\mathfrak {co}(2),\mathfrak {d},\mathbb {R}\cdot \mathrm {diag}(1,\mu )\) or \(\mathbb {R}\cdot C_a\).
First, exclude \(\mathfrak {a}=\mathbb {R}\cdot C_a\). In Table 1 this implies the system of linear equations
for an arbitrary parameter \(\alpha \in \mathbb {R}\). The system has only the trivial solution, which is a contradiction to Berger’s first criterion \(h(C_a,v_0,y_0) \in \underline{\mathfrak {h}}\), for some \(v_0 \in \mathbb {R}\) and \(y_0 \in \mathbb {R}^{2}\).
Next, note that in the remaining cases \(\mathfrak {v} = \left\{ v \in \mathbb {R} \;\big |\; h(0,v,y) \in \mathfrak {h}, y\in \mathbb {R}^2 \right\} \ne 0\). In order to see this assume \(\mathfrak {v} = 0\) and consider first the case \(\mathfrak {a} = \mathfrak {sl}(2,\mathbb {R})\). By indecomposability of the holonomy representation the kernel of \(\mathfrak {h}\) is necessarily isotropic. Then, for each \(A \in \mathfrak {a}\) there exists a unique element \(v_a\) such that \(h(A,v_a,y)\in \mathfrak {h}\) for some \(y \in \mathbb {R}^{2}\). Otherwise the non-isotropic vector \(b_4\) would be in \(\ker \mathfrak {h}\). The map \(\omega : A \mapsto v_A\) is a cocycle with respect to the representation \(\rho : \mathfrak {a} \rightarrow \mathfrak {gl}(\mathbb {R}) \cong \mathbb {R}\), \(\rho (A)v = \mathrm {tr}(A)\cdot v\), which is just the trivial representation in the case of \(\mathfrak {sl}(2,\mathbb {R})\). This can be easily seen by calculating \(v_{\left[ A,B\right] } = \mathrm {tr}(A) \cdot v_B - v_A \cdot \mathrm {tr}(B)\) via Eq. (3).
By semi-simplicity of \(\mathfrak {sl}(2,\mathbb {R})\) and Whitehead’s first lemma \(\omega \) is a coboundary such that \(v_A = \mathrm {tr}(A)\cdot \hat{v}\) for some \(\hat{v} \in \mathbb {R}\). Now, conjugating with the element \(\exp \!\left( h(0,\hat{v},0)\right) \) according to (4), the projection to \(\left\{ h(0,v,0) \;\big |\; v \in \mathbb {R} \right\} \) is trivial. This implies \(b_4 \in \ker \mathfrak {h}\) which is a contradiction to \(\ker \mathfrak {h}\) being necessarily isotropic. Hence, \(\mathfrak {v} \ne 0\).
For the other algebras one can argue similarly. Again, assume \(\mathfrak {v} = 0\) and by indecomposability \(\ker \mathfrak {h}\) is isotropic which implies the existence of a unique \(v_A\) for each \(A\in \mathfrak {a}\) such that \(h(A,v_a,y)\in \mathfrak {h}\) for some \(y \in \mathbb {R}^{2}\). The map \(\omega : A \mapsto v_A\) is still a cocycle. Now, there are two subcases: firstly, for the unit \(I\in \mathfrak {a}\), by above considerations, \(0 = v_{[I,A]} = I(v_A) - A(v_I)\) implies \(v_A = 2\,A \cdot v_I\). After conjugation with \(\exp (h(0,2\cdot v_I,0)\), the projection to \(\left\{ h(0,v,0) \;\big |\; v \in \mathbb {R} \right\} \) is again trivial and the contradiction follows as before. Secondly, for \(\mathfrak {a} = \mathbb {R}\cdot \mathrm {diag}(1,\mu )\) choose \(I' = \mathrm {diag}(1,\mu )\). Then, the same argument holds using \(I'\) instead of the unit I. For \(\mathfrak {a} = 0\) the proposition follows directly from indecomposability.
Next, by \(\mathfrak {v}\ne 0\), Table 1 obtains \(v_1 \ne 0\) or \(v_2 \ne 0\); hence, \(\mathfrak {y} = \left\{ y \in \mathbb {R}^2 \;\big |\; h(0,0,y) \in \mathfrak {h}\right\} \ne 0\).
Now, if \(\mathfrak {a} \in \{0,\mathfrak {gl}(2,\mathbb {R}),\mathfrak {sl}(2,\mathbb {R}),\mathfrak {co}(2)\}\) one has \(\mathfrak {y}=\mathbb {R}^{2}\), as there is no one-dimensional, invariant subspace of \(\mathbb {R}^{2}\). Thus, \(\mathfrak {a}\subset \mathfrak {h}\) and \(\mathfrak {h} \cap \mathfrak {m} = \mathfrak {m}(1,2)\), which implies \(\mathfrak {h} = \mathfrak {a} \ltimes \mathfrak {m}(1,2)\).
Assuming \(\mathfrak {a} \subset \mathfrak {d}\), it follows that the parameters in column A of Table 1 are identically zero, except \(d_1,c_4\). Table 1 immediately follows in the case \(\mathfrak {a} = \mathfrak {d}\) that \(\mathfrak {y} = \mathbb {R}^{2}\) and subsequently \(\mathfrak {h} = \mathfrak {d} \ltimes \mathfrak {m}(1,2)\). If \(\mathfrak {a} = \mathbb {R} \cdot \mathrm {diag}(1,\mu ) \subset \mathfrak {d}\), Table 1 implies \(\mu = 0\) and \(d_1 \ne 0\) such that, possibly after conjugation, \(\mathfrak {h} \cap \mathfrak {m} = \mathfrak {m}(1,k)\), \(k = 1,2\) and consequently \(\mathfrak {h} = \mathbb {R} \cdot \mathrm {diag}(1,0) \ltimes \mathfrak {m}(1,k)\).
Finally, in the case \(\mathfrak {a} = 0\) follows \(\mathfrak {y} = \mathbb {R}^{2}\) or \(\mathfrak {y} = (1,0)^{\top }\) in Table 1 after suitable conjugation. \(\square \)
3 Local Type III metrics
In this section a procedure is developed in order to construct (quasi-)normal forms for the metric induced by the \(\mathrm {G}_{2}^{*}\)-invariant 3-form \(\omega \) [cf. (1)]. Then, these (quasi-)normal forms are used to find metrics which realize each of the algebras in Theorem 2. This will prove Theorem 1. The approach is fairly the same used by Fino and Kath for Type I algebras [7].
Assume M has holonomy \(H \subset \mathrm {G}_{2}^{*}\). Then, M admits a torsion-free H-structure. Holonomy is here considered with respect to the metric g and the Levi-Civita connection \(\nabla \) induced by the \(\mathrm {G}_{2}^{*}\)-invariant (hence H-invariant) 3-form \(\omega \) as described in Sect. 2. Note, every torsion-free H-structure is 1-flat [4] and Cartan’s first structure equation is given by
where \(\eta : TP \rightarrow \mathbb {R}^{n}\) and \(\theta : TP \rightarrow \mathfrak {h}\) is the connection form associated with the Levi-Civita connection. Here, the principal bundle P is the reduction of the frame bundle along \(H \hookrightarrow \mathrm {G}_{2}^{*}\hookrightarrow \mathrm {GL}(7,\mathbb {R})\). Choosing a local frame \((b_i)\) in P the components of the connection form are given by \(\theta _{j}^{i} = b^{i}(\nabla b_j)\), where \((b^j)\) denotes the dual frame. For any tangent vector X one has \(b^{i}(\nabla b_j)(X)\)\(=b^{i}(\nabla _{X} b_j)\). The construction ‘machinery’ now consists of three steps. First, choose a local frame \((b_i)\) and write down the structure equations as an exterior differential system, where the connection form takes values in the holonomy algebra \(\mathfrak {h}\). Choosing local coordinates \(x_i\) on M, the frame is expressible in terms of local functions using exterior differential calculus methods, i.e., Frobenius theorem and suitable transformations of the local frame by elements of H. As the second step, use this adapted frame and calculate the components of the connection form, which reformulates as a PDE system for the local functions on M. With respect to this system lastly use Ambrose–Singer holonomy theorem [2] and calculate the components of the curvature tensor (and their covariant derivatives, if necessary; cf. [20]) such that they span the holonomy algebra \(\mathfrak {h}\).
In the relevant case of manifolds (M, g) with holonomy contained in \(\mathrm {G}_2^{*}\) the connection form takes values in the algebras of Theorem 2. Applying the approach described above, main Theorem 1 is proven in the following subsections by calculating a metric for each of the 8 cases.
Remark 2
Below bold letters denote differential 1-forms. Since the procedure is quite the same in each case, detailed calculations are provided in the first and most general one while omitting some details of these somewhat laborious calculations later on. Furthermore, note that all metrics finally turn out to be real analytic. This guarantees that the infinitesimal holonomy calculated in the following subsections coincides with the holonomy.
3.1 Holonomy of Type III 1a
Proposition 1
The holonomy of \((M^{4,3},g)\) is contained in \(\mathrm {G}_2^{*}\) and is of Type III 1a if and only if there are local coordinates \(x_1,\ldots ,x_7\) such that \(g = 2(b^1\cdot b^5 + b^2 \cdot b^6 + b^3\cdot b^7) - (b^4)^2\), where
with functions \(r_5,r_6,r_7,s_7\) given by
for arbitrary functions \(F_5,F_6,F_7\) and functions \(u,s_6,t_6,t_7,F_4\) satisfying the differential equations
Proof
The structure equation
implies that coordinates exist such that \(b^6,b^7\) lie in the ideal \(\mathscr {I}_0=\mathscr {I}(\mathrm {d}x_6,\mathrm {d}x_7)\) generated by \(\mathrm {d}x_6,\mathrm {d}x_7\). Transforming the basis pointwise with an appropriate element
yields \(b^6 = \mathrm {d}x_6\) and \(b^7 = \mathrm {d}x_7\). This implies \(\mathbf {a}_1,\ldots ,\mathbf {a}_4 \in \mathscr {I}_0\), since \( \mathrm {d}b^6 = \mathrm {d}\mathrm {d}x_6 = 0\) and \(\mathrm {d}b^7 = \mathrm {d}\mathrm {d}x_7 =0\). Furthermore, by \(\mathrm {d}b^5 \in \mathscr {I}(b^5)\) the structure equation implies \(b^5 = \mathrm {e}^{u} \cdot \mathrm {d}x_5 \) for a suitable local function u and coordinate \(x_5\). Since \(\mathbf {a}_1,\mathbf {a_4}\in \mathscr {I}_0\), one has \(u = u(x_5,x_6,x_7)\). Using the exponential of u here and in comparable cases has practical reasons, as it slightly simplifies some calculations.
From the structure equation deduce \(\mathrm {d}b^4 \in \mathscr {I}(\mathrm {d}x_5)\), the ideal generated by \(\mathrm {d}x_5\). Thus, \(b^4 = \mathrm {d}x_4 + q\cdot \mathrm {d}x_5\) and after a change of basis by a suitable element \(\exp (h(0,v,0))\) follows \(b^4 = \mathrm {d}x_4\). Then, \(\mathrm {d}b^4 = 0\) implies \(\mathbf {v} \in \mathscr {I}(\mathrm {d}x_5)\).
Since \(\mathbf {a}_1,\ldots ,\mathbf {a}_4 \in \mathscr {I}_0\) and \(\mathbf {v} \in \mathscr {I}(\mathrm {d}x_5)\), it follows from the structure equation that \(\mathrm {d}b^2\), \(\mathrm {d}b^3\in \mathscr {I}_1 = \mathscr {I}(\mathrm {d}x_5,\mathrm {d}x_6,\mathrm {d}x_7)\), the ideal generated by \(\mathrm {d}x_5,\mathrm {d}x_6,\mathrm {d}x_7\). This allows the assumption
Transforming the basis with an appropriate element \(\exp (h(0,0,(y_1,y_2)^{\top }))\) yields
Then,
implies
and \(\mathbf {y}_1,\mathbf {y}_2 \in \mathscr {I}_1\). Using the latter, \(\mathbf {a}_1,\ldots ,\mathbf {a}_4 \in \mathscr {I}_0\), \(\mathbf {v} \in \mathscr {I}(\mathrm {d}x_5)\) and the equation for \(\mathrm {d}b^1\), by an analogue consideration obtain
with functions
Now, with respect to the local coordinates and the metric defined above, the holonomy is contained in \(\mathrm {G}_2^{*}\) and of Type III 1a if and only if the following relations between the components of the local connection form are satisfied:
The remaining relations are either fulfilled trivially or identically zero, i.e., they do not contain any further information. The relations mentioned above lead to a system of partial differential equations given by
\(b^1 (\nabla b_1) = b^2 (\nabla b_2) +b^3 (\nabla b_3){:} \)
\(b^1 (\nabla b_4) = \sqrt{2}\cdot b^2 (\nabla b_7){:}\)
\( b^2 (\nabla b_1) = 0{:}\)
\( b^3 (\nabla b_1) = 0{:}\)
After some substitutions and integrations this system gives rise to the dependencies of \(r_5,r_6\), \(r_7,s_7\) on local coordinates as proposed in the theorem. Functions \(F_4,F_5,F_6,F_7\) are appropriate ‘integration constants,’ and Eqs. (6)–(9) are equivalent to the system of conditional equations for \(u,s_6,t_6,t_7,F_4\) as stated. \(\square \)
Example 1
One can easily check by direct calculation that the functions
satisfy Eqs. (6)–(9), and the metric defined by them has holonomy \(\mathfrak {h} = \mathfrak {gl}(2,\mathbb {R}) \ltimes \mathfrak {m}(1,2) \subset \mathfrak {h}^{I\!I\!I}\).
3.2 Holonomy of Type III 1b
Proposition 2
The holonomy of \((M^{4,3},g)\) is contained in \(\mathrm {G}_2^{*}\) and is of Type III 1a if and only if there are local coordinates \(x_1,\ldots ,x_7\) such that \(g = 2(b^1\cdot b^5 + b^2 \cdot b^6 + b^3\cdot b^7) - (b^4)^2\), where
with functions \(r_5,s_7\) given by
for arbitrary functions \(F_5,r_6,r_7\) and functions \(s_6,t_6,t_7,F_4\) satisfying the differential equations
Proof
The proof is essentially the same as in case 1a. The structure equation
implies the choice of \(b^5 = \mathrm {d}x_5\), since \(\mathrm {d}b^5 = 0\). Thus, set \(u\equiv 0\) in the proof of Proposition 1. Apart from that, following the same considerations as before proves Proposition 2.
Example 2
One can easily check that the functions
satisfy the conditional equations of the theorem and the metric defined that way has holonomy \(\mathfrak {h} = \mathfrak {sl}(2,\mathbb {R}) \ltimes \mathfrak {m}(1,2) \subset \mathfrak {h}^{I\!I\!I}\).
3.3 Holonomy of Type III 1c
Proposition 3
The holonomy of \((M^{4,3},g)\) is contained in \(\mathrm {G}_2^{*}\) and is of Type III 1c if and only if there are local coordinates \(x_1,\ldots ,x_7\) such that \(g = 2(b^1\cdot b^5 + b^2 \cdot b^6 + b^3\cdot b^7) - (b^4)^2\), where
with functions \(r_5, r_6, r_7,t_6,s_6,s_7, t_7 \) given by
for arbitrary functions \(F_5,F_6,F_7\) and functions \(u,v,F_1,\ldots ,F_4\) satisfying the differential equations
Proof
The structure equation
implies the existence of local coordinates \(y_6,x_7\) such that \(b^6,b^7\) lie in the ideal generated by \(dy_6,\mathrm {d}x_7\). Thus, assume
for suitable functions \(k_1,\ldots ,k_4\). Transforming the basis pointwise by an appropriate element
yields \(b^7 = \mathrm {d}x_7\) and \(b^6 = g_1 \cdot \mathrm {d}y_6 + g_2 \cdot \mathrm {d}x_7\) for some new functions \(g_1,g_2\). Since \(\mathrm {d}b^7=\mathrm {dd}x_7 = 0\), \(\mathbf {a}\) and \(\mathbf {b}\) lie in \(\mathscr {I}(\mathrm {d}y_6,\mathrm {d}x_7)\), the ideal generated by \(\mathrm {d}y_6\) and \(\mathrm {d}x_7\), and \(g_1,g_2\) depend on \(y_6,x_7\) only. Therefore, it is possible to introduce a new local coordinate \(x_6\) by
such that \(b^6 = \mathrm {d}x_6 + v(x_6,x_7) \cdot \mathrm {d}x_7\) with an appropriate function v. Consequently, one has \(\mathbf {a},\mathbf {b}\)\(\in \mathscr {I}(\mathrm {d}x_6,\mathrm {d}x_7)\).
The structure equation for \(\mathrm {d}b^5\) allows the choice \(b^5 = \mathrm {e}^{u} \cdot \mathrm {d}x_5\) for a suitable local function u and coordinate \(x_5\). Since \(\mathbf {a} \in \mathscr {I}(\mathrm {d}x_6,\mathrm {d}x_7)\), it follows \(u = u(x_5,x_6,x_7)\).
From the structure equation deduce \(b^4 = \mathrm {d}x_4 + q \cdot \mathrm {d}x_5\). After a change of basis using a suitable element \(\exp (h(0,v,0))\) obtain \(b^4 =\mathrm {d}x_4\) and \(\mathrm {d}b^4 = 0\). Hence, \(\mathbf {v} \in \mathscr {I}(\mathrm {d}x_5)\).
Next, the structure equation implies \(\mathrm {d}b^2,\mathrm {d}b^3 \in \mathscr {I}(\mathrm {d}x_5,\mathrm {d}x_6,dx_7)\), as \(\mathbf {a},\mathbf {b} \in \mathscr {I}(\mathrm {d}x_6,\mathrm {d}x_7)\), \(\mathbf {v} \in \mathscr {I}(\mathrm {d}x_5)\) and \(b^5 = \mathrm {e}^{u} \cdot \mathrm {d}x_5\). It follows
which reduces to
after transforming the basis with a suitable element \(\exp (h(0,0,(y_1,y_2)^{\top }))\). Comparing both sides of the equations
yields \(\mathbf {y}_1,\mathbf {y}_2\in \mathscr {I}(\mathrm {d}x_5,\mathrm {d}x_6,\mathrm {d}x_7)\) and
An analogue consideration for \(b^1\), keeping \(\mathbf {y}_1,\mathbf {y}_2\in \mathscr {I}(\mathrm {d}x_5,\mathrm {d}x_6,\mathrm {d}x_7)\) in mind, leads to
Again, the metric g is used, with respect to the local coordinates \(x_1,\ldots ,x_7\) considered so far, in order to calculate the components of the local connection form \(\theta \). The holonomy of g is contained in \(\mathfrak {co}(2) \ltimes \mathfrak {m}(1,2)\) if and only if the following relations between the components hold
The remaining relations are either trivial or identically satisfied. The relations give rise to the following system of partial differential equations
\(b^1 (\nabla b_1) = b^2 (\nabla b_2) +b^3 (\nabla b_3){:} \)
\( b^2 (\nabla b_2) = b^3 (\nabla b_3){:}\)
\(b^3 (\nabla b_2) = -b^2 (\nabla b_3){:}\)
\( b^1 (\nabla b_4) = \sqrt{2} b^2 (\nabla b_7){:}\)
\( b^2 (\nabla b_1) = 0{:}\)
\( b^3 (\nabla b_1) = 0{:}\)
The system can be solved by substitution and integration. Along with the integration one has to introduce new functions \(F_1,\ldots ,F_7\). Finally the system is equivalent to the form of functions \(r_5,r_6,r_7,t_6,t_7,s_6,s_7\) as stated in the proposition, except Eqs. (13) and (14) which are equivalent to conditional Eqs. (10) and (11). \(\square \)
Example 3
It is easy to verify that the functions given by the choice
satisfy the conditional equations, and that the holonomy, with respect to the metric g as defined, is \(\mathfrak {h} = \mathfrak {co}(2) \ltimes \mathfrak {m}(1,2)\).
3.4 Holonomy of Type III 1d
Proposition 4
The holonomy of \((M^{4,3},g)\) is contained in \(\mathrm {G}_2^{*}\) and is of Type III 1d if and only if there are local coordinates \(x_1,\ldots ,x_7\) such that \(g = 2(b^1\cdot b^5 + b^2 \cdot b^6 + b^3\cdot b^7) - (b^4)^2\), where
with functions \(r_5, r_6, r_7,s_6, t_7 \) given by
for arbitrary functions \(F_1,F_2,F_4,\ldots ,F_7\) and a function u satisfying the equations
where \(K_1,K_2\) are arbitrary functions.
Proof
The structure equation
allows the choice of \(b^6 = \mathrm {d}x_6\) and \(b^7 = \mathrm {d}x_7\) after changing the basis with a suitable element
Therefore, \(\mathbf {a} \in \mathscr {I}(\mathrm {d}x_6)\) and \(\mathbf {d} \in \mathscr {I}(\mathrm {d}x_7)\). The equation for \(\mathrm {d}b^5\) implies \(b^5 = \mathrm {e}^{u} \cdot \mathrm {d}x_5\) for a suitable local function u and coordinate \(x_5\). Then, \((\mathbf {a}+\mathbf {d}) \in \mathscr {I}(\mathrm {d}x_6,\mathrm {d}x_7)\) implies \(u = u(x_5,x_6,x_7)\).
Next, the equation for \(\mathrm {d}b^4\) implies \(b^4 = \mathrm {d}x_4 + q \cdot \mathrm {d}x_5\), and with a transformation using a suitable element \(\exp (h(0,v,0))\) one arrives at \(b^4 = \mathrm {d}x_4\). From \(\mathrm {d}b^4 = 0\) deduce \(\mathbf {v} \in \mathscr {I}(\mathrm {d}x_5)\).
Since \(\mathbf {a} \in \mathscr {I}(\mathrm {d}x_6)\), \(\mathbf {d} \in \mathscr {I}(\mathrm {d}x_7)\), \(\mathbf {v} \in \mathscr {I}(\mathrm {d}x_5)\) and \(b^5 = \mathrm {e}^{u} \cdot \mathrm {d}x_5\), from the structure equation follows \(\mathrm {d}b^2 \in \mathscr {I}(\mathrm {d}x_5,\mathrm {d}x_6)\) and \(\mathrm {d}b^3 \in \mathscr {I}(\mathrm {d}x_5,\mathrm {d}x_7)\). Thus, choose
and after a change of basis with an appropriate element \(\exp (h(0,0,(y_1,y_2)^{\top }))\) obtain
Comparing both sides of the equations
yields \(\mathbf {y}_1,\mathbf {y}_1 \in \mathscr {I}(\mathrm {d}x_5,\mathrm {d}x_6,\mathrm {d}x_7)\), \(s_6=s_6(x_2,x_5,x_6)\) and \(t_7 = t_7(x_3,x_5,x_7)\).
Finally the structure equation implies \(\mathrm {d}b^1 \in \mathscr {I}(\mathrm {d}x_5,\mathrm {d}x_6,\mathrm {d}x_7)\) so that the assumption
is possible. Comparing the expressions for \(\mathrm {d}b^1\)
leads to the dependencies
Using the metric g with respect to the local coordinates allows the calculation of the components of the local connection form. The holonomy of g is contained in \(\mathfrak {d} \ltimes \mathfrak {m}(1,2)\) if and only if the following relations are satisfied:
These relations are equivalent to the following partial differential system:
\(b^1 (\nabla b_1) = b^2 (\nabla b_2) +b^3 (\nabla b_3){:} \)
\(b^1 (\nabla b_4) = \sqrt{2} \cdot b^2 (\nabla b_7){:} \)
\( b^2 (\nabla b_1) = 0{:}\)
\( b^3 (\nabla b_1) = 0{:}\)
which can be easily integrated and yield the form of functions \(r_5,r_6,r_7,s_6,t_7\) as stated in the proposition. Since \(s_6\) and \(t_7\) depend on \(x_5,x_6\) and \(x_5,x_7\), respectively, Eqs. (15) and (16) give rise to the constraints on the derivatives of u. \(\square \)
Example 4
With the choice
the conditional equations are fulfilled and the holonomy with respect to the metric defined by that functions is \(\mathfrak {h} = \mathfrak {d} \ltimes \mathfrak {m}(1,2)\).
3.5 Holonomy of Type III 2a
Proposition 5
The holonomy of \((M^{4,3},g)\) is contained in \(\mathrm {G}_2^{*}\) and is of Type III 2a if and only if there are local coordinates \(x_1,\ldots ,x_7\) such that \(g = 2(b^1\cdot b^5 + b^2 \cdot b^6 + b^3\cdot b^7) - (b^4)^2\), where
with functions \(r_5,r_6\) given by
and \(F_5, F_6\) are arbitrary.
Proof
Obviously, the structure equation
allows the choice of \(b^7 = \mathrm {d}x_7\). Furthermore, it implies \(b^5 = u \cdot \mathrm {d}x_5\) and \(b^6 = v' \cdot \mathrm {d}x_6\) for appropriate functions \(u,v'\) and local coordinates \(x_5,x_6\). Changing the basis by an element
one obtains \(b^5 = \mathrm {d}x_5\) and \(b^6 =\mathrm {d}x_5+ v \cdot \mathrm {d}x_5\) with a new function v. Since \(\mathrm {d}b^5 = 0\), it follows that \(\mathbf {x} \in \mathscr {I}(\mathrm {d}x_5)\). Thus, \(v = v(x_5,x_6)\).
Next, the structure equation allows the choice \(b^4 = \mathrm {d}x_4 + q \cdot \mathrm {d}x_5\). Transforming with a suitable element \(\exp (h(0,v,0))\) results in \(b^4 = \mathrm {d}x_4\) and therefore \(\mathbf {v} \in \mathscr {I}(\mathrm {d}x_5)\).
Similar, the equation for \(\mathrm {d}b^3\) implies \(\mathrm {d}b^3 \in \mathscr {I}(\mathrm {d}x_5)\), since \(\mathbf {v} \in \mathscr {I}(\mathrm {d}x_5)\), which is why it is possible to choose \(b^3 = \mathrm {d}x_3 + t_5 \cdot \mathrm {d}x_5\). Comparing both sides of
gives \(t_5 = t_5(x_5,x_6)\). From the structure equation deduce \(\mathrm {d}b^2 \in \mathscr {I}(\mathrm {d}x_5)\), as \(\mathbf {x},\mathbf {v} \in \mathscr {I}(\mathrm {d}x_5)\). This allows the choice
and transforming the basis with an appropriate element \(\exp (h(0,0,(y_1,0)^{\top }))\) leads to \(b^2 = \mathrm {d}x_2\).
Finally, the structure equation implies, since \(b^6 \in \mathscr {I}(\mathrm {d}x_5,\mathrm {d}x_6)\) and \(\mathbf {x},\mathbf {v}\in \mathscr {I}(\mathrm {d}x_5)\), \(\mathrm {d}b^1 \in \mathscr {I}(\mathrm {d}x_5,\mathrm {d}x_6)\) such that the choice
is allowed. The dependencies of functions \(r_5,r_6\) on the local coordinates are due to
and result in \(r_5 = r_5(x_1,x_2,x_4,x_5,x_6,x_7)\) and \(r_6 = r_6(x_2,x_5,x_6,x_7)\).
Now, the metric g, with respect to the local coordinates, is used to calculate the components of the local connection form. The holonomy of g is contained in \(\mathbb {R}\cdot \mathrm {diag}(1,0) \ltimes \mathfrak {m}(1,1)\) if and only if the following relations between the components are satisfied
These relations form a system of partial differential equations given by
\(b^1 (\nabla b_1) = b^2 (\nabla b_2){:}\)
\(b^1 (\nabla b_4) = \sqrt{2} b^2 (\nabla b_7){:}\)
\(b^1 (\nabla b_2) = 0{:} \)
\(b^1 (\nabla b_7) = 0{:} \)
Straightforward substitution and integration lead to expressions for \(r_5,r_6\) as stated in the theorem, while \(v,t_5\) and functions \(F_5,F_6\), which arise by integration, are arbitrary. \(\square \)
Example 5
It is easy to verify that with the choice
the holonomy of (M, g) is \(\mathfrak {h} = \mathbb {R}\cdot \mathrm {diag}(1,0) \ltimes \mathfrak {m}(1,1)\).
3.6 Holonomy of Type III 2b
Proposition 6
The holonomy of \((M^{4,3},g)\) is contained in \(\mathrm {G}_2^{*}\) and is of Type III 2b if and only if there are local coordinates \(x_1,\ldots ,x_7\) such that \(g = 2(b^1\cdot b^5 + b^2 \cdot b^6 + b^3\cdot b^7) - (b^4)^2\), where
with functions \(r_5, r_6\) of the form
for arbitrary functions \(v,F_5,F_6\).
Proof
The structure equation
allows the choice of \(b^7 = \mathrm {d}x_7\). Next, the equations for \(\mathrm {d}b^5\) and \(\mathrm {d}b^6\) imply \(b^5 = u \cdot \mathrm {d}x_5\) and \(b^6 = v' \cdot \mathrm {d}x_6\). Transforming the basis with an element
yields \(b^5 = \mathrm {d}x_5\), \(b^6 = \mathrm {d}x_6+ v \cdot \mathrm {d}x_5\) and \(\mathbf {x} \in \mathscr {I}(\mathrm {d}x_5)\), since \(\mathrm {d}b^5 = 0\). It follows \(v = v(x_5,x_6)\).
From the structure equation deduce \(\mathrm {d}b^4 \in \mathscr {I}(\mathrm {d}x_5)\), which is why the choice \(b^4 = \mathrm {d}x_4 + q \cdot \mathrm {d}x_5\) is feasible. A change of basis with an appropriate element \(\exp (h(0,v,0))\) leads to \(b^4 = \mathrm {d}x_4\). Consequently, one has \(\mathbf {v} \in \mathscr {I}(\mathrm {d}x_5)\), as \(\mathrm {d}b^4 = 0\).
Next, the structure equation implies \(\mathrm {d}b^2,\mathrm {d}b^3 \in \mathscr {I}(\mathrm {d}x_5)\), since \(\mathbf {x},\mathbf {v} \in \mathscr {I}(\mathrm {d}x_5)\) and \(b^5 = \mathrm {d}x_5\). Then,
and after transforming with a suitable element \(\exp (h(0,0,(y_1,y_2)^{\top }))\) obtain \(b^2 = \mathrm {d}x_2\) and \(b^3 =\mathrm {d}x_3\). This implicates \(\mathbf {y}_1 \in \mathscr {I}(\mathrm {d}x_2,\mathrm {d}x_5,\mathrm {d}x_6)\) and \(\mathbf {y}_2 \in \mathscr {I}(\mathrm {d}x_5,\mathrm {d}x_6)\).
Finally, as \(\mathbf {v} \in \mathscr {I}(\mathrm {d}x_5)\), \(\mathbf {y}_2 \in \mathscr {I}(\mathrm {d}x_5,\mathrm {d}x_6)\) and \(b^6 = \mathrm {d}x_6 + v\cdot \mathrm {d}x_5\), one has \(\mathrm {d}b^1 \in \mathscr {I}(\mathrm {d}x_5,\mathrm {d}x_6)\) by the structure equation. Thus,
and from the equation
obtain \(r_5 = r_5(x_1,x_2,x_4,x_5,x_6,x_7)\) and \(r_6 = r_6(x_2,x_5,x_6,x_7)\).
Consider the metric g with respect to the local coordinates given as above. The holonomy of g is contained in \(\mathbb {R}\cdot \mathrm {diag}(1,0)\ltimes \mathfrak {m}(1,2)\) if and only if the following relations between the components of the local connection form hold:
The system of partial differential equations associated with these relations is given by
\(b^1 (\nabla b_1) = b^2 (\nabla b_2){:}\)
\(b^1 (\nabla b_4) = \sqrt{2} b^2 (\nabla b_7){:}\)
\(b^1 (\nabla b_2) = 0{:}\)
Again, the system can be solved straightforward by substitution and integration in order to obtain the form of functions \(r_5,r_6\) as stated in the theorem. New functions \(F_5,F_6\), arising due to integration, and function v are arbitrary. \(\square \)
Example 6
By simple calculations one can check that the choice
leads to a metric with holonomy \(\mathfrak {h} = \mathbb {R} \cdot \mathrm {diag}(1,0) \ltimes \mathfrak {m}(1,2)\).
3.7 Holonomy of Type III 2c
Proposition 7
The holonomy of \((M^{4,3},g)\) is contained in \(\mathrm {G}_2^{*}\) and is of Type III 2c if and only if there are local coordinates \(x_1,\ldots ,x_7\) such that \(g = 2(b^1\cdot b^5 + b^2 \cdot b^6 + b^3\cdot b^7) - (b^4)^2\), where
with functions \(r_5,r_7\) given by
for arbitrary functions \(t_5,F_5,F_7\) which fulfill
Proof
Obviously, the structure equation
allows the choices \(b^5 = \mathrm {d}x_5\), \(b^6 = \mathrm {d}x_6\), \(b^7 = \mathrm {d}x_7\). Furthermore, \(\mathrm {d}b^4 \in \mathscr {I}(\mathrm {d}x_5)\) such that \(b^4 = \mathrm {d}x_4 + q \cdot \mathrm {d}x_5\) can be chosen. A change of basis with an element \(\exp (h(0,v,0))\) yields \(b^4 = \mathrm {d}x_4\), \(\mathrm {d}b^4 = 0\) and \(\mathbf {v} \in \mathscr {I}(\mathrm {d}x_5)\). Using the latter, the structure equation implies \(\mathrm {d}b^3 \in \mathscr {I}(\mathrm {d}x_5)\). Thus, choose \(b^3 = \mathrm {d}x_3 + t_5 \cdot \mathrm {d}x_5\) and by comparing the expressions for \(\mathrm {d}b^3\) we have \(t_5 =t_5(x_5,x_6)\).
Next, from the structure equation deduce \(\mathrm {d}b^2 \in \mathscr {I}(\mathrm {d}x_5)\) which leads to \(b^2 = \mathrm {d}x_2 + s_5 \cdot \mathrm {d}x_5\). After a transformation with a suitable element \(\exp (h(0,0,(y_1,0)^{\top }))\) obtain \(b^2 = \mathrm {d}x_2\) and \(\mathbf {y}_1 \in \mathscr {I}(\mathrm {d}x_5,\mathrm {d}x_7)\).
Lastly, \(\mathrm {d}b^1 \in \mathscr {I}(\mathrm {d}x_5,\mathrm {d}x_7)\) by the structure equation and \(\mathbf {y}_1 \in \mathscr {I}(\mathrm {d}x_5,\mathrm {d}x_7)\). Thus,
and by comparing both sides of
leads to \(r_5 =r_5 (x_4,x_5,x_6,x_7)\) and \(r_7 = r_7(x_5,x_6,x_7)\).
With respect to the local coordinates, the metric g has holonomy contained in \(\mathfrak {m}(1,1)\) if and only if the following relations between the components of the local connection form are satisfied:
This is equivalent to the partial differential system
\(b^1 (\nabla b_4) = \sqrt{2} \cdot b^2 (\nabla b_7){:} \)
\( b^1 (\nabla b_7) = 0{:}\)
Solving the system by integration and substitution gives rise to the dependencies of \(r_5,r_6\) on \(t_5\) and new functions \(F_5,F_7\) as proposed in the proposition. The latter functions are arbitrary. \(\square \)
Example 7
With the choice
it is simple to check that the holonomy of the corresponding metric g is \(\mathfrak {h} = \mathfrak {m}(1,1)\).
3.8 Holonomy of Type III 2d
Proposition 8
The holonomy of \((M^{4,3},g)\) is contained in \(\mathrm {G}_2^{*}\) and is of Type III 2d if and only if there are local coordinates \(x_1,\ldots ,x_7\) such that \(g = 2(b^1\cdot b^5 + b^2 \cdot b^6 + b^3\cdot b^7) - (b^4)^2\), where
with \(r_5\) is of the form
for arbitrary functions \(r_6\) and F.
Proof
The structure equation
allows the choice of \(b^5 = \mathrm {d}x_5\), \(b^6 = \mathrm {d}x_6\), \(b^7 = \mathrm {d}x_7\). As a consequence one has \(\mathrm {d}b^4 \in \mathscr {I}(\mathrm {d}x_5)\) such that one can choose \(b^4 = \mathrm {d}x_4 +q \cdot \mathrm {d}x_5\). A change of basis with a suitable element \(\exp (h(0,v,0))\) leads to \(b^4 = \mathrm {d}x_4\) and \(\mathbf {v} \in \mathscr {I}(\mathrm {d}x_5)\), since \(\mathrm {d}b^4 = 0\).
Next, using \(\mathbf {v} \in \mathscr {I}(\mathrm {d}x_5)\), the structure equation implies \(\mathrm {d}b^2,\mathrm {d}b^3 \in \mathscr {I}(\mathrm {d}x_5)\) such that the assumption \(b^2 = \mathrm {d}x_2 + s_5 \cdot \mathrm {d}x_5\) and \(b^3 = \mathrm {d}x_3 + t_5 \cdot \mathrm {d}x_5\) is possible. After a transformation using an appropriate element \(\exp (h(0,0,(y_1,y_2)^{\top }))\) obtain \(b^2 = \mathrm {d}x_2\) and \(b^3 = \mathrm {d}x_3\). Consequently, \(\mathbf {y}_1 \in \mathscr {I}(\mathrm {d}x_5,\mathrm {d}x_7)\) and \(\mathbf {y}_2 \in \mathscr {I}(\mathrm {d}x_5,\mathrm {d}x_7)\) by the structure equation.
Finally, this implies \(\mathrm {d}b^1 \in \mathscr {I}(\mathrm {d}x_5,\mathrm {d}x_6)\), since \(\mathbf {v} \in \mathscr {I}(\mathrm {d}x_5)\) and \(b^6 =\mathrm {d}x_6\). Thus,
and comparing both sides of
yields \(r_5 =r_5(x_4,x_5,x_6,x_7)\) and \(r_6 = r_6(x_5,x_6,x_7)\).
A metric g as given by the proposition has, with respect to the local coordinates, holonomy contained in \(\mathfrak {m}(1,2)\) if and only if the relation
between the components of the local connection form is satisfied. This results in the partial differential equation
which is, by integration, equivalent to the stated dependence of \(r_5\) on \(r_6\) and a new function F. \(\square \)
Example 8
It is easy to check that the metric g associated with the choice
has holonomy \(\mathfrak {h} = \mathfrak {m}(1,2)\).
Remark 3
The algebras of Type III 2c and 2d are Abelian and of dimension two or three. In [16], indefinite symmetric spaces were classified and it turned out that their holonomy algebras are also Abelian and of dimension two or three. They indeed coincide, which can be seen by an appropriate change in notation. Thus, the algebras of Type III 2c and 2d are holonomy algebras of (locally) symmetric spaces.
References
Agricola, I.: Old and new on the exceptional group \(G_2\). Notices Amer. Math. Soc. 55(8), 922–929 (2008)
Ambrose, W., Singer, I.M.: A theorem on holonomy. Trans. Amer. Math. Soc. 75(3), 428–443 (1953). http://www.jstor.org/stable/1990721
Berger, M.: Sur les groupes d’holonomie homogene des variétés à connexion affine et des variétés riemanniennes. Bull. Soc. Math. France 83, 279–330 (1955)
Bryant, R.L.: Metrics with exceptional holonomy. Ann. Math. 126, 525–576 (1987)
Cartan, Élie: Sur une classe remarquable d’espaces de Riemann. Bulletin de la Société Mathématique de France 54, 214–264 (1926)
Engel, F.: Ein neues, dem linearen Komplexe analoges Gebilde. Berichte der Sächsischen Akademie der Wissenschaften 52(63–76), 220–239 (1900)
Fino, A., Kath, I.: Local Type I Metrics with Holonomy in \({\rm G}_{2}^*\). https://doi.org/10.3842/SIGMA.2018.081
Fino, A., Kath, I.: Holonomy groups of \(G_2^{\ast }\)-manifolds. arXiv:math.DG/1604.00528v1 (2016)
Fino, A., Luján, I.: Torsion-free G*2(2)-structures with full holonomy on nilmanifolds. Adv. Geom. 15, (2015). https://doi.org/10.1515/advgeom-2015-0015
Fulton, W., Harris, J.: Representation Theory. Springer study edition. Springer, New York, NY [u.a.] (2004). Includes bibliographical references and index
Galaev, A.S.: Holonomy Groups of Lorentzian Manifolds. https://doi.org/10.1070/RM2015v070n02ABEH004947
Galaev, A.S.: Holonomy classification of Lorentz-Kähler manifolds. J. Geom. Analy. 1–34 (2016). https://doi.org/10.1007/s12220-018-0027-1
Galaev, A.S.: Holonomy algebras of Einstein pseudo-Riemannian manifolds. J. Lond. Math. Soc. 98(2), 393–415 (2018)
Graham, C.R., Willse, T.: Parallel tractor extension and ambient metrics of holonomy split \(G_2\). J. Differential Geom. 92, 463–506 (2012). https://doi.org/10.4310/jdg/1354110197
Kath, I.: \(G_{2(2)}^{\ast }\)-structures on pseudo-Riemannian manifolds. J. Geom. Phys. 27(3–4), 155–177 (1998)
Kath, I.: Indefinite symmetric spaces with \(G_{2(2)}\)-structure. J. Lond. Math. Soc. 87(3), 853–876 (2013). https://doi.org/10.1112/jlms/jds068
Leistner, T.: On the classification of Lorentzian holonomy groups. J. Differential Geom. 76(3), 423–484 (2007)
Leistner, T., Nurovski, P.: Ambient metrics with exceptional holonomy. Ann. Sc. Norm. Super. Pisa Cl. Sci. 5(11), 407–436 (2012)
Niedzialomski, K.: Geometry of \(g\)-structures via the intrinsic torsion. https://doi.org/10.3842/SIGMA.2016.107
Ozeki, H.: Infinitesimal holonomy groups of bundle connections. Nagoya Math. J. 10, 105–123 (1956)
Reichel, W.: Über trilineare alternierende Formen in sechs und sieben Veränderlichen und die durch sie definierten geometrischen Gebilde. Ph.D. thesis, Universität Greifswald (1907)
Acknowledgements
I am very grateful to Ines Kath for introducing me into the field of holonomy theory as well as her support and useful advices on this article.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Volkhausen, C. Local Type III metrics with holonomy in \(\mathrm {G}_2^*\). Ann Glob Anal Geom 56, 113–136 (2019). https://doi.org/10.1007/s10455-019-09659-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10455-019-09659-8