Dynamic column breakthrough experiments for measurement of adsorption equilibrium and kinetics

Abstract

This paper provides a set of comprehensive guidelines for the use of dynamic column breakthrough experiments to measure single and multi-component equilibria and kinetics. Recommendations are made for the design of the experimental rig, experimental procedures, and data processing methods to minimize errors and increase data reliability. Designing experiments to identify the transport mechanism, and quantitatively interpreting the breakthrough responses via modeling and optimization are also enumerated. Results reported in relevant published literature are also used to illustrate the ideas and concepts.

1 Introduction

The response observed at the exit of an adsorbent packed column to a step-change in the concentration of one or more absorbable component(s) in the feed is the breakthrough response of the column. A breakthrough response contains both equilibrium and kinetic information of the adsorbate in adsorbent pores. The residence time of the response contains equilibrium information, and its spread contains kinetic information. Both of these are affected by the dead volume of the breakthrough apparatus. Hence, central to the usefulness of a breakthrough study is firstly to properly design the apparatus to minimize dead volume before and after the column, and then to apply an appropriate method to correct the effects of the dead volume on the residence time and spread of the concentration breakthrough front. The corrected breakthrough responses may then be analysed to extract adsorption equilibrium (data or isotherm model parameters) and mass transfer rate constants, and even some idea of the transport mechanism if the experiments are carefully designed. A breakthrough experiment may be easily extended to measure mixture equilibrium. The breakthrough responses also capture axial dispersion and heat transfer characteristics in an adsorption column, thus allowing an avenue to check the validity of available correlations for an a priori estimation of axial dispersion for flow through the packed bed, and heat transfer coefficients at the column wall. At the process level, a breakthrough study is useful to validate mixture equilibrium and kinetic models that constitute a complete process simulation model. Variants of breakthrough experiments may also be designed to validate the model for each step of a cyclic process individually.

In this article, we provide recommendations for designing a breakthrough experimental rig and then discuss the experimental procedure and analysis of a breakthrough response for single component equilibrium measurements. We further show how it can be easily extended to measure multi-component equilibrium. After that, we discuss its usefulness as a tool to characterize adsorption kinetics in the context of the literature available on this important experimental technique. For the sake of brevity, the review is focussed on gas adsorption. While parallels can be drawn to liquid phase systems, we advise caution in doing so. In liquid systems, solute concentrations are low, columns are efficient owing to the use of smaller particle sizes, and thermal effects are usually negligible. These aspects, as will be shown later, cannot be ignored in gas systems. A detailed description of extracting equilibrium and kinetic information from liquid phase adsorption breakthrough studies can be found elsewhere (Guiochon et al. 2006; Seidel-Morgenstern 2004). The reader is referred to standard textbooks to be conversant with the fundamental principles that govern adsorption processes (Ruthven 1984; Ruthven et al. 1994; Wankat 1986; Yang 2013). Finally, the literature is replete with breakthrough studies, and it is not the aim of this work to provide a comprehensive review. Instead, the goal is to propose recommendations for setting-up and analysing breakthrough experiments and provide a limited set of examples.

2 Recommendations for the design of an experimental rig

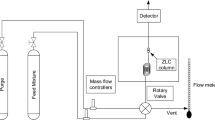
A representative schematic of a breakthrough apparatus is shown in Fig. 1. The abbreviations and significance of the various lines are explained in the figure caption. The adsorption column is packed with the adsorbent under investigation. The mass flow controllers (MFCs) help control the feed flow rate and composition at the desired level. The mass flow meter (MFM) measures the flow leaving the adsorption column. In the figure, a mass-spectrometer (MS) is used to represent any instrument used to analyze the gas composition leaving the column as a function of time. The use of an inline mass spectrometer will give the flexibility of studying a wide variety of gases and their mixtures. The back-pressure regulator (BPR) is used to control the column pressure at the desired level. The valves (V1–9) are used to guide the flow and introduce a step-change in concentration at the column inlet. The pressure indicators (PIs) at the column inlet and outlet keep track of the operating pressure and pressure drop across the column. The column is immersed in a circulating water bath connected to a thermostat to help maintain a constant column wall temperature.

Fig. 1

Schematic of a breakthrough apparatus. MFC flow controller, MFM flow meter, MS mass spectrometer/gas chromatograph/effluent analyser, NV needle valve, PI, TI pressure, temperature indicators, V1–9 valves. Black lines (K): common, green lines (G): measurement of column response including extra-column volume, red line (R): bypass lines for measurement of extra-column volume, purple line (P): flow stabilization, grey line (Y): for column regeneration (Color figure online)

Industrial adsorption processes operate close to adiabatic conditions. However, for lab-scale experiments, specifically, where the quantity of adsorbent available is in the gram-scale, it is difficult to achieve the adiabatic limit. Hence, it is a common practice to use temperature-controlled systems to remove heat so that isothermal conditions can be approached. Water cooling is more effective than air cooling to remove the heat of adsorption. Water circulation can adequately maintain the temperature above its freezing point and below its boiling point at atmospheric pressure. Fluids are available to operate at a modest temperature below the freezing point or above the boiling point of water. Typically, an adsorbent bed is first regenerated by a combination of heating (while purging with an inert gas, typically helium) and periodically pulling a vacuum. If the required regeneration temperature is very high (like in the case of zeolites), either heating in a high-temperature oven or furnace or heating in-situ, using heating tapes or a jacket furnace, may be required. The vacuum pump is used to periodically pull a vacuum while heating. This enhances the effectiveness of regeneration. The thermocouples (TI) are located along the column length in order to monitor the adsorbent bed temperature during breakthrough runs. A needle valve (NV) is placed between the MFM and BPR to send part of the column exit gas to the composition analyzer (MS). The rig can be fully automated for operation and data acquisition by replacing the manual valves with solenoid valves, and analog pressure and temperature indicators with electronic devices capable of sending and receiving electronic signals.

The green lines before and after the adsorption column represent the dead volume. Additional dead volumes can arise from tubing, fittings, instruments, portions of the column that are either empty or filled with glass-wool or other inert solids. While the dead volume cannot be completely eliminated, every attempt has to be made to minimize it. Whatever dead volume remains should be measured and corrected from the total response. The red line is used to bypass the column in order to measure the dead volume. It is known as the dead volume or blank correction. The purple line is used to stabilize the flow before introducing a step-change in the adsorbate concentration at the column inlet. A mass flow controller takes some time to reach the set point. This is not a problem when we can allow a long residence time of the adsorbate in the adsorption column. When we deal with a weakly adsorbing system and/or we have only a small amount of the adsorbent for testing, then it is advisable to use the flow stabilization line. If solenoid valves are used, this will give almost an ideal step-change without any noise. If there is any concern about the complete mixing of the feed mixture prepared in situ, that may be solved by either using premixed gas cylinders or a short mixing tube in the feed line.

In addition to the above, the following recommendations are made for obtaining reliable breakthrough data. The diameter of the column should be at least 10 times of the adsorbent particle diameter in order to reduce the channeling effect at the wall. It is also recommended that the column length to diameter ratio is greater than 3. The column length should be chosen to ensure that the dead volume is not dominant. In other words, care should be taken to ensure that the mean residence time of the blank run is not more than 20 to 30% of the uncorrected mean residence time of the column response. This becomes a problem when only a small amount of a newly synthesized adsorbent is available, and breakthrough is measured for a weakly adsorbing adsorbate. Pressure measurements at the inlet and exit are important for correctly estimating equilibrium capacity. Increasing the flow rate increases the pressure drop and decreases the residence time. Low flow rates are recommended if only an equilibrium measurement is the target of the experiment. An appropriate choice of length to velocity ratio becomes critical when we also want to extract kinetic information from a breakthrough study. The adsorbent should be regenerated before experimentation and periodically in between runs. During regeneration, the column should be slowly heated to the required regeneration temperature and alternated between purging with an inert gas and pulling a vacuum for more effective regeneration. A table (Table S1) summarizing these guidelines is provided in the Supporting Information.

3 Experimental protocol and sample breakthrough responses

First in the protocol is to make the experimental rig leak proof. The column should be pressurized to the maximum pressure level expected in the investigation, and the pressure must be held for the duration of the longest experiment. Although the flow controllers and the flow meter are factory calibrated, they will change over time. Also, the calibration conditions at the factory may be different from actual experimental conditions in the laboratory. Hence in-situ flow calibration against an independent standard like a bubble flow meter or any other hand-held flow calibrator is recommended. The flow controllers facilitate the preparation of various mixture compositions in order to calibrate the detector. Having a stable baseline of the detector for the inert carrier gas, helium, for example, is essential. The baseline may drift if the breakthrough run is very long. Therefore, baseline drift should be checked and corrected. Unless we are dealing with very strongly adsorbing gases, purging with the inert gas and pulling vacuum for some time may be sufficient for regenerating in between runs. The dead volume must be measured at the same flow and pressure conditions as in the actual experiment while bypassing the column using the red line (c.f. Figure 1). It is indeed advantageous if the dead volume correction is negligible. However, this should be an informed decision and not an assumption.

After regeneration, the column and the detector are initialized by flowing an inert gas such as helium. This is done by opening valves V1, V4, V5, and V6. In this case, V4 (c.f. Figure 1) is opened toward the green line. The BPR and the thermostat are set at the desired levels. The gas will flow all the way up to the vent with a small stream taken to the detector. Valves V4 and V6 are closed once the detector stabilizes at the baseline. The next step is to set the flow and composition of helium and the adsorbate (CO₂, for example) to be tested in the MFCs, and open V9 to stabilize the flow. The BPR in this line is also adjusted to the same pressure level used to initialize the column. The second BPR in the purple line is required to ensure that the flow does not reach the detector, so the baseline is not disturbed. Once the MFCs stabilize, a step change of the adsorbate concentration to the column inlet is introduced by simultaneously opening valves V4 and V6, and closing V9. Again, V4 is opened towards the green line. The response at the column exit is monitored until the detector signal reaches a stable constant value, the bed temperature returns to the initial value, the exit mole fraction of the adsorbate becomes equal to the inlet fraction, and the total outlet flow also becomes equal to the inlet flow. This marks the end of the adsorption breakthrough experiment.

The outcome of the experimental procedure narrated above is schematically shown in Fig. 2. In order to illustrate this, we consider a common test system of CO₂ (adsorbate) and He (inert). Naturally, the same discussion will apply to any other system. In Fig. 2a, the input graph shows that a controlled constant flow of a CO₂/He mixture is introduced as a step-change in the adsorbate mole fraction at the column inlet. The corresponding responses measured at the exit are shown on the right under output. CO₂ is retained by the adsorbent, and depending on the absorbent capacity and the feed flow rate, it will take some time to show up at the exit. Until CO₂ leaves the column, only the inert helium fraction of the feed flow will leave at the other end, so there will be a reduction in the exit flow rate compared to the inlet flow. The fractional reduction of the exit flow is a good indication of the mole fraction of CO₂ in the feed. In the plot, the exit flow rate normalized with the feed flow rate, $\left(\frac{Q\left(t\right)}{{Q}_{\mathrm{in}}}\right),$ begins at 0.7, which is an indication that the CO₂ mole fraction in the feed is about 0.3. The exit flow rate will rise along with the rise of CO₂ in the exit stream. This is the beginning of the breakthrough and will continue until the exit flow rate and CO₂ mole fraction both become equal to the inlet valves. The temperature curves are not shown here to keep things simple. However, in an actual experiment, it is also important to check that the entire bed has returned to the feed temperature. The output of a step-change in CO₂ concentration at the inlet yields a very spread out response at the exit. We will discuss later that, under isothermal conditions and for a system that obeys a type-I isotherm, this is a consequence of the mass transfer resistance encountered by CO₂ to diffuse from the bulk to the pore interior adsorption sites, and axial dispersion in the adsorption column and dead volume. It is also influenced by the shape of the equilibrium isotherm and, under non-isothermal conditions, by the heat generated by the exothermic adsorption.

Fig. 2

Representative dimensionless concentration and flow curves measured at the column exit for a adsorption and b desorption breakthrough. y_in in b is the adsorbate mole fraction in the feed during the adsorption breakthrough run

At this point, if we want to measure the desorption breakthrough, one choice is to just close valve V2. This will introduce a reverse step change in concentration at the inlet, but the desorption run will be at a reduced flow rate. In order to conduct the desorption run at the same flow rate as the adsorption step, valves V4 and V6 are closed, and valve V9 is opened. Valve V2 is closed to stop the CO₂ flow, and the helium flow is adjusted to make it equal to the total feed flow rate of the adsorption run. Valves V4 and V6 are opened, and V9 is closed simultaneously after allowing some time for the increased helium flow to stabilize. The figures on the second row are for a helium flow rate equal to the feed flow rate in the adsorption run. Pure helium flows through the bed and eventually completely desorbs all the adsorbate (CO₂ in our discussion) from the bed for a reversible physical adsorption process. The desorbing CO₂ is added to the inlet helium flow, so now the flow rate increases at the exit, as may be seen from $\left(\frac{Q\left(t\right)}{{Q}_{\mathrm{in}}}\right)>1$ on the second y-axis. Starting from the feed mole fraction attained at the end of the previous run, shown as $\left(\frac{y\left(t\right)}{{y}_{\mathrm{in}}}=1\right),$ the CO₂ mole fraction drops monotonically to zero when all the adsorbed CO₂ has been desorbed. The exit flow rate, starting from a higher value than that at the inlet, also drops to ultimately become equal to the flow rate at the inlet when CO₂ desorption is complete. Unless the CO₂ concentration is in the linear range of the isotherm, the desorption curve is mostly governed by the shape of the equilibrium isotherm and not so much by the mass transfer kinetics for a Langmuirian (type 1) isotherm. Due to this fact, it is even possible to estimate the entire adsorption isotherm from a desorption curve under specific conditions (Malek and Farooq 1996).

3.1 Importance of measuring flow rate at the exit

A change in the exit flow rate due to adsorption or desorption may be neglected only when the fraction of the adsorbable component in the feed during the adsorption breakthrough is very small. Hence, in general, the changing flow-rate at the exit should be measured. It is particularly important if breakthrough experiments are used to accurately measure equilibrium capacity.

It is worth noting that both the composition and the flow rate change at the column exit during a breakthrough experiment. Directly measuring this changing flow rate using a Coriolis mass flow meter is preferred. If a volumetric flow meter is used, it should be carefully calibrated to account for the changing composition. In order to calibrate a volumetric flow meter for a range of adsorbate:inert compositions, the mixtures can be prepared either by using multiple MFCs or using pre-mixed cylinders. Once the desired composition and flow-rates are set, the flowmeter readings can be read along with the readings of an independent flow-calibrator, e.g., a bubble flow meter connected inline. From a set of these measurements, the flowmeter can be calibrated for a variety of compositions and flow-rate ranges. Attempts to express the exit flow rate with a function of the measured effluent mole fraction of the absorbable component by assuming a constant inert carrier flow rate at the exit (Malek et al. 1995) and also relaxing that assumption (Brandani 2005) have shown limited success. It has been shown that either approach works reasonably well up to 50% adsorbable component in the feed for an adsorption breakthrough run, but the threshold for a desorption breakthrough run is much lower (circa 10%) for the constant carrier flow rate assumption (Brandani 2005). In Fig. S1 in the Supporting Information, the exit flow rate obtained from adsorption run for 10 mol% of the adsorbable component in the feed using the constant inert carrier flow approximation (designated as the helium reference method) is compared with the measured flow rate using a Coriolis mass flow meter (Goyal et al. 2019).

3.2 Impact of extra-column volume

The extra-column volume, or dead volume, increases the residence time of a breakthrough response and leads to an over-estimation of the equilibrium capacity calculated from the uncorrected column breakthrough response. Dead volume also affects the spread, i.e., the shape of the breakthrough curve, which in turn affects the information on adsorption kinetics extracted. Hence, the measured breakthrough responses must be corrected from the blank response in order to obtain the true response of the breakthrough column, which can then be analysed to obtain reliable equilibrium and kinetic information. Correcting only the residence time is relatively simple, and it also does not matter whether the dead volume is upstream or downstream of the adsorption column. Correcting for the additional spread contributed by the dead volume is more involved, and different methods have been proposed in the literature (Joss and Mazzotti 2012; Rajendran et al. 2008). It should also be noted that the proposed methods assume that the additional spread of the mass transfer front is contributed by the dead volume downstream of the adsorption column. Thus, the implied assumption is that the dead volume upstream of the adsorption column is in plug flow, and hence the column inlet sees a perfect step change as introduced. Any (significant) deviation from a perfect step change at the inlet, if it can be accurately measured, should ideally be reflected in the inlet boundary condition in the simulation.

3.2.1 Methods of correcting dead volume

A common practice for the blank or dead volume correction that is adopted in several studies is to measure a blank response under the same flow rate, pressure, and temperature conditions as the actual experiment by simply bypassing the adsorption column with a tube (or a connector) of negligible volume. This blank response is then subtracted point-by-point (PBP) from the composite response (i.e., including the adsorption column) on a $\frac{c\left(t\right)}{{c}_{\mathrm{in}}}$ versus time plot to account for extra-column contributions. The underlying assumption of this method is that the blank and the column responses are linearly additive, which fails when the adsorbable component in the feed is concentrated, and consequently the flow rate change at the column exit (due to adsorption) is not negligible (Rajendran et al. 2008). A tank in series (TIS) method was proposed where the blank response due to a step concentration change in the feed is modelled as a collection of continuous stirred tanks, which is used to invert the TIS model to predict the expected response at the column exit from the measured composite/combined response from column and blank.

In a recent study (Goyal et al. 2019), it was argued that the PBP method of blank correction should yield the same result as the TIS method if we use the normalized molar flow rate (of the adsorbable component) at the exit, i.e., we use $\frac{y\left(t\right)Q(t)}{{y}_{\mathrm{in}}{Q}_{\mathrm{in}}}$ versus time plots instead of $\frac{c\left(t\right)}{{c}_{\mathrm{in}}}$ versus time. Here, $Q(t)$ is the changing standard molar flow rate at the exit, and ${Q}_{\mathrm{in}}$ is the controlled constant standard molar flow rate at the inlet. The method is illustrated in Fig. 3a, and the results presented in support of this claim are shown in Fig. 3b.

Fig. 3

a Illustration of the point-by-point blank correction method. b Close agreement between the PBP correction of the breakthrough responses in normalized exit molar flow rate vs. time plot and the TIS correction. The results are for N₂ breakthrough in a bed packed with silica gel (Goyal et al. 2019). In this study, the subscript ‘o’ was used to denote values at the column inlet

4 Analysis of breakthrough experiments

4.1 Single component equilibrium

The breakthrough response for a step-change in the concentration of an adsorbable component in the feed, after a dead volume correction, should ideally contain the same equilibrium information obtainable from an uptake experiment conducted in a gravimetric balance or a constant volume apparatus. The adsorption column should start with a uniform temperature equal to the feed and must return to that same state at the end. So, an isothermal mass balance is adequate to calculate the equilibrium capacity of the adsorbent equilibrated with the feed composition at a given temperature and pressure. A general mass balance of an adsorption column that includes a velocity change but neglects pressure drop will be derived first.

$$\mathrm{Input}=\frac{{Q}_{\text{in}}{P}_{\text{ref}}}{{R}_{\text{g}}{T}_{\text{ref}}}{y}_{\text{in}}{t}_{\infty }=\frac{A\varepsilon {v}_{\text{in}}{P}_{\text{in}}}{{R}_{\text{g}}{T}_{\text{in}}}{y}_{\text{in}}{t}_{\infty }.$$

(1)

In the above expression, $y, Q, P$ and $T$ refer to the mole fraction of the adsorbate, total volumetric flow-rate, total pressure, and temperature. $Q$ is at some reference (“ref”) states of $P$ and $T$ at which the flowmeter is calibrated (usually specified by the flowmeter manufacturer). The parameters $A,$ $\varepsilon ,$ and v refer to the cross-sectional area of the column, the bed voidage, and the interstitial velocity, respectively. We have a constant molar flow rate of the adsorbate at the inlet for the entire duration of the adsorption run. Hence, the total number of moles of the adsorbate into the column is its molar flow rate multiplied by the duration of the adsorption run indicated here as ${t}_{\infty }.$ Infinity is used to remind us that we have to give sufficient time for the column to be completely equilibrated with the feed composition.

$$\mathrm{Output}={\int }_{0}^{{t}_{\infty }}\frac{Q\left(t\right){P}_{\text{ref}}}{{R}_{\mathrm{g}}{T}_{\mathrm{ref}}}y\left(t\right)dt={\int }_{0}^{{t}_{\infty }}\frac{A\varepsilon v\left(t\right){P}_{\text{out}}\left(t\right)}{{R}_{\mathrm{g}}{T}_{\text{out}}\left(t\right)}y\left(t\right)dt.$$

(2)

We have a changing molar flow rate of the adsorbate, leaving the adsorption column. Hence, the total amount of adsorbate out of the column is the integral of the changing amount from time 0 to infinity. At the end of an experiment, the accumulation in the column can be written as:

$$\mathrm{Accumulation}=LA\varepsilon \frac{{{y}_{\mathrm{in}}P}_{\mathrm{in}}}{{R}_{\mathrm{g}}{T}_{\mathrm{in}}}+LA\left(1-\varepsilon \right){q}_{\mathrm{in}}^{*}.$$

(3)

The accumulation consists of two contributions. The first and the second term represent the accumulation in the void spaces and the solid phase, respectively. Note that ${q}_{\mathrm{in}}^{*}$ represents the solid phase loading that is in equilibrium with the fluid phase concentration, ${c}_{\mathrm{in}}\left(=\frac{{{y}_{\mathrm{in}}P}_{\mathrm{in}}}{{R}_{\mathrm{g}}{T}_{\mathrm{in}}}\right)$.

When the breakthrough is complete, the overall mass balance is given by:

$${\text{Input}} - {\text{Output}} = {\text{Accumulation}}.$$

(4)

By combining Eqs. (1) to (4), we obtain

$$\frac{{Q}_{\text{in}}{P}_{\text{ref}}}{{R}_{\text{g}}{T}_{\text{ref}}}{y}_{\text{in}}{t}_{\infty }-{\int }_{0}^{{t}_{\infty }}\frac{Q\left(t\right){P}_{\text{ref}}}{{R}_{\text{g}}{T}_{\text{ref}}}y\left(t\right)dt=LA\left[\varepsilon \frac{{{y}_{\text{in}}P}_{\text{in}}}{{R}_{\text{g}}{T}_{\text{in}}}+\left(1-\varepsilon \right){q}_{\text{in}}^{*}\right]$$

(5)

which, upon rearrangement gives:

$${\int }_{0}^{{t}_{\infty }}\left(1-\frac{y\left(t\right)Q\left(t\right)}{{{y}_{\mathrm{in}}Q}_{\mathrm{in}}}\right)dt={\stackrel{-}{t}}_{\mathrm{ads}}= \frac{L}{{v}_{\mathrm{in}}}\left[1+\frac{\left(1-\varepsilon \right)}{\varepsilon }\frac{{q}_{\mathrm{in}}^{*}}{{c}_{\mathrm{in}}}\right].$$

(6)

The definition of the mean residence time (${\stackrel{-}{t}}_{\mathrm{ads}}$) is given by the integral on the left-hand side of Eq. (6). It is worth noting that ${Q}_{\text{in}}$ is at a reference pressure and temperature but, ${v}_{\text{in}}$ is at the column inlet pressure and temperature: $\frac{{v}_{\mathrm{in}}{P}_{\mathrm{in}}}{{T}_{\mathrm{in}}{R}_{\mathrm{g}}}\varepsilon A=\frac{{Q}_{\mathrm{in}}{P}_{\mathrm{ref}}}{{T}_{\mathrm{ref}}{R}_{\mathrm{g}}}$. The constant mole fraction, ${y}_{\mathrm{in}}$, of the adsorbate and the constant total flow rate, ${Q}_{\mathrm{in}}$, are measured at the inlet. At the exit, the changing mole fraction of the adsorbate $y(t)$ and total flow rate $Q(t)$ as a function of time are measured. The flow rates are typically in standard volumetric flow rate units, i.e., at some reference temperature and pressure conditions. Therefore, it is recommended to use a $\frac{y\left(t\right)Q\left(t\right)}{{y}_{\mathrm{in}}{Q}_{\mathrm{in}}}$ vs. time plot after a blank correction (see Fig. 4). Since both the volumetric flow rates are at the same reference conditions, the ratio represents the adsorbate molar flow rate at the exit normalized with its constant molar flow rate at the inlet. Therefore this plot, for the case of single-component breakthrough experiments, will always change from 0 to 1 on the y-axis. In such a plot, the shaded area in Fig. 4a represents the integral on the left-hand side of Eq. (6).

Fig. 4

The shaded areas represent the integral on the left-hand side of a Eq. (6) and b Eq. (7)

When a reverse step change in the adsorbate mole fraction (from ${y}_{\mathrm{in}}$ to 0) is introduced at the inlet of the adsorption column, in order to completely desorb the adsorbate after reaching an equilibrium with the feed concentration in the adsorption run (${c}_{\mathrm{in}}$), Eq. (6) becomes:

$${\int }_{0}^{{t}_{\infty }}\left(\frac{y\left(t\right)Q\left(t\right)}{{{y}_{\mathrm{initial}}Q}_{\mathrm{in}}}\right)dt={\stackrel{-}{t}}_{\mathrm{des}}= \frac{L}{{v}_{\mathrm{in}}}\left[1+\frac{\left(1-\varepsilon \right)}{\varepsilon }\frac{{q}_{\mathrm{initial}}^{*}}{{c}_{\mathrm{initial}}}\right].$$

(7)

Note that for the case of desorption runs, the subscript “initial” refers to conditions at which the column was saturated prior to desorption. Here the adsorbate molar flow rate at the exit is normalized with the molar flow rate used to equilibrate the bed prior to the desorption run. The shaded area in Fig. 4b represents the integral on the left-hand side of Eq. (7).

For a reversible physical adsorption process that does not show hysteresis, ${q}_{\mathrm{in}}^{*}$ and ${q}_{\mathrm{initial}}^{*}$ obtained from the adsorption and desorption runs must be equal. If the mole fraction of the adsorbable component is very low, such that it is within the linear range of the isotherm and the change in exit flow rate due to adsorption is negligible, then $Q(t)\approx {Q}_{\mathrm{in}}$ and $\frac{{q}_{\mathrm{in}}^{*}}{{c}_{\mathrm{in}}}=K$ (Henry’s constant), and the adsorption and desorption breakthrough curves will be practically mirror images of one another. For systems that show a highly non-linear type-1 isotherm, complete desorption could take an impractically long time. In such cases, significant discrepancies could be noticed between the adsorption and desorption capacities.

The same procedure can be repeated at different feed concentrations. The water bath (see Fig. 1) may also be maintained at different temperatures. Clearly, the breakthrough method may also be used to measure equilibrium isotherms over a wide range. However, at least two different methods of equilibrium data measurement are recommended to confirm data reliability and reproducibility.

While a negligible pressure drop is a good approximation for breakthrough runs conducted in laboratory-scale columns packed with commercial adsorbent particles (2–3 mm in diameter), the assumption may not hold when breakthrough experiments are conducted in even small columns (5 to 10 cm) packed with as-synthesized crystals of a variety of new adsorbents. In this case, the mass balance equations must be modified to account for a non-negligible pressure drop in the adsorption column. Since the exact pressure profile along the length of the adsorption column is not known, a linear pressure profile assumption will change Eqs. (6) and (7) as follows:

$${\int }_{0}^{{t}_{\infty }}\left(1-\frac{y\left(t\right)Q\left(t\right)}{{{y}_{\mathrm{in}}Q}_{\mathrm{in}}}\right)dt={\stackrel{-}{t}}_{\mathrm{ads}}= \frac{L}{{v}_{\mathrm{in}}}\left[1+\frac{\left(1-\varepsilon \right)}{\varepsilon }\frac{{q}_{\mathrm{avg}}^{*}}{{c}_{\mathrm{avg}}}\right],$$

(8)

$${\int }_{0}^{{t}_{\infty }}\left(\frac{y\left(t\right)Q\left(t\right)}{{{y}_{\mathrm{initial}}Q}_{\mathrm{in}}}\right)dt={\stackrel{-}{t}}_{\mathrm{des}}= \frac{L}{{v}_{\mathrm{in}}}\left[1+\frac{\left(1-\varepsilon \right)}{\varepsilon }\frac{{q}_{\mathrm{avg}}^{*}}{{c}_{\mathrm{avg}}}\right],$$

(9)

$${c}_{\mathrm{avg}}=\frac{{(P}_{\mathrm{in}}+{P}_{\mathrm{out}}){y}_{\text{in}}}{2{R}_{\mathrm{g}}{T}_{\mathrm{in}}}.$$

(10)

In Eq. (10), ${P}_{\mathrm{in}}$ and ${P}_{\mathrm{out}}$, are the inlet and exit pressures of the adsorption column at the end of the adsorption breakthrough run. ${q}_{\mathrm{avg}}^{*}$ is the adsorbed phase loading in equilibrium with ${c}_{\mathrm{avg}}$.

Breakthrough results are also presented in the literature as $\frac{c\left(t\right)}{{c}_{\mathrm{in}}}$ versus time, $\frac{y\left(t\right)}{{y}_{\mathrm{in}}}$ versus time, $\frac{c\left(t\right)v(t)}{{c}_{\mathrm{in}}{v}_{\mathrm{in}}}$ versus time and $\frac{y\left(t\right)v(t)}{{y}_{\mathrm{in}}{v}_{\mathrm{in}}}$ versus time plots. When the breakthrough is complete, we have $y\left(t\right)={y}_{\mathrm{in}}$, $T\left(t\right)={T}_{\mathrm{in}}$, $c(t)=\frac{{y}_{\mathrm{in}}{P}_{\mathrm{out}}}{{R}_{\mathrm{g}}{T}_{\mathrm{in}}}$ and $v\left(t\right)=\frac{{v}_{\mathrm{in}}{P}_{\mathrm{in}}}{{P}_{\mathrm{out}}}$. Therefore, while $\frac{y\left(t\right)}{{y}_{\mathrm{in}}}$ versus time plot, and $\frac{c\left(t\right)v\left(t\right)}{{c}_{\mathrm{in}}{v}_{\mathrm{in}}}$ versus time plot will always ultimately reach one, $\frac{c\left(t\right)}{{c}_{\mathrm{in}}}$ versus time plot will only reach one when the pressure drop is negligible. This plot will settle below one when the pressure drop across the adsorption column is non-negligible. Similarly, $\frac{y\left(t\right)v\left(t\right)}{{y}_{\mathrm{in}}{v}_{\mathrm{in}}}$ versus time plot will settle above one when there is pressure drop across the adsorption column. Hence, a reliable estimate of equilibrium data from a breakthrough run depends on the blank correction and unambiguous presentation of experimental data as a $\frac{y\left(t\right)Q\left(t\right)}{{y}_{\mathrm{in}}{Q}_{\mathrm{in}}}$ versus time plot commensurate with the definition of the mean residence time (Peter et al. 2013).

The equilibrium data for N₂, CH_4, and CO₂ on a metal–organic framework adsorbent, Cu-BTC (copper benzene-1,3,5-tricarboxylate), from breakthrough and volumetric experiments (Najafi Nobar and Farooq 2012) at two different temperatures are compared in Fig. 5. Similar comparisons for N₂, CO_2, and H₂O on zeolite 13X (Wilkins et al. 2020; Wilkins and Rajendran 2019) are shown in Fig. S2 in the Supplementary Information. For the concentration range covered, N₂ and CH₄ exhibit a fairly linear equilibrium on Cu-BTC with increasing concentration, while CO₂ is slightly nonlinear at higher concentrations. On 13X zeolite, N₂ is quite linear, CO₂ is nonlinear, and H₂O is very nonlinear. The results also represent a wide range of solid loading ranging from very low N₂ adsorption on Cu-BTC to very high loadings for water adsorption on 13X zeolite. As seen, no matter how strong the affinity is to the adsorbent, breakthrough experiments can match static equilibrium measurements, if performed properly.

Fig. 5

Adsorption and desorption breakthrough curves for N₂, CH_4, and CO₂ on Cu-BTC (Najafi Nobar and Farooq 2012). The adsorbate mole fraction is measured at the column exit, and the temperature is measured at a fixed location along the column. In the legend, BTC stands for dynamic column breakthrough equilibrium measurements, while CV stands for equilibrium measurements from a constant volume experiment. Note that ${q}_{i}^{*}$ and ${c}_{i}$ are in units of mmol/cm³

The experimental adsorption and desorption breakthrough curves, the mole fraction measured at the column exit, and the temperature measured at a fixed location along the column for N₂, CH_4, and CO₂ on Cu-BTC are also shown in Fig. 5 (Najafi Nobar and Farooq 2012). They represent, from the bottom row to the top row, increasing non-linearity of the isotherm at the inlet feed conditions. N₂ exhibits a practically linear isotherm; therefore the adsorption and desorption breakthrough curves are symmetric. This is also observed in the temperature breakthrough curves. Both the maximum adsorption temperature and minimum desorption temperature occur at the same time, and both return to the feed temperature at the same time. Although the CH₄ isotherms look almost linear, the breakthrough curves exhibit mild asymmetry between adsorption and desorption. The desorption temperature curve also takes longer to return to the feed temperature compared to its adsorption counterpart. The asymmetry is more pronounced for CO₂. The adsorption temperature curve has a much greater amplitude than the desorption curve. The latter also takes much longer to come back to the initial temperature. In a type 1 equilibrium system, the desorption (concentration) breakthrough curve becomes increasingly equilibrium controlled with increasing nonlinearity. Hence, a desorption breakthrough is not recommended for studying mass transfer kinetics.

The effect of isotherm nonlinearity on the breakthrough time, while keeping the feed flow rate unchanged, is shown in Fig. S3 in the Supporting Information (Wilkins and Rajendran 2019). The N₂ runs at three compositions are shown. In Fig. S3e, the red, blue, and black curves correspond to 25, 50, and 85 mol% N₂ in helium at the same pressure and temperature. Although the concentration of N₂ in the feed has increased, all three breakthroughs occur around the same time ($\approx$ 12 dimensionless time). The dimensionless time is the ratio of the actual time to the time it would take an inert component to travel through the column. This is expected, according to Eq. (6). It clearly shows that for the same $L$, ${v}_{\mathrm{in}}$ and $\varepsilon$ the mean residence time only depends on $\frac{{q}_{\mathrm{in}}^{*}}{{c}_{\mathrm{in}}}$, which is the slope of the chord from zero loading to the respective equilibrium point. Since all three chords practically overlap in the linear range of the isotherm, the breakthrough curves all have the same mean residence time. It is important to note that while the compositional breakthrough appears complete at 30 dimensionless time, the thermal waves do not come back to the inlet temperature until at least 300 dimensionless time. In order to obtain accurate equilibrium data temperature breakthrough curves must return to the inlet conditions. It should be noted that more heat is generated for a larger step change in concentration. In the case of breakthrough curves for CO₂ on zeolite 13X, also included in Fig. S3, the breakthrough times for different feed concentrations (at the same feed flow rate) are no longer equal since $\frac{{q}_{\mathrm{in}}^{*}}{ {c}_{\mathrm{in}}}$ is not constant outside of the Henry region. The lower the concentration is of the step input, the longer it will take for the breakthrough curve to be seen at the column exit. The same is true for the temperature curves. This experiment also illustrates the fact that it takes much longer for the temperatures to return to the initial condition. Therefore, in order to obtain good data, the breakthrough experiment should be continued not just until the composition appears to have reached the inlet value, but also the temperature to reach the inlet or initial conditions. It will be shown later that for macropore controlled transport, the mass transfer rate is inversely affected by $\frac{{q}_{\mathrm{in}}^{*}}{{c}_{\mathrm{in}}}$. This partly explains the higher spread of the breakthrough front at a lower CO₂ feed concentration. The sharper breakthrough front at a higher CO₂ partial pressure is also due to the self-sharpening of its concentration wave front due to a higher nonlinearity of the isotherm at this feed condition. Hence, the adsorption breakthrough experiments should be conducted in the linear to the modest nonlinear range to reliably estimate the mass transfer rate.

4.2 Presentation of multicomponent breakthrough results

In the adsorption literature on new adsorbents, mixture breakthrough results are commonly presented as a $\frac{y(t)}{{y}_{\mathrm{in}}}$ versus time plot or $\frac{c(t)}{{c}_{\mathrm{in}}}$ versus time plot to demonstrate the selectivity of the adsorbent for a given mixture of components. These two types of plots are often interchangeably used and considered as equivalents. A representative breakthrough response for a binary system plotted as $\frac{y\left(t\right)}{{y}_{\mathrm{in}}}$ versus time for both components is shown in Fig. S4 in the Supporting Information. The maximum value of $\frac{y\left(t\right)}{{y}_{\mathrm{in}}}$ for the weaker components attains a value greater than one. This overshoot is commonly referred to as a roll-up. It is an important signature for a competitive mixture breakthrough. In an n-component system, there will be $\mathrm{n}-1$ roll-ups, and only the strongest adsorbing component will not show any roll-up. $\mathrm{n}-1$ roll-ups in an n-component adsorption system is a phenomenon of equilibrium origin (Basmadjian et al. 1987; Rhee et al. 2001). Roll-up of both the components of kinetic origin in a binary system has also been reported in the literature (Farooq and Ruthven 1991; Kapoor and Yang 1987). When the equilibrium capacity of two components differs significantly, the weaker component will be practically pure in the exit stream until the stronger component begins to breakthrough. Hence, the maximum value of $\frac{y(t)}{{y}_{\mathrm{in}}}$ for the weaker component is $\frac{1}{{y}_{\mathrm{in}}}$ where ${y}_{\mathrm{in}}$ is the mole fraction of the weaker component in the feed. The other method of representing breakthrough curves is to use the ratio of the concentrations at the outlet to that of the inlet, i.e., $\frac{c\left(t\right)}{{c}_{\mathrm{in}}}=\frac{y\left(t\right)P\left(t\right){T}_{\mathrm{in}}}{{y}_{\mathrm{in}}{P}_{\mathrm{in}}T\left(t\right)}$. It should be noted that even for systems with large heat effects, the exit temperature is greatly attenuated by the large capacity of the end metal plate of the adsorption column. Therefore, in multi-component breakthroughs, whether a $\frac{c\left(t\right)}{{c}_{\mathrm{in}}}$ versus time plot for a weaker component will have roll-up will depend on the pressure drop and its mole fraction in the feed. Hu et al. (2017) have shown the pressure drop in a small column packed with different types of MOF crystals can be quite large and depending on the feed composition and that is it entirely possible for the maximum value of $\frac{c\left(t\right)}{{c}_{\mathrm{in}}}$ to remain below one for the weaker adsorbate. This discussion is a reminder of an important fact that the roll-up that can be seen in a $\frac{y(t)}{{y}_{\mathrm{in}}}$ versus time or $\frac{c\left(t\right)}{{c}_{\mathrm{in}}}$ versus time plot in gas phase studies is not a confirmation of competitive adsorption. In the gas phase breakthrough, the roll-up will also occur even when the isotherms are linear or nonlinear and cooperative so long as the components travel at different velocities owing to the differences in affinity. Our recommendation to use a $\frac{y\left(t\right)Q\left(t\right)}{{y}_{\mathrm{in}}{Q}_{\mathrm{in}}}$ versus time plot also applies for a multi-component breakthrough study where measurable roll-up is a confirmation of competitive adsorption.

4.3 Analysis of a multicomponent breakthrough run for mixture equilibrium

There is a limited amount of multi-component equilibrium data in the literature. Often, multi-component equilibrium is estimated through ideal adsorbed solution theory or simple extensions to models fitted with single-component equilibrium data. While in some systems, these approximations or extensions may be reasonable, it is always advisable to at least perform a limited validation of mixture equilibrium using experiments. It should be reiterated that multi-component breakthrough experiments can offer insight into competitive adsorption equilibrium and provide validation to the process model used in simulation studies.

A multi-component adsorption breakthrough experiment is performed the same way that a single-component experiment is performed. Some attention needs to be given to the calibration of the exit flow rate and composition. A similar method to what was described in Sect. 3.1 can be used with multiple adsorbates and an inert gas. Depending on the detectors, the signal might change drastically with different gas mixtures. For example, a detector signal for CO₂ in N₂ could be different from that in helium for the same CO₂ composition. The column mass balance for each component in a multi-component breakthrough experiment the same as the one derived for a single adsorbable component in Sect. 4.1. The equilibrium capacity of the mixture components may be obtained from experimental breakthrough data plotted as $\frac{{\mathrm{y}}_{i}\left(t\right)\mathrm{Q}\left(t\right)}{{\mathrm{y}}_{i,\mathrm{in}}{\mathrm{Q}}_{\mathrm{in}}}$ versus time. The multi-component versions of Eqs. (6) and (7), shown as Eqs. (11) and (12), apply for adsorption and desorption runs, respectively. Similarly, multi-component versions of Eqs. (8) and (9), using ${\mathrm{c}}_{i,\mathrm{avg}}$ and ${\mathrm{q}}_{i,\mathrm{avg}}^{*}$ instead, are applicable when the pressure drop is significant.

$${\int }_{0}^{{\mathrm{t}}_{\infty }}\left(1-\frac{{\mathrm{y}}_{i}\left(\mathrm{t}\right)\mathrm{Q}\left(\mathrm{t}\right)}{{{\mathrm{y}}_{i,\mathrm{in}}\mathrm{Q}}_{\mathrm{in}}}\right)\mathrm{dt}=\frac{\mathrm{L}}{{\mathrm{v}}_{\mathrm{in}}}\left[1+\frac{\left(1-\upvarepsilon \right)}{\upvarepsilon }\frac{{\mathrm{q}}_{i,\mathrm{in}}^{*}}{{\mathrm{c}}_{i,\mathrm{in}}}\right],$$

(11)

$${\int }_{0}^{{\mathrm{t}}_{\infty }}\left(\frac{{\mathrm{y}}_{i}\left(\mathrm{t}\right)\mathrm{Q}\left(\mathrm{t}\right)}{{{\mathrm{y}}_{i,\mathrm{initial}}\mathrm{Q}}_{\mathrm{in}}}\right)\mathrm{dt}=\frac{\mathrm{L}}{{\mathrm{v}}_{\mathrm{in}}}\left[1+\frac{\left(1-\upvarepsilon \right)}{\upvarepsilon }\frac{{\mathrm{q}}_{i,\mathrm{initial}}^{*}}{{\mathrm{c}}_{i,\mathrm{initial}}}\right].$$

(12)

When a mixture feed is introduced in an initially clean bed, the breakthrough for a binary mixture will qualitatively look like the curves shown in Fig. 6a. The blue adsorption breakthrough is for the light component and the red for the heavy component. The heavy component qualitatively looks the same as any single-component breakthrough. After a period of time, the breakthrough is seen at the effluent of the column. The light component will breakthrough before the heavy component. In normalized mole flow, $\frac{{\mathrm{y}}_{i}\left(t\right)\mathrm{Q}\left(t\right)}{{\mathrm{y}}_{i,\mathrm{in}}{\mathrm{Q}}_{\mathrm{in}}}$, it will go above 1 for some time. The light component will come back to 1 when the heavy component breaks through. The roll-up (the part above 1) in this plot is a confirmation of competitive adsorption, unlike the roll-ups in a $\frac{{\mathrm{y}}_{i}(t)}{{\mathrm{y}}_{i,\mathrm{in}}}$ $\left(\mathrm{or} \frac{{\mathrm{c}}_{i}\left(t\right)}{{\mathrm{c}}_{i,\mathrm{in}}}\right)$ versus time plot as discussed earlier. For the weaker component, the integral in Eq. (11) is given by area A minus area B (Wilkins and Rajendran 2019). For the stronger component area C represents the integral, which (as already mentioned) is similar to a single component breakthrough.

Fig. 6

Binary breakthrough response for a adsorption in a clean bed and b desorption from the equilibrated bed from the adsorption step showing areas related to equilibrium calculations (Wilkins and Rajendran 2019). The figures in the top row, shown in blue, correspond to the light component, while the figures in the bottom row, shown in red, correspond to the heavy component (Color figure online)

4.4 Challenges of handling mixtures of very strong and very weak components

If the capacity of the weaker component is low and the capacity difference with the strongly adsorbed component is very large, measuring area B accurately becomes challenging (Wilkins et al. 2020; Wilkins and Rajendran 2019). For such systems, area B may have a similar magnitude to area A; small errors can accumulate during the experiment and yield an incorrect equilibrium. This often comes from uncertainties associated with flow and composition measurements. When there is a large selectivity, a small displaced amount is eluted over a long time, so the roll-up may not appear to be significant. If the flow meter is not able to measure this, it could mislead one to conclude that there is no roll-up and hence no competition. Thus it may appear that the integral is just area A. In such cases, a good alternative is to first equilibrate the adsorption column with a known mixture and then desorb the co-adsorbed weaker component by purging the bed with a pure feed of the stronger component (Goyal et al. 2019). It is also possible to desorb both the components by purging the equilibrated bed with helium (Wilkins and Rajendran 2019). The desorption breakthrough curves of the two components obtained in the latter case are shown in Fig. 6b, where the blue curve is for the light (weaker) component, and the red curve is for the heavy (stronger) component. The integral in the mass balance given by Eq. (12) now contains terms that refer to the initial conditions of the bed instead of the inlet conditions. Area D corresponds to the integral for the light component, and area E is integral for the heavy component. It is relatively easy to measure area D for the light component in a desorption experiment than to measure the areas A–B in an adsorption experiment. It is also possible to measure area E for the heavy component, but that may take a long time; for some very strongly adsorbed systems (such as H₂O on zeolite 13X), it is practically impossible to desorb completely with only an inert sweep gas (Wilkins and Rajendran 2019).

To summarize, for a given set of conditions, we recommend measuring the heavy component equilibrium loading using an adsorption breakthrough experiment and measuring the light component loading with a desorption experiment. This idea is illustrated in Fig. S5 in the Supporting Information (Wilkins and Rajendran 2019). The CO₂ equilibrium capacity was obtained from the red area via Eq. (11) and that of N₂ was obtained from the grey area using Eq. (12). One set of equilibrium points is obtained from two breakthrough experiments. Experiments were repeated at other CO₂:N₂ compositions to obtain the other pairs of equilibrium points. These results are shown in Fig. S6a in the Supporting Information.

With post-combustion carbon capture being a popular topic at the moment, many researchers want to perform breakthrough experiments using humid-CO₂ (Xiao et al. 2008). CO₂ and water breakthrough curves and the corresponding temperature curves on 13X zeolite at three different relative humidities are shown in Fig. 7. Attention should be paid to the fact that H₂O takes much longer to breakthrough than CO₂. As seen, all three CO₂ compositions initially breakthrough at the same time. When compared to a single-component CO₂ experiment at the same conditions, nearly the same breakthrough curve will be found. Often, this observation is used as proof that CO₂ is unaffected by H₂O in the breakthrough experiment and that the material shows high CO₂ capacity even in the presence of H₂O. Such a conclusion is incorrect, as this analysis fails to account for the CO₂ roll-up and subsequent H₂O breakthrough. In these experiments, H₂O travels very slowly through the column. As water travels through the column, CO₂ is pushed out and replaced with H₂O. At the beginning of the breakthrough, what CO₂ sees is almost a clean bed, a situation similar to what it will see even in the absence of water. Over time, water will remove most of the accumulated CO₂. When water breaks through, the CO₂ roll-up ends, the effluent temperature returns to the inlet temperature, equilibrium has been reached, and now very little CO₂ is left behind in the adsorbent (Xiao et al. 2008). This is evident from the CO₂:H₂O mixture equilibrium isotherms shown in Fig. S6b in the Supporting Information, measured following the same procedure described for CO₂:N₂ mixture in the previous section.

Fig. 7

Competitive a CO₂ and b water breakthrough curves, and c the corresponding temperature breakthrough curve on 13X zeolite at three different relative humidities (Wilkins et al. 2020)

5 Adsorption kinetics from breakthrough experiments

A breakthrough study is an important transition between particle scale characterization of single-component adsorption equilibrium and kinetics, and process investigation and design. The adsorption separation processes are broadly classified into two types: equilibrium controlled and kinetically controlled. We include steric hindrance (or size-exclusion) in the latter category as an extreme case of kinetic separation. The modeling and design of either type of separation require knowledge of adsorption kinetics. Kinetically controlled separation processes are controlled by adsorbate transport in the micropores and require experimentally validated detailed kinetic models, including the concentration dependence of micropore transport for reliable process design. On the one hand, breakthrough studies on kinetically controlled systems are limited. On the other hand, there is a significant body of published work where breakthrough studies are used as a way to validate the column dynamics models on a limited scale before extending it for preliminary equilibrium-controlled separation process investigation by simulation. A closer look at these studies reveals two main approaches. One approach is to choose or develop a column dynamics model and compare it with single component experimental breakthrough results for each component of the mixture to be separated using independently measured equilibrium and diffusion parameters usually obtained from a batch method. In many cases, diffusivity obtained from a low-pressure uptake is used to estimate the mass transfer rate constant to simulate experimental breakthroughs also conducted at low pressures. In another approach, the single component equilibrium isotherm measured in a batch method is used, but the mass transfer rate constant is estimated by fitting the simulation result to the experimental breakthrough curve. Some mixture equilibrium model is assumed that directly uses the single component parameters. It is further assumed that the impact of any change in the mass transfer rate constants under the process conditions is secondary in equilibrium-controlled separations where the transport resistance is mostly in the macropores. We will show later that independent of the transport mechanism; the macropore controlled transport rate constant is also affected by the nonlinearity of the isotherm. In the equilibrium part of this review, we highlighted the importance of validating the mixture equilibrium model used in a process exploration study and showed how dynamic column breakthrough experiments could be extended to generate reliable mixture equilibrium data. In this section, we advocate the importance of understanding the transport mechanism in the adsorbent pores and show how breakthrough experiments can be an effective tool to achieve that. The text above classifies different ways in which breakthrough has been used in studies in the literature. They will be illustrated with appropriate examples. Before we move on, it is important to remind that in breakthrough experiments, unlike other small-scale techniques, such as the zero-length-column, heat, flow effects, and the local-equilibrium conditions impact the estimation of kinetic information. However, by careful experimental design and analysis, it would be possible to estimate kinetic information with reasonable confidence.

5.1 Transport mechanisms in adsorbent pores

According to the IUPAC (International Union of Pure and Applied Chemistry) classification, pore diameters < 20 Å are classified as micropores, between 20 and 50 Å as mesopores and > 50 Å as macropores (Thommes et al. 2015). In this discussion, we will not distinguish between mesopores and macropores, and consider pore diameters > 20 Å as macropores. Commonly encountered transport mechanisms in adsorbent pores are molecular diffusion, Knudsen diffusion, surface diffusion, and micropore diffusion (Kärger et al. 2012). The first three mechanisms occur in the macropores of an adsorbent particle, and the radius of a spherical particle is the characteristic dimension that affects the diffusional time constant. For non-spherical adsorbents of cylindrical or irregular shapes, the radius of an equivalent sphere is often used, which is obtained by equating the (external) surface area to volume ratio of the actual geometry.

The mass transfer rate is proportional to the macropore diffusivity and inversely proportional to the square of the particle radius. Similarly, for transport in the micropores, the mass transfer rate is proportional to the micropore diffusivity and inversely proportional to the square of the (equivalent) crystal radius when the adsorbent is a crystalline material (examples are zeolites, Engelhard titanosilicates, metal–organic frameworks, etc.). Unlike the case of crystalline materials, in the case of non-crystalline adsorbents (like activated carbons, carbon molecular sieves, etc.), a hypothetical radius is used. Therefore, for non-crystalline adsorbents, it is not possible to separately estimate the micropore diffusivity from macroscopic experiments (gravimetry, volumetry, breakthrough, etc.). It is presented as the diffusional time constant (ratio of micropore diffusivity over the square of a hypothetical radius). While the kinetic theory of gases allows the estimation of the molecular diffusivity and Knudsen diffusivity from physical properties and operating conditions, surface diffusivity and micropore diffusivity are still determined experimentally.

In the macropores, the changes in the length of the diffusion path due to the pore structure of the passage must be taken into consideration. Thus, the effective molecular diffusivity, ${\left({D}_{\mathrm{m}}\right)}_{\mathrm{macro}}$, in the macropores of a porous adsorbent is related to the molecular diffusivity in the homogeneous bulk fluid ${(D}_{\mathrm{m}})$ as follows:

$${\left({D}_{\text{m}}\right)}_{\text{macro}}=\frac{{D}_{\text{m}}}{\tau },$$

(13)

where τ is the tortuosity factor (typical value of 3 is used in the absence of a better estimate (Ruthven 1984)). It is worth noting that D_m, according to the Chapman–Enskog equation, is inversely proportional to the pressure and proportional to ${T}^{1.5}$:

$${D}_{\text{m}}=\frac{0.001859{T}^{1.5}{\left(\frac{1}{{M}_{1}}+\frac{1}{{M}_{2}}\right)}^{0.5}}{P{\sigma }_{12}^{2}\Omega (\epsilon /kT)}\,({\text{cm}}^{2}/{\text{s}}),$$

(14)

where M is the molecular mass of a given species, ${\sigma }_{12}$ is the average collision diameter, and $\Omega (\epsilon /kT)$ is the collision integral (Bird et al. 1964). Molecular diffusion in the adsorbent pores is hindered by more frequent collisions with the pore wall in small diameter pores at low pressure. Unlike molecular diffusion, Knudsen diffusivity $({D}_{\mathrm{K}})$ is independent of pressure and is calculated using:

$$D_{{\text{K}}} = 9700r_{\mu } \sqrt {\frac{T}{M}} \;({\text{cm}}^{2} /{\text{s}}),$$

(15)

where ${r}_{\mu }$ is the pore size in cm, $T$ is the temperature in K, and $M$ is the molecular weight of the gas in g/mol. Knudsen diffusion occurs in series with molecular diffusion. The tortuosity correction is similar to that for the molecular diffusivity.

Surface diffusion refers to the direct contribution to flux in a pore from transport through a physically adsorbed layer on the surface of the macropore. Surface diffusion increases with increasing pressure in the non-linear range of the isotherm. It occurs in parallel with Knudsen diffusion.

$${(D}_{\mathrm{K}+\mathrm{s}}) ={D}_{\text{K}}+\left(\frac{1-{\varepsilon }_{p}}{{\varepsilon }_{p}}\right)\left(\frac{{q}^{*}}{c}\right){D}_{\mathrm{s}}.$$

(16)

${q}^{*}$ (mol/m³) is the adsorbed phase concentration in equilibrium with the adsorbate concentration $c$ (mol/m³) in the macropore gas, and ${D}_{\mathrm{K}+\mathrm{s}}$ is the effective diffusivity due to the Knudsen and surface diffusion. In the linear limit, $\frac{{q}^{*}}{c}$ approaches the Henry’s constant, $K$. The effective diffusivity is also subjected to the tortuosity correction. Since molecular diffusivity is in series with Knudsen and surface diffusion, the effective particle diffusivity ${D}_{p}$, can be written as

$$\frac{1}{{D}_{\text{p}}}=\tau \left(\frac{1}{{D}_{\text{m}}}+\frac{1}{{D}_{\text{K} + \text{s}} }\right).$$

(17)

In the micropores, the adsorbate is always under the adsorption force field of the pore wall. There is no free gas phase within the confines of the micropores. The micropore diffusivity $({D}_{\mathrm{c}})$ is obtained by fitting an appropriate diffusion model to the measured batch uptake versus time curve of adsorbate in an adsorbent. It can also be obtained from breakthrough experiments. Like surface diffusivity, micropore diffusivity may also be a function of the adsorbed phase concentration in the nonlinear range of a favourable isotherm. Hence, attention should be paid to the initial condition and size of the step perturbation used in the experiment for a proper interpretation of the measured diffusivity value. In order to avoid ambiguity, it is customary to report the micropore (and also surface) diffusivity values measured in the linear range of the isotherm called the limiting diffusivity $({D}_{\mathrm{c},0})$.

5.2 The linear driving force model

The linear driving force (LDF) approach, a lumped-parameter model, is commonly used to describe the mass transfer kinetics in an adsorption column. In this approach, the lumped parameter, the LDF coefficient, $k$, is related to the various resistances by the following equation:

$$\frac{1}{k}=\frac{{R}_{\mathrm{p}}K}{3{k}_{\mathrm{f}}}+\frac{{R}_{\mathrm{p}}^{2}K}{15{\varepsilon }_{\mathrm{p}}{D}_{\mathrm{p}}}+\frac{{r}_{\mathrm{c}}^{2}}{15{D}_{\mathrm{c}}}.$$

(18)

Haynes and Sarma derived the above equation using a moment analysis of the pulse response from a chromatographic column model that explicitly allowed for linear adsorption equilibrium and external film, macropore, and micropore resistances (Haynes and Sarma 1973). This linear additivity rule has been widely used in the literature beyond Henry’s law region by replacing K with $\frac{{q}_{\mathrm{in}}^{*}}{{c}_{\mathrm{in}}},$ as shown in Eq. (19) (Hassan et al. 1985)

$$\frac{1}{k}=\frac{{R}_{\mathrm{p}}}{3{k}_{\mathrm{f}}}\left(\frac{{q}_{\mathrm{in}}^{*}}{{c}_{\mathrm{in}}}\right)+\frac{{R}_{\mathrm{p}}^{2}}{\begin{array}{c}15{\varepsilon }_{\mathrm{p}}{D}_{\mathrm{p}}\end{array}}\left(\frac{{q}_{\mathrm{in}}^{*}}{{c}_{\mathrm{in}}}\right)+\frac{{r}_{\mathrm{c}}^{2}}{15{D}_{\mathrm{c}}}.$$

(19)

It should be noted that both $\frac{{q}_{\mathrm{in}}^{*}}{{c}_{\mathrm{in}}}$ and ${D}_{\mathrm{c}}$ depend on the single component and mixture equilibrium isotherms. The contribution of ${D}_{\mathrm{m}}$ in ${D}_{\mathrm{p}}$ is also affected by the feed mixture composition. Therefore, the estimated LDF coefficient is dependent on the quality of the equilibrium data and the goodness of the isotherm model fitted to the data.

5.3 Qualitative identification of transport mechanisms

Like carefully designed gravimetric and volumetric experiments, well-thought-out breakthrough experiments can shed light on the transport mechanism of an adsorbate in the pores of an adsorbent. This is then followed by a detailed analysis for confirmation and transport property estimation to inform process design.

Since macropore resistance is inversely related to the square of particle size, by conducting breakthrough experiments by varying particle size at the same flow, pressure, and feed composition, it is possible to easily distinguish between macropore and micropore controlled transport. Amanullah et al. measured the breakthrough of a small fraction of methyl ethyl ketone in an inert (helium) carrier in an activated carbon bed (Amanullah et al. 2000). As shown in Fig. 8, a sharper breakthrough response for the smaller particle size suggested dominance of macropore diffusional resistance. Macropore molecular diffusion control was confirmed by showing that the ratio of extracted mass transfer coefficients was practically equal to the inverse ratio of squares of the particle diameters. In order to confirm micropore controlled transport of methane in 5A zeolite, Cen and Yang showed that the shape of the breakthrough curve was unaffected for two significantly different adsorbent particle sizes (1587 μm versus 250–420 μm) (Cen and Yang 1986). Hejazi performed breakthrough experiments of N₂ on Ag-ETS-10 with crushed and un-crushed particles (Hosseinzadeh Hejazi 2017). Since batch experiments revealed a fast uptake, the contribution from micropore resistance was considered minimal. Further, by carefully using the same adsorbent mass and identical flow rates, it was shown that the two breakthrough curves were practically identical, revealing that macropore diffusion did not contribute to the mass transfer resistance either. The results suggested that the system was most likely controlled by axial-dispersion.

Fig. 8

Comparison of breakthrough curves for two different particle sizes confirming the presence of resistance in the macropores (Amanullah et al. 2000)

Breakthrough runs carried out at the same partial pressure of the adsorbate gas and same gas velocity, but at different total pressures, may offer immediate guidance to what is the controlling transport mechanism in the macropores. The same partial pressure and velocity are necessary to ensure the same residence time for the runs conducted at different total pressures. Since molecular diffusivity is inversely proportional to the operating column pressure, an increase in mass transfer resistance manifested by an increased spreading of the mass transfer zone with an increase in column operating pressure is an indication that the transport mechanism is dominated by molecular diffusion. On the other hand, if the breakthrough responses obtained at different operating column pressures remain unchanged, then it rules out molecular diffusion as the dominant transport mechanism. However, it does not immediately confirm Knudsen diffusion control because surface diffusion along the physically adsorbed adsorbate layer on the macropore walls may also be present. At constant partial pressure, mass transfer resistances due to Knudsen and surface diffusion are unaffected by a change in total pressure. The presence of surface diffusion will reduce the effective mass transfer resistance in the pores. Therefore, further differentiation requires simulating the breakthrough response using the established equilibrium isotherm model and the LDF mass transfer rate constant estimated from the relevant equations for Knudsen controlled transport. A reduced spread of the mass transfer front in the experimental breakthrough response (i.e., a sharper breakthrough response) compared to the response from the simulation will indicate that both Knudsen and surface diffusion are present.

By conducting the aforementioned experiments, Goyal et al. showed that transport of N₂ in the pores of the silica gel sample they were investigating was not macropore molecular diffusion-controlled (Goyal et al. 2019). The breakthrough results are shown in Fig. 9. Further analysis confirmed that it was completely controlled by Knudsen diffusion. The modelling of the breakthrough response required for this confirmation is detailed later. Similar results were also reported for CO₂ breakthrough. However, from the further analysis, the transport of CO₂ was found to be a combination of Knudsen and surface diffusion. The CO₂ partial pressure range of interest in this study was approximately in the linear part of the isotherm. Hence, only limiting surface diffusivity was reported, and its concentration dependence was not investigated. By conducting breakthrough experiments at different temperatures, surface diffusivity was further analysed to determine the activation energy.

Fig. 9

Experimental breakthrough curves for the identification of the transport mechanism of N₂ in silica gel pores (Goyal et al. 2019). In these runs, the N₂ partial pressure was maintained at 0.15 bar, and the operating pressures were 1.1 and 3 and bar in runs S1 and S2, respectively

5.4 Modelling and simulation of breakthrough experiments

So far, we have considered the evaluation of single- and multi-component equilibrium information from DCB experiments. It was shown that this requires writing a simple integral mass balance for a particular component performed over the entire breakthrough experiment. It is also shown that a qualitative evaluation of the controlling mass transfer mechanisms is possible by merely performing a range of experiments as dictated by the features associated with the various mass transfer resistances that can be present in the adsorbent particle. However, the quantitative estimation of kinetic information from DCB experiments requires the solution of a set of equations often collectively called “column dynamics equations”. These equations represent the transport of mass and heat across the column, along with suitable descriptions of pressure drop and the adsorption isotherm. The complexity of the models typically differs in the level of detail to which the mass transfer is described. The model equations presented here, have been discussed in many textbooks and papers in the literature (Casas et al. 2012; Effendy et al. 2017; Farooq and Ruthven 1991; Haghpanah et al. 2013; Ruthven 1984). Hence, only the final equations are presented here.

The equations provided here are based on the following assumptions:

• (1) The gas phase is ideal.

• (2) The adsorption column is homogenous in terms of packing density and porosity. This can be practically approached through suitable packing of the column.

• (3) An axially-dispersed plug flow model can adequately describe the fluid flow. This is typically sufficient, provided the ratio of the column diameter to the particle diameter exceeds 10.

• (4) Two types of mass transfer models are used for transport in the adsorbent pores: (i) the linear driving force (LDF) model when all the transport processes are lumped into a single LDF rate constant and (ii) the detailed pore diffusion model where both macropores and micropores are recognized, and concentration dependence of the micropore diffusivity is described according to the chemical potential gradient as the driving force for diffusion.

• (5) A one-dimensional model is sufficient to describe the dynamics. Although lab-scale columns have a finite rate of heat transfer through the walls and hence the possibility of radial gradients, the use of one-dimensional models is usually considered sufficient. A detailed discussion can be found elsewhere (Casas et al. 2012; Farooq and Ruthven 1990).

• (6) The adsorbent particle is radially homogenous in terms of temperature.

• (7) The thermal properties of the adsorbed phase are identical to that of the gas phase (Walton and LeVan 2005).

• (8) Heat transfer is finite at the column wall and can be adequately represented by a one-dimensional heat transfer model with film heat transfer coefficients on two sides of the wall.

Based on the above assumptions, the equations describing the column dynamics can be derived. These are provided in Table 1. The boundary conditions required to solve these equations are provided in Table S2 in the Supporting Information. Note that the boundary conditions are provided assuming that there is no spread in the inlet lines, and the concentration perturbation is a perfect step. While negligible spread in the inlet line is a reasonable assumption in most cases, it can be an issue in weakly adsorbing macropore molecular diffusion-controlled systems. In such a case, an accurate prediction of the breakthrough response requires measuring the actual concentration change at the inlet and using that as the inlet boundary condition instead of the usual constant inlet boundary condition.

Table 1 Constitutive equations for describing breakthrough experiments

A number of analytical solutions for column dynamics models have been proposed in the literature over the years. A comprehensive summary of these studies was covered by Ruthven (1984). The analytical solutions, while elegant and insightful, are subjected to many simplifying assumptions, e.g., isothermal, dilute, and linear equilibrium, which is difficult to match for strongly adsorbed systems and bulk separation studies. The commonly used semi-infinite boundary condition at the exit is also difficult to justify for breakthrough studies with a small quantity of a new adsorbent. From these considerations, we limit our discussion to the numerical solution of a comprehensive breakthrough model. It offers the flexibility to explore a variety of systems over a wide range of conditions necessary for a reliable scale-up study. We recognize that using a full simulation numerical model runs the risk of making it a fitting exercise instead of paying attention to the underlying essential physics of the process. We also note that using analytical solutions without a full understanding of the conditions for its validity is equally risky.

As can be seen from Table 1, the complete non-isothermal, non-isobaric model equations are coupled with algebraic equations that represent the adsorption equilibrium isotherms. Very often, these isotherms are explicit nonlinear equations (e.g., Langmuir isotherm or its multi-process version) (Ritter et al. 2011) and occasionally implicit nonlinear equations such as the multi-site Langmuir isotherm (Nitta et al. 1984). Hence, solving these equations, while not straightforward, can be conveniently performed on modern software tools on standard desktop computers. It is worth noting that depending on the type of adsorption equilibria, sharp fronts (degenerated-forms of discontinuities) can propagate along the column. This requires the use of either a fine discretization of space and time domains and/or the use of high-resolution numerical techniques. While finite difference and finite element techniques have been used, recent developments in finite-volume techniques have made it possible to solve these equations in a robust and rapid manner (Haghpanah et al. 2013; Todd et al. 2001; Webley and He 2000). Techniques such as orthogonal collocation have been used to discretize the particle mass balance together with finite-volume schemes at the column-level (Effendy et al. 2017).

5.4.1 Estimation and impact of axial dispersion

In single-component batch uptake measurements, a pure gas is used, and hence there is no external film resistance. In a single component dynamic column breakthrough, the adsorbate is mixed with an inert gas (commonly helium) to feed the column. External mass transfer resistance and axial dispersion are the two additional resistances that distinguish a dynamic column breakthrough measurement from batch uptake measurement. In general, the contribution of external film resistance is considered negligible in gas adsorption studies. But axial dispersion must be formally accounted for if experimental breakthrough results are analysed to extract intra-particle mass transport information. In order to study adsorption kinetics, very small particles that tend to agglomerate and strongly non-linear isotherms where axial dispersion begins to dominate over other resistances should be avoided. Away from these extreme limits, available correlations provide good estimates of the axial dispersion coefficient, which are discussed next.

The following correlation for estimating axial dispersion in a packed bed was proposed in a comprehensive study by Edwards and Richardson (1970):

$${D}_{\mathrm{L}}=\gamma {D}_{\mathrm{m}}+\frac{P{e}_{\infty }^{-1}\left(v{d}_{\mathrm{p}}\right)}{1+\left(\frac{\beta \gamma {D}_{\mathrm{m}}}{v{d}_{\mathrm{p}}}\right)},$$

(20)

where ${D}_{\mathrm{m}}$ is the molecular diffusivity, given by the Chapman–Enskog equation for a particular gas mixture, $v$ is the interstitial velocity and, ${d}_{\mathrm{p}}$ is the particle diameter. In Eq. (20), $P{e}_{\infty }$ is the limiting value of the Peclet number, which is a function of the adsorbent particle size. Based on literature data, Langer et al. have proposed Eq. (21) to calculate $P{e}_{\infty }$ with ${d}_{\mathrm{p}}$ in units of cm (Langer et al. 1978). The interstitial inlet feed velocity, ${v}_{\mathrm{in}}$, is used for a priori estimate of axial dispersion contribution, but in a numerical simulation, it is possible to use the local velocity to allow varying axial dispersion along the column length.

$$\begin{aligned} & P_{{e_{\infty } }} = 2,\quad d_{p} > 0.3\;{\text{cm,}} \\ & P_{{e_{\infty } }} = 6.7d_{p} ,\quad d_{p} \le 0.25\;{\text{cm}}{\text{.}} \\ \end{aligned}$$

(21)

Wicke has proposed the following expression to estimate $\gamma$ (Wicke 1973).

$$\gamma =0.45+0.55\varepsilon .$$

(22)

After estimating $P{e}_{\infty }$ and $\gamma$, the following expression proposed by Bischoff can give an estimate for $\beta$ (Bischoff 1969).

$$\frac{1}{P{e}_{\infty }}=\frac{\beta }{\alpha }.$$

(23)

Here $\alpha$ accounts for the velocity distribution and is a function of particle diameter. $\alpha$ values reported by Langer et al. at four different particle diameters from 0.056 to 0.225 cm are well correlated by Eq. (24):

$$\alpha =8.1352\mathrm{ln}\left({d}_{\mathrm{p}}\right)+24.807.$$

(24)

In the wide range of experimental data from several studies analysed by Langer et al., any systematic effect of the column to particle diameter ratio was not obvious, but it should be noted that the minimum column to particle diameter ratio used in these studies was 10.

5.4.2 Estimation of external film mass transfer and wall heat transfer coefficient

The external film mass transfer resistance is commonly neglected in gas phase adsorption studies. Nevertheless, the following correlation for mass transfer in a packed bed proposed by Wakao and Funazkri, which reconciles differing results from a large number of studies, is recommended for estimating the film mass transfer resistance between the bulk gas and the adsorbent particle surface (Wakao et al. 1979):

$$Sh=2.0+1.1S{c}^{1/3}R{e}_{\mathrm{p}}^{0.6},$$

(25)

where $Sh \left(=\frac{{k}_{\mathrm{f}}{d}_{\mathrm{p}}}{{D}_{\mathrm{m}}}\right)$ is the Sherwood number, $Sc \left(=\frac{\mu }{{D}_{\mathrm{m}}\rho }\right)$ is the Schmidt number and ${Re}_{\mathrm{p}} \left(=\frac{{d}_{\mathrm{p}}u\rho }{\mu }\right)$ is the particle-Reynolds number based on particle diameter ${(d}_{\mathrm{p}}),$ and superficial velocity $(u)$.

The one-dimensional heat transfer model, used in a non-isothermal breakthrough simulation to analyze the propagation of the thermal front at various locations in an adsorption column, requires two heat transfer coefficients: one between the packed bed and the wall, and the other between the wall and outside air or the circulating fluid in the temperature-controlled bath. The following Sieder–Tate correlation may be used for the external heat transfer coefficient (Holman and Lloyd 2008).

$$Nu=0.027 {Re}^{0.8}{Pr}^{1/3},$$

(26)

where $Nu=\left(\frac{{h}_{\mathrm{out}}{d}_{\mathrm{co}}}{k}\right)$ is the Nusselt number, $\mathit{Pr }\left(=\frac{{C}_{\mathrm{p}}\mu }{k}\right)$ is the Prandtl number and $Re$ $\left(=\frac{{d}_{\mathrm{co}}u\rho }{\mu }\right)$ is the Reynolds number based on the column outside diameter. ${d}_{\mathrm{co}}$ is the column’s outer diameter. The other symbols have their usual meanings. Typically, a velocity of 0.5 m/s is used for airflow in a confined (laboratory) environment (American Industrial Hygiene Association 2003).

The Leva correlation, given by Eq. (27), is commonly used for heat transfer between the packed bed and the column wall (Leva and Grummer 1948).

$$Nu=\frac{{h}_{\mathrm{in}}{d}_{\mathrm{ci}}}{k}=0.813 {e}^{\left(-6\frac{{d}_{\mathrm{p}}}{{d}_{\mathrm{ci}}}\right)}{R{e}_{\mathrm{p}}}^{0.9}.$$

(27)

In the above equation ${d}_{\mathrm{ci}}$ is the column inner diameter. It is common to estimate the inside heat transfer coefficient, ${h}_{\mathrm{in}}$, by using it as a fitting parameter to match the temperature curve measured along the column length. Although the one-dimensional heat transfer model assumes that the resistance to heat transfer in the radial direction is confined in a small gas film at the wall, the radial temperature profile is not entirely flat. There is some resistance to heat transfer through the adsorbent in the radial direction. Hence, the fitted inside heat transfer coefficient includes this effect. It also accounts for any thermal resistance between the gas and adsorbent if an instantaneous gas–solid thermal equilibrium is assumed.

The correlation of Yagi et al., given by Eq. (28), is recommended in the literature for estimating the effective bed thermal conductivity ${(K}_{\mathrm{z}})$ of an adsorption column in a non-isothermal simulation (Farooq and Ruthven 1991; Knox et al. 2016; Yagi and Kunii 1957):

$$\frac{{K}_{\mathrm{z}}}{{k}_{\mathrm{g}}}=\frac{{K}_{\mathrm{z}}^{o}}{{k}_{\mathrm{g}}}+ \delta \left(PrR{e}_{\mathrm{p}}\right),$$

(28)

where ${K}_{\mathrm{z}}^{o}$ is the effective bed thermal conductivity at $R{e}_{\mathrm{p}}=0,$ and ${k}_{\mathrm{g}}$ is the gas thermal conductivity. $\delta$ varied from 0.7 to 0.8 in the experiments conducted by the authors with glass beads, metallic balls, broken pieces of limestone, and Raschig rings. Knox et al. (2016) used a value of 0.75 in their study on the breakthrough of CO₂ and H₂O in 5A zeolite. Wakao and Kato (1969) obtained numerical solutions of combined conduction and radiation heat transfer for packed beds filled with a stationary fluid. Their results are shown as a chart of $\frac{{K}_{\mathrm{z}}^{o}}{{k}_{\mathrm{g}}}$ vs.$\frac{{K}_{\mathrm{s}}}{{k}_{\mathrm{g}}}$ in Fig. S7 in the Supporting Information. The effective axial thermal conductivity of the fluid used in the inlet boundary condition for the column energy balance equation follows from the similarity assumed between the mechanism of fluid-phase mass and heat transfer $\left(Pe=P{e}_{\mathrm{h}}\right)$ (see Table S2 in the Supporting Information).

5.5 Transport mechanism from analysis of LDF constant

Only the mass transfer coefficient (either the LDF constant or the limiting micropore diffusivity) may be obtained from measured breakthrough responses using an independently established equilibrium isotherm model. The transport mechanism may then be established from further analysis of the LDF constant.

By analysing the extracted mass transfer coefficients, Malek and Farooq concluded that transport of C₁ to C₄ hydrocarbons in silica gel was by Knudsen diffusion, and by a combination of Knusden and surface diffusion in activated carbon (Malek and Farooq 1997). Similar conclusions were reached in other laboratories from particle-scale measurements (Doong and Yang 1986; Huang and Fair 1988).

Nobar and Farooq established molecular diffusion-controlled transport of three gases, CO₂, CH_4, and N₂, in Cu-BTC by comparing estimated and extracted mass transfer coefficients from a large number of breakthrough runs conducted over a wide range of operating pressures, temperatures and feed mole fractions (Najafi Nobar and Farooq 2012). The parity plot used for this comparison is shown in Fig. S8 in the Supplementary Information. Independently measured single component adsorption equilibrium data for the three gases were fitted to the Langmuir isotherm model, and the obtained isotherm parameters were used in a non-isothermal simulation model to extract the mass transfer parameters.

In a study on adsorption and diffusion of oxygen and nitrogen in RS-10, a modified 4A zeolite, single-component isotherms were independently measured and fitted to the Langmuir isotherm model (Farooq et al. 1993). Using these isotherm parameters, an isothermal, constant diffusivity pore diffusion model was fitted to the experimental single component breakthrough results in Henry’s law region for oxygen and nitrogen to extract the limiting diffusivity values. The results are shown in Fig. 10. The limiting diffusivity values obtained gave an excellent prediction of the experimentally measured binary breakthroughs in an operating regime where the concentration dependence of micropore diffusivity was important. The mixture pore diffusion model, including concentration dependence of the micropore diffusivity, depends on the accurate prediction of the mixture isotherm curvature. Therefore, these results also confirm the adequacy of the assumed extended Langmuir mixture equilibrium isotherm, in addition to confirming the model adopted for transport kinetics. The validated mixture breakthrough model was further extended to simulate kinetically controlled PSA nitrogen enrichment from the air that matched very well with the laboratory-scale experimental process performance.

Fig. 10

Comparison of experimental and theoretical breakthrough curves for a oxygen and b nitrogen in molecular sieve RS-10 (Farooq et al. 1993). The fits of the pore diffusion model to the breakthroughs in Henry’s law region using independently measured equilibrium isotherms gave the limiting diffusivity values

5.6 Breakthrough used to validate equilibrium and kinetics from elsewhere

Dynamic column breakthrough experiments can be used for validating independently measured equilibrium and kinetics information. It is well known that for many materials, it is challenging to obtain uniform crystal or particle morphologies at larger scales. These can arise because of inhomogeneity that is due to the use of large equipment for manufacturing, improper removal of solvents, variability in crystal size, and various other reasons. Hence, relying solely on experiments that are carried out with mg-scale samples in order to scale-up processes that employ hundreds of kilograms of adsorbents is not advisable. Since most commercial static measurements are specifically designed to handle small samples, DCB experiments lend themselves as a method to verify scaled-up performance.

There are possibly two approaches in which breakthrough experiments can be used to validate independently measured kinetic data. The first one is to compute the second moment of the breakthrough curve, which contains information about both dispersion and adsorption kinetics and compare it with those mass transfer coefficients calculated from independent measurements. This approach is more common for pulse chromatographic measurements in the literature (Haq and Ruthven 1986). Although in principle it should be applicable for step perturbation also, there is no readily available moment analysis with velocity and temperature changes necessary for breakthrough studies more commonly conducted with large concentration step changes. The second method is to use the models described earlier to compute the breakthrough curves using kinetic data from independent measurements and check them against the experimentally measured breakthrough experiments.

Cen and Yang described the breakthrough of CH₄ and N₂ on a bi-dispersed zeolite 5A beads based on the independent measurements from literature (Cen and Yang 1986). They showed a good match between experiments and the calculated breakthrough curves. Brandani et al. measured the kinetics of CO₂ in a carbon monolith using a zero-length column (ZLC) and also conducted breakthrough experiments using the monolith (Brandani et al. 2004). ZLC is a chromatographic experiment where a few pellets of an adsorbent are exposed to a change in sorbate composition, and the response is measured. The diffusion parameters are extracted by analyzing this response. They showed that diffusion parameters measured from the ZLC measurements were reasonably consistent with those from the breakthrough experiments. The authors concluded that the controlling mechanisms were molecular and Knudsen in the macropores with some possible contributions from the micropores.

Grande and Rodrigues measured the kinetics of propane and propylene in zeolite 4A using ZLC, constant volume, and breakthrough experiments. The pore diffusion constants measured from the three methods were in good agreement (Grande and Rodrigues 2004). In another study, Grande et al. studied the kinetics of propane and propylene on CMS, again using the previous three methods (Grande et al. 2003). The diffusion parameters calculated from DCB experiments and those from ZLC experiments varied by two orders of magnitude. Differences in the sizes of the microparticles were the suspected cause.

5.7 Breakthrough used to have a quick estimate of the LDF constant

Another common way to estimate mass transfer from a breakthrough experiment is to perform an experiment and fit the spread of the adsorption breakthrough curve to a model, such as the linear driving force model. A series of these experiments at different flow rates and compositions can yield data to span the desired set of process conditions. This method is one of the more common ways in which breakthrough experiments are used to determine the mass transfer rate. Many examples exist in the literature, some of which will be detailed in the following paragraphs. This method requires prior knowledge of the isotherm and will yield inaccurate results if the isotherm fit is poor.

There is a wide variety of modelling approaches in the studies using this technique. They range from simple models that are analytical to numerical solutions of partial differential equations that account for mass, momentum, and heat transfer. The choice of model will depend on how complex a given adsorbent–adsorbate system is. For some of these studies, the step change is so small (ppm of adsorbate) that very little heat is generated, and therefore the system is practically isothermal. Others deal with concentrated adsorbate systems that generate a significant amount of heat. A few examples are described below.

Chauveau et al. used a constant-pattern analytical solution to estimate LDF coefficients on an activated carbon for methyl acetate and vinyl chloride (Chauveau et al. 2013). These experiments were performed at concentrations below 500 ppm. The constant-pattern model, comprising the linear driving force rate equation and Langmuir equilibrium isotherm, assumes that the breakthrough curve has attained a constant shape unaffected by the column length. The minimization of error between the analytical solution and the experimental breakthrough was used to fit the LDF coefficient. In order to analyze the breakthrough of various volatile organic compounds on activated carbon Brosillon et al. solved the plug-flow model for fluid flow along with the LDF model to describe the solid–fluid mass transfer (Brosillon et al. 2001). The simulation was fitted to the experimental breakthrough to extract the LDF coefficient. A similar procedure was also done by Murillo et al. for phenanthrene on an activated carbon (Murillo et al. 2004). Fournel et al. used an axially dispersed plug flow model to calculate the breakthrough for various volatile organic compounds on activated carbon (Fournel et al. 2010). Saleman et al. performed a similar analysis for CH₄ and N₂ on H⁺-mordenite (Saleman et al. 2013). In this study, the energy balance was also considered to account for the large heat effect arising from much larger quantities of adsorbate and an operating pressure of approximately 900 kPa. The authors were able to obtain a satisfactory match of the composition and thermal breakthrough curves. Their model accounted for three transport mechanisms in the column, such as in Eq. (19). The minimization of error between the simulation and the experimental breakthrough was used to fit the LDF coefficient. Many studies have used this framework to estimate the LDF coefficient. Hwang et al. measured the mass transfer resistance of CO₂ and CO on an activated carbon (Hwang and Lee 1994). Casas et al. found the LDF coefficients for H₂ and CO₂ on an activated carbon and a hybrid MOF, UiO-67/MCM-41, for pre-combustion carbon capture at high pressure (Casas et al. 2013, 2012). Wu et al. performed this analysis for O₂ and N₂ on LiLSX for a PSA air separation process (Wu et al. 2016). Wilkins et al., Son et al., and Ribeiro et al. used the same approach to study H₂O on zeolite 13X at ambient conditions (Ribeiro et al. 2008; Son et al. 2019; Wilkins et al. 2020). Clearly, the method of fitting a column dynamics model to measured breakthrough responses have been widely used to estimate the LDF coefficient for a variety of different adsorbate–adsorbent systems from very small to large concentration step changes.

To estimate the LDF coefficient from a particular breakthrough curve, the following recommendations are made. First, it is advisable to perform the experiment as closely as isothermal as possible, or heat effects must be considered in the model. It should be noted that any significant departure from isothermal conditions will influence the breakthrough curve in addition to the spread caused by mass transfer. Second, an independent check, based on the recommendations made earlier, should be made to confirm that the right form of the equilibrium relationship is used in the simulations. Finally, when attempting to describe the mass transfer coefficient, if a non-isothermal model is to be used, there are two possible approaches to obtain the LDF coefficient. A simple approach is to estimate the heat transfer coefficients from the correlations provided earlier or from independent measurements (Kim et al. 2017), and minimize the objective function defined by Eq. (29a):

$$\sum\limits_{i=0}^{{t}_{\infty }}{\left({y}_{\mathrm{exp}}\left({t}_{i}\right)-{y}_{\mathrm{sim}}\left({t}_{i}\right)\right)}^{2}.$$

(29a)

A more elaborate approach is to simultaneously optimize the LDF coefficient along with the inside and outside heat transfer coefficients by minimizing the objective function defined by Eq. (29b):

$$\sum\limits_{i=0}^{{t}_{\infty }}{\left({y}_{\mathrm{exp}}\left({t}_{i}\right)-{y}_{\mathrm{sim}}\left({t}_{i}\right)\right)}^{2}+\sum\limits_{i=0}^{{t}_{\infty }}{\left(\frac{{T}_{\mathrm{exp}}\left({t}_{i}\right)-{T}_{\mathrm{sim}}\left({t}_{i}\right)}{{T}_{\mathrm{exp}}\left({t}_{i}\right)}\right)}^{2}.$$

(29b)

Studies that have considered the second approach, report that the fitted values of the heat transfer coefficient indeed lie in the neighborhood of the values provided by the correlations (Casas et al. 2013; Hefti et al. 2015).

5.7.1 LDF versus pore diffusion models

It is commonly assumed that the breakthrough dynamics obtained using the linear driving force approximation, with the LDF coefficient estimated by Eq. (30) known as the Glueckauf approximation, is practically indistinguishable from that obtained using the full pore diffusion model with constant diffusivity, $D$ (Glueckauf and Coates 1947).

$$k=\frac{15D}{{R}_{\mathrm{p}}^{2}}.$$

(30)

Equation (18) derived by Haynes and Sarma (1973) is an important extension of the Glueckauf approximation for systems in which more than one mass transfer resistance is significant.

The modeling of transport through a barrier resistance confined at the micropore mouth is mathematically equivalent to the linear driving force (LDF) model (Kärger et al. 2012). The wide success of the Glueckauf approximation in column dynamics calculations has given rise to a misconception that the details of the transport mechanism in a micropore controlled adsorbent are not captured in the breakthrough response from a column. However, by comparing the pore diffusion and LDF models for a dynamic column response for a linear isotherm, it has been shown that the extent of agreement between the two models depends on the product of the two parameters, $\alpha \left[=\frac{\left(1-{\varepsilon }_{\mathrm{p}}\right){K}_{\mathrm{c}}}{{\varepsilon }_{\mathrm{p}}}\right]$ and $\gamma \left[=\frac{{D}_{\mathrm{c}}L}{{r}_{\mathrm{c}}^{2}{v}_{\mathrm{in}}}\right]$ (Farooq et al. 2002). By an appropriate choice of operating conditions, it is indeed possible to clearly distinguish between the two mechanisms. Figure 11 gives the range of $\alpha \gamma$ in which the pore and LDF models diverge (shown as E). The proposed criterion was verified experimentally for the breakthrough of oxygen and nitrogen in a 4A zeolite and two carbon molecular sieve samples.

Fig. 11

Effect of $\alpha \gamma$ on E, the measure of the difference between the pore and LDF models (Farooq et al. 2002)

5.7.2 Rapid validation of mixture equilibrium and kinetics for process calculations

We observe that there is a trend in the literature to use independently measured single component equilibrium isotherms for the components in a mixture using gravimetry or volumetry, and then use them to extract mass transfer rates from breakthrough experiments, and form some idea about the mass transfer mechanism. Although limited in number, detailed binary mixture equilibrium data from breakthrough studies are also reported. A process model requires a mixture equilibrium description and some framework to extend a single component transport mechanism to mixture transport. Instead of postulating models for mixture equilibrium and kinetics based on single-component studies without any validation, at least some validation on a limited scale is desirable. It is possible to use mixture breakthrough experiments to fill that gap. As a case study, we present results for the binary breakthrough of CH₄:N₂ and CO₂:N₂ mixtures in Cu-BTC in Fig. 12. The Langmuir isotherm model and macropore molecular diffusion-controlled transport mechanisms for each of these gases in Cu-BTC were discussed in a previous section. The model predictions in Fig. 12 are for the extended Langmuir model using single component parameters and for the single component transport mechanism adjusted for mixture equilibrium.

Fig. 12

Comparison of an experiment and simulation model prediction for a and b breakthrough of a 30:70 CO₂:N₂ mixture in a Cu-BTC bed saturated with N₂ at 23 °C and 2 bar; c and d breakthrough of a 70:30 CH₄:N₂ mixture in a bed saturated with N₂ at 23 °C and 2 bar. Data reported from the work of Nafaji Nobar and Farooq (2012)

6 Cautionary notes for the use of breakthrough data for process evaluation

There are several breakthrough studies, especially with MOF materials, where selectivity, as demonstrated by the time lag between the breakthrough of the light and the heavy components, is used to claim process success. Although selectivity is an important metric for the purity-recovery performance of an adsorption process (like other separation processes), there is no direct relationship between selectivity and processing cost and plant footprint in an adsorption separation process (Khurana and Farooq 2016; Leperi et al. 2019; Park et al. 2020; Rajagopalan et al. 2016). These latter considerations may not be critical for small scale niche applications. However, these are key considerations for carbon capture and concentration (CCC) from dilute industrial flue gases or from air capture where the required processing volume is a few orders of magnitude higher than that of the largest known chemical plant. In summary, while breakthrough studies should be viewed as an important step towards process evaluation, they should not be used to make estimates of process performance without the use of appropriate process simulations and/or experimentation.

An economical solution to the unprecedented challenge of CCC requires high capacity adsorbents with negligible mass transfer resistance and contacting devices to allow high throughput at a minimum pressure drop. These represent orthogonally opposite demands in the context of current practices based on the packed bed technology. The level of adsorbent particle size required to reduce mass transfer resistance in high capacity adsorbents will exponentially increase the pressure drop at high throughput in a packed bed. Hence, alternative contacting devices such as parallel passage contactors made of thin laminates of stacked adsorbent sheets with small channels in between the sheets or extruded structured adsorbents have been explored (Ahn and Brandani 2005; Couck et al. 2017; Rezaei and Webley 2010; Ruthven and Thaeron 1997). Parallel passage contactors are known to significantly reduce pressure drop compared to a packed bed at comparable bulk density. The characteristic dimension that controls the mass transfer rate in laminates is its thickness. The challenge is to make very thin laminates that are large enough and have sufficient strength to meet industrial-scale process demands. Mass balance equations for dynamic column breakthrough developed in this paper are valid for breakthrough runs in these advanced contacting devices. The breakthrough simulation model will also be applicable with the LDF constant appropriately modified for the relevant geometry, the Ergun equation replaced with the pressure drop equation in a parallel passage contactor, and the inlet velocity distributions appropriately captured (Farooq et al. 1998; Sharma et al. 2020). While some preliminary studies mentioned here have successfully implemented these modifications, more investigations are required to make impactful contributions.

7 Conclusions

The design of an experimental rig, its critical features and systematic operating procedures to conduct good breakthrough experiments have been presented. An appropriate presentation of breakthrough data and correction methods for the measured data and their analyses were discussed. Breakthrough experiments conducted and analyzed following the recommendations can give reliable single component and mixture equilibrium data. Equilibrium data obtained from adsorption and desorption runs (for a reversible physical adsorption system that does not show hysteresis) are reproducible. For a binary mixture with a large difference in selectivity, it is recommended to obtain the equilibrium data for the heavy component from an adsorption breakthrough and the light component equilibrium data from a desorption breakthrough following an adsorption breakthrough experiment. The recommendation for the intermediate components in a multi-component mixture is similar to that for the light component.

Procedures to investigate the transport mechanism of an adsorbate in adsorbent pores and determine the relevant mass transfer parameter(s) are illustrated. In such breakthrough experiments, the preference should be to minimize heat effects, failing which an appropriate non-isothermal model should be used to extract the mass transfer rate parameter. Extracting a lumped LDF coefficient without attempting any further analysis to examine the intrinsic transport mechanism seems to the overwhelming general trend. Understanding the transport mechanism is important to reliably extend the extracted mass transfer information to other operating conditions and feed compositions; this should be routinely studied going forward. Especially with the explosion of research activities in the material synthesis domain, the number of adsorbents has increased rapidly, and reproducing results is becoming a challenge (Han et al. 2019). Standardizing data presentation and analysis provides an opportunity to improve reliability and reproducibility.

Summarizing, the dynamic column breakthrough method is a useful tool to characterize the equilibrium and transport of adsorbates in adsorbents under process conditions. However, we should be mindful that a breakthrough experiment does not directly shed light on the potential separation performance of the adsorbate–adsorbent system. Suitable process studies should be performed after breakthrough experiments to arrive at such decisions.