1 Introduction

Composite sandwich structure is composed of two thin composite laminates and a thick core. Due to the high specific strength and modulus, good energy absorption and thermal insulation, it is widely employed in the aerospace and other high-tech industries as a typical light-weight structure [1,2,3]. In practical engineering application, the sandwich structure is extremely susceptible to LVI occasions leading to damage such as delamination and fiber fracture, which will critically reduce its residual compressive strength and significantly increase the potential failure risk [4,5,6,7,8]. Therefore, it is necessary to study the LVI performance and damage mechanism of sandwich structure and further analyze the influence of LVI damage on the residual compressive strength of the material structure.

The LVI response and damage behavior of sandwich structures have been extensively investigated up to now. He et al. [9] studied the effects of face sheet thickness and core parameters on the low-velocity impact response and damage mode of aluminum honeycomb sandwich panels with CFRP skin. They found that the thickness of the face sheet can significantly improve the impact resistance of sandwich panel. Zhang et al. [10] explored the influence of the face sheet, core and adhesive layers on the energy absorption of sandwich panels with aluminum sheets and core under LVI, and figured out that the core of sandwich panel plays a critical role in energy absorption. Sun et al. [11] conducted an experimental and numerical study on the LVI behavior of aluminum honeycomb sandwich panels with various structural parameters, which showed that by altering the thickness ratio of the front and back face sheets, the impact response of sandwich panel was optimized without changing the total thickness of face sheets. Ivanez et al. [12] simulated the LVI response of composite sandwich beams and found that the core absorbed up to 80% impact energy at lower velocities while the face sheet absorbed much more energy due to the rupture at higher velocities. Qin et al. [13] investigated the dynamic behavior of metal honeycomb sandwich panels subjected to LVI in various positions. From the center to non-center positions, the impact resistance of the sandwich panel decreased significantly. The other works on the LVI response and damage mechanism of sandwich structures can also be found in Ref [14,15,16,17,18].

However, most works have only investigated the impact resistance of sandwich structures while less attention had been put on the residual properties of impacted sandwich structures. The residual strength of composite materials mainly includes residual compressive strength, residual flexural strength and residual tensile strength. Through experimental test and numerical simulation, He et al. [19] evaluated the residual flexural strength of aluminum honeycomb sandwich panels with impact induced damage. It was found that under bending load, when the core stiffness was lower, the sandwich panel failed owing to core buckling and crushing; when the core stiffness was higher, it failed due to face sheet fracture. Through the three-point bending test, Khosravani et al. [20] found that the flexural modulus and strength of honeycomb core were higher after thermal aging and the hexagonal lattice core had higher load carrying capabilities than triangular lattice. Akatay et al. [21] analyzed the effect of repeated LVI on the residual compressive strength of aluminum honeycomb sandwich with GFRP panels. For single impact, a direct but moderate reduction of compressive strength was formed. However, it was catastrophic reduction in repeated impacts case. Wang et al. [22] conducted an experimental and analytical study on LVI and CAI behavior of foam sandwich with GFPR skins. The main failure mode of CAI for sandwiches without lattice webs was face sheet debonding whereas they are panel delamination and foam crushing with lattice webs. Ge et al. [23] designed a sandwich structure with bi-directional corrugated core and tested it in both flatwise and edgewise compression conditions. Bi-directional corrugated core sandwich panels were shown to own superior compression performance than unidirectional counterpart. In addition, Mazaev et al. [24] investigated the influence of discretization, relative density and thickness of a honeycomb core on the stress state of three-layered composite plates with a tetrachiral honeycomb interlayer during static bending.

At present, there are few studies on the CAI performance of honeycomb core sandwich panels. Most studies only discuss the effect of minor surface damage while there is fewer study of CAI performance under penetration. It is necessary to study the CAI strength of honeycomb sandwich panels from the aspects of impact damage and core parameters. Moreover, it is very essential to propose an integrated and efficient modeling technique for investigating the LVI and CAI behavior to support aerospace certification requirements.

This work aims to develop an FE model to investigate the edgewise compression buckling behavior and damage mechanism of impacted honeycomb sandwich structures. Johnson-Cook material model and bilinear traction-separation model are respectively used to predict the aluminum core damage response and inter-laminar delamination. The CAI performance under three impact damage scenes, minor damage, top face sheet penetration and overall penetration, are analyzed in detail. The influences of the core geometric parameters on the residual compressive strength are also discussed.

2 Dynamic Damage Constitutive Model

2.1 Constitutive Model of CFRP Laminates

Fiber tension, fiber compression, matrix tension and matrix compression are four main failure modes of unidirectional fiber-reinforced composites subjected to LVI. These four failure models can be well predicted by Hashin criteria with the following expressions [25].

Fiber tension failure \(\left( {{{\hat {\sigma }}_{11}} \geqslant 0} \right)\):

$${F_{ft}}={\left( {\frac{{{{\hat {\sigma }}_{11}}}}{{{X^T}}}} \right)^2}+\alpha {\left( {\frac{{{{\hat {\sigma }}_{12}}}}{{{S^L}}}} \right)^2}=1$$
(1)

Fiber compression failure \(\left( {{{\hat {\sigma }}_{11}}<0} \right)\):

$${F_{fc}}={\left( {\frac{{{{\hat {\sigma }}_{11}}}}{{{X^C}}}} \right)^2}=1$$
(2)

Matrix tension failure \(\left( {{{\hat {\sigma }}_{22}} \geqslant 0} \right)\):

$${F_{mt}}={\left( {\frac{{{{\hat {\sigma }}_{22}}}}{{{Y^T}}}} \right)^2}+{\left( {\frac{{{{\hat {\sigma }}_{12}}}}{{{S^L}}}} \right)^2}=1$$
(3)

Matrix compression failure \(\left( {{{\hat {\sigma }}_{22}}<0} \right)\):

$${F_{mc}}={\left( {\frac{{{{\hat {\sigma }}_{22}}}}{{2{S^T}}}} \right)^2}+\left[ {{{\left( {\frac{{{Y^C}}}{{2{S^T}}}} \right)}^2} - 1} \right]\frac{{{{\hat {\sigma }}_{22}}}}{{{Y^C}}}+{\left( {\frac{{{{\hat {\sigma }}_{12}}}}{{{S^L}}}} \right)^2}=1$$
(4)

where \({X^T}\) and \({X^C}\) are the longitudinal tensile and compressive strengths; \({Y^T}\) and \({Y^C}\) are the transverse tensile and compressive strengths; \({S^L}\) and \({S^T}\) denote the longitudinal and transverse shear strengths \({\hat {\sigma }_{11}}\) and \({\hat {\sigma }_{22}}\) are the effective normal stresses and \({\hat {\sigma }_{12}}\) is the shear stress; \(\alpha\) is the shear contribution factor and it is defined as 1 to fully consider the shear stress; F is the failure index of corresponding failure mode.

Once the damage initiation criterion is met, the stiffness of the material will be reduced and the damage evolution begins. The stress-strain relation of the material considering damage is [26]:

$$\left\{ \begin{gathered} {\sigma _{11}} \hfill \\ {\sigma _{22}} \hfill \\ {\tau _{12}} \hfill \\ \end{gathered} \right\}=\frac{1}{{{D_m}}}\left[ {\begin{array}{*{20}{c}} {\left( {1 - {d_f}} \right){E_1}}&{\left( {1 - {d_f}} \right)\left( {1 - {d_m}} \right){v_{21}}{E_1}}&0 \\ {\left( {1 - {d_f}} \right)\left( {1 - {d_m}} \right){v_{12}}{E_2}}&{\left( {1 - {d_m}} \right){E_2}}&0 \\ 0&0&{D\left( {1 - {d_s}} \right)G} \end{array}} \right]\left\{ \begin{gathered} {\varepsilon _{11}} \hfill \\ {\varepsilon _{22}} \hfill \\ {\gamma _{12}} \hfill \\ \end{gathered} \right\}$$
(5)

In the above equation, \({D_m}=1 - \left( {1 - {d_f}} \right)\left( {1 - {d_m}} \right){v_{12}}{v_{21}}>0\), \({E_1}\) and \({E_2}\) are the Young’s modulus, G is the in-plane shear modulus, \({v_{12}}\) and \({v_{21}}\) are the Poisson ratios; \({d_f}\) is the damage state variable of fiber; \({d_m}\) is the damage state variable of matrix ; \({d_s}\) is the shear damage state variable.

\({d_f}\), \({d_m}\) and \({d_s}\)can be determined by:

$$\begin{gathered} {d_f}=\left\{ {\begin{array}{*{20}{c}} {{d_{ft}}}&{{\text{~if }}{{\hat {\sigma }}_{11}} \geqslant 0} \\ {{d_{fc}}}&{{\text{~if }}{{\hat {\sigma }}_{11}}<0} \end{array}{\text{,}}} \right.{\text{ }}{d_m}=\left\{ {\begin{array}{*{20}{c}} {{d_{mt}}}&{{\text{~if }}{{\hat {\sigma }}_{22}} \geqslant 0} \\ {{d_{mc}}}&{{\text{~if }}{{\hat {\sigma }}_{22}}<0} \end{array}} \right. \hfill \\ {\text{ }}{d_s}=1 - \left( {1 - {d_{ft}}} \right)\left( {1 - {d_{fc}}} \right)\left( {1 - {d_{{\text{mt}}}}} \right)\left( {1 - {d_{mc}}} \right) \hfill \\ \end{gathered}$$
(6)

The damage state variable d is defined by:

$${d_I}=\frac{{\delta _{{eq}}^{{f,I}}\left( {{\delta _{eq}} - \delta _{{eq}}^{{0,I}}} \right)}}{{{\delta _{eq}}\left( {\delta _{{eq}}^{{f,I}} - \delta _{{eq}}^{{0,I}}} \right)}}$$
(7)

where index I represents the different failure modes; \(\delta _{{eq}}^{{}}\) and \(\sigma _{{eq}}^{{}}\) are the equivalent displacement and stress; \(\delta _{{eq}}^{0}\) and \(\sigma _{{eq}}^{0}\) are the initial equivalent displacement and stress; \(\delta _{{eq}}^{f}\) is the final equivalent displacement.

Under different failure modes, the expressions of equivalent displacement and stress are also different, namely.

Fiber tension failure \(\left( {{{\hat {\sigma }}_{11}} \geqslant 0} \right)\):

$$\delta _{{eq}}^{{ft}}={L^C}\sqrt{{{\left\langle{{\varepsilon _{11}}}\right\rangle }^2}+\alpha\varepsilon _{{12}}^{2}}\sigma _{{eq}}^{{ft}}=\frac{{\left\langle {{\sigma _{11}}} \right\rangle \left\langle {{\varepsilon _{11}}} \right\rangle +\alpha {\tau _{12}}{\varepsilon _{12}}}}{{\delta _{{eq}}^{{ft}}/{L^C}}}$$
(8)

Fiber compression failure \(\left( {{{\hat {\sigma }}_{11}}<0} \right)\):

$$\delta _{{eq}}^{{fc}}={L^C}\left\langle { - {\varepsilon _{11}}} \right\rangle \quad \sigma _{{eq}}^{{fc}}=\frac{{\left\langle { - {\sigma _{11}}} \right\rangle \left\langle { - {\varepsilon _{11}}} \right\rangle }}{{\delta _{{eq}}^{{fc}}/{L^C}}}$$
(9)

Matrix tension failure \(\left( {{{\hat {\sigma }}_{22}} \geqslant 0} \right)\):

$$\delta _{{eq}}^{{mt}}={L^C}\sqrt {{{\left\langle {{\varepsilon _{22}}} \right\rangle }^2}+\varepsilon _{{12}}^{2}} \quad\sigma _{{eq}}^{{mt}}=\frac{{\left\langle {{\sigma _{22}}} \right\rangle \left\langle {{\varepsilon _{22}}} \right\rangle +{\tau _{12}}{\varepsilon _{12}}}}{{\delta _{{eq}}^{{mt}}/{L^C}}}$$
(10)

Matrix compression failure\(\left( {{{\hat {\sigma }}_{22}}<0} \right)\):

$$\delta _{{eq}}^{{mc}}={L^C}\sqrt {{{\left\langle { - {\varepsilon _{22}}} \right\rangle }^2}+\varepsilon _{{12}}^{2}} \quad \sigma _{{eq}}^{{mt}}=\frac{{\left\langle { - {\sigma _{22}}} \right\rangle \left\langle { - {\varepsilon _{22}}} \right\rangle +{\tau _{12}}{\varepsilon _{12}}}}{{\delta _{{eq}}^{{mc}}/{L^C}}}$$
(11)

where\({L^C}\)is the characteristic length of the element.

The damage initiation displacement under different failure modes is:

$$\begin{array}{*{20}{c}} {\delta _{{eq}}^{{0,ft}}={{\left. {\delta _{{eq}}^{{ft}}} \right|}_{{F_{ft}}=1}}} \\ {\delta _{{eq}}^{{0,fc}}={{\left. {\delta _{{eq}}^{{fc}}} \right|}_{{F_{fc}}=1}}} \\ {\delta _{{eq}}^{{0,mt}}={{\left. {\delta _{{eq}}^{{mt}}} \right|}_{{F_{mt}}=1}}} \\ {\delta _{{eq}}^{{0,mc}}={{\left. {\delta _{{eq}}^{{mc}}} \right|}_{{F_{mc}}=1}}} \end{array} \begin{array}{*{20}{c}} {\sigma _{{eq}}^{{0,ft}}={{\left. {\sigma _{{eq}}^{{ft}}} \right|}_{{F_{ft}}=1}}} \\ {\sigma _{{eq}}^{{0,fc}}={{\left. {\sigma _{{eq}}^{{fc}}} \right|}_{{F_{fc}}=1}}} \\ {\sigma _{{eq}}^{{0,mt}}={{\left. {\sigma _{{eq}}^{{mt}}} \right|}_{{F_{mt}}=1}}} \\ {\sigma _{{eq}}^{{0,mc}}={{\left. {\sigma _{{eq}}^{{mc}}} \right|}_{{F_{mc}}=1}}} \end{array}$$
(12)

The final equivalent displacement under different failure modes is:

$$\delta _{{eq}}^{{f,I}}=\frac{{2G_{{\text{I}}}^{C}}}{{\sigma _{{eq}}^{{0,I}}}}$$
(13)

where \(G_{{}}^{C}\) represents the fracture energy of the material.

2.2 Constitutive Model of Aluminum Honeycomb Core

The plastic hardening and strain-rate hardening processes of common metals can be described using Johnson-Cook model [27, 28]. The effective stress is defined as:

$$\sigma =\left( {A+B{\varepsilon ^n}} \right)\left( {1+C{\text{In}}{{\dot {\varepsilon }}^ * }} \right)\left( {1 - {T^{ * m}}} \right)$$
(14)

where A is the yield stress; B is the hardening constant and n is the hardening exponent; C is the strain rate constant; \(\varepsilon\) is the effective plastic strain, \({\dot {\varepsilon }^ * }\) is the normalized effective plastic strain rate; m is the thermal softening exponent. The dimensionless temperature, \({T^ * }\), can be expressed by:

$${T^ * }=\left( {T - {T_r}} \right)/\left( {{T_m} - T} \right)$$
(15)

where, \({T_r}\) is the room temperature; \({T_m}\) is the material melting point.

The Johnson-Cook model adopts a linear accumulation method to reflect the failure depending upon the material deformation process. The plastic fracture strain\({\varepsilon _f}\)is represented by:

$${\varepsilon _f}=\left[ {{D_1}+{D_2}\exp {\sigma ^ * }} \right]\left[ {1+{D_4}In{{\dot {\varepsilon }}^ * }} \right]\left[ {1+{D_5}{T^ * }} \right]$$
(16)

where \({\sigma ^ * }\)is the normalized mean stress; \({D_1}\)–\({D_5}\) are failure parameters determined by experimental data.

When the damage parameter D in Eq. (17) accumulates to be 1, the damage of metal material happens.

$$D=\sum {{{\Delta}}}{\varepsilon _{eq}}/{\varepsilon _f}$$
(17)

where \({\Delta}{\varepsilon _{eq}}\) is the equivalent plastic strain increment.

2.3 Constitutive Model of Cohesive Element

Cohesive interface is considered between adjacent layers. Only a normal stress \({t_1}\) and two shear stresses \({t_2}\) and \({t_3}\) exist since the cohesive interface is extremely thin. The interface behavior is governed by a bilinear traction-separation law, which adopts an initial linear elastic response followed by a linear damage evolution.

The initial elastic response of cohesive elements can be expressed as [29]:

$$\left\{ {\begin{array}{*{20}{l}} {{t_1}} \\ {{t_2}} \\ {{t_3}} \end{array}} \right\}=\left[ {\begin{array}{*{20}{c}} {{k_1}}&0&0 \\ 0&{{k_2}}&0 \\ 0&0&{{k_3}} \end{array}} \right]\left\{ {\begin{array}{*{20}{l}} {{\delta _1}} \\ {{\delta _2}} \\ {{\delta _3}} \end{array}} \right\}$$
(18)

where k is the initial stiffness and\(\delta\)is the separation displacement. To recognize the damage initiation of cohesive elements, Camanho and Davila [29] suggested the quadratic nominal stress criterion, which is specified by:

$${\left( {\frac{{\left\langle {{t_1}} \right\rangle }}{N}} \right)^2}+{\left( {\frac{{{t_2}}}{S}} \right)^2}+{\left( {\frac{{{t_3}}}{T}} \right)^2}=1$$
(19)

where N, S and T are the interface strengths in tensile and two shear directions.

The normal compressive stress does not contribute to the damage initiation of cohesive elements. Hence, the Macaulay operator in Eq. (19) is defined by:

$$\left\langle a \right\rangle =\left\{ {\begin{array}{*{20}{c}} {a{\text{ }}a>0} \\ {0{\text{ }}a \leqslant 0} \end{array}} \right.$$
(20)

After damage initiation, the linear damage evolution of interface is represented by a scalar damage variable d, namely

$$d=\frac{{\delta _{m}^{f}\left( {{\delta _m} - \delta _{m}^{0}} \right)}}{{{\delta _m}\left( {\delta _{m}^{f} - \delta _{m}^{0}} \right)}}\quad (d \in [0,1])$$
(21)

Here, \({\delta _m}\), involving the combination of normal and shear separations, is the equivalent strain determined by Eq. (22). \(\delta _{m}^{0}\) is the equivalent strain upon which material is initially damaged and \(\delta _{m}^{f}\) is the equivalent strain upon which material is totally damaged.

$${\delta _m}=\sqrt {{{\left\langle {{\delta _1}} \right\rangle }^2}+\delta _{2}^{2}+\delta _{3}^{2}} =\sqrt {{{\left\langle {{\delta _1}} \right\rangle }^2}+\delta _{{shear}}^{2}}$$
(22)

Then, the damage variable d is introduced into the constitutive relationship of cohesive elements as:

$$\left\{ {\begin{array}{*{20}{l}} {{{\hat {t}}_1}} \\ {{{\hat {t}}_2}} \\ {{{\hat {t}}_3}} \end{array}} \right\}=\left[ {\begin{array}{*{20}{c}} {1 - d\left\langle {{t_1}} \right\rangle /{t_1}}&0&0 \\ 0&{1 - d}&0 \\ 0&{}&{1 - d} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{k_1}}&0&0 \\ 0&{{k_2}}&0 \\ 0&0&{{k_3}} \end{array}} \right]\left\{ {\begin{array}{*{20}{l}} {{\delta _1}} \\ {{\delta _2}} \\ {{\delta _3}} \end{array}} \right\}$$
(23)

Here, the hat symbol (^) denotes the actual stress.

3 Description of FE Model

3.1 Configuration of Sandwich Structure

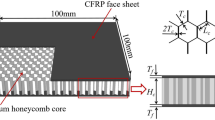
Figure 1 shows the sandwich structure, which is made up of two thin CFRP skins and a thick aluminum honeycomb core. In this work, four different geometric configurations of sandwich panel are set up by changing the height of core, wall thickness and side length of honeycomb cell in order to fully explore the role of core under LVI and its influence on CAI strength. The overall dimension of the sandwich panel is 100 × 100 mm. The geometric parameters of sandwich panels are summarized and provided in Table 1. The CFRP face sheet is laminated with eight unidirectional T700 carbon-fiber reinforced epoxy layers (0.125 mm each layer) in 0°/90° stacking sequence, with the material parameters listed in Table 2. The material parameters of AA3003 aluminum alloy applied in aluminum honeycomb core are given in Table 3.

Fig. 1
figure 1

Schematic diagram of geometric structure of aluminum honeycomb sandwich panel [9]

Full size image
Table 1 Geometric parameters of sandwich panel [9]
Full size table
Table 2 Material properties of the unidirectional laminate [9]
Full size table
Table 3 Material properties of AA3003 aluminum alloy foil [9]
Full size table

3.2 FE Modeling

The CAI of sandwich panel can be separated into three steps in simulation, as illustrated in Fig. 2. First, the sandwich panel is subjected to LVI. Then, it is the stabilization process, which eliminate stress oscillation in the sandwich panel and prepares it for compression. Lastly, the edgewise compression simulation is conducted. The damage state in sandwich panel obtained after LVI will be the initial condition of compression simulation.

Fig. 2
figure 2

Analysis steps for FE simulation

Full size image

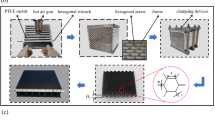
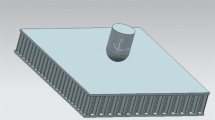
The FE model of LVI of sandwich structure is established in ABAQUS/Explicit, which is composed of the impactor, clamps and sandwich panel, as presented in Fig. 3. The diameter of impactor is 12 mm and the mass is 13.2 kg. The center of the clamp provides a 75 mm diameter impact region. Both the impactor and clamp are discrete with four-node rigid quadrilateral elements (R3D4), which are set as rigid bodies since only slight deformation occurs in impact. CFRP laminates are discretized with hourglass-controlled 8-node reduced-integration continuous shell elements (SC8R). 8-node zero-thickness cohesive elements (COH3D8) are inserted between each layer of laminates to simulate the interfacial delamination. The honeycomb core is discrete with hourglass controlled 4-node traditional shell elements (S4R). To make the simulation results more accurate, mesh-refine is performed in the impact area of the sandwich panel.

Fig. 3
figure 3

FE model of LVI of sandwich panel

Full size image

The bottom clamp is fixed and a clamping pressure of 0.02 MPa is applied to the top clamp in the LVI simulation. The Z-direction displacement of the impactor is allowed by setting different velocities of the impactor (0.87 m/s, 1.23 m/s and 2.46 m/s) to achieve corresponding impact energies of 5, 10 and 40 J. Since there is no visible debonding observed between the skins and core during the impact process, the “tie contact” available in ABAQUS/explicit is adopted. The interaction between impactor and sandwich panel is set as “general contact” with the normal direction as “hard contact” and the tangential direction as “penalty contact”. Here, the coefficient of friction is set as 0.3.

After impact, the boundary conditions of the sandwich panel are adjusted for edgewise compression simulation. One side of the sandwich panel is fixed, while the other is loaded with a 0.7 mm displacement along X-direction.

3.3 Verification of Proposed FE Model

The experimental data obtained from the LVI of aluminum honeycomb sandwich panels with CFRP skins (specimen T0.06-H10-L3.0) are compared with the results of numerical simulations to verify the applicability of the proposed FE model. The damage patterns of the sandwich panels obtained by simulation with three impact energies (5, 10 and 40 J) are consistent well with the experimental results, as shown in Fig. 4.

Fig. 4
figure 4

Comparison of experimental [9] and simulated damage patterns of specimen T0.06-H10-L3.0 under different impact energies

Full size image

The experimental and simulated impact load-time curves and energy absorption-time curves of specimen T0.06-H10-L3.0 are illustrated in Fig. 5. The predicted impact load curves and energy absorption curves agree with the experimental data. However, when the impact energy is 40 J, the predicted second peak load is much lower than the experimental value. It can be attributed to the deletion of damaged element in the simulation leading to the loss of interaction with the impactor. As provided in Table 4, the peak impact load derived from numerical simulation has a maximum error of 4.90%, and the energy absorption has a maximum error of 13.02%, which verifies the effectiveness of the proposed FE model. Later, the verified FE model will be utilized to predict the CAI mechanical response of sandwich panel in diverse structural configurations.

Fig. 5
figure 5

Comparison of experimental [9] and simulated impact load-time curves and energy absorption-time curves of specimen T0.06-H10-L3.0 under different impact energies a 5 J b 10 J c 40 J

Full size image
Table 4 Experimental [9] and predicted peak load and energy absorption of specimen T0.06-H10-L3.0
Full size table

4 Numerical Results and Discussions

4.1 LVI Damage Characterization

Figure 6 depicts the LVI damage patterns of four sandwich panels with various core geometrical parameters. From Fig. 6, it can be found that no evident damage formed on the top face sheet of the sandwich panel when the impact energy is 5 J. However, the core buckled and folded at the impact point and the damage extended from the center to the periphery. In the case of 10 J, the top face sheet is penetrated resulting in the increase of core damage depth. In addition, the skin sheet and core of the sandwich panel are both penetrated under 40 J impact with damage also occurring around the center of bottom sheet. By comparing the damage patterns of these sandwich panels, it can be found that the core damage area and panel deflection around impact point of specimen T0.06-H10-L1.5 are significantly smaller than those of other sandwich panels. It can be concluded that reducing the side length of honeycomb cells will increase the stiffness of sandwich panel and make the damage region smaller.

Fig. 6
figure 6

LVI damage patterns of sandwich panels under different impact energies

Full size image

The impact force and energy absorption curves of sandwich panels with four core characteristics under LVI are provided in Fig. 7. Energy absorption of the sandwich plate is obtained by subtracting the kinetic energy from the initial impact energy of the impactor. The energy absorption curve of sandwich panel expresses a trend of first rise and then decrease under the impact energy of 5 and 10 J. It is caused by the rebound of sandwich panel after impact. According to the trend and peak of the curves, the variation of the height of the core (T0.06-H5-L3.0) and the wall thickness of honeycomb cells (T0.03-H10-L3.0) has a slight effect on the peak contact force and energy absorption. However, the energy absorption increases significantly when the side length of the honeycomb cells decreases (T0.03-H10-L1.5). Due to the improved stiffness of the sandwich panel, this peak impact force arrives earlier and becomes larger. Furthermore, the decrease of core thickness (T0.06-H5-L3.0) causes the impactor to have a shorter impact period. That is, it will impact the bottom face sheet earlier resulting in the earlier appearance of second peak in the case of 40 J.

Fig. 7
figure 7

Impact load and energy absorption curves of sandwich panels under different impact energies a 5 J b 10 J c 40 J

Full size image

To further investigate the damage behavior of sandwich panel under LVI, specimen T0.06-H10-L3.0 is selected to describe the failure mode of skin sheets, as shown in Fig. 8. It can be observed that the damage area of fiber tension, fiber compression, matrix tension and matrix compression of the face sheets increases steadily with increasing impact energy. In these damage modes, matrix tension failure is most evident. Besides, the delamination area of sandwich panels grows noticeably compared to other failure modes while only the central part of the cohesive elements are completely deleted due to interface penetration.

Fig. 8
figure 8

Failure modes in skin sheets of specimen T0.06-H10-L3.0 under different impact energies

Full size image

4.2 Analysis of CAI Process

Due to the lack of experimental results on CAI of the CFRP aluminum sandwich composites under LVI, only the numerical prediction results are provided here. Figure 9 displays the out-of-plane displacement field of the top sheet after edgewise compression of non-impacted and impacted sandwich panels. The buckling in non-impacted sandwich panel caused by compression can result in fiber fracture at the corner of face sheet. The fracture pattern consists mostly of two cracks with an uneven fracture position. It is worth noting that the fracture morphology of the non-impact specimen T0.06-H10-L1.5 shows a crack. It is due to that the reduction of side length of honeycomb cells increases the in-plane stiffness of sandwich panel. Specially, the buckling results of impacted specimen T0.06-H10-L3.0 (40 J) during the compression process are exhibited in Fig. 10. The buckling level of the impact position increases with the compression process, and it extends along the center to the ends of the face sheet causing the panel to break. A straight line runs through the impact position forming the pattern. The buckling of the panel during compression can be greatly reduced by decreasing the side length of the honeycomb cells (T0.06-H10-L1.5). On the other hand, the buckling level of the panel increases with the decrease of core height (T0.06-H05-L3.0) and cell wall thickness (T0.03-H10-L3.0).

Fig. 9
figure 9

Out-of-plane displacement field of top sheet of the sandwich under edgewise compression

Full size image
Fig. 10
figure 10

Buckling displacement of the top sheet of 40 J impacted specimen T0.06-H10-L3.0 under compression

Full size image

To analyze the failure mechanism of sandwich panel under edgewise compression, the specimen T0.06-H10-L3.0 in non-impacted and 40 J impacted conditions, is selected, as illustrated in Fig. 11. The compression damage of the non-impacted sandwich panel mainly spreads along two irregular cracks, and the impacted sandwich panel spreads along the vertical crack. Matrix compression and matrix tension are the most obvious failure modes for these two sandwich panels, and the overall damage area of non-impacted sandwich panel is greater. Compared with non-impacted sandwich panel, the fiber and delamination damage caused by edgewise compression to the impacted case is more noticeable.

Fig. 11
figure 11

Compressive failure of top face sheet of sandwich panel a non-impacted panel b 40 J impacted panel

Full size image

4.3 Load-displacement Curves in Compression

The load-displacement curves of the sandwich panels subjected to compressive load are depicted in Fig. 12. The load on the sandwich panel gradually increases as the compressive displacement increases, and shows a linear trend before reaching the peak load. The sandwich panel is broken when the ultimate load is reached, and the curve decreases rapidly. LVI has a great influence on the residual compressive strength of the sandwich panel, even under low impact energy of 5 J. The ultimate load-bearing capacity is significantly reduced. Moreover, for sandwich panels T0.06-H05-L3.0 and T0.03-H10-L3.0, the impact energy from 5 to 40 J has non-significant effect on the residual compressive strength. However, for sandwich panel T0.06-H10-L1.5, the residual compressive strength decreases with the increase of impact energy.

Fig. 12
figure 12

Load-displacement curves of specimens with different structural parameters under various impact energies

Full size image

Due to the different failure mechanism in non-impacted and impacted cases, the core geometric parameters has little effect on the compressive strength of non-impacted sandwich panel but has a considerable effect on the CAI performance of impacted sandwich panel. As displayed in Fig. 13, the edgewise compressive strength of the non-impacted sandwich panels are mostly determined by face sheets, whereas the CAI strength of impacted sandwich panels are primarily determined by the deflection at the impact position. By decreasing the height of core (T0.06-H05-L3.0) and wall thickness of honeycomb cells (T0.03-H10-L3.0), the stiffness of the sandwich panel decreases while the deflection of the impact pit increases. It results in a 50% reduction in CAI strength. The CAI strength of the sandwich panel will be greatly improved by reducing the side length of honeycomb cells (T0.06-H10-L1.5), which improves the stiffness of sandwich panel and lessen the deflection of impact pit. The CAI strength of the sandwich panel retains close to 80% with impact energy of 5 J.

Fig. 13
figure 13

Residual compressive strengths and normalized residual compressive strengths of specimens

Full size image

5 Conclusion

In this paper, a FE model of aluminum honeycomb sandwich panels with CFRP face sheets is established to predict the LVI and CAI properties. The influences of honeycomb core height, cell side length and wall thickness on the impact resistance and residual strength of sandwich panel are investigated in detail. Several main conclusions drawn from this work are summarized as follows.

  1. 1.

    The geometric parameters of core have a significant effect on the LVI resistance of sandwich panel. The smaller side length of the honeycomb cell, the larger core height and the thicker cell wall will increase the stiffness of the sandwich panel. They also result in an increase in peak impact load, a decrease in damaged core area and a decrease in deflection of impact position. The greater the overall stiffness of the sandwich panel leads the better resistance to LVI.

  2. 2.

    The CAI damage response of impacted and non-impacted sandwich panels is completely different. The compression fracture of non-impacted sandwich panel mostly displays two cracks whereas the crack of the impacted sandwich panel extends from the center position to the ends into a straight line. Therefore, the impact cave caused by LVI determines the damage shape of sandwich panel under CAI.

  3. 3.

    The deformation near the impact point caused by LVI significantly affects the CAI strength of sandwich panels. The impact has a significant influence on the compression performance of sandwich panels, even under a low-energy impact. The residual compressive strength of sandwich panels reduce dramatically compared to non-impacted cases.

  4. 4.

    The upper and lower panels of the sandwich panel determine the edgewise compression load-bearing capacity of sandwich panel. The overall stiffness of core determines the deflection of impact point. The geometric parameters of core have little effect on the edgewise compressive strength of non-impact sandwich panel while a great influence on the CAI strength of impacted sandwich panel. The CAI strength of a sandwich panel is proportional to its overall structural stiffness.