Digital Image Correlation (DIC) Validation of Engineering Approaches for Bending Stiffness Determination of Damaged Laminates

Abstract

During the last decade new models for bending stiffness prediction of damaged composite laminates have been proposed in the literature advancing the earlier developed engineering approaches in accuracy and in complexity. However, experimental data for validation of complex analytical or engineering models are almost non-existent in the literature. In the present work a detailed experimental study was performed to investigate the bending stiffness reduction of composite cross-ply laminates with evolving micro-damage. Intralaminar cracks and local delaminations in the bottom surface 90-degree layer of carbon/epoxy and glass/epoxy cross-ply laminates were introduced in 4-point bending tests. Digital Image correlation (DIC) technique was used to experimentally determine the midplane curvature. The accuracy of beam theory for bending stiffness determination was assessed. The measured bending stiffness reduction with respect to transverse crack density was also compared with FEM predictions. The results show that the beam theory gives slightly underestimated curvature at low deflections, whereas at large deflections the beam theory overestimates the curvature and the moment–curvature relation becomes nonlinear. Nevertheless, the overall agreement between beam theory and DIC-based results is still very good, which leads to conclude that beam theory based data reduction schemes have sufficient accuracy for predicting bending stiffness even for highly damaged laminates.

1 Introduction

Prediction of bending stiffness reduction due to micro-cracking is highly relevant in many engineering applications of high performance composites, such as, for example, wings of the aeronautical structures, wind turbine blades, automotive frame components, etc. Regarding the state of the art prediction methods, the in-plane stiffness reduction of laminated composites due to micro-cracking has been thoroughly understood. Some of the better-known research works on this topic discuss modeling approaches [1, 2], analysis of progressive matrix cracking [3, 4], reduction of thermo-elastic properties [5] and delamination starting from matrix cracks [6]. These works have been complemented by a vast amount of related publications and the prediction models for in-plane loading have now matured.

In recent decades, a significant progress has also been made in developing and improving models for predicting the bending stiffness (out-of-plane loading) of composites with evolving intralaminar damage in plies and with interlaminar cracks (delaminations) [7,8,9,10,11,12,13]. In this context at least three research directions can be distinguished with respect to the approach and computational tools used. The first group is purely based on numerical models, in most cases using FEM for response calculation of some structural element with explicitly modelled cracks, considering them as discontinuities [10]. In the second group [11,12,13], semi-analytical methods are developed refining approximate analytical solution by dividing plies into sub-layers. On one hand such models may have high accuracy, on the other hand the calculation methodology is very complex and difficult to apply for other researchers. The third group is suggesting probably less accurate but more application friendly methods based on simple models [7, 8], variational approach [9] or Classical Laminate Theory (CLT), where the stiffness of damaged plies is replaced by the so-called “efficient stiffness” that depends on the damage state [10, 14]. A significant obstruction for validation of the described bending stiffness models is the lack of experimental data in the literature.

Recently, some experimental data for validation of the effective stiffness models for bending stiffness prediction have been presented by the authors [14]. In few other examples in the literature [15, 16] damage in 90-plies was introduced in tensile test and then the bending of the laminate was studied in mechanical loading or as thermal curvature change. Experimental data on micro-damage evolution and corresponding bending stiffness reduction in laminates were presented in [17] for static loading and in [18] for cyclic loading.

In the present work, extensive experimental data for bending stiffness of laminates with intralaminar cracks and delaminations are presented and compared with beam theory engineering models and FEM results. Micro-damage was introduced in [90_n/0]_s cross-ply laminates in a 4-point bending test by subjecting the specimens to relatively large displacements, which lead to large strains in surface layers. The bending stiffness of previously damaged laminates was determined by performing a small-displacement bending test in linear-elastic region.

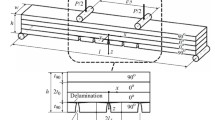
In the 4-point bending test the damage state is not uniform along the length of the specimen: the central region between loading points, where the curvature is larger, is usually more damaged than the peripheral regions near the supports (Fig. 1). During the 4-point bending test, intralaminar cracks and subsequent delaminations may only be introduced in the bottom 90-degree layer of the laminate, where the transverse stresses are tensile. The load bearing capacity of the damaged 90-degree layer becomes smaller and correspondingly the laminate behavior becomes more and more unsymmetrical. Due to progressing damage, the thermal stresses in layers are also changing and the initially symmetric and flat laminate obtains a certain curvature that changes with damage development.

Fig. 1

Schematic depiction of a cross-ply laminate subjected to 4-point bending with damage in bottom surface 90-degree layer

In a real experiment the damage distribution is never perfectly uniform, which means that even in the central zone with constant applied moment ${M}_{x}$ the bending stiffness has variation and there is no symmetry with respect to the middle-point.

The above brief description of potential problems points towards necessity to gather reliable experimental data for bending stiffness reduction due to micro-damage development. Hence, it also motivates revisiting the most common analysis method used for this purpose: the 4-point bending test. The common data reduction routine is based on beam theory that states that in the central region between the loading points the displacement distribution profile is parabolic. In geometrically small deformation theory it leads to constant curvature in the zone between the loading points that in normalized form does not depend on effective elastic constants (i.e., on the effective flexural modulus that depends on damage state, see Sect. 3). Another postulate regarding accuracy that should be assessed is that, quite typically, the only recorded set of data used in estimation of bending stiffness are the load and the cross-head displacement of the testing machine.

One way for a robust assessment of accuracy of such beam theory-based assumptions and methods is to use Digital Image Correlation (DIC) technique, which makes it possible to perform full-field strain and displacement measurements on specimen edges. Full field displacement measurement techniques such as DIC have been developed during the last 2–3 decades [19,20,21,22,23,24,25,26,27,28,29] and they have the capability to give a deeper insight into complex deformation problems. DIC systems allow obtaining a complete displacement distribution in a region of interest and can even be applied to measure local strains in the damaged regions. Research works include comprehensive overviews on image correlation for shape, motion and deformation measurement [19], 3-D surface profile and displacement measurements [20], 2D DIC for displacement and strain field measurements [21]. Specific applications of DIC in composite materials characterization has been described in [22]. Alternative approach of using electronic speckle pattern interferometry for measurement of plane strain surface displacements is presented in [23]. Many papers are published on using DIC for analysis of damaged composites, some focusing on micro-scale deformations [24], some focusing on specific damage modes, such as transverse cracking [25, 26], others analyzing local variation of homogenized properties, for example, laminate stiffness [27]. DIC methods have also been used in context of flexural tests of composites, however, mostly focusing on delamination and buckling analysis [28] and shear strain distribution near the loading points [29].

In the present study Digital Image Correlation (DIC) based experimental program was carried out, recording the displacement distribution during the 4-point bending test, with the following objectives:

• (a) To assess the assumptions used in the beam theory regarding displacement distribution and curvature determination for severely damaged laminates

• (b) To inspect the range of applicability and validate usage of robust, reliable and simple beam theory-based testing methods for bending stiffness determination of damaged composite laminate specimens

• (c) To analyse damage modes in plies and their change during large deflection bending, comparing test results with FEM modelling.

Hence, in the present paper bending stiffness reduction in cross-ply laminates with intralaminar cracks in surface 90-degree layers was calculated in two different ways:

• (a) using testing machine force data and DIC displacement distribution data;

• (b) using testing machine force and cross-head displacement data and simple beam theory expressions.

The bending stiffness dependence on crack density is compared with 3-D FEM model predictions, where the region between load application points was modelled with explicit, uniformly distributed intralaminar cracks (with or without local interlaminar delaminations in the crack tip region).

2 Methods of Analysis

2.1 Mechanics of the 4-point Bending Test

Initially symmetric [90_n/0]_s cross-ply laminate is subjected to 4-point bending, introducing damage in central region of the bottom surface 90-degree layer, see Fig. 1. The coordinate system shown in Fig. 1 is consistently used in the further text.

The possible damage modes under 4-point bending are intralaminar cracks in the bottom 90-degree layer and local delaminations (interlaminar cracks) as shown in a detail view in Fig. 2a and a typical micrograph Fig. 2b.

Fig. 2

a Schematic image of intralaminar (transverse) cracks and delaminations due to bending in a cross-ply laminate. b Typical micrograph of micro-damage in laminate

Bending stiffness reduction is analysed using the relationship between the applied bending moment ${M}_{x}$ and midplane curvature ${k}_{x}$. Particular case, where the whole specimen length $l$ between two supports is divided in three equal parts $(l/3)$, is analyzed in this paper.

Uniform, displacement ${u}_{z}(t)$ monotonously increasing with respect to time $t$ is applied on both loading points ($x=\pm l/6$ in Fig. 1) and the corresponding force $P(t)$ is measured in the test or calculated numerically with FEM. As follows from equilibrium considerations, see Sect. 2.4, the region between both loading points is subjected to constant (coordinate independent) bending moment ${M}_{x}(t)$.

By increasing ${u}_{z}\left(t\right)$, the curvature of the specimen ${k}_{x}$ increases and so does the axial strain ${\varepsilon }_{x}$, that, according to CLT, is linear with respect to the thickness coordinate $z$ measured from the laminate middle-plane (Figs. 1 and 2). Hence, the axial strain ${\varepsilon }_{x}$ is tensile in the bottom surface 90-degree layer of the laminate and intralaminar cracks may be created in this layer (Figs. 1 and 2), reducing the bending stiffness of the damaged region of the laminate.

Intralaminar cracks, with a crack tip at the interface with the adjacent 0-degree layer, cause very high shear stresses ${\sigma }_{xz}$ and tensile out-of-plane normal stresses ${\sigma }_{zz}$ in this region, often resulting in formation of local delaminations (interlaminar cracks) growing from the intralaminar crack tip in the $x$ axis direction during increasing loading as shown in Fig. 2. Thus, damage parameters are the crack density ${\rho }_{c}$ in the layer with average spacing between the cracks $2{l}_{c}=1/{\rho }_{c}$, and delamination length ${l}_{d}$, see Fig. 2.

When intralaminar cracks are introduced in the surface 90-degree layer, the laminate becomes unsymmetrical: the $B$ matrix of the damaged laminate is not zero and some middle-plane strains ${\varepsilon }_{x0}$, ${\varepsilon }_{y0}$ may also be present. When damage evolves, the laminate extensional, coupling and bending stiffness matrices ($A,B,D$ respectively) change, each in a different way. Experimentally and also in FEM simulations we analyse the laminate bending resistance, plotting the slope of the bending moment-curvature curve (trendline in low curvature region) versus the crack density in the layer, i.e., ${M}_{x}/{k}_{x}\sim {\rho }_{c}$.

2.2 CLT Formulation

According to CLT, an unsymmetrical cross-ply laminate should have double curvature (nonzero curvature even before mechanical loading, due to thermal stresses in plies). However, many observations have shown that the state with double curvature is unstable and usually unsymmetrical laminate curved by thermal stresses has one or another stable cylindrical shape. Therefore, in CLT calculations we assume that only ${k}_{x}$ is applied leading to ${M}_{x}$ to be calculated and to boundary conditions with

$${\gamma }_{xy0}={k}_{xy}={k}_{y}=0$$

(1)

The out-of-plane normal strains ${\varepsilon }_{z}$ are also neglected.

The CLT equations for this case are

$$\begin{cases}0={A}_{11}{\varepsilon }_{x0}+{A}_{12}{\varepsilon }_{y0}+{B}_{11}{k}_{x}\\ 0={A}_{12}{\varepsilon }_{x0}+{A}_{22}{\varepsilon }_{y0}+{B}_{12}{k}_{x}\\ {M}_{x}={B}_{11}{\varepsilon }_{x0}+{B}_{12}{\varepsilon }_{y0}+{D}_{11}{k}_{x}\\ {M}_{y}={B}_{12}{\varepsilon }_{x0}+{B}_{22}{\varepsilon }_{y0}+{D}_{12}{k}_{x}\end{cases}$$

(2)

where

$${A}_{ij}=\sum\nolimits_{k=1}^{N}{\overline{Q} }_{ij}^{k}{t}_{k},\,{B}_{ij}=\sum\nolimits_{k=1}^{N}{\overline{Q} }_{ij}^{k}\frac{{z}_{k+1}^{2}-{z}_{k}^{2}}{2}, \,{D}_{ij}=\sum\nolimits_{k=1}^{N}{\overline{Q} }_{ij}^{k}\frac{{z}_{k+1}^{3}-{z}_{k}^{3}}{3}$$

(3)

In (3) ${t}_{k}$, $k=\mathrm{1,2}\dots N$ is the thickness of the $k$-th layer; the overbar is used to denote the stiffness of the layer in the global system of coordinates, see, for example, [30]. Solving (2) with respect to ${M}_{x}$, we can express it in form

$${M}_{x}={C}_{11}({\rho }_{c}){k}_{x}$$

(4)

where the expression for ${C}_{11}$ follows from solving (2):

$${C}_{11}=\frac{{B}_{11}\left({A}_{22}{B}_{11}-{A}_{12}{B}_{12}\right)+{B}_{12}\left({A}_{11}{B}_{12}-{A}_{12}{B}_{11}\right)}{{A}_{12}^{2}-{A}_{11}{A}_{22}}+{D}_{11}$$

(5)

According to (4), (5), by measuring ${M}_{x}$ and ${k}_{x}$ during the experimental test, we can determine ${C}_{11}$, which is not exactly equal to ${D}_{11}$, when the laminate has evolving damage and the symmetry is lost.

In (5), the elements of the $A,B,D$ matrices are changing differently with increasing crack density ${\rho }_{c}$. In this study the dependence of ${C}_{11}$ on intralaminar crack density ${\rho }_{c}$ was investigated experimentally and also by using FEM simulation. Corresponding results are presented in Sect. 5.

The boundary conditions in an experimental test could be slightly different than described above, for example, ${\gamma }_{xy0}={M}_{xy}={M}_{y}=0$ instead of Eq. (1), however, the differences due to changed boundary conditions are expected to be small.

2.3 FEM Modelling

The 3-D FEM model according to schematic geometry shown in Fig. 3 was generated using finite element software ANSYS [31]. The model consisted of layers representing the given [90_n/0]_s cross-ply lay-ups. The laminate was subjected to a 4-point bending loading scheme by applying constant vertical displacement ${u}_{z}$ = 3 mm at the loading lines at $x=\pm l/6$ (Fig. 3).

Fig. 3

Schematic image of a 3-D FEM model of damaged cross-ply laminate subjected to 4-point bending

Simple supports, allowing rotation around $y$ axis, were added at specimen ends: the nodes corresponding to coordinates$x=-l/2$, $z=h/2$ were constrained against displacement in $x$ and $z$ axis directions; the node at coordinate$x=-l/2$, $z=h/2$, $y=-0.5w$ was additionally constrained against displacement in the $y$ axis direction to ensure stability of deformation. The nodes corresponding to coordinates$x=+l/2$, $z=h/2$ were constrained against displacement in the z axis direction and the node corresponding to coordinate$x=+l/2$, $z=h/2$, $y=-0.5w$ was additionally constrained against displacement in $y$ axis direction. Displacement ${u}_{y}$ coupling was applied on the nodes of each edge of the laminate ($y=0$,$y=-w$) ensuring generalized plane strain conditions and satisfying conditions (1).

The length of the model $l$ was taken equal to 150 mm in accordance with experimental tests described in Sect. 3. The width of the model in $y$-axis direction $w$ was set equal to 20 mm. The thickness of the 90 and 0-degree layers was modelled according to the average thickness of respective lay-up samples described in Table 1 in Sect. 3.2. Rectangular finite element mesh with element size approximately equal to 0.78 mm was generated in all FEM simulations in the present study. This particular size of element was found by performing a convergence analysis validating the obtained FEM results with respect to theoretical values of bending stiffness calculated by CLT. No refinement of mesh was used in vicinity of intralaminar cracks and delaminations since only the structural response of the whole test specimen was modelled in this study and the analysis of local stress concentrations due to micro-damage was beyond the scope of the present study.

Table 1 Elastic constants of materials, list of lay-ups and specimen geometry

The top 90-degree layer and the 0-degree layers were modelled without discontinuities (no cracks). In the bottom 90-degree layer discontinuities in form of transverse cracks were explicitly introduced in the FEM model, however, only in the constant bending moment zone, i.e., in the region between the load/displacement application lines as shown in Fig. 3. All cracks were modelled flat shaped and initially closed in the unloaded state. The number of intralaminar cracks was parametrically varied from 0 to 33 uniformly spaced cracks, which means that the intralaminar crack density ${\rho }_{c}$ was changed from 0 to $99/l$ cracks per mm.

Apart from transverse cracks, the effect of local delaminations at transverse crack tip on laminate bending stiffness was also parametrically investigated using the FEM calculations. Delaminations (interlaminar cracks) were introduced between the damaged bottom 90-degree layer and 0-degree layer as schematically shown in Fig. 2. Delaminations were created symmetrically with respect to the transverse crack plane. The delamination length ${l}_{d}$ was parametrically varied from 0 to $0.5{t}_{90}$, where ${t}_{90}$ is thickness of the 90-degree layer. For better visual clarity, the transverse cracks and delaminations are schematically shown in deformed shape in Figs. 2a and 3. In the particular case of 4 point bending loading of cross-ply laminate with intralaminar damage in the bottom 90-degree layer and delamination at the interface between the bottom 90-degree layer and the neighbouring 0-degree layer (Fig. 2), the crack surfaces of the representative volume element in the loaded state are fully open regardless of the ply thickness or crack length, hence no contact elements were used in the FEM calculation. This was verified with trial calculations which showed no change in the obtained results, when contact elements were generated on the crack surfaces. Under in-plane tensile loading, when ply interface delaminations initiate from intralaminar crack tips, the delamination crack surfaces are typically closed and the crack grows predominantly in Mode II [32].

The bending stiffness ${C}_{11}$ was calculated according to definition (4), where the bending moment ${M}_{x}$ was calculated from the reaction forces, and the curvature ${k}_{x}$ was calculated from the mid-plane displacement ${u}_{z}$ distribution in the constant bending moment zone between the load application lines, approximating the deformed shape with parabolic function. In accordance with CLT, the mid-plane curvature ${k}_{x}$ in this region is also constant and can be found as the second derivative of displacement distribution ${u}_{z}(x)$:

$${k}_{x}=-\frac{{\partial }^{2}{u}_{z}}{\partial {x}^{2}}$$

(6)

Reaction forces and displacement ${u}_{z}$ distributions were found in the post-processing stage and derivation according to (6) and calculation of ${C}_{11}$ was performed.

2.4 Beam Theory Analysis

The deformed shape of a beam subjected to 4-point bending and the corresponding moment diagram are schematically shown in Fig. 4. In the used geometrical configuration shown in Fig. 4a, the load application points $x=\pm l/6$ divide the total length $l$ of the specimen into three equal parts (i.e., $AB=BD=DE=l/3$). According to the bending moment diagram for this loading scheme, shown in Fig. 4b, the maximum bending moment value is ${M}_{x}=Pl/6$ and the bending moment is constant between the load application points. Hence, it is expected that with increasing load the central region of the laminate with the maximum bending moment will be damaged more than the peripheral regions near supports. In result, the flexural modulus of the laminated beam in the central region ${E}_{(2)}$ will be lower than ${E}_{(1)}$ in the peripheral region.

Fig. 4

Schematic representation of a 4-point bending test: a undeformed loading scheme (continuous line) and deformed shape of the beam (dashed line); b bending moment ${M}_{x}$ diagram

The expected displacement ${u}_{z}(x)$ distribution of the specimen middle-plane for the given boundary conditions and loading scheme, is shown as a dashed line in Fig. 4a, with the highest value expected to be in the specimen midpoint C. In structural mechanics, the displacement distribution ${u}_{z}\left(x\right)$ can be analytically calculated using the bending moment distribution and boundary conditions. Neglecting the contribution of shear and axial forces, the displacement at any arbitrary point $i$ of the beam can be calculated using expression:

$$\Delta_i=\int_0^l\frac{{\overline M}_iM_x}{EI}dx$$

(7)

where $i$ denotes an arbitrary point, $l$ is the total length of the beam, ${\overline{M} }_{i}$ is the bending moment distribution from unit force applied at the point $i$ in the direction of displacement of interest, ${M}_{x}$ is the bending moment distribution from the externally applied forces, $E$ is the flexural elastic modulus of the beam, $I$ is the cross-sectional moment of inertia of the beam. For a homogeneous beam with constant rectangular cross-section of width $b$ and height $h$, the expression (7) after substituting the ${M}_{x}$ distribution shown in Fig. 4b yields following expressions for displacements in points B, D and C of a simply supported beam

$${u}_{z}^{B}={u}_{z}^{D}=\frac{5P{l}^{3}}{27Eb{h}^{3}},\quad {u}_{z}^{C}=\frac{23P{l}^{3}}{108Eb{h}^{3}}$$

(8)

For a non-homogeneous beam with different flexural modulus in regions, ${E}_{(1)}$ and ${E}_{(2)}$

$${u}_{z}^{B}={u}_{z}^{D}=\frac{P{l}^{3}}{27b{h}^{3}}\left(\frac{2}{{E}_{(1)}}+\frac{3}{{E}_{(2)}}\right),\quad {u}_{z}^{C}=\frac{P{l}^{3}}{108b{h}^{3}}\left(\frac{8}{{E}_{(1)}}+\frac{15}{{E}_{(2)}}\right)$$

(9)

In beam theory the shape of the midplane displacement distribution ${u}_{z}(x)$ of the beam is parabolic, hence the analytical expression for curvature in the region $BD$ between the load application points is

$${k}_{x}=\frac{2\left({u}_{z}^{C}-{u}_{z}^{B}\right)}{{\left(l/6\right)}^{2}}$$

(10)

For both, the homogeneous and the non-homogeneous beam the result after using (8) and (9), respectively, is the same

$${k}_{x}=\frac{2Pl}{Eb{h}^{3}}$$

(11)

In (11), $E={E}_{(2)}$ (see Fig. 4a) in case of a non-homogeneous beam: the midplane curvature ${k}_{x}$ in the region between the load application points depends only on the stiffness of the beam in this region and it is not affected by the stiffness of the peripheral regions.

For a homogeneous beam it follows from (8) that ${u}_{z}^{B}=\frac{20}{23}{u}_{z}^{C}$ and Eq. (10) yields

$$k_x=\frac{216}{23}\frac{u_z^C}{l^2}\quad{\mathrm{or}}\quad{k_x}=\frac{54}5\frac{u_z^B}{l^2}$$

(12)

It can be also expressed trough normalized curvature ${k}_{xn}$

$${k}_{x}={k}_{xn} {u}_{z}^{C}\quad {\mathrm{with}}\quad {k}_{xn}=\frac{216}{23{l}^{2}}$$

(13)

In (13) ${k}_{xn}$ is the normalized curvature that corresponds to normalized displacement profile ${u}_{z}/{u}_{z}^{C}$. The normalized displacement profile was also measured experimentally using DIC, see Sect. 4.

Relationship similar to (13) can be derived also in the non-homogeneous beam case. The expression for normalized curvature contains also flexural moduli ${E}_{(1)}$ and ${E}_{(2)}$

$${k}_{xn}=\frac{216}{\left(8\left({E}_{(2)}/{E}_{(1)}\right)+15\right){l}^{2}} ,\quad {k}_{x}=\left(\frac{216}{8\left({E}_{(2)}/{E}_{(1)}\right)+12}\right)\frac{{u}_{z}^{B}}{{l}^{2}}$$

(14)

In results presented in Sect. 4, expression (12) was used to calculate the curvature ${k}_{x}$ from the recorded displacement ${\Delta }_{B}$, when beam theory analysis was used for predictions.

3 Experimental Details

3.1 Experimental Methods

Experimental 4-point bending tests were performed using an Instron 4411 testing machine equipped with a ± 5kN load cell. The laminate specimens were subjected to 4-point bending with distance between supports $l$ = 150 mm and the distance between the loading points was equal to $l/3$ = 50 mm. Optional span-to-thickness ratios of 40:1 and 60:1 recommended by ASTM D7264/D7264M-15 testing standard [33] were adopted for carbon/epoxy and glass/epoxy laminates respectively, see more details in Sect. 3.2. The cross-head displacement is assumed to represent the displacement at both load application points. The test was run under displacement control with a vertical cross-head displacement rate of 7 mm/min. Such loading rate was chosen so that the maximum strain rates at the tensile faces of the test samples would be in range between 0.32%/min up to 0.63%/min. The discrepancy of strain rates for specimens with different thickness is expected to have no influence on the damage evolution and the objective of the present paper. The load and the corresponding cross-head displacement values from the Instron 4411 machine were recorded and saved after each test and they were later used in conjunction with beam theory expressions. The test rig with specimen during the test is shown in Fig. 5a.

Fig. 5

Measurements of displacement in a 4-point bending test with a DIC system: a test rig and captured displacement distributions, b Camera and illumination system

Loading was performed in multiple steps reaching a certain predetermined maximum displacement value, after which the specimen was completely unloaded. Each load step was carried out up to a larger maximum displacement value than in the previous loading step in order to gradually increase the amount of micro-damage (transverse cracks, delamination length) in laminate and to observe gradual reduction of bending stiffness due to damage propagation. The bending stiffness corresponding to a certain state of damage was measured from the initial linear slope of the bending moment – curvature relation (${M}_{x}$ vs. ${k}_{x}$).

In addition to load and cross-head displacement recordings directly from the Instron testing machine, a DIC 3-D deformation analysis system ARAMIS from GOM GmbH was used for measuring the complete distribution of vertical displacements along the specimen length. These data were used as means for direct experimental determination of bending stiffness of damaged laminates and to validate the beam theory assumptions. The ARAMIS DIC measurement system consisted of two optical lenses and an illumination unit as shown in Fig. 5.

In relation with the objective of the present work, displacement distribution was measured only in the central region between the load application points, where the bending moment is constant. The full-field displacement data recorded by the ARAMIS system (Fig. 5a) were synchronized with the corresponding force/displacement data from the Instron 4411 testing machine using a signal cable connecting the two systems. Due to not fully exact calibration constants of the load signal, small differences may be observed for exactly the same load data recorded directly by the Instron 4411 testing machine. The DIC system also contained a standalone computer running the measurement software. The laminate specimens were moderately polished on one edge, on which a black and white paint pattern was sprayed to enable the speckle pattern based measurement of displacements with the ARAMIS DIC system. The other edge of each specimen was finely polished to mirror quality for enabling the optical microscopy investigations (for quantification (manual counting) of transverse cracks and for qualitative assessment of delaminations). Mid-plane displacement distribution along the specimen length were recorded with the ARAMIS system software using data acquisition frequency of 0.5—1 Hz. Each recording of data consisted of the value of applied force and the corresponding complete displacement distribution along the length of the laminate midplane. The recorded test data in text format were processed with Matlab software to calculate the bending moment – midplane curvature relation ${M}_{x}$ vs. ${k}_{x}$.

It was clearly observed in all performed tests that the experimental displacement distributions between the load application points recorded by ARAMIS system very accurately correspond to a parabolic shape, as it is also assumed within the CLT. Hence, the displacement distribution data were in all cases fitted with a parabolic function. Derivation of the fitted polynomial function was performed according to (6). Thus, the experimental value of mid-plane curvature ${k}_{x}$ was obtained for each recorded time/force instant. The corresponding bending moment ${M}_{x}$ was calculated using the recorded load data and the geometry of the loading scheme (Fig. 4). An example of processed experimental data is shown in Fig. 8, Sect. 4. The experimental values of bending stiffness ${C}_{11}$ were obtained as the slope of the linear part of the ${M}_{x}$ vs. ${k}_{x}$ curve, as shown in Fig. 9, Sect. 4. The linear fit to find the bending stiffness from the ${M}_{x}$ vs. ${k}_{x}$ relation data was always performed in a maximum strain region 0.05% $\le {\varepsilon }_{x}^{h/2}\le$ 0.40%, where ${\varepsilon }_{x}^{h/2}$ is the tensile strain at the lower face of the laminate ($z=h/2$).

As mentioned above, the opposite edge of each sample, which was not used for DIC measurements, was finely polished for optical microscopy inspection. The objective of optical microscopy inspection was foremost to accurately quantify the transverse crack density in the bottom 90-degree layers of tested [90_n/0]_s laminates. This was done by manually counting the amount of transverse cracks in the middle region of the specimen (between the load application points) after each loading–unloading step. A standard optical microscope by Olympus was used with 100 × and 200 × magnification. To perform the optical microscopy inspection, specimens were removed from the testing rig after each loading–unloading step. After completing the optical microscopy inspection the specimens were mounted back on the testing rig to continue with the next loading–unloading step. In addition, optical microscopy was also used to qualitatively inspect the presence and magnitude of delaminations between the surface 90-degree layer and the neighboring 0-degree layer of the tested laminates.

3.2 Material and Specimen Data

For the experimental study, carbon fiber/epoxy and glass fiber/epoxy (denoted as CF/ep and GF/ep respectively) [90_n/0]_s cross-ply laminates were manufactured. CF/ep plates were manufactured from unidirectional Toray T700S carbon fiber non-crimp fabrics (NCF) and Araldite epoxy resin with Aradur hardener from Huntsman. The plates were manufactured using vacuum infusion technique with curing time of 24 h at room temperature. After curing, 4 h long post-curing cycle at 100 °C was performed. CF/ep plates were stacked in the lay-up [90₂/0]_s. GF/ep plates were manufactured from unidirectional glass fiber/epoxy pre-preg sheets, which were manually stacked and compacted using vacuum bag technique. Plates were cured in a hot-press for 1 h at 125 °C temperature without any post-curing. Low mechanical pressure was applied on the plate to ensure compaction while preventing fiber distortion. The lay-up for GF/ep plates was [90₃/0]_s. Longitudinal modulus ${E}_{L}$, transverse modulus ${E}_{T}$, Poisson’s ratio ${\nu }_{LT}$ and in-plane shear modulus ${G}_{LT}$ of CF/ep and GF/ep materials were determined by performing standard tensile tests on UD and [± 45] angle-ply specimens. The resulting elastic properties are summarized in Table 1. The values of out-of-plane Poisson’s ratio ${\nu }_{23}$ were not measured experimentally, but assumed based on typical values for carbon and glass fiber UD composites. Although not used in the present study, and hence not shown in Table 1, the values of transverse thermal expansion coefficient ${\alpha }_{2}$ for GF/ep were also determined experimentally being equal to 46.7‧10^–6 [1/°C]. The thermal expansion properties of CF/ep were not measured experimentally therefore they remain unknown. Table 1 also shows the average ply thickness, ${t}_{ply}$, for the tested CF/ep and GF/ep laminate specimens. The NCF-based CF/ep laminates have notably thicker plies (${t}_{ply}$ ≈ 0.62 mm) compared to pre-preg type GF/ep laminates (${t}_{ply}$ ≈ 0.32 mm). The length of the test specimens was approximately 200 mm to suit the distance between the supports $l$ = 150 mm (Fig. 1). 3 specimens from each material were tested under 4-point bending loading conditions as described above.

4 Comparison and FEM Validation of DIC and Beam Theory Based Data Reduction Schemes

Typical load versus loading point displacement curves ($P$ vs. ${u}_{z}^{B}$) for CF/ep and GF/ep specimens are shown in Fig. 6. Using beam theory, these data were recalculated to ${M}_{x}$ versus ${k}_{x}$ by expression (12) and the bending moment diagram (Fig. 4b). In the present section and in further text we refer to notation used in Fig. 4a to describe the location of a specific point. Using the beam theory-based approach, the loading nose displacement ${u}_{z}^{B}$ values were the ones recorded from the cross-head displacement. They were used in (12) to calculate ${k}_{x}(t)$ at any instant of time $t$. By subjecting the specimens to relatively large deflections, damage in form of transverse matrix cracks and delaminations was introduced in the bottom 90-degree layer. Intralaminar cracks and delaminations reduce the bending stiffness of the beam in the damaged region, which is mostly between the load application points, and lead to rather sudden drop of the applied force $P$ clearly visible in the vicinity to the maximum in each loading step in Fig. 6.

Fig. 6

Examples of load–displacement curves for: a CF/ep [90₂/0]s laminates; b GF/ep [90₃/0]s laminates. Legends indicate the maximum tensile strain on the specimen surface reached during the corresponding loading step

The obtained load–displacement curves in Fig. 6 are not linear even during the unloading, where the damage state is not changing. An interesting feature is that the uploading and unloading curves are both concave. Hence, we can exclude viscoelasticity as a potential reason for the nonlinear behavior in the high deflection/curvature region. Among other possible reasons for nonlinearity at large deflections we have to notice the increasing arc length between the points $B$ and $D$ of the specimen between load application points (see Fig. 4). The distance between the loading noses of the test rig (Fig. 5a) does not change during loading. This means that at very large ${u}_{z}$ (comparable with the distance $l/3$) the specimen is sliding in x-axis direction and the specimen length (arc length) between both loading noses is significantly larger than the initial length of $l/3$. During unloading the specimen is sliding back and the arc length decreases returning to linear behavior.

The average axial stress in damaged layers is lower than before damage appearance, which means that the contribution of this layer to laminate bending resistance is reduced, which is reflected in reduced bending stiffness of the laminate. This is also indicated by the reducing slopes of the test curves in Fig. 6.

As an alternative to the beam theory-based data reduction and to validate its accuracy, a DIC system was also used to measure vertical displacement distribution on the laminate middle-plane (as described in Sect. 3.1). The deformed shape of the laminate middle-plane for CF/ep and GF/ep laminates obtained by DIC at different selected values of the applied cross-head displacement is shown in Fig. 7a for CF/ep and in Fig. 7b for GF/ep. The data are shown for one representative specimen of each respective material. For a better comparison of shapes, the displacement values in Fig. 7a, b are normalized with respect to the maximum value of the displacement, ${u}_{z}^{C}$, i.e., ${u}_{z}^{n}={u}_{z}(x)/{u}_{z}^{C}$, see Fig. 4a.

Fig. 7

Normalized mid-plane displacement distribution of cross-ply specimens: a CF/ep [90₂/0]_s; b GF/ep [90₃/0]_s. Data in legends are values of ${u}_{z}^{B}$ at the instant of data capture

According to (13), the normalized curvature ${k}_{xn}$ should be independent on the material system and on the damage state. This is also reflected in the experimental results shown in Fig. 7a, b.

Noteworthy, the three very similar normalized curves in each figure represent the same material with 3 different states of damage. It is also important to note that each curve is recorded at the instant of the maximum displacement in the loading step, which is different in each case. For purpose of clarity, the value of the loading nose displacement ${u}_{z}^{B}$ at the instant of data capture is given in the legend.

Data presented in Fig. 7 show that the deformed shape of the midplane neither depend on the loading level nor on the damage state. The three curves for GF/ep [90₃/0]_s in Fig. 7b look slightly different but that is mostly an artefact because the curves are not entirely symmetric. This discrepancy could be caused by slightly non uniform damage distribution and small differences in deflection of both loading noses.

It was found that fitting these experimental displacement data with parabolic function gives an excellent agreement. According to (6) the second derivative of the parabolic fitting function gives the required ${k}_{x}$. Examples of normalized curvatures ${k}_{xn}$ calculated using these data are given in Table 2. Data for one representative specimen of each material (specimen “Sp.2” for CF/ep and specimen “Sp.3” for GF/ep) at different levels of maximum displacements and with different damage states are presented in Table 2.

Table 2 Normalized curvature ${k}_{xn}$ for selected representative specimens

The specimen identification in Table 2 shows the material, the lay-up, the specimen number and ${u}_{z}^{B}$ at the instant of data capture. Results in Table 2 show that the normalized curvature of any specimen is almost independent on the material system used, on the applied displacement level and on the damage state. This conclusion is in line with expression (13) in beam theory. According to (13), for the given geometrical configuration ${k}_{xn}$ is equal to $0.000417 1/{mm}^{2}$.

According to beam theory, the normalized curvature of a beam with constant elastic properties over its whole length depends on geometrical parameters only. Equation (14) shows that the normalized curvature of a damaged laminate depends on the stiffness values in the different regions of the beam, and hence it is subject to change with different damage evolution in those regions. For damaged specimens, the damage state, due to variation of the bending moment along the length of the beam, may be more severe in region between the loading points. In such case in the central region between B and D (Fig. 4) the flexural modulus is ${E}_{(2)}$, whereas in peripheral regions it is ${E}_{(1)}$. Since ${E}_{(2)}<{E}_{(1)}$, the normalized curvature calculated using (15) is larger than before damage. The difference can be estimated using experimental results presented in Sect. 5 that show almost 20% lower bending stiffness of CF/ep specimens with damage. That would increase the normalized curvature to ${k}_{xn}=0.000449 1/{mm}^{2}$. This value is a rough overestimation, because the peripheral regions are also damaged and hence ${E}_{(1)}$ is also lower than before. Due to experimental limitations, the damage state change outside the central region was not documented in the present study. The reduction of flexural modulus should be more pronounced in laminates with relatively thick damaged plies and not too high longitudinal and transverse modulus ratio of the ply material such as, for example, GF/ep composites.

Nevertheless, the effect of different flexural stiffness in different regions cannot be seen in DIC measurements of curvature in Table 2. In some specimens, the normalized curvature slightly increased with increasing damage whereas in some it even became smaller. Obviously, the observed variation is just a reflection of the accuracy of measurements.

From the above discussion, we conclude that assumptions of the beam theory regarding the deformed shape of damaged beam are rather accurate and are validated by DIC results. The normalized curvature calculated according to (13) is very close to experimental values in Table 2. The only concern using beam theory could be the accuracy of loading nose displacement data (${u}_{z}^{B}, {u}_{z}^{D}$) obtained from the displacement of the cross-head of the testing machine without the use of external displacement transducers: it can be different for various testing machines. This problem is well known and is partially related to the compliance of the testing system.

Using DIC, at each time instant during loading–unloading, the displacement ${u}_{z}\left(x\right)$ curve obtained by DIC was recorded, the data fitted with a parabolic function and curvature was calculated using (6). The applied bending moment ${M}_{x}$ was plotted against the calculated curvature ${k}_{x}$ and the slope of the obtained curve in maximum tensile strain region $0.05\%\le {\varepsilon }_{x}^{h/2}\le 0.4\%$ was used to calculate the bending stiffness ${C}_{11}$. In Fig. 8a, b examples of the ${M}_{x}-{k}_{x}$ curves for studied materials obtained from DIC are shown together with similar curves obtained using beam theory.

Fig. 8

${M}_{x}$ vs ${k}_{x}$ curves for cross-ply specimens: a CF/ep [ 90₂/0]_s, in loading step with ${u}_{z}^{B}=$ 18 mm; b GF/ep [ 90₃/0]_s, in loading step with ${u}_{z}^{B}=$ 14 mm

Noteworthy, the ${M}_{x}$ vs. ${k}_{x}$ curves obtained by DIC and the beam theory have a horizontal shift. The reason is that with damage development the laminate is losing symmetry and the middle-plane has a small residual curvature even in an unloaded state (part of thermal stresses in the damaged ply are released). In the DIC system the reference midplane at the start of the test is always assumed to be a straight line despite that the actual specimen midplane is initially slightly curved. Thus DIC based curves ${M}_{x}-{k}_{x}$ always start at zero curvature and the measurement is the curvature change. For the beam theory ${M}_{x}-{k}_{x}$ curves, the zero point for displacements is as for the undamaged specimen and load is zero until the nose displacement reach the specimen that is slightly curved due to thermal stresses. It has to be noted that the recorded tensile machine displacement was zeroed only at the beginning of the test. Therefore Fig. 6 accurately represents the residual deformations and curvatures of damaged laminates.

One can notice a good agreement in slopes of curves from DIC and the beam theory in Fig. 8 in low strain region. This means that for both approaches the bending stiffness calculated from the corresponding slopes is rather similar. An example of bending stiffness determination using DIC data is shown in Fig. 9. Results of the bending stiffness dependence on damage state are analyzed in Sect. 5.

Fig. 9

${M}_{x}$ vs ${k}_{x}$ data for CF/ep [90₂/0]_s laminate in loading step with ${u}_{z}^{B}=$ 4 mm used for bending stiffness ${C}_{11}$ determination. Curvature is calculated using DIC data

5 Bending Stiffness of Damaged Laminates

5.1 Damage Evolution in Loading–unloading Cycles Under 4-point Bending

In this section we present selected results for damage evolution in the tested laminates. The amount of intralaminar cracks was determined using optical microscopy and manual counting. The crack density ${\rho }_{c}$ reached after loading to certain tensile strain in the surface 90-degree layer, was defined as the number of cracks in the region between the load application points divided by the length of this region ($l/3$) (Fig. 1).

From here on we will use crack density is a normalized form, which is a common formulation when damage effect on stiffness is analysed. It is defined as:

$${\rho }_{cn}={\rho }_{c}{t}_{90}$$

(15)

The normalized form is preferable, because it defines the average distance between cracks in units of ply thickness. This measure defines the level of overlapping of stress perturbations. Empirically, it is well known that ${\rho }_{cn}\approx 1$ corresponds to so-called “saturation crack density” seldom exceeded experimentally. The amount of stiffness reduction depends on the normalized crack density ${\rho }_{cn}$, not on ${\rho }_{c}$.

In Fig. 10 the normalized crack density ${\rho }_{cn}$ for CF/ep and GF/ep laminates (three specimens of each kind) is plotted versus the maximum tensile strain ${\varepsilon }_{x}$ in the surface 90-degree layer (calculated from the curvature and the specimen thickness as ${\varepsilon }_{x}^{h/2}={k}_{x}\frac{h}{2}$. The maximum strain data ${\varepsilon }_{x}^{h/2}$ in Fig. 10 were obtained by taking the mid-plane curvature data ${k}_{x}$ from DIC measurements and assuming that midplane strain is zero.

Fig. 10

Normalized crack density as a function of maximum strain in the surface 90-degree layer of cross-ply laminates

According to Fig. 10, the damage development at low strain levels is very similar in CF/ep and GF/ep cross-ply laminates: first transverse cracks appear at strain slightly below 0.5%. The difference at large strains is more distinct. For example, at 1.2% strain the normalized crack density ${\rho }_{cn}$ in the CF/ep [90₂/0]_s specimens is significantly higher than in GF/ep [90₃/0]_s specimens (approximately 0.2 versus 0.15). However, these values are rather low and cracks in both laminates can be considered as “non-interactive”, which means that stress perturbation caused by one crack does not have large effect on the neighbouring cracks. For non-interactive cracks the “non-normalized” crack density ${\rho }_{c}$ is a good measure for comparison of damage evolution, except the cases when the ply is exceptionally thin. For the used laminates we obtain almost the same value of 0.16 cracks/mm (${\rho }_{cn}/{t}_{90}=0.2/1.2$ for CF/ep and $0.15/0.9$ correspondingly for GF/ep).

After 1.2% strain the damage development in [90₂/0]_s CF/ep specimens is rather peculiar (a sharp reduction in crack density increase rate). The reason for this behaviour is extensive local delaminations initiated from intralaminar crack tips. Delaminations were only qualitatively inspected and not quantified in the present study. Delaminations growing from transverse crack tip significantly reduce the stress between cracks hindering development of new transverse cracks.

5.2 Bending Stiffness Dependence on Crack Density: Experiments and FEM Modelling

In this section dependence of the normalized crack density ${\rho }_{cn}$ on curvature ${k}_{x}$ (according to (15) the values are proportional to data in Fig. 10) and the bending stiffness dependence on the maximum curvature reached in the loading step are combined un order to present the bending stiffness reduction as a function of intralaminar crack density, i.e., ${C}_{11}\left({\rho }_{cn}\right)$.

The results are shown in Fig. 11a, b for CF/ep and GF/ep specimens respectively. In Fig. 11 the bending stiffness ${C}_{11}\left({\rho }_{cn}\right)$ is normalized with respect to bending stiffness of the undamaged specimen ${C}_{11}\left({\rho }_{cn}=0\right)$. The legend “Sp.1”, “Sp.2”, “Sp.3” in Fig. 11a, b represents normalized bending stiffness ${C}_{11n}$ obtained from DIC data for 3 tested specimens (as described in Sect. 4). Also in Fig. 11, beam theory results are presented showing the bending stiffness of one specimen (Sp.1) of each material obtained using beam theory expressions (as described in Sect. 4). Beam theory data are shown for only one representative specimen for visual clarity of the graphs.

Fig. 11

Normalized bending stiffness dependence on normalized crack density in the surface 90-degree layer of cross-ply laminates: a CF/ep [90₂/0]_s; b GF/ep [90₃/0]_s

Ply discount model-based bending stiffness results are shown as horizontal lines (asymptotic value) in Fig. 11. In general, the reduction of bending stiffness for the tested materials is considerable and experimental data approach to the asymptotic value defined by the ply-discount model. With infinite transverse crack density and with delaminations connecting the crack tips, the assumed zero stress in the damaged ply within the ply-discount model would become realistic.

Comparing “Sp.1” and “Beam theory” values (they correspond to the same specimen) for each material, we see that the beam theory based data reduction leads to slightly higher bending stiffness than the one obtained from DIC, but considering the scatter, the agreement is reasonably good.

The FEM predicted bending stiffness reduction, assuming that there is no delamination (notation FEM ${l}_{dn}=$ 0), for GF/ep composite shown as solid line in Fig. 11b, follows the experimental trend. That indicates that delaminations were very small during the main part of the test. For CF/ep laminate the agreement between FEM predictions and experimental bending stiffness data is good until normalized crack density ${\rho }_{cn}$ approaches 0.20 (Fig. 11a). This is the same crack density value in Fig. 10, when cracking rate reduces and stops, because of large delaminations. One can see in Fig. 11a, that indeed the experimental bending stiffness deviates from the FEM predicted and drops much faster than in predictions with assumed zero delamination length.

In studies of the effect of delaminations on bending stiffness, the extent of delamination is characterized by normalized delamination length. Normalized delamination length, see Fig. 2, is defined as delamination length ${l}_{d}$ divided by 90-degree layer thickness ${t}_{90}$, ${l}_{dn}={l}_{d}/{t}_{90}$ .

The curve showing FEM results under assumption of rather large (but constant) value of the normalized delamination length ${l}_{dn}=0.5$ (the delamination length on each side of the intralaminar crack is 50% of the 90-ply thickness), is systematically below the experimental data for GF/ep specimens. Bending stiffness of the [90₂/0]_s CF/ep laminate, which at normalized crack density below 0.2 follows the prediction with zero delamination, turns towards the FEM curve with assumed fixed delamination length, ${l}_{dn}=0.5$. Thus, the presence of large delaminations is demonstrated by optical observations, by large bending stiffness drop, by stopped intralaminar cracking (Fig. 10) and by FEM calculations.

6 Conclusions

Experimental and theoretical studies with the aim to characterize bending stiffness reduction in laminated structures with intralaminar damage in layers and local interlaminar delaminations arising from intralaminar cracks, motivate revisiting the well-known 4-point bending test and to validate the accuracy of the beam theory based data reduction schemes in gathering experimental data. In the presented work, the Digital Image Correlation (DIC) technique is used to measure the full-field displacement distribution on the specimen edge and the vertical displacement distribution is used to find the mid-plane curvature ${k}_{x}$ of the specimen. The recorded data are used to construct the applied bending moment ${M}_{x}$ versus ${k}_{x}$ curve, the initial slope of which defines the bending stiffness of a laminate. Comparing the curvature with the one obtained using simple expressions from beam theory it was found that the latter slightly underestimates ${k}_{x}$, however, values are still sufficiently accurate in low deflection region. At large deflections, when the specimen arc length between the loading noses is much larger than the distance between them, the beam theory overestimates the curvature and the ${M}_{x}$ versus ${k}_{x}$ curves become more nonlinear than they should. Due to these features the beam theory based data reduction leads to slightly overestimated bending stiffness, however, the agreement with the DIC based results is still good. We conclude that the beam theory based data reduction scheme has sufficient accuracy even for highly damaged laminates.

By applying relatively large displacements, intralaminar cracks were introduced in the bottom surface layer of CF/ep and GF/ep cross-ply [90_n/0]s laminates, which leads to reduction of the bending stiffness with increasing density of transverse cracks. 3-D FEM calculations were performed for validation of two extreme cases: a) assuming idealized transverse cracks perpendicular to the mid-plane and with no delaminations between layers at the crack tip; b) assuming that independent on the loading level, the introduced cracks have fixed size local delaminations. Comparison with data shows that in the initial stage of cracking development, the experimental bending stiffness degradation follows the FEM curve for a case with no delaminations and after large deflections, when more damage is introduced, the bending stiffness degradation curve better fits the FEM predictions with relatively large delaminations. We consider this behaviour as an evidence that with increasing applied deflection, first the transverse cracks with no delaminations appear and their number increases, however, later on, the already existing and newly created cracks start to develop extensive delaminations.