1 Introduction

Continuous Silicon carbide fibers–reinforced silicon carbide matrix (SiCf/SiC) composites have been identified as promising candidate thermo-structural materials in gas turbine engines due to their high specific strength/modulus, oxidation resistance, and stability at high temperatures [1, 2]. Creep resistance is one of the main requirements for SiCf/SiC composites in applications such as turbine rotor blades, which requires maintaining the material properties over long periods (thousands of hours) at high temperatures [3]. However, the existence of oxidants such as oxygen, water vapor in service environment leads to the oxidation of SiCf/SiC composites, which further results in the degradation of the mechanical properties of the composites including the creep resistance [4, 5].

Plenty of experimental efforts have been devoted to study the creep behavior and failure mechanism of SiCf/SiC composites under the oxidizing atmosphere [6,7,8]. Many of these investigations have pointed out the critical influence of the interphase on the creep behavior of the composites [3]. Pyrolytic carbon (PyC) was most commonly used as interphase in SiCf/SiC composites as a result of its strong anisotropy in properties and microstructure, as well as the fact that it serves to protect the fibers during manufacturing [9]. However, the PyC interphase is readily oxidized at temperatures as low as 500℃ with the formation of gaseous oxides [10]. The SiC fibers and matrix may undergo passive oxidation at high temperatures (> 800℃) under the atmosphere of high oxygen pressures with the formation of gaseous and solid oxides [11]. The oxidation of PyC interphase and the other constituents induces the oxidation embrittlement of SiCf/SiC composites at intermediate temperatures (600 °C–850 °C), which leads to the stress rupture of the composite under the stresses that are well below their ultimate strength in the pristine state [12]. Much work has been done to model the stress rupture behavior at intermediate temperatures taking the effect of loss of interphase by oxidation on load transfer at intermediate temperatures where creep is not relevant [13,14,15].

Different from the failure mechanism of SiC fibers at intermediate temperatures, the creep of SiC fibers at high temperature is a crucial issue for the mechanical properties of SiCf/SiC composites, which should be considered [16]. In addition, with the requirement of a higher thrust-weight ratio of gas turbine engines, the service temperature of SiCf/SiC composites has been increased up to 1200℃. Thus, the research of the creep behavior of SiCf/SiC composites at high temperatures should be accelerated. However, limited attention has been focused on modeling the effect of oxidation on the creep behavior of SiCf/SiC composites at high temperatures (> 900℃). Xihui et al. [17] modeled the residual strength of the SiCf/SiC mini-composites under a stressed oxidizing atmosphere in the temperature range of 900 ~ 1300℃. The model considered the healing of the matrix cracks due to the oxidation of the constituents and gave the degradation rule of the residual tensile strength of the composite before the matrix crack healing. However, the creep of SiC fibers was not taken into account due to the short time of healing of matrix cracks at high temperatures. Casas et al. [3] modeled the creep behavior of SiCf/SiC composites at 1000 ~ 1100℃ in dry air oxidizing environment, which takes the effect of the oxidation of PyC interphase and SiC fibers and the creep of fibers into account. However, the model just described the effect of dry oxygen on the constituents but not considered the influence of water vapor on the oxidation behavior of the constituents. Since the combustion of hydrocarbon fuel in the combustion chamber of gas turbine engines will produce about 10% water vapor, SiCf/SiC composites are exposed to a complex oxidation environment composed of oxygen and water vapor. Previous studies show that the existence of water vapor will change the oxidation mechanism [18, 19], however, the effect of water vapor on the creep failure mechanism of the SiCf/SiC composites in the air was still not clear. Therefore, it is essential to study the creep behavior of SiCf/SiC composites in the environment coupled with oxygen and water vapor at high temperatures (> 900℃). On the other hand, the model used by Casas et al. [3] only takes the effect of oxide layer on fiber strength not considers the influence of grain growth and thermal decomposition of fiber caused by the high temperature. The grain growth and thermal decomposition of fiber will lead to the increase of defects, which cause the fiber degradation.

The present work aims to incorporate the effect of the oxidation of constituents in a complex oxidation environment composed of oxygen and water vapor, the grain growth, thermal decomposition and creep of fiber into the mechanical response of the composite accounting for the synergistic creep-oxidation interactions at high temperatures.

The remainder of the paper is organized as follows. In Sect. 2, a new model for predicting the creep behavior in wet oxygen environment involving the thermal–mechanical model, environmental micro-model, fiber strength degradation model, creep-oxidation model was established. Subsequently, in Sect. 3, the selection of the parameters used in these models was illustrated. Then, in Sect. 4, model predictions and experimental data were presented and discussed. Besides, the effect of creep and oxidation on the matrix crack spacing is discussed. Finally, Sect.  5 concluded with a summary of the analysis and results.

2 Description of the Model

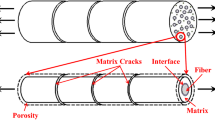
As shown in Fig. 1, a model for predicting the creep behavior of SiC/SiC mini-composites in a wet oxygen atmosphere is presented. The model includes four parts: thermal–mechanical model, environmental micro-model, fiber strength degradation model, and the creep oxidation model. Firstly, the initial matrix crack spacing and the width of the matrix cracks are calculated by the thermal–mechanical model. Then the initial matrix crack spacing and the width of the matrix cracks are substituted to the environmental micro-model to calculated the oxidation morphology of the component materials including the consumed length of the PyC interphase, the thickness of the silica layer grown on the surface of the fiber and matrix. The fiber strength degradation model gives the degradation rule of fiber strength and the criterion judging fiber failure considering the effect of grain growth of fibers, the thermal decomposition of fibers. According to the consumed length of the PyC interphase, the stress distribution of fibers and matrix can be obtained based on the shear-lag model. Combining the stress distribution of fibers, the fraction of fiber failure with the creep model of fibers, the creep-model of the mini-composites is established and the creep curves in wet oxygen atmosphere are modeled. The details of these models are as follows.

Fig. 1
figure 1

Schematic of the thermal–mechanical model (a), environmental micro-model (b), fiber strength degradation model (c), creep-oxidation model (d)

Full size image

2.1 Thermal–Mechanical Model

The SiC/PyC/SiC mini-composites refer to a single fiber tow coated with an interphase material and then finally coated with a substantial thickness of sheath material which represents the matrix shown in Fig. 1(a). Such a mini-composite can be simplified as a collection of elemental composites with an axisymmetrical assembly of (i) a single straight fiber (with constant radius \(r_{f0}\)), (ii) a layer of carbon interphase with a constant thickness e, (iii) a shell of dense SiC matrix with a constant thickness \(r_{t} - r_{m0}\).

The elemental composite is assumed to have the same length \(L_{com}\) as the mini-composite (Fig. 1(a)). Besides, the values of the fiber volume fraction \(V_{f}\) and density keep same in elemental and mini-composite. The above conditions lead to the following two equations:

$$r_{f0}^{2} /r_{com}^{2} = V_{f}$$
(1)
$$r_{com}^{2} \rho_{com} = (r_{t}^{2} - r_{m0}^{2} )\rho_{m} + (r_{m0}^{2} - r_{f0}^{2} )\rho_{c} + r_{f0}^{2} \rho_{f}$$
(2)

where \(\rho_{com}\),\(\rho_{m}\),\(\rho_{c}\),\(\rho_{f}\) are density for mini-composite, matrix, carbon, and fiber, respectively. Solving the above two equations with measured geometric parameters,\(r_{f0}\),\(e\) and \(r_{m0}\), yields the values of \(r_{t}\) and \(r_{com}\) necessary to fully define the hypothetical composite. When the mini-composites are subjected to a constant tensile stress level higher than the matrix cracking stress, a distribution of approximately parallel cracks perpendicular to the loading direction appears in the matrix, as shown schematically in Fig. 1(a).

The average matrix crack spacing \(L_{c}\) used in this work was determined by experimental data. The matrix crack width,\(2d\), versus temperature and stress has been derived by Sun et al. [20] in Eq. (3):

$$\frac{2d}{{2d_{0} }} = \frac{1}{{T_{0} }}\left[ {\Delta T + \frac{1}{{E_{f} V_{f} \left( {\alpha_{m} - \alpha_{f} } \right)}}\sigma } \right]$$
(3)

where \(T_{0}\) is the heat treatment (HT) temperature of the composite,\(2d_{0}\) denotes the initial crack opening distance at room temperature, \(\Delta T\) is the temperature difference between ambient temperature and HT temperature, \(E_{f}\) is Young’s modulus of fiber,\(\alpha_{m}\) and \(\alpha_{f}\) are the thermal expansion coefficients of matrix and fiber and \(\sigma\) is the tensile stress applied to the both ends of the mini-composite.

2.2 Environmental Micro-Model

2.2.1 Chemical Reactions

The kinetics for the oxidation between silicon carbide and H2O/O2 mixtures differs from those in either pure oxygen or pure steam. The previous test results [21] show that oxidation of SiC in wet oxygen environment takes place according to the straightforward Reaction (4):

$$SiC\left( s \right) + 2O_{2} \left( g \right) \to SiO_{2} \left( s \right) + CO_{2} \left( g \right)$$
(4)

The water vapor has been proved to act as a catalyst, which can significantly accelerate the reaction rate of SiC and oxygen by enhancing oxygen permeability of the scale [22]. From the work of Opila [23], the oxidation kinetics of SiC are modeled using a permeation constant that depends on the partial pressure of water vapor, which can be expressed as:

$$K_{{H_{2} O}} = K_{{O_{2} }} \left[ {1{ + }\varsigma \left( {P_{{H_{2} O}} } \right)^{\eta } } \right]$$
(5)

where \(K_{{H_{2} O}}\)(in \(mol/\left( {m \cdot s \cdot Pa} \right)\)) is the enhanced permeability for oxygen in the scale with the existence of water vapor.\(K_{{O_{2} }}\) is the permeability factor for oxygen in the silica scale. The partial pressure dependence,\(\eta\), and the factor \(\varsigma\) are obtained using a fit to experimental data from Oplia’s report [23].

The parabolic rate constant B (in \(m^{2} /s\)) related to the growth of the silica scale on SiC surface can be written in terms of oxygen concentration and oxygen permeability as:

$$B = \frac{{2RTK_{{H_{2} O}} C_{{O_{2} }} }}{N}$$
(6)

where \(C_{{O_{2} }}\)(in \(mol/m^{3}\))is the concentration of the oxygen, R is the gas constant. N (in \(mol/m^{3}\)) is the mole number of oxygen molecules that are incorporated into a unit volume of the silica scale. T is the absolute temperature. The oxidation of both the SiC matrix and fibers yields an overall weight increase associated with a positive volume change. As a consequence, the annular pore resulting from the oxidation of the carbon interphase will become progressively filled with silica as the oxidation of the annular pore walls proceeds.

The oxidation of carbon in an atmosphere of wet oxygen results in the formation of gaseous carbon dioxides, with an overall weight loss, according to

$$C\left( s \right){ + }O_{2} \left( g \right) \to CO_{2} \left( g \right)$$
(7)

The values of reaction constant, \(k_{c}\)(in \(kg/\left( {m.s} \right)\)), which have been used in the present work for the oxidation of the carbon interphase, were dependent on the oxygen concentration according to the following relationship:

$$\frac{{k_{c} }}{{k_{0} }} = \left( {\frac{{C_{{O_{2} }} }}{{C_{atm} }}} \right)^{n}$$
(8)

where \(k_{0}\) is liner rate constant at P = 100 kPa in pure oxygen, \(C_{atm}\) is oxygen concentration at P = 100 kPa in pure oxygen. n is the apparent reaction exponent for carbon oxidation.

In the following, the calculations have been performed taking into account either Eqs. (4) and (7) to involve the O2/CO2 couples.

2.2.2 Oxidation of the Internal Channel

The approach used for modeling of the oxidation of the mini-composite in an environment of flowing gases containing oxygen and water vapor is based on the one described in prior work for the occasion without water vapor [17]. Briefly, the variations of the concentration,\(C_{{O_{2} }}\), were modeled using equations for oxygen flux through the matrix crack and for silica scale growth on the matrix and fiber surface. The difference is that the binary diffusion of O2 and CO was considered in the prior work, while in this paper the O2/CO2 couples will take their place, as shown in Fig. 1(b). More details can be found in prior work. The results from that work used here can be summarized and modified as follows.

a) The first stage: When oxygen diffuses along the matrix crack, it reacts with the matrix on both walls of the crack. At a specific location z, the equation of mass conservation used to depict the variations of the concentration,\(C_{{O_{2} }}\), can be rewritten as

$$\frac{d}{dz}\left[ {2\left( {r_{t} - z} \right)\left( {2d - 2\overline{h}_{m} \left( {z,t} \right)} \right)\frac{{ - D_{1} C_{0} }}{{C_{0} - C_{{O_{2} }} \left( {1 - \alpha_{1} } \right)}}\frac{{dC_{{O_{2} }} }}{dz}} \right] + \frac{{4g_{m} \left( {r_{t} - z} \right)\rho_{s} }}{{M_{s} }}\frac{{dh_{m} \left( t \right)}}{dt} = 0$$
(9)

where \(D_{1}\) is an effective diffusion coefficient of O2 taking into account the molecular diffusion regime and the Knudsen diffusion, the subscript 1 represents the first stage. \(C_{0}\) is the total concentration. \(\alpha\) is the ratio between the molar fluxes of O2 and CO2. \(g_{m}\) is the number of moles of O2 necessary to form 1 mol of silica during oxidation of SiC matrix.\(\rho_{s}\) is the density of silica.\(M_{s}\) is the molar mass of silica.\(h_{m}\) is the thickness of silica scale on the matrix, the growth rate of which can be expressed as:

$$\frac{{dh_{m} \left( t \right)}}{dt} = \frac{{B_{m} }}{{2h_{m} }} = \frac{{RTK_{{H_{2} O}} C_{{O_{2} }} }}{{N_{m} h_{m} }}$$
(10)

\(\overline{h}_{m}\) is the thickness of the expansion of silica scale on the wall of matrix cracks, which can be expressed as \(\overline{h}_{m} = h_{m} /\nu_{m}\), where \(\nu_{m}\) is the volume expansion ratio of SiC matrix, which is given by \(\nu_{m} = M_{s} \rho_{m} /\left( {\rho_{s} M_{m} } \right)\), where \(\rho_{m}\) and \(M_{{\text{m}}}\) are the density and molar mass of silica, respectively.

b) The second stage: When oxygen goes through the annular pore, the matrix and the fiber on both walls of the pore also consume oxygen. Assuming that the direction along the fiber axis is x, the differential equation for this stage at a specific time t is:

$$\frac{d}{dx}\left[ {\left( {r_{m}^{2} - r_{f}^{2} } \right)\frac{{ - D_{2} C_{0} }}{{C_{0} - C_{{O_{2} }} \left( {1 - \alpha_{2} } \right)}}\frac{{dC_{{O_{2} }} }}{dx}} \right] + \frac{{g_{m} r_{m} \rho_{s} }}{{2M_{s} }}\frac{{dh_{m} \left( t \right)}}{dt} + \frac{{g_{f} r_{f} \rho_{s} }}{{2M_{s} }}\frac{{dh_{f} \left( t \right)}}{dt} = 0$$
(11)

where \(g_{f}\) is the number of moles of O2 necessary to form 1 mol of silica during oxidation of SiC fiber.\(r_{m}\) and \(r_{f}\) are the inner diameter and outer diameter of annular pores, respectively.\(h_{f} \left( t \right)\) is the oxide scale thickness of fiber, the growth rate of which can be expressed as:

$$\frac{{dh_{f} \left( t \right)}}{dt} = \frac{{B_{f} }}{{2h_{f} }} = \frac{{RTK_{{H_{2} O}} C_{{O_{2} }} }}{{N_{f} h_{f} }}$$
(12)

\(\overline{h}_{f}\) is the thickness of expansion of the silica scale on the fiber surface, which can be expressed as \(\overline{h}_{f} = h_{f} /\nu_{f}\), where \(\nu_{f}\) is the volume expansion ratio of SiC fiber, which is given by \(\nu_{f} = M_{s} \rho_{f} /\left( {\rho_{s} M_{f} } \right)\), where \(\rho_{f}\) and \(M_{f}\) are the density and molar mass of silica, respectively.

The boundary conditions are given by:

  • 1. At the top of matrix crack (z = 0), with

    $$C_{{O_{2} }} {\text{ = C}}_{0}$$
    (13)

  • 2. At the end of interfacial oxidation \(\left( {z = r_{t} - r_{m0} ,x = L_{r} } \right)\), with

    $$\frac{{ - D_{2} C_{0} }}{{C_{0} - C_{{O_{2} }} \left( {1 - \alpha_{2} } \right)}}\frac{{dC_{{O_{2} }} }}{dx} = \frac{{\beta k_{0} }}{{M_{c} }}\left( {\frac{{C_{oxy} }}{{C_{atm} }}} \right)^{n}$$
    (14)

    where \(\beta\) refers to the number of moles of oxygen consumed by one mole of carbon, \(M_{c}\) is the molar mass of carbon.\(L_{r}\) is the length of the carbon interphase consumed by oxidation. The oxidation rate of the carbon interphase at t is given by

    $$\frac{{dL_{r} }}{dt} = \frac{{ - D_{{2,L_{r} }} C_{0} }}{{C_{0} - C_{{O_{2} ,L_{r} }} \left( {1 - \alpha_{{L_{r} }} } \right)}}\left( {\frac{{dC_{{O_{2} }} }}{dx}} \right)_{{L_{r} }} \frac{{M_{c} }}{{\beta \rho_{c} }}$$
    (15)

  • 3. At the bottom of matrix crack \(\left( {z = r_{t} - r_{m0} ,x = 0} \right)\), it is assumed that there is no consumption of oxygen in this region where the number of moles of oxygen entering the bottom of matrix crack is equal to that entering the two entrances of the annular pore, with

    $$2\pi \left( {r_{t} - z} \right)\left( {2d - 2\overline{h}_{m} \left( {z,t} \right)} \right)\frac{{ - D_{1} C_{0} }}{{C_{0} - C_{{O_{2} }} \left( {1 - \alpha_{1} } \right)}}\frac{{dC_{{O_{2} }} }}{dz}{ = }\left( {r_{m}^{2} - r_{f}^{2} } \right)\frac{{ - D_{2} C_{0} }}{{C_{0} - C_{{O_{2} }} \left( {1 - \alpha_{2} } \right)}}\frac{{dC_{{O_{2} }} }}{dx}$$
    (16)

2.3 Fiber Strength Degradation Model

2.3.1 Thermal Exposure Induced Fiber Strength Degradation

Under an inert atmosphere, thermal instability of the microstructure accompanied by fiber strength loss has been observed in Hi-Nicalon™ (HN) and Hi-Nicalon type S (HNS) fibers by several investigators Fig. 1(c) [24, 25]. The most significant and measurable change in microstructure reported as accompanying strength loss is grain growth. Typically, an average crystallite size has been measured using X-ray diffraction; and in some instances, the data is supported by high-resolution TEM investigations. Grujicic et al. [26] gave the grain size of Nicalon fiber versus time and temperature as:

$$G^{3} \left( {T,t} \right){ = }\left( {3.26 \times 10^{{{ - }9}} } \right)^{3} { + }\left( {2.42 \times 10^{{{ - }18}} } \right) \cdot t \cdot \exp \left( {\frac{{ - 3.42 \times 10^{5} }}{RT}} \right)$$
(17)

where G is the average grain size. The first term on the right-hand side represents the original grain volume. In addition to grain growth, Nicalon fibers also exhibit thermal decomposition due to their high oxygen content at high temperatures, which can also cause fiber strength degradation (Fig. 1(c)). The change of pore volume fraction with time and temperature caused by thermal decomposition of fiber can be expressed as [26]:

$$P\left( {T,t} \right) = 38\left\{ {1 - \exp \left[ { - 1.36 \times 10^{30} \times \exp \left( {\frac{{ - 0.935 \times 10^{6} }}{RT}} \right)t^{1.08} } \right]} \right\}$$
(18)

The strength degradation caused by the increase of grain size and thermal decomposition of fiber can be expressed by the following formula [26]:

$$\sigma_{0} \left( {T,t} \right){ = }10.77 \times 10^{6} \left( {G\left( {T,t} \right)} \right)^{ - 0.26} \times \left[ {2 - \frac{1}{{1 - \left( {\frac{{P\left( {T,t} \right)}}{100}} \right)^{0.32} }}} \right]$$
(19)

According to fracture mechanics, the size of defects,\(a_{c}\), on the surface of the fiber before oxidation can be estimated:

$$a_{c} = \left( {\frac{{K_{IC} }}{{Y\sigma_{0} \left( {T,t} \right)}}} \right)^{2}$$
(20)

where Y is a shape factor,\(K_{IC}\) is fiber fracture toughness.

2.3.2 Oxidation Induced Fiber Strength Degradation

As suggested by Evans et al. [13] and Helmer et al. [27], the oxide scale can be assumed to fail first because of the high failure strain of the fibers. Thus, it can be assumed that the fiber strength is determined by the larger one between the flaw in the oxide scale and the preexisting fiber flaw. In addition, the flaw size in the oxide scale is assumed to be the same size as the scale thickness, which has been proved to be true in detail by Ohiai et al. [28].

Therefore, when the oxide scale thickness on the fiber surface is smaller than the pre-existing flaw, the fiber strength will not be affected. On the contrary, when the thickness of silica scale on the fiber surface is larger, the fiber strength will be determined by the thickness of the silica scale. From the standpoint of fracture mechanics, the strength of the fiber can be expressed as:

$$\sigma_{c} \left( {x,t} \right) = \left\{ \begin{gathered} \sigma_{0} ,a_{c} \left( t \right) \ge h_{f} \left( {x,t} \right) \hfill \\ \frac{{K_{IC} }}{{Y\sqrt {h_{f} \left( {x,t} \right)} }},a_{c} \left( t \right) < h_{f} \left( {x,t} \right) \hfill \\ \end{gathered} \right.$$
(21)

2.4 Creep-Oxidation Model

2.4.1 The Stress Distribution of Fiber and Matrix

The intrusion of oxidizing gas along the cracks of the matrix will greatly affect the load transfer between the fiber and the matrix Fig. 1(d). For example, the consumption of the interphase will make the exposed area of the fiber increase, and the oxidation of the fiber will lead to an increase in stress and a decrease in strength in a local area, and ultimately affect the creep characteristics and failure probability of the fiber, resulting in the degradation of the mechanical properties of the composite material.

As shown in Fig. 2, a characteristic unit is used as the object of mechanical analysis. \(L_{d}\) is the length of the debonding region at one side of the crack. The length of the characteristic unit is equal to the average matrix crack spacing \(L_{c}\). Considering the symmetry of the material, only the stress distribution within the range \(\left( {0,L_{c} /2} \right)\) is discussed here.

Fig. 2
figure 2

Stress distribution along the fiber axis: before oxidation(a), after oxidation (the debonded regions have not been overlapped) (b), after oxidation (the debonded regions have been overlapped) (c), the interphase is completely consumed (d)

Full size image

During the oxidation process of mini-composite, there are four regions on a single fiber, including the matrix crack region \(\left( {x \in \left( {0,d} \right)} \right)\), interphase consumed region \(x \in \left( {d,d + L_{r} } \right)\),interphase debonded region \(x \in \left( {d + L_{r} ,d + L_{r} + L_{d} } \right)\), and interphase bonded region \(x \in \left( {d + L_{r} + L_{d} ,L_{c} /2} \right)\), as shown in Fig. 2(b). The axial stress distribution of fibers and matrix in these two regions can be written as:

$$\sigma_{f} = H,x \in \left( {0,d + L_{r} } \right)$$
(22)
$$\sigma_{m} = 0,x \in \left( {0,d + L_{r} } \right)$$
(23)

where H is the maximum fiber stress within the matrix crack region and interphase consumed region (If oxidation duration \(t > 0\)). Away from these two regions, the fiber stress decreases and satisfies the following equation:

$$\frac{{d\sigma_{f} }}{dx} = - \frac{2\tau }{{r_{f0} }}$$
(24)

where \(\tau\) is the interfacial shear stress and \(x\) represents the axial distance to the centerline of matrix cracks.

Therefore, the axial stress distribution of fibers and matrix in the interphase debonded region can be expressed as:

$$\sigma_{f} \left( {x,t} \right) = H - \frac{2\tau }{{r_{f0} }}\left( {x - d - l_{r} } \right),x \in \left( {d + L_{r} ,d{\text{ + L}}_{r} + L_{d} } \right)$$
(25)
$$\sigma_{m} \left( {x,t} \right) = \frac{\sigma }{{V_{m} }} - \frac{{V_{f} }}{{V_{m} }}\left[ {H - \frac{2\tau }{{r_{f0} }}\left( {x - d - L_{r} } \right)} \right],x \in \left( {d + L_{r} ,d + L_{r} + L_{d} } \right)$$
(26)

In the loading process, the value of H will change with time considering the impact of fiber fracture failure. According to the assumption of global load sharing, the maximum stress of the fiber in the matrix cracking and interphase consumption area can be expressed as [29]:

$$\frac{\sigma }{{V_{f} }} = H\left( {1 - \phi_{L} } \right) + \frac{2\tau }{{r_{f0} }}\lambda \phi_{L}$$
(27)

where \(\phi_{L}\) is the fraction of failed fibers, which can be calculated as \(\phi_{L} = 1 - \left( {N/N_{0} } \right)\) where N is the number of surviving fibers and \(N_{0}\) is the original number of fibers.\(\lambda\) is the average fiber pullout length. The first term on the right side of Eq. (27) represents the load bearing of the intact fiber, and the second term represents the contribution of the broken fiber through friction. As the fraction of broken fibers increases, the stress of the remaining fibers increases and further increases the probability of fiber failure.

The interphase bonded region retains the complete structure, so firstly the distribution of stress follows the mixing rate formula:

$$\sigma { = }\sigma_{f0} V_{f} \left( {1 - \phi_{L} } \right) + \sigma_{m0} V_{m}$$
(28)

Secondly, considering the influence of high-temperature creep of the fiber, the fiber stress in the interfacial bonded region should also satisfy the following relation:

$$\frac{{\sigma_{f0} }}{{E_{f} }} + \varepsilon_{fc} = \frac{{\sigma_{m0} }}{{E_{m} }} + \varepsilon_{mc}$$
(29)

where \(\varepsilon_{fc}\) and \(\varepsilon_{mc}\) represent the creep strain of fiber and matrix, respectively. Since the creep resistance of the SiC matrix far exceeds that of the SiC-based fiber [30], the creep strain of the SiC matrix can be ignored here. The thermally activated fiber creep,\(\varepsilon_{fc}\), can be described using a simplified Bailey-type relationship [31]:

$$\varepsilon_{fc} = A_{0} \sigma_{f0} t^{{P_{cr} }}$$
(30)

where \(A_{0}\)(in \(GPa^{ - 1}\)) is a parameter related to the creep rate, which depends on temperature. \(P_{cr}\) is a creep parameter. Combine Eqs. (28), (29), and (30), the fiber and matrix stress in the interfacial bonded region can finally be expressed as:

$$\sigma_{f0} = \frac{{\sigma /E_{m} }}{{V_{f} \left( {1 - \phi_{L} } \right)/E_{m} + A_{0} V_{m} t^{{P_{cr} }} + V_{m} /E_{f} }}$$
(31)
$$\sigma_{m0} = \frac{{\sigma \left( {\frac{{E_{m} }}{{E_{f} }} + A_{0} E_{m} t^{{P_{cr} }} } \right)}}{{V_{f} \left( {1 - \phi_{L} } \right) + V_{m} \left( {\frac{{E_{m} }}{{E_{f} }} + A_{0} E_{m} t^{{P_{cr} }} } \right)}}$$
(32)

Therefore, the general distribution of fiber and matrix stress can be uniformly expressed as

$$\sigma_{f} \left( x \right) = \left\{ \begin{gathered} \frac{1}{{1 - \phi_{L} }}\left( {\frac{\sigma }{{V_{f} }} - \frac{2\tau }{{r_{f0} }}\lambda \phi_{L} } \right),x \in \left( {0,d + L_{r} } \right) \hfill \\ \frac{1}{{1 - \phi_{L} }}\left( {\frac{\sigma }{{V_{f} }} - \frac{2\tau }{{r_{f0} }}\lambda \phi_{L} } \right) - \frac{2\tau }{{r_{f0} }}\left( {x - d - L_{r} } \right),x \in \left( {d + L_{r} ,d + L_{r} + L_{d} } \right) \hfill \\ \frac{{\sigma /E_{m} }}{{V_{f} \left( {1 - \phi_{L} } \right)/E_{m} + A_{0} V_{m} t^{{P_{cr} }} + V_{m} /E_{f} }},x \in \left( {d + L_{r} + L_{d} ,L_{c} /2} \right) \hfill \\ \end{gathered} \right.$$
(33)
$$\sigma_{m} \left( x \right) = \left\{ \begin{gathered} 0,x \in \left( {0,d + L_{r} } \right) \hfill \\ \hfill \\ \frac{\sigma }{{V_{m} }} - \frac{{V_{f} }}{{V_{m} }}\left[ {\frac{1}{{1 - \phi_{L} }}\left( {\frac{\sigma }{{V_{f} }} - \frac{2\tau }{{r_{f0} }}\left( {x - d - L_{r} } \right)} \right)} \right],x \in \left( {d + L_{r} ,d + L_{r} + L_{d} } \right) \hfill \\ \frac{{\sigma \left( {\frac{{E_{m} }}{{E_{f} }} + A_{0} E_{m} t^{{P_{cr} }} } \right)}}{{V_{f} \left( {1 - \phi_{L} } \right) + V_{m} \left( {\frac{{E_{m} }}{{E_{f} }} + A_{0} E_{m} t^{{P_{cr} }} } \right)}},x \in \left( {d + L_{r} + L_{d} ,L_{c} /2} \right) \hfill \\ \end{gathered} \right.$$
(34)

It is noticeable that there exist some special situations during the oxidation of mini-composite. Initially, the interphase consumption has not started, that is \(L_{r} = 0\). Only the matrix crack region, interphase debonded region and interphase bonded region need to be considered in this case, as shown in Fig. 2 (a). Another special case is called complete debonding, that is \(d + L_{r} + L_{d} = L_{c} /2\). Only matrix crack region, interphase consumed region, and interphase debonded region need to be considered in this case, as shown in Fig. 2(c). In the extreme case when the carbon is completely consumed, the fiber and matrix are completely separated, which means the fiber will support the entire load applied to the composite, as shown in Fig. 2(d).

The strength of the fiber can be described by a two-parameter Weibull distribution [32], and the failure probability of the fiber can be expressed as:

$$\phi_{L} = 1 - \exp \left[ { - \int {\frac{1}{{A_{0} }}\left( {\frac{{\sigma_{f} \left( {x,t} \right)}}{{\sigma_{c} \left( {x,t} \right)}}} \right)^{m} dA} } \right]$$
(35)

where \(\sigma_{c} \left( {x,t} \right)\) is the characteristic strength for a fiber of surface \(A_{0} { = }2\pi r_{f0} L_{com}\) under monotonic tension, m is the Weibull modulus. The strength \(\sigma_{c} \left( {x,t} \right)\) will be considered to vary with time and location as mentioned in the previous section. Due to the assumption of a periodic matrix crack spacing,\(L_{c}\), the probability of failure of fiber along the gauge length,\(L_{com}\), of a monotonic tension specimen is

$$\phi_{L} = 1 - \exp \left[ { - \int_{0}^{{L_{com} }} {\frac{1}{{L_{com} }}\left( {\frac{{\sigma_{f} \left( {x,t} \right)}}{{\sigma_{c} \left( {x,t} \right)}}} \right)^{m} dx} } \right]$$
(36)

Using the symmetry in the fiber stress distribution on both sides of the crack plane, the integration is performed only along the length \(L_{c} /2\).

$$\phi_{L} = 1 - \exp \left[ { - \frac{2}{{L_{c} }}\int_{0}^{{L_{c} /2}} {\left( {\frac{{\sigma_{f} \left( {x,t} \right)}}{{\sigma_{c} \left( {x,t} \right)}}} \right)^{m} dx} } \right]$$
(37)

2.4.2 Strain of the Composite

The fiber axial stress at the crack of the matrix, H, is an important parameter that determines the stress distribution. The dependence of the value of this parameter and the fiber failure volume fraction,\(\phi_{L}\), is mutual. This nonlinear problem needs to be solved by numerical methods.

Once the relationship of fiber stress with time and position has been calculated, the axial elastic strain of the fiber can be determined by integration:

$$\varepsilon_{e} \left( t \right) = \frac{2}{{E_{f} L_{c} }}\int_{0}^{{L_{c} /2}} {\sigma_{f} \left( {x,t} \right)} dx$$
(38)

The deformation of fiber and matrix at high temperature is time-dependent. After the matrix is cracked, the creep of the minicomposite material mainly depends on the creep of the fiber. Therefore, the average creep of the minicomposite material can be expressed as an integral:

$$\varepsilon_{c} \left( t \right) = \frac{{2A_{0} t^{{P_{cr} }} }}{{L_{c} }}\int_{0}^{{L_{c} /2}} {\sigma_{f} \left( {x,t} \right)} dx$$
(39)

The total strain,\(\varepsilon_{t} \left( t \right)\), is the sum of the elastic strain and the creep strain:

$$\varepsilon_{t} = \varepsilon_{e} \left( t \right) + \varepsilon_{c} \left( t \right)$$
(40)

As shown in Fig. 3, a numerical method based on a classical Runge and Kutta algorithm was applied to solve the above differential equation. Besides, the bisection method was used to search for the unknown boundary conditions with the help of the known boundary conditions.

Fig. 3
figure 3

Numerical calculation method based on Runge Kuta algorithm and dichotomy

Full size image

3 Parameter of the Model

A list of variables used in the model is shown in Table 1 with a brief description. In the last column, the type of variable is also given. The environmental variables define the absolute temperature, T, and the partial pressure of water vapor,\(P_{{H_{2} O}}\), of the ambient. The environment of interest is ambient with a temperature range of 900 ~ 1200℃, 1 atm total pressure, 21%O2, water vapor of 1%-50%H2O.

Table 1 A list of variables and acronyms used in this work
Full size table

The material parameters are obviously dependent on the testing conditions. For the fibers, Young’s modulus of 100 GPa and a radius of 6 μm has been considered. The volume fraction of fibers is considered to be 0.1 ~ 0.3. In this work, the PyC interphase thickness is considered to be 1.5 μm, the length of the mini-composite is 130 mm, the heat treat temperature for the composite is 1200℃.

The model for fiber creep has two unknown parameters,\(A_{0}\) and \(P_{cr}\), which are related to the creep rate. These two parameters were obtained from the bend stress relaxation (BSR) test, which has been demonstrated to be an effective method for comparing the relative creep resistance of a wide variety of ceramic fibers [31].

The oxidation kinetics of the SiC fiber and matrix were calibrated to data in Oplia’s report [23]. The temperature-dependent oxygen permeability used for both fiber and matrix was 2.2e-14exp(-113873 /R/T) moles/m s Pa. The parameter \(\varsigma\) and \(\eta\) that accounts for the dependence on \(P_{{H_{2} O}}\) were 60.254 and 1.5365 respectively based on the best fit to experimental data.

For calibration of PyC interphase degradation, the linear rate constant describing interphase consumption at P = 100 kPa in pure oxygen was \(1070exp\left( { - 153620/RT} \right)\) kg/(m.s). The reaction exponent for carbon oxidation, n, was adjusted to fit data, with sufficient goodness of fit obtained to infer that the carbon oxidation rate dependence of oxygen concentration is well represented.

For the fiber stress distribution model, the average fiber pullout length,\(\lambda\), is considered to be 137 ~ 240 μm [3]. The interfacial shear stress,\(\tau\), is assumed to be in the range of 4 ~ 30 MPa. The Weibull modulus, m, is considered to be 3 ~ 7. The value of fracture toughness,\(K_{IC}\), is in the range of 0.1 ~ 2.4 \(MPa \cdot m^{1/2}\).

4 Results and Discussion

4.1 Variation of Oxygen Concentration

Figure 4(a) shows the oxidation morphology of the internal channels including the matrix cracks and interphase annular gap. The z-axis denotes the direction from the outer surface of the matrix along the centerline of matrix crack to the fiber and x-axis denotes the direction parallel to the fiber. The O2 concentration along the diffusion path (z + x) with different times under the wet oxygen atmosphere (10% H2O) at 1200℃ is shown in Fig. 4(b). It can be observed firstly that the O2 concentration continuously decreases with the diffusion path. Secondly, the O2 concentration gradient gradually decreases with the increase of time, which is mainly caused by the reduction of O2 diffusion rate in silica due to the growth of the silica scale. Thirdly, the amount of the consumption of O2 increases with time and, PyC interphase consumed length. This is because the increase of interphase consumed length leads to the increase of exposure area of fiber and matrix in the oxidizing atmosphere, which consumes more O2[10].

Fig. 4
figure 4

Scheme of oxidation morphology of internal channel (a), Variation of O2 concentration along diffusion path with different times under the wet oxygen atmosphere (10% H2O) at 1200℃ (b), Consumption length of PyC interphase versus time at different temperatures under the wet oxygen atmosphere (10% H2O) (c), Consumption length of PyC interphase versus time under different water vapor pressure at 900℃ (d), Silica scale thickness on the surface of fiber versus time in wet oxygen (1% H2O) (e), Evolution of the thickness of silica scale along interphase annular gap at different times in wet oxygen (1% H2O, 1200℃) (f), Evolution of the thickness of silica scale on the fiber surface along x axis at 900℃ at the time of 10000 s under different water vapor pressure (g), Fiber strength versus time at 900℃ under wet oxygen (1% H2O) atmosphere (h), Evolution of the thickness of silica scale on the wall of matrix crack along z axis at 900℃ at the time of 10000 s under different water vapor pressure (i), Scheme of interphase consumed length and silica scale on the surface of fiber (j), Evolution of crack opening with time under wet oxygen atmosphere (1% H2O) at different temperatures (k), Variation of gap width with time at different temperatures (l)

Full size image

4.2 Oxidation of the PyC Interphase

Based on the oxygen concentration profile, the PyC interphase consumed length is calculated. Figure 4(c) shows the consumption length of the PyC interphase versus time at different temperatures under a wet oxygen atmosphere (1%H2O). The consumption length of the PyC interphase increases with time and the increasing rate of consumption length of the PyC interphase grows as the temperature rises, which can illustrate the accelerating effect of temperature on the reaction rate of the PyC interphase. To investigate the effect of water vapor pressure on the consuming rate of interphase, the consumption length of PyC interphase versus time at 1200℃ under different water vapor pressure is simulated (Fig. 4(d)). It can be observed from Fig. 4(d) that there exists little difference between the curves of consumption length of the PyC interphase versus time. The increase of water vapor pressure doesn’t improve the consuming rate of the PyC interphase but reduces that slightly. According to Xiaowei’ experimental work [33], the existence of water vapor will inhibit the reaction between carbon and O2 to a certain degree under the wet oxygen atmosphere (700 ~ 1300℃). At the same O2 pressure, the increase of water vapor pressure will inhibit the reaction between carbon and O2 more obviously, which leads to the reduction of the consuming rate of the PyC interphase.

4.3 Oxidation of the SiC-Based Fiber

Figure 4(d) shows the growth rule of the thickness of the silica scale on the fiber surface with time at different temperatures under wet oxygen atmosphere (1%H2O). It can be concluded that the oxidation rate and thickness of the silica scale on the fiber surface increase as the temperature rises. It also can be inferred from this figure that the growth of the silica scale obeys the parabolic line law. Figure 4(e) shows the evolution of the thickness of silica scale along the interphase annular gap at different times in wet oxygen (1% H2O, 1200℃). It can be seen that the distribution of silica scale along the interphase annular gap is nonlinear. Due to the higher O2 concentration and longer exposure time to the oxidants in the area near the matrix crack, the accumulated thickness of the silica scale is larger. To explore the effect of water vapor pressure on the growth rate of the thickness of silica scale on the fiber surface, the evolution of the thickness of silica scale on the fiber surface along x-axis at 900℃ at the time of 10000 s under different water vapor pressure is simulated shown in Fig. 4(g). It can be found that the thickness of the silica scale on the fiber surface at the same x position increases significantly with the rise of water vapor pressure, which is mainly due to the catalysis of water vapor to the chemical reaction between O2 and SiC. The previous study [34] show that the existence of water vapor promotes the volatilization of the silica scale and make the silica scale loose and porous, which thus accelerates the diffusion rate of O2 in silica scale to make the oxidation reaction faster. When the thickness of the silica scale,\(h_{f}\), exceeds the pre-existing flaw,\(a_{c}\), the fiber strength will decrease, which is shown in Fig. 4(h).

4.4 Variation of Matrix Crack Opening and Gap Width

Based upon the calculated thickness of the silica scale at the entrance of the matrix crack and interphase annular gap, the matrix crack opening and gap width can be obtained. Figure 4(i) shows the scheme of interphase consumed length and silica scale on the surface of the fiber. As the temperature rises, the initial matrix crack opening under the creep load, 2d0, decreases firstly due to the thermal expansion of the matrix. Then the matrix crack opening will further decrease due to oxidation of the wall of the matrix crack. Figure 4(j) shows the evolution of the thickness of the silica scale on the wall of the matrix crack along the z axis at 900℃ at the time of the 10000 s under different water vapor pressure. Firstly, it can be observed that the thickness of the silica scale decreases along z-axis due to the reduction of O2 concentration. Secondly, the effect of water vapor pressure on the thickness of the silica scale is obvious. According to the previous description in Sect. 4.3, the oxidation of SiC will result in volume expansion, which leads to the decrease of matrix crack opening. Figure 4(k) shows the evolution of crack opening with time under the wet oxygen atmosphere (1%H2O) at different temperatures. It can be observed that the matrix crack opening decreases with time due to the growth of the silica scale on the wall of the matrix crack, however, the decreasing rate of matrix crack opening remains slow as the time increases, which is mainly due to two reasons. Firstly, the matrix crack opening under the creep load before oxidation reaches over 30 \(\mu m\), which is much larger than the silica thickness of the silica scale. Thus, the variation of matrix crack opening seems to increase slowly. Figure 4(l) shows the variation of gap width with time at different temperatures under the wet oxygen atmosphere (1%H2O). The initial gap width is the thickness of the interphase, which equals 1.5 \(\mu m\). With the increase of time, the gap width decreases gradually. Similar to the matrix crack opening, the temperature accelerates the oxidation rate of SiC matrix and fiber and therefore increases the sealing rate of the gap width.

4.5 Creep-Oxidation of the Mini-Composite

To validate the model in this paper, the predicted strain–time curve was compared with the experimental data with a creep load of 40 N under wet oxygen atmosphere (about 1% H2O) at 900℃ [35] in Fig. 5. The values of parameters such as \(V_{f} ,\lambda ,\tau ,m,K_{IC}\) were selected shown in Fig. 5.

Fig. 5
figure 5

Experimental curve and prediction of the model (strain and evolution of \(\phi_{L}\)) for the creep test of the sample (900℃, about 1%H2O, 21%O2, 40 N)

Full size image

The results show that the predicted strain–time curves agree well with the test data, which verifies the validity of the model. It can be inferred from Fig. 5 that the strain–time curves can be divided into three stages: The time-dependent strain is transient, and a continuously decreasing strain rate (primary stage) appears at first. Then it goes to a steady state (constant strain rate, secondary) stage, at last accelerating (tertiary stage) to rupture. In addition, it can be observed from Fig. 5 that the fraction of failed fibers increases with time and the growth rate becomes greater with time. The fraction of failed fibers, \(\phi_{t}\), increase from 0 to 11% when the mini-composite fails, which is consistent with the results obtained by Casas et al. [3] This also reflects the acceleration of fiber failure with time as a consequence of load transfer to the intact fibers and loss of strength of the surviving fibers.

To illustrate the effect of temperature and partial pressure of water vapor on the strain of the mini-composites, the strain–time curves under different temperatures and partial pressures of water vapor are simulated. Figure 6(a) shows the strain–time curves under different water vapor pressure (1%-50%) at 900℃. Firstly, it can be observed that the tertiary stage of the strain–time curves in 1% water vapor pressure is not very obvious compared with that under the atmosphere of 5% ~ 50% water vapor pressure. Secondly, the failure time of the mini-composites becomes shorter with higher water vapor pressure. According to the simulated results in Sects. 4.2 and 4.3, the increase of water vapor pressure has little effect on the consuming rate of the PyC interphase but affects the growth rate of the thickness of the silica scale on the fiber surface seriously. This fact illustrates that the increase of water vapor pressure only accelerates the failure rate of fibers but has little influence on the stress distribution in various interphase regions. Figure 6(b) shows the strain–time curves under different water vapor pressure at 1000℃. Compared with the strain–time curve at 900℃ under 1%H2O, the tertiary stage is more obvious in the strain–time curve at 1000℃ under 1%H2O. This is because the effect of temperature on both the consuming rate of the PyC interphase and the growth rate of silica scale is significant, which accelerates the change of stress distribution and the failure of fibers. The strain–time curves under different water vapor pressure (1%-50%) at 1100℃ and 1200℃ are shown in Fig. 6(c) and (d). It can be found that the time for steady state (constant strain rate, secondary) stage decreases with the increase of water vapor pressure. When the water vapor pressure reaches 50%, the steady state almost disappears. Besides, the higher water vapor pressure, the tertiary stage appears earlier. Thus, it can be inferred that the higher water vapor pressure leads to the shorter creep life of the mini-composites when O2 pressure is constant in the wet oxygen atmosphere.

Fig. 6
figure 6

Variation of strain versus time under different water vapor pressure at 900℃ (a), 1000℃ (b), 1100℃ (c), 1200℃ (d), the strain versus time under 1%H2O at different temperatures (e), the strain versus time under 50%H2O at different temperatures (f)

Full size image

To analyze the effect of temperature on the strain under high and low water vapor pressure, the strain–time curves under 1% and 50% H2O at different temperatures are obtained in Fig. 6(e) and (f). It can be found from Fig. 6(e) that the three stages involving the primary stage, steady state stage, and tertiary stage are obvious under 1%H2O although the time for the primary stage, steady state stage decreases as the temperature rises. Besides, it can be seen from Fig. 6(e) that there exists a larger deviation in the primary stage of strain–time curves compared to that in Fig. 5a-d. The slope of the primary stage of strain–time curves in Fig. 6e increases with the raise of temperature, which shows the accelerating effect of temperature on the strain in the primary stage. This is mainly due to the increase of consumption rate of PyC interphase with the raise of temperature, which leads to the increase of growth rate of the axial stress of fiber. It can be inferred from Eq. (38) and (39) that the integral of the axial stress of fiber with greater growth rate results in higher rate of strain. It can be found from Fig. 6(f) that the steady state stage completely disappears even at 900℃ under 50% H2O, and the time in the primary stage becomes short with the raise of temperature. This phenomenon is different from the behavior in Fig. 6(e) and the main reason is that the high water vapor pressure accelerates the degradation of SiC fibers, which increases the failure probability of the fibers. Zhu’s [36] study shows the existence of one, two or three stages depends on the stress and temperature conditions and the tertiary stage appears at low stresses (45-75 MPa), which is consistent with the strain–time curves obtained in this work.

4.6 The Effect of Creep and Oxidation on the Matrix Crack Spacing

It is assumed that the matrix crack spacing is constant in this work. To check the effect of creep and oxidation on the matrix crack spacing, the critical matrix strain energy (CMSE) criterion [37] is used to judge the variation of matrix crack spacing. The CMSE criterion generally considers that the matrix crack spacing is uniform and there exists a critical value of strain energy \(U_{cr}\) for the matrix between two adjacent cracks, beyond which the matrix will not be able to support an extra load as more energy is placed into the composites. Subsequently, new cracks form so that the matrix strain energy \(U_{m}\) remains constant. The CMSE criterion is expressed as:

$$U_{m} = U_{cr}$$
(41)

where

$$U_{m} = \int_{V} {\int_{\varepsilon } {\sigma_{m} } } \left( x \right)d\varepsilon dV$$
(42)

Figure 7 shows the stress distribution and strain energy of the matrix after different oxidation times (0.01 h, 0.1 h, 1 h, 6.5 h) at 900℃ under1%H2O. It can be observed that the matrix stress gradually decreases with time, which leads to the reduction of matrix strain energy. The matrix strain energy decreases from \(1.3 \times 10^{{{ - }3}} J\) to \(0J\) when oxidation time from 0.01 h to 6.5 h, which validates the assumption that the matrix crack spacing remains constant during the process of creep oxidation of the mini-composites.

Fig. 7
figure 7

The stress distribution and strain energy of matrix after different oxidation times (0.01 h, 0.1 h, 1 h, 6.5 h) at 900℃ under1%H2O

Full size image

5 Conclusions

A model for predicting the creep-oxidation behavior of SiC/PyC/SiC mini-composites in a wet oxygen atmosphere is presented. The model involves the thermal–mechanical model, environmental-micro model, fiber strength degradation model, and creep-oxidation model. The water vapor is considered as the catalyzer in the environmental-micro model. The effects of grain growing, thermal decomposition, and the growth of silica scale are taken into account in the fiber strength degradation model. The change of stress distribution due to the consumption of the PyC interphase and the creep of fibers are considered in the creep-oxidation model. The following conclusions were drawn as follows:

  1. 1.

    The model predictions show the obvious accelerating effect of temperature on the consumption of interphase and the growth of the silica scale. The water vapor has little influence on the consuming rate of the PyC interphase but promotes the growth of silica scale on the matrix and fiber significantly.

  2. 2.

    The predicted strain–time curves are composed of the primary stage, steady state stage, and tertiary stage, which is consistent with the experimental data. The increase of temperature and water vapor pressure leads to the reduction of creep life and makes the tertiary stage appear in advance. The increase of water vapor pressure results in the disappearance of steady state stage.

  3. 3.

    The effect of temperature on the creep life of the mini-composites is mainly reflected in two aspects: firstly, the rise of temperature increases the stress in the fiber by accelerating the consumption of interphase. Secondly, the increase of temperature accelerates the reduction rate of fiber strength by increasing the growth rate of the silica scale on the fiber surface. While water vapor only affects the reduction rate of fiber strength by increasing the growth rate of the silica scale.

  4. 4.

    The creep and oxidation of the constituents have no effect on the matrix crack spacing, which means the set of constant matrix crack spacing in this work is suitable.

  5. 5.

    The model proposed in this work is a good tool to study the creep behavior of unidirectional SiC/SiC composites under wet oxygen atmosphere. This work also contributes to analysis of the oxidation and creep mechanism of SiC/SiC composites with more complexed structures, such as 2D woven, 3D braided composites.