Introduction

Pulmonary embolism (PE) is a life-threatening condition that occurs when an embolus travels into the pulmonary arteries and occludes blood flow to the lungs. Although PE is normally prevented using anticoagulation therapy, when anticoagulants are contraindicated, an inferior vena cava (IVC) filter may instead be placed to act as a mechanical barrier to embolus passage.

Most IVC filters are composed of a series of round or rectangular metal struts arranged in a conical shape and connected at a central hub (e.g., Greenfield (Boston Scientific Corporation, Natick, MA); Günther Tulip and Celect (Cook Medical, Bloomington, IN); Option (Angiotech, Vancouver, BC, Canada); ALN (ALN Implants Chirurgicaux, Ghisonaccia, France); and G2 Express, Eclipse, Meridian, Denali, and Simon Nitinol filters (Bard Peripheral Vascular, Tempe, AZ)). The filter struts direct emboli toward the filter hub at the center of the IVC lumen where the emboli are captured and, ideally, slowly undergo lysis under the influence of fluid shear stresses.43,45 However, the presence of the IVC filter may also disrupt IVC hemodynamics, causing secondary flow downstream of the filter struts and hub that can promote thrombosis.39,40,43,45,50

The number of filters placed in the United States annually has increased rapidly over the past few years, from 2000 in 19794 to 132,000 in 2007,28 to an estimated 250,000 in 2012.41 Despite decades of clinical use and development, complications with modern IVC filters remain common13 and include recurrence of PE, persistence or worsening of deep-vein thrombosis, filter fracture, filter perforation, and filter migration. Furthermore, although previous studies23,50 have outlined the attributes of an “ideal” IVC filter (e.g., nonthrombogenic, high embolus-trapping efficiency, and resistance to tilt or migration), a single “ideal” IVC filter may not exist for all patients, as the best combination of filter characteristics is likely patient-specific.43

Computational modeling has the ability to predict the local mechanical and hemodynamic parameters that determine the in vivo performance of IVC filters and could, with further development and validation, be used as a tool to guide clinical decisions (e.g., filter selection and filter placement location) on a patient-specific basis. To date, previous studies used finite element analysis to predict vein-IVC filter contact forces,1,16 the force required for an IVC filter to migrate downstream,19 and the force required for penetration of an IVC filter strut through the IVC wall.24 Researchers have also used computational fluid dynamics (CFD) to predict the effect of IVC filter placement on secondary flow patterns and wall shear stresses (WSS) in the IVC.1,38,39,43,50

In these computational studies, two primary simplifications are made. First, the geometry of the human IVC is idealized, either as a single straight tube,39,43,45 or as a smooth tube with straight side branches.38,50 In reality, the IVC and its branches pass through the abdomen in close proximity to the aorta, the lumbar spine, and the various organs of the gastrointestinal system. Consequently, the morphology of the IVC is complex: the cross section of the IVC is non-circular and varies in shape and size along the length of the vessel, the IVC and its branches are curved, and anatomical variants such as asymptomatic iliac vein compression are common.36

Second, in previous studies blood is approximated as a Newtonian fluid,1,38,39,43,50 neglecting its shear-thinning and viscoelastic properties. High shear rates disrupt red blood cell (RBC) aggregates and deform RBCs into shapes that reduce drag.11 Thus, the effective viscosity of blood decreases with increasing shear rate until reaching an asymptotic value for shear rates above approximately 100 s−1 (Fig. 1a). In most computational hemodynamic studies, shear rates are assumed to be sufficiently high to justify the approximation of blood as a Newtonian fluid with a viscosity equal to its asymptotic value. Shear rates in the IVC, however, are among the lowest in the circulation (Fig. 1b), in part due to the lack of flow pulsatility (Fig. 1c). Furthermore, a recent study10 shows that secondary flows patterns are sensitive to hemorheology in large, curved blood vessels like the IVC.

In this study, we investigate hemorheological and morphological effects on IVC hemodynamics. Specifically, we compare velocity profiles, secondary flows, IVC and thrombus WSS, and thrombus wake volumes among three IVC geometries with varying levels of idealization. Newtonian and non-Newtonian blood flow simulations are performed, and non-Newtonian effects are quantified by calculating non-Newtonian importance factors and the local and mean errors in velocities, shear rates, and shear stresses due to the Newtonian approximation. Accurately predicting these quantities (in particular, WSS) is important for modeling and simulation of thrombosis, thrombolysis, embolization, and embolus migration.

Figure 1
figure 1

(a) Shear rate–viscosity curve for blood with RBC disaggregation and deformation illustrated. (b) Mean wall shear rate (WSR) in various vessels of the human circulation (data from Goldsmith and Turitto22). The dashed line indicates a WSR of 100 s−1. (c) Flow waveforms for the human descending aorta and infrarenal IVC under resting conditions based on in vivo magnetic resonance imaging measurements.9 The data show that flow through the IVC is approximately steady.

Full size image

Materials and Methods

Computational Geometries

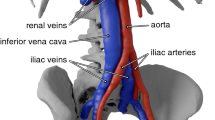
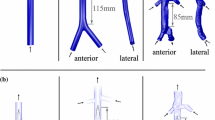
Three IVC geometries are considered (Fig. 2a): (1) a straight, circular tube IVC, (2) a patient-averaged IVC based on measurements from ten computed tomography (CT) datasets,38 and (3) a patient-specific IVC representative of a normal patient with a healthy level of left common iliac vein compression by the right iliac artery (approximately 41% compression here vs. an observed range for asymptomatic compression of 0–68%;36 Fig. 2b). The CT data for the patient-specific IVC was acquired (in-plane resolution of 0.59 mm and slice offset of 0.7 mm) at the Hershey Medical Center after obtaining an IRB exemption. As in Aycock et al.,1 the CT data were then segmented and reconstructed to produce a three-dimensional model of the patient IVC. The patient-specific IVC was uniformly scaled by a factor of 0.88 to obtain a mean hydraulic diameter of 2 cm, approximately the same as that of the patient-averaged and straight-tube IVCs (Fig. 2c). This was required to achieve both dynamic similarity and comparable mean shear rates in each IVC geometry, thereby enabling consistent comparisons when examining the influence of non-Newtonian effects.

Figure 2
figure 2

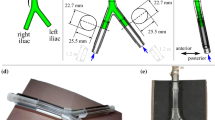
(a) Anterior and lateral views of the three-dimensional models for the (i) straight tube IVC, (ii) patient-averaged IVC, and (iii) patient-specific IVC, with the following vessel segments: 1—infrarenal IVC, 2—iliac veins, 3—renal veins, and 4—suprarenal IVC. Geometries are shown in order of increasing geometric complexity from left to right. (b) Anatomical details captured in the patient-specific IVC geometry: (i) compression of the left iliac vein between the right iliac artery (anterior) and the spine (posterior); (ii) curvature of the infrarenal IVC along the lumbar spine. (c) Hydraulic diameters for the infrarenal regions of the IVCs. The average hydraulic diameter for the straight tube, patient-averaged, and scaled patient-specific IVCs is approximately 2 cm. The location \(x=0\) mm is approximately 2 cm upstream of where the renal veins meet the IVC in the patient-averaged and patient-specific IVCs. (d) Computational model of the G2 Express IVC filter and (e) teardrop-shaped thrombus.

Full size image

Partial occlusion of the IVCs by an IVC filter (G2 Express, Bard Peripheral Vascular, Tempe, AZ; Fig. 2d) and a teardrop-shaped15,38,43 thrombus (approximately 1.06 cm3 in volume; maximum occlusion of approximately 30% of the cross-sectional area of the infrarenal IVC; Fig. 2e) was considered using a nonlinear finite element-based computational method for virtual filter placement from a previous study.1 In brief, an inverse analysis was performed to approximate the in vivo stress state of each IVC. The sheathed IVC filter was then positioned in the infrarenal region of each IVC and virtually placed by simulating contact between the vein wall and the IVC filter. The IVC was modeled as a compliant anisotropic, hyperelastic vessel1,20 during the filter placement simulation, but was modeled as a rigid structure in the hemodynamics simulations. The virtual placement simulations reveal that the normal contact forces between the vein wall and the IVC filter struts are increasingly non-uniform with increasing geometric complexity (Table 1), in agreement with a recent study on IVC filter forces.16

Table 1 Maximum (max.), minimum (min.), and average (avg.) contact normal force magnitudes for the three IVC geometries.
Full size table

Characteristic Shear Rate and Viscosity

In previous literature,2,8,21,30 a characteristic viscosity has been used to improve the accuracy of the Newtonian approximation. Phenomenologically, use of a characteristic viscosity scales the Reynolds number of the Newtonian flow so that it approximately matches the Reynolds number of the non-Newtonian flow.21 The characteristic viscosity may be calculated based on either the wall shear rate (WSR),12,31 which is usually the highest shear rate in the flow, or based on the mean shear rate.2,3,8,21,46

For simple Poiseuille flow of a Newtonian fluid in a vessel of circular cross section, the mean shear rate30,46 is:

$$\begin{aligned} \dot{\gamma }_{p}=\frac{16U}{3D} \end{aligned}$$
(1)

where U is the characteristic velocity and D is the vessel diameter. However, because the patient-averaged and patient-specific IVC geometries considered in the current study are more complex, with curved vessels and bifurcations, the flow deviates significantly from Poiseuille flow. Therefore, we used a more rigorous procedure for estimating the characteristic shear rate and viscosity:

  1. (1)

    Perform a Newtonian simulation using an asymptotic viscosity \(\mu _{\infty }\) for blood.

  2. (2)

    Calculate a characteristic shear rate \(\dot{\gamma }_{c}\) for the flow based on a representative mean shear rate. For example, for a cell-centered finite volume method, a volume-weighted shear rate may be calculated as:

    $$\begin{aligned} \dot{\gamma }_{c}=\frac{\sum _{i=1}^{n}\dot{\gamma }_{i}\, V_{i}}{\sum _{i=1}^{n}V_{i}} \end{aligned}$$
    (2)

    where \(\dot{\gamma }_{i}\) are the cell-centered shear rate values and \(V_{i}\) are the cell volumes.

  3. (3)

    Use the characteristic shear rate \(\dot{\gamma }_{c}\) to calculate a corresponding characteristic viscosity with the chosen non-Newtonian viscosity model, i.e. \(\mu _{c}=\mu (\dot{\gamma }_{c})\).

  4. (4)

    Perform a second Newtonian simulation using the obtained characteristic viscosity \(\mu _{c}\).

Following this procedure, a Newtonian simulation was first performed in each of the IVCs using the asymptotic viscosity. Characteristic shear rates were calculated based on the volume-weighted mean shear rate in the infrarenal regions of the IVCs, where IVC filters are generally placed. A second Newtonian simulation was then performed in each IVC using the resulting characteristic viscosity. This process was repeated for the partially occluded IVCs.

Non-Newtonian Model and Non-Newtonian Reynolds Number

Non-Newtonian simulations were performed in each IVC using the Carreau model.6 Unlike other models (e.g., power-law), the Carreau model captures the asymptotic behavior of shear-thinning fluids at both low and high shear rates, making it a popular choice for modeling blood flow.8,21,32,45,48 The Carreau model assumes that the viscosity is a function of the local shear rate:

$$\begin{aligned} \mu (\dot{\gamma })=\mu _{\infty }+(\mu _{0}-\mu _{\infty })\left( 1+(\lambda \dot{\gamma })^{2}\right) ^{\frac{n-1}{2}} \end{aligned}$$
(3)

where \(\mu _{\infty }\) is the asymptotic viscosity, \(\mu _{0}\) is the zero shear rate viscosity, \(\lambda\) is the relaxation time for blood, \(\dot{\gamma }\) is the scalar shear rate, and n determines the transition between the low and high viscosities. The scalar shear rate (\(\dot{\gamma }\)) may be defined in tensor notation as:6

$$\begin{aligned} \dot{\gamma }=\sqrt{2e_{ij}e_{ij}} \end{aligned}$$
(4)

where \(e_{ij}\) is the strain rate tensor:27

$$\begin{aligned} e_{ij}=\frac{1}{2}\left( \frac{\partial u_{i}}{\partial x_{j}}+\frac{\partial u_{j}}{\partial x_{i}}\right) . \end{aligned}$$

Constants used for the Carreau model were the same as those used in a previous study45 of non-Newtonian blood flow in a simplified IVC (\(\mu _{\infty }\) = 2.57 cP, \(\mu _{0}\) = 162.66 cP, \(\lambda\) = 57.49 s, and n = 0.435).

For the non-Newtonian simulations, the Reynolds number (Re) was calculated as:2,3,21,30

$$\begin{aligned} Re=\frac{\rho \, UD}{\mu _{c,n\text {-}N}} \end{aligned}$$
(6)

where \(\rho\) is the fluid density, U is the characteristic velocity, D is the characteristic diameter, and \(\mu _{c,n\text {-}N}\) is the characteristic viscosity calculated from the Carreau model using the volume-weighted mean shear rate (Eq. 2) from the non-Newtonian flow. Because the cross sections of the infrarenal IVCs are not perfectly circular, the hydraulic diameter (calculated as \(D_{h}=4A/P\), where A is the cross-sectional area and P the wetted perimeter) was used as the characteristic diameter in the Reynolds number (Eq. 6).

Quantifying Non-Newtonian Effects

To quantify the non-Newtonian effects and the error incurred by the Newtonian approximation, percent standard deviation (%SD) and percent mean error (%ME) were calculated as:

$$\begin{aligned} \%SD(\phi )=\frac{1}{\bar{\phi }_{n\text {-}N}}\sqrt{\frac{\sum _{i=1}^{n}\left( \bar{\phi }_{n\text {-}N}-\phi _{n\text {-}N,i}\right) ^{2}\, A_{i}}{\sum _{i=1}^{n}A_{i}}}\times 100 \end{aligned}$$
(7)
$$\begin{aligned} \%ME(\phi )=\frac{1}{\bar{\phi }_{n\text {-}N}}\frac{\sum _{i=1}^{n}\left( \phi _{N}-\phi _{n\text {-}N,i}\right) \, A_{i}}{\sum _{i=1}^{n}A_{i}}\times 100 \end{aligned}$$
(8)

respectively, where \(\phi\) is either the wall viscosity (\(\mu _{\rm{wall}}\)), WSR, or WSS, \(\phi _{N}\) is the corresponding value obtained using the Newtonian approximation, \(\phi _{n\text {-}N}\) is the corresponding value obtained from the non-Newtonian simulations, \(A_{i}\) are the areas for face-area weighting (e.g., see Fortuny et al. 17), and i sums over all faces in the infrarenal region of each IVC. Mean values of \(\phi\) were also calculated using face-area weighting:

$$\begin{aligned} \bar{\phi }=\frac{\sum _{i=1}^{n}\phi _{i}\, A_{i}}{\sum _{i=1}^{n}A_{i}}. \end{aligned}$$
(9)

The %SD quantifies the variability of the non-Newtonian values and, thereby, the importance of non-Newtonian effects (i.e., the larger the spread in WSR and \(\mu _{\rm{wall}}\), the greater the importance of considering hemorheological effects), while the %ME quantifies the bias in the Newtonian approximation (i.e., whether the Newtonian approximation under-predicts or over-predicts values, on average). Mean error values normalized by the field means are reported rather than the average of percent error values calculated on a per cell basis due to the occurrence of some values of \(\phi\) close to zero (e.g., in stagnation regions), which would result in percent error values approaching positive or negative infinity. That is, we normalize the mean errors by the mean field values to accommodate zero-valued regions that would otherwise be problematic.

The importance of non-Newtonian effects was also characterized using the non-Newtonian importance factor proposed by Ballyk et al.,3 which is the ratio of the characteristic viscosity to the asymptotic viscosity (\(\mu _{c}/\mu _{\infty }\)). According to Ballyk et al.,3 for values of \(\mu _{c}/\mu _{\infty }\) > 1.75, non-Newtonian effects are significant.

Quantifying Geometric Effects

The geometric tortuosity of the each infrarenal IVC was quantified using the non-dimensional tortuosity index7 (\(\tau\)):

$$\begin{aligned} \tau =\frac{L}{L_{0}} \end{aligned}$$
(10)

where \(L_{0}\) is the shortest distance between two points lying at the ends of a section of a vessel and L is the distance between the two endpoints following the centerline of the vessel lumen. Tortuosity was calculated for the infrarenal region of each IVC by extracting the infrarenal centerlines in Avizo (VSG Inc., Burlington, MA, USA) using the skeletalization tool. The tortuosity indices are 1, 1.01, and 1.05 for the straight-tube, patient-averaged, and scaled patient-specific IVCs, respectively.

The Dean number (De) was also calculated for the infrarenal regions of the IVCs to quantify the effect of infrarenal curvature on IVC hemodynamics. The Dean number is a dimensionless parameter that characterizes the strength of counter-rotating vortices (i.e., Dean flow) in curved pipes and is a function of geometry and Reynolds number:

$$\begin{aligned} De=Re\left( \frac{D}{2R}\right) ^{1/2} \end{aligned}$$
(11)

where D is the (hydraulic) diameter of the pipe and R is the radius of curvature of the pipe along the flow direction. The presence of Dean vortices in the IVCs was confirmed by visualizing velocity vectors and contours on slices perpendicular to the direction of the bulk flow.

The influence of geometric complexity on IVC hemodynamics was also evaluated by comparing shear rate histograms, velocity, shear rate, and shear stress profiles, non-Newtonian importance factors, and Newtonian approximation errors among the three IVCs.

Numerical Methods

Blood flow was simulated using the finite volume method to solve the laminar, incompressible Navier-Stokes equations in OpenFOAM (version 2.3.x, OpenCFD, Ltd). Hexahedral-dominant volume meshes of the IVCs were created before and after filter and thrombus placement. Meshes were generated with the same spatial resolution as the patient-specific IVC meshes in a previous study,1 yielding meshes containing approximately 8 million to 13 million computational cells. Wall normal layers were added on the surfaces of the IVC, the filter, and the thrombus to improve the accuracy of near-wall velocity gradient calculations. A mesh refinement study was performed previously in a patient-specific IVC at a higher Reynolds number than considered in the current study, which yielded a grid convergence index of approximately 6%.1

Simulations were performed in each IVC considering three occlusion scenarios (unoccluded, partially occluded by an IVC filter, and partially occluded by an IVC filter and thrombus) and three different viscosity models (27 CFD simulations, total). Newtonian simulations were performed using asymptotic and characteristic viscosities (\(\mu _{\infty }\) and \(\mu _{c}\)), and non-Newtonian simulations were performed using the Carreau model. Blood was modeled with a constant density of ρ = 1060 kg m−3. Boundary conditions were specified as in Aycock et al.1 Specifically, a zero-pressure Dirichlet boundary condition was specified at the outlet and the gradient of the pressure was fixed at zero at the inlets (Neumann boundary condition). Steady flow rates were specified at the inlets, consistent with in vivo magnetic resonance imaging measurements of normal resting flow in the IVC:9 0.6 LPM inflow for each iliac vein and 0.4 LPM inflow for each renal vein.9 For the straight-tube IVC, a steady flow rate of 1.2 LPM was specified at the inlet, representative of the combined flow from the left and right iliac veins. Fully-developed Newtonian or non-Newtonian flow was specified at all inlets by extruding the inlets beyond their entry lengths and computing the fully developed flow that was then prescribed to each respective inlet.

The CFD results were post-processed to obtain velocity, viscosity, shear rate, and shear stress information. Thrombus wake volumes were also quantified by integrating the volume of the flow in the vicinity of the thrombus where the velocity magnitude was less than 1 cm s−1, similar to the stasis or stagnation volume definitions used in previous hemodynamic studies.18,25 The elapsed computational time (or “wall clock” time) required for convergence (defined as a reduction of the residuals to less than \(10^{-6}\) and \(10^{-9}\) for pressure and velocity, respectively) was recorded to compare the computational cost of the Newtonian vs. the non-Newtonian simulations.

Results

Unoccluded IVCs

Hemorheological Comparison

More than 99% of the internal shear rates in the infrarenal region of the IVCs are found to lie in the nonlinear region (i.e., less than 100 s−1) of the shear rate–viscosity curve for blood (Fig. 3). The Newtonian simulations performed using the asymptotic viscosity for blood over-predict the non-Newtonian Reynolds numbers by more than a factor of two (Table 2). The Newtonian and non-Newtonian Reynolds numbers are much closer when the characteristic viscosity is used in the Newtonian simulations (Table 2). Non-Newtonian importance factors (\(\mu _{c}/\mu _{\infty }\)) are also higher than the threshold of 1.75 suggested by Ballyk et al.3 for all IVCs (Table 2).

Figure 3
figure 3

Internal and wall shear rate histograms from the non-Newtonian simulation results (bars), non-Newtonian shear rate–viscosity curve for blood (blue), and cumulative shear rate (red) for the (a) straight tube, (b) patient-averaged, and (c) scaled patient-specific IVCs. The cumulative shear rates annotated at the location \(\dot{\gamma }=100~{\rm s}^{-1}\) quantify how much of the IVC volume or wall surface area lies in the nonlinear region of the shear rate–viscosity curve for blood (\(\dot{\gamma }<100~{\rm s}^{-1}\)).

Full size image
Table 2 Average shear rate calculated using the Poiseuille approximation (\(\dot{\gamma _{p}}\); Eq. 1), characteristic shear rate calculated using a volume-weighted average of the asymptotic Newtonian simulation results (\(\dot{\gamma }_{c}\); Eq. 2), characteristic shear rate calculated using a volume-weighted average of the non-Newtonian simulation results (\(\dot{\gamma }_{c,n\text {-}N}\)), characteristic viscosity (\(\mu _{c}\)), non-Newtonian importance factor (\(\mu _{c}/\mu _{\infty }\)), and Reynolds numbers in the infrarenal region of the IVCs.
Full size table

Use of a characteristic viscosity improves the prediction of velocity, viscosity, shear rate, and shear stress profiles (Fig. 4). When using the asymptotic viscosity, velocity profiles are less smooth and have an increased number of inflection points compared with the characteristic viscosity and non-Newtonian results (Fig. 4). The mean non-Newtonian WSS is under-predicted when using the asymptotic viscosity (%ME of −29% to −54%), and slightly over-predicted when using the characteristic viscosity (%ME of 5−11%; Table 3).

Figure 4
figure 4

Velocity, viscosity, shear rate, and shear stress profiles along lines identified in the left-most images for the unoccluded (a) straight-tube, (b) patient-averaged, and (c) scaled patient-specific IVCs. The radius is normalized by the maximum radius (\(R\approx\) 1 cm).

Full size image
Table 3 Average flow parameters and Newtonian approximation errors for flow through the infrarenal region of the straight-tube, patient-averaged, and scaled patient-specific IVCs unoccluded, with an IVC filter, and with an IVC filter and a thrombus.
Full size table

Secondary flows are also better predicted using the characteristic viscosity compared with the asymptotic viscosity (Figs. 5 and 6). Secondary flow velocities are larger when using the asymptotic viscosity compared with the characteristic viscosity or non-Newtonian model (Fig. 5c). Additionally, the asymptotic Newtonian viscosity simulations reveal regions of swirling flow (e.g., Fig. 6a) and different streamline trajectories than those predicted by the characteristic Newtonian viscosity or non-Newtonian simulations (e.g., Figs. 6b, 6c).

Figure 5
figure 5

Secondary flow in the (a) patient-averaged and (b) scaled patient-specific IVC geometries. (c) Enlarged view of the middle cross-sections from (a) and (b) showing the effect of the viscosity model on the secondary flow patterns.

Full size image
Figure 6
figure 6

Streamlines in the scaled patient-specific IVC for the three viscosity models considered. The streamlines are seeded from three different locations (x,y,z coordinates, in cm) in the (a) anatomical right and (b,c) anatomical left iliac veins.

Full size image

Effect of IVC Morphology on Hemodynamics

The range of observed internal and wall shear rates is smallest in the straight-tube IVC (Fig. 3a), larger in the patient-averaged IVC (Fig. 3b), and largest in the patient-specific IVC (Fig. 3c; see also %SD in Table 3). Mean WSR and WSS also increase with increasing morphological complexity of the IVC (Table 3).

Mean shear rates calculated using the Poiseuille flow assumption (Eq. 1) are approximately 17 s−1 for each infrarenal IVC (Table 2). However, using the cell-volume weighted approach proposed in this study (Eq. 2), the mean shear rate is approximately 40% higher in the patient-specific IVC (24 s−1) than in the straight-tube or patient-averaged IVCs (17.0 and 17.1 s−1, respectively; Table 2). Thus, the characteristic viscosity is approximately 10% lower in the patient-specific IVC (Table 2). Furthermore, the non-Newtonian importance factor decreases slightly with increasing geometric complexity (Table 2) due to the attendant increase in the average shear rate.

Using the characteristic viscosity, WSS errors are approximately the same for all IVC geometries (%ME of 5–11%; Table 3). When using the asymptotic viscosity, WSS errors are larger than when using the characteristic viscosity, but decrease in magnitude with increasing geometric complexity (from a %ME of −54 to −29%; Table 3).

Increasing geometric complexity of the IVC is also associated with an increase in secondary flow velocities (Dean numbers from the non-Newtonian simulations are 0, 27, and 75 for the straight-tube, patient-averaged, and patient specific IVCs, respectively; see Figs. 5a vs. 5b). Dean vortices are symmetric in the patient-averaged IVC (Fig. 5a), but are stronger (i.e., higher secondary flow velocities) in the anatomical left side of the patient-specific IVC (Fig. 5b).

Partially Occluded IVCs

Hemorheological Comparison

Partial occlusion of the IVC increases the characteristic shear rate (making it higher than the average shear rate predicted by the Poiseuille approximation; Table 2), thus decreasing the characteristic viscosity and increasing the Reynolds number slightly (Table 2). The non-Newtonian importance factors also decrease slightly with increasing occlusion (Table 2), but are still above the threshold of 1.75 specified by Ballyk et al.3

As in the unoccluded IVC, mean IVC WSS is again predicted more accurately using the characteristic viscosity than using the asymptotic viscosity (%ME of 8−13% vs. %ME of −28% to −50%, respectively; Table 3). Mean WSR and WSS increase with partial occlusion of the IVC by the IVC filter, and further increase with partial occlusion of the IVC by the thrombus (Table 3). As the mean WSR and WSS increase, the mean error in WSS decreases slightly using the asymptotic viscosity, but increases slightly using the characteristic viscosity (Table 3).

Thrombus WSR values reach well over 100  s−1 in the region of maximum occlusion (\(x=-23\) mm to \(-20\) mm; Figs. 7a*–7c*). In contrast to the previous results, in the region of maximum occlusion, the non-Newtonian WSS on the thrombus is predicted more closely using the asymptotic viscosity than using the characteristic viscosity (Figs. 7a*–7c*) due to the higher thrombus WSR and lower viscosity in this region. In general, the mean thrombus WSS is under-predicted relative to the non-Newtonian results when using the asymptotic viscosity (by as much as 80%) and over-predicted when using the characteristic viscosity (by as much as 50%; Fig. 7a).

The non-Newtonian thrombus wake volumes range from 13% to 15% of the thrombus volume (Table 4) and are predicted more accurately using the characteristic viscosity than using the asymptotic viscosity in the Newtonian simulations (Table 4; Fig. 8).

Table 4 Wake volumes normalized by the thrombus volume (1.06 cm3) for the Newtonian and non-Newtonian simulations in the IVCs partially occluded by the filter and thrombus.
Full size table
Figure 7
figure 7

Distribution of the circumferential averages of thrombus wall viscosity, thrombus WSR, thrombus WSS, and normalized thrombus WSS vs. axial position (x) along the thrombus in the (a) straight-tube, (b) patient-averaged, and (c) scaled patient-specific IVCs. The location \(x=0\) mm is approximately 2 cm upstream of where the renal veins meet the IVC and corresponds to the bottom surface of the IVC filter hub.

Full size image

Effect of IVC Morphology on Hemodynamics

The trends noted for the unoccluded IVCs are present again in the partially occluded IVCs: mean IVC WSR and WSS increase with increasing morphological complexity of the IVC, and IVC WSS errors decrease with increasing morphological complexity of the IVC when using the asymptotic viscosity (although the WSS errors are still much larger when using the asymptotic viscosity compared with the characteristic viscosity; Table 3). However, the peak thrombus WSR and thrombus WSS decrease with increasing geometric complexity of the IVCs (Figs. 7a*–7c*).

Additionally, while the flow is approximately symmetric in the straight tube and patient-averaged IVCs (Figs. 8a–8b), the flow around the model thrombus is biased toward the anterior side in the scaled patient-specific IVC (Fig. 8c).

Figure 8
figure 8

Contours of velocity magnitude on a sagittal plane in the IVCs partially occluded by an IVC filter and thrombus. The flow is approximately symmetric in (a) the straight-tube and (b) the patient-averaged IVCs, but the flow velocity is higher along the anterior side of (c) the scaled patient-specific IVC (arrows).

Full size image

Computational Cost of Newtonian vs. Non-Newtonian Simulations

Using the same number of CPUs (96) for all simulations, elapsed computational times are lowest using the characteristic viscosity, higher using the asymptotic viscosity, and highest using the non-Newtonian viscosity model (Table 5). At most, the non-Newtonian simulations require approximately 24% more computational time than the individual Newtonian simulations (Table 5). Compared to the sum of the computational time for the asymptotic and characteristic Newtonian simulations required in the two-step process for obtaining an improved characteristic viscosity (see “Characteristic Shear Rate and Viscosity”), the non-Newtonian simulations require approximately 50% less time (Table 5).

Table 5 Elapsed computational times (or wall clock times) in hours using 96 CPUs for the Newtonian (\(t_{N}\)) and non-Newtonian (\(t_{n\text {-}N}\)) simulations performed using the scaled patient-specific IVC geometry.
Full size table

Discussion

In contrast to a previous study on IVC hemodynamics,45 we found that non-Newtonian effects are strong in the IVC: mean errors in WSS in the infrarenal region of the IVC are approximately −50 to −30% when using the asymptotic viscosity for blood whereas Swaminathan et al.45 reported errors in WSS to be less than 10% using the same asymptotic viscosity. This discrepancy may be due to the higher flow rate and Reynolds number investigated in the previous study (approximately 2.31 LPM and 1000 in Swaminathan et al. 45 vs. 1.2 LPM and 225–250 here, respectively). Additionally, in the current study, over 99% of the internal shear rates in the infrarenal IVC are less than 100 s−1 (Fig. 3), non-Newtonian importance factors are above the threshold suggested by Ballyk et al.3 of 1.75 (Table 2), and secondary flows are sensitive to the viscosity model (Figs. 5 and 6), collectively indicating that non-Newtonian effects are important during resting flow conditions in the IVC.

Previous studies of pulsatile blood flow have also suggested that non-Newtonian effects are generally negligible in large blood vessels like the IVC.3,26,30 The discrepancy between those studies and the results reported herein may be explained by the differences in shear rates, which are well over 100 s−1 in most large blood vessels during systole (Fig. 1) but much less than 100 s−1 in the IVC (an average of approximately 17 to 24 s−1 based on our analysis; Table 2). Previous studies have shown that non-Newtonian effects can be significant in large arteries,3,26,30 but the effects are isolated to the diastolic phase of the cardiac cycle, when the shear rates are low. Furthermore, Ballyk et al.3 reported that non-Newtonian effects are more significant when simulating steady flow than when simulating a pulsatile flow with the same mean flow rate. Because of the damping effect of vascular compliance and the associated relatively steady flow rate in the IVC (Fig. 1c), the shear rates in the IVC are comparable to the shear rates observed in arteries during diastole. Thus, while non-Newtonian effects may be neglected in most arterial flows, where the high stresses that occur during systole are of primary interest (e.g., for predicting atherosclerosis), non-Newtonian effects are significant in the IVC throughout the entire cardiac cycle.

As shown in previous studies,2,8,21,30 the use of a characteristic viscosity improves the accuracy of the Newtonian approximation for predicting the non-Newtonian WSS (%ME of 5–13%) and Reynolds numbers (Table 2) compared with the use of the asymptotic viscosity. Because the characteristic viscosities in the current study are much higher than the Newtonian viscosities used in previous studies (5.27–5.85 cP here vs. 2.57–4 cP38,39,43,50), the Reynolds numbers in the current study are the lowest reported for resting flow in the infrarenal IVC (approximately 225–250 here vs. 320–370 in the literature38,39,43,50). Consequently, the previously published studies contain greater flow disturbances (e.g., wakes) due to the IVC filter and are probably more representative of the hemodynamics that occur in the IVC under elevated flow conditions (e.g., light exercise).

However, when considering partial occlusion of the IVC, local errors in thrombus WSS are large in the high-shear region of maximum IVC occlusion (up to approximately 50%; Figs. 7a*–7c*) even when using a characteristic viscosity in the Newtonian simulations. The thrombus WSS errors are lower when using the asymptotic viscosity in the high-shear regions (Figs. 7a*–7c*). But, as the shear rate decreases downstream of the site of maximum thrombus diameter, the thrombus WSS is again predicted more accurately using the characteristic viscosity (Fig. 7). Additionally, the volume of the low-shear wake region downstream of the thrombus is predicted more accurately using the characteristic viscosity (Table 4). Indeed, when considering partial occlusion of the IVC, a single viscosity cannot simultaneously predict the flow in the region of the occlusion, where shear rates are high and the viscosity is relatively low (Figs. 7a*–7c*), and in the regions upstream and downstream of the occlusion, where the shear rates are low and the viscosity is relatively high (Fig. 7). Thus, use of a non-Newtonian model is preferable if accurate predictions of thrombus WSS are required—e.g., for predicting thrombolysis, thrombosis, and embolization,4 all of which are mediated by fluid stresses either directly (e.g., mechanical lysis43), indirectly (e.g., platelet activation leading to thrombus growth34), or both.

The added computational cost of using a non-Newtonian model was found to be relatively low (at most 24% more expensive; Table 5). Furthermore, the computational cost of performing a single non-Newtonian simulation is approximately 50% of the time required to perform two Newtonian simulations to better approximate the non-Newtonian characteristic viscosity (Table 5) using the approach presented herein. Other recent studies29,32,48 have also shown that non-Newtonian simulations can be performed with approximately the same computational cost as Newtonian simulations, or even less. Collectively, these results challenge the notion (e.g., see discussion in Benard et al.,5 Mejia et al.,33 Vahidi and Fatouraee,49 and Marrero et al. 32) that added computational cost is a strong justification for neglecting non-Newtonian effects.

The inherent simplicity (e.g., Surovtsova44) and stability (e.g., Vahidi and Fatouraee 49) of the Newtonian model are also sometimes provided as justification for neglecting non-Newtonian effects, but we found that the non-Newtonian Carreau model was no more challenging to use and was just as numerically stable as the Newtonian model. Thus, the strongest justification for neglecting non-Newtonian effects in CFD simulations of blood flow is the prevalence of high shear rates (e.g., Torii et al. 47 and Clark et al. 14) in the flow field of interest. However, even then, one must ensure that regions of low shear rate are not simultaneously present, where non-Newtonian effects could affect the solution.

In addition to hemorheology, our results show that IVC morphology has a strong influence on IVC hemodynamics. Specifically, as IVC complexity increases, the range of shear rates present in the IVC also increases (Fig. 3) and the flow patterns in the IVC become increasingly complex (Fig. 4). Furthermore, in the patient-averaged and patient-specific IVCs, Dean vortices develop in the infrarenal IVC due to the curvature of the IVC along the lumbar spine (Fig. 5), introducing swirl into the flow and altering the fluid streamlines (e.g., Fig. 6). We suspect that, as shown in a recent study on arterial emboli,35 patient-specific secondary flow features may affect the trajectory of migrating emboli in the IVC and possibly influence the embolus-trapping efficiency of IVC filters.

Some limitations should be noted. Only one non-Newtonian model (Carreau) and one set of model constants were considered. Furthermore, the asymptotic viscosity of blood is approximately 3.5 cP for a nominal hematocrit of 45%,12,37 while a value of 2.57 cP was used in the current study, which was based on the curve fit of Swaminathan et al.45 to the experimental data of Chien.11 Blood viscosity and shear-thinning behavior are patient-specific and increase with increasing blood hematocrit;12 therefore, a wide range of model constants should be studied. However, the purpose of this study was to investigate representative physiological conditions, and to determine if, in general, non-Newtonian effects are important in the human IVC. We chose to use the same model and model constants as those in Swaminathan et al.45 to permit a direct comparison with that study, which is often cited as justification for neglecting non-Newtonian effects in the human IVC. We expect that the use of different model constants and a higher asymptotic viscosity (e.g., 3.5 cP) would affect the quantitative comparison of the Newtonian and non-Newtonian results, but would not change the overall results and conclusions of this study, namely that non-Newtonian effects are significant in the human IVC and should be considered in future studies of IVC hemodynamics.

Additionally, IVC hemodynamics were investigated in only one patient-specific IVC using an idealized thrombus model and average boundary conditions rather than patient-specific measurements. Other patient geometries would have different levels of infrarenal curvature, iliac vein compression,36 and cross-sectional variation. However, the patient-specific IVC in the current study is representative of a normal, healthy patient. Furthermore, the results of this study demonstrate that subtle differences in IVC morphology can influence IVC filter placement mechanics (e.g., contact forces; Table 1) and IVC hemodynamics (e.g., secondary flow; Figs. 5 and 6), thus motivating the need for further investigation of the influence of patient-specific IVC morphology on IVC filter performance. These results also motivate future fluid-structure interaction studies to quantify the effect of wall motion on IVC mechanics and hemodynamics. Finally, although beyond the scope of the present study, validation studies should be performed in future work to compare results from the computational model to results from in vitro models and, eventually, to state-of-the-art in vivo measurements of IVC mechanics and hemodynamics.

Summary

  1. (1)

    Shear rates are low in the IVC geometries considered, with over 99% of the infrarenal IVC volume in the highly nonlinear region of the shear rate–viscosity curve. Furthermore, non-Newtonian importance factors are above the threshold specified by Ballyk et al.3 in all cases, indicating that non-Newtonian effects are important in the IVC.

  2. (2)

    The Newtonian simulations performed using an asymptotic viscosity greatly under-predict the non-Newtonian WSS (%ME of -28% to -54%). Simulations performed using the characteristic viscosity predict the non-Newtonian WSS more closely (%ME of 5–13%), but cannot accurately model the hemodynamics for the full range of shear rates that occur, especially in the presence of the high shear rates generated during partial occlusion of the IVC.

  3. (3)

    Non-Newtonian simulations required only a marginal increase in computational time (15–24% longer wall clock time) compared with the Newtonian simulations. Therefore, we recommend that future studies of blood flow in the IVC consider non-Newtonian effects, especially when accurate predictions of both low (<100 s−1) and high (>100 s−1) shear rate phenomenon are required.

  4. (4)

    Infrarenal IVC flow patterns become increasingly complex with increasing anatomical complexity of the IVC. Secondary flow features are also sensitive to the viscosity model and are more prominent in the Newtonian simulations performed using the asymptotic viscosity due to the associated higher Reynolds number. We anticipate that these secondary flow patterns may influence embolus trajectories and IVC filter embolus-trapping efficiencies. Thus, future studies should also recognize the potential limitations of using an idealized IVC model to predict IVC filter performance.