Length and stiffness effects of the attached flexible plate on the flow over a traveling wavy foil

Abstract

Flow over a traveling wavy foil attached with a flexible plate has been numerically investigated using the lattice Boltzmann method combined with the immersed boundary method. The influence of the flexibility and length of the caudal fin on the locomotion of swimming fish through this simplified model, whereas the fish body is modeled by the undulating foil and the caudal fin by the plate passively flapping as a consequence of fluid-structure interaction. It is found that the plate flexibility denoted by the bending stiffness, as well as the length ratio of tail and body, plays an important role in improving thrust generation and propulsive efficiency. It is also revealed that there exists a parameter region of the plate length and stiffness, in which positive propeller efficiency can be achieved. The effect of the passively flapping flexible plate on the pressure field and the vortex production on the wake is further discussed. It is found that when the length ratio of caudal fin and body is greater than 0.2, a reverse von Kármán vortex street occurs when the bending stiffness is about greater than 1.0, and a great thrust is generated as a result of a large pressure difference occurring across the flexible plate. This work provides physical insight into the role of the caudal fin in fish swimming and may inspire the design of robotic fish.

Graphic abstract

1 Introduction

Aquatic animals have evolved multiple propulsion mechanisms to move efficiently in the water [1, 2], they generate hydrodynamic thrust through the movements of their bodies and appendages. Changing the locomotion mode has a marked effect on drag reduction, thrust production, and propulsive efficiency. Gray et al. [3] observed that dolphin swimming consumes only one-seventh of the power required to drag a rigid dolphin model at the same speed. Barrett et al. [4] found that the power needed to push a swimming body may be less than that of pulling a straight rigid body. The above work indicates that there exists a special drag reduction mechanism in fish swimming. Fish swimming can be divided into two basic patterns: body and/or caudal fin (BCF) and median and /or paired fins (MPF) modes according to the mode of locomotion [5]. In statistics, 85 percent of the fish in the world use BCF as their main mode of locomotion, fish swing their bodies and caudal fins that interact with the surrounding fluids to push themselves forward [6]. Therefore, it is particularly important to investigate the role of the fish body and caudal fin in the swimming process.

The mechanisms of force generation have been extensively investigated through the dynamic analysis of the flow around the body [1, 7, 8]. The undulating and pitching foils have been adopted to model the fish body in previous work, both of them can produce oscillating lift and thrust [9,10,11]. Fish swimming is commonly associate with evident bending of the flexible body in nature, the oscillatory motion of the body can not be ignored [12, 13]. In that, the rigid pitching foil is insufficient to reflect the locomotion characteristics of the fish. Typically, the fish-like undulating foil is generally adopted as a primary model to study fish swimming [14,15,16], where the body and tail are often treated integrally as a single undulating foil [17,18,19].

It has been indicated by previous studies, although relatively few, that the coupling between body movement and caudal fin flapping intriguingly affects the vortex shedding in the wake and further influences the propulsion performance. Liu et al. [20, 21] adopted a rigid plate attached to a wave-like swimming motion airfoil with a torsional spring to model the caudal fin. These researches found that both the joint flexibility and the length of the caudal fin affect the fish locomotion remarkably. Promode et al. [22] investigated the motion of a pair of flapping foils attached behind a rigid cylinder by experiments and found that the foils greatly influence the drag force acting on the cylinder. Yeh and Alexeev [23] found that the flexible plate actuators obtain a larger moving speed and a higher propulsive efficiency with a passive attachment. Eldredge et al. [24] used a model composed of two rigid elliptical sections joined by a torsion spring and demonstrated that passive deflection contributes to drag reduction. However, in the above studies, the caudal fin is modeled to be rigid thus could not be deformed by the fluid-structure interaction.

In reality, the caudal fin is flexible and deformable, which is not supposed to be seen as an extension of the body simply [2, 25]. It has been illustrated that the true caudal fin can significantly improve the flapping-based fish locomotion [16, 26,27,28,29,30,31]. Kinematic studies showed that the tail of fish may undergo complex deformations independent of the body [32, 33], the instantaneous shape of the caudal fin can greatly influence the surrounding fluid flows [27, 29, 31, 34,35,36]. Heathcote and Gursul [37] demonstrated changing the flexibility of the attached aluminum plate can remarkably improve the thrust and the propulsion efficiency of the pitching airfoil upstream. David et al. found the pitching foil attached with a flexible foil has greater thrust than that with a rigid foil by experiment [38]. Therefore, the caudal fin flexibility greatly affects the locomotion of fish. However, the coupled effect of the fish body and the flexible caudal fin has not received enough research attention, and numerical studies on such coupled effects are highly desirable to obtain physical insight into fish swimming.

According to our previous work [20, 21], two-dimensional studies utilizing an undulating foil are indicative as they bring insight into the hydrodynamic forces and the detailed wake flow structures modulated by the caudal fin. The swimming fish body is modeled by a wavy foil undergoing a specified undulation, and a passively flapping flexible plate models the caudal fin. We will illustrate the impact of the caudal fin on swimming performance in thrust force generation and propulsion efficiency improvement. Our main objective is to investigate the combined effect of the plate’s length and stiffness on the propulsion performance through this simplified model, thus understanding some typical basic phenomena, like why different fish have caudal fins with varying combinations of length and stiffness.

The rest of the article is structured as follows. Section 2 introduces the calculation model and governing equation. Section 3 presents the numerical methods and validations. Section 4 discusses the typical results. Finally, Sect. 5 gives the conclusions and the outlook.

2 Problem definition and governing equations

Fig. 1

Wavy foil body with a flexible plate

Viscous flow over a traveling wavy foil attached with a passively flapping flexible plate is considered to study the coupled effects of the body and caudal fin, which is shown in Fig. 1. The Reynolds number Re is defined as $Re=\frac{U_{\infty } L}{v}$, $U_\infty$ is the free-stream velocity, L is the length of the wavy foil, v is the kinematic viscosity. The non-dimensional governing equations are given as

$$\begin{aligned}&\nabla \cdot \varvec{u}=0, \end{aligned}$$

(1)

$$\begin{aligned}&\begin{array}{c} \frac{\partial \varvec{u}}{\partial t}+ \varvec{u}\cdot \nabla \varvec{u} = -\frac{1}{\rho }\nabla p + \frac{1}{Re} \nabla ^{2} \varvec{u}, \end{array} \end{aligned}$$

(2)

where $\varvec{u}$ is the flow velocity, $\rho$ is the fluid density, p is the pressure. The above governing equations are solved with the boundary conditions supplemented as $\varvec{u}=(U_\infty ,0)$ for the inlet and lateral boundaries of the computational domain, and $\frac{\partial \varvec{u}}{\partial x}=0$ for the outlet boundary.

As shown in Fig. 1, The profile of undulating foil at the equilibrium position is described by the NACA0012 airfoil, the starting point of the foil is located at the coordinate origin O(0,0), the midline of the foil oscillates laterally, the motion equation along the midline is described by [39,40,41]:

$$\begin{aligned} y(x,t)=A_m(x) \mathrm{cos}[2 {\uppi } L(x-ct)/\lambda ] ,\quad \quad 0 \le x \le 1, \end{aligned}$$

(3)

where c is the phase speed, $A_m(x)$ is the amplitude of the midline, which is estimated as a quadratic polynomial in order to reasonably simulate the lateral fluctuation of fish swimming [42], the quadratic polynomial is

$$\begin{aligned} A_m(x)=C_0+C_1x+C_2x^2, \end{aligned}$$

(4)

where the coefficients $C_0$, $C_1$ and $C_2$ are solved from the kinematic data of the stabile fish swimming [43], which makes $A_m(0)=0.02$, $A_m(0.2)=0.01$, and $A_m(1)=0.10$. We assume that the body length keeps unchanged and fix $\frac{L}{\lambda }=1$, Eq. (3) is simplified as

$$\begin{aligned} y(x,t)=A_m(x)\mathrm{cos}[2 {\uppi } (x-ct)] ,\quad \quad 0 \le x \le 1. \end{aligned}$$

(5)

The flexible plate extends out along the tangential direction of the midline from the joint P, therefore, it flaps passively with the traveling wavy foil. The motion of the plate is forced to keep consistent with the foil at the joint point P, while another end Q is free. The flexible plate deforms passively due to the fluid-plate interaction. The length of the flexible plate is set as l. The governing equation of the flexible plate is given as

$$\begin{aligned}&\rho _{s} h \frac{\partial ^{2} \varvec{X}}{\partial t^{2}}-E h \frac{\partial }{\partial s}\left\{ \left[ 1-\left( \frac{\partial \varvec{X}}{\partial s} \cdot \frac{\partial \varvec{X}}{\partial s}\right) ^{-1 / 2}\right] \frac{\partial \varvec{X}}{\partial s}\right\} \nonumber \\&\quad +E I \frac{\partial ^{4} \varvec{X}}{\partial s^{4}}=\varvec{F}, \end{aligned}$$

(6)

where s is the Lagrangian coordinate along the surface, ${\rho }_s$ is the mass density of the plate, $\varvec{X}=(X(s,t),Y(s,t))$ is the plate position, Eh and EI respectively denote the structural stretching stiffness and bending stiffness. $\varvec{F}$ is the Lagrangian forcing exerted on the flexible plate by the surrounding fluids. At the joint P (s=0), the boundary condition used is

$$\begin{aligned} Y(t)=y(L,t), \quad \frac{{\partial } \varvec{X}}{\partial s}=(1,0). \end{aligned}$$

(7)

At the free end Q (s=l), we have

$$\begin{aligned} -E h\left( 1-\left| \frac{\partial \varvec{X}}{\partial s}\right| ^{-1}\right) \frac{\partial \varvec{X}}{\partial s}\!+\! E I \frac{\partial ^{3} \varvec{X}}{\partial ^{3} \varvec{s}}\!=\!0, \quad \frac{\partial ^{2} \varvec{X}}{\partial s^{2}}=0.\qquad \end{aligned}$$

(8)

The dimensionless stretching stiffness is defined as $K_S=E h / (\rho c^{2} l^3)$, and the dimensionless bending stiffness is $K_B=E I / (\rho c^{2} l^{5})$, the mass ratio of the flexible plate and the fluid is $M ={\rho }_s h/(\rho L)$, where h is the thickness of the flexible plate. The caudal fins of most fish in nature are around 0.1 to 0.3 times the length of their body. For example, the length ratio of the caudal fins to the body is around 0.11 for sandfish, 0.13 for sablefish, 0.15 for herring, 0.25 for bonefish, ladyfish, carp, and lanternfish, 0.3 for milkfish [44]. Therefore, the length of the flexible plate is varied from 0.1 to 0.3, to investigate the impact on the hydrodynamics and swimming propulsive performance. The flexible plate is considered to be very thin ($h \ll l$) and have a mass ratio of $M=0.2$, and to be unstretchable and approximated as $K_S=1000$, the bending stiffness $K_B$ range of the plate is chosen as 0.01–250 based on previous studies on fish swimming [26, 45,46,47].

3 Numerical method

In this study, the lattice Boltzmann method is applied to solve fluid equations, the governing equation of the plate is solved by the finite element method. The immersed boundary method is applied to couple the two solvers to deal with the flow over a moving deformable body.

3.1 The lattice Boltzmann method

Benefit from the parallel simplicity and high computational efficiency, the lattice Boltzmann equation (LBE) has been extensively used as an alternative to solve the Navier-Stokes equations to simulate complex flows [48,49,50]. The LBE using the Bhatnagar-Gross-Krook model is

$$\begin{aligned}&f_{i}\left( \varvec{x}+\varvec{e}_{i} {\Delta } t, t+\mathrm{\Delta } t\right) -f_{i}(\varvec{x}, t)\nonumber \\&\quad =-\frac{1}{\tau }\left[ f_{i}(\varvec{x}, t)-f_{i}^{e q}(\varvec{x}, t)\right] +{\Delta } t F_{i}, \end{aligned}$$

(9)

where $f_{i}(\varvec{x},t)$ is the particle distribution function, $\tau$ is the relaxation time, and $\varvec{e}_i$ is discrete speed. The equilibrium distribution function $f_i^{eq}$ is defined as

$$\begin{aligned} f_{i}^{e q}=\omega _{i} \rho \left[ 1+\frac{\varvec{e_{i}} \cdot \varvec{u}}{c_{s}^{2}}+\frac{\varvec{u} \varvec{u}:\left( \varvec{e_{i}} \varvec{e_{i}} -c_{s}^{2} I\right) }{2 c_{s}^{4}}\right] , \end{aligned}$$

(10)

the forcing term $F_i$ that corresponds to $\varvec{f}$ is

$$\begin{aligned} F_{i}=\left( 1-\frac{1}{2 \tau }\right) \omega _{i}\left( \frac{\varvec{e_{i}} -\varvec{u}}{c_{s}^{2}}+\frac{\varvec{e_{i}} \cdot \varvec{u}}{c_{s}^{4}} \varvec{e_{i}}\right) \cdot \varvec{f}, \end{aligned}$$

(11)

where $c_s$ is the speed of sound and $\omega _{i}$ is the weighting factor. The velocity $\varvec{u}$ and mass density $\rho$ can be obtained via

$$\begin{aligned}&\rho =\sum _{i} f_{i}, \end{aligned}$$

(12)

$$\begin{aligned}&\rho \varvec{u}=\sum _{i} \varvec{e}_{i} f_{i}+\frac{1}{2} \varvec{f} {\Delta } t. \end{aligned}$$

(13)

Fig. 2

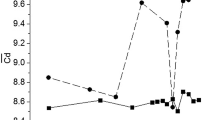
Code validation by time histories of a the trailing-edge of the single flapping plate in the y-direction [53] and b the drag and lift coefficients $C_D$, $C_L$ of the traveling wavy foil attached by a rigid plate of $l=0.1$, the solid lines represent the present results, the symbols represent the previous results [20]

3.2 Immersed boundary method

In the immersed boundary method [51], the body force term $\varvec{f}$ accounts for the interaction force between the fluid and the solid boundary. The boundary of the plate is represented by a series of Lagrange points, the position of the boundary point s is $\varvec{X}(s,t)$ for $0 \le s \le 1$.

The plate velocity is $\varvec{V}_s = \frac{\partial \varvec{X}}{\partial t}$, the fluid velocity $\varvec{V}_f$ at position $\varvec{X}(s,t)$ is interpolated by the velocity of the surrounding fluid point:

$$\begin{aligned} \varvec{V}_{f}(s, t)=\int \varvec{u}(x, t) \mathrm{\delta }[\varvec{x}-\varvec{X}(s, t)] \mathrm{d} \varvec{x}. \end{aligned}$$

(14)

The Lagrangian interaction force F between the fluid and the immersed boundary in Eq. (6) can be calculated by penalty method [51]:

$$\begin{aligned} \begin{aligned} \varvec{F}(s, t)&= \alpha \int _{0}^{t}\left[ \varvec{V}_{f}\left( s, t^{\prime }\right) -\varvec{V}_{s}\left( s, t^{\prime }\right) \right] \mathrm{d} t^{\prime }\\&\quad +\beta \left[ \varvec{V}_{f}(s, t)-\varvec{V}_{s}(s, t)\right] . \end{aligned} \end{aligned}$$

(15)

Based on the previous studies, the penalty parameters are chosen as $\alpha =1000$ and $\beta =1$ to satisfy the equations:

$$\begin{aligned} \frac{\partial \varvec{u}}{\partial t}+\varvec{u} \cdot \nabla \varvec{u}=-\nabla p+\frac{1}{Re} \nabla ^{2} \varvec{u}+\varvec{f}, \end{aligned}$$

(16)

where the body force $\varvec{f}$ on the Eulerian points can be calculated by the Lagrangian force $\varvec{F}$ via

$$\begin{aligned} \varvec{f}(\varvec{x}, t)=\int _{\varGamma } \varvec{F}(s, t) {\updelta }[\varvec{x}-\varvec{X}(s, t)] \mathrm{d}s. \end{aligned}$$

(17)

The smooth approximation of the two-dimensional Dirac $\delta$ function is:

$$\begin{aligned}&\delta _{h}=\frac{1}{{\Delta } x {\Delta } y} \phi \left( \frac{x}{{\Delta } x}\right) \phi \left( \frac{y}{{\Delta } y}\right) , \end{aligned}$$

(18)

$$\begin{aligned}&\begin{array}{c} \phi (r)=\left\{ \begin{array}{ll} \left( 3-2|r|+\sqrt{1+4|r|-4 r^{2}}\right) / 8, &{} |r|<1, \\ \left( 5-2|r|-\sqrt{-7+12|r|-4 r^{2}}\right) / 8, &{} 1 \leqslant |r|<2, \\ 0, &{} |r| \geqslant 2. \end{array}\right. \end{array}\nonumber \\ \end{aligned}$$

(19)

It is important to note that the wavy foil boundary is prescribed to be an undulating motion rather than being solved from the problem of coupled fluid-structure interaction. The motion of the passively flapping flexible plate is determined by the boundary force F acting by surrounding fluids, the governing equation is solved by the finite element method [52].

Fig. 3

Time histories of a drag coefficient $C_D$ and b lift coefficient $C_L$ of the traveling wavy foil attached by a plate of $l=0.3$ and $K_B$=100 for ${ \Delta } x/L=0.02,0.01$, and 0.005

3.3 Code validation

To validate our code, two typical problems are considered here. The first one is the flow over a single passive flapping flexible plate with a heaving amplitude of 0.01 at the leading edge. The simulation parameters are consistent with Huang et al. [53]. Figure 2a shows the trajectory of the trailing-edge of the single flapping flexible plate, it is seen that our result is consistent with that obtained by Huang et al. [53]. The second one is the flow over a traveling wavy foil attached by a rigid plate of $l=0.1$ and compared them with the previous results [20]. The hydrodynamic forces obtained for $Re=500$ and $c=2.0$ during one cycle plotted in Fig. 2b are compared well with the previous results.

Simulations using different grid sizes of ${\Delta } x/L=0.02,0.01$, and 0.005 were carried out to check the grid independence. The force coefficients that vary with time are shown in Fig. 3. It is seen that a grid size of ${\Delta } x/L=0.01$ is sufficient for the research. Besides, the numerical method has been extensively validated in our previous studies [26, 54].

4 Results and discussion

In this section, some typical results of flow over the traveling wavy foil attached with different passive flexible plates are present, the dynamic behaviors and propulsive performance are analyzed detailedly, along with the effects of flexibility and length of the caudal fin on the propulsion performance. Inspired by the previous studies of animal locomotion [26, 37, 39], Reynolds number $Re=500$ and the phase speed of traveling wave $c=2.0$ are considered here, the length of attached plate are chosen as $l=0.1,0.15,0.2,0.25$, and  0.3, the bending stiffness $K_B$ varies from 0.01 to 250. Based on detailed examinations, the computational domain of the fluid flow is selected as $-5 \le x \le 25$ and $-15 \le y \le 15$, which is large enough so that the boundary effects are trivial.

4.1 Propulsion performance

In this subsection, the combined effects of length and stiffness on propulsive performance are discussed. We examine the drag force exerting on the traveling wavy foil and the attached flexible plate, the propulsion efficiency, and the power consumed, which are closely related to fish swimming. The drag force $F_D$ exerts on the fish is characterized by the corresponding drag coefficient defined as

$$\begin{aligned} C_{D}=\frac{F_{D}}{\frac{1}{2} \rho U_{\infty }^{2} L}. \end{aligned}$$

(20)

The total power needed for the propulsive motion is composed of two parts. The first part is the swimming power required to produce the vertical oscillation, which is defined as

$$\begin{aligned} P_{S}=-\int _{S F} f_{y} \frac{\mathrm{d} y_{w}}{\mathrm{d} t} \mathrm{d} s-\int _{S P} f_{y} \frac{\mathrm{d} y_{w}}{\mathrm{d} t} \mathrm{d} s, \end{aligned}$$

(21)

where SF is the surface of the wavy foil, SP is the surface of the flexible plate, $f_y$ is the lateral force per unit length on the surface, $y_w$ is the displacement in the y-direction along the surface, and ds is the element length on the surface. The second part is the power, $P_{D}=F_{D} U_{\infty }$, required to overcome drag force. The total drag force $F_{D}$ can be obtained by $F_{D}=F_{D F}+F_{D P}$, where $F_{DF}$ and $F_{DP}$ are the drag forces of the traveling wavy foil and the flapping flexible plate, respectively. Therefore, the total power is calculated by $P=P_{S}+P_{D}$ [20, 55]. The propulsion efficiency is defined as the the ratio of $-P_{D}$ to P in time-averaged manner, i.e., ${\bar{\eta }}=\frac{-{\bar{P}}_{D}}{{\bar{P}}}$.

Fig. 4

Variation of a the mean drag force coefficient $\bar{C_D}$, b the propulsion efficiency ${\bar{\eta }}$ and c the power ${\bar{P}}$ for different values of bending stiffness and length of the flexible plate

The averaged drag force coefficient ${\bar{C}}_D$, the power consumed ${\bar{P}}$, and the propulsion efficiency ${\bar{\eta }}$ vary with the plate stiffness are shown in Fig. 4. It can be observed in Fig. 4a that the plate length can change the drag force magnitude and even the sign of the drag force. The positive sign of the average drag force coefficient ${\bar{C}}_D$ means drag force, and the negative one denotes thrust force. For $l=0.1,0.15$, ${\bar{C}}_D$ is positive for all the plate stiffness $K_B$ considered. For $l=0.2-0.3$, the force changes with the plate stiffness significantly, ${\bar{C}}_D$ is positive (acts as drag force) for small $K_B$ and turns to be negative approximately when $K_B \gtrsim 1.0$ corresponds to the thrust force generation. The thrust force increases as $K_B$ continue to increase, indicating that the plate flexibility greatly contributes to the propulsive force.

It is seen in Fig. 4b that the propulsion efficiency ${\bar{\eta }}$ has a significant variation with the increase of $K_B$. When the flexible plate is short, i.e., $l=0.1,0.15$, the propulsion efficiency is always negative, corresponding to the drag force. For $l=0.2-0.3$, the propulsion efficiency increases obviously with the stiffness enhancement and becomes positive at the critical stiffness around $K_B=1.0$, it keeps increasing until $K_B=25$. For $K_B>25$, further increasing $K_B$ leads to a slight enhancement of propulsion efficiency, indicating a weak improvement for fish swimming locomotion when the attached plate has a stiffness increase approaching to be rigid. For $K_B>100$, the plate can be regarded as a purely flapping rigid plate. By comparing Fig. 4b and c, it can be observed that the improvement of propulsion efficiency usually accompanies an increase in power consumption. The overall trend of P demonstrates that the power consumed increases with the stiffness enhancement for each l. It is interesting to note that increasing l from 0.25 to 0.3 leads to a significant increase in power consumed especially for $K_B>1$, much greater than those when l increases from 0.15 to 0.2 and from 0.2 to 0.25. This observation indicates that increasing the length of the attached flexible plate can result in optimization in terms of propulsion efficiency and power consumption, which can explain why the ratio of the caudal fin to body length is around 0.25 for a large number of fish in nature.

Fig. 5

Variation of the root-mean-square values of a drag force coefficient ${\bar{C}}_{Drms}$ and b lateral force coefficient ${\bar{C}}_{Lrms}$

The root-mean-square values of the drag force and the lateral force are plotted in Fig. 5 to study the influence of the flexible plate on the stability of the movement. The more steadily the fish swims, the smaller the corresponding rms value. It is demonstrated that the flexible plate length distinctly affects the stability of fish swimming. For $l=0.1$ and 0.15, the rms values are small, indicating that the fish swims with lower-level oscillations, namely, a fish with a short caudal fin has more steady locomotion. Also, it is seen that when l increases from 0.25 to 0.3, the rms values of drag and lift coefficients almost doubled, which can explain why the power consumption for $l=0.3$ is much greater, as shown in Fig. 4c.

To better understand the effects of the traveling foil and the attached flexible plate in swimming, the mean drag coefficients of the two parts are shown separately in Fig. 6. When the plate is very flexible such as $K_B=0.01$, ${\bar{C}}_{DF}$ is negative, a thrust force is generated on the traveling foil surface, which is shown in Fig. 6a. Nevertheless, the flapping flexible plate is subjected to great resistance, resulting in the total drag force shown in Fig. 4a. When the flexible plate stiffness becomes larger, the thrust force is mostly generated by the flapping motion of the attached plate, which pushes the surrounding fluids into the wake. It agrees well with the previous findings that when the undulating motion of the swimmer is limited to the last third of the length of the body, the swimmer adopts a quite rigid caudal fin to produce thrust force [6].

Fig. 6

Variations of the mean drag force coefficients of the traveling foil ${\bar{C}}_{DF}$ (a) and the plate ${\bar{C}}_{DP}$ (b)

Fig. 7

Comparison of the vortical structures in the wake at the instants $t/T = 1/2$: a–c for $K_B=0.01$, d–f for $K_B=1$, and g–i for $K_B=100$. The vectors in each figure represent the velocity at $x/L=2.0$

4.2 Wake flow

It is known that the vortical structures of the wake flow are closely associated with the hydrodynamic features, this subsection is to examine the influence of the attached flexible plate on the wake. In order to show the influence of the effect of length and stiffness on the wake flow, the vortical structures behind the traveling wavy foil attached with the flexible plate are presented for typical values of plate stiffness and length, i.e., $K_B=0.01$, 0.1, and 10 for soft, flexible and almost rigid plates and $l=0.1$, 0.2, and 0.3 for short, middle and long plates. As a representative instant, the flow pattern at $t/T=1/2$ is plotted in Fig. 7 to explain the generation of force.

Fig. 8

a Deformation and b passive deflection angle of the flexible plate at $t/T=1/2$

Fig. 9

Jetlike velocity of one cycle of a $l=0.2$, b $l=0.3$ at $K_B=10$

Flow over the traveling wavy foil has a complex interplay with the passively flapping flexible plat deformed by the hydrodynamics force exerted by the surrounding fluids, resulting in intriguing vortex shedding in the wake flow. As shown in Fig. 7a–c, with the increase of the length of the flexible plate, the structure of the wake vortex changes significantly, which is in connection with the deformation of the flexible plate. Figure 8a shows the deformation of the flexible plate with different lengths at $t/T=1/2$, quantified as the passive deflection angle ($\alpha$) of the flapping flexible plate. As illustrated for $l=0.3$ in Fig. 8a, $\alpha$ is the angle at which the end of the flexible plate deviates from the midline of the wavy foil as extended out from the point P. As shown in Fig. 8b, the passive deflection angle increases clearly for $l=0.2$ and 0.3 of $K_B=0.01$, leading to a greater vertical separation distance between the positive and negative vortices. Positive and negative vortices are located above and below the axis $y=0$ respectively, resulting in drag force as obtained in Fig. 4a.

Fig. 10

a Profiles of the wavy foil and flexible plate in one cycle (a)–(d), and contour plots of effective pressure $p_e$ in the wake flow for $K_B=0.1$ (e)–(h) and $K_B=10$ (i)–(l). The arrow points to the direction of the force induced by the pressure difference across the flexible plate or the traveling foil

Fig. 11

a Time evolution of the passive deflection angle $\alpha$. The time depended drag coefficient of b the overall model $C_D$, c the traveling foil $C_{DF}$ and d the flexible plate $C_{DP}$ at $l=0.25$

For $K_B=0.1$, the lateral distance between the positive and negative vortices decreases as plate length increases, increasing the number of vortex pairs. This can explain why the drag force increases at $K_B =0.1$ when l varies from 0.1 to 0.3 as shown in Fig. 4a. When the plate becomes almost rigid, for example, $K_B=10$, clearly seen in Fig. 7g–i, with the increase of the length of the plate, the intensity of the shedding vortex increases obviously. For the short plate such as $l=0.1$, a nearly in-line vortex street is formed in the wake, corresponding to $\bar{C_D}$ is close to zero in Fig. 4a. For $l=0.2$ and 0.3, a reverse von Kármán vortex appears at $K_B=10$. This vortical structure induces jet wake flow, which makes the advection velocity downstream of the vortex higher than the imposed background flow, thus forming the average thrust force plotted in Fig. 4a. With the plate length increasing from 0.2 to 0.3, the vortex shedding intensity increased clearly, and the lateral distance of positive and negative vortices increases. In theory, these two vortical transitions are expected to generate more intensive jet wake vortices after the plate of $l=0.3$. The corresponding wake jetlike velocity of $K_B=10$ at $x/L=2.0$ for $l=0.2$ and 0.3 is shown in Fig. 9, the jetlike flow becomes more intense when the plate length increases, which contributes to larger thrust force generation. This kind of phenomenon can quantitatively explain the increase of thrust force for the attached plate with larger stiffness and length, which is consistent with the hydrodynamic force obtained in Fig. 4a. The above findings demonstrate explicitly that the stiffness of the caudal fin plays an important role in physics to the fish swimming locomotion.

4.3 Pressure field

The drag force is composed of friction drag and drag caused by the pressure distribution. It has been proved that the friction drag force overtime is almost unaltered over one period for the traveling wavy foil in previous studies [39]. Therefore, the force caused by the pressure distribution is pivotal in the propulsion. The effective pressure contours for different $K_B$ values is shown in Fig. 10, the contour plots of positive effective pressure are colored by brown and those of negative one by green, the arrow points to the direction of the force induced by the pressure difference. Two representative calculation examples at $l=0.25$ are chosen to illustrate how the flapping flexible plate affects the wake pressure field and in turn generates thrust force.

As shown in Fig. 10a and e, the joint P starts to move down at $t/T= 1/4$. Time evolution of passive deflection angle $\alpha$ is shown in Fig. 11a. The flexible plate of $K_B=0.1$ has an obvious lag of almost 1/8 cycle relative to the rigid plate due to its flexibility, as shown in Fig. 11a. Resulting from the unfavorable position of the plate, the top of the flexible plate appears a positive pressure area, and the bottom appears a negative pressure area, which leads to a drag force and is helpful to explain why $C_D$ in Fig. 11b is positive for $K_B=0.1$. For $K_B=10$, the plate moves almost in line with the wave foil midline. As a result of the favorable relative position at $t/T= 1/4$, a negative pressure area and positive pressure area appear at the top and bottom of the flexible plate, respectively, which contributes to a thrust force and explains why $C_D$ in Fig. 11b is negative for $K_B=10$ at this instant. At $t/T=2/4$, the joint P is at the lowest position and then tends to move up. The positive pressure area is above the flexible plate, the negative pressure area is below the flexible plate. Because of the large deformation, the flexible plate of $K_B=0.1$ releases elastic energy to restore deformation, it forms a positive angle above the horizontal direction, as shown in Fig. 11d, $C_{DP}$ is negative at this instant, the plate is pushed forward. However, the back part of the wavy foil forms a negative angle below the horizontal direction, thus contributes to the generation of drag force depicted in Fig. 11c. In integral, the fish are subjected to a small drag force as obtained in Fig. 4a. For $K_B=10$, negative pressure appears on the top at $t/T= 2/4$, however, the flexible plate forms a small angle below the horizontal line, which corresponds to the small drag force generated in Fig. 11b. Since the anti-phase pressure field is symmetric about the horizontal axis, the specific analysis for the hydrodynamics force of $t/T=3/4$ and $t/T =4/4$ are similar to that described above.

5 Conclusions

The flow problem on a traveling wave foil with a flexible plate is studied numerically. The traveling wavy foil represents the swimming fish body, and the flexible plate describes the passively flapping caudal fin. The bending stiffness $K_B$ of the plate is utilized to describe the flexibility of the caudal fin. Combined influences of caudal fin length and bending stiffness on propulsive features are examined via the hydrodynamic force, power consumption and propulsion efficiency, as well as the related flow behaviors like the wake vortices and effective pressure.

The findings obtained in the present study confirm that the caudal fin is not supposed to be seen as an extension of the fish body simply, in other words, it should be treated as a distinct propeller in the study of fish swimming locomotion. It is indicated that the stiffness and length of the caudal fin greatly influence the propulsive performance of fish swimming. Specifically, when the caudal fin is short as $l\le 0.15$, the fish has more steady locomotion, but its propulsive performance is not significantly improved for all the stiffness $K_B$ considered. When the caudal fin is long as $l\ge 0.2$, the propulsion performance is greatly improved. The propulsion efficiency improves obviously with the increase of the caudal stiffness, it obtains a positive value at the critical stiffness of $K_B=1.0$ approximately at which the thrust force is generated.

The thrust generation mechanism is also explained in detail through the analysis of vortex production and pressure distribution. The influence of the caudal fin on the wake vortices and effective pressure field demonstrate a great dependence on the stiffness and length of the attached flexible plate, namely, the caudal fin. For the different combinations of the stiffness and length, the attached flexible plate flaps passively with quite different deformations, which in turn modify the wake flow feature and the hydrodynamic force significantly. When the length ratio of caudal fin and body is greater than 0.2 and the bending stiffness $K_B$ is approximately greater than 1.0, a reverse von Kármán vortex street appears in the wake, related to the thrust force generated in fish swimming. The effective pressure distribution is pivotal in the generation of thrust force which appears resulting from effective pressure difference across the flexible plate at its favorable position and pushes the undulating swimmer forward.

The findings of this study contribute to understanding how the flexibility and length of the caudal fin affect the fish locomotion to improve propulsion performance. It is better to use more realistic structural models to research the fish swimming locomotion, such as the caudal fin modeled with non-uniformly distributed stiffness along the surface in a three-dimensional simulation. These will be the research issues of our future work.