1 Introduction

The recent advances in microfluidics technology have enabled precise fluid and particle manipulation for various biomedical and chemical analyses on the microscale. The microfluidics techniques have the characteristics of small sample consumption, short reaction time, and low waste generation rate (Talebjedi et al. 2021a, b). The commonly used microfluidics techniques for particle separation applications include, acoustophoresis (Taatizadeh 2021; Ohiri et al. 2018; Abedini-Nassab et al. 2021), on-chip centrifugation(Nasiri et al. 2020), optical based method(Geiger et al. 2019; Gao et al. 2017; Wang et al. 2021), magnetic technology (Shen and Park 2018; Abedini-Nassab 2019; Abedini-Nassab and Bahrami 2021) and dielectrophoresis separation (Dalili et al. 2021). The dielectrophoresis separation technique stands out as a label-free, non-invasiveness, cost-effective, high throughput and yield compared to conventional particle manipulation methods.

Dielectrophoresis (DEP) refers to a technique of moving electrically polarizable matter with an inhomogeneous electric field. The fundamental idea was introduced by Pohl in the 1950s (Pohl 1951), and has made its way into numerous applications involving the separation and purification of inorganic (Arnold et al. 2006; Krupke et al. 2003; Kullock et al. 2020; Lorenz et al. 2020) organic (Becker et al. 1995; Voldman 2006; Fiedler et al. 1998; Pohl and Hawk 1966; Sang et al. 2016; Yu et al. 2020) and living materials (Green et al. 1997; Hamada et al. 2013; Madiyar et al. 2013). In addition to DEP, other electrokinetic phenomena, such as AC electro-osmosis (ACEO) (Ramos et al. 1999) and AC electrothermal effects (ACET), (Castellanos et al. 2003), will also induce motion in suspended particles, particularly in fluids of high ionic strength. A discussion of the various electrokinetic phenomena can be found in several review papers (Castellanos et al. 2003; Gascoyne and Vykoukal 2002; Pethig 2010; Gagnon 2011; Ramos et al. 1998), which describe the length, time, and force scales where the different types of phenomena are dominant. DEP is the preferred method for manipulating objects inside microfluidic environments due to the lack of heating and the better spatial control of particles.

There have been several efforts in DEP force prediction through numerical calculations. For example, equations for expressing the acting force on a straight, slender body are proposed (Lin et al. 2009). Also, a theory for calculating the DEP force acting on a chain of spherical particles is suggested (Techaumnat et al. 2004). Moreover, mathematical modeling of the force produced with interdigitated electrode geometry is proposed (Crews et al. 2007).

Though DEP has been the subject of much scientific interest in the field of lab on a chip and microelectromechanical systems (MEMS), there have been surprisingly few attempts to make quantifiable comparisons between experiments and theoretical predictions (Wang et al. 1993; Saucedo-Espinosa and Lapizco-Encinas 2015). Moreover, little attention has been paid to the electrical circuit requirements to hone and optimize the DEP effect. To fill this gap, here we conduct a comprehensive set of experiments and simulations to directly measure the DEP force on colloidal particles in a microfluidic chip over a wide range of field strengths and driving frequencies. We can precisely calibrate the system by employing electrode geometries that can be solved analytically and compared with numerical solutions. The numerical solutions are used to confirm our analytical model. Finally, we develop an equivalent circuit model for the nDEP microfluidic instrument, which can be used to assess the system power requirements, range of operating frequencies, and the optimal chip dimensions for the desired particle manipulation capabilities.

Consistent with prior investigations, here we use interdigitated electrode arrays (IDT), as these geometries can induce strong electric fields throughout the fluid volume (Javanmard et al. 2012; Yan et al. 2014; Albrecht et al. 2004). Prior experiments with IDTs have been conducted with various electrode shapes (e.g., straight bars, saw tooth (Morgan and Green 1997; Sedgwick et al. 2008), square traps (Rosenthal and Voldman 2005), quadrupole traps (Fuhr et al. 1992; Voldman et al. 2003), octupole traps (Schnelle et al. 1993, 2000)) and different modes of excitation (e.g., stationary (Gerard et al. 1997), traveling wave (Cheng et al. 2009), pulsed signals (Cui et al. 2009), and multiple frequencies (Wang et al. 2009; Urdaneta and Smela 2007)). As our goal is to characterize the DEP force precisely, we limit our analysis to the simplest possible electrode geometry and driving conditions, consisting of an array of rectangular electrodes excited by a sine wave (Fig. 1b). This geometry is ideal because the fields are analytically solvable, and the resulting DEP force is primarily directed towards (or away) from the plane of the electrodes.

Fig. 1
figure 1

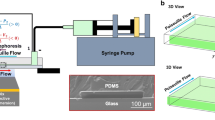
Experimental setup. The chip and connectors are shown in (a) with a magnified view of the electrode array (b). A representative confocal microscopy image of beads levitating above the surface is shown in (c), where the red and blue dashed lines show the equilibrium position of the beads at 1 and 3 V, as compared to those non-specifically adhered to the substrate depicted by the green dashed line. The applied frequency in these experiments is 1 MHz. Representative brightfield microscopy images show the beads when the applied voltage (peak to peak) is d \(0 \mathrm{V}\), or e \(3 \mathrm{V}\)

Full size image

We believe that the most reliable characterization method is based on negative dielectrophoresis (nDEP) to repel the particles away from the substrate. Because the DEP force decays exponentially with distance away from the IDT array, the particle will find an equilibrium vertical position where the nDEP force exactly balances that of gravity (Gerard et al. 1997). By measuring these equilibrium positions over a wide range of field strengths and operating frequencies and comparing these results against the theoretically predicted locations, it is possible to directly quantify the applied force and determine relevant material properties.

Here, we use a confocal microscope to measure the equilibrium particle locations and then fit the entire data set to estimate the dielectric contrast factor of the particle, also known as the Clausius–Mossotti factor (CM). We believe this approach is preferable to other methods based on the measurement of particle migration velocities in laminar flow fields (Wang et al. 1998) or the holding forces on particles in shear flow (Voldman et al. 2001), which are less easy to calibrate against than gravity.

After carefully calibrating the experimental system, we then analyze the influence of the geometry of the IDT array (i.e., electrode width and array periodicity) on both the magnitude and the distance dependence of the nDEP force. We also develop an equivalent circuit model and plot the frequency–response function for our experimentally tested IDT geometry. This comprehensive theoretical and experimental analysis can serve as a useful guide for designing improved nDEP systems for manipulating colloidal particles inside fluids.

This work, for the first time to our knowledge, provides a good reference for researchers in the field, covering the required information in one place. (i) It presents a new analytical model as well as (ii) numerical simulation results, predicting the nDep behavior, and (iii) confirms the results with experiments. This combination of the three studies and agreements between them without any fitting parameter is rare. (iv) It also provides the practical requirements for running nDEP microfluidic instruments, including the whole nDep system circuit model for enhancing the delivered power to the chip, the IDT geometry design, and the required operational frequencies and voltages. This complete circuit model with the ability to predict the delivered voltages to the chip, to our knowledge, is new, and it is fundamentally required for people in the field to design their nDep systems accordingly.

2 Experimental methods

Figure 1 provides an overview of the experimental system, including a magnified view of the test clips used for electrical connections and the chip (Fig. 1a), a zoomed-in view of the IDT array (Fig. 1b), a representative image of the data obtained in the confocal microscope (Fig. 1c), and a representative bright-field microscopy image of particles levitating above the substrate in the absence (Fig. 1d) or presence (Fig. 1e) of an AC electric field.

Confocal imaging is performed with an upright Zeiss 780 microscope using a 20× objective and a slice width of \(0.89 \mu {\rm m}\). Care is taken to level the microscopy stage and quickly scan through the slices to reduce the amount of bead motion during image acquisition. Measurements are conducted on 30-μm-wide platinum electrodes spaced 10 microns apart. We use two different procedures to determine the separation distance between the bead and substrate depending on the conditions. In one method, we take advantage of the tendency of some beads to non-specifically adhere to the chip surface, which is used as a reference point to measure the relative separation of the nearby levitating beads (see Fig. 1c). When there was an insufficient number of beads adhered to the substrate to generate a reliable measure of separation distance, we employ a second method that uses the image reflections of beads to determine the levitation height. At least ten measurements are collected for each driving frequency and field strength to obtain means and standard deviations. The measurement precision is limited by the slice thickness (here, approximately \(1 \mu \mathrm{m}\)).

We ran our experiments in de-ionized water as a low ionic strength fluid. The study was not conducted for higher conductive fluids, such as cell culture media or diluted KCL, which need careful system engineering to minimize ACEO and ACET effects.

3 Theory and simulation

We ran the simulations using our developed custom Matlab codes. To obtain an analytically tractable solution, we develop a 2-D theoretical model for the IDT array, which is a reasonable approximation when the electrode fingers are long (e.g., \(\sim 1300 \mu {\rm m}\)) compared to the array period (e.g., \(40 {\mu} {\rm m}\)). In essence, the potential along the direction of the electrode length is assumed to remain constant (see the coordinate system of Fig. 2a). This problem is easily solved through the separation of variables, subject to suitable boundary conditions.

Fig. 2
figure 2

Schematic of the nDep chip and potential simulation. a The negative-dielectrophoresis chip layout is illustrated. The interdigitated electrode array has a period, 2 L, electrode width b, and is connected to an oscillating electrical potential V0. The particle levitates to a height, y, above the substrate due to the repulsive negative-dielectrophoresis force. b The XY-potential energy landscape is depicted for an AC potential 1 Volt (peak to peak), and using the dimensions of our experimental system. The energy minima and maxima are depicted as the red and purple regions, respectively. c The solid line depicts the assumed boundary conditions for the analytical solutions, while the dash-dotted line shows the solution obtained from finite difference equations

Full size image

To find the electric potential, the Laplace equation can be written as \({\nabla }^{2}\varphi =0.\) In this work, the boundary conditions are specified on the electrodes, which are held at potentials, \(\pm ({V}_{0}/2) {\sin}(\omega t).\) The electrodes are assumed to be infinitely thin. In between the electrodes, along the boundary of the fluid domain, we assume that the potential is linear and piece-wise continuous, such as that shown in Fig. 2c. Given these assumptions, the electrical potential can be expressed in the Fourier series as

$$\varphi \left( {x,y} \right) = \frac{{4V_{0} }}{{\pi^{2} }}\left( {\frac{L}{L - b}} \right)\sum\limits_{n = 1}^{N} {\frac{1}{{n^{2} }}f\left( n \right)\sin \left( {\frac{n\pi }{L}x} \right)e^{{ - \frac{n\pi }{L}y}} } ,$$
(1)

where

$$f\left( n \right) = \sin \left( {\frac{n\pi }{2}} \right)\cos \left( {\frac{n\pi b}{{2L}}} \right).$$
(2)

Equation (2) is a function of the electrode width, \(b\), and the array period, \(2L\). What we do here is similar in shape, but different in general, to the one introduced by Morgan and coworkers (Morgan et al. 2001). The electric field distribution is determined from the negative gradient of the electrical potential, given by Eq. (3).

$$\vec{E}\left( {x,y} \right) = \frac{4}{\pi }\left( {\frac{{V_{0} }}{L - b}} \right)\sum\limits_{n = 1}^{N} {\frac{1}{n}f\left( n \right)e^{{ - \frac{n\pi }{L}y}} \left[ { - \cos\left( {n\pi xL^{ - 1} } \right)\hat{x} + \sin\left( {n\pi xL^{ - 1} } \right)\hat{y}} \right]} ,$$
(3)

where \(\hat{x}\) and \(\hat{y}\) represent the unit vectors in \(x\) and \(y\) directions, respectively. A solid spherical particle of radius, \(a\), exposed to this field distribution behaves identically as an electric point dipole with a dipole moment (Jones 1995):

$$\vec{p}\left( \omega \right) = 4\pi a^{3} \varepsilon_{0} Re\left[ {\tilde{K}\left( \omega \right)} \right]\vec{E},$$
(4)

where \({\varepsilon }_{0}\) is the dielectric constant of free space, and \(E\) is the strength of the electric field at the particle center, while \(\tilde{K}\left( \omega \right)\) is the frequency-dependent Clausius–Mossotti factor (Jones 1995):

$$\tilde{K}\left( \omega \right) = \frac{{\tilde{\varepsilon }_{p} \left( \omega \right) - \tilde{\varepsilon }_{f} \left( \omega \right)}}{{\tilde{\varepsilon }_{p} \left( \omega \right) + 2\tilde{\varepsilon }_{f} \left( \omega \right)}}.$$
(5)

The complex electrical permittivity \(\tilde{\varepsilon }\left( \omega \right)\), is a function of the dielectric permittivity of the particle,\(\varepsilon_{p}\), and fluid, \(\varepsilon_{f}\), and each medium’s electric conductivity, \(\sigma_{p}\) and \(\sigma_{f}\), respectively. These properties are related as Eq. (6) (Jones 1995).

$$\tilde{\varepsilon }_{p,f} \left( \omega \right) = \varepsilon_{p,f} + j\frac{{\sigma_{p,f} }}{\omega }.$$
(6)

From Eq. (5), it is clear that the CM factor is thus bounded in the range of \(- 0.5 \ge \tilde{K}\left( \omega \right) \ge 1\). The potential energy of a point dipole exposed to an external electric field is given by Eq. (7).

$$U_{e} = - \frac{3}{2}\varepsilon_{0} V_{p} Re\left[ {\tilde{K}\left( \omega \right)} \right]\vec{E}^{2} ,$$
(7)

where \({V}_{p}\) is the volume of the particle. Equation (7) indicates that particles will move towards the local electric field maxima (minima) when the CM factor is positive (negative). Since the CM factor is negative for the particles and frequencies of interest here, the particles tend to move away from the electrodes, causing them to levitate in the y-direction. For this system, the potential energy can be expressed explicitly as (Eq. (8)).

$$U\left( {x,y} \right) = - \frac{{24\varepsilon_{0} \tilde{K}\left( \omega \right)V}}{{\pi^{2} }}\left( {\frac{{V_{0}^{{}} }}{L - b}} \right)^{2} \sum\limits_{n = 1}^{N} {\sum\limits_{m = 1}^{N} {\left( \frac{1}{nm} \right)} } f\left( n \right)\, f\left( m \right)\cos\left( {\frac{{\left( {n - m} \right)\pi }}{L}x} \right)e^{{ - \frac{{\left( {n + m} \right)\pi }}{L}y}} ,$$
(8)

For one particular IDT array geometry (Fig. 2a, b), in which \(b / L = 0.75\), there exists an energy minimum located at \(\sim 15 \mu {\rm m}\) above the electrode center. This plot also indicates that a stable vertical position can be achieved by nDEP force alone (i.e., even without the counterbalancing force of gravity). The addition of gravity merely shifts the equilibrium vertical position relative to the nDEP energy landscape. For smaller electrodes, however, the energy minimum is directly in between the electrodes and located at infinity; therefore, gravity is required to achieve a stable equilibrium.

The force acting on the particle is determined by taking the negative gradient of the potential energy represented in Eq. (9).

$$\vec{F}_{e} \left( {x,y} \right) = - F_{mag} \sum\limits_{n = 1}^{N} {\sum\limits_{m = 1}^{N} {f\left( n \right)f\left( m \right)e^{{ - \frac{{\left( {n + m} \right)\pi }}{L}y}} \left[ {\left( {\frac{n - m}{{nm}}} \right)\sin\left( {\left( {n - m} \right)\pi \frac{x}{L}} \right)\hat{x} + \left( {\frac{n + m}{{nm}}} \right)\cos\left( {\left( {n - m} \right)\pi \frac{x}{L}} \right)\hat{y}} \right]} } ,$$
(9)

where Fmag is the characteristic magnitude of the dielectric force, and is given by Eq. (10).

$$\vec{F}_{{{\text{mag}}}} \left( {x,y} \right) = \frac{{24\varepsilon_{0} \tilde{K}\left( \omega \right)V_{p} }}{\pi L}\left( {\frac{{V_{0} }}{L - b}} \right)^{2} .$$
(10)

When the particle has moved a sufficient distance away from the substrate, the short-range forces from the substrate (e.g., Van der Waals, hydrophobic/hydrophilic interactions) become negligible, and the only remaining long-range force arises from the particle’s buoyancy relative to the surrounding fluid (Eq. (11)).

$$F_{g} = \Delta \rho V_{p} g.$$
(11)

Since the polystyrene beads are denser than the fluid, the net buoyancy force is directed towards the substrate, resulting in a stable equilibrium point when \({F}_{g} = {F}_{e}\). For notational convenience, it is possible to define a dimensionless quantity that is the ratio of these characteristic force scales (Eq. (12)).

$$\Lambda = \frac{{F_{{{\text{mag}}}} }}{{F_{g} }} = \frac{{24\varepsilon_{0} \left| {{\text{Re}} \left[ {\tilde{K}\left( \omega \right)} \right]} \right|}}{\Delta \rho g\pi L}\left( {\frac{{V_{0}^{{}} }}{L - b}} \right)^{2} ,$$
(12)

where \({V}_{0}\) is set to be 0.5 V for this scaling analysis. As a rough estimate for this system assuming the values in Table 1, the force scale is approximately \(\Lambda \approx 10\). Since this parameter is derived from experimental values, it is not considered a fitting parameter.

Table 1 Values used for beads in de-ionized water
Full size table

Due to the strong non-linearity of the dielectric forcing function, it is not possible to obtain an explicit expression of the equilibrium position, \({y}_{\mathrm{eq}}\), as a function of the system parameters, such as voltage and CM factor. However, it is possible to solve Eq. (10) for V0 and multiply the numerator and denominator by the right-hand side and left-hand side of Eq. (11), respectively. Then, by replacing \({F}_{\mathrm{mag}}/{F}_{g}\) with Λ (using Eq. (12)), Eq. (13) can be derived.

$$V_{0} \left( {y_{{{\text{eq}}}} } \right) = V_{s} \sqrt {\sum\limits_{m = 1}^{N} {\sum\limits_{n = 1}^{N} {\Lambda^{ - 1} \left( {\frac{n + m}{{nm}}} \right)f\left( n \right)f\left( m \right)} } \cos \left( {\left( {n - m} \right)\pi } \right)e^{{ - \frac{{\left( {n + m} \right)\pi }}{L}y_{{{\text{eq}}}} }} } .$$
(13)

In the asymptotic limit, where the particle is levitated to distances comparable to the electrode spacing, Eq. (13) can be simplified by retaining the first expansion term only.

$$\frac{{y_{{{\text{eq}}}} }}{a} = \frac{1}{\pi }\frac{L}{a}\left[ {\ln \left( {{{V_{0} } \mathord{\left/ {\vphantom {{V_{0} } {V_{s} }}} \right. \kern-\nulldelimiterspace} {V_{s} }}} \right) - \ln \left( {\sqrt {2\Lambda^{ - 1} } \cos \left( {\frac{\pi b}{{2L}}} \right)} \right)} \right].$$
(14)

Equation (14) predicts that the stable vertical position increases logarithmically with the applied voltage. The first term in the forcing approximation is nearly equal to the numerical solution when the separation distance between the particle and substrate exceeds one particle radius.

The frequency range for which the dielectric force is dominant over other electrohydrodynamic effects can be estimated from the values of Table 1 using the characteristic charge relaxation time scale, τ = ε/σ. The timescale for de-ionized water, with the conductivity of \(5.5 \mu {\rm S}/\mathrm{m}\), is in the order of a millisecond, implying that the capacitive field associated with dielectrophoresis will dominate at frequencies above \(1 \mathrm{kHz}\). On the other hand, in high ionic strength fluids like cell culture media, the timescale is typically on the order of nanoseconds and suggests that nDEP will dominate only at GHz frequencies and beyond.

3.1 Simulation methods

The analytical model of Eqs. (1–3) approximates the electric fields and potentials inside the fluid and is based on an implicit assumption that the surface potential between the electrodes is piecewise and linear. To test the validity of this assumption, we develop a finite difference approach to determine the exact potential in the fluid. Here, we solve the Poisson equation at each point on a square grid having \(N \times N\) grid points spaced apart by a distance, h. The equation can be written as \(\nabla^{2} \varphi = \frac{{\varphi_{i + 1,j} + \varphi_{i - 1,j} + \varphi_{i,j + 1} + \varphi_{i,j - 1} - 4\varphi_{i,j} }}{{h^{2} }} = 0\), where the indices \(i\) and \(j\) correspond to the \(x\)- and \(y\)-directions, respectively. For charge-balanced conditions, the solution of the electrostatic potential is thus an arithmetic average of the neighboring grid points, i.e., (Eq. (15)).

$$\varphi_{i,j} = \frac{1}{4}\left( {\varphi_{i + 1,j} + \varphi_{i - 1,j} + \varphi_{i,j + 1} + \varphi_{i,j - 1} } \right).$$
(15)

At the chip surface, the potential is only specified on the electrodes as either \(+{V}_{0}\) or \(-{V}_{0}\). Meanwhile, for the regions in between the electrodes, the grid points are solved as Eq. (16).

$$\varphi_{i,0} = \frac{1}{3}\left( {\varphi_{i + 1,0} + \varphi_{i - 1,0} + \varphi_{i,1} } \right).$$
(16)

Periodic boundary conditions are used along the lateral edges of the container and chosen to satisfy the conditions, \(\varphi_{0,j} = \varphi_{N,j}\), \(\varphi_{1,j} = \varphi_{N + 1,j}\), and \(\varphi_{ - 1,j} = \varphi_{N - 1,j}\). The height of the fluid container was chosen to be several array periods in total height, which allows us to specify the upper boundary condition as the far-field approximation of Eq. (1). A grid size of \(N = 100 \mathrm{h}\) was found to achieve numerical convergence, where \(h = L / 25\).

The solution procedure involves establishing an initial guess for all interior regions of the fluid and then iterating Eqs. (15–16) until the potential reaches convergence. We found that the discrepancy between the analytical and numerical model is relatively small, with the most significant error occurring near the electrode surface (~3.2%). As shown in Fig. 2c, the difference between the approximate piecewise boundary condition and the numerical solution is quite small. It justifies the use of the analytical model to calibrate the experimental apparatus.

3.2 Equivalent circuit model

Maximizing the nDEP effect requires a circuit design in which most of the voltage is dropped across the fluid. Thus, it is essential to consider the behavior of the experimental system in terms of an equivalent circuit model (Ngo et al. 2014). For example, the capacitance per unit length of the IDT array can be determined from the relationship between the surface charge density and surface voltage on the electrode array. In conductors, one can write \({E}_{n}=\sigma (x)/\varepsilon ,\) where \({E}_{n}\) is the normal component of the electric field. Thus, the surface charge density can be determined from the normal component of the electric field as follows:

$$\sigma \left( x \right) = \frac{4\varepsilon }{\pi }\left( {\frac{{V_{0} }}{L - b}} \right)\sum\limits_{n = 1}^{N} {\frac{1}{n}f\left( n \right)\sin\left( {n\pi xL^{ - 1} } \right)} .$$
(17)

The capacitance per unit area of the interdigitated electrode array can then determine by integrating the total charge on the electrode surface (Eq. 18).

$$C_{f} = \left( {\frac{2\varepsilon A}{{L - b}}} \right)\sum\limits_{n = 1}^{N} {\frac{f\left( n \right)}{{\left( {n\pi } \right)^{2} }}\cos\left( {\frac{n\pi b}{{2L}}} \right)}$$
(18)

which for our system amounts to a capacitance of approximately \(40\, \mathrm{ pF}\) for an electrode array of \(5\, {\mathrm{mm}}^{2}\). A similar expression can be obtained for the electrical resistance of the electrode array (Eq. 19).

$$R_{f} = \left[ {\left( {\frac{2\sigma A}{{L - b}}} \right)\sum\limits_{n = 1}^{N} {\frac{f\left( n \right)}{{\left( {n\pi } \right)^{2} }}\cos\left( {\frac{n\pi b}{{2L}}} \right)} } \right]^{ - 1}$$
(19)

which for the same electrode geometry and size is calculated to be \(3 \mathrm{M}\Omega\) when the fluid has a bulk conductivity of de-ionized water, but only 1 \(8\Omega\) when the fluid is cell culture media (assuming conductivity of \(1 \mathrm{S}/\mathrm{m}\)).

In addition to the field distribution between the electrodes, there is also a resistance and inductance associated with the wire leads and the impedance of the power supply. The inductance between a pair of wires is computed approximately as

$$L_{p} = \frac{{\mu_{0} }}{\pi }\cosh^{ - 1} \left( \frac{S}{w} \right),$$
(20)

where S is the center-to-center distance between the wires of width, w. The dominant inductance of this circuit is produced by the electrical traces to and from the chip connector, which is estimated to be on the order of \(1 \mu {\rm H}\). The diagram shown in Fig. 3a represents the equivalent circuit of a typical nDEP system. Based on this circuit model, the voltage drop across the fluid is determined by calculating the relative impedance across the fluid compared to that of the entire circuit. For the circuit illustrated in Fig. 3, the transfer function is given as Eq. (21).

$$\frac{{V_{\rm out} }}{{V_{\rm in} }} = \frac{{\left( {1 + R_{t} R_{f}^{ - 1} - \omega^{2} \omega_{R}^{ - 2} } \right) - j\omega \left( {\omega_{L}^{ - 1} + \omega_{C}^{ - 1} } \right)}}{{\left( {1 + R_{t} R_{f}^{ - 1} - \omega^{2} \omega_{R}^{ - 2} } \right)^{2} + \omega^{2} \left( {\omega_{L}^{ - 1} + \omega_{C}^{ - 1} } \right)^{2} }}.$$
(21)
Fig. 3
figure 3

Equivalent circuit model. a In the equivalent circuit model, \({R}_{t}\) and \({L}_{t}\) represent the resistance and inductance of the wire leads, respectively. \({R}_{f}\) and \({C}_{f}\) represent the resistance and capacitance of the interdigitated electrodes and the media, respectively. b The real part (dotted line), imaginary part (dashed line), and the magnitude of the circuit transfer function are plotted

Full size image

The following definitions are used for the characteristic frequencies: \(\omega_{R} = \sqrt {L_{t} C_{f} }^{ - 1}\), \(\omega_{L} = R_{f} L_{t}^{ - 1}\), and \(\omega_{C} = \left( {R_{t} C_{f}^{{}} } \right)^{ - 1}\). These characteristic values are associated with the circuit's resonance, inductance, and capacitive time constants. Given our estimated parameters for this circuit, \(L_{t} = 1\;{\mu H}\), \(C_{f} = 40\;{\text{pF}}\), \(R_{f} = 3\;{\text{M}}\Omega\), and using \(R_{t} = 50\Omega\) as the resistance of the co-axial cable and leads, these characteristic frequencies are found to be \(\omega_{R} = 10^{8} {\text{Hz}}\), \(\omega_{L} = 10^{13} Hz\), and \(\omega_{C} = 10^{9} {\text{Hz}}\). The real part, imaginary part, and magnitude of Eq. (21) are plotted in Fig. 3b. As seen in this figure, the real part has a peak at ~130Mz and then it drops. That means at frequencies higher than ~130 MHz, the delivered voltage to the chip is lower than the input voltage, and it may not be enough for desired particle levitation. Hence, this analysis suggests that our circuits can operate at frequencies up to tens of MHz, consistent with our experimental results described in Sect. 4. Going beyond these frequencies will require more complicated circuit designs.

4 Results and discussion

The vertical equilibrium positions were measured as a function of the applied voltages of 0–6 V for operating frequencies ranging from \(0.1\, \mathrm{to}\, 20 \,\mathrm{MHz}\). To guide the eye, we also plot the predicted equilibrium positions as a function of the voltage from Eq. (13). The four curves in each plot are calculated based on assumed CM factors of \(\tilde{K} = - 0.05\)\(, -0.1, -0.3\), and \(-0.5\). Overlaid on top of this graph are the predictions of Eq. (14), averaged over the spatial period, \(2L\), for considering the minor variation in the vertical force with lateral position. As predicted, the equilibrium position increased logarithmically with voltage. In nearly all instances, the experimental data typically lie between the set of curves with CM factors of \(-0.3\) and \(-0.5\), which is not surprising since \(\tilde{K}\) is expected to be near the limit of \(-0.5\) for low dielectric polystyrene beads inside water. To provide a relevant forcing scale, we also introduce another reference axis denoted as “contact force”, which represents the calculated force of the bead when in direct contact with the IDT array at each of the corresponding applied voltages. This force is essential since it is the force levitating the particles at rest on the chip. This can be considered as a maximum force that can be applied in different experimental conditions, which for particular IDT array and bead size is in the range of 1–100 pN.

For the highest frequencies tested, ranging from 10 to 20 MHz, the power supply was unable to output the required voltages, which is reflected in the compression of the experimental measurements for these operating conditions. As the experimental data for this frequency regime fall outside expectations, it could also imply that other effects are at play. For our current experimental apparatus, the measurements at frequencies below 10 MHz appear to be most reliable. Thus, to cover the widest range possible for our setup, we focused on frequencies lower than 10 MHz as well as low voltages at 20 MHz.

By comparing the experimental data to theoretical predictions across each dataset of Fig. 4, we provide our best estimate of the fitting values of \(K(w)\) as a function of frequency in Fig. 5. The CM factors tend to be around \(-0.5\) for most of the lower frequency range but diverge at frequencies above 10 MHz due to the effects discussed above. The data points for which we have reasonable confidence are plotted as open circles, whereas the remainder is plotted as open diamonds.

Fig. 4
figure 4

Particle levitation measurement together with its theoretical predictions. The average vertical position and standard deviation of particles floating in water are plotted as a function of the applied voltage and for different frequencies of a \(100\, \mathrm{kHz}\), b \(215\, \mathrm{kHz}\), c \(464\, \mathrm{kHz}\), d\(1\, \mathrm{MHz},\) e \(2.15\, \mathrm{MHz}\), f \(4.64\, \mathrm{MHz}\), g \(10\, \mathrm{MHz}\), and h \(20\, \mathrm{MHz}\). The figure axis labeled “Contact Force” is used to indicate the magnitude of the force that the beads would experience when resting on the substrate for the different applied voltages. The theoretical curves show the predicted equilibrium positions for different Clausius–Mossotti factor having values of \(-0.5\) (solid line), \(-0.3\) (dashed line), \(-0.1\) (dashed-dotted line), and \(-0.05\) (dotted line)

Full size image
Fig. 5
figure 5

Clausius–Mossotti factor estimates. Based on the experimental data of Fig. 4; the best fitting Clausius–Mossotti factor is provided. Below \(10\, \mathrm{MHz}\), the Clausius–Mossotti factor is estimated to be in the range of \(-0.4\) to \(-0.5\), in good agreement with theoretical expectations (see open circle data points). Data above \(10\, \mathrm{MHz}\) (indicated by open diamond data points) do not fit with the expected negative dielectrophoresis model

Full size image

The plots in Fig. 5 can also be used for particle separation system design. Since based on these plots, the particles with different CM factors are levitated to different heights, they can predict the separation distance between the particles.

One of the interesting design questions for nDEP systems is determining the optimal geometry for specific particle sizes. For example, manipulating \(100\, \mathrm{nm}\) diameter virus particles, which experience weak DEP forces, would require a different type of electrode spacing than manipulating 10–20 μm diameter mammalian cells. From Eqs. (9–10), it is clear that the forcing function varies exponentially with the dimensionless ratio of the particle size relative to the electrode period. Thus, the maximum force will be achieved when the IDT array spacing is commensurate with the particle size (see the dashed line of Fig. 6).

Fig. 6
figure 6

Forcing profile of various interdigitated electrode array geometries. The force on a \(10 \mu {\rm m}\) diameter particle is plotted as a function of the dimensionless separation distance for substrate periods of \(L = 5 \mu {\rm m}\) (solid line), \(10 \mu {\rm m}\) (dashed line), \(20 \mu {\rm m}\) (dash-dotted line), and \(40 \mu {\rm m}\) (dotted line). The dotted line corresponds to the experimentally tested conditions. The strongest forces are achieved when the substrate period is commensurate with the particle diameter

Full size image

On the other hand, when the electrode spacing is much larger than the particle size, such as in our experiments, the contact force is lower at the surface; however the force is longer ranged. Thus, if the goal is better controlling the vertical position of the bead, it is recommended to use a larger array period. Whereas if the goal is to remove non-specifically adhere beads, it is recommended to use electrodes matched to the particle size to achieve the largest forces.

The other geometric parameter that we analyzed is the ratio of the electrode width relative to the array period \((b / L).\) Figure 7 plots the distance-dependent force profile for different ratios of \(b / L\) values, including our experimental ratio of \(0.75\). We found that for ratios of \(b / L > 0.3\), the equilibrium position is located directly above the center of the electrodes rather than in between the electrodes (see also Fig. 1d). For ratios \(b / L < 0.3\), on the other hand, the equilibrium positions are located directly in between the electrodes. To indicate these different lateral equilibrium positions, we use either blue or black coloration in Fig. 7. It should also be noted that as the \(b / L\) ratio decreases, the agreement between our analytical and numerical solutions surface is less accurate since the assumption of a piecewise linear electrical potential begins to break down. Regardless, the set of curves in Fig. 7 indicates that the ideal electrode geometry should consist of electrodes widths that are \({\sim} 1/3\) of the array period.

Fig. 7
figure 7

The force on a 10 μm diameter particle is plotted as a function of the dimensionless separation distance for different \(b / L\) ratios of \(0.75\) (black solid line), \(0.5\) (black dotted line), \(0.35\) (black dashed line), \(0.25\) (blue dash-dotted line) and \(0.10\) (blue solid line). The color coding depicts whether the equilibrium position is directly on top of the electrodes (black) or in between the electrodes (blue)

Full size image

5 Conclusion

Though there are many prior experimental demonstrations of negative dielectrophoresis (nDEP) (Arnold et al. 2006; Pohl and Hawk 1966), as well many theoretical analyses of nDEP (Castellanos et al. 2003; Gascoyne and Vykoukal 2002; Morgan et al. 2001), few prior works have combined theoretical (including analytical and numerical) and experimental analyses to directly quantify the nDEP forces on particles inside microfluidic devices, such as what we did here. To provide a firmer foundation for the nDEP field, we combine analytical models, numerical calculations, and experiments to carefully calibrate the nDEP system. We show that dielectrophoretic forces can be quantified with the nearly perfect agreement between theory and experiment. We also show that the range of operating frequencies can be adequately predicted from equivalent circuit models of the interdigitated electrode array (IDT) electrode geometry. Using the equivalent circuit model, this study is fundamentally important and provides essential information about the proper operational conditions. Finally, we conduct a theoretical analysis that indicates that the ideal IDT array consists of electrode widths that are \(\sim 1/3\) of the array spacing, which is matched to the intended particle size. The results achieved in this work and the difference between experienced nDEP forces acting on the particles with various sizes or dielectric permittivity can be further used for designing size-specific or permittivity-specific robust nDEP particle separation systems.

Though our experiments are conducted in de-ionized water, which is a low ionic strength fluid, in principle, it should be possible to achieve nDEP in fluids with higher conductivity, such as cell culture media or phosphate-buffered saline. However, achieving this goal will require careful system engineering to minimize AC electro-osmosis and AC electrothermal effects, which can dominate nDEP at frequencies below 1 GHz. Thus, if the goal is to conduct experiments on mammalian cells without significant heating, then the circuits need to be optimized for the GHz range to minimize these other electrokinetic effects. Unfortunately, function generators capable of generating GHz range frequency signals are highly expensive. Additionally, the external circuit surrounding the nDEP chip will have to be carefully tuned to enable their reliable operation at GHz frequencies. Though difficult, we expect that it is still possible to achieve nDEP at higher frequencies. Thus, our results should serve as a useful guide for designing dielectrophoretic particle manipulation microchips for the biological and non-biological research fields.