Bubble formation in viscous fluids by a microfluidic flow-focusing junction: a computational study

Abstract

A three-dimensional (3D) numerical study of bubble formation process in viscous fluids in a microfluidic flow-focusing junction is carried out in the present study. The numerical approach is first validated by the experimental data and shows a very good agreement, and a reciprocal relationship can be derived between the normalized bubble length and liquid fraction. Afterwards, the numerical approach is further applied to study bubble formation in fluids with different viscosities ranging from 5.6 to 400 mPa s, and the viscosity ratio of liquid phase to gas phase (μ_l/μ_g) is up to 2.2 × 10⁴. Two different interpolation treatments including the Geo-Reconstruction method and the CICSAM are implemented when dealing with the situation for high viscosity, and the results are compared with the experimental data, indicating a better performance of the Geo-Reconstruction method. The numerical results of the bubble shapes are also compared with the experimental visualization results, showing good agreements. The evolution of the gas tip is further investigated quantitatively, and the liquid film is found to play a very important role in affecting the velocity of the gas tip. Finally, the hydrodynamic behaviors of the Taylor bubble formed in the junction including velocity and pressure distributions are studied in detail, and the contribution of pressure drop within the channel is also discussed.

1 Introduction

The microchannel reactors are extremely important in heat and mass transfer and monodispersion, and they have been widely applied in a variety of fields such as biotransformations (Bolivar et al. 2011), emulsions generation (Garstecki et al. 2005) or chemical synthesis (Castrohernández et al. 2016), where the multiphase flow, especially gas–liquid flow, occurs frequently and plays an important role. For example, the micro-bubbles in the liquid or solution were used as efficient reactant cores or carriers for targeted drug delivery or tracer agents which were available for imaging device (Bolivar et al. 2011; Garstecki et al. 2005; Castrohernández et al. 2016). Consequently, great efforts have been devoted to study the corresponding bubble formation process in microchannel reactors in the past 2 decades (Cubaud and Ho 2004; Cubaud et al. 2005). The two most common micro-devices for bubble formation are the T-junction and the flow-focusing junction, where the gas of the former is injected perpendicular to the liquid flow, while the gas of the latter is injected into a crossing-liquid-flow. The dynamics underlying both the T-junctions and flow-focusing devices are controlled by the inlet pressures of liquid phase and gas phase as well as physical properties. The flow-focusing geometry leads to more straightforward numerical and theoretical descriptions due to its geometrical symmetry, from which the fundamental information for understanding the bubble formation process in microchannel reactor can be drawn. Cubaud and Ho (2004), Cubaud et al. (2005), Jose and Cubaud (2012) and Sauzade and Cubaud (2013) have presented systematic experimental studies on the two-phase flow in flow-focusing junctions and have shown the great potential of the microfluidic flow-focusing junction in producing the cellular material. Moreover, to improve the modeling and practical utilization of bubble dissolution in carbonated microfluidics where the fluid is generally with a very high viscosity, their studies were expanded to highly viscous fluids (Dietrich et al. 2008). A sequence of interesting visualization results about the formation and shrinkage of the Taylor bubble caused by dissolution of gas phase have been presented and studied quantitatively. CastroHernández et al. (2016) developed a method to produce monodisperse micro-droplets based on a planar flow-focusing device fabricated by soft lithography techniques. The droplet was generated at the tip of a long and stable liquid ligament, and it was possible to obtain droplets of 1 μm in diameter from a channel of 50 µm in width. Dietrich et al. (2008) experimentally studied the dynamics of bubble formation in three types of flow-focusing microdevices with different mixer angles. The bubble size and formation behavior were studied in detail, and the influences of flow rate ratio as well as the physical proprieties including the viscosities and surface tensions were taken into account. Furthermore, the correlations to predict the bubble size were proposed and showed a good agreement with the experimental data. Garstecki et al. (2005, 2006) made important contributions to understand multiphase flow phenomena in microfluidic junctions, and they presented an experimental study of bubble formation in a flow-focusing device with orifice (Garstecki et al. 2005). The breakup process was studied in detail and it was found that the evolution of the bubble neck and gas thread showed significant difference from the bubble formation in an infinite fluid. They concluded that the confinement of the orifice in the device could be used as a tool to control the dynamics of the breakup of immiscible fluids. They also experimentally studied the bubble and droplet formations in a microfluidic T-junction (Garstecki et al. 2006). It was found that the breakup was dominated by the pressure drop rather than by the shear stress from their experimental results with relatively small capillary numbers Ca (Ca = μu/σ), based on which a simple scaling correlation to predict the bubble or droplet length was proposed. Fuerstman et al. (2007) conducted an interesting analysis on the influence of surfactant on the pressure drop along the rectangular channel with bubbles. The pressure drop was found to be determined by three factors: the liquid slug between bubbles, the gutters along the corners and the curved caps at the bubble rear, which were the three parts of a general model for the pressure drop along a channel containing bubbles.

The numerical investigation has become an increasingly important approach in the study of the bubble formation in micro-devices because of its capability to solve very complex conjugated problem. Menech et al. (2008) studied the droplet formation within microfluidic T-junction in a wide range of viscosity, and the breakup dynamics of gas streams were studied in detail based on the phase-field model. They identified three distinct regimes for the droplet formation, i.e., squeezing, dripping and jetting, and they also proposed a critical capillary number above which the shear stress started to play an important role in the breakup process. Jensen et al. (2006) presented a simple two dimensional (2D) axisymmetric numerical study based on the experimental study by Garstecki et al. (2005). They managed to find the scaling between the bubble volumes and the channel radius. However, due to the restriction of the simplification of 2D axisymmetric geometry, the numerical method failed to catch up the steady bubble formation process. Qian and Lawal (2006) performed a comprehensive 2D numerical study of the bubble formation in the T-junctions with various cross-sectional widths (0.25, 0.5, 0.75, 1, 2 and 3 mm) based on the volume of fluid (VOF) method. They proposed a series of empirical correlations to predict the bubble length and slug length, and it was also concluded that the bubble size was primarily dependent on the velocities of the liquid phase and gas phase. Guo and Chen (2009) also presented a 2D numerical study of the Taylor bubble formation in a microfluidic T-junction based on the VOF method. Different mechanisms of bubble breakup were observed in the numerical results and the transitional capillary number from squeezing regime to shearing regime was identified. Similarly, Yu et al. (2007) presented the transitional behavior of the bubble formation in the numerical investigation. It was found that the bubbles showed bullet shapes and the formation process was mainly dominated by the shear stress at higher Ca number (Ca > 0.03). Dang et al. (2014) have presented a 3D numerical study of the bubble formation process in a Y-type junction using the coupled level set and VOF (CLSVOF) method. The evolution of bubble shape during the formation process was compared with the visualization results and showed a good agreement. In addition, they numerically investigated several factors that influenced the Taylor bubble formation, i.e., the flow rate ratio, contact angle and surface tension. The VOF method was also used by Shivhare et al. (2016) to study the sheath-to-sample flow in the 2D and 3D hydrodynamic focusing reactors, and the width of sample stream at different viscosity ratios and flow rate ratios were investigated in detail. More recently, Borgogna et al. (2018) conducted a 3D simulation on the mixing process in microfluidic focusing-junction based on a combined Eulerian/Lagrangian approach. It was interesting that the reconstruction method from the noisy trajectories provided a novel way to study the mixing behavior quantitatively in complex 3D flows.

The parameters in the previous numerical studies mentioned above are summarized in Table 1. It can be found that there are apparent limitations in these numerical studies. For example, the numerical studies were mainly 2D investigations which were quite different from the practical conditions. As a result, the particular phenomena in the microchannel like the gutter flow were not able to be captured. Another limitation is that the previous investigations mainly focused on the conventional fluids like the water and alcohol with low viscosities and rarely managed to study the bubble formation in viscous fluids. The only attempt on bubble formation in viscous fluid was carried out by Yu et al. (2007) who proposed a 2D numerical study on the air bubble formation in silicon oil, but the numerical results did not agree with the optical visualization results. Contrary to the numerical studies, there were many experimental investigations on this topic, and the bubble formation in viscous oil has been widely studied experimentally (Pancholi et al. 2008; Lu et al. 2013, 2014, 2016). For example, glycerol with the viscosity of 1100 mPa s was used as the working fluid whose viscosity ratios nearly reached 10⁵ in the study of Lu et al. (2016). Moreover, the bubble formation process in viscous fluids with the viscosities ranging from 5 to 400 mPa s were studied experimentally, and the precise visualization images were recorded by a high-speed digital camera and the phenomena were very interesting. For example, the bubbles in high viscous fluids were spindle and the bubble tips were much sharper, which are very different from those under the conventional condition. Such a fact motivates us to study the particular behaviors in detail. Additionally, Sauzade and Cubaud (2013) have studied CO₂ dissolution in viscous oil and the related mass transfer of bubble in viscous fluids, where the viscosity was found to play a vital role in both bubble dynamic and mass transfer. In a word, the numerical study of the bubble formation in viscous fluids is extremely rare, and the bubble dynamics and the corresponding multiphase flow behaviors for viscous fluids necessarily need to be understood.

Table 1 The viscosities of the numerical studies in references

The present study aims to investigate the bubble formation in microfluidic flow-focusing junctions with viscous fluids and to provide essential information to understand the related mechanics. The numerical approach is based on three dimensional VOF method and different interpolation treatments are utilized to study the bubble formation when dealing with high viscous fluids. The numerical approach is first valuated by the experimental data from the literature, and then the entire bubble formation processes in viscous fluids in a wide range of viscosities are investigated. Finally, the behaviors of the formed Taylor bubble by the flow-focusing junction in micro-channel at different viscosities are also studied in detail.

1.1 Mathematic model and numerical procedures

1.1.1 The volume of fluid method

The volume of fluid (VOF) method is a popular interface tracking method in which the volume fraction α is defined as the volume of the primary phase divided by the volume of the cell. In the present study, the primary phase is specified as the liquid phase, and hence the volume fraction α equals 1 when the cell is full of liquid phase while it is 0 when the cell is full of gas phase. Additionally, the interfacial cell is indicated by ε < α < 1 − ε, where ε is a small value of 10^–6. The continuity equation for the volume faction is shown as follows:

$$\frac{{\partial \left( {\alpha \rho } \right)}}{\partial t} + \nabla \cdot \left(\alpha \rho {{\mathbf{u}} } \right) = 0.$$

(1)

In the finite volume solver used in the present study, the convection and diffusion fluxes through the cell faces should be calculated when solving the above continuity equation. Two kinds of interpolation treatments for the cells near the interface are implemented to estimate the fluxes at the cell faces. The first is the widely-used geometric reconstruction (Geo-Reconstruction) method. Once the linear interface position within each interfacial cell is known based on a piecewise-linear approach, the advection across the cell faces can be estimated by geometrical relations using the distributions of the normal and tangential velocities on the faces. The other approach is the compressive interface capturing scheme for arbitrary meshes (CICSAM) which is a modified high resolution differential scheme based on the normalized variable diagram (Leonard 1991). Coupled by the donor–acceptor scheme, the advection of fluid through the face can be estimated, and unlike the Geo-Reconstruction method, the CICSAM does not have to introduce geometrical representation of the interface but to satisfy the aforementioned conditions by choosing proper discretization scheme. The CICSAM has been considered to be more suitable for fluid flow with high viscosity ratio between the liquid and gas phases (Wacławczyk and Koronowicz 2008). Therefore, the CICSAM is also employed to discretize the convective term in the continuity equation of volume fraction in the case of relatively high viscosity.

A single momentum equation is solved throughout the domain, which can be written as:

$$\frac{{\partial \rho {\mathbf{u}}}}{\partial t} + \nabla \cdot \left( {\rho {\mathbf{u}} {\mathbf{u}}} \right) = - \nabla p + \nabla \cdot \left( {\mu \left( {\nabla {\mathbf{u}} + {\nabla {\mathbf{u}}} ^{{\text{T}}} } \right)} \right) + \rho {\mathbf{g}} + {\mathbf{f}}_{\sigma } ,$$

(2)

where u represents the velocity vector which is shared among phases. It should be noticed that the momentum equation is dependent on the volume fraction through the volume-fraction-averaged properties, i.e., ρ and μ. f_σ is the volumetric surface tension which can be estimated based on the continuum surface force (CSF) model.

$${\mathbf{f}}_{\sigma } = \sigma \kappa \nabla \alpha ,$$

(3)

where σ is the surface tension coefficient and κ is the curvature at interface and can be computed by the local gradients at the interface as:

$$\kappa = \nabla \cdot {\hat{\mathbf{n}}},$$

(4)

where ${\hat{\mathbf{n}}}$ is the unit normal of the interface in the following form:

$${\hat{\mathbf{n}}} = \frac{\nabla \alpha }{{\left| {\nabla \alpha } \right|}}.$$

(5)

As mentioned above, the Geo-Reconstruction scheme and the CICSAM (Ubbink 1997) are both implemented in the present study. Correspondingly, the implementations for the surface terms differ slightly based on Eq. (3). The CICSAM does not have to consider any density averaging while surface tension term of Geo-Reconstruction scheme should be rewritten in a smoothed superposition form:

$${\mathbf{f}}_{\sigma } = \frac{{\sigma \rho \kappa \left( {\nabla \alpha } \right)}}{{{1 \mathord{\left/ {\vphantom {1 {2\left( {\rho_{{\text{g}}} + \rho_{{\text{l}}} } \right)}}} \right. \kern-\nulldelimiterspace} {2\left( {\rho_{{\text{g}}} + \rho_{{\text{l}}} } \right)}}}}.$$

(6)

The properties appearing in the equations are determined by the presence of the component phases in each control volume. For example, ρ in each cell is calculated by the following equation:

$$\rho = \rho_{{\text{l}}} \alpha + \rho_{{\text{g}}} \left( {1 - \alpha } \right).$$

(7)

The wall adhesion is also taken into account by a contact angle which is used to estimate the interface normal in the cells near the wall. The normal to the interface at the wall is defined as follows:

$${\hat{\mathbf{n}}} = {\mathbf{n}}_{{\text{w}}} \cos \theta + {\mathbf{n}}_{{\text{t}}} \sin \theta .$$

(8)

where θ is the contact angle, n_w is the unit normal vector to the wall and n_t is the unit tangential to the wall toward the primary phase which is liquid phase in the present study. Based on the above interface normal, the local curvature is calculated and implemented to estimate the surface tension force, and more detail can be found in Jia et al. (2014).

1.2 Numerical procedures

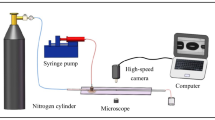
In nearly all the experimental studies, the inlet lengths upstream the junction were many times of the channel width to achieve steady supply of each phase. In some studies (Garstecki et al. 2006; Fuerstman et al. 2007), even the “resistors” containing mesh or serpentuator was applied to improve the flow stability. The flow-driven approaches in the experiments can be categorized into two types: one is to use the pressurized tanks which can maintain a constant high pressure and propel the fluid stream into the micro-channel; while the other is using the syringe pump that leads to a constant flow rate (Dang et al. 2014; Lu et al. 2014, 2016). It should be noticed that the constant inlet flow rates can also be achieved in the steady experimental stage using pressure-driven approach (Garstecki et al. 2005, 2006; Cubaud and Ho 2004; Dietrich et al. 2008). In order to follow the inlet conditions of the experimental studies in the literature, we implement constant velocity inlet condition in all numerical cases even in the pressure-driven experiments using the reported inlet flow rates.

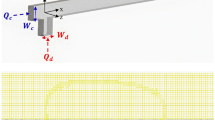
Figure 1 is the computational domain for a typical microfluidic flow-focusing junction in the present study. Following the experimental setup (Cubaud et al. 2005; Lu et al. 2014), the gas is injected through the middle inlet and the liquid is emitted from both side-inlets which are colored by green in the figure. The experiments were carried out in a flow-focusing devices with square cross-section of w × w, where w is the channel width, as shown in the figure. The bubble length d is estimated by the distance between the front and rear ends for a specific bubble, as shown in Fig. 1a, and the slug distance L is defined as the length between the rear ends for the neighboring bubbles. The normalized hydrodynamic entrance length for laminar flow in a square duct can be estimated by ${{x_{{\text{c}}} } \mathord{\left/ {\vphantom {{x_{{\text{c}}} } w}} \right. \kern-\nulldelimiterspace} w} = \left[ {\frac{3.44}{{f{\text{Re}} }}} \right]^{2}$(Plessis and Collins 1992), where f is the local friction factor. The largest hydrodynamic entrance length x_c in the present study is much smaller than 0.5w; hence, the inlet length is chosen to be larger than 0.5w and is designated to be 1.0w for all the cases in the numerical calculation. Consequently, the channels upstream the junction are simplified, and the computational cost can be therefore significantly reduced. In the previous study, the gravity effect was found possibly ignored in a horizontal microchannel when the confinement number (${\text{Co}} = \sqrt {{\sigma \mathord{\left/ {\vphantom {\sigma {g\Delta \rho D^{2} }}} \right. \kern-\nulldelimiterspace} {g\Delta \rho D^{2} }}}$) is larger than 1.0 (Menech et al. 2008), and the confinement numbers in the present study are all larger than 3.8. Due to the symmetry of the geometrical configuration, the computational domain for calculation can be largely simplified by setting two symmetry interfaces in the domain shown in Fig. 1b, and the entire domain is structured by hexahedral mesh grid which is densified in the flow-focusing region and the downstream region while it is coarsened in the inlet region. The finest grid size is about 0.025w to achieve grid independence in the calculations, and more details can be found in the appendix.

Fig. 1

The typical computational domain of the microfluidic flow-focusing junction. a The computational domain, b the illustration of symmetrical mesh

In the present study, the finite volume Computational Fluid Dynamics (CFD) solver ANSYS Fluent (V14.0) is used to solve the governing equations, and the pressure–velocity coupling is achieved by algorithm of pressure implicit with splitting of operators (PISO). Due to the poor convergence performance of CICSAM for low Ca (Ca < 10^–3) in the preliminary numerical tests, the CICSAM is only used for the cases with high viscosity while the Geo-Reconstruction method is implemented for all the cases. In order to ensure the convergence for the cases with wide ranges of viscosity and gas–liquid flow ratio, variable time step is utilized in which the time step automatically varies according to restriction by the Courant number (Cont) that is defined as the time step to the characteristic time of transit of a fluid element across a control volume.

$${\text{Cont}} = \frac{\Delta t}{{{{V_{{{\text{cell}}}} } \mathord{\left/ {\vphantom {{V_{{{\text{cell}}}} } {\sum\nolimits_{{\text{f}}}^{N} {{\mathbf{u}}_{{\text{f}}} \cdot {\mathbf{n}}_{{\text{f}}} A_{{\text{f}}} } }}} \right. \kern-\nulldelimiterspace} {\sum\nolimits_{{\text{f}}}^{N} {{\mathbf{u}}_{{\text{f}}} \cdot {\mathbf{n}}_{{\text{f}}} A_{{\text{f}}} } }}}},$$

(9)

where $\Delta t$ is the time step. The Courant number is maintained at 0.2 and the time step is adjusted between 1 × 10^–5 s and 1 × 10^–7 s according to Eq. (9) during the iterations.

2 Results and discussion

2.1 Validation of the numerical method

In this section, the numerical approach is first verified to validate the numerical method. As mentioned above, Cubaud et al. (2005) have presented the systematic experimental studies of bubble formation in a microchannel with focusing-junction, and the results were confirmed by other researchers (Li et al. 2013). Therefore, such experimental results (Cubaud et al. 2005) can be a very good reference to validate our numerical approach. Both the height and width of microchannel were 100 μm, and the experiments were performed on the air bubble formations in water or water with surfactants of sodium dodecyl sulfate (SDS, 8.0 mM/l), and the corresponding surface tensions for these two liquids were 73.0 mN/m and 38.0 mN/m, respectively. Nevertheless, the differences of density and viscosity between the pure water and surfactant solution were negligibly small. The viscosity of water was about 1.0 mPa s, and the corresponding Ca numbers for the cases were less than 4.0 × 10^–3. The inlet flow rates for the gas phase and liquid phase are shown in Table 2, and the liquid fractions defined as $\phi_{{\text{l}}} = {{Q_{{\text{l}}} } \mathord{\left/ {\vphantom {{Q_{{\text{l}}} } {\left( {Q_{{\text{l}}} + Q_{{\text{g}}} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {Q_{{\text{l}}} + Q_{{\text{g}}} } \right)}}$ are also listed.

Table 2 The inlet flow rates of the gas phase and liquid phase

Shown in Fig. 2 is a typical numerical result of bubble formation process in the microfluidic flow-focusing junction, where the liquid phase penetrates into the main channel from the side inlets while the gas is injected from the upstream of the main channel. The two immiscible fluids form an interface at the junction, and the gas thread begins to expand downstream. Correspondingly, a neck connecting the inlet and gas tip appears, and the interface approaches the centerline until the neck breaks. Then, a new bubble flows downstream in the main channel, while the tip of the gas stream retracts to the inlet and the bubble formation process repeats. Due to the relatively small Ca (Ca < 4 × 10^–3), the bubble formation process shows an apparent peculiarity that the gas thread is squeezed by the blocking liquid in the junction. Herein, the viscous force of the liquid phase is suppressed and the channel is refilled by the gas easily before the next pinch-off occurs. This is the bubbling regime which contrasts to the shearing regime that occurs only for larger Ca number where the gas thread is not confined by channel wall.

Fig. 2

A typical bubble formation process (air/water, u_g = 0.286 m/s, u_l = 0.113 m/s). The time interval is 0.3 ms

Figure 3 shows the comparison of the bubble length between the experimental results and numerical results. It can be found that the numerical results agree fairly well with the experimental data, and there is a reciprocal relationship between the normalized bubble length and the liquid fraction, i.e., ${d \mathord{\left/ {\vphantom {d w}} \right. \kern-\nulldelimiterspace} w} = \phi_{{\text{l}}}^{ - 1}$. The reciprocal relationship can be derived from the evolution of gas thread within the squeezing process during the bubble formation. A typical schematic of bubble formation process is shown in the inset. It can be seen that the gas thread gradually grows into main channel, and then the neck appears and is squeezed by the liquid due to the blocking. Finally, the pinch-off occurs and a new bubble is formed. The bubble size seems to depend on the pinch-off time (rupture time) which can be estimated by $\tau = w/u_{{\text{l}}}$ (Cubaud et al. 2005; Pohorecki and Kula 2008; Lu et al. 2014). Moreover, the gas thread grows with an average velocity u_ave which can be estimated by $u_{{{\text{ave}}}} = \left( {Q_{{\text{l}}} + Q_{{\text{g}}} } \right)/w^{2}$ in the square channel within the pinch-off time. Consequently, the approximation of the bubble length can be written as:

$$d = u_{{{\text{ave}}}} \tau = \phi_{{\text{l}}}^{ - 1} w,$$

(10)

where it displays a reciprocal relationship. Coincidentally, the same correlation to predict the bubble size in the Y-type flow junction was also developed in an analytical study of Pohorecki and Kula (2008), i.e., ${d \mathord{\left/ {\vphantom {d w}} \right. \kern-\nulldelimiterspace} w} = \frac{{u_{{\text{l}}} + u_{{\text{g}}} }}{{u_{{\text{l}}} }} = \phi_{{\text{l}}}^{ - 1}$. In addition, a simple scaling correlation was also proposed to predict droplet length by ${d \mathord{\left/ {\vphantom {d w}} \right. \kern-\nulldelimiterspace} w} = 1 + {{Q_{{{\text{oil}}}} } \mathord{\left/ {\vphantom {{Q_{{{\text{oil}}}} } {Q_{{{\text{water}}}} = }}} \right. \kern-\nulldelimiterspace} {Q_{{{\text{water}}}} = }}\phi_{{{\text{oil}}}}^{ - 1}$ in the experimental study of Garstecki et al. (2006). It can be found that these studies led to a very similar expression of the bubble or droplet length, whether the cross section is rectangle or circle. The common feature for these studies is that their bubble formations were all squeezing process due to the blocking of the fluid thread which occupied the main channel, and the bubble formation is dominated by the pinch-off which is determined by the flow rate from the side inlets.

Fig. 3

Comparison of the bubble length between the experimental results and numerical results

The distance L between bubbles is also an important factor for the Taylor bubble flow and has always been used as the characteristic length of the unit cell proposed in the dissolution and reaction processes (Plessis and Collins 1992). The liquid film is thin when the Ca is small, and hence the bubble shape can be simplified as a rectangular plug with a volume of dh². Based on the mass conservation, the distance between bubbles can be simply expressed as a function of bubble length in which the distance L can be derived from the above analysis and is formulated as $1{ - }\phi_{{\text{l}}} = {d \mathord{\left/ {\vphantom {d L}} \right. \kern-\nulldelimiterspace} L}$, and then the approximation of ${L \mathord{\left/ {\vphantom {L w}} \right. \kern-\nulldelimiterspace} w} = {{\left( {{d \mathord{\left/ {\vphantom {d w}} \right. \kern-\nulldelimiterspace} w}} \right)^{2} } \mathord{\left/ {\vphantom {{\left( {{d \mathord{\left/ {\vphantom {d w}} \right. \kern-\nulldelimiterspace} w}} \right)^{2} } {\left( {{d \mathord{\left/ {\vphantom {d {w - 1}}} \right. \kern-\nulldelimiterspace} {w - 1}}} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {{d \mathord{\left/ {\vphantom {d {w - 1}}} \right. \kern-\nulldelimiterspace} {w - 1}}} \right)}}$ can be obtained based on the above relations between the bubble length and flow rate ratio (Cubaud et al. 2005). The distance L is also numerically calculated in the present study and compared with the above approximation. As can be seen in Fig. 4, the numerical results agree fairly well with the approximation for the normalized slug length. Moreover, it can be found that the minimum appears when the bubble lengths approximately equal 2w when the gas flow rate equals liquid flow rate.

Fig. 4

Variation of the normalized distance L/w with the normalized bubble length d/w

2.2 Bubble formation in viscous fluids

In the above section, the numerical method has been validated for the conventional fluids with relatively small viscosities. In order to study the bubble formation process in viscous fluids, the experimental study of Lu et al. (2014) is chosen as reference in which the aqueous solutions with different mass fractions of glycerol were used as the working fluids with a wide range of viscosity, as shown in Table 3. The experiments were also carried out in a square microchannel with cross section of 600 × 600 μm, and both the solution and nitrogen gas were injected into the channel by syringe pumps at constant flow rates. Hence, the constant inlet boundary condition is also used in the numerical calculation, and both the liquid and gas inlet flow rates are specified following the experimental conditions. Additionally, the static contact angle is 70° according to the estimation of Lu et al. (2014).

Table 3 The properties of the aqueous solutions

Figure 5 shows the comparison between the experimental data and the numerical results by different interface interpolation treatments. It can be found that the Geo-Reconstruction method yields better results than the CICSAM that fails to converge due to large instability at very small Ca and shows larger derivation when the Ca is up to 0.13. The numerical results calculated by the Geo-Reconstruction scheme agree fairly well with the experimental data while it also shows large derivation at small Ca. The possible reason might be due to inaccurate wetting properties which was proved to significantly influence the bubble length (Dang et al. 2014). The contact angle estimated from the optical visualization is found to be much smaller than the reported value by Lu et al. (2014) which is used in our study. Taylor (1961) had proved that the thickness of the liquid film between bubble and side wall increased with the increase of the Ca number, which can be described as ${\delta \mathord{\left/ {\vphantom {\delta d}} \right. \kern-\nulldelimiterspace} d} = 0.66{\text{Ca}}^{2/3}$. Consequently, the influences of the contact angle are weakened due to thick liquid film at relatively large capillary number. Thus, the numerical results agree much better with the experimental data under the conditions with larger Ca number. Another possible reason might be the existence of the contaminant in the experiments. The accumulation of the contaminant at the bubble rear induces a gradient of surface tension which leads to surface deformation compared to the non-contaminant cases (Parhizkar et al. 2015).

Fig. 5

The normalized bubble length for bubble formed in fluids with different viscosities. a Comparison of the experimental data with numerical results based on different interpolation treatments, b the difference of the bubble shapes between the capturing methods, (b-1) μ_l = 69.5 mPa s, Ca = 0.0248 (b-2) μ_l = 400 mPa s, Ca = 0.139. The blue lines represent the bubbles calculated by CICSAM, while the black lines correspond to the Geo-Reconstruction method. Q_l = Q_g = 30 mL/h

Furthermore, there are two distinct regimes in the evolution of the bubble length, as shown in Fig. 5a, where a transition can be noticed. When the Ca is smaller than 7 × 10^–3, the bubble length decreases significantly while the bubble length almost keeps constant with further increase of the Ca. A similar phenomenon was also found by Loo et al. (2016) and Guo and Chen (2009), in which a transition capillary number from squeezing regime to shearing regime was found around 5.8 × 10^–3. This phenomenon can be attributed to the change of the bubble formation scheme. When the Ca is small, the bubble formation is dominated by the squeezing process, whereas the bubble formation is determined by the shear force at high Ca. As shown in Fig. 5b, it can be found that the thicknesses of the liquid films δ become larger with increasing the Ca. Moreover, the thicknesses of the liquid film and the bubble shapes calculated by the Geo-Reconstruction method and CICSAM are almost the same. The difference between two methods mainly lies in the bubble length which is determined during the bubble formation process. In general, the Geo-Reconstruction method is more suitable than the CICSAM even in the cases of large viscosity ratio in the present study.

The bubble formation is dominated by the competition of surface tension, static pressure and viscous shear stress (Dietrich et al. 2008), and the pressure difference between the liquid phase and gas phase is the most dominant driving force (Cubaud et al. 2005; Garstecki et al. 2005). In the present study, the evolutions of the pressure difference between the liquid and gas inlets are calculated, where the local pressure is calculated by the area-weighted-average method, i.e., $P_{{{\text{ave}}}} = \frac{1}{A}\int {P{\text{d}}A} = \frac{1}{A}\sum\nolimits_{i = 1}^{n} {P_{i} \left| {A_{i} } \right|}$. It can be found that the pressure condition is closely linked with the bubble formation process, as shown in Fig. 6a. Moreover, the regular fluctuations appear after initial one or two cycles, and an entire bubble formation cycle can be clearly observed by the peaks and valleys during various stages from I to IV, as shown in Fig. 6b. When the breakup occurs, a new Taylor bubble is formed and the pressure difference reaches the valley (i.e. stage I). Afterwards, the pressure difference increases gradually with the moving gas tip until the neck appears which connects the emerging bubble with the gas-inlet (i.e., stages I–II). Subsequently, the gas tip expands on the main duct and the liquid phase keeps on squeezing gas thread, as shown in stages II–III. When the neck is thin enough, the gas thread breaks up due to the increasing surface tension. Correspondingly, the pressure difference decreases quickly to the valley at stage IV, and the entire process repeats periodically. It can be found that the pressure difference differs due to the variations of viscosities. With the increase of the liquid viscosity, the cycle is shorter with smaller amplitude. As mentioned above, the liquid film becomes thicker due to larger viscosity, and the bubble formation changes from squeezing mode to shearing mode. The viscous force of the liquid phase becomes dominant and the gas thread cannot fill the entire cross section due to the thick liquid film, and the neck appears and retracts earlier and more quickly before pick-off occurs. Sullivan and Stone (2008) have experimentally studied the bubble generation frequency within microfluidic flow-focusing junction, and they found that the frequency in steady state can be approximated by $f \propto Q_{{\text{l}}} {{\left( {P_{{\text{g}}} - \Delta P_{{\text{l}}} } \right)} \mathord{\left/ {\vphantom {{\left( {P_{{\text{g}}} - \Delta P_{{\text{l}}} } \right)} {P_{{\text{g}}} }}} \right. \kern-\nulldelimiterspace} {P_{{\text{g}}} }}$, where ΔP_l is the liquid pressure drop along the entire channel, and P_g is the pressure at gas inlet. It can be found that when the P_g is specified, the larger ΔP_l, the smaller f is. Consequently, the frequency decreases with the increase of liquid pressure drop due to the increasing liquid viscosity. In addition, an interesting phenomenon is that the peak value of the pressure difference at 5.7 mPa s is larger than that at 69.5 mPa s. As mentioned above, the bubble formation scheme for the case of μ_l = 5.7 mPa s is squeezing process, in which the gas tip almost fills the whole rectangular groove, blocking the flow channel and causing pressure accumulations at the junction region. Here, the gas–liquid interface contacts the channel wall, which induces a wall adhesion force shown in the Fig. 6c. Therefore, the pressure difference for the case of μ_l = 5.7 mPa s not only have to overcome the effect of viscous force, but also the extra adhesion force, and hence the peak pressure difference is a little higher.

Fig. 6

The fluctuation of the pressure difference between the gas and liquid inlets, ΔP = P_ave,l − P_ave,g, and the instantaneous profiles

Figure 7 shows the comparison of the experimental results and numerical results during the bubble formation where the bubble shapes are indicated by the iso-surface of α = 0.5. As can be seen in the figure, a sequence of pictures of the bubble formations are shown and compared with the experimental visualization results. The time is normalized to the period of bubble formation and the instantaneous numerical results are chosen at the similar normalized time instants. As depicted in the figures, the shape and size of the bubble of the numerical results agree fairly well with those of the experimental results at difference moments. Moreover, the bubble tip connecting the gas inlet after the bubble formation is apparently sharper in the case of larger viscosity (μ_l = 400 mPa s), as shown in Fig. 7b. The reason is that the viscous force is strong enough to suppress the surface tension force, which smooths and minimizes the phase interface, and the interface maintains a sharp tip. Due to the continuous inlet flow, the emerging gas tip extends in the flow-focusing region, and gas thread prolongs into the main channel along the flow direction. The gas thread also approaches the side wall until touching the liquid film whose thickness is proportional to the viscosity, i.e.,$\delta \propto \mu_{{\text{l}}}$ (Parhizkar et al. 2015). The bubble keeps on growing and a neck appears connecting the gas tip to the gas inlet. When the concave neck is tiny enough, the bubble pinch-off occurs and a new bubble is formed finally. In the case of larger viscosity, the liquid film becomes thicker and leads to slender bullet bubble whose rear is approximately flat. The reason can also be attributed to the significant influence of the viscous force at relatively large viscosity.

Fig. 7

Comparison of the experimental results (left) and the numerical results (right) of the bubble formation process. a 90 wt% glycerol in water, μ_l = 163 mPa s, Ca = 0.0575; b 98 wt% glycerol in water, μ_l = 400 mPa s, Ca = 0.139. Q_l = Q_g = 30 mL/h

Figure 8 shows the normalized bubble volume at different viscosities and flow rate ratios. The liquid flow rate is 30 mL/h following the experimental condition of Lu et al (2014). The bubble volumes are calculated directly by integrating the gas phase, i.e.,$V_{{\text{B}}} \propto \left( {\mu_{{\text{l}}} Q_{{\text{l}}} } \right)^{ - 1}$. Apparently, it can be found that the bubble volume decreases with the increase of the viscosity, which can be attributed to the decrease in the pinch-off time. At larger viscosity, the liquid film between the gas and side wall is thicker, and the neck for bubble formation appears earlier and is narrower than at smaller viscosity. Consequently, bubbles form more frequently. Similar phenomena were observed in the experimental study of Garstecki et al. (2005), and it was found that the bubble volume was inversely proportional to the viscosity and can be scaled by a correlation of $V_{{\text{B}}} \propto \left( {\mu_{{\text{l}}} Q_{{\text{l}}} } \right)^{ - 1}$. However, in the present study, the numerical results of bubble volume follows a power-law trend of the flow rate ratio (Q_g/Q_l) and can be written as $V_{{\text{B}}} \propto \left( {{{Q_{{\text{g}}} } \mathord{\left/ {\vphantom {{Q_{{\text{g}}} } {Q_{{\text{l}}} }}} \right. \kern-\nulldelimiterspace} {Q_{{\text{l}}} }}} \right)^{\gamma }$. As shown in the figure, at γ = 0.52, the trend of the numerical results agrees with the experimental results (Lu et al. 2014) within a maximal derivation of 17%. Based on the relation between the bubble length and liquid fraction φ_l shown in Eq. (10), the bubble volume can be derived as:

$$V_{{\text{B}}} = dw^{2} = \phi_{{\text{l}}}^{ - 1} w^{3} ,$$

(11)

where

$$\phi_{{\text{l}}}^{ - 1} = \left( {1 + {{Q_{{\text{g}}} } \mathord{\left/ {\vphantom {{Q_{{\text{g}}} } {Q_{{\text{l}}} }}} \right. \kern-\nulldelimiterspace} {Q_{{\text{l}}} }}} \right).$$

(12)

Fig. 8

The normalized bubble volume in viscous fluids at various viscosities and flow ratios Q_l = 30 mL/h

The results of Eq. (11) are also shown by blue line in Fig. 8 as well as in the inset in which the normalized bubble volume is plotted with the liquid fraction. It can be found that the results at μ_l = 5.7 mPa s agree very well with the predictions by Eq. (11). As mentioned above, the approximation of Eq. (11) is more reasonable at relatively small viscosity; therefore, the results of Eq. (11) is valid at small viscosity. Herein, the bubble formation is dominated by the squeezing process which is determined by the liquid flow rate. With the increase of the viscosity, the normalized bubble volumes decrease gradually and deviate from the approximation of Eq. (11).

During the bubble formation, the gas tip moves downstream along the main channel until a new bubble is formed and a new tip appears; hence, the evolution of the gas tip can be a good indicator for the evolution of the gas thread and helpful to understand the bubble formation in detail. Figure 9 shows the positions of the gas tip front and the bubble profiles during a bubble formation process. It can be seen that the position of the gas tip moves downstream slightly at the beginning until the neck appears and then it moves almost linearly. The transition delays with the decrease of the viscosity because the gas thread spends more time to refill the junction due to thinner liquid film at smaller viscosity. Based on the mass balance of the liquid in a reference frame moving with the bubble tip at an arbitrary axial position of x, the following equation can be formulated (Taylor 1961):

$$u_{{\text{t}}} \left( {A_{{{\text{ch}}}} - A_{{\updelta }} } \right) = u_{{{\text{in}}}} A_{{{\text{ch}}}} ,$$

(13)

where u_t is the velocity of the tip, and A_ch and A_δ are the cross-section area of the channel and liquid film, respectively. u_in is the inlet velocity of the main channel and equals 0.023 m/s in the present study. It can be found that the gas tip velocities are proportional to the cross-section area of the liquid film, and hence the corresponding u_t increases with the viscosity.

Fig. 9

The evolutions of the gas tip at different viscosities. Q_l = Q_g = 30 mL/h. The solid lines are eye guides

2.3 The behaviors of the formed Taylor bubbles in the main channel in viscous fluids

As shown in the above sections, the shapes and sizes of the Taylor bubbles formed in viscous fluids by the flow-focusing junction are significantly influenced by the viscosity. In this section, the details of the flow behavior of the Taylor bubble and the surrounding liquid in viscous fluids are presented, which include the local flow field characteristics and the pressure profiles.

The mass transfer of the Taylor bubbly flow has shown that the recirculation flow within the liquid slug promotes the mixing of species (Yu et al. 2007; Jia and Zhang 2016). Fries et al. (2008) experimentally studied the flow characteristics in the liquid slug using micro-resolution particle image velocimetry (μ-PIV), and the rotating vortices symmetrical to channel center axis were clearly observed. Shown in Fig. 10 are the flow characteristics of the Taylor bubbly flow at μ_l = 69.5 mPa s and μ_l = 400 mPa s. The streamlines in the liquid slug of the numerical results on the xz-plane are also shown by white curves in the figure, and it should be noticed that the superficial velocity along the flow direction is calculated by u_x,s = u_x − U_B, where U_B is the bubble velocity. At equal flow rate of each phase, symmetrical vortices appear in the liquid slug in the case of smaller viscosity while there is no recirculation flow in the liquid slug in the case of larger viscosity. Whether the recirculation flow exists can be judged by a discriminant (Taylor 1961):

$$\left\{ {\begin{array}{*{20}c} {{{u_{{\text{B}}} } \mathord{\left/ {\vphantom {{u_{{\text{B}}} } {u_{{{\text{tot}}}} }}} \right. \kern-\nulldelimiterspace} {u_{{{\text{tot}}}} }} < C} & {\text{recirculation flow}} \\ {{{u_{{\text{B}}} } \mathord{\left/ {\vphantom {{u_{{\text{B}}} } {u_{{{\text{tot}}}} }}} \right. \kern-\nulldelimiterspace} {u_{{{\text{tot}}}} }} \ge C} & {\text{bypass flow}} \\ \end{array} } \right.{ ,}$$

(14)

where u_tot = 0.046 m/s, C = 2 for a circle tube and 2.096 for a square channel. The bubble velocities are estimated by the bubble positions shown in Fig. 10c, where the bubble position changes almost linearly with time, and the bubble velocities u_B can be estimated by the slope and are 0.067 m/s and 0.097 m/s at μ_l = 69.5 mPa s and μ_l = 400 mPa s, respectively. Consequently, it can be found that the value of ${{u_{{\text{B}}} } \mathord{\left/ {\vphantom {{u_{{\text{B}}} } {u_{{{\text{tot}}}} }}} \right. \kern-\nulldelimiterspace} {u_{{{\text{tot}}}} }}$ for the case of large viscosity (μ_l = 400 mPa s) is about 2.11 which meets the condition of C = 2.096 for the bypass flow in Eq. (14).

Fig. 10

Flow characteristics of the liquid plug, a μ_l = 69.5 mPa s, b μ_l = 400 mPa s, c the bubble positions. The gas phase and liquid phase are denoted in blue and red, respectively. The solid lines are the linearly fitted results

In the previous numerical studies (Qian and Lawal 2006; Guo and Chen 2009; Yu et al. 2007), only the pressure drop at the center axis was discussed, and the sharp pressure rise or drop at the phase interface may mask other important information in cap region or gutters at the corners (Fuerstman et al. 2007). To this end, the pressure along the flow direction at the center axis (black line) and gutter (red line) as well as the average pressure of the cross sections are obtained, and the schematic illustrations are shown in Fig. 11a. The evolutions of the pressure differences at μ_l = 163 mPa s and μ_l = 400 mPa s are chosen as examples and are shown in Fig. 11b and c. It can be found that the average pressure is indeed between the pressures along the center and gutter, which indicates that the contribution of the pressure drop in the channel gutter cannot be ignored. As shown in the figure, the pressure drop along the center axis is sharp due to the surface tension force on the interface. However, both average pressure and gutter pressure seem to change gradually, and four distinct regions can be noticed in the pressure profiles: single phase region, the rear cap, the body and the front cap. Besides, remarkable differences can be identified within these regions. The pressure drop at caps are significant at μ_l = 163 mPa s, while the pressure drop becomes insignificant at the rear cap at larger viscosity due to the viscous force in the liquid. Moreover, the rear surface of bubble at μ_l = 400 mPa s is nearly flat.

Fig. 11

The pressures of the Taylor bubble along the flow direction at different locations a schematic of the locations, and the pressure profiles for the cases of b μ_l = 163 mPa s and c μ_l = 400 mPa s

All the pressures decrease linearly along the channel in the single phase regions. The pressure drop of laminar flow of single phase through a rectangular channel can be estimated by the following equations (Fuerstman et al. 2007):

$$\Delta P = \frac{a\mu QL}{{h^{3} w}} = kL$$

(15)

$$a = 12\left[ {1 - \frac{192h}{{\pi w}}\tanh \left( {\frac{\pi w}{{2h}}} \right)} \right]^{ - 1} ,$$

(16)

where w is the width of channel, h is the height of the channel and equals w for the square channel here, and a is the dimensionless parameter that is determined by the aspect ratio w/h in the above equation. It can be found that the pressure drop changes linearly with the channel length in the single phase region. The corresponding parameter k are estimated to be 606.7 and 1444.6 for the cases of μ_l = 163 mPa s and μ_l = 400 mPa s, respectively, and the predicted results (i.e., the dash line) agree well with the numerical results, as shown in the figure.

3 Conclusion

In the present study, a systematic 3D numerical study of the bubble formation process in viscous fluids in a microfluidic flow-focusing junction is carried out based the VOF method. The viscosities range are from 5.6 to 400 mPa s, and the viscous ratio (μ_l /μ_g) is up to 2.2 × 10⁴. Both the Geo-Reconstruction method and the CICSAM are implemented to solve the continuity equation of the volume faction in the present study. The numerical results are compared with the experimental results and show good agreements, and the following conclusions can be drawn:

• 1. For the conditions that the capillary number is small, i.e., Ca < 4 × 10^–3, the gas thread easily expands to occupy the channel and is squeezed by the blocking liquid, and consequently a reciprocal relationship can be derived to predict the bubble length. The Geo-Reconstruction method is found to be more suitable than the CICSAM in the case of high viscosity ratio in the present study.

• 2. For the bubble formation process in the viscous fluids at various viscosities, the fluctuation of the inlet pressure difference is significantly influenced by the liquid viscosity, and the bubble lengths decrease with the increase of the viscosity at the same flow rate. In addition, a transition from the squeezing scheme to shearing scheme is found to occur at about Ca = 7 × 10^–3.

• 3. With the increase of viscosity, the gas thread becomes sharp at the tip, and the bubble rear cap turns to be much flat. Moreover, the gas tip moves more quickly at higher viscosity and the pinch-off time becomes shorter, and the liquid film between the gas thread and wall is found to play a very important role in that the thickness significant influences the velocity of gas tip.

• 4. At the same flow rate, the recirculation flow is found around the Taylor bubble at relatively low viscosity while there is a bypass flow at high viscosity. The pressure drop along the channel can be divided into four regions including the single phase region, the rear cap, the body and the front cap. In addition, the flow along the channel gutter is found to play an important role that leads to smaller pressure drops in the regions of the body and the caps.

This article helps to understand the hydraulic mechanisms of bubble formation in viscous fluid in microfluidic flow-focusing junction, and we hope to expand the 3D CFD for applications in microfluidics. One of the most significant advantages of the 3D calculation is that it is closer to the practical condition, while the physical quantity in the 2D calculation is constant in the third axial direction, which will inevitably result in a certain distortion. For example, in this study, we observed a gutter flow at the corner of the square channel even though the bubble surface touches the wall, and hence the hydrodynamic behavior is indeed three dimensional. In addition, such 3D feature has also been found in mixing behavior of species on the cross-junction of microfluidic (Borgogna et al. 2018), in which the calculation could not be simplified to two dimension either. Moreover, with the improvement of micro-reactor manufacturing technology and the increasing diversity of application requirements, non-planar three-dimensional microfluidic structure has become popular (Shivhare et al. 2016; Tripathi et al. 2016), which can only be predicted by 3D calculation. On the other hand, the 2D simulation is simple and easy to implement, which can greatly simplify the algorithm and solution. When dealing with complex multiphysical field coupling problems, such as phase change in multiphase flow, multiphase chemical reaction, fluid solid coupling and so on, the 2D simulation is always a good choice for reducing the model complexity and saving debugging time (Peng et al. 2020; Hill et al. 2018). Nevertheless, with the improvement of computational capacity, the 3D computing is always worth further research to obtain more realistic results.

Appendix

As mentioned, the flow-focusing junctions in the present study consists of square channels, and the hexahedral mesh is used. The aspect ratio of the main computational region, i.e., the bubble forming region shown in Fig. 12a, is maintained at about 1.0, and its grids are generated with constant cell size. Several structured meshes are analyzed to establish the optimal one, and the grid size (g) is varied from w/20 to w/60. The cases of the viscous fluids with different viscosities (Lu et al. 2014) are simulated with the different mesh densities, and the predicted contour lines (α = 0.5) in the x–y plane are shown in Fig. 12b, in which the lines are depicted with different colors corresponding to the grid densities. It can be seen that, with the exception of the g = w/20, the predicted results are in good agreement among one another, which presents similar shapes and identical liquid film thickness. Moreover, the difference of the predicted results between the mesh densities of g = w/40 and g = w/60 is negligible, while the case of g = w/60 has triple the number of cells in comparison with the case of g = w/40, and the computational time of the former is nearly twice that of the latter with the present resources (2.3 GHz CPUs, 2 processors, 16 cores, 128 GB RAM). Therefore, the mesh size with w/40 (i.e., 0.025w) is adopted in the calculations of the viscous fluid, which is able to offer both accurate results and reasonable computational time. Moreover, the grid size of 0.025w is also used for the calculations of Cubaud’s cases, and the corresponding grid density has met the grid independence requirement proposed by Cubaud et al. (2005), i.e., g < w/32. In addition, the gird size is only 2.5 μm, which has been proved to be small enough to accurately obtain the hydraulic characteristics of micro-reactor in our previous studies (Jia and Zhang 2016).

Fig. 12

The mesh convergence analysis. a The schematic of main region for the complete computational domain, and the predicted bubble shapes for the cases of b-I μ_l = 5.7 mPa s, b-II μ_l = 69.5 mPa s, b-III μ_l = 163 mPa s and b-IV μ_l = 400 mPa s