1 Introduction

Microfluidic devices are widely used in food (Weng and Neethirajan 2017), materials (Kulkarni and Sebastian Cabeza 2017), and biological fields (Bonn et al. 2009), with characteristics of high safety, fast reaction rate, and well controllability (Chen et al. 2015), compared with conventional equipment. The microfluidics is also a promising tool for the measurement of viscosity of fluids. Livak-Dahl et al. (2013) developed a droplet viscometer, which measures the velocity of a droplet passing through a sag to obtain viscosity at a constant pressure. Li et al. (2017) developed a simple water-in-oil continuous viscometer, which is capable for the measurement of the viscosity of Newtonian and non-Newtonian fluids with small sample volumes. Yao et al. (2018) reviewed the transport and reaction of highly viscous ionic liquids in the microreactor and found that viscosity affects fluid dynamics greatly. New correlations considering both shear and inertial forces are proposed to predict the flow regime transitions in a wide range of fluid viscosity. Several studies have been focused on the characteristics of fluid flowing in microchannels, with the features of low Reynolds number, high shear rate, and high heat transfer rate (Chevlier and Ayela 2008), among which the pressure drop of single phase flow in microchannels is a fundamental issue. Up to now, most of these studies have concerned Newtonian fluids in microchannels (Li et al. 2006; Roumpea et al. 2017; Liu et al. 2017; Al-housseiny et al. 2013; Singhal et al. 2004; Zhang et al. 2018). It is found that the expression of pressure drop of fluid flow in microchannels is in good agreement with Darcy’s law and Hagen–Poiseuille equation, to some extent. However, some studies have also found that the pressure drop of fluids in microchannels is influenced by fluid properties such as shear-thinning property, complex channel configurations, and boundary conditions; thus the results deviate from Darcy’s law and Hagen–Poiseuille equation (Wang et al. 2017; Afzal and Kim 2015; Pomeau and Villermaux 2006).

There exists deviation between the experimental data and theoretical value of the pressure drop for fluids in a microchannel, due to the size and shape of microchannels, the relative roughness, and the measurement method. Duryyodhan et al. (2014) used deionized water as the working medium to study the effect of mass flow rate, hydraulic diameter, length, and divergence angle of the microchannel on the pressure drop. The numerical analysis shows that the pressure drop has a nonlinear relationship with the mass flow rate and is inversely proportional to the square of hydraulic diameter and the divergence angle. Bahrami et al. (2007) proposed that the Poiseuille number is a function of the geometric parameters of cross-section at fixed flow rate for a certain fluid and obtained the expressions for the pressure drop in microchannels with rectangular, elliptical, and trapezoidal sections. In this model, the square root of area is used as the characteristic length, which is superior to the traditional hydraulic diameter. Akbari et al. (2011) introduced a new dimensionless number for the calculation of pressure drop for single-phase flow in microchannels with varied cross-section in laminar regime and pointed out that the perimeter of cross-section can be used as a suitable characteristic scale.

However, the flow behavior of non-Newtonian fluids in microchannels has been less concerned. Fluids that flow through microchannels and porous media exhibit high shear rates, which beyond the measurement range of the conventional rheometer (Chevlier and Ayela 2008). The rheology of non-Newtonian fluids depends on the shear rate (Pan and Arratia 2012). For example, when blood flows through small capillaries, the shear viscosity decreases with increasing shear rate. Hydraulic fracturing is an effective technique to improve the recovery of shale gas reservoirs (Sun et al. 2014). Augmented pressure generates fracture networks, which are similar to porous media (Armstrong et al. 2016). Sodium carboxymethyl cellulose, polyacrylamide, polyethylene oxide, and polyisobutylene are widely used as drag reducers for these applications, which belong to non-Newtonian fluids. When the drag reducing agent is added into porous channels, characteristics of fluid flowing in the channel are complicated due to the complex shape, length, and varied diameter of the channel, the tortuous path, and directions (Tan et al. 2017). In addition, inertial instability and secondary flow often occur in viscous flow during macroscopic rheological measurements. Up to now, the rheological characteristics of non-Newtonian fluids in microchannels have not been fully understood. In this paper, the pressure drop of Newtonian and non-Newtonian fluids in microchannels is experimentally studied to obtain the rheological properties of fluids in microchannels, from the engineering point of view.

2 Experimental materials and methods

2.1 Material

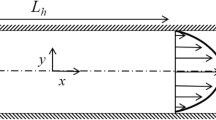
The polymethyl methacrylate (PMMA) microfluidic device used in the experiment is manufactured by Tianjin Micronano Manufacturing Technology Company. The microchannel is machined on a PMMA flat plate using a precision milling machine. The PMMA plate engraved with microchannels is attached to a piece of PMMA plate of the same size and sealed by a nut. The mechanical seal ensures no leakage. Figure 1 shows a microchannel structure with a rectangular cross-section. The actual diameter of the microchannel is calibrated using an electron microscope, with the cross-section of 393 μm × 400 μm (width × height), and the accuracy is ± 1 μm. The corners of the square cross-section in microchannels are smooth, and slight differences in manufacturing defects are negligible (Supplementary Material). The length of channel is measured to be 40 mm by a vernier caliper.

Fig. 1
figure 1

Structure of the rectangular microchannel used in the experiment

Full size image

2.2 Experimental process

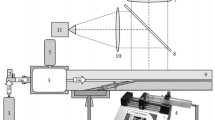
Experimental devices include microfluidic devices and fluid control systems. The fluid control system includes a peristaltic pump, a differential pressure transmitter, and a reservoir. The fluids are transported by a peristaltic pump (Lander, BT100-1F/YZ1515X, Baoding) and the flow rates of fluids range from 0.27 to 162 ml/min with an accuracy of ± 0.002 ml. The differential pressure transmitter (Honeywell, ST800, USA) is used to measure pressure drop of fluids in the microchannel, with a range of 0–200 kPa and an accuracy of 0.025%. The pressure drop is measured for the entire channel, that is, ΔPtotal = ΔPentrance + ΔPstraight. The pressure drop at the inlet is \(\frac{\Delta P}{{\frac{1}{2}\rho u^{2} }} = \lambda \frac{x}{d} + m,\) where λ is the friction factor, x is the length of the inlet section, and m is the correction coefficient for the calculation of the pressure drop for the inlet section where the fluid flow is not fully developed, usually 1.31 (Dai and Chen 2015). Then the pressure drop of fluids is calculated in the straight section. The flow rate controlled by the peristaltic pump is calibrated by the electronic balance (ST Instrument, JA5003B, Shanghai) with an accuracy of ± 1 mg, at the outlet of the channel before the experiment. Before each experiment, the liquid in the microchannel is discharged to facilitate the measurement of pressure. Prior to each experiment, the liquid in microchannels is first purged using a syringe filled with nitrogen; a small amount of glycerol adhered to the wall of the microchannel during the discharge process, and then water is injected into the microchannel using a syringe. The purpose of this procedure is to dilute the glycerol attached to the wall, which takes about 2 min. Finally, the liquid in the microchannel is purged with a syringe filled with nitrogen. The next set of experiments is not performed until no liquid is observed in the channel under the high-speed camera. Furthermore, the entire system is cleaned before experiments to ensure the accuracy of the experimental data. The sketch of the experimental procedure is shown in Fig. 2. The liquid is poured from the reservoir through the peristaltic pump into the test microchannel and finally flows into the reservoir. When a constant value has been shown for at least 3 min by the differential pressure transmitter, the fluid flow is considered as a stable state. Then, the pressure and flow rate of fluids of the experiment are recorded. All of the experiments are conducted at 20 °C and atmospheric pressure.

Fig. 2
figure 2

Experimental diagram for the measurement of pressure drop for single phase flow in a microchannel

Full size image

2.3 Fluid properties

Deionized water (Wahaha pure water, China) and aqueous glycerol–water mixtures (Analytical purity, Komiou Chemical Reagent, Tianjin) are used as Newtonian fluids. Carboxymethyl Cellulose (CMC) aqueous solutions are used as the shear-thinning non-Newtonian fluids in experiments. The viscosity of aqueous glycerol solution is measured with a capillary Ubbelohde viscometer (Ivisc, LAUDA, Germany), and the results are shown in Table 1.

Table 1 Density and viscosity of newtonian fluid at 20 °C
Full size table

The 0.1%, 0.25%, and 0.5% CMC solutions are used as a shear-thinning, non-viscoelastic fluid (USP grade, Aladdin Reagents, China). The solution is prepared in a beaker by a stirrer with the stirrer speed of 2 r/s, and an appropriate amount of CMC reagent, weighed using an electronic balance, is added slowly to water to be stirred continuously for 24 h. The rheological properties of CMC solutions are measured by a programmable rheometer (Waters, DHR-2, CHINA) at 20 °C within the range of the shear rate from 100 to 1000 s−1. Figure 3 shows the dependence of the viscosity of CMC solution on the shear rate.

Fig. 3
figure 3

The rheological property of CMC solutions measured by DHR-2 rheometer

Full size image

The viscosity of CMC can be expressed by a power law equation within a range of shear rates:

$$\eta = k\gamma^{n - 1}$$
(1)

where η is the viscosity, k represents the consistency coefficient of the fluid, and n is the flow characteristic index of the fluid. The physical properties of CMC solutions and the fitting parameters for the power law model are shown in Table 2.

Table 2 Density, power law coefficient of CMC solutions at 20 °C
Full size table

3 Results and discussion

Pressure drops of several different fluids in the microchannel are studied experimentally. The effects of fluid velocity and viscosity on the pressure drop of single-phase flow in the microchannel are investigated. In addition, the relationship between the apparent viscosity and characteristic values of the shear rate in a specific system is obtained from the measured pressure drop.

3.1 Effects on pressure drop of fluids in microchannels

The influence of different factors on the pressure drop for single phase flow in microchannels is shown in Fig. 4. Figure 4(a) shows the linear relationship between the pressure drop and the flow rate of Newtonian fluids in microchannels. As seen from the figure, basic trend of the effect of flow rates on the pressure drop is the same for Newtonian fluids in the same microchannel. However, the slope of the pressure and flow rate curve increases with the increase of the liquid viscosity, due to the augmentation of resistance with the increase of the liquid viscosity. This phenomenon coincides with the numerical results demonstrated by Fuerstman, and Morris and Henrik (Fuerstman et al. 2007; Morris and Forster 2004; Henrik 2004). The linear relationship between the pressure drop and the Reynolds number Re is also shown in Fig. 4b, which shows also that the slope is viscosity-dependent, as \(Re = {{D_{\text{h}} u\rho } \mathord{\left/ {\vphantom {{D_{\text{h}} u\rho } \mu }} \right. \kern-0pt} \mu },\) where Dh is the characteristic diameter of the microchannel, u, ρ, and µ are, respectively, the velocity, density, and viscosity of fluid. Under certain conditions, Re is proportional to the velocity of fluids, with fixed diameter of the microchannel, fluid density, and viscosity.

Fig. 4
figure 4

Dependence of pressure drop on flow rate and Reynolds number. a–b Newtonian fluids; c–d non-Newtonian fluids. The Reynolds number in Fig. 4d is the generalized Reynolds number Re*

Full size image

As shown in Fig. 4c and d, the pressure drop of non-Newtonian fluids increases nonlinearly with the increase of the flow rate and Reynolds number Re* of fluids, respectively. At low flow rates of fluids, the pressure drop increases more significantly with the increase of flow rates, which is also observed by Tang, who attributed this phenomenon to the electro-viscous effect of fluids in microchannels (Tang et al. 2012).

3.2 Comparison between the experimental results and theoretical prediction for pressure drop

3.2.1 Pressure drop of Newtonian fluids

The pressure drop of Newtonian fluid in a microchannel can be expressed by a dimensionless friction factor f (Tang et al. 2012) as follows:

$$f = \frac{2\Delta P}{{\rho u^{2} }}\frac{{D_{\text{h}} }}{L}$$
(2)

where L is the length of the microchannel, f  = 4ffanning. The Reynolds number Re indicates the ratio of the inertial force to the viscous force and is used to distinguish whether the fluid flow is laminar or turbulent. When u \(\in\) [0, 0.5], Re \(\in\) [0, 150], the fluid flow in the microchannel falls into the laminar flow region. Thus, the relationship between the friction coefficient and the Reynolds number for Newtonian fluids in the microchannel can be expressed as follows (Fig. 5):

$$\frac{f}{2} = \frac{26}{Re}$$
(3)
Fig. 5
figure 5

Relationship between the friction factor f and Reynolds number Re for Newtonian fluids in the microchannel

Full size image

It can be seen from Eq. 3 that the relationship between the friction factor f and the Reynolds number Re is close to the theoretical value fRe = 56.92, which is obtained by solving the Navier–Stokes equations for fully developed Newtonian in a rectangular section. A rectangular microchannel is used in the experiment, and the uncertainty analysis of the friction factor and Reynolds number is performed by the root and square expressions:

$$y = f(x_{1} ,x_{2} , \ldots ,x_{N} )$$
(4)
$$\delta y = \sqrt {\left( {\frac{\partial f}{{\partial x_{1} }}\delta x_{1} } \right)^{2} + \left( {\frac{\partial f}{{\partial x_{2} }}\delta x_{2} } \right)^{2} + \ldots \left( {\frac{\partial f}{{\partial x_{N} }}\delta x_{N} } \right)^{2} } ,$$
(5)

where δx1 to δxN are the uncertainties analyses for each parameter. Based on the error analysis, the errors for Reynolds number and friction factor are estimated to be ± 0.3% and ± 1.3%. Thus for fRe, the experimental value is less than the theoretical prediction.

3.2.2 Pressure drop of non-Newtonian fluids

The generalized Reynolds number of shear-thinning non-Newtonian fluids listed in Table 2 are calculated based on the power law equation (Kozicki et al. 1966, the detailed deduction is presented in Supplementary Material):

$$Re* = \frac{{\rho D_{\text{h}}^{n} u^{2 - n} }}{k}\left( {\frac{n}{a + bn}} \right) \cdot 8^{1 - n}$$
(6)

where Dh is the hydraulic diameter of the channel. The constants a = 0.2121 and b = 0.6766 for square cross-sectional channel microchannels. Because of the cross-section of 393 μm × 400 μm (width × height), microchannel section can be approximated square. Here the values of k and n have been measured by the rheometer. u \(\in\) [0, 0.8], Re \(\in\) [0, 250], indicating that the fluid flow falls into the laminar flow in the experiment. The dependence of the measured results of the friction coefficient and the Reynolds number of CMC solution is shown in Fig. 6. There exists divergence between the experimental data and the estimated value predicted by the traditional theory fRe* = 64 (Jiang 2004), which is determined by the rheological properties of the non-Newtonian fluid.

Fig. 6
figure 6

Relationship between the friction factor f and Reynolds number Re* for non-Newtonian fluids in the microchannel

Full size image

The reason why the friction factor deviates from the theoretical prediction value is mainly the loss of the import effect, which were studied by some researchers. But the import effect has been removed in the present study. In our experiment,there are three aspects that may cause the above phenomenon. First, deviations from traditional theoretical predictions due to roughness have also been studied by researchers (Judy 2011; Kandlikar et al. 2005; Yamada et al. 2011). Tang et al. (2012) found that for non-Newtonian fluid polyacrylamide (PAM) solutions in the microchannels of the three types (fused silica tubes, fused silica square channel, and stainless steel tubes), the experimental friction factors are higher than the traditional theoretical values, due to the surface roughness, inertia, and entrance length effects. The increase in surface roughness leads to an increase in the flow resistance of the fluid in microchannels. This should be responsible for the greater product of friction factor f and Re* in comparison with the traditional value for larger Re* as shown in Fig. 6. Second, the reason for the large deviation may be due to the existence of non-uniform shear field in the flow of non-Newtonian fluid in the microchannel. The non-uniform shear field of the fluid in the microchannel might be out of the range for the measurement of the rheological properties by conventional rheometer. Generally speaking, the range of the shear rate obtained by a common rheometer is 102 ~ 103s−1. However, the shear rate in the microchannel may be out of this range. A generalized Reynolds number is used in the present study, where k and n are measured using a rheometer, which may be not suitable for the relatively large or small range of shear rate in some area in microchannels. Finally, the wall slip may be present for polymer solution in microchannels in our experiments (Cuenca and Bodiguel 2013), and the wall slippage leads to the product of friction factor f and Re* less than 64.

4 Viscosity measurement based on the pressure drop of fluids in the microchannel

Pressure drops for Newtonian and non-Newtonian fluids are measured in the same microchannel and the results show that experimental data deviate from the theoretical values. Previous studies attributed the deviation to the choice of microchannel size, the measurement methods, channel shape, and wall slip (Cuenca and Bodiguel 2013) and ignored deviation due to viscosity measurements. Due to the limitation of the minimum torque, macroscopic rheometers (Gupta et al. 2016) are inaccurate in obtaining shear viscosity data for low shear rates. In addition, inertial instability and secondary flow are often encountered in rheological measurements by rheometers. Therefore, it is difficult to obtain shear viscosity data at high shear rates. The fully developed two-dimensional flow in a microchannel with the aspect ratio less than 1 can be deemed as steady flow. The pressure drop ΔP that drives the fluid flow and the fluid flow distance L can be related to the wall shear stress τw:

$$WD\Delta P = 2L(W + D)\tau_{\text{w}} ;$$
(7)

then

$$\tau_{\text{w}} = \frac{WD\Delta P}{2L(W + D)},$$
(8)

where τw is the wall shear stress, ΔP is the pressure drop of the fluid in the channel, W, D, and L are the channel width, the channel depth, and the channel length, respectively. The apparent shear rate \(\dot{\gamma }_{\text{w}}\) can be expressed as (Macosko 1994):

$$\dot{\gamma }_{\text{w}} { = }\frac{6Q}{{WD^{2} }}$$
(9)

where Q is the flow rate of fluids. As shown in Fig. 7, the wall shear viscosity and the apparent shear rate of glycerol aqueous solution with different concentrations are calculated using Eqs. (8) and (9). Hence, the viscosity in rectangular microchannel can be expresses as follows:

$$\eta = \frac{{W^{2} D^{3} \Delta P}}{12LQ(W + D)}$$
(10)
Fig. 7
figure 7

Relationship between the apparent viscosity and shear rate for Newtonian fluids in microchannels. The dotted line in the figure indicates the fitted viscosities of 20%, 40%, 60%, and 80% glycerol aqueous solutions are 0.0015 Pa·s, 0.00383 Pa·s, 0.0084 Pa·s, and 0.04434 Pa·s

Full size image

It is found that the apparent viscosity is not sensitive to the apparent shear rate as shown in Fig. 7. Meanwhile, Fig. 7 shows that the viscosities of 20%, 40%, 60%, and 80% glycerol aqueous solutions are 0.0015 Pa·s, 0.00383 Pa·s, 0.0084 Pa·s, and 0.04434 Pa·s, respectively. The values are the same as the viscosity measured by a capillary viscometer. Results of using a viscometer are 0.0015 Pa s, 0.0038 Pa s, 0.0086 Pa s, and 0.0443 Pa s. Using percentage error to describe the accuracy of the viscosity measurement, the formula is as follows:

$${\text{error}}\% = \frac{{\left| {x_{1} - x_{2} } \right|}}{{x_{2} }} \times 100\% ,$$
(11)

where x1 is the experimental value and x2 is the standard value. Calculated that percentage errors of 20%, 40%, 60%, and 80% glycerol aqueous solutions are 0%, 0.079%, 0.2%, and 0.009%. Errors are small and can be ignored. The concept of continuum mechanics as regards the viscosity as a resistance to the fluid flow in microchannels. From the molecular point of view, the viscosity can be considered as a transport coefficient in the liquid, which determines the rate at which the molecules of liquid transport momentum.

Previous verification shows that the viscosity of Newtonian fluids in the microchannel is close to the measurement by using the viscometer. Since it is a Newtonian fluid, there is no change with the shear rate, and it can be introduced when the shear rate is lower than 1000 s−1. It is consistent with the situation above 1000 s−1. Due to the viscosity in the fluid, a part of the mechanical energy of the fluid will irreversibly transform into thermal energy, and the fluid flow will have many complicated phenomena, such as boundary layer effect, friction effect, non-Newtonian flow effect, and so on (Kuttan et al. 2019; Ashish and Satyendra 2019). For the 80% aqueous glycerol solution, due to the high viscosity, it exhibits instability at low shear rates, so some of data initially appeared to be slightly deviated from the curve. It should be pointed out that more experimental work is urgent for the measurement of viscosity and rheological property of fluids based on pressure drop in a more wider range such as less than 1000 s−1, which may be of interest to biological or physiological applications of microfluidics. Sun et al. (2014) studied the flow behavior of polyacrylamide anion-deionized water mixtures in circular microchannels. From Darcy’s law, \(\eta_{\text{app}} \text{ = }k\frac{{A\text{d}P}}{{q\text{d}L}}\), where k, A, and q are fixed values for the same microchannel. Thus a simplified model of apparent viscosity is proposed as \(\eta_{\text{app}} = \frac{{({\text{d}}P/{\text{d}}L){\text{FR}}}}{{({\text{d}}P/{\text{d}}L){\text{DIwaterz}}}}\), where (dP/dL)FR is pressure gradient of friction reducer, (dP/dL)DIwater is pressure gradient of DI water. But this method ignores the instability of fluid flow and the complexity of non-Newtonian fluid properties. In this experiment, for non-Newtonian fluids, the same formula (8) and (9) are also used to calculate the wall shear stress and apparent shear rate for CMC solutions with different concentrations. Then the relationship between the apparent viscosity and the shear rate is obtained as shown in Fig. 8. The apparent viscosity of CMC solution increases with the increase of solution concentration, whereas decreases with the increase of shear rate to exhibit shear-thinning characteristics. The apparent viscosity shows a nonlinear relationship with the apparent shear rate. This relationship can be represented by a power law, which has been given in Fig. 8 and the parameters for the fitted power law equation are listed in Table 3. However, the power law equation does not agree with the rheometer measurements.

Fig. 8
figure 8

Relationship between the apparent viscosity and shear rate of non-Newtonian Fluids in microchannels. The dotted line in the figure indicates power laws of viscosities

Full size image
Table 3 Parameters in power-law relation for CMC solutions flowing in the microchannel
Full size table

In our experiment, it is considered that there exists a non-uniform shear field in the microchannel due to the velocity distributions in the radial direction in confined microchannels, leading to the viscosity distribution in the radial direction for non-Newtonian fluid in microchannels. A simple one-dimensional constitutive model of velocity distribution for non-Newtonian fluids in laminar flow in microchannels can be described as (Suman 2012) follows:

$$u(y) = \frac{{16a^{2} \Delta P}}{{\pi k\left( {\frac{{{\text{d}}u}}{{{\text{d}}y}}} \right)^{n} L}}\left[ {\left( {1 - \frac{{\cosh \left( {\frac{\pi y}{2a}} \right)}}{{\cosh \left( {\frac{\pi b}{2a}} \right)}}} \right)\sin \left( {\pi \frac{z}{2a}} \right) + \frac{1}{27}\left( {1 - \frac{{\cosh \left( {\frac{3\pi y}{2a}} \right)}}{{\cosh \left( {\frac{3\pi b}{2a}} \right)}}} \right)\sin \left( {3\pi \frac{z}{2a}} \right)} \right],$$
(12)

where u is the velocity of the fluid at y, n is the power law exponent, ΔP is the pressure drop of the fluid in the channel, L is the length of the microchannel, a, b, z are the directions of three-dimensional axis, respectively, and y is the distance from a point in the channel cross-section to the center of the channel. Figure 9 shows the velocity distribution of the fluid in microchannels. The power law index n satisfies the following relationship: n1 > n2 > n3. The curve for n1 = 1 indicates that the fluid is a Newtonian fluid and the velocity distribution is parabolic. When n < 1 and n is smaller, the curve for the velocity distribution of the non-Newtonian fluid is flatter. Equation (12) can be used to obtain the shear rate as follows:

$$\dot{\gamma } = \frac{{{\text{d}}u}}{{{\text{d}}y}} = Any^{2} \left( {\frac{{{\text{d}}u}}{{{\text{d}}y}}} \right)^{ - n - 1} \frac{{{\text{d}}^{2} u}}{{{\text{d}}y^{2} }} + 2An\left( {\frac{{{\text{d}}u}}{{{\text{d}}y}}} \right)^{ - n}$$
(13)
$$\dot{\gamma } = Any^{2} \dot{\gamma }^{ - n - 1} \dot{\gamma }^{\prime } + 2An\dot{\gamma }^{ - n} ,$$
(14)

where \(A = \frac{{16a^{2} \Delta P}}{\pi kL}\left[ {\left( {\frac{{ - \pi^{2} }}{{8a^{2} + \pi^{2} b^{2} }}} \right)\sin (\pi \frac{z}{2a}) + \frac{1}{27}\left( {\frac{{9\pi^{2} b^{2} }}{{8a^{2} + 9\pi^{2} b^{2} }}} \right)\sin \left( {3\pi \frac{z}{2a}} \right)} \right]\) is constant in certain conditions, indicating that the shear rate is a function of the distance from a certain point to the center y, the power law index n and the coefficient k. Then from the constitutive equations, the viscosity of fluid for non-Newtonian fluids in microchannels should be also width-dependent. Thus, from engineering point of view, the expression for the apparent viscosity ηapp of non-Newtonian fluids, as shown in Fig. 8, is convenient and promising for the characterizing of the rheological property of non-Newtonian fluid flow in microchannels. This kind of apparent rheological curve for the flow of non-Newtonian fluids in microchannels is completely different from the inherent one measured by the rheometer.

Fig. 9
figure 9

The velocity profile of the fluid in the microchannel. n denotes the power law exponent of fluids, n1 > n2 > n3, D is the channel height

Full size image

5 Conclusion

This paper presents a microfluidics method to characterize the apparent rheological properties of fluids in microchannels based on pressure drop measurement. For Newtonian fluids, the pressure drop increases linearly with the increase of velocity, viscosity, and Reynolds number of fluids, respectively. The experimental results agree well with the calculated values estimated by the classical prediction model for pressure drop of Newtonian fluids in microchannels. For non-Newtonian fluids, the pressure drop increases nonlinearly with the increase of fluid’s velocity, viscosity, and Reynolds number, which deviates from the traditional theoretical predictions. This is caused by the rheological properties of non-Newtonian fluids in confined spaces. Based on the measured pressure drop, the apparent viscosity of non-Newtonian fluids in a given microchannel can be scaled with the characterized shear rate by a power-law, which is completely different from the rheological property characterized by the rheometer measurements. This can be understood by the existence of viscosity distribution due to the heterogeneous shear rate distribution at radial direction for non-Newtonian fluids in a microchannel. Thus, it is necessary to define the apparent viscosity of non-Newtonian fluids in the microchannel to characterize the fluid properties. This result shows that there exists divergence between the characteristic apparent rheological curve for non-Newtonian fluids flowing in microchannels of this engineering significance and the inherent rheological property for such fluids measured by the rheometer, which deserves further theoretical and simulation studies. This work paves the way for studies in dynamics of complex fluids in porous media and complex networks of microchannels.