Effects of micron scale surface profiles on acoustic streaming

Abstract

Conventional models of boundary-driven streaming such as Rayleigh–Schlichting streaming typically assume smooth device walls. Using numerical models, we predict that micron scale surface profiles/features have the potential to dramatically modify the inner streaming vortices, creating much higher velocity, smaller scale vortices. Although inner streaming is hard to observe experimentally, this effect is likely to prove important in applications such as DNA-tethered microbeads where the flow field near a surface is important. We investigate here the effect of a sinusoidally structured surface in a one-dimensional standing wave field in a rectangular channel using perturbation theory. It was found that inner streaming vortex patterns of scale similar to the profile are formed instead of the much larger eight-vortices-per-wavelength classical inner streaming patterns seen in devices with smooth surfaces, while the outer vortex patterns are similar to that found in a device with smooth surfaces (i.e., Rayleigh streaming). The streaming velocity magnitudes can be orders of magnitude higher than those obtained in a device with smooth surfaces, while the outer streaming velocities are similar. The same inner streaming patterns are also found in the presence of propagating waves. The mechanisms behind the effect are seen to be related to the acoustic velocity gradients around surface features.

1 Introduction

Acoustic streaming is a nonlinear effect in which a steady, time-averaged flow is generated by the absorption of acoustic oscillations in a viscous fluid (Lighthill 1978). Based on the dissipation mechanisms of energy attenuation, various acoustic streaming patterns have been analysed, most notably Eckart-type streaming (Eckart 1947) and boundary-driven streaming (Nyborg 1958). The former is associated with the sound attenuation in the bulk of the fluid, while the latter is a result of the interaction between acoustic oscillations and no-slip boundaries.

In most bulk acoustofluidic manipulation devices in which the dimensions of the fluid-channel cross sections are of the same order of magnitude as the acoustic wavelengths, the acoustic streaming fields are generally dominated by boundary-driven streaming due to the presence of the viscous boundary layer, as Eckart-type streaming generally requires acoustic attenuation over longer distances than those observed in such devices. Acoustic streaming effects in acoustofluidic manipulation devices are often considered as a disturbance, as they place a practical lower limit on the particle sizes that can be manipulated by the primary acoustic radiation force (Bruus et al. 2011; Barnkob 2012). However, acoustic streaming flows can also play an active role in such systems, and have been used to enhance particle trapping (Hammarstrom et al. 2012, 2014; Chung and Cho 2008; Lutz et al. 2006; Yazdi and Ardekani 2012; Li 2012), particle focusing (Antfolk et al. 2014), particle propulsion (Nadal and Lauga 2014), and particle separation (Devendran et al. 2014). Understanding their formation mechanisms, either theoretically or numerically, and effectively predicting them are important to create designs for enhancing or minimizing the streaming effects in acoustofluidic manipulation devices.

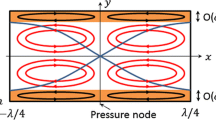
Rayleigh (1883) was the first to present an analytical solution to explain the boundary-driven streaming fields outside the viscous boundary layer, which thus is usually referred as outer streaming ‘or Rayleigh streaming’. A description of boundary-driven streaming fields inside the viscous boundary layer was first derived by Schlichting (1932), and such fields are known as inner streaming or ‘Schlichting streaming’. In general, their solutions describe the boundary-driven streaming fields in one-dimensional (1D) standing wave fields, which have a regular pattern of four vortex pairs per acoustic half-wavelength, as shown in Fig. 1. Following this early work, complimentary approaches have been developed (Lighthill 1978; Nyborg 1953, 1958; Riley et al. 1998; Hamilton et al. 2003), which have paved the theoretical foundations for understanding acoustic streaming, as reviewed recently by Valverde (2015).

Fig. 1

(Colour online) Schematic presentation of the classical boundary-driven streaming flows in a two-dimensional rectangular channel, where $\lambda$ is the acoustic wavelength, ${\delta _{\text{v}}}$ is the thickness of viscous boundary layer, and the curves are the distribution of acoustic pressure magnitudes

The rapid advance of computational technology in the past decades has allowed the simulations of boundary-driven streaming fields in models at the sizes of practical experimental devices, which has made it a great tool for the estimation of the performance of acoustofluidic manipulation systems too complex for analytical solutions. Modelling of boundary-driven streaming flows showed good consistency with theoretical solutions (Muller et al. 2012; Aktas and Farouk 2004; Tang and Hu 2015a) and with measurements under real experimental conditions (Muller 2013; Lei et al. 2013, 2014, 2016, 2017; Lei 2017; Tang and Hu 2015b).

Most acoustic streaming fields in acoustofluidic devices that have been reported in the literature are based on the condition that the fluid channels have flat boundaries. Boundary-driven streaming fields around objects with regular, simple surfaces, such as cylinders and spheres (Stuart 1965; Riley 1975, 1987, 1992; Amin and Riley 1990; Rednikov and Sadhal 2004, 2011), have also been explored. More recent work has demonstrated significant acoustic streaming patterns around macroscale structures and sharp edges (generally of mm scale) (Oberti et al. 2009; Wiklund et al. 2012; Nama et al. 2014; Ovchinnikov et al. 2014; Leibacher et al. 2015; Costalonga et al. 2015). Limited research has been conducted on the boundary-driven streaming fields in acoustofluidic manipulation devices with non-flat surfaces and it is unclear whether microscale curvilinear boundaries affect the boundary-driven streaming fields.

In this paper, we present a numerical study on the effects of sinusoidally shaped surfaces on the acoustic and streaming fields in acoustofluidic devices, including the acoustic pressure amplitudes, inner and outer streaming patterns, and the magnitudes of streaming velocities. In reality, surfaces of fluid channels are likely to exhibit some roughness, rather than being perfectly flat as generally considered in the literature. Therefore, the results presented here are important and indicate that the inner streaming fields found in real experimental acoustofluidic manipulation devices may be significantly different to those generally assumed to exist. While the results are presented for a representative standing wave device, we discuss below that the same patterns are also predicted to arise in the presence of propagating waves that travel along a surface.

Section 2 presents the fundamental governing equations of acoustic streaming, and Sect. 3 presents the numerical methods and model configurations. In Sect. 4, the modelled results are presented and discussed. Overall conclusions are drawn in Sect. 5.

2 Theory

In the following, we use bold and normal-emphasis fonts to represent vector and scalar quantities, respectively. The fundamental governing equations of acoustic streaming theory have been extensively presented in the literature. Here, we assume a homogeneous isotropic fluid, in which the continuity and momentum equations for the fluid motion are

$$\frac{{\partial \rho }}{{\partial t}}+\nabla \cdot (\rho {\varvec{u}})=0,$$

(1a)

$$\rho \left( {\frac{{\partial {\varvec{u}}}}{{\partial t}}+{\varvec{u}} \cdot \nabla {\varvec{u}}} \right)= - \,\nabla p+\mu {\nabla ^2}{\varvec{u}}+\left( {{\mu _{\text{b}}}+\frac{1}{3}\mu } \right)\nabla \nabla \cdot {\varvec{u}},$$

(1b)

where $\rho$ is the fluid density, $t$ is time, ${\varvec{u}}$ is the fluid velocity, $p$ is the pressure, and $\mu$ and ${\mu _{\text{b}}}$ are, respectively, the dynamic and bulk viscosity coefficients of the fluid. The left-hand side of Eq. (1b) represents the inertia force per unit volume on the fluid with the two terms in the bracket being the unsteady acceleration and convective acceleration of a fluid particle, respectively. The right-hand side indicates the divergence of stress, including the pressure gradient and the viscosity forces. Other forces, such as the gravity force, are not considered, as they are generally negligible compared to the forces presented.

There are two main numerical methods for the modelling of boundary-driven streaming fields in acoustofluidic devices (Lei et al. 2017), both of which are based on perturbation theory (Bruus 2012a; Sadhal 2012) and assume that the second-order time-averaged acoustic streaming velocity is superposed on the first-order acoustic velocity field. Following this theory, the fluid density, pressure, and velocity can, respectively, be expressed as

$$\rho ={\rho _0}+{\rho _1}+{\rho _2}+ \cdots ,$$

(2a)

$$p={p_0}+{p_1}+{p_2}+ \cdots ,$$

(2b)

$${\varvec{u}}={{\varvec{u}}_1}+{{\varvec{u}}_2}+ \cdots ,$$

(2c)

where the subscripts 0, 1, and 2 represent the static (absence of sound), first-order, and second-order quantities, respectively.

Substituting Eqs. (2a, b, c) into Eqs. (1a, b) and considering the equations to the first-order, Eqs. (1a, b) take the form:

$$\frac{{\partial {\rho _1}}}{{\partial t}}+{\rho _0}\nabla \cdot {{\varvec{u}}_1}=0,$$

(3a)

$${\rho _0}\frac{{\partial {{\varvec{u}}_1}}}{{\partial t}}= - \,\nabla {p_1}+\mu {\nabla ^2}{{\varvec{u}}_1}+\left( {{\mu _b}+\frac{1}{3}\mu } \right)\nabla \nabla \cdot {{\varvec{u}}_1}.$$

(3b)

Repeating the above procedure, considering the equations to the second-order and taking the time average of Eqs. (1a, b) using Eqs. (2a, b, c), the continuity and momentum equations for solving the second-order time-averaged acoustic streaming velocity can be expressed as

$$\nabla \cdot \overline {{{\rho _1}{{\varvec{u}}_1}}} +{\rho _0}\nabla \cdot {{\varvec{u}}_2}=0,$$

(4a)

$$- \,{\varvec{F}}= - \,\nabla {p_2}+\mu {\nabla ^2}{{\varvec{u}}_2}+\left( {{\mu _{\text{b}}}+\frac{1}{3}\mu } \right)\nabla \nabla \cdot {{\varvec{u}}_2},$$

(4b)

where the upper bar means a time-averaged value and ${\varvec{F}}= - \,{\rho _0}\overline {{{{\varvec{u}}_1}\nabla \cdot {{\varvec{u}}_1}+{{\varvec{u}}_1} \cdot \nabla {{\varvec{u}}_1}}}$ is the Reynolds stress force (RSF)(Lighthill 1978). The divergence free velocity ${\varvec{u}}_{2}^{{\varvec{M}}}={{\varvec{u}}_2}+\overline {{{\rho _1}{{\varvec{u}}_1}}} /{\rho _0}$, derived from Eq. (4a), is the mass transport velocity of the acoustic streaming, which is generally closer to the velocity of tracer particles in a streaming flow than ${{\varvec{u}}_2}$ (Nyborg 1998).

Taking the curl of both sides of Eq. (4b), the following equation is established:

$$\mu {\nabla ^2}(\nabla \times {{\varvec{u}}_2})= - \,\nabla \times {\varvec{F}}.$$

(5)

One advantage of this equation over Eq. (4b) is that the second-order pressure, ${p_2}$, does not need to be considered. Thus, it can be established whether acoustic streaming vortices can be generated in a plane from the rotationality of the RSF field in that plane, although Nyborg (Mason 1965) points that for certain boundary conditions, some knowledge of ${p_2}$ is necessary to determine ${{\varvec{u}}_2}$. The use of Eq. (5) to investigate the potential existence of streaming vortices is very useful to many problems, including the question of boundary-driven streaming in bulk acoustofluidic devices discussed here, in which the acoustic streaming fields usually appear as regular vortex patterns.

3 Numerical methods and model configurations

3.1 Model configurations

In this paper, we investigate the effects of sinusoidally shaped surfaces on the boundary-driven streaming fields in 1D standing wave fields in two-dimensional (2D) rectangular channels, in which the streaming fields associated with flat surfaces are usually referred to as the Rayleigh–Schlichting streaming. A sinusoidal profile could arguably be considered the simplest (lowest Fourier order), periodic structure, and also has the benefit that results can be obtained in computationally shorter times than are required for profiles with sharper radiuses of curvature. We discuss below the implications from our results for more general surface profiles.

Figure 2 shows the model configuration. The top boundary has a sinusoidally profile, and is parallel to the propagation direction of the standing wave field. Here, only half of the rectangular chamber is modelled for numerical efficiency, as boundary-driven streaming fields in 2D rectangular chambers are symmetric to the channel axis, and thus, as shown in Fig. 2a, the bottom boundary was set as a symmetric boundary condition. The origin of the coordinates was set at the centre of the bottom boundary. Figure 2b shows a magnification of the sinusoidally shaped surface profile, which is determined by two parameters, ${h_0}$ and $T$, the profile amplitude and wavelength, respectively. A range of values for these parameters are explored in this paper. It is noteworthy that for all the cases, the sinusoidally shaped surface covers the whole boundary, such that the total areas of these 2D chambers with different profiles on $T$ or ${h_0}$ are the same, which is $A=h \times w$, the area of the chamber with flat surfaces.

Fig. 2

(Colour online) Schematic illustration of the model: a excitation and coordinates and b magnification of the structured surface, where ${\delta _{\text{v}}}$ is the thickness of the viscous boundary layer (orange layer, exaggerated, not to scale), $f$ and ${v_0}$ are, respectively, the frequency and amplitude of the excitation, $\lambda$ is the acoustic wavelength, and $T$ and ${h_0}$ are the wavelength and amplitude of the sinusoidally shaped boundary, respectively

The 1D standing wave fields in these rectangular channels were established by a harmonic excitation of the left boundaries at a frequency $f \approx 1$ MHz. The thickness of the viscous boundary layer in water at this frequency (Bruus 2012), ${\delta _{\text{v}}}=\sqrt {2\nu /\omega }$, is close to 0.53 µm, where $\nu =\mu /{\rho _0}$ is the kinematic viscosity coefficient of the fluid and $\omega =2\pi f$ is the angular frequency.

3.2 The Reynolds stress method

In acoustofluidic systems, where the boundaries have significant curvature relative to ${\delta _{\text{v}}}$, the limiting velocity method is not applicable (Nyborg 1958). Instead, the acoustic streaming fields can be solved from the Reynolds stress method (RSM), which can be applied to solve both the inner and outer streaming fields in devices regardless of surface shapes of fluid channels (Lei et al. 2017).

The numerical simulations were conducted in COMSOL 4.4 (2015). Mesh dependency for this approach has previously been established (Lei et al. 2017). First, a COMSOL ‘Thermoacoustics, Frequency Domain’ interface was used to solve the first-order acoustic pressure and velocity fields, which solves

$${\nabla ^2}{p_1}+\frac{{{\omega ^2}}}{{{c^2}}}{p_1}=0,$$

(6)

where $c$ is the sound speed and ${p_1}$ is defined at position $r$ using the relation ${p_1}(r,t)=Re{\text{[}}~{p_1}(r){e^{i\omega t}}{\text{]}}$. In this step, the left boundary of the rectangular channel was set as a harmonic excitation, the bottom boundary was a symmetric condition, and the remaining boundaries were sound reflection boundary conditions. In terms of excitations, a normal stress boundary condition was chosen in a previous work (Lei et al. 2017) to stabilise the acoustic pressure amplitude in devices with various dimensions. Here, a velocity excitation was chosen to reflect the boundary vibration generated from the transducer in practical acoustofluidic manipulation devices, such that the effects of surface profile on the acoustic pressure amplitudes were also examined in this work.

Then, a COMSOL ‘Creeping Flow’ interface was used to simulate the acoustic streaming fields, which neglects inertial terms (Stokes flow), as the inertial force (${{\varvec{u}}_2} \cdot \nabla {{\varvec{u}}_2}$) is generally negligible compared to the viscosity force ($\mu {\nabla ^2}{{\varvec{u}}_2}$) in such low velocity streaming systems. In this interface, the acoustic streaming velocities were solved Eqs. (4a, b). In 2D Cartesian coordinates shown in Fig. 2a, the two RSF components (${F_x},~{F_y}$) can be calculated from

$${F_x}={\rho _0}(\partial \overline {{u_{1}^{2}}} /\partial x+\partial \overline {{{u_1}{v_1}}} /\partial y),$$

(7a)

$${F_y}={\rho _0}(\partial \overline {{{u_1}{v_1}}} /\partial x+\partial \overline {{v_{1}^{2}}} /\partial y),$$

(7b)

where ${u_1}$ and ${v_1}$ are the two components of the acoustic velocity vector ${{\varvec{u}}_1}$ along coordinates $x$ and $y$, respectively. In this step, all the boundaries were set as no-slip boundary conditions besides the symmetric boundary condition of the bottom boundary.

To verify our model code, we replicated the results of (both modelled and experimentally measured) acoustic streaming fields near a sharp edge as presented by Ovchinnikov et al. (2014). The results (shown in Sect. 4.2.5) are in close agreement.

4 Results and discussion

A series of sinusoidally shaped surfaces for two cases, respectively, $h=40{\delta _{\text{v}}}$ and $h=80{\delta _{\text{v}}}$, are compared in this paper. For both cases, as in devices with flat surfaces, the $y$-extent of the inner streaming vortices are negligible compared with those of the outer streaming vortices, as typically found in acoustofluidic devices. Initial results are presented below with a wavelength of the sinusoidally shaped surface of $T=3.7$ µm (an arbitrary choice that gives $~T=~\lambda /200$), with the effect of varying T explored later on.

4.1 First-order acoustic fields

As expected, it was found that, under the same velocity excitation, a similar half-wavelength standing wave field was established in the $x$-direction of the chambers, with an acoustic pressure node at the centre ($x=0$) and two pressure antinodes at the two ends ($x= \pm \,w/2$), as plotted in Fig. 3a. However, a shift in the resonant frequencies and variations in the magnitudes of the acoustic pressure amplitudes were found in models with different profile amplitudes, although they were driven with the same excitation. The detailed relationships between these two quantities and the amplitudes of the sinusoidally structured surfaces are shown in Fig. 3b, c, where the resonant frequencies and the corresponding acoustic pressure amplitudes (free-field magnitudes at the pressure antinodes) in chambers with a sinusoidally shaped surface for two cases, $h=40{\delta _{\text{v}}}$ and $h=80{\delta _{\text{v}}}$, are presented.

Fig. 3

(Colour online) a Modelled first-order acoustic pressure fields ($h=80{\delta _{\text{v}}},\,{h_0}=0$); b, c variations of the half-wavelength resonant frequencies, ${f_{\text{r}}}$, and the modelled pressure amplitudes, ${\left| {{p_1}} \right|_{{\text{max}}}}$, with the amplitudes of the sinusoidally shaped surface profiles, ${h_0}$, for two cases, $h=40{\delta _{\text{v}}}$ (diamond line) and $h=80{\delta _{\text{v}}}$ (square line), respectively. The pressure amplitudes (units of Pa) were obtained from the same excitation, ${v_0}=1$ mm/s. The wavelength of these sinusoidally shaped surface profiles was the same: $T=3.7$ µm

For both cases, as shown in Fig. 3, a general downward trend in the resonant frequencies and the pressure amplitudes can be seen with the rise of ${h_0}$. The resonant frequency for each case was obtained by a sweep of frequencies around the ideal frequency, ${f_0}=c/2w$, where $c$ is the sound speed in the fluid, to find the frequency with maximum average acoustic energy density in the chamber. In these simplified fluid-channel-only models, these variations may be attributed to the fact that the losses in the viscous boundary layer are augmented with the curved boundary compared to that in a device with flat boundaries [i.e., more damping (Hahn and Dual 2015)]. Similar results have been reported in Muller and Bruus (2014). It is interesting to note the grating-like ‘blocking’ of waves from the non-flat boundaries described by Hawwa (2015). However, the surface profile wavelength considered here is much smaller than the acoustic wavelength and this is not likely to be a significant effect.

4.2 Acoustic streaming fields

In this section, the effects of a sinusoidally shaped boundary on the boundary-driven streaming fields, including the acoustic streaming patterns and streaming velocity magnitudes, are presented.

4.2.1 Chambers with flat walls

First, we describe the modelled acoustic streaming fields in chambers showing conventional Rayleigh–Schlichting streaming as a base line [though the reduced chamber height means that the modified analytical solution of Hamilton et al. (2003) is required]. The acoustic pressure field and streaming field are shown in Fig. 4. To show the inner streaming field, a plot of the $x$-component mass transport streaming velocity, $u_{2}^{M}$, along $x=w/4$, as plotted in Fig. 4c. The streaming velocities compare well with Hamilton et al.’s analytical solution. The inner streaming pattern is not shown explicitly here, but follows the pattern, as shown in Fig. 1. Modelling shows that small (e.g., ${h_0}=50$ nm) surface profiles do not significantly modify this pattern.

Fig. 4

(Colour online) Modelled second-order acoustic streaming fields in chambers ($h=80{\delta _{\text{v}}}$) for a flat boundary: a acoustic pressure field (units of Pa); b outer acoustic streaming fields, where the white lines plot the streaming patterns and the colours show the magnitudes of streaming velocities (units of m/s); and c vertical distribution of $u_{2}^{M}$ ($=\,{u_2}+\overline {{{\rho _1}{u_1}}} /{\rho _0}$) along $x=w/4$ shown in b. The modelled streaming velocities were compared to Hamilton et al.’s analytical solution (Hamilton et al. 2003)

4.2.2 Profiles with various amplitudes in µm region

The acoustic streaming fields in chambers with larger ${h_0}$ (non-negligible amplitudes compared to ${\delta _{\text{v}}}$) are shown in this section. The detailed relationship between the magnitudes of the streaming velocities and the amplitudes of the sinusoidally shaped profiles will be shown later in Fig. 6. Figure 5 shows the modelled streaming field for a device with ${h_0}=0.53$ µm. The pattern seen in this example is representative of the pattern found for a wide range of values of ${h_0}$ (at least up to ${h_0}=4{\delta _{\text{v}}}$).

Fig. 5

(Colour online) a Modelled acoustic streaming field in a chamber ($h=80{\delta _{\text{v}}}$), where the amplitude of the surface profile is ${h_0}=0.53$ µm; b magnification of the inner streaming fields near the sinusoidal surface at the centre of the channel ($x=0$) shown in a. The white lines plot the streaming patterns, the arrows show the streaming velocity vectors, and the colours show the magnitudes of streaming velocities (units of m/s)

Fig. 6

(Colour online) Enhancement (compared to a flat boundary) in inner streaming velocity magnitude, $\gamma _{{{\text{in}}}}^{n}$, with varying amplitudes of the sinusoidally shaped surface, ${h_0}$. $\gamma _{{{\text{in}}}}^{n}={\gamma _{{\text{in}}}}/\gamma _{{{\text{in}}}}^{0}$, where ${\gamma _{{\text{in}}}}={\left| {{\varvec{u}}_{2}^{{\varvec{M}}}} \right|_{{\text{max}}}}/\left| {{p_1}} \right|_{{{\text{max}}}}^{2}$ ($\gamma _{{{\text{in}}}}^{0}$ is ${\gamma _{{\text{in}}}}$ when ${h_0}=0$). $\gamma _{{{\text{in}}}}^{0}$ for $h=40{\delta _{\text{v}}}$ and $h=80{\delta _{\text{v}}}$ at ${h_0}=0$ are 96 and 107, respectively. The wavelength of these surface profiles was the same: $T=3.7$ µm

It can be seen that the outer streaming patterns in these models are still the same as those shown in the previous section, two vortices within each half-wavelength standing wave field. Overall, the magnitudes of streaming velocities close to the chamber walls show dramatic enhancement, while the outer streaming remains similar. The largest enhancement is seen at ($x=0$), where the acoustic velocity is maximum.

A magnified view of the local area near the profiled top boundary at the centre of the chamber is shown in Fig. 5b. It can be seen that a series of streaming vortices are generated creating fluid motion away from the high points of the profile. The shift from an inner streaming pattern of acoustic wavelength scale (e.g., Fig. 1) to a pattern with scale dependent on the much smaller profile wavelength, $T$, is significant. The mechanism on the formation of this vortex pattern will be analysed in more detail in the following sections.

4.2.3 Effects of surface profile amplitude on the magnitudes of streaming velocities

As both the modelled magnitudes of acoustic pressure and acoustic streaming velocity change with the amplitude of the sinusoidally shaped surface, ${h_0}$, here a coefficient $\gamma$, defined as the ratio of the maximum streaming velocity and the square of acoustic pressure amplitudes, is introduced. The reason for choosing this coefficient to characterise the magnitudes of acoustic streaming velocities is based on the fact that the amplitude of the streaming velocity scales with the square of the pressure amplitude in an acoustic standing wave field and it is independent of the variations in damping (which determines the pressure amplitude for a given excitation) that are seen with different values of ${h_0}$.

Two coefficients, ${\gamma _{{\text{in}}}}$ and ${\gamma _{{\text{out}}}}$, are used to characterise respectively the inner streaming velocity and the streaming velocity in the bulk of the chamber, which are calculated by

$${\gamma _{{\text{in}}}}=\frac{{{{\left| {{\varvec{u}}_{2}^{{\varvec{M}}}} \right|}_{{\text{max}}}}}}{{\left| {{p_1}} \right|_{{{\text{max}}}}^{2}}},$$

(8a)

$${\gamma _{{\text{out}}}}=\frac{{{{\left| {{\varvec{u}}_{2}^{{\varvec{M}}}} \right|}_{{\text{out}}}}}}{{\left| {{p_1}} \right|_{{{\text{max}}}}^{2}}},$$

(8b)

where ${\left| {{p_1}} \right|_{{\text{max}}}}$ is the standing wave pressure amplitude away from the boundary, ${\left| {{{\varvec{u}}_2}} \right|_{{\text{max}}}}$ is the maximum streaming velocity amplitude, and ${\left| {{\varvec{u}}_{2}^{{\varvec{M}}}} \right|_{{\text{out}}}}$ is the magnitude of streaming velocity at ($w/4$, 0) used to measure the outer streaming velocity amplitude. By normalising these coefficients to their value for a flat surface, a measure of the enhancement caused by surface profiles of varying amplitude can be plotted, as shown in Fig. 6. It can be seen that the magnitudes of the streaming velocities rise rapidly with the increase of ${h_0}$. For ${h_0}=2$ µm, for example, the maximum inner streaming velocities can be more than 100 times higher than those found in a device with flat surfaces for the same acoustic pressure amplitude. Although the results report enhancements for surface profile amplitudes as low as 5 nm, we are cautious about the validity of the model for these extreme values given existing uncertainty over slip lengths of potential boundaries (Mishra et al. 2014).

Figure 7 plots the normalised relationship between ${\gamma _{{\text{out}}}}$ and the amplitudes of sinusoidally shaped surface, ${h_0}$. As shown in the graph, with the growth of ${h_0}$, ${\gamma _{{\text{out}}}}$ first decreases slowly to the minimum value when ${h_0}$ is just greater than ${\delta _{\text{v}}}$ and then rises gradually with the further increase of ${h_0}$. However, compared to the inner streaming velocities, this structured surface has much less effect on the outer streaming velocities, as it can be seen that, in the whole range of ${h_0}$ considered here, the magnitudes of outer streaming velocities plotted are in the same order of magnitude. In both inner and outer streaming plots, it can be seen that the effect of chamber height is not too significant for these cases when the chamber height is significantly larger than ${\delta _{\text{v}}}$, a situation likely to be found in experimental devices.

Fig. 7

(Colour online) Relationships between the normalised magnitude of the outer streaming velocity $\gamma _{{{\text{out}}}}^{n}$ and the amplitudes of sinusoidally shaped surface, ${h_0}$. $\gamma _{{{\text{out}}}}^{n}={\gamma _{{\text{out}}}}/\gamma _{{{\text{out}}}}^{0}$, where ${\gamma _{{\text{out}}}}={\left| {{\varvec{u}}_{2}^{{\varvec{M}}}} \right|_{{\text{max}}}}/\left| {{p_1}} \right|_{{{\text{max}}}}^{2}$. $\gamma _{{{\text{out}}}}^{0}$ ($\gamma _{{{\text{out}}}}^{0}$ is ${\gamma _{{\text{out}}}}$ when ${h_0}=0$) for $h=40{\delta _{\text{v}}}$ and $h=80{\delta _{\text{v}}}$ at ${h_0}=0$ are 51 and 53, respectively. The wavelength of these surface profiles was the same: $T=3.7$ µm

Similarly, the effects of profile wavelength on the acoustic and streaming fields have been examined, as shown in Fig. 8. The acoustic and streaming fields in four chambers, where the sine-wave shaped boundaries have fixed ${h_0}=0.53$ µm and various profile wavelengths, $T$, ranging from 2.5 to 5 µm were modelled. In all these cases, a half-wavelength standing wave in the $x$-direction of the chambers was established. It can be seen that, under the same excitation, the magnitudes of pressure amplitudes and streaming velocities vary in these models, and similar vortex patterns to those reported in the paper are found in all cases. Figure 8 compares the simulated results. In all the models considered, with the increase of wavelength, $T$: (1) a global growth can be seen on the modelled acoustic pressure amplitudes (Fig. 8a); (2) the inner streaming vortices near $x=w/4$ increase in size (Fig. 8b); (3) the streaming velocity first experiences a rise and then see a slight drop (Fig. 8c); and (4) a similar distribution on the variations of the net streaming velocity and the outer streaming velocity, a general fall on the magnitudes, can be seen. The figure uses the coefficient ${\gamma _n}$ which is defined as

Fig. 8

(Colour online) Relationships between the modelled results and the wavelength of the sine-wave shaped boundary, $T$: a acoustic pressure amplitudes; b size of inner streaming vortex near $x=w/4$; c maximum (inner) streaming velocity, ${\gamma _{{\text{in}}}}$; and d outer streaming velocity, ${\gamma _{{\text{out}}}}$, and net streaming velocity, ${\gamma _n}$. The amplitude of these sine-wave shaped boundaries was the same: ${h_0}={\delta _{\text{v}}}$

$${\gamma _n}=\frac{{\left| {{{\varvec{u}}_{2{\varvec{n}}}}} \right|}}{{\left| {{p_1}} \right|_{{{\text{max}}}}^{2}}},$$

(9)

where ${{\varvec{u}}_{2{\varvec{n}}}}$ is the net streaming velocity. Compared to the effect of profile amplitude on the modelled streaming fields, it can be seen that the wavelength of the sine-wave surface profile has less impact.

4.2.4 Investigating mechanisms

To investigate the mechanism by which these inner streaming patterns are formed, we consider an example in which ${h_0}={\delta _{\text{v}}}$. Figure 9 shows the distributions of the acoustic velocity, the RSF, the vorticity of RSF field, and the acoustic streaming fields near the top wall of the chamber. It can be seen that, due to the presence of the sinusoidally shaped boundary, both the acoustic velocity magnitudes and the RSF have a periodic distribution (wavelength of $T$) in the $x$-direction of the chamber, with the maximum values staying just below the peaks of sine-wave with a distance of approximately 2 ${\delta _{\text{v}}}$ and ${\delta _{\text{v}}}$ from the peaks, respectively. Figure 9c plots the vorticity of the RSF field near the top boundary. As shown, it is zero in most areas of the chamber except those small regions near each peak of the boundary. In addition to showing the magnitude of $\nabla \times F$, signs are used to demonstrate the vorticity of the RSF fields following the ‘right-hand rule’. It can be seen that, due to the different rotationality of the RSF at the two sides of each peak of the sine wave, two vortices can be generated in each wavelength of the surface, which explains the modelled acoustic streaming fields near the top boundary, as shown in Fig. 9d. Our interpretation is that the acoustic velocity gradients caused by the streamlines coming closer together to pass over the peaks are the root cause of the RSF forces which drive jets away from each peak, resulting in the vortical pattern.

Fig. 9

(Colour online) Distributions of the modelled results near the top boundary of the chamber for ${h_0}={\delta _v}$: a acoustic velocity (units of m/s); b Reynolds stress force (units of N/m³); c normalised vorticity of the Reynolds stress force (units of N/m⁴); and d acoustic streaming (units of m/s), where the arrows and colours show the corresponding vector fields and magnitudes, respectively. The values were obtained from an oscillation excitation amplitude of ${v_0}=1$ mm/s

Choosing the sinusoidal profile made the model sufficiently simple as to produce accurate results in reasonable timescales for devices much larger than the profile wavelength. However, the results and discussion presented here indicate that similar results might also be produced for other profile shapes. Figure 10 shows the modelled inner streaming fields around some example (single) protuberances. A general pattern of a jet directed away from the protuberance continues to hold. We attribute this to velocity gradients caused as the flow passes around the protuberance generating the requisite RSFs. It is interesting that, for the rectangle and trapezoid surfaces, only two streaming vortices were obtained although four distinct RSF areas can be seen around the protuberance for the cases presented. This is attributed to the fact that the rotationality of RSF fields in the central two areas is much weaker than the two adjacent outer areas. For the two cases presented, the widths of the protuberances (${w_0}$) is smaller than the heights (${h_0}$). It was found that two small vortices were formed at each corner of the shape when the ${w_0} \gg {h_0}$ (i.e., four vortices for four distinct area of rotationality of RSF fields in these cases). The modelled streaming fields presented here compare well with those measured and modelled streaming fields around similar shapes reported in the literature (Oberti et al. 2009; Wiklund et al. 2012; Nama et al. 2014; Ovchinnikov et al. 2014; Leibacher et al. 2015; Costalonga et al. 2015).

Fig. 10

(Colour online) Modelled boundary-driven streaming fields and the corresponding rotationality of Reynolds stress force fields (normalised) around some typical non-flat surfaces: a semi-circular surface; b triangular surface; c square surface; and d trapezoidal surface, where the arrows plots the streaming vector fields and the colours (black, orange and white for − 1, 0 and 1, respectively) represent the magnitudes of the rotationality of the Reynolds stress force fields. The standing wave fields were established at the $x$-direction of the fluid chambers. ${\delta _{\text{v}}} \approx 0.6$ µm is the thickness of the viscous boundary layer

In the second part of this section, we illustrate the driving mechanism of the outer streaming vortices in the chambers. Figure 11 shows the modelled inner streaming field near the top surface of the chamber, where only a portion of the chamber near $x=w/4$ is presented to show the detailed information. Here, as emphasized in the figure, the two inner streaming vortices near $x=w/4$ was chosen as an example. It can be seen that the vortex pairs have different strengths, stronger on the left-hand side due to the higher acoustic velocities, which decrease from the maximum value at the centre ($x=0$) to the side boundary of the chamber ($x=w/2$). Therefore, there is a net streaming velocity at the edge ($y$-extent) of the competing two inner streaming vortices (the vortex edge is defined as the point at which streamlines cease to re-circulate and instead join the outer streaming pattern) in each wavelength of the surface. This net streaming velocity is approximated as

Fig. 11

(Colour online) Explanations for the formation mechanism of outer streaming vortices—the competing of two inner streaming vortices (size of ${S_{{\text{in}}}}$) in each wavelength of the surface, where ${u_{2{\text{c}}}}$ and ${u_{2{\text{ac}}}}$ are the $x$-component streaming velocities at the edge of the clockwise and anti-clockwise inner streaming vortex pairs in a wavelength, respectively. ${u_{2{\text{n}}}}={u_{2{\text{ac}}}} - {u_{2{\text{a}}}}$ is the net $x$-component streaming velocity of the competing inner streaming vortex pairs, the limiting velocities that drive the outer streaming vortex

$${u_{2{\text{n}}}}={u_{2{\text{ac}}}} - {u_{2{\text{a}}}},$$

(10)

where ${u_{2{\text{c}}}}$ and ${u_{2{\text{ac}}}}$ are the $x$-component streaming velocities at the edge of the clockwise and anti-clockwise inner streaming vortex pairs, respectively. The $y$-extent of inner streaming vortices is controlled by the competition between the rotationality of the RSF along the height of the chamber, which is the same as that of a device with flat surfaces (Lei et al. 2017).

As the inner vortex pattern is continuous along the top surface, this net streaming velocity exists across the whole of that surface and has the same sign between each acoustic velocity antinode and its adjacent node (with a change signs in every $\lambda /4$ of the standing wave). This is why the modelled outer streaming fields have the same pattern in all the models, with two vortices being obtained in each $\lambda /2$ of the standing wave in these half devices.

The formational mechanism of the continuous flows outside the non-flat surfaces presented here is similar to the case described by Huang et al. (2014), in which acoustic streaming flows around vibrating sharp edges were successfully applied to continuously pump fluid and particles in an acoustofluidic device.

Based on the observation that it is the acoustic velocity gradients near the surface that gives rise to the driving terms, one might also expect a similar effect to arise from the gradients that occur when a propagating wave travels with a component parallel to the surface over a profiled surface. By changing the right-hand boundary conditions of the model to absorb incident acoustic waves (using a radiation boundary condition), we were also able to model this situation. The acoustic velocity amplitude above the viscous boundary layer (i.e., at ${\delta _{\text{v}}} \ll {h_0}<(h - y)$) was set to be the same magnitude as in the centre of the device in the corresponding standing wave case. It was found that the inner acoustic streaming pattern in these cases was indistinguishable in both magnitude and shape to that found at the centre of the device for the standing wave case. In contrast, there was no net outer streaming pattern in accord with the lack of streaming expected in the smooth-walled case (Eckhart streaming flow is not considered here).

4.2.5 Verification and experimental approaches

To verify our numerical method and code, we here apply it to replicate the results of Riley (1992) who both model and experimentally measure the acoustic streaming field near a mm scale sharp edge. Results are shown in Fig. 12. A similar acoustic velocity field to Fig. 2 in Riley (1992) was first modelled (Fig. 12a) using the COMSOL ‘Thermoacoustics, Frequency Domain’ interface. The standing wave field was created by a velocity boundary condition at the side walls ($x= \pm \,1$ mm). Then, with the Reynolds stress forces calculated from the acoustic velocity fields acting as a volume force, the acoustic streaming field was modelled from the COMSOL ‘Creeping flow’ interface, as shown in Fig. 12b. The detailed acoustic streaming fields near the tip are plotted in Fig. 12c–e. It can be seen that the modelled results presented here compare well with those shown in Figs. 4 and 6 in Riley (1992).

Fig. 12

(Colour online) Verification of model: acoustic and streaming fields around a macroscale sharp edge: a acoustic velocity field (units of m/s); b acoustic streaming field (units of m/s); c zoomed area near the tip shown in b; d, e modelled horizontal and vertical distributions of the streaming velocity magnitudes near the tip shown in the insets. These results accord with those of Ovchinnikov et al. (2014) and support our implementation of the perturbation approach used above

To our knowledge, inner streaming patterns in microfluidic devices operating in the MHz region or above have not been directly probed experimentally to date. Discussion of possible experimental techniques can be derived from the similar problem of looking for slip boundary conditions as reviewed by Mishra et al. (2014) Possible techniques include particle image velocimetry (PIV) or velocimetry of photo-bleached fluid volumes using near field illumination techniques. However, Lauga cautions on many complicating factors including dissolved gases and bubbles near the surface and electro-kinetic effects (including the influence of charges on tracer particles). Recent work (Tietze et al. 2013, 2015) examining the enhancement of electrochemical systems in the presence of boundary-driven streaming created by plate and surface waves may be able to provide indirect confirmation of the results we present here, with the hypothesis that in such systems that are limited by diffusion at the electrode surface, the enhanced streaming will significantly increase electrochemical reaction rates.

5 Conclusions

In this paper, the effects of profiled surfaces on the boundary-driven streaming fields in 2D rectangular chambers were numerically investigated. Our models predict that profiles with amplitudes comparable to the viscous boundary layer have the potential to dramatically enhance (and change the pattern of) acoustic streaming patterns with up to 100 fold enhancement in both standing and propagating wave systems.

In terms of first-order acoustic fields, it was shown that the sinusoidal surfaces do not have any effect on the standing wave pattern, but affect the magnitudes of pressure amplitudes due to the augmentation of damping from the non-flat surfaces.

For standing wave excitation, the outer streaming pattern remained similar to that found in Rayleigh–Schlichting streaming, and the addition of the surface profile resulted in a pair of vortices pointing away from each peak of the surface profile, directing fluid away from the highest points of the profile. While the existence of such effects for larger scale protuberances has previously been explored, the dramatic enhancement predicted here is surprising given the small scale of the required profiles. The patterns can be understood as resulting from Reynolds stress forces created by the acoustic velocity gradients produced by the fluid passing around the high points of the profile.

The results in this paper are from a 2D model. We anticipate that the method could also be extended to implement a 3D-model to predict the streaming from more general surface textures. This would be more challenging as we already experience memory issues when applying the COMSOL solver to the 2D case. It is also not immediately clear how generalizable the results presented here are to a rough surface with a random 2D fractal-like profile. We suspect that the current model (which could be considered to represent long sinusoidal ridges across the depth of a chamber) produces enhancements that will be larger than would be found in a randomly distributed collection of surface high points. However, it seems likely from the modelling that each high point of a rough surface will result in velocity gradients (similar to those seen in Fig. 10) that will lead to Reynolds stress forces that seek to drive fluid away from the high point, and will lead to vortices if the spacing and amplitude of the high points is suitable. Nevertheless, the profiles modelled here could be fabricated for cases when intentional enhancement of near-surface streaming is required.

Ordered or unordered micron or nanoscale surface profiles may exist in many real acoustofluidic devices, especially those without surface finish. In addition, micron and nanostructured surfaces can be fabricated by many techniques, such as interference lithography (Bläsi et al. 2011), electron-beam lithography (Chen 2015), soft lithography (Zhao et al. 1997), and nanoparticle-assisted lithography (Li et al. 2011). Although the major contents presented in this paper are acoustic streaming fields near structured surfaces at the micron scale, we have also verified this numerical approach with results from macron scale surface structures shown in the literature (see Fig. 12). We foresee applications of the enhanced near-surface streaming we predict in cases, where diffusion limited processes occur near boundaries. This includes battery systems (particularly flow batteries), drug delivery, and surface-based sensor systems. There is also the possibility of disrupting biofouling formed on surfaces that are not accessible by other means, e.g., in microfluidic systems. The effect of enhanced near-surface streaming may also be important in systems that bring microbeads into proximity with surfaces, such as DNA stretching, and bead affinity assays.