Pressure-driven flow through PDMS-based flexible microchannels and their applications in microfluidics

Abstract

Flexible microchannels have soft walls which undergo deformation under the influence of fluid flow. The dimensional and flexural similarity of flexible microchannels make them ideal candidates for mimicking biological structures such as blood vessels and air pathway in lungs. The analysis of fluid flow and the dynamics of interaction of cells through flexible arteries provide valuable insights about cardiovascular-related diseases. Flexible microchannels can be instrumental in the in vitro investigation of such diseases. This review discusses the recent developments in pressure-driven flow through flexible microchannels and their applications. Here we present the existing theoretical models that predict the deformation and pressure-flow characteristics of flexible microchannels and the corresponding experimental validations. We compare the models for laminar flow of Newtonian fluids through flexible microchannels with their corresponding experimental validation and enlist their limitations. We discuss in detail the various applications of flexible microchannels and their relevance in cell mechanophenotyping, micropumps, microflow stabilizers, and organ-on-chip devices. The insight into the flow dynamics provided herein will extend using flexible microchannels to develop organs-on-chip and other microfluidic applications.

1 Introduction

In the last few decades, polydimethylsiloxane (PDMS) has gained enormous popularity for fabricating microfluidic devices, surpassing silicon and glass. High cost, opacity (in visible/UV region of spectrum) and time-consuming fabrication processes with hazardous chemicals are a few demerits that limit the applications of silicon (Becker and Gärtner 2000; Chen et al. 2008). In comparison, PDMS provides numerous benefits because of its biocompatibility (Brown et al. 2005; Eroshenko et al. 2013; Zhang et al. 2013), non-toxicity, permeability to oxygen and carbon dioxide (Whitesides 2006), optical transparency down to approximately 256 nm (Michel et al. 2001), tunability of surface properties (Sneha Maria et al. 2016; Maria et al. 2017), ease of fabrication and low cost. Furthermore, its elastic and soft nature makes PDMS suitable for analytical operations involving reversible deformation. PDMS can be bonded to itself and other surfaces, creating a watertight seal. Using this property, PDMS membranes with different thicknesses have been used to form three-dimensional microstructures such as microchambers and micropumps (Iyer et al. 2015; Kumar et al. 2016).

In the biomedical field, diseases such as atherosclerosis and stenosis require precise understanding of the fluid–structure interaction within the blood vessels. Blood vessels are usually flexible in nature, vary in size from 10 μm diameter and 1 μm wall thickness (small capillaries) to as much as $25\,{\text{mm}}$ diameter and 2 mm wall thickness (aorta) (Mazumdar 1992). As in situ investigation of blood flow through blood vessels is extremely challenging, an accurate physical model is required to simulate fluid flow conditions. PDMS-based flexible microchannels mimicking blood vessels can play a vital role in such investigations (Hardy et al. 2009; Palchesko et al. 2012; Raj and Sen 2016). Fluid–structure interplay in the flexible microchannel is highly necessary for the design of such microfluidic devices.

PDMS-based microfluidic devices exhibit interesting flow physics as the walls deform internally when the fluid pressure inside the microchannel exceeds a critical value. However, modeling the flow physics through flexible channels is challenging because of the complex fluid–structure interaction involved. Despite the challenges, the models hold vital importance because of the practical significance of flexible microchannels in organ-on-chip models (Huh et al. 2007, 2010; Zheng et al. 2009), deformable droplet generators (Pang et al. 2014; Raj et al. 2016), cell mechanophenotyping (Guan et al. 2012; Huang et al. 2014), microscale pressure sensors (Hosokawa et al. 2002), cell sorting (Beech and Tegenfeldt 2008) and other applications.

Internal wall deformation of PDMS flexible microchannels was first observed by Adzima et al. who noticed non-linear pressure-flow characteristic curve with high-aspect ratio rectangular PDMS microchannels (Adzima and Velankar 2006). The slope of the pressure versus flow rate curve decreased at higher flow rates. Without any theoretical justification, such deviation was simply attributed to the deformation of the internal walls of the channel. In a parallel work, Gervais et al. reported a complete analytical model, along with the experimental validation, demonstrating the internal deformation of the walls of the PDMS microchannel (Gervais et al. 2006). The internal wall deformation was characterized by considering the PDMS wall to be a semi-infinite structure, which is discussed in detail in the next section. The model derived by Gervais et al. (2006),valid for high aspect ratio (width to height ratio), was later modified by Cheung et al. (2012) and validated for various aspect ratios and liquid viscosities. Hardy et al. (2009) demonstrated that the model presented by Gervais et al. (2006) fails below a wall thickness of $2\,{\text{mm}}$. However, since the wall thickness for certain blood vessels are on the order of 100 μm (Mazumdar 1992), analytical models for channels of such dimensions hold vital importance, similar to the one developed in our previous work (Raj and Sen 2016). Later, Raj et al. developed a theoretical model for the wall thickness on the order of $1\,{\text{mm}}$ using thick plate approximations (Raj et al. 2017). Till now, the models developed assumed that the PDMS wall deformation is parabolic, which is highly unlikely at lower input flow rates or pressure drop applied for thicker wall channels. Towards improving this model, Christov et al. (2018) recently reported a theoretical model which does not assume the parabolic deformation but considers the fluid–structure interaction. Later, the same group investigated the validity of all the important models developed till date and compared with a numerical model developed by them (Shidhore and Christov 2017). In the first part of this review, we discuss the existing theoretical models for pressure-flow and deformation characteristics of deformable PDMS microchannels, and their corresponding experimental validations. Then, we present the applications of pressure-driven flow in flexible microchannels in organ-on-chip, cell mechanophenotyping, investigation of interaction between deformable objects with compliant boundaries and other microfluidics systems.

2 Theoretical model: pressure-flow and deformation characteristics

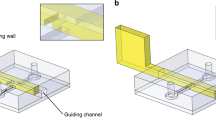
Conventionally, PDMS microchannels are fabricated by bonding a PDMS layer containing microchannel with a glass slide which results in a microchannel having three walls fabricated of PDMS and the fourth wall fabricated of glass (refer to Fig. 1a). Although PDMS is softer than glass, the conventional PDMS microchannels deform only above a critical pressure range, as discussed later in this section. Alternatively, the glass slide in the conventional fabrication technique is replaced by a thin PDMS membrane as shown in Fig. 1b. Such devices are referred as compliant microchannels. Thus, flexible microchannels can be of two types: conventional microchannels and compliant microchannels. In this section, we will discuss the theoretical models available in the existing literature for pressure-flow and deformation characteristics of conventional and compliant microchannels. Figure 1c–e shows the various notational parameters as well as the coordinate system used in theoretical modeling. Under the influence of flow, one of the walls of a flexible channel deforms internally as shown in Fig. 1d–e. Fig. 1d shows the cross-sectional deformation of the channel at a location $~z$. Here, the deformation is approximated to be parabolic. The deformation of the channel is maximum at $z=0$ and reduces to zero at $~z=L$. The deformation and pressure-flow characteristics of conventional and compliant microchannels are presented in the following subsection,

Fig. 1

Schematic of the PDMS-based microfluidic device a conventional, b compliant microchannel, c top view, d cross-sectional view of a deformed compliant channel, e side view of a deformed compliant channel (Raj and Sen 2016)

2.1 Conventional PDMS microchannels

In conventional microchannels, the deformation of the thick PDMS walls (considered as semi-infinite) is similar to soil deformation on application of load (Timoshenko and Woinowsky-Krieger 1959). An analytical model was developed by Gervais et al (2006) to predict the deformation and pressure-flow characteristics of conventional PDMS microchannel. Here, the pressure-flow characteristic of Newtonian incompressible fluid flow through a rigid rectangular microchannel with high aspect ratio (height to width ratio) is given by (Bruus 2008)

$$\frac{{\partial p(z)}}{{\partial z}}=\frac{{12\mu }}{{{h^3}w}}$$

(1)

where $p(z)$ is the pressure in the stream-wise position $z$, $Q$ is the flow rate, $\mu$ is the viscosity of fluid, $h$ and $w$ are height and width of the channel, respectively. The pressure-flow characteristic (Eq. 1) scales as the third power of the channel height. Such strong dependency suggests that even a small change in the height of the microchannel (as observed with PDMS microchannels at high flow rates; refer to Fig. 1) can give rise to a significant modification in the pressure-flow characteristics. The height of PDMS microchannel is maximum at the beginning $(z=0)$ and reduces to the nominal height at the outlet $~z=L$. To derive the pressure-flow characteristics of the deformable microchannel, we must incorporate the height of the channel as a function of position along the channel $(z)$ and pressure along with other parameters into Eq. 1. The above relationship $h(z)$, was developed using scaling analysis based on the assumption that Hooke’s law is valid for stress–strain dependency. In general, the thickness of the PDMS layer containing the microchannel is on the order of few millimeters. So, for the stress–strain analysis, an approach similar to soil mechanics was used, where the pressure imposed by a large structure will deform the soil under it, and this deformation becomes negligible at distances far away from the source of pressure (Timoshenko and Woinowsky-Krieger 1959). In the case of a semi-infinite medium, the characteristic length scale of strain decay is proportional to the width of the channel. This implies that for higher channel widths, the deformation becomes negligible at distances far away from the solid–liquid interface. Using this approach, the lateral and vertical strains were related to the pressure and channel deformation across the width $\Delta W$ and height $\Delta h$ as follows:

$${\varepsilon _{{\text{vertical}}}}\sim \frac{{\Delta h}}{w}\sim \frac{p}{E}$$

(2)

$${\varepsilon _{{\text{lateral}}}}\sim \frac{{\Delta w}}{h}\sim \frac{p}{E}$$

(3)

where $E$ is the Young’s modulus of the wall material. Comparing Eqs. 2 and 3, it is found that the lateral deformation across the channel width $\Delta w$ becomes negligible for the case of $~w \gg h$ (i.e, for high aspect ratio channels). Hence, only channel deformation in the vertical direction (i.e., the direction normal to the flow) is significant. This gives the relation between the maximum deformation in the vertical direction Δh_max(z) at the center of the channel under deformation and the local pressure $p\left( z \right)$ as

$$\frac{{\Delta {h_{\hbox{max} }}}}{{{h_0}}}={C_1}\frac{{pw}}{{E{h_0}}}$$

(4)

where C₁ is a dimensionless proportionality constant whose magnitude is of the order of unity and $~{h_o}$ is the undeformed height of the channel.

Now, assuming parabolic function for wall deformation, the average deflection $<\Delta h>$ in the channel height at any distance $z$ can be given as $\Delta h\sim \frac{2}{3}\Delta {h_{\hbox{max} }}$. Hence, the effective channel height at any location is related to the local pressure as follows,

$$h\left( z \right)={h_0}\left( {1+\alpha \frac{{p\left( z \right)w}}{{E{h_0}}}} \right)$$

(5)

where, $\alpha =\frac{2}{3}{C_1}$. Please note that the above equation represents the deflection of the upper wall of the channel which is in the form of a taper. Thus, the problem is simplified as the flow between tapering plates. Finally, the pressure-flow characteristics of the deforming channel (Eq. 6) is derived by incorporating Eq. 5 into the Eq. 1 and solving the differential equation along with the boundary condition $~p\left( {z=L} \right)=0$, which is given as

$$Q=\frac{{{h_0}^{4}E}}{{48\alpha \mu (L - z)}}\left[ {{{\left( {1+\alpha \frac{{p\left( z \right)w}}{{E{h_0}}}} \right)}^4} - 1} \right]$$

(6)

The total pressure drop for an imposed flow rate $Q$ is given by Eq. 6 as $~p\left( {z=0} \right)={P_o}$. From Eqs. 5 and 6, it is clear that pressure-flow characteristics as well as the deformation characteristics are strong functions of the parameter $~\alpha$. The value of $\alpha$, which is determined by fitting Eq. 6 with the experimental data, is on the order of unity. Once $\alpha$ for a microchannel of arbitrary dimensions is known, Eq. 6 can be used to determine the pressure-flow characteristics of the conventional PDMS microchannel.

Please note that Eq. 6 is valid only for high aspect ratio channels (i.e., $w \gg {h_o}$). However, in applications such as droplet formation for material synthesis (Tice et al. 2003) and other lab on-chip devices (Ichikawa et al. 2004; Adzima and Velankar 2006; Li and Olsen 2006; Kim and Yoo 2008; Zheng et al. 2012), often channels having aspect ratio closer to unity are used. Towards this, Cheung et al. (2012) have developed an analytical expression for pressure-flow characteristics of square channels as follows (Cheung et al. 2012). By solving the Navier–Stokes equation for steady-state, fully developed Newtonian flow through rigid rectangular channel and approximating the resulting Fourier sum representation, the pressure-flow characteristic, which is accurate within 13% for a square microchannel, is available (Bruus 2008),

$$\Delta p=\frac{Q}{{{h^3}w}}\frac{{12\mu L}}{{\left( {1 - 0.63\frac{h}{w}} \right)}}$$

(7)

Cheung et al. (2012) have utilized Eq. 7 along with Eq. 5 (as a constitutive relation) to develop the pressure-flow characteristic of a PDMS microchannel. The resulting differential equation was solved with outlet boundary condition $~p(z=L)~=~0$, which gives us the expression shown below.

$$Q=\frac{{{h_0}^{4}E}}{{48\alpha \mu (L - z)}}\left\{ {\left[ {{{\left( {1+\alpha \frac{{p\left( z \right)w}}{{E{h_0}}}} \right)}^4} - 1} \right] - 0.504\frac{{{h_0}}}{w}\left[ {{{\left( {1+\alpha \frac{{p\left( z \right)w}}{{E{h_0}}}} \right)}^5} - 1} \right]} \right\}$$

(8)

Equation 8 is valid for channels of different aspect ratios unlike Eq. 6 which is only applicable to high aspect ratio channels. Further, Cheung et al. (2012) have found out the value of the parameter $\alpha$ similar to Gervais et al. (2006) and have provided further insights into this parameter for channels of different dimensions. Experiments were performed with high viscous liquid (50 wt % glycerol solution) through the same channel and it was found that change in the viscosity of the fluid flowing through the channel does not change the value of $\alpha$ significantly. Further, both Eqs. 6 and 8 were utilized to fit the experimental data and calculate the best fit value of $\alpha$ and found that there is no significant variation in the value of $\alpha$ determined using the two methods. Hence, it was concluded that $\alpha$ is solely dependent on the channel dimensions, confirming the observation of Gervais et al. (2006). Please note that this method of finding the value by fitting procedure will only provide an approximate prediction (Cheung et al. 2012). Though, the exact value of $\alpha$ can be found by fluid–material structure computation, which is very challenging.

Gervais et al. (2006) and Cheung et al. (2012) investigated the flow dynamics of conventional PDMS microchannels having higher wall thicknesses ($\geq 6\,{\text{mm}}$) and concluded that the value of $\alpha$ is solely dependent on the channel dimensions. Later, Hardy et al. (2009) investigated the effect of wall thickness on deformation characteristics of the channel (discussed in details in the next section). In the work of Hardy et al. (2009) when the wall thickness was reduced to $1.5~\,{\text{mm}}$, it was observed that for the same channel dimensions, the experimental data for wall deformation deviated from that predicted by Eq. 6. This shows that the value of $\alpha$ is different for different wall thicknesses and semi-infinite model approximation fails for $t<2\,{\text{mm}}$. Towards this, Raj et al. (2017) suggested a different approach by considering the wall thickness (500 μm $\leq t \leq$ 2000 μm) as a thick membrane and using the relationship between the local pressure, channel dimensions, wall thickness $t~$and wall properties as

$$p\left( z \right)=\left[ {\frac{{66{t^3}}}{{{w^4}}}\frac{E}{{\left( {1 - {\nu ^2}} \right)}}} \right]\left( {\Delta {h_{\hbox{max} }}} \right)$$

(9)

which is a constitutive relation for Eq. 7. Here, $\nu$ is Poisson’s ratio of the wall material. Please note that the Eq. 9 plays a similar role as Eq. 4, except that the basic approach taken for deriving the two equations are different. While Eq. 4 is derived using scaling analysis whereas Eq. 9 is derived by assuming the wall as a thick membrane. In Raj et al. (2017), by solving the resulting differential equation, the pressure-flow characteristic was established as

$$Q=\frac{{wh_{o}^{3}p(z)}}{{12\mu \Omega (L - z)}}\left[ {\frac{{{\Omega ^3}}}{4}p{{\left( z \right)}^3}+{\Omega ^2}p{{\left( z \right)}^2}+\frac{\Omega }{2}p\left( z \right)+\,1 - 0.63\frac{{{h_o}}}{w}\left( {\frac{{{\Omega ^4}}}{5}p{{\left( z \right)}^4}+{\Omega ^3}p{{\left( z \right)}^3}+\frac{\Omega }{2}p\left( z \right)+1} \right)} \right]$$

(10)

where, $\Omega$ is defined as “deformability parameter” given by $~\Omega =\left[ {\frac{{a\left( {1 - {\nu ^2}} \right){\xi ^3}}}{{99E{h_o}}}} \right]$, $a~$ is the aspect ratio $(w/{h_o})~$and $\xi$ is the channel width-to-wall thickness ratio $(w/t)$. We discuss the experimental validation of the above models in the next section. Also, we discuss the analytical framework developed for flow dynamics through PDMS microchannels having wall thickness smaller than 100 μm, referred as “compliant microchannels” (Anoop and Sen 2015; George et al. 2015; Raj and Sen 2016; Raj et al. 2016; Reddy et al. 2016).

2.2 Compliant PDMS microchannels

As discussed, for the case of conventional PDMS microchannels, the thick PDMS walls that undergo deformation are considered to be semi-infinite. However, when the wall thickness decreases to ~ 100 μm, the entire PDMS wall deforms such that the outer as well as the inner surfaces of the thin wall undergo stretching. In this case, the deformation of the two side walls and the lower wall of the channel is negligible, so the channel cross-section could be assumed to be rectangular throughout. Under imposed flow condition, at a fixed cross-section along the microchannel, the local pressure $p(z)$ induces deflection of the compliant membrane wall. The expansion of the channel cross-section in turn modifies the fluid velocity and pressure distribution, which further controls channel deformation and so on.

Raj and Sen (2016) introduced an approach to establish the pressure-flow and deformation characteristics of compliant microchannels. To find a relationship between the local pressure $p(z)$ and the maximum deformation of the channel wall $\Delta {h_{\hbox{max} }}$, the force balance over an infinitesimally small element of the thin membrane wall yielded the expression

$$p(z) \approx \frac{{64}}{3}\frac{{{t_{\text{m}}}{E_{\text{m}}}}}{{w(1 - {v_{\text{m}}})}}{\left( {\frac{{\Delta {h_{\hbox{max} }}}}{w}} \right)^3}$$

(11)

where ${t_{\text{m}}}$, ${E_{\text{m}}}$ and ${v_{\text{m}}}$ are thickness, Young’s modulus and Poisson’s ratio of membrane, respectively. This gives the effective channel height as

$$h\left( z \right)={h_0}\left[ {1+\frac{2}{{3{h_0}}}{{\left( {\frac{{3{w^4}\left( {1 - {v_{\text{m}}}} \right)p(z)}}{{64{t_{\text{m}}}{E_{\text{m}}}}}} \right)}^{\frac{1}{3}}}} \right]$$

(12)

In Eq. 12, a group of parameters combined together, termed “compliance parameter” $~{f_p}=~{w^4}(1 - {\nu _{\text{m}}})/(72{t_{\text{m}}}{E_{\text{m}}}h_{o}^{3})$ govern the deformation of the thin wall. For a channel of fixed dimensions $w$ and${h_0}$, as the thickness and the value of Young’s modulus of the thin membrane wall decreases, ${f_p}$ increases, which provides higher membrane deflection $\Delta h\left( z \right)$. Now, Eq. 12 is utilized as a constitutive relation for Eq. 7, and the resulting differential equation is solved using outlet boundary condition $~p(z=L)~=~0$ to determine the pressure-flow characteristics of the compliant microchannel as

$$Q=\frac{{w{h_o}^{3}p}}{{12\mu (L - z)}}\left[ {1+\frac{9}{4}{{({f_{\text{p}}}p)}^{\frac{1}{3}}}+\frac{9}{5}{{({f_{\text{p}}}p)}^{\frac{2}{3}}}+\frac{1}{2}\left( {{f_{\text{p}}}p} \right) - 0.63\frac{{{h_0}}}{w}\left\{ {1+3{{({f_{\text{p}}}p)}^{\frac{1}{3}}}+\frac{{18}}{5}{{({f_{\text{p}}}p)}^{\frac{2}{3}}}+2\left( {{f_{\text{p}}}p} \right)+\frac{3}{7}{{({f_{\text{p}}}p)}^{\frac{4}{3}}}} \right\}} \right]$$

(13)

It is observed from Eq. 13 that the pressure-flow characteristics of the compliant microchannel is non-linear, unlike that in case of the rigid channel. However, the above equation reduces to a linear term at $~{f_{\text{p}}}=0$, which then describes the pressure-flow characteristics of Newtonian fluid flow through a rigid rectangular microchannel.

Further, Eq. 12 may be rearranged as $p\left( z \right)=\frac{1}{{{f_{\text{p}}}}}{\left[ {\frac{{h\left( z \right)}}{{{h_o}}} - 1} \right]^3}$ and used as a constitutive relation for Eq. 7 to find an expression for the effective height of the channel $h\left( z \right)$, as follows

$$\left( {\frac{w}{{4{h_0}}}} \right){h^4} - \left( {\frac{{2w+0.63{h_0}}}{{5{h_0}^{2}}}} \right){h^5}+\left( {\frac{{w+1.26{h_0}}}{{6{h_0}^{3}}}} \right){h^6} - \left( {\frac{{0.09}}{{{h_0}^{3}}}} \right){h^7}=4\mu {f_p}Q\left( {L - z} \right)+\frac{1}{{60}}w{h_0}^{3} - (0.006){h_0}^{4}$$

(14)

All the theoretical models presented above assume the deformation of the flexible wall to be parabolic, which may not satisfy the actual deformation profile at low applied pressure drops. Towards this, recently Christov et al. (2018) have developed a theoretical model for $L \gg w \gg {h_o}$ using Kirchhoff–Love plate expression (Timoshenko and Woinowsky-Krieger 1959) as a constitutive relation to the Navier–Stokes equation. The derived pressure-flow characteristics is given by Eq. 15.

$$Q=\frac{{h_{o}^{3}wp\left( z \right)}}{{12\mu \left( {L - z} \right)}}\left[ {1+\frac{1}{{480}}~\frac{{{w^4}}}{{B{h_o}}}~p\left( z \right)+\frac{1}{{362880}}{{\left( {\frac{{{w^4}}}{{B{h_o}}}} \right)}^2}p{{\left( z \right)}^2}+\frac{1}{{664215552}}{{\left( {\frac{{{w^4}}}{{B{h_o}}}} \right)}^3}p{{\left( z \right)}^3}~} \right]$$

(15)

where, $B=\frac{{{E_{\text{m}}}t_{{\text{m}}}^{3}}}{{\left[ {12\left( {1 - {\nu _{\text{m}}}} \right)} \right]}}$ is the bending rigidity of the thin PDMS membrane wall. Equation 15 works well for the compliant microchannel of high aspect ratios (width to height ratio). Further, Shidhore and Christov (2017) has investigated the validity of Eq. 15 and compared it with experimental data for channels with various wall thicknesses ${t_{\text{m}}}$. Equation 15 was found to work well for membrane thickness ${t_{\text{m}}}=$ 50 μm and 200 μm.

This completes the up-to-date review on existing theoretical models for pressure-driven flow through flexible microchannels. In the next section, we present the validation of the presented theoretical models and methods to measure the wall deformation of flexible microchannels. The nomenclature and corresponding units in the SI system for terminology used in the equations for deriving pressure-flow and deformation characteristics of compliant microchannels are listed in Table 1.

Table 1 Nomenclature of terminology used in the characterization of compliant microchannels

3 Validation of the theoretical models for flexible PDMS microchannels

In the previous section, we presented theoretical models that enable prediction of the deformation of soft microchannels. To experimentally characterize the deformation of such channels, two types of techniques, namely fluorescence and confocal microscopy, were utilized. These techniques enable measurement of the deformed height of the channel by studying the shape of the fluid flowing through it, which is the same as that of the deformed channel cross-section. Gervais et al. (2006) used confocal microscopy to characterize the deformed height of the channel. The experiments confirmed internal wall deformation at higher flow rates (Fig. 2a). While the deformation of the upper PDMS wall of the microchannel was significant at an imposed flow rate of 300 μL/min, negligible deformation was observed at 1 μL/min (bottom image of Fig. 2a). Further, numerical simulations performed using CFDACE software (CFDRC Inc.) also clearly shows that the PDMS wall deformation takes place in the transverse direction (Fig. 2b). While deformation and fluid pressure are maximum at the inlet, these reduce to zero and atmospheric pressure respectively at the outlet.

Fig. 2

a Confocal microscopic image of the PDMS microchannel at imposed flow rate of 300 μL/min (top) and 1 μL/min (bottom). b Numerically simulated pressure, velocity and deformation profile of the PDMS microchannel (Gervais et al. 2006)

In contrast, Hardy et al. (2009) characterized the deformation of the walls of soft microchannels under pressure-driven flow via fluorescence microscopy. Rhodamine 6G dye (a fluorescence dye) at 6 µM concentration was pumped through the microchannel and was illuminated using a fluorescence excitation light source (Exfo X-Cite 120). The pressure and fluorescence intensity at five different points along the channel were measured. As observed, in the fluorescence images and the intensity plots in Fig. 3, the channel is illuminated more at higher flow rates, giving rise to an increase in brightness of the fluorescence images, compared to the zero flow rate condition (Fig. 3a). High fluorescence intensity along the channel cross-section shows that the thickness of the liquid is highest at this location. For the concentration of Rhodamine dye used in the experiments, the thickness of the dye layer is linearly proportional to the fluorescence intensity (Holden et al. 2003). Using this relation, the thickness of the fluid layer (mixed with rhodamine) is correlated with the intensity level, which is proportional to channel wall deformation along the cross-section. The deformation along the channel length measured using this technique is shown in Fig. 4c, d. The deformation is maximum at the beginning of the channel ($z=0)$ and gradually decreases until the end of the channel. Figure 3b (left image) shows that the deformation increases with an increase in the flow rate, as expected. These results also show that the proposed fluorescence technique is highly reliable for measuring microchannel deformation. Compared to confocal microscopy, this technique is less expensive, as the former requires sophisticated setup.

Fig. 3

a Fluorescence image showing the higher intensity of the illumination by the fluid layer at a positive imposed flow rate of 200 μL/min (right) compared to zero flow rate condition (left). b The variation of fluorescence intensity with the increase in the imposed flow rate along the marked cross-section of the microchannel (Hardy et al. 2009)

Fig. 4

Measured pressure profile along the microchannel stream-wise direction for two distinct wall thicknesses; $3\,{\text{mm}}$ (a) and $1.5\,{\text{mm}}$ (b), measured deformation profile of the microchannel for two distinct wall thicknesses; $3\,{\text{mm}}~$ (c) and $1.5\,{\text{mm}}$ (d), Solid line shows the predictions from Eq. 7 by utilizing the best-fitted $\alpha$ value (Hardy et al. 2009)

Next, we compare the experimental data with the predictions of the theoretical models. Figure 5 shows the comparison between the experimental observations and the theoretical prediction of the pressure-flow characteristics (Eqs. 6, 8 and 10). Equation 6 is valid for high aspect ratio ($w/{h_o})$ channels, as evident from its agreement with the experimental data for channel aspect ratios greater than 10 (Fig. 5a). However, it starts failing at low aspect ratios (close to 1.0), whereas Eq. 8 shows a better comparison, as seen in Fig. 5b. In these studies, wall thickness greater than $6\,{\text{mm}}$ was chosen and its effect on channel wall deformation as well as pressure-flow characteristics was considered. However, as discussed in the theoretical section, Hardy et al. (2009) have investigated the effect of wall thickness on the fitting parameter $\alpha$. Figure 4 demonstrates the results for the pressure (a–b) and the deformation plots (c–d) along the stream-wise direction at various imposed flow rates for microchannels of PDMS wall thicknesses $3\,{\text{mm}}$ (Fig. 4a, c) and $1.5\,{\text{mm}}$ (Fig. 4b, d). As seen in Fig. 4, the total pressure drop in the 1.5 mm thickness channel is smaller than that in the 3 mm thickness channel. This difference suggests that the 1.5 mm thickness channel experienced greater deformation and less restricted flow. Further, Hardy et al. (2009) have estimated the approximate value of $\alpha$ for PDMS wall thickness $3.0\,{\text{mm}}$ and $1.5\,{\text{mm}}$ to be 0.48 and 0.62, respectively. Thus, reducing the wall thickness from 3.0 to 1.5 mm, increases the value of $\alpha$ by 30% for fixed channel dimensions, which suggests that at these thicknesses and deformations, possibly the semi-infinite medium approximation becomes invalid. The findings of Hardy et al. (2009) shows that the semi-infinite assumption and hence the modeling proposed by Gervais et al. do not hold good for low wall thicknesses ($1\,{\text{mm}}$). The small capillaries and aorta in the human circulatory system have wall thickness ranging from 1 μm to $2\,{\text{mm}}$ (Mazumdar 1992). None of the above two models are valid for predicting flow behavior in case of flexible microchannels having lower (< 1 mm) wall thicknesses, which limit the applications of such models in the in vitro investigation of blood vessels.

Fig. 5

a Comparison between experimental and theoretical pressure-flow characteristics (Eq. 7) (Gervais et al. 2006), $\frac{w}{{{h_o}}}\sim 10$ and 20, wall thickness $t\sim 6\,{\text{mm}}$. b Comparison of theoretical model (Eq. 9) with the experimental data for channel (Cheung et al. 2012) with$~\frac{w}{{~{h_o}}}=2$, wall thickness $t\sim 6\,{\text{mm}}$. c Comparison of theoretical prediction (Eq. 11) with the experimental data for channel with various wall thicknesses and wall properties (Raj et al. 2017), $\frac{w}{{{h_o}}}=7$. d The compiled value of $\alpha$ for various wall thicknesses (Raj et al. 2017)

Toward this, Raj et al. (2017) developed a model that predicts the pressure-flow characteristics of microchannels and have validated for various wall thicknesses ranging from 500 to 2000 μm precisely (Fig. 5c). The value of $\alpha$ for various $\xi$ determined from these experiments is presented in Table 2 for reference. Also, Fig. 5d shows that ${\xi ^3}$ varies linearly with $\alpha$, which indicates $~\alpha \sim {\left( {\frac{w}{t}} \right)^3}$. This has also been concluded by Christov et al. (2018) when they compare their theoretical model (Eq. 15) with that of Gervais et al. (2006) (Eq. 6). Furthermore, the theoretical model for the flow through compliant microchannel reported by Raj and Sen (2016) can be used to describe accurately the fluid flow in flexible microchannels having wall thicknesses as low as 100 μm. Figure 6 shows the comparison of the experimental results and the theoretical predictions (Eqs. 13 and 14) for pressure-flow and deformation characteristics, respectively, which agree within an error of $~18~\%$. Equation 15 also works well for the wall thickness ~ 100 μm as shown in Fig. 6c. Shidhore and Christov (2017) have developed a numerical model for the fluid flow through deformable microchannel and compared their model with experimental data reported by Raj and Sen (2016) as well as the theoretical models (Eqs. 13 and 15) as shown in Fig. 6c. The numerical model was found to predict the experimental data very well, as observed.

Table 2 The experimental parameters utilized by Raj et al. (2017), reference for Fig. 5c

Fig. 6

a Comparison of pressure drop $\Delta p$-flow rate $Q$ characteristics obtained from experiments with that predicted using the model (Eq. 1) (Raj and Sen 2016). b Comparison of theoretical (Eq. 14) and experimental axial average deflection profile of the thin membrane wall (Raj and Sen 2016) ($Q=$ 1000 μl/min), w = 500 μm, ho = 83 μm, μ = 0.000914 Pas, f_p = 1.023446 × 10⁻⁵ Pa⁻¹. c Comparison of experimental data from Raj and Sen (2016) with the theoretical models and the simulation data by Shidhore and Christov (2017), Raj and Sen (2016) and Christov et al. (2018) represents Eqs. 13 and 15, respectively

The integration capability of PDMS-based microfluidics devices allows bonding thin PDMS membranes with microchannels and micro chambers. Recently, Debadi et al. investigated the hydrodynamics of a PDMS microchannel having a thin PDMS membrane (60 μm thickness) integrated over a short length as the channel wall (Chakraborty et al. 2012). Two-dimensional finite element model was developed to study the fluid–structure interaction between fluid flowing in the channel with this thin PDMS layer. Figure 7a, b shows the schematic of the device used for experimental investigation, which is a double-layer device. The bottom PDMS layer contains the channel of dimension $W \times H$ and the top layer has a microchannel connected with pneumatic pressure source (see Fig. 7) which are bonded together with the thin PDMS membrane. This arrangement allows having the thin PDMS layer only over a short length of the channel. The deformation of the thin layer under the application of varying externally applied pressure (with zero imposed flow rate through the microchannel) was studied. One of the major findings of this work is the pressure-flow characteristics of the channel with varying width $W$, as shown in Fig. 7c. For width $~W=3L$ ($L$ is marked in Fig. 7b for reference), no significant deformation of the thin layer was observed. However, under an imposed flow rate condition for $~W=0.5~L$, the thin PDMS layer was deformed, and the observed pressure drop deviated from that expected for a rigid microchannel of identical dimension. The theoretical models for pressure-flow characteristics of fluid flow through flexible microchannels are summarized in Table 3.

Fig. 7

a Schematic of the device used by Chakraborty et al. (2012) to investigate the fluid–structure interaction at the thin PDMS layer (thickness 60 μm). b Schematic showing the doubled layered arrangement of microchannels and the thin PDMS membrane. c Pressure-flow characteristics of microchannel with thin PDMS membrane integrated over a short length of the wall (Chakraborty et al. 2012)

Table 3 List of existing theoretical models (equations) for pressure-flow characteristics of Newtonian laminar fluid flow through flexible microchannels along with their validity and limitations

4 Applications of flexible PDMS microchannels

Thin PDMS membranes have been employed for various applications such as flow stabilization (Yang and Lin 2009; Iyer et al. 2015), cell manipulation (Ho et al. 2016; Ravetto et al. 2016), pneumatic actuation, micropumps and organ-on-a-chip (Huh et al. 2010). Iyer et al. (2015) utilized such membranes to fabricate a compliant microchamber to stabilize fluid flow within microfluidic devices . Huh et al. (2010) designed a lung-on-a-chip module by utilizing PDMS membranes coated with extra-cellular matrix (ECM) to compartmentalize microchannels, mimicking lungs. Besides these, thin PDMS membranes have been exploited in elastocapillary studies and applications (Anoop and Sen 2015; George et al. 2015; Reddy et al. 2016). Here, the various applications of the compliant microchannels in microfluidics and its benefits over conventional microchannels are discussed.

4.1 Organ-on-a-chip models using compliant PDMS microchannels

The dimensional and flexural similarity of PDMS-based compliant microchannels with blood vessels and tissues allows use of these devices to mimic various organs -on-chip, such as airway, lung, kidney, gut, and blood vessels (Huh et al. 2007, 2010; Zheng et al. 2009; Jang and Suh 2010). Huh et al. (2007) have designed and fabricated a microfluidic airway system and demonstrated its utility in in vitro investigation of pulmonary diseases. Often, the incapability of pulmonary surfactant to reduce surface tension at the air–liquid interface leads to two-phase instability in the small airway epithelium. This instability creates a liquid plug inside the airway lumen, which obstructs the small airway, and hinders gas exchange in the alveoli. During inhalation, the lung expands, and the liquid plug migrates through the airway tubes, and finally ruptures. The propagation and rupture of the liquid plug opens the sealed airway, and injures small airway epithelial cells due to mechanical stress. Towards this, Huh et al. (2007) investigated the effect of artificially created liquid plug propagation and rupture on cell viability, and found that cell viability decreases with an increase in the number of propagated and ruptured plugs within a certain time scale. Figure 8 shows the schematic of the microfluidic device designed for this work. To mimic the basement membrane in vitro, two PDMS microchannels were separated by a porous polyester membrane ($400\,{\text{nm}}$ pore size), which served as the chamber for growing cells. The upper and lower chambers mimicked the apical (airway lumen) and basal compartments of the airway epithelium, respectively. The dimensions of the microchannel (300 μm width and 100 μm height) were chosen to match the dimensional similarity of the conducting airways and bronchioles. Further, to create a tissue-like environment similar to airways, small airway epithelial cells (SAECs) were seeded into the upper and lower chambers. Once the cells were grown over the porous membrane to confluency, the culture media from the upper chamber was removed, which created an air–liquid interface over the cells. Then, liquid plugs were created artificially in the lower channel, and propagated by controlling the valve switches. As the plug propagated through the lower channel, the liquid adhered to the walls and the plug ruptured downstream. This generated transient pressure wave, produced harmful stresses on the membrane surface and damaged the cells. Figure 8f clearly shows that cell viability decreases with an increase in the number of such plugs. Thus, using a compliant microchannel, the effect of unstable wave on cell viability could be easily investigated.

Fig. 8

Design of the airway system a the fabricated airway system consists of two PDMS microchannels with a porous membrane sandwiched between them. b SAECs are seeded and grown till confluency over the porous membrane in both upper and lower chambers. c The culture media in the upper chamber is drained to create an air–liquid interface over the cultured cells. d Plugs are created artificially and flown through the lower chamber. e Plug propagates and ruptures along its movement in the lower chamber, reopening the in vitro small airways. f The viability of grown cells as a function of number of plugs that ruptured during propagation through the lower chamber (Huh et al. 2007)

Similarly, Zheng et al. (2009) mimicked small airway using a compliant microchannel and studied the deformation of the compliant wall with the propagation of liquid plug (suspension of DI water with fluorescent particles). Figure 9a shows the microscopic image of the plug propagating through the compliant microchannel, for a capillary number ($Ca$, ratio of inertia force to the surface tension force) of 0.001 and 0.0015. The lower image for every $Ca~$ represents the quantitative extraction and polynomial fitting of the wall position. Figure 9b shows the variation of the wall deformation with $Ca$. It implicitly indicates that the wall deformation increases with increase in plug velocity as well as plug length. Furthermore, the pressure drop across the plug was monitored for both rigid and compliant microchannels and was found to increase with an increase in the plug velocity. However, the pressure drop was slightly lower in the compliant microchannel than the rigid microchannel.

Fig. 9

a Microscopic images of the plug propagating inside the compliant microchannel where the upper wall is rigid and the lower wall is flexible. The compliant wall deforms with the plug propagation. b Change in the deformation of the compliant wall with change in $Ca$ for various plug lengths (Zheng et al. 2009)

Further, Jang et al. (2010) utilized a multilayered PDMS microfluidic device [similar to Huh et al. (2007)] to analyze renal tubular cells, and demonstrated the applicability of the compliant microchannel in drug screening and advanced tissue engineering. A thin porous membrane similar to Huh et al. (2007) was utilized to mimic the renal tubular space. The primary rat inner medullary collecting duct (IMCD) cells were cultured on the inner walls of the tubular space. In vivo-like tubular environment was mimicked by flowing fluid at a shear rate of $1\,{\text{dyn/c}}{{\text{m}}^2}~$over the renal cells for a period of 5 h, which was optimal for culturing cells.

Later, using a similar arrangement, Huh et al. mimicked the alveoli–capillary interface to study the effect of silica nanoparticles on lungs (Huh et al. 2010). The design and investigation presented in this work play a major role in drug delivery applications. Figure 10 shows the schematic of the microfluidic device fabricated to mimic the alveoli–capillary interface. The microfluidic platform reproduces key structural, functional, and mechanical properties of the human alveolar–capillary interface, which is a vital part of the human lung. A thin PDMS membrane, sandwiched between two microchannels, was seeded with epithelial and endothelium cell lines on both sides, respectively, and grown to confluency. This membrane, shown in Fig. 10a, mimics the human alveolar–capillary interface. To mimic air inhalation, vacuum was applied to the two side chambers (Fig. 10a), which inflated the main channel, and in turn stretched the cultured cells over the thin membrane. The main aim of this design was to investigate the effect of the dynamic mechanical stress on the inflammatory and toxic responses of the lung in the presence of silica nanoparticles during breathing. The investigation in this study using the in vitro model showed significant insights regarding the inflammatory response. Repeated mechanical strain was found to enhance the inflammatory and toxic response of the lung in the presence of silica nanoparticles. Also, it increases the uptake of nanoparticles and induces their transport into the microvascular channel. Thus, such organ-on-chip microdevices, which mimic tissue–tissue interfaces, play a vital role as an economical substitute to clinical investigations for drug testing and other toxicological studies.

Fig. 10

Lung-on-a-chip model a Membrane coated with ECM is cultured with epithelium and endothelium cell lines. b In vivo alveoli–capillary interface mimicked in the work. c, d Cross-sectional view of the mimicking microchannel with porous membrane separating the two microchannels. e Image of the fabricated microfluidic device (Huh et al. 2010)

The transplanted cells require the transport of nutrients, oxygen delivery and waste removal for the regeneration of vital organs such as liver and heart. Since the diffusion process alone is not sufficient to fulfill the transport needs, convective pathways, i.e., a vasculature network, is highly desired. Towards this, Shin et al. designed an artificial vasculature network using PDMS microchannel (Michael Shin et al. 2004). In this design, a rectangular PDMS microchannel having thick PDMS walls on three sides and a thin PDMS membrane as the fourth wall, were used to mimic the circular arteries. Human mammary endothelial cells (HMEC-I) were cultured on the internal walls of the microchannel (Fig. 11a, b), which provides the cell environment in the vasculature network. This proposed device can be used for studying blood flow through diseased arteries.

Fig. 11

Artificially mimicked vasculature network using a flexible microchannel. a Vasculature network. b Zoomed view of the microchannel network showing the cultured HPMEC-I cells on the internal walls of the channel (Michael Shin et al. 2004)

4.2 Biomechanics studies in compliant PDMS microchannels

Compliant microchannels find interesting applications in cell mechanophenotyping. Constriction-based microfluidic devices, having channels of dimension smaller than that of the cells, are most widely used for such studies. The size of the micro-constriction determines the range of cell sizes that can be handled/manipulated in a rigid, constriction-based microchannel. For cell samples exhibiting high polydispersity, channels of various dimensions must be fabricated. Towards this, Guan et al. (2012) designed and demonstrated a flexible microchannel-based device for mechanophenotyping, which can handle cells of various size ranges. Figure 12 shows the assembly of the proposed microfluidic device. This technique utilizes a thin, deformable PDMS membrane as one of the walls of the micro-constriction (Fig. 12b). This thin wall deforms inward with the application of pressure, and thus decreases the size of the micro-constriction. This approach allows active control of the size of the micro-constriction. Once a single cell moves closer to the constriction channel, its size is measured. Then, the size of the micro-constriction is adjusted, keeping the size ratio (i.e., ratio of cell diameter to constriction size) fixed. When the cell migrates through the channel, its passage time is also measured. It is observed that the passage time varies with different gap sizes (Fig. 12c) and for different cell lines (Fig. 12d).

Fig. 12

a Schematic of the size-independent cell deformability cytometry. b Cross-sectional view of the constriction channel showing the deformed cell. c Dependence of passage time on cell diameter for various gap dimensions. d Dependence of passage time on the size ratio (Gap height/Cell diameter) for various cell types (Guan et al. 2012)

Further, compliant microchannel devices have been used to overcome channel clogging, which is commonly observed with constriction-based microfluidic devices. The small size of the constriction channel in comparison to the cell size, and aggregates of cells in the constriction channel are the main reasons for clogging. To overcome this difficulty, Huang et al. (2014) presented a device, which utilized a control chamber across a deformable wall channel, which permits applying positive as well as negative pressure depending upon the user’s need (Fig. 13). If the device is clogged, a negative pressure is applied in the control channel, which increases the size of the constriction channel to a value greater than the cell size or the overall size of the debris and clears the clog.

Fig. 13

a Schematic of the thin membrane microfluidic device used for single cell analysis. b Schematic showing unclogging of the micro-constriction device by applying vacuum at the other side of the constriction (Huang et al. 2014)

4.3 Other compliant PDMS microchannel-based microfluidic devices

In addition to the above, flexible channels find applications as micropumps (Singh et al. 2015; Kumar et al. 2016), microflow stabilizers (Iyer et al. 2015) and deformable droplet generators (Pang et al. 2014; Raj et al. 2016). For example, Iyer et al. developed a microflow stabilizer device, which transforms pulsatile flow into steady flow (Iyer et al. 2015). A series of compliant chambers, having a thin PDMS membrane of thickness 75–250 µm as one of the walls of each of the chambers, were used along the flow directions (Fig. 14). The capability of the thin wall to expand allows it to gather more and more fluid during excess flow and release them during underflow, due to spring-back effect. Thus, the compliant boundaries of the chambers act as capacitors, and transform the incoming pulsatile flow into a more stabilized flow. A PZT actuated, valveless micropump was used to supply pulsatile flow into the developed microflow stabilizer, and the pulsation of flow at the outlet of the device was measured. The device performance was measured in terms of “Attenuation Factor (AF)”, which is defined in the equation below.

Fig. 14

a Design of the microflow stabilizer device. b Experimental data showing smoothening of pulsatile input from the micropump (Iyer et al. 2015)

$$AF=\frac{{{Q_{0,~{\rm max} }} - {Q_{0,~{\rm min} }}}}{{{Q_{i,~{\rm max} }} - {Q_{i,~{\rm min} }}}}$$

(16)

where ${Q_{o,{\rm max} }}$ and ${Q_{o,{\rm min} }}$ are the maximum and minimum flow rates at the outlet, and ${Q_{i,{\rm max} }}$ and ${Q_{i,{\rm min} }}$ are the maximum and minimum flow rates at the inlet, respectively. Using three microflow chambers of 4 mm diameter as shown in Fig. 14a, the proposed device could significantly reduce the attenuation factor to 0.05, thus demonstrating its potential incorporation for real-world microfluidics circuits to reduce flow pulsation.

Further, thin PDMS membranes have been used in micropumps. The thin membrane wall is actuated by various mechanisms such as piezoelectric (Singh et al. 2015) and solenoid (Kumar et al. 2016). Figure 15 shows the schematic of the solenoid-actuated micropump device by Kumar et al. (2016). The thin PDMS membrane walled chamber acted as a capacitor, which with the help of nozzle and diffusor arrangement, pumped the liquid into the microchannel. As shown in Fig. 15a, the solenoid actuated the membrane wall by supplying a square waveform signal force. A positive value of the force results in the pumping of fluid through the system, and zero force level helps the chamber to suck the liquid inside due to the spring-back effect generated by the membrane. Figure 15b shows the schematic of the piezoelectric actuated micropump. The thin PDMS membrane (bonded as one of the wall of the micropump chamber) is bonded with a piezoelectric element which expands and contracts under the application of potential difference across it. With the expansion and contraction of PZT element, PDMS membrane (150 μm thick) also expands and contracts. This drives the liquid across the micropump with the help of nozzle and diffusor channel arrangement.

Fig. 15

a The schematic of the solenoid-actuated micro pump (Kumar et al. 2016). b Schematic of piezoelectric actuator-based micropump (Singh et al. 2015)

Recently, microfluidic peristaltic pumping techniques were developed using compliant microchannels (Darby et al. 2010; Zhang et al. 2015; Xiang et al. 2016). Zhang et al. (2015) demonstrated peristaltic pumping on-chip by utilizing a spring-and-cam arrangement over the compliant microchannel. Figure 16a, b shows the schematic and working principle of the device, respectively. The PDMS chip having the embedded compliant microchannel was installed over a sliding linear rail, and connected to a spring, as shown in Fig. 16a. A nylon cam of radius 6 mm was placed over the compliant microchannel and adjusted, such that it blocked the channel by deforming the compliant wall. The shape of the cam was designed specifically for this purpose. As the cam rotated, the spring was stretched, and the chip was pulled along the sliding rail, thus creating the pumping action. As soon as the cam rotated further such that its flat part was in contact with the channel wall, it lost grip of the chip and the microfluidic chip was pulled back by the spring, thus completing the cycle (Fig. 16b). Using this technique, Zhang et al. (2015) demonstrated a uniform flow in the range 1–500 nL/s with a back pressure of 340 kPa. Later, Xiang et al. (2016) reported another on-chip peristaltic pumping technique using cam follower system as shown in Fig. 16c–g. Here, three cams with a 120-degrees phase difference were installed over the compliant microchannel along its length. By rotating specific combination of the cam structures, the connected pins at the cam compressed the channel synchronously, such that the liquid was pumped and flowed forward in the channel (Fig. 16f–g). Using this technique, Xiang et al. (2016) demonstrated the highest pumping flow rate of 274 μL/min and maximum back pressure of 36 kPa.

Fig. 16

On-chip microfluidic peristaltic pumping technique reported by Zhang et al. (2015) showing a the schematic of the device and b the working principle; (Zhang et al. 2015). On-chip microfluidic peristaltic pumping technique reported by Xiang et al. (2016). c, d Schematic of the device showing the arrangement of a single cam e phase difference between the three cams, and f, g schematic showing the synchronous action of cams creating the pumping action (Xiang et al. 2016)

5 Dynamics of deformable objects through compliant PDMS microchannels

Next, we discuss the existing literature on the interaction of deformable objects such as droplets and cells with deformable boundaries. Although well-explored for macroscale flow (Lighthill 1968), this topic has received limited attention in the microscale. The topic has significance because of its utility in in vitro investigations for cardiovascular and cell migration-related diseases. The interaction between a deformable object and a deformable boundary involves multilevel complexities. In the case of single phase flow through flexible microchannels, the rheology of the liquid and the mechanical property of the wall together influence the hydrodynamics. However, in a suspension consisting of deformable objects, the analysis has two perspectives. The first perspective is the change in the rheology of the fluid sample induced by the presence of deformable objects. For example, emulsions exhibit different rheological property because of the presence of droplets. Here, the bulk behavior of the sample is considered for studying the hydrodynamics. The second perspective is to investigate the dynamics of interaction between a single deformable object, such as a cell, with a flexible wall boundary. Here, both the deformability of the single cell and the mechanical property of the compliance wall hold vital importance.

Deformable walls were utilized to generate droplets of sizes smaller than the throat dimensions (Lee et al. 2007). Pang et al. investigated the effect of wall compliance on droplet generation (Pang et al. 2014). In this study, compliant PDMS membranes were employed as one of the walls of the T-junction type droplet generator (Fig. 17a). PDMS membranes of varying bending stiffness $B$ were used for experimentation, and polydispersity in the generated droplets (i.e., standard deviation in droplet length relative to the average length of the droplets) was compared (Fig. 17d). The results showed a decrease in the polydispersity of the generated droplets with decrease in bending stiffness. Also, droplet generation was more controlled when softer droplet generators were used (Fig. 17c). The increased monodispersity was attributed to the flexibility of the membrane wall, which allows the droplets to expand and release stresses.

Fig. 17

a Cross-sectional view of the soft droplet generator having a thin PDMS membrane as one of the walls. b Conventional rigid droplet generator. c Droplet breakup in the conventional and soft droplet generator showing control of droplet generation. d Comparison of polydispersity in the generated droplet size for PDMS membranes having different bending stiffness (Pang et al. 2014)

Later, Raj et al. (2016) investigated droplet generation using a deformable droplet generator shown in Fig. 18a, b. Deformable droplet generator is a double layered microfluidic device. Droplet generator device is coupled with a controlling channel by sandwiching a thin PDMS membrane between them such that, the droplet generator junction has thin PDMS membrane as one of its walls. A highly viscous liquid is flown through the controlling channel which creates a pressure gradient across the membrane at the droplet generator junction and reduces the height of the droplet generator junction. In contrast, at zero flow rate through the controlling channel, the thin membrane wall expands outward and thus height of the droplet generator junction increases. This enables to generate droplets of desired size (in a range) by monitoring the flow rate of the controlling liquid through the controlling channel. A non-dimensional parameter, i.e., controlling parameter $~{K_{\text{p}}}=\frac{{w_{{\text{t}}}^{3}\Delta {p_{\text{t}}}}}{B}$ was defined to characterize the performance of the droplet generator. Here, ${w_{\text{t}}}\;{\text{and}}\;\Delta {p_{\text{t}}}$ denotes the width of the droplet generator throat and the pressure gradient across the membrane at the throat, respectively, and $B$ is flexural rigidity of the membrane. $\Delta {p_{\text{t}}}$ was found out by utilizing the theoretical model developed by Raj and Sen (2016).

Fig. 18

Schematic of the controllable deformable flow-focusing droplet generator device. a Top view of the focusing deformable droplet generator. b Cross-sectional view of the junction region. c Generation of droplets of sizes smaller than throat size. d Effect of increase in capillary number ($Ca$) on the droplet breakup regime for rigid and deformable droplet generator (Raj et al. 2016)

A thin membrane (22.5 ± 2 μm) was used for fabricating the device. The effect of ${K_{\text{p}}}$ on the droplet generation was studied. Figure 18c shows the variation of non-dimensional droplet size ${D_{\text{d}}}/w$ with ${K_{\text{p}}}$ by keeping flow rate ratio $r$, capillary number $Ca$ and viscosity ratio λ fixed. As visible, a droplet of size 75 ± 3.5 μm was possible to generate at ${K_{\text{p}}}=7.79$ with a throat size of 100 μm × 100 μm. Furthermore, effect of capillary number over the droplet generation was investigated. Figure 18d shows the comparison of generated droplet size between rigid and deformable droplet generator with the increase in capillary number. Droplet breakup was found to transit from a stable dripping regime to an unstable jetting regime at $Ca=0.24$ for a rigid droplet generator. However, droplet breakup was maintained as dripping regime even at $Ca=0.45$, which increases the throughput of the droplet generation significantly with the monodispersity of droplet generation maintained. The droplet size at $~Ca=0.45$was found to be 45 μm, which is significantly smaller the throat size (100 μm × 100 μm).

Furthermore, the interaction of biological cells with deformable structures was also studied previously. For this purpose, Walter et al. fabricated a flexible PDMS cantilever inside a microchannel to create a narrow confinement that mimics the tight spaces in the micropores or narrow vessels (Walter et al. 2011). Figure 19a shows the scanning electron microscopy image of the fabricated confinement within the microchannel. Once the cell suspension was flowed through the microchannel, a single cell was forced to move through the narrow flexible confinement. The cell size prior to deformation was measured upstream of the confinement (Fig. 19b). Once the cell moved to the position of the cantilever, it deformed the cantilever, the value of which provided an estimate of the cell deformability (Fig. 19c).

Fig. 19

a Scanning electron micrographic image of the fabricated cantilever in the microchannel. Microscopic image of b the undeformed cell just before entering into the cantilever zone and c the deformed cell at the cantilever junction (Walter et al. 2011)

More recently, Raj et al. (2016) characterized the entry and transit behavior of cells through compliant microchannels, theoretically and experimentally, using a device having thick PDMS walls on three sides and a thin PDMS membrane (25 µm) on the fourth side (Raj and Sen 2018). The device consisted of three zones, namely zones I, II and III. The constricted microchannel formed the zone II, and the cells entered and exited this channel via zones I and III, respectively. A rigid microchannel having thick PDMS walls on three sides and a microscope glass slide on the fourth was used for comparison. The behavior of cells at the constriction entrance was characterized in terms of the cell entry time (i.e., the duration between time period when the leading edge of the cell enters into the micro-constriction and the time period until the rear end of the cell is completely inside the micro-constriction), and their transit behavior in terms of the average transit velocity (micro-constriction length/entry time). While flowing HeLa cells through the compliant micro-constriction, it was found that the entry time was lower and the transit velocity was higher in compliant micro-constriction than the rigid one (Fig. 20a–d). With further increase in the compliance parameter (which defines the softness and flexibility of the microchannel), the entry time and the transit velocity decreased and increased further, respectively (Fig. 20c, d). Comparison of the flow behavior of HeLa and MDA-MB-231 cells showed that the compliant micro-constriction is less sensitive to variation in size ratio (cell diameter/hydraulic diameter of the constriction channel). However, the entry time of cells is more sensitive to the compliance factor. While for a fixed value of the size ratio and compliance factor, the more deformable MDA-MB-231 cells entered the compliant micro-constriction relatively quicker than the stiffer HeLa cells, for small values of the size ratio, the extension ratio of cells (deformed length/undeformed cell diameter) in transit through the micro-constriction decreased with increase in the compliance parameter (Fig. 20e). This resulted in reduced cell deformation, and therefore an increase in the average transit velocity with increase of the compliance parameter. As the change in cell deformability is dynamic under these conditions, cells experience acceleration and steady velocity periodically, due to the effect of the stiffness of the micro-constriction and the viscous drag force (Fig. 20f). Finally, theoretical investigations showed that the induced hydrodynamic resistance on the cell increases with increase in size ratio due to the scaling of drag force with cell size, and for a fixed value of the size ratio, the hydrodynamic resistance decreases with increase in compliance parameter (Fig. 20g). Characterization of flexible microchannels similar to the one in this study will help to mimic blood flow through arteries and other blood vessels under certain disease conditions such as atherosclerosis, coronary artery disease, hypertension, and diabetes.

Fig. 20

Microscopy image of a HeLa cell entering a rigid and b compliant micro-constriction. Variation of c entry time, d average transit velocity and e extension ratio of HeLa cells with size ratio in rigid (${f_{{\text{p}}0}}=0$) and compliant (${f_{{\text{p}}1}},{f_{{\text{p}}2}}$) micro-constrictions with the corresponding fit for the experimental data (solid line). f Variation of local velocity of HeLa cell in compliant micro-constriction showing periodic recurrence of stiffness-dominated regime (blue) and mixed regime influenced by both stiffness and viscous drag (green). g Theoretical plot of the variation of the induced hydrodynamic resistance with size ratio in rigid (${f_{p0}}=0$) and compliant (${f_{{\text{p}}1}},{f_{{\text{p}}2}}$) micro-constrictions (Raj and Sen 2018). (Color figure online)

The range of applications of flexible microchannels demonstrated in prior literature studies is summarized in Table 4.

Table 4 Summary of the wide range of applications of flexible PDMS microchannel

6 Conclusion

In this review, we have discussed the flow dynamics through flexible and/or compliant microchannels. A comprehensive study of the existing theoretical models for pressure-flow and deformation characteristics of conventional and compliant microchannels was presented. It was observed the semi-infinite approach for solving the fluid–structure interaction problem fails below a wall thickness $t \leq 2\,{\text{mm}}$. However, considering the channel wall as a thin plate helps to predict the pressure-flow and deformation characteristics of fluid flow accurately. The discussion concludes that the flexibility of the channel offers additional degrees of freedom for liquid flow, and provides lower pressure drop through microchannels. Further, we have seen the applications of flexible microchannels in cell mechanophenotyping, micro-pumps, microflow stabilization, and organ-on-chip devices. The thin flexible structures reviewed herein act as the substrate for culturing cells. Furthermore, the flexibility of the structure permits mimicking the functions of human organs. However, there is scope for more development in the field of flexible microchannels, and we have identified a few questions that still need to be answered. First, the validity of the assumptions used to develop the theoretical models presented here must be reconsidered, and more comprehensive analytical models must be developed for channels of wall thickness ranging from 3 μm to the order of a few millimeters. Next, studies involving dynamics of pulsatile flow through compliant microchannels are very limited and require attention to mimic pulsatile blood flow through compliant blood vessels. Finally, compliant microchannels having flexibility comparable to the actual artery walls and with the internal surfaces coated with epithelial cells must be engineered, to be able to accurately conduct in vitro analysis of cardiovascular diseases. These advances will help to design flexible microchannels-based systems for mimicking blood vessels and organs in the human body.