1 Introduction

Capillary flow phenomena are ubiquitous in nature (Shirtcliffe et al. 2006) and have profound influence on our day-to-day life (Prothero 1961). Such flows are inherent in various situations such as transportation of water from the soil to the leaves, drying of paper towels, tissue rolls over a liquid spillage, and flow through microcapillaries in our body. Although capillary flow has been studied for more than a century, it has still remained a subject of significant interest due to its wide variety of applications in many areas such as inkjet printing (Fuchiwaki et al. 2016), lab-on-a chip (Squires and Quake, Anoop and Sen 2015; George et al. 2015; Samy et al. 2017; Reddy et al. 2016; Maria et al. 2016, 2017), DNA manipulation (Yeo et al. 2011), diagnostic testing (Weigl et al. 2008), microfluidic-based separation (Sanders et al. 2001; Di Carlo et al. 2007), chemical microreactors (Dummann et al. 2003), micromolding (Enoch Kim et al. 1996), capillary chromatography (Bouffard et al. 1994), porous media (Delker et al. 1996; Mullins and Braddock 2012), and multiphase systems (Sorbie et al. 1995). Microfluidic-based pumping technologies (Ashraf et al. 2011) (such as micropumps, electro-wetting) have been developed for precise manipulation and handling of liquids in various physical systems. However, most of these devices either require electrical energy or some other active energy sources, thus, limiting the applications of such systems particularly for portable and on-field applications. On the other hand, capillary flow-based pumping technique has proven to be one of the simplest and cost-effective tools for the manipulation of liquids without aid of any external energy, which facilitates a wider range of applications.

Capillary flow, driven by the Laplace pressure across a curved meniscus, corresponds to spontaneous penetration of a liquid into a confinement usually a channel or pore (e.g., capillary tube, porous soil, and paper) to displace another fluid. For closed cylindrical channels, the capillary-driven flow is well described by the famous Washburn’s law (also known as Lucas–Washburn equation) (Lucas 1918; Washburn 1921). According to the Washburn’s law, as fluid wets the wall inside the channel, the driving force raised by the decrease in the free energy is balanced against the viscous drag of the liquid. The location of the liquid meniscus \(x\) with time \(t\) is given as \({x^2}=\left( {\gamma R\cos \theta /2\mu } \right)t\), where \(R\) is the channel radius, \(\mu {\text{~}}\) is the dynamic viscosity of the liquid, \(\gamma\) is the surface tension of the liquid, and \(\theta\) is the static contact angle of the liquid on the channel wall. Thus, advancement of the liquid meniscus along the channel \(x\) is proportional to the square root of time \(~t\), i.e., \({x^2}=kt\), where \(k\) is the ‘mobility parameter’ that depends on the channel dimensions and geometry, liquid properties, and liquid-wall wettability. So far, studies on capillary flow have mostly been focused on the Washburn’s regime (i.e., balance between the capillary and viscous effects) involving either modification in channel geometry or variation in the liquid-surface wettability in both closed and open channels. Some works have been reported on the existence of inertial regime (i.e., balance between the capillary and inertial effects) at the beginning of capillary flow in closed confinements.

Capillary flow in open channels and surfaces has gained a significant interest in the recent past as it offers ease of surface modifications, straight forward cleaning, and relatively simpler fabrication methods (since no bonding is required), thus, have the potential to play an important role in the future of microfluidics technology. Moreover, the risk of the microchannel clogging is eliminated that enables the reusability of devices for repeated use. Open channel/surface capillary flows have been investigated experimentally and theoretically (Bouaidat et al. 2005; Yu et al. 2015; Romero and Yost 1996; Ouali et al. 2013; Yang et al. 2014; Shin et al. 2016) in the past, which showed that the liquid meniscus follows Washburn’s regime, i.e., \({x^2}=kt\). Capillary flow of PDMS in open rectangular silicone microchannels was studied which showed that flow rates measured from experiments matched well with that predicted using a theoretical model for small aspect ratios (Sowers et al. 2016). Experimental study involving capillary flow of water and water–glycerol mixtures in open hydrophilic microchannels showed that the capillary meniscus follows Washburn’s regime (Yang et al. 2014).

A review of the literature clearly indicates that most of the prior studies on the capillary flows in open channels dealt with different channel configurations and liquids mainly in the Washburn’s regime. However, the effect of extreme wetting condition of the channel surface (e.g., superhydrophobicity and superoleophilicity), aspect ratio of the channel, inertial (or, early), and visco-inertial regimes in open-channel capillary flows have not been attempted. In this work, we report the dynamics of capillary flow of oil in open superoleophilic channels of different aspect ratios. The occurrence of inertial and viscous-inertial regimes in capillary flow through open channels is studied. A simple analytical model is developed to predict the meniscus dynamics both in the inertial, visco-inertial, and Washburn regimes and the theoretical predictions compare well with the experimental data. The literature review also indicates that the applications of capillary flows in open channels have not received much attention. This work demonstrates the use of a superoleophilic (which is also superhydrophobic) open-channel device integrated with electrodes for impedance-based sensing of oil from oil-in-water emulsions.

2 Experiments: fabrication, materials, and methods

Figure 1a shows the process flow used for fabrication of the open superoleophilic microchannel. First, a PMMA template having the negative replica (i.e., a protruding structure) of the microchannel was machined using high-precision CNC micro-milling (Minitech Machinery Inc., USA). The width of the structure was varied in the range of 0.3–1.0 mm while keeping the depth of the channel fixed at 0.5 mm to obtain channels of aspect ratios greater and lesser than one. At one of the ends, the structure expands into a cylindrical reservoir of diameter of 3.0 mm (and height 0.5 mm) which serves as the microchannel inlet. After machining, the structure was exposed to chloroform for 1 min to smoothen the machined surfaces.

Fig. 1
figure 1

a Process flow used for the fabrication of the open superoleophilic microchannel. b Procedure used for creating the superoleophilic microchannel. c Cross section of the channel before and after the spin coating and soot deposition process

Full size image

Next, the proposed microchannel was fabricated by performing soft lithography using the PMMA template. PDMS (Sylgard 184, 10:1 ratio, Dow Corning, USA) was poured onto the PMMA template and the setup was cured in oven at 85 °C for 2 h. After curing, the PDMS layer was peeled off the PMMA template to obtain the PDMS microchannel. The procedure followed for creating the superoleophilic microchannel is presented in Fig. 1b. To make the PDMS channel superoleophilic, the PDMS channel was spin coated with a mixture of PDMS + n-hexane (10% by weight) at 4000 rpm to create a very thin layer (thickness < 5 µm) of (PDMS + n-hexane) over the entire microchannel surface. Then, candle sooting was performed on the uncured (PDMS + n-hexane) surface by following the procedure reported in our earlier work (Iqbal et al. 2017). After the soot deposition, the channel was washed under high-speed water jet followed by drying with compressed nitrogen gas to yield a superoleophilic microchannel device.

In the above protocol, the purpose of n-hexane is to reduce the viscosity of PDMS to facilitate spin coating and increase solidification time (from 30 s to 1.0 min under candle sooting), so that carbon particles get adequate time to penetrate into PDMS during candle sooting. Without n-hexane, PDMS would solidify quickly within 30 s, and in that case, carbon particles would not find enough time to penetrate into PDMS. This would cause improper bonding between the soot particles and PDMS, and the soot particles would be easily removed away when washed with water jet. Figure 1c shows the cross section of the channel before and after the spin coating and soot deposition processes. As observed, the channel cross section has rounded corners due to deposition of the (PDMS + n-hexane) and soot particles. The contact angle of olive oil on the channel surface thus created was found to be \(<5^\circ\) and the roll-off angle \(<1^\circ\).

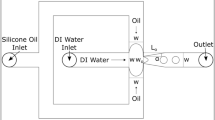
DI water (ELGA, minimum resistivity \(\sim\) 18.2 MΩ cm) and olive oil (SRL, India, 99% purity) were used as received for the experiments. Figure 2a shows a schematic of the experimental setup. The superoleophilic microchannel device was placed on an XY stage and sample liquid of volume 10 µL (olive oil) was dispensed at the device inlet using a micropipette. The cylindrical inlet of the channel prevents liquid spillage. The capillary flow meniscus was captured from the top using a digital microscope (Dinolite, Taiwan). Later, the device was also used for the detection of oil from oil-in-water emulsion (Fig. 2b). A pair of aluminium electrode was patterned on the glass slide using evaporation and etching. In oil detection experiments, oil-in-water emulsion was prepared by dispensing 30 µL of oil with 30 mL of water followed by vortex mixing and then sonication for 10 min. When the open microchannel device is dipped into the emulsion, oil from the emulsion rises along the superoleophilic microchannel. The capillary flow of oil in the channel and, hence, the presence of oil in the water sample were detected by measuring the impedance between the pair of electrodes. All the experiments were carried out at an ambient temperature of 25 °C in a quiescent atmosphere. The channels were reused after washing with IPA (Isopropyl alcohol, Thermo Fisher) followed by drying with compressed nitrogen.

Fig. 2
figure 2

a Schematic of the experimental setup used for the open superoleophilic channel capillary flow experiments. b Schematic of the experimental setup used for the detection of oil in oil-in-water emulsion

Full size image

3 Analytical modelling

The theoretical formulation describes the capillary flow in a superoleophilic open channel in the Washburn’s regime which is driven by the surface tension and opposed by the viscous drag. Besides, the inertial regime is also described where the effect of liquid inertia is considered in the formulation. Since the flow is of very low Reynold’s number (\(Re \approx 8 \times {10^{ - 3}}\)), Stokes’ flow is considered in calculating the viscous drag. The flow is treated to be incompressible and Newtonian, and it is assumed that the shape of the liquid–air advancing meniscus remains unchanged and contact angle of the meniscus with the channel walls remains constant during the flow. It is assumed that velocity gradient along the flow direction is negligible as compared to that in the other two directions and flow is two dimensions for the purpose of calculating the viscous force. Furthermore, we also have considered that there is no spillage of the oil and flow is confined within the channel.

A schematic of the capillary flow through the open channel is presented in Fig. 3. The viscous force is represented in terms of the simplified N–S equation for 2D flow through a rectangular microchannel as follows:

Fig. 3
figure 3

Schematic of the capillary flow of oil through the open superoleophilic channel: a isometric view, b top view, and c side view showing the capillary meniscus

Full size image
$$\mu \left( {\frac{{{\partial ^2}u}}{{\partial {y^2}}}+\frac{{{\partial ^2}u}}{{\partial {z^2}}}} \right)=\frac{{\Delta P}}{L},$$
(1)

where \(\frac{{\Delta P}}{L}\) is the total driving potential, \(\mu\) is the dynamic viscosity of liquid, and \(u\) is the flow velocity. By solving the above equation (see detailed derivation in the Electronic Supplementary Information), the viscous drag is expressed as follows:

$${F_{\text{v}}}=~\frac{{{\pi ^4}\mu }}{{8\left[ {1 - \left( {\frac{{2h}}{{\pi w}}} \right){\text{~tanh}}\left( {\frac{{\pi w}}{{2h}}} \right)} \right]}}\left( {\frac{w}{h}} \right)\left( {x\frac{{{\text{d}}x}}{{{\text{d}}t}}} \right),$$
(2)

where \(w\) and \(h\) are the width and height of the channel, respectively, and \(x\) is the meniscus location, which is a function of time \(t\). By considering that the top side of the channel is open to atmosphere and the bottom wall is semi-circular in shape (of radius equal to half of the channel width), the driving capillary is obtained as follows:

$$\begin{aligned} {F_c} & =\left( {\gamma \frac{h}{2}\cos {\theta _{\text{L}}}+\gamma \frac{h}{2}\cos {\theta _{\text{R}}}+\gamma \frac{{\pi w}}{2}\cos {\theta _{\text{B}}}+\gamma w\cos {\theta _{\text{T}}}} \right) \\ & =\left( {\gamma h\cos \theta +~\gamma \frac{{\pi w}}{2}\cos \theta - \gamma w~} \right)=\gamma w\left\{ {\left( {\frac{1}{\varepsilon }+\frac{\pi }{2}} \right)\cos \theta - 1} \right\}, \\ \end{aligned}$$
(3)

where \(\gamma\) is the surface tension of the liquid. In the above, it is assumed that the channel has the same wetting property over its entire surface (i.e., \(\theta\) is the same on the three surfaces) and contact angle between oil and air is 180°, \(\left( {h/2} \right)\) is the effective channel height, and \(\varepsilon =\left( {w/h} \right)\) represents aspect ratio of the microchannel.

In addition to viscous and capillary forces, inertia force may be relevant in the beginning of the capillary flow similar to the Bosanquet solution (Bosanquet 1923). From Newton’s second law, the inertial force is given as \(\frac{{\text{d}}}{{{\text{d}}t}}\left( {mV} \right)\), where \(m\) is the mass of the liquid in the channel and \(V\) = \(\frac{{{\text{d}}x}}{{{\text{d}}t}}\) is the meniscus velocity.

Depending on the relative magnitude of the viscous, capillary, and inertia forces, three different regimes can be identified that are illustrated as follows.

3.1 Inertial regime

In this regime, the viscous force is negligible and the capillary force is balanced by the inertia force to give \({F_{\text{c}}}={F_{\text{I}}}\). Using the expressions for inertia force and capillary force from (3), we get

$$\gamma w\left\{ {\left( {\frac{1}{\varepsilon }+\frac{\pi }{2}} \right)\cos \theta - 1} \right\}=\frac{{\text{d}}}{{{\text{d}}t}}\left[ {\rho Ax\left( {\frac{{{\text{d}}x}}{{{\text{d}}t}}} \right)} \right].$$
(4)

If we integrate the above equation, we get \({x^2}=\frac{{w\gamma }}{{\rho A}}\left\{ {\left( {\frac{1}{\varepsilon }+\frac{\pi }{2}} \right)\cos \theta - 1} \right\}{t^2}+{c_1}.\)

Now, using the initial condition, \(t=0,\;~x=0\), we get \({c_1}=0\). Therefore, we have

$$x=\sqrt {\frac{{w\gamma }}{{\rho A}}\left\{ {\left( {\frac{1}{\varepsilon }+\frac{\pi }{2}} \right)\cos \theta - 1} \right\}} \times t.$$
(5)

3.2 Visco-inertial regime

In this regime, the capillary force is balanced by the inertia and viscous forces. Therefore, the inertial force \(\frac{{\text{d}}}{{{\text{d}}t}}\left( {mV} \right)=\mathop \sum \nolimits^{} F\), where \(F\) represents the sum of the capillary as well as the viscous forces. Using the expressions for viscous and capillary forces from Eqs. (2) and (3), respectively, we get

$$\frac{{\text{d}}}{{{\text{d}}t}}\left[ {\rho Ax\left( {\frac{{{\text{d}}x}}{{{\text{d}}t}}} \right)} \right]=\gamma w\left\{ {\left( {\frac{1}{\varepsilon }+\frac{\pi }{2}} \right)\cos \theta - 1} \right\} - \frac{{{\pi ^4}\mu }}{{8\left[ {1 - \left( {\frac{{2h}}{{\pi w}}} \right)~\tanh \left( {\frac{{\pi w}}{{2h}}} \right)} \right]}}\left( {\frac{w}{h}} \right)\left( {x\frac{{{\text{d}}x}}{{{\text{d}}t}}} \right).$$
(6)

The above equation can be non-dimensionalized using \({x^*}=\frac{x}{{{x_{{\text{ref}}}}}}\), where \({x_{{\text{ref}}}}=\frac{{8h\left\{ {1 - \left( {\frac{{2h}}{{\pi w}}} \right)\tanh \left( {\frac{{\pi w}}{{2h}}} \right)} \right\}}}{{{\pi ^4}\mu }}\sqrt {2\rho h\gamma }\) and \({t^*}=\frac{t}{{{t_{{\text{ref}}}}}}\) where \({t_{{\text{ref}}}}=\frac{{8\rho {h^2}\left\{ {1 - \left( {\frac{{2h}}{{\pi w}}} \right)\tanh \left( {\frac{{\pi w}}{{2h}}} \right)} \right\}}}{{{\pi ^4}\mu }}\) to yield

$$\frac{{\text{d}}}{{{\text{d}}{t^*}}}\left[ {{x^*}\frac{{{\text{d}}{x^*}}}{{{\text{d}}{t^*}}}} \right]=\frac{1}{2}\left\{ {\left( {\frac{1}{\varepsilon }+\frac{\pi }{2}} \right)\cos \theta - 1} \right\} - {x^*}\frac{{{\text{d}}{x^*}}}{{{\text{d}}{t^*}}}~~.$$
(7)

Now, if we solve Eq. (6) with the initial conditions of \(t=0\): \({x^*}={x_0}^{*}~\;{\text{and}}\;~\frac{{{\text{d}}{x^*}}}{{{\text{d}}{t^*}}}=0\), (see detailed solution steps in the Electronic Supplementary Information), we get

$${x^2}={x_0}^{2}+\left( {\frac{{16h\gamma }}{{{\pi ^4}\mu }}} \right)\left\{ {\left( {\frac{1}{\varepsilon }+\frac{\pi }{2}} \right)\cos \theta - 1} \right\}\left\{ {1 - \left( {\frac{{2h}}{{\pi w}}} \right)\tan \left( {\frac{{\pi w}}{{2h}}} \right)} \right\}\left\{ {t+{t_{{\text{ref~}}}}{e^{ - t/{t_{{\text{ref}}}}}} - {t_{{\text{ref}}}}} \right\},$$
(8)

where \({x_0}=\frac{{\pi h}}{8}\) is calculated from the initial virtual mass in channel \({m_0}=\frac{{\rho \pi {h^2}w}}{8}\) by doing potential flow analysis. At large time scales \(t>{t_{\text{c}}}\), the inertial effects become negligible as compared to the capillary and viscous forces, and in that case, the meniscus follows a modified Washburn’s equation:

$${x^2}={x_0}^{2}+\left( {\frac{{16h\gamma }}{{{\pi ^4}\mu }}} \right)\left\{ {\left( {\frac{1}{\varepsilon }+\frac{\pi }{2}} \right)\cos \theta - 1} \right\}\left\{ {1 - \left( {\frac{{2h}}{{\pi w}}} \right)\tan \left( {\frac{{\pi w}}{{2h}}} \right)} \right\}t,~$$
(9)

which is of the form \({x^2}={k_{{\text{vi}}}}t\) where \({k_{{\text{vi}}}}\) is the mobility parameter, \({k_{{\text{vi}}}}=\frac{{16h\gamma }}{{{\pi ^4}\mu }}\left\{ {\cos \theta \left( {\frac{1}{\varepsilon }+\frac{\pi }{2}} \right) - 1} \right\}\left\{ {1 - \left( {\frac{{2h}}{{\pi w}}} \right)\tan \left( {\frac{{\pi w}}{{2h}}} \right)} \right\}.\)

3.3 Lucas–Washburn (or viscous) regime

In this regime, the inertia force is negligible and the capillary force is balanced by the viscous force to give \({F_{\text{c}}}={F_{\text{v}}}\). Using the expressions for viscous and capillary forces from Eqs. (2) and (3), we get

$$~\gamma w\left\{ {\left( {\frac{1}{\varepsilon }+\frac{\pi }{2}} \right)\cos \theta - 1} \right\}=\frac{{{\pi ^4}\mu }}{{8\left[ {1 - \left( {\frac{{2h}}{{\pi w}}} \right)~\tanh \left( {\frac{{\pi w}}{{2h}}} \right)} \right]}}\left( {\frac{w}{h}} \right)\left( {x\frac{{{\text{d}}x}}{{{\text{d}}t}}} \right).$$
(10)

Upon solving, we get

$${x^2}=\left( {\frac{{16h\gamma }}{{{\pi ^4}\mu }}} \right)\left\{ {\left( {\frac{1}{\varepsilon }+\frac{\pi }{2}} \right)\cos \theta - 1} \right\}\left\{ {1 - \left( {\frac{{2h}}{{\pi w}}} \right)\tanh \left( {\frac{{\pi w}}{{2h}}} \right)} \right\}t.$$
(11)

Equations (5), (9), and (11) are used for the theoretical predictions of the meniscus location with time, which is compared with the experimental data, as presented in the following section.

4 Results and discussion

Experimental images of capillary flow meniscus of oil at various time instants \(t\) in an open superoleophilic channel of 800 µm width and 500 µm height are presented in Fig. 4a. The variations in the meniscus location \(x\) with time \(t\) from experiments and models are depicted in Fig. 4b. Here, similar to the close channel case (Fries and Dreyer 2008), three distinct regimes, namely the inertial, visco-inertial, and Lucas–Washburn regimes, are observed. In the inertial regime (between \(0<t<0.2\;~{\text{s}}\)), mainly flow is driven by the capillary force and opposed by the inertia force. In this regime, the relationship between the distance travelled by the meniscus \(x\) and time \(t\) is linear, i.e., \(x\sim t\) (Eq. 5) or the meniscus velocity remains constant, as shown in the inset of Fig. 4b. The timescale that represents the transition between the inertial and visco-inertial regimes is estimated by the time at which both solutions attain within 3% of disagreement (Fries and Dreyer 2008). Using \(0.03=\frac{{{x_{{\text{Inertia}}}} - {x_{{\text{Visco-inertia}}}}}}{{{x_{{\text{Inertia}}}}}}\), we get \(t=\frac{{0.72\rho {h^2}\left\{ {1 - \left( {\frac{{2h}}{{\pi w}}} \right)\tanh \left( {\frac{{\pi w}}{{2h}}} \right)} \right\}}}{{{\pi ^4}\mu }} \approx 0.2~\;{\text{s}}\). The transitional time \(t~\) can be physically explained as the time required for the viscous boundary layer to diffuse over a length scale of the order of the characteristic length scale of the channel (i.e., \(\sim \left( {w/2} \right)\)).

Fig. 4
figure 4

a Experimental images of capillary flow of oil at various time instants \(t\) in an open superoleophilic channel (of 800 µm width and 500 µm height), white regions appearing in the liquid are caused due to reflection of light, meniscus is indicated by dotted line, b variations in the meniscus location \(x\) with time \(t\) from experiments and models for 500 µm width 500 µm height superoleophilic channel, and variations in the velocity \(\frac{{{\text{d}}x}}{{{\text{d}}t}}\) with time \(~t\) are shown in the inset

Full size image

For \(0.2~\;{\text{s}}<t<15\;~{\text{s}}\), the effect of the driving capillary force is balanced by the inertia and viscous force which gives rise to the visco-inertial regime. In this regime, the relationship between the distance travelled by the meniscus \(x\) and time \(t\) is given by Eq. (8). The exponential term in Eq. (8) decays with time and vanishes as time \(t \to \infty\) to provide \(x\sim \sqrt t\). Figure S1 in the Electronic Supplementary Material shows a zoomed view of the difference between the predictions of \(x\) vs. \(t\) characteristics in the inertial and visco-inertial regimes, which is rather small. Thus, to obtain the inertial to visco-inertial transition time scale, we take \({x_{{\text{Pure~}}\;{\text{viscous}}}}={x_{{\text{Visco-inertia}}}}\) which yields a transition time of 15 s.

For \(t>15~\,{\text{s}}\), the effect of inertia force becomes negligible, and in that case, the driving capillary force is mainly balanced by the viscous force which leads to the Lucas–Washburn’s regime, i.e., \(x\sim \sqrt t\), indicating a decay in the meniscus velocity with time, as shown in the inset (Fig. 4b). The difference between the model and experimental results observed in Fig. 4b is mainly attributed to the following: (a) in the model, fully developed flow approximation is used, whereas, in the beginning, flow is still developing; (b) in the model, static contact angle value is used instead of the more realistic dynamic contact angle (Coney and Masica 1969; Joanny and de Gennes 1984; Popescu et al. 2008; Eral et al. 2013), which is diffiult to implement in the analytical model; (c) the meniscus may not have a single curvature and may, instead, have irregular shape (as seen in Fig. 4a).

Next, we compare the variations in the meniscus location \(x\) with time \(t\) from experimental data obtained for the superhydrophilic open channel with that for a oleophilic open channel (made of PDMS), as shown in Fig. 5. The contact angles of olive oil with the superoleophilic and oleophilic channels are measured to be \(5^\circ \pm 1^\circ\) and \(50^\circ \pm 1^\circ\), respectively. In case of the oleophilic channel, the inertial regime is observed over a much smaller timescale of \(t=0.09\;~{\text{s}}\) as compared to that in case of the superoleophilic channel, which occurs over timescale of \(t=0.2~\;{\text{s}}\). This is explained as follows: due to the micro-roughness on the superoleophilic channel, capillary action also takes place in the grooves of the micro-structure (see SEM image in Fig. 1b). Therefore, a thin layer of liquid wicks into the micro-roughness grooves ahead of bulk liquid meniscus (see schematic in Fig. 6a and experimental images in Fig. 6b for a droplet dispensed over a superoleophilic surface). Owing to the filling of liquid in the micro-structure grooves, bulk liquid meniscus moves much faster on the solid–liquid composite surface by satisfying the Cassie–Baxter state (Gennes et al. 2004).

Fig. 5
figure 5

a Variations in the meniscus location \(x\) with time \(t\) from the experimental data obtained for the superhydrophilic open channel with that for a oleophilic open channel (made of PDMS). b \(x\) vs. \(t\) comparison for superoleophilic and oleophilic channels in inertia regime, c \(x\) vs. \(t~\)comparison between superoleophilic and oleophilic channels in visco-inertia regime

Full size image
Fig. 6
figure 6

a Schematic and b experimental images showing movement of capillary flow meniscus and droplet contact line in case of spreading of an oil droplet on a superoleophilic surface

Full size image

In Sect. 3, for each of the operating regimes, mobility parameters were determined, which signify flow rate per unit length of the channel. The variation in the mobility parameter \(k\) in the three different regimes with aspect ratio \(\varepsilon =\left( {w/h} \right)\) of the superoleophilic channel obtained from theory and experiments is presented in Fig. 7. Figure 7a shows the theoretical and experimental results match within 10% for visco-inertia regime and pure viscous regime. In the visco-inertial regime, it is observed that mobility parameter \(k\) initially increases with increase in the aspect ratio \(\varepsilon\) and attains a maximum value of \(k=\) 25 for aspect ratio \(\varepsilon =1.6\). Beyond this aspect ratio \(\varepsilon =1.6\), the mobility parameter \(k\) decreases with increase in the aspect ratio \(\varepsilon\). When the aspect ratio \(\varepsilon <1.6\), the mobility parameter \(k\) decreases rapidly due to the rapid increase in the viscous force (since the channel is narrow) as compared to the capillary force in the channel. For \(\varepsilon>1.6\), the mobility parameter \(k\) decreases due to decrease in the ratio of the surface area to the cross-sectional area that leads to the reduction in the driving capillary force. However, in the inertial regime, mobility parameter \(k\) decreases with increase in the aspect ratio \(\varepsilon\), because inertia force increases with increase in the channel size (see Fig. 7b).

Fig. 7
figure 7

a Variation in the mobility parameter \(k\) in the visco-inertia and pure-viscous regimes with aspect ratio \(\varepsilon\) of the superoleophilic channel obtained from theory and experiments. b Variation in the mobility parameter \(k\) in the pure-inertia regime with aspect ratio \(\varepsilon\) of the superoleophilic channel

Full size image

As stated in the Sect. 1, one of the advantages of the open channel is that such channels can be easily cleaned and reused. The reusability of the superoleophilic channel was demonstrated by repeated use of the channel and cleaning of the channel with IPA before reusing each time. Figure 8a shows the variations in the meniscus location \(x\) with time \(t\) from experiments in case of an open superoleophilic channel of width 0.5 mm and height 0.5 mm during its repeated use. As observed, all the curves overlap, indicating that the superoleophilic channel can be reused without any degradation in the capillary flow performance.

Fig. 8
figure 8

a Variations in the meniscus location \(x\) with time \(t\) from experiments in case of an open superoleophilic channel of width 0.5 mm and height 0.5 mm during its repeated use. b Variation in the meniscus location \(x\) and impedance across the electrode with time \(t\) in the microchannel device used for detection of oil. c Variation in the meniscus location \(x\) and impedance across the electrode with time t in the microchannel device used for the detection of oil from oil–water emulsion

Full size image

Next, we demonstrate the impedance-based sensing of oil by integrating electrodes (at \(x=20\) mm) with the superoleophilic channel (see Fig. 8b). The impedance between the electrodes before and after the spacing between the electrodes gets filled with oil (due to capillary action) is monitored using an oscilloscope. First, the device was tested by dipping one end of the capillary channel in pure oil at \(20^\circ\) angle with the horizontal. When oil rises through the gap between the electrodes (see \(x~\) vs. \(t\) in Fig. 8b), a change in the impedance was noted, as shown in Fig. 8b. Next, a superoleophilic channel, integrated with electrodes across the channel length, is put into an emulsion (30 μl of olive oil in 30 ml of DI water after 2 min of vortex mixing followed by 10 min of ultra-sonication) at \(20^\circ\) inclination angle. Oil drops spread and fill the channel inlet as soon as the drops come in contact with the channel wall. Then, due to the capillary action, oil flows through channel and fills the gap between the electrodes. The change in the impedance when the oil meniscus crosses the spacing between the electrodes is depicted in Fig. 8c. There is a difference between the impedance values observed in case of experiments with pure oil (15.18 k\({{\varvec{\Omega}}}\)) and oil–water emulsion (12.83 k\({{\varvec{\Omega}}}\)), which is explained as follows. It is possible that, during the capillary flow of oil from the oil–water emulsion, some amount of water might have also come along with the oil phase, which gives rise to a smaller impedance as compared to the pure oil case. The effective impedance \(({Z_{\text{t}}})\) of this oil–water mixture mainly depends on volume percentages of both the phases present in the gap between the electrodes, which is given as follows (Zubair and Tang 2014):

$$\frac{1}{{{Z_{\text{t}}}}}=\frac{{\frac{{{v_{\text{w}}}}}{{{Z_{\text{w}}}}}+\frac{{{v_0}}}{{{Z_0}}}}}{{{v_{\text{t}}}}},$$
(12)

where \({v_{\text{w}}}\) is the volume of water in the channel between electrodes, \({Z_{\text{w}}}\) is the impedance of water, \({v_0}\) is the volume of oil in the channel between electrodes, and \({Z_0}\) is the impedance of oil. Using impedance of water (0.25 k\({{\varvec{\Omega}}}\)) and oil, and volume of oil (5 µl), the volume percentage of water present in the oil between the electrodes is estimated as < 2%.

5 Conclusions

We presented the dynamics of capillary flow of oil in open superoleophilic channels. The superoleophilic channel was fabricated by spin coating a thin layer of PDMS + n-hexane (10% by weight) over a PDMS channel at 4000 rpm for 10 s followed by candle sooting for 3 min. The occurrence of various flow regimes, including the inertial, visco-inertial, and Lucas–Washburn regimes, were studied using analytical modelling as well as experiments. From analytical model and experiments, inertial regime was observed between \(0<t<0.2\;~{\text{s}}\), in which, owing to the balance of inertia and capillary forces, a linear relationship between the distance travelled by the meniscus \(x\) and time \(t\) was observed, i.e., \(x\sim t\). For \(0.2~\;{\text{s}}<t<15~\;{\text{s}}\), the effect of the driving capillary force is balanced by the inertia and viscous force, thus, giving rise to the visco-inertial regime. For \(t>15~\;{\text{s}}\), the effect of inertia force becomes negligible, and in that case, the driving capillary force is mainly balanced by the viscous force, which leads to the Lucas Washburn’s regime. In both the visco-inertial and Lucas–Washburn’s regimes, a decay in the meniscus velocity with time was observed, i.e., \(x\sim \sqrt t\). In case of a superoleophilic channel, much longer inertial regime is observed due to the wicking of oil into the micro-roughness grooves ahead to bulk liquid meniscus. Owing to the filling of liquid in the micro-structure grooves, bulk liquid meniscus moves much faster on the solid–liquid composite surface by satisfying the Cassie–Baxter state. The study of the effect of channel aspect ratio \(\varepsilon\) on the mobility parameter \(k~\) showed that the mobility parameter \(k\) is maximum for an aspect ratio of \(\varepsilon =1.6\), which is attributed to the balance between the capillary and viscous forces. When the aspect ratio \(\varepsilon <1.6\), the mobility parameter \(k\) decreases rapidly due to the rapid increase in the viscous force (since the channel is narrower) as compared to the capillary force in the channel. For \(\varepsilon>1.6\), the mobility parameter \(k\) decreases due to decrease in the ratio of the surface area to the cross-sectional area that leads to the reduction in the driving capillary force. Finally, we demonstrate application of the superoleophilic channel integrated with electrodes for impedance-based sensing of oil from an oil–water emulsion. The proposed superoleophilic channel has potential to be used for sensing of oil contaminants in water.