Experimental observations of bands of suspended colloidal particles subject to shear flow and steady electric field

Abstract

Manipulating suspended colloidal particles flowing through a microchannel is of interest in microfluidics and nanotechnology. However, the flow itself can affect the dynamics of these suspended particles via wall-normal “lift” forces. The near-wall dynamics of particles suspended in shear flow and subject to a dc electric field was quantified in combined Poiseuille and EO flow through a ~ 30 μm deep channel. When the two flows are in opposite directions, the particles are attracted to the wall. They then assemble into very high aspect ratio structures, or concentrated streamwise “bands,” above a minimum electric field magnitude, and, it appears, a minimum near-wall shear rate. These bands only exist over the few micrometers next to the wall and are roughly periodic in the cross-stream direction, although there are no external forces along this direction. Experimental observations and dimensional analysis of the time for the first band to form and the number of bands over a field of view of ~ 200 μm are presented for dilute suspensions of polystyrene particles over a range of particle radii, concentrations, and zeta potentials. To our knowledge, there is no theoretical explanation for band assembly, but the results presented here demonstrate that it occurs over a wide range of different particle and flow parameters.

1 Introduction

The dynamics of suspended neutrally buoyant colloidal particles near planar surfaces has been of interest in colloid science for more than a half-century, starting from the classic Derjaguin, Landau, Verwey, and Overbeek (DLVO) theory describing how electric double layer (EDL) interactions and van der Waals forces affect a single particle near a surface (Saville 1977; Probstein 2003). More recently, novel applications in microfluidics and nanotechnology have renewed interest in suspended particle electrokinetics, and how externally applied electric fields affect the dynamics of dielectric suspended particles and cells (Bousse et al. 2000; Stone et al. 2004; Ohno et al. 2008; Chang and Yeo 2010). Manipulating and assembling such particles and cells is a key technology in various microfluidics applications including particle and cell trapping, separation and sorting, and bead-based immunoassays (Lim and Zhang 2007; Nilsson et al. 2009; Ng et al. 2010; Sajeesh and Sen 2014). The dynamics of suspended particles near a planar surface, i.e., a wall, are of particular interest because: (1) most of the transduction elements (e.g., sensors, actuators) in microfluidic devices are surface- or wall-mounted structures; and (2) the particles spend a significant fraction of their residence time near the walls of the device due to their relatively large surface areas and small volumes.

Understanding the electrokinetics of colloidal particles near surfaces is also of interest in nanomaterials synthesis (Velev and Bhatt 2006). A common method for fabricating such materials involves assembling colloidal particles into 1D “pearl chains” (Stauff 1955) and 2D colloidal crystals (Trau et al. 1996) by depositing them directly on a solid surface. A variety of such “colloidal lithography techniques” have been developed for rapid and selective deposition of charged particles (Yang et al. 2006; Lotito and Zambelli 2017).

Yet, a fundamental understanding of near-wall particle dynamics, especially for suspended particles in a flow (vs. in a quiescent fluid), e.g., shear flow or a flow driven by an electric field, remains limited. Several researchers have observed and analyzed electroviscous, or shear-induced electrokinetic, lift, on charged suspended particles of radii a = O(1 µm) in a shear flow (Bike et al. 1995; Tabatabaei et al. 2006; Schnitzer and Yariv 2016). Here, “lift” refers to forces normal to the wall. The magnitude of this usually repulsive force scales as ${\dot {\gamma }^2}$, where $\dot {\gamma }$ is the shear rate, although there appear to be significant discrepancies between experimental estimates and theoretical predictions (Bike and Prieve 1996; Wu et al. 1996).

Williams et al. (1994) observed in their field-flow fractionation studies an additional “hydrodynamic” lift force for suspended a = O(1–10 µm) particles that was instead directly proportional to $\dot {\gamma }$. Subsequent studies have reported a lift force with this scaling for much smaller a = O(10–100 nm) particles (Cevheri and Yoda 2014a; Ranchon et al. 2015), but there are, to our knowledge, no theoretical analyses of this force.

Yariv and his co-workers (Yariv 2006; Yariv et al. 2011; Schnitzer and Yariv 2012, 2016; Schnitzer et al. 2012) have extensively analyzed the lift on a suspended particle near a wall due to an applied electric field of magnitude |E|. For a steady, or dc, electric field, the particle experiences a “dielectrophoretic-like” repulsive lift with a magnitude proportional |E|². A number of experimental studies have observed repulsive lift forces with this scaling in electroosmotic (EO) flow driven by a dc electric field (Liang et al. 2010; Kazoe and Yoda 2011), and even exploited this phenomenon to separate particles based on their size (Lu et al. 2015). Significant discrepancies have also been reported, however, between the experimental estimates and theoretical predictions of dielectrophoretic-like lift (Liang et al. 2010; Kazoe and Yoda 2011). The discrepancies with Kazoe and Yoda, who only considered particles within a few radii of the wall, may be due in part to the assumption in Yariv’s analyses that the particles are many radii away from the wall.

Recently, we have considered the combination of both effects by studying the near-wall dynamics of particles suspended in a shear flow and subject to an electric field in the combined Poiseuille and EO flow of a particle suspension through a microchannel. Although a number of groups have studied inertial particle focusing on the same type of flow for a ≥ 5 μm particles (Kim and Yoo 2009; Yuan et al. 2016; Li and Xuan 2018), this work considers instead colloidal a < 400 nm particles within 1 μm of the wall. The parabolic velocity profile for Poiseuille flow is therefore well approximated in these studies by a linearly varying velocity profile near the wall with constant shear rate $\dot {\gamma }$.

Surprisingly, the lift force acting on the particles changes from repulsive to attractive depending upon the relative directions of the shear and EO flows. For “co-flow,” where the shear and EO flows are in the same direction, the force is repulsive; for “counter-flow,” where the shear and EO flows are in opposite directions, the flow is attractive. The magnitude of this attractive or repulsive lift appears to scale with |E|, suggesting that it is electrophoretic (vs. dielectrophoretic) and with ${\dot {\gamma }^N}$, where N ≈ 0.5 (Cevheri and Yoda 2014a).

Moreover, the particles in this dilute suspension (nominal bulk volume fraction ${\varphi _\infty }$ < 4 × 10⁻³) assemble into “bands” above a minimum |E| and, in most cases, a minimum $\dot {\gamma }$. These “bands” (cf. Fig. 4b, c) are very high-aspect ratio structures aligned with the flow direction or channel axis with a cross-sectional dimension of a few micrometers and a length of at least 2.5 cm, comparable to that of the channel itself (Cevheri and Yoda 2014b). They exist only within a few micrometers of the wall, based on fluorescence microscopy observations in the bulk of the flow. Unpublished astigmatic particle-tracking visualizations suggest that the particle concentration is at a maximum ~ 3 μm from the wall (M. Rossi, private communication).

This study builds upon these initial observations. Results are presented here for band formation to quantify how particle properties such as radius a, surface charge, characterized by the particle zeta potential ${\zeta _{\text{p}}}$, and particle concentration, characterized in terms of ${\varphi _\infty }$, affect band characteristics over a broad range of experimental parameters. Although the fundamental mechanisms underlying band formation remain unresolved, these results show that our observations of the attraction and subsequent concentration of colloidal particles near the wall, followed by band formation, are “robust”: these phenomena occur over a range of dielectric particle sizes, surface charges, concentrations, and flow parameters, namely electric field magnitudes |E| and shear rates $\dot {\gamma }$. Moreover, the characteristics of band formation are reproducible and quite stable for a given set of conditions.

The remainder of this paper is organized as follows. The microchannels, the procedures used to generate the flow, and the properties of the particle suspensions are described first, followed by a description of the experimental procedures and image acquisition. The processing used to identify the bands and their characteristics are detailed. Results on the band characteristics are presented and discussed, followed by a summary and conclusions.

2 Microchannel flow and particle suspensions

Dilute suspensions of colloidal polystyrene particles flowing through fused-quartz microchannels are studied in this work. The microchannels are an “upside-down” channel trench isotropically wet etched in a 2.3 mm-thick fused quartz substrate (Telic Company) and sealed on the bottom via thermal bonding to a fused-silica microscope slide “lid” (Esco Optics R120110) of dimensions 50.8 mm × 25.4 mm × 1 mm. The cross section of the microchannel is roughly “C”-shaped (Fig. 1) with a depth (z-dimension) H ≈ 34 μm and a width (y-dimension at half-depth) W ≈ 305 μm. The S-shaped microchannel (Fig. 2a) has a central straight section with a length of 2.8 cm; the x-direction is defined to be along the direction of Poiseuille flow in this straight section. The imaged region is the gray square in the center of the straight section. A hole is drilled at both ends of the microchannel, and reservoirs about 3.2 mm in diameter are bonded to the fused quartz over the holes with epoxy (Loctite E-60HP) cured for 24 h at 50 °C (Fig. 2b).

Fig. 1

Cross section of the microchannel showing fluorescent particles illuminated by evanescent waves at the interface between the fused silica “lid” and the solution flowing through the channel. Dimensions are given in micrometers

Fig. 2

a Bottom view of the microchannel. A close-up view is shown of the imaged region (gray square) in the center of the straight portion of the channel. The pressure difference applied from the upstream (left) to downstream (right) reservoirs drives Poiseuille flow to the right, while the voltage gradient (electric field) applied from the right to the left reservoirs drives the counterions (here, cations) to the left. b Side view of the channel showing the four-way connectors used to apply the pressure and voltage gradients and channel reservoirs. The arrows indicate the direction of the Poiseuille flow

The microchannel is illuminated using evanescent waves created by the total internal reflection (TIR) of light at the interface between the fused-silica lid (i.e., the bottom of the channel) and the fluid inside the channel as seen in Fig. 1. The wavelength λ = 488 nm beam from an argon-ion laser (Innova I305) with an output power of about 1.5 W is shuttered by an acousto-optic modulator (IntraAction Corp AFM-803A1) to create pulses at a frequency of 10 Hz and a width of 0.5 ms. The angle of incidence of the beam θ_i ≈ 70° is determined from the distance between two adjacent TIR positions and the thickness of the lid. The length scale for the exponential decay of the intensity, the penetration depth z_p, is estimated to be 110 nm.

An electron multiplying CCD camera (Hamamatsu C9100-13) connected to a microscope (Leica DM-IRE2) images the region of the flow shown in Fig. 2a through a magnification 40, numerical aperture 0.55 microscope objective (Leica 506,059). The camera acquires a sequence of 512 × 512 pixel, 16-bit grayscale images at 10 Hz and an exposure time of 0.5 ms.

The external pressure and voltage gradients are supplied via four-way connectors attached to both reservoirs with a short section of flexible tubing (Fig. 2b). The pressure gradient, which is to the left (i.e., along the − x direction), is generated hydrostatically by connecting the upstream four-way connector to a water container at an adjustable height with the downstream connector open to the surroundings. A manometer is used to measure the applied pressure drop Δp. The ambient temperature (typically 21 °C) is measured by a thermometer and used to estimate the properties of the fluid, assumed to be those of water.

The total channel length L ≈ 4.3 cm, estimated from combined images of the channel, is defined to be the distance from the bottom centers of the inlet and outlet reservoirs. The near-wall shear rate $\dot {\gamma }$ is taken to be that at the channel wall, or z = 0, and determined by modeling the flow in the channel as that between two parallel plates separated by a distance of H driven by a pressure gradient Δp/L. Within the region illuminated by the evanescent waves, z ≤ a + 3z_p, this shear rate varies by at most 4%. In all cases, $\dot {\gamma }$ < 1800 s⁻¹, and the uncertainty in $\dot {\gamma }$ at a given z is 15 s⁻¹.

The voltage difference ΔV is generated by a power supply (Stanford Research Systems PS325; Instek GPR-3510 HD) connected to platinum electrodes inserted through a hole in the end of a rubber sleeve over one of the ports of both four-way connectors. The electric field magnitude $\left| E \right|=\Delta V/L$; in all cases $\left| E \right|$ < 500 V/cm.

Five different colloidal suspensions (Table 1) are studied to elucidate how banding is affected by various particle properties. Suspensions 1, 2, and 3 are compared to examine the effect of bulk volume fraction φ_∞; 3 and 4 the effect of particle zeta-potential ζ_p; and 4 and 5 the effect of a.

Table 1 Properties of the colloidal particle suspensions; the values for a and ζ_p are given in terms of the average value ± standard deviation

The 1 mM sodium tetraborate (Na₂B₄O₇) solution (pH ~ 9) is made by dissolving sodium tetraborate decahydrate (VWR AA40114-36), or borax, in UltraPure water. The sodium tetraborate + boric acid (H₃BO₃) solution is made by adding a very small amount of the 1 mM Na₂B₄O₇ solution to 4 mM H₃BO₃ solution to achieve a pH of ~ 7. The boric acid solution is made by dissolving boric acid (VWR AA12305-A1) in UltraPure water. The pH of the solutions is measured by a pH meter (Oakton pH11 Economy Meter).

Two different particles are used for these studies: (1) a = 245 nm carboxylate-modified polystyrene (PS) spheres labeled with green fluorescent dye with excitation and emission peaks at 505 nm and 515 nm, respectively (ThermoFisher F8813); and (2) a = 355 nm sulfate-modified polystyrene (PS) spheres labeled with green fluorescent dye with excitation and emission peaks at 502 nm and 518 nm, respectively (microparticles GmbH PS-FluoGreen-Fi132-1). The values for a and the solids concentration are from the manufacturer. The particles are nearly density matched to the aqueous solutions, with a density ρ = 1.05 g/cm³. The particle ζ-potential is measured for particles suspended at a volume fraction of 0.02% by dynamic light scattering using a Malvern ZetaSizer ZS.

In all cases, the colloidal suspension was prepared, sonicated, and filtered using a syringe filter with a pore size of 0.8 μm (Millex SLAA033SS) for the a = 245 nm particles, and a syringe filter with a pore size of 1.2 μm (Whatman 104-62267) for the a = 355 nm particles, to remove flocculated particles. Finally, the solution was degassed.

3 Experimental procedures

The channel is cleaned before each experiment to remove any particles and contamination by rinsing it with DI water, methanol (FisherSci A412P-4, 99.9%), acetone (FisherSci A18P-4, 99.7%), and 1 M sodium hydroxide (ACROS 12426-0010) using a syringe pump attached to the right reservoir to apply suction. The microchannel is then flushed with the appropriate electrolyte solution without particles. The channel is also cleaned every ~ 20 h of experiments by driving Nanostrip (Cyantek 539400) through the channel at a flow rate of 8 μL/h for 24 h to remove any organic matter (e.g., PS).

The microchannel, cleaned tubing, manometer, and upstream container are assembled using short sections of flexible tubing and filled with the appropriate solutions. Air bubbles within the tubing are removed as required by inserting a needle into the open ends of the tubing and applying suction.

After aligning the optical setup to illuminate the center of the channel, the channel is fixed to the microscope stage with paper tape and platinum electrodes are inserted through the holes in the sleeve stoppers. The (x, y) position of the channel center is calculated from dial indicator readings. A prism is coupled to the top of the microchannel using index-matching fluid of refractive index n = 1.4587 (Cargille 19571) and used to couple the laser beam into the microchannel at the angle of incidence required for TIR.

In most cases, images are obtained at a given $\dot {\gamma }$ for several different values of |E|. The height of the upstream container is first set to achieve the desired pressure difference and $\dot {\gamma }$. Image acquisition starts at least 10 min after starting Poiseuille flow at this constant value of $\dot {\gamma }$; the desired electric field is applied 30 s after the start of image acquisition. At the end of an image sequence at a given |E|, the electric field is turned off, and image acquisition at the next value of |E| starts at least 5 min afterward.

At the beginning and end of the experiment at a given shear rate, the electrodes and power supply are connected in series to an ammeter (Keithley 485 Autoranging Picometer) to determine the resistance of the fluid inside of the channel. Variations in the resistance over the course of the experiment would indicate that there is significant Joule heating; in all cases, the resistance over a typical experiment lasting about 8 h varies by less than 4%.

4 Data processing

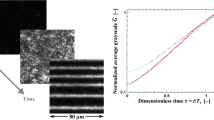
Figure 3 shows a typical time sequence of grayscale images of band formation where the dc electric field is applied at t = 0. The grayscale images are processed to estimate the time when the first band forms after applying the electric field, and the cross-stream, or y-, locations of the band centers, once formed, as detailed in the Supplementary Material.

Fig. 3

Three (contrast enhanced) grayscale images from a sequence acquired for a shear rate $\dot {\gamma }$= 1760 s⁻¹ at a t = 6.15 s; b t = 10.15 s; and c t = 28.15 s after a dc electric field |E| = 117 V/cm is applied (at t = 0). The Poiseuille flow is to the right, while the EO flow is to the left

The number of bands, which is determined by counting the number of band centers at a given time t, is plotted as a function of t. A sigmoid function of the form ${C_1}/[1+\exp \{ - {C_3}(t - {C_2})\} ]$ is curve fit to these data using the least-squares method (Fig. 4). The banding time, T_o, is then defined to be the time when the first band appears based on the sigmoid curve fit. The steady-state number of bands over the 203 µm vertical extent of the images, N, is defined to be the average number of bands over a sequence of 1000 frames starting at t = 5 min, where the electric field (at a given value of |E|) is applied at t = 0. Figure 4 shows that the number of bands shortly after T_o is much greater than N (cf. Fig. 3b). These initial bands are short-lived, and after some seconds merge into more stable bands with a typical y-extent of 5–6 μm (Cevheri and Yoda 2014b), as can be seen in a 10 s video sequence for the case shown in Figs. 3 and 4 starting at t = 5.15 s (Supplementary Material). In all cases, T_o and N are then averaged over at least three trials at a given set of conditions to determine their average values and standard deviations.

Fig. 4

Plot of the number of bands as a function of time for the case shown in the previous figure. The solid line is the sigmoid curve fit; the dashed vertical line denotes T_o = 8.15 s, the time when the first band is formed based upon the sigmoid curve fit

5 Results

The flow of each particle solution (cf. Table 1) through the microchannels was visualized over a wide range of near-wall shear rates $\dot {\gamma }$ and electric field magnitudes |E|. In all cases, the particles are attracted to the wall, but they do not always assemble into bands. The conditions under which the particles form bands are shown in what are termed “banding maps” (Fig. 5), plots in |E| − $\dot {\gamma }$ space where combinations of shear rate and voltage gradient that result in band formation are shown as filled symbols, and (|E|, $\dot {\gamma }$) combinations where no bands are observed are shown as open symbols. These banding maps are averages over three independent realizations. The standard deviations in |E_min| for Fig. 5a–c (ζ_p = − 44 mV) are 3.6 V/cm; those for Fig. 5d (a = 355 nm) are much greater, 47 V/cm.

Fig. 5

Banding maps for solutions 1–3 and 5 (cf. Table 1), comparing ζ_p = − 44 mV and a = 245 nm PS particles in pH 9 Na₂B₄O₇ solution at a φ_∞ = 0.08%; b φ_∞ = 0.17%; and c φ_∞ = 0.33%; and d ζ_p = − 55 ± 7 mV and a = 355 nm particles in pH7 Na₂B₄O₇–H₃BO₃ solution at φ_∞ = 0.33%

These plots show that banding occurs above a minimum |E| and, in most cases, above a minimum $\dot {\gamma }$. We suspect that there is a minimum shear rate for all cases, since banding, or for that matter, particle attraction, does not occur when $\dot {\gamma }$ = 0 (i.e., for the case of “pure” EO flow), but it is impractical in this experimental setup to reproducibly achieve low shear rates $\dot {\gamma }$ < 90 s⁻¹.

It appears in Fig. 5a, b that the minimum electric field magnitude for band formation |E_min| increases with shear rate; however, |E_min| has little variation with $\dot {\gamma }$ for the other cases. A comparison of Fig. 5a–c shows that as the particle concentration increases from φ_∞ = 0.08–0.33%, |E_min| decreases from about 76 V/cm to 25 V/cm at $\dot {\gamma }$ > 10³ s⁻¹. This minimum field also appears to increase slightly with $\dot {\gamma }$. Moreover, |E_min| increases drastically as a increases from 245 to 355 nm (Figs. S2 and 5d) from 39 to 105 V/cm, respectively. For the a = 245 nm particles, |E_min| increases from 25 to 39 V/cm as particle zeta potential decreases (slightly) from ζ_p = − 44 to − 53 mV (Fig. 5c and S2).

The results for the time for the first band to form T_o suggest that they scale with electric field offset from the threshold value (|E| − |E_min|), vs. |E| itself. Figure 6 therefore shows a semi-log plot of T_o vs. |E| − |E_min| for φ_∞ = 0.08%, 0.17% and 0.33% at a = 245 nm and ζ_p = − 44 mV. Clearly, bands form more rapidly as φ_∞ increases. At the lowest particle concentration of φ_∞ = 0.08%, the relationship between T_o and |E| − |E_min| is different from that at φ_∞ = 0.17% and 0.33%, where T_o decreases as |E| − |E_min| increases. The time for the first band to form appears instead to decrease, then reaches a minimum value, and then increases as |E| − |E_min| increases. This behavior suggests that the near-wall particle dynamics are fundamentally different at the lowest concentration, i.e., for very dilute (perhaps φ_∞ < 10⁻³) particle suspensions.

Fig. 6

Semi-log plot of T_o as a function of |E| − |E_min| for φ_∞ = 0.08% (hatched); 0.17% (filled) and 0.33% (open symbols) at $\dot {\gamma }$ = 730 s⁻¹ (gray triangle), 1070 s⁻¹ (blue circle), 1390 s⁻¹ (purple diamond), and 1760 s⁻¹ (red square) for a = 245 nm and ζ_p = − 44 mV. The error bars denote the standard deviation in these data over three independent realizations

Given the lack of fundamental understanding of these phenomena, dimensional analysis was used to analyze and, if possible, simplify, these data. We assume that T_o and N (which is proportional to the spatial frequency, or period, of the bands) are functions of the flow, particle, and channel parameters $(\dot {\gamma },|E| - |{E_{{\text{min}}}}|$, a, ζ_p, ${\varphi _\infty }$, H, ζ_w U, ν), where H is the channel depth, ζ_w is the ζ-potential of the channel walls, U is the maximum (centerline) flow velocity in the channel including the EO flow and assuming two-dimensional Poiseuille flow, and ν is the fluid kinematic viscosity. The electrical permittivity of the fluid was not considered directly as a parameter, but is indirectly considered through U.

With ten parameters involving four primary dimensions, namely mass M, length L, time T and current I, there are six independent dimensionless groups based on the Buckingham Pi theorem. The two dimensionless groups involving the independent variables are ${T_{\text{o}}}\dot {\gamma }$ and N. For the five dimensionless groups involving dependent variables, we use the standard channel- and particle-based Reynolds numbers $Re=UH/\nu$ and $R{e_{\text{p}}}={a^2}\dot {\gamma }/\nu$, respectively, ${\varphi _\infty }$, ${\Pi _4} \equiv a(|E| - |{E_{{\text{min}}}}|)/|{\zeta _{\text{p}}}|$, and ${\Pi _5} \equiv a(|E| - |{E_{{\text{min}}}}|)/|{\zeta _{\text{w}}}|$. Here, Re = 0.16–0.56, $R{e_{\text{p}}}$ = 4.4 × 10⁻⁵–2.5 × 10⁻⁴, ${\varphi _\infty }$ = 8.0 × 10⁻⁴–3.3 × 10^–3, ${\Pi _4}$ = 9.5 × 10⁻⁴ − 0.17, and ${\Pi _5}$ = 4.8 × 10⁻⁴–6.9 × 10⁻².

At the two higher concentrations φ_∞ = 0.17% and 0.33%, T_o decays exponentially with |E| − |E_min|. Based on the dimensional analysis, Fig. 7 plots ${T_{\text{o}}}\dot {\gamma }$ as a function of ${\Pi _4}=a(|E| - |{E_{{\text{min}}}}|\,)/{\zeta _{\text{p}}}$; the collapse of the data at both φ_∞ clearly demonstrates that the time scale for band formation is the inverse of the shear rate, and that band formation is a convective phenomenon, at least for a = 245 nm and ζ_p = − 44 mV. The decay constants for ${T_{\text{o}}}\dot {\gamma }$, based on a curve fit over all the data at a given φ_∞ (lines), are 5.6 × 10⁻² and 3.0 × 10⁻² for φ_∞ = 0.17% and 0.33%, respectively. The uncertainties in ${T_{\text{o}}}\dot {\gamma }$ and ${\Pi _4}$ are determined using standard error-propagation methods. Note that the standard deviation in ζ_p, which exceeds 20% for a = 245 nm (cf. Table 1), leads to large uncertainties in ${\Pi _4}$.

Fig. 7

Semi-log plot of ${T_{\text{o}}}\dot {\gamma }$ (note the vertical axis labels are scaled by 10³) vs. $a\,(|E| - |{E_{{\text{min}}}}|\,)/{\zeta _{\text{p}}}$ showing the same data as the previous Figure for φ_∞ = 0.17% (filled) and 0.33% (open symbols) at $\dot {\gamma }$ = 730 s⁻¹ (gray triangle), 1070 s⁻¹ (blue circle), 1390 s⁻¹ (purple diamond), and 1760 s⁻¹ (red square). The dashed and solid lines are curve fits to the data (R² = 0.96 and 0.98 for φ_∞ = 0.17% and 0.33%, respectively). The error bars represent the uncertainty in the data

Figure 8 shows a semi-log plot of ${T_{\text{o}}}\dot {\gamma }$ vs. ${\Pi _4}=a(|E| - |{E_{{\text{min}}}}|\,)/{\zeta _{\text{p}}}$ for ζ_p = − 53 mV (filled symbols) and − 44 mV (open symbols) at a = 245 nm and φ_∞ = 0.33%. Although the time scale of ${\dot {\gamma }^{ - 1}}$ collapses the data for both ζ_p, it is less clear that there is an exponential decay with electric field offset. Nevertheless, ${T_{\text{o}}}\dot {\gamma }$ clearly decreases as ζ_p increases. Figure 9 considers instead the effect of particle size, showing ${T_{\text{o}}}\dot {\gamma }$ vs. |E| − |E_min| for a = 245 nm (filled symbols) and 355 nm (open symbols) at ζ_p = − 53 mV and − 55 mV, respectively, and φ_∞ = 0.33%. The dimensionless band formation time increases with a. Figures 8 and 9 suggest that ${\Pi _4}$ is not sufficient to account for the effects of particle size and surface charge, and that ${\zeta _{\text{p}}}/a$ may not be the appropriate scale for |E| − |E_min|.

Fig. 8

Semi-log plot of ${T_{\text{o}}}\dot {\gamma }$ (again scaled by 10³) as a function of $a\,(|E| - |{E_{{\text{min}}}}|\,)/{\zeta _{\text{p}}}$ for ζ_p = − 53 mV (filled) and − 44 mV (open symbols) at $\dot {\gamma }$ = 1070 s⁻¹ (blue circle), 1390 s⁻¹ (purple diamond), and 1760 s⁻¹ (red square). The error bars denote the uncertainty in the data

Fig. 9

Similar to the previous Figure, but for a = 245 nm (filled) and 355 nm (open symbols) particles. Unless stated otherwise, the error bars in all the plots denote the uncertainty

Given that N is defined to be the average number of bands in steady state over the fixed 203 µm vertical dimension of the images, its inverse ${N^{ - 1}}$ is proportional to the spatial period, or frequency, of the bands. Figure 10 plots ${N^{ - 1}}$ as a function of |E| − |E_min| for (a) φ_∞ = 0.08%, 0.17% and 0.33%, then splits the data for (b) φ_∞ = 0.08% and (c) φ_∞ = 0.17% and 0.33%, again at a = 245 nm and ζ_p = − 44 mV. Figure 10a suggests that there is no clear relation between ${N^{ - 1}}$ and φ_∞, while Fig. 10b, c show that ${N^{ - 1}}$ increases linearly with electric field offset; the lines are linear curve fits with R² > 0.96. Although ${N^{ - 1}}$ appears to be essentially independent of ζ_p (Fig. S3), at least over the limited range studied here, it increases with a (Fig. 11). The rate at which ${N^{ - 1}}$ increases with $a(|E| - |{E_{{\text{min}}}}|\,)/{\zeta _{\text{p}}}$ also increases with a.

Fig. 10

Graphs of ${N^{ - 1}}$ vs. |E| − |E_min| for a φ_∞ = 0.08% (hatched), 0.17% (filled) and 0.33% (open symbols); b of ${N^{ - 1}}$ vs. $a\,(|E| - |{E_{{\text{min}}}}|\,)/{\zeta _{\text{p}}}$ for φ_∞ = 0.08% with linear curve fits (dashed lines); and c of ${N^{ - 1}}$ vs. $a\,(|E| - |{E_{{\text{min}}}}|\,)/{\zeta _{\text{p}}}$ for φ_∞ = 0.17% (filled) and 0.33% (open symbols) with linear curve fits (solid and dotted lines, respectively) at $\dot {\gamma }$ = 730 s⁻¹ (gray triangle), 1070 s⁻¹ (blue circle), 1390 s⁻¹ (purple diamond), and 1760 s⁻¹ (red square). Only curve fits with R² > 0.96 are shown. The error bars in a represent a standard deviation. Note that c shows a subset of the data to improve clarity

Fig. 11

Plot of ${N^{ - 1}}$ as a function of $a\,(|E| - |{E_{{\text{min}}}}|\,)/{\zeta _{\text{p}}}$ for a = 245 nm (filled) and 355 nm (open symbols) at $\dot {\gamma }$ = 730 s⁻¹ (gray triangle), 1070 s⁻¹ (blue circle), 1390 s⁻¹ (purple diamond) and 1760 s⁻¹ (red square) and linear curve fits (solid and dotted lines, respectively) with R² > 0.97. The error bars denote the uncertainty in the data

Finally, a plot of the average number of bands in steady state over the 203 μm field of view N (vs. ${N^{ - 1}}$) as a function of shear rate $\dot {\gamma }$ for a = 245 nm and a = 355 nm particles at ζ_p = − 53 mV and − 55 mV, respectively, and φ_∞ = 0.33% (Fig. 12) shows that N increases linearly with the shear rate. The standard deviations in N for the a = 355 nm results (open symbols) are much greater than those for the smaller particles. Interestingly, N appears to be a linear function of $\dot {\gamma }$ alone; although results are not shown here, there is no obvious functional relationship between N and ${T_{\text{o}}}\dot {\gamma }.$ Note that ζ_p appears to have little effect on N, though N does increase linearly with ζ_p for ζ_p = − 53 mV and − 44 mV (Fig. S4).

Fig. 12

Graph of N vs. $\dot {\gamma }$ for a = 245 nm at |E| − |E_min| = 22 ± 3 V/cm (gray filled square) and 34 ± 3 V/cm (blue filled diamond) and a = 355 nm at |E| − |E_min| = 20 ± V/cm (gray open square) and 31 ± 1 V/cm (blue open diamond). The linear curve fits (solid and dotted lines, respectively) have R² > 0.99 and R² > 0.95, respectively

6 Summary and discussion

The results presented here show that the assembly of colloidal dielectric (nearly) neutrally buoyant particles in a dilute suspension in combined Poiseuille and electroosmotic counterflow through microchannels is a “robust” phenomenon, occurring over a range of particle sizes a = 245 nm–355 nm, ζ-potentials = − 55 to − 44 mV, and bulk volume fractions φ_∞ = 0.08–0.33%. Although results are not shown here, banding has been observed (but not quantified) for a = 500 nm, a = 245 nm particles suspended in a buffered potassium nitrate–potassium hydroxide solution, and in PDMS-fused silica microchannels.

In all cases, the particles are first attracted to, and concentrated at, the wall where they are subject to an applied pressure gradient and dc electric field. We conjecture that particle attraction is due to polarization of the counterion cloud screening the particle, and hence only dielectric (vs. conducting) particles are attracted to the wall. However, the particles only assemble into bands above a minimum electric field |E_min|, which decreases as φ_∞ increases. This |E_min| increases, however, as ζ_p and a increase. The results also suggest that the particles only assemble into bands above a minimum shear rate, although the value of this shear rate could not be determined in some cases due to limitations in the experimental setup.

The time for the first band to form T_o after the dc electric field is applied, where the particles are initially subject to steady Poiseuille flow, scales with the inverse of the near-wall shear rate. This result suggests that band assembly is a convective phenomenon. In this creeping flow with channel Reynolds numbers < 0.6, the velocity field is simply the superposition of the parabolic and uniform velocity profiles of Poiseuille and EO flows, respectively, and so the shear rate is determined by the Poiseuille flow. The dimensionless time for band formation ${T_{\text{o}}}\dot {\gamma }$ decays exponentially with the electric field offset, i.e., the difference between the applied electric field magnitude and |E_min|. This time also decreases as ζ_p increases, and increases with a.

Once the first band forms, there is an initial phase where there are several short-lived bands, which then merge after several seconds into more stable bands. Although results are not shown here, the standard deviation of the number of bands in the latter “steady-state” phase is less than two in all cases. The average number of bands N in steady state over a fixed field of view of ~ 200 μm (over three independent realizations) appears to increase linearly with shear rate; its inverse, ${N^{ - 1}}$, which is proportional to the spatial frequency of the bands, decreases linearly with electric field offset. Although N decreases as a increases, the average number of bands in steady state appears to be independent of ζ_p and there appears to be no consistent relationship between N and the bulk volume fraction.

The observation that bands only form when |E| exceeds |E_min|, and probably also when the shear rate also exceeds a minimum value, suggests that colloidal particles only assemble into bands once the near-wall particle concentration exceeds a minimum, or threshold, value. The particles are attracted to the wall with a force whose magnitude is proportional to |E| and ${\dot {\gamma }^N}$, where N ≈ 0.5 (Cevheri and Yoda 2014a). If the particles are subject to this force over the entire length of the channel, the near-wall particle concentration at a given location in the channel will increase with the electric field magnitude and shear rate due to the resultant increase in the magnitude of this attractive force. We suspect that the effect of |E| on band formation is more evident in these experiments, because the attractive force has a stronger dependence on |E|. Moreover, the near-wall particle concentration should increase with x for a given set of flow conditions, because the particles will have been subject to this attractive force over a longer period of time.

If, however, the concentration of near-wall particles does not exceed this threshold value because the attractive force magnitude is too small, or because the particle concentration in the bulk is too low, the particles do not assemble into bands. This conjecture is supported by the observations that |E_min| decreases as φ_∞ increases and increases as a increases for a given volume fraction, since the number density of the a = 355 nm particles is one-third that for the a = 245 nm particles at a given φ_∞.

The current work focuses on resolving how the near-wall particle concentration and |E_min| depend upon channel position x. In terms of future work, we plan to consider conducting particles to verify our earlier conjecture that these phenomena are observed only for dielectric particles, and to consider the effect of ac electric fields, although the attractive force appears to be electrophoretic, vs. dielectrophoretic, in its scaling.

Unfortunately, the questions of why these suspended particles are attracted to the wall when subject to a shear flow and an electric field in opposite directions, or why they subsequently assemble into bands, remain unanswered. Nevertheless, these experimental studies demonstrate that band formation is “robust”, and even if their origin can be attributed to entropic effects, e.g., random interparticle interactions in a confined domain (Zurita-Gotor et al. 2012), these colloidal particle structures are reproducible and stable enough to quantify their characteristics, and their dependence upon, and scaling with, various flow and particle properties.