Droplet formation by squeezing in a microfluidic cross-junction

Abstract

In microfluidics, flow focusing is widely used to produce water-in-oil droplets in microchannels at high frequency. We here report an experimental study of droplet formation in a microfluidic cross-junction with a minimum number of geometrical parameters. We mostly focus on the squeezing regime, which is composed of two distinct steps: filling and pinching. The duration of each step (and corresponding volumes of each liquid phase) is analyzed. They vary according to both water and oil flow rates. These variations provide several insights about the fluid flows in both phases. We propose several scaling laws to relate the droplet volume and frequency to the flow rate of both phases. We also discuss the influence of surfactant and channel compliance on droplet formation.

1 Introduction

Droplet microfluidics is a powerful tool for both fundamental and applied research in biology-related fields. The key advantage offered by water-in-oil droplets is the confinement of biological content: Each droplet is seen as an individual micro-reactor, isolated from the outer phase. The technology provides a new way of studying microorganisms (e.g., cells, bacteria) at the scale of single units Brouzes et al. (2009); Mazutis et al. (2013); Clausell-Tormos et al. (2008). Monodisperse droplets Abate et al. (2009) can be produced with controlled volume at a frequency reaching several tens of kHz (Bardin et al. 2013). They are easily manipulated in microchannel networks (merging, splitting, sorting, mixing) (Huebner et al. 2008). Droplets are able to transport and incubate solid reagents, biological content, or anything else that can be immersed in an aqueous phase while being immiscible with the oil phase. Droplet microfluidics is now encountered in numerous applications, from single-cell analysis (Brouzes et al. 2009; Mazutis et al. 2013; Clausell-Tormos et al. 2008) to DNA amplification (deMello 2006), material synthesis (Gunther and Jensen 2006) and various chemical reactions (Song et al. 2003).

Fig. 1

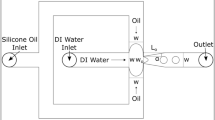
Top-view of water-in-oil droplet formation in a cross-junction. The continuous oil phase consists of 10 % of surfactant PFO in FC-$40$ oil. The capillary number of the continuous phase is $Ca = 0.006$ and the flow-rate ratio is $\phi = 1$ ($Q_{\rm{D}}=10.5$ $\mu$L/min, $Q_{\rm{C}}=11$ $\mu$L/min). The droplet length and channel width are denoted $L_{\rm{d}}$ and W, respectively

The first step in any droplet-based microfluidic device is the droplet formation. While all droplet production units deliver the dispersed phase through a single channel, there are several different ways of introducing the continuous phase. In T-junctions (TJ) (Tice et al. 2003; Thorsen et al. 2001; Garstecki et al. 2006; Christopher et al. 2009), the continuous phase is brought from one side of the dispersed phase. By contrast, in co-flow/flow focusing (FF) (Anna et al. 2003; Utada et al. 2007; Josephides and Sajjadi 2015; Nie et al. 2008), the continuous phase pinches the dispersed phase from at least two sides simultaneously. The corresponding geometries often involve a large number of parameters (incl. restriction, enlargement, orifice) and are therefore difficult to fully characterize and optimize. A few recent studies Abate et al. (2009); Cubaud and Mason (2008); Chen et al. (2014); Liu and Zhang (2011) have introduced simplified FF designs called cross-junctions (Fig. 1), in which the number of dimensionless geometry parameters can be reduced to one: the aspect ratio $W^* = W/H$ between the channel width W and the channel height H.

In addition to geometry, the production mostly depends on five physical parameters: the flow rates $Q_{\rm{D}}$, $Q_{\rm{C}}$ and the dynamical viscosities $\mu _{\rm{D}}$, $\mu _{\rm{C}}$ of the dispersed and continuous phases, respectively, and the interfacial tension $\sigma$. Based on these, three additional dimensionless parameters are defined, the capillary number Ca, the flow-rate ratio $\phi$, and the viscosity ratio $\eta$:

$$\begin{aligned} Ca = \frac{1}{WH}\frac{\mu _{\rm{C}} Q_{\rm{C}}}{\sigma }, \qquad \phi = \frac{Q_{\rm{D}}}{Q_{\rm{C}}}, \qquad \eta = \frac{\mu _{\rm{D}}}{\mu _{\rm{C}}}. \end{aligned}$$

(1)

A comparison of TJ, co-flow and FF was provided by Christopher and Anna (2007), in which they provide scaling laws for the droplet size (length or diameter) as a function of $\phi$, Ca and other geometry parameters for the TJ and co-flow. Abate et al. (2009) also compared several designs of TJ and FF. They provided measurements of the droplet volume as a function of the flow-rate ratio, $\phi$, as well as diagrams of the monodisperse production regime as a function of Ca and $\phi$. In subsequent work (Abate and Weitz (2011)), the same group demonstrated better control of the droplet size at a cross-junction by adding resistor channels at each inlet. However, scaling laws that relate the droplet size and frequency to the inlet parameters and geometry are still lacking for FF. Furthermore, the models available for TJ designs are not directly applicable to the FF geometry.

Two main production regimes have been recurrently identified in every geometry: squeezing and dripping (the latter is also called jetting) (Baroud et al. (2010); Nunes et al. (2013); Anna (2016)). In squeezing, the dispersed phase breaks up at the junction or in its immediate vicinity. After break-up, the remaining liquid retracts in the junction area (Cubaud and Mason (2008); Derzsi et al. (2013)). The squeezing regime yields monodisperse droplets which size is mostly prescribed by the channel dimensions. The droplet length is usually larger than H and W so the resulting droplet cannot be spherical; it is instead strongly confined by the channel walls. A distinct mode of squeezing identified in FF units with orifice is referred as geometry-controlled (Anna and Mayer (2006); Lee et al. (2009)). There the dispersed phase protrudes and retracts (Bardin et al. (2013)), forming droplets with dimensions close to the orifice width. In the dripping (or jetting) mode, the dispersed phase breaks up farther from the junction, and the interface does not recoil afterward (Derzsi et al. (2013)). The droplets produced are usually much smaller than the junction/orifice dimensions, and the production frequency is significantly higher. The transition from squeezing to dripping always occurs when local velocities are increased to the point where viscous and/or inertial effects can overcome surface tension (Abate et al. (2012)). Several criteria were proposed to capture this transition (Utada et al. (2007)), based on either the capillary number Ca or the Weber number $We_{\rm{in}}=\rho d U_{\rm{in}}^2/\sigma$ (where $\rho$ is the density of the dispersed phase, d is the inner channel diameter, and $U_{\rm{in}}$ is the velocity of the dispersed phase at the inlet). The Weber number is preferred as soon as the channel dimensions are sufficiently large for inertia to dominate viscous forces. In cross-junctions (Fu et al. (2012)), the proposed transition criterion is $We \simeq 7.10^{-6}Ca_{\rm{D}}^{-1.9}$, with $Ca_{\rm{D}}>10^{-2}$.

Flows of each phase can be driven through either flow-rate or pressure control. Ward et al. (2005) compared both options in a flow-focusing unit and showed that droplets could be equivalently produced, in a similar range of droplet size for both systems. Quantitative differences were nevertheless observed in the dependence of drop size to flow control parameters. In pressure-controlled systems, flow rates are hard to measure accurately (the error made by most flow sensors at this scale can be of the order of 10 %). Therefore, we will here focus on flow-rate control, for which the flow rates are known a priori.

The viscosity ratio $\eta$ also influences the droplet formation process Tice et al. (2003); Christopher and Anna (2007); Nie et al. (2008); Cubaud and Mason (2008). Cubaud and Mason (2008) investigated this effect in squared channels cross-junctions for viscous droplets in a less viscous continuous phase: $\eta \in [22, 1500]$. They identified five distinct production regimes and a scaling law for the droplet length $L_{\rm{d}}$ in the squeezing regime, valid for $\eta > 15$. Nie et al. (2008) outlined that the dispersed phase viscosity strongly affects the droplet size in FF units with orifice. Another important aspect to take into account is the presence of surfactant. A recent extensive study of drop formation in TJ Glawdel and Ren (2012) demonstrated that surfactant adsorption can occur at the same time-scale as the droplet formation, in which case it strongly influences the production.

A detailed comprehension of squeezing and dripping regimes is still missing, though it is required to exploit the full potential of droplet microfluidics (Nunes et al. (2013)). Many empirical and numerical models have been proposed for various geometries and parameter ranges. For example, Tan et al. (2008) proposed that the droplet length $L_{\rm{d}}$ empirically satisfies $L_{\rm{d}}/W = 1.59 (\phi /Ca)^{0.2}$ for $L_{\rm{d}}/W \in [1,6]$, in a flow-focusing cross-junction with two inlets of different rectangular cross-section (i.e., four geometric parameters) and some surfactant in the continuous phase. Another empirical relation was proposed by Liu and Zhang (2011), based on numerical simulations in a similar cross-junction:

$$\begin{aligned} \frac{L_{\rm{d}}}{W}= (\epsilon + \omega \phi ) Ca^{-m}. \end{aligned}$$

(2)

The fitting parameters $\epsilon$, $\omega$ and m are positive but otherwise unconstrained, and they depend on both the geometry and the viscosity ratio $\eta$. More recently, Chen et al. (2014) provided a sophisticated model of droplet formation in the squeezing regime in a cross-junction. The model evaluated the volume of the dispersed phase at various stages of the break-up process, with only one constrained fitting parameter. They validated this model with experiments for several values of $\eta$, W/H, $\phi$ and Ca, although not for a large range of theses parameters.

The comparison of these models is often not straightforward, owing to the different output variables involved in each, e.g., the droplet length $L_{\rm{d}}$, the droplet volume $V_{\rm{d}}$ or the production frequency $F_{\rm{d}}$. There are two trivial relations between these parameters. First, a mass balance of the dispersed phase indicates that

$$\begin{aligned} Q_{\rm{D}} = V_{\rm{d}} F_{\rm{d}}. \end{aligned}$$

(3)

Second, since droplets are here confined by the channel walls, there must exist a geometrical relationship between the droplet length $L_{\rm{d}}$ and its volume $V_{\rm{d}}$. This relation might depend on Ca, as does the shape of the droplet. Therefore, the knowledge of either $F_{\rm{d}}$, $V_{\rm{d}}$ or $L_{\rm{d}}$ as a function of input parameters is sufficient to characterize the production. Practically, $F_{\rm{d}}$ can be measured very accurately from top-view recordings, while the measurement of $L_{\rm{d}}$ is limited by the spatial resolution of the camera. The droplet volume cannot be directly measured from images (unless some geometrical assumptions are made on the three-dimensional shape), but it is easily retrieved from the measured $F_{\rm{d}}$. Chen et al. (2014) therefore suggested to use the dimensionless droplet volume

$$\begin{aligned} \varOmega = \frac{V_{\rm{d}}}{W^2 H} = \frac{Q_{\rm{D}}}{F_{\rm{d}} W^2 H} \end{aligned}$$

(4)

as the main output parameter.

In this work, we revisit the production of droplets in a microfluidic cross-junction and provide a new series of experimental data. After a description of the experimental setup, we describe the different production regimes observed as Ca and $\phi$ are varied. In particular, we analyze the motion of tiny satellite droplets between the main drops, from which we infer the real dimensions of the microchannels. We then focus on the squeezing regime, and we investigate the corresponding relation between $\varOmega$, Ca and $\phi$ through a thorough quantitative analysis of video recordings. We consider the entire range of squeezing and the possible influence of adding surfactant. We finally compare our data to the recent model of Chen et al. (2014), and discuss the possible effect of compliance in the experimental setup.

2 Experiments

2.1 Liquids

We study the formation of water-in-oil droplets for two different continuous phases: ($\mathcal {S}_{\rm{o}}$) without and ($\mathcal {S}_{\rm{w}}$) with surfactant. In both cases, the dispersed phase is made of de-ionized (DI) water of viscosity $10^{-3}$ mPa s at $20\,^{\circ }$C. The first continuous phase ($\mathcal {S}_{\rm{d}}$) consists in silicone oil (Xiameter, 5 cSt, Sigma Aldrich) without surfactant. The second continuous phase ($\mathcal {S}_{\rm{d}}$) is a mixture of FC-40 fluorocarbon oil (3M, INVENTEC Benelux) and the surfactant 1H, 1H, 2H, 2H-Perfluoro-1-octanol (PFO, Sigma Aldrich) in a volume ratio of 9:1. The viscosity of both oil mixtures was measured at $20\,^{\circ }$C with a rheometer Haake Mars III (ThermoScientific). It is 5.4 mPa s for silicone oil, 4.9 mPa s for pure FC-40, and 5.4 mPa s again for the mixture of FC-40 and PFO. Therefore, the viscosity ratio $\eta = \mu _{\rm{D}} / \mu _{\rm{C}} = 0.18$ is constant for both configurations. Similarly, the interfacial tension between the oil mixture and DI water was measured with an optical contact angle meter (KSV instruments LTD CAM 200 – pending drop method). It is 36.4 mN/m for silicone oil, 54 mN/m for pure FC-40 and 14 mN/m for the FC-40 + PFO mixture. The critical micellar concentration (CMC) of PFO in FC-40 was determined by the same method (cf. Supplementary Information): it is highly soluble, since its CMC approaches $10\,\%$ vol./vol. Our surfactant/oil mixture is therefore slightly above the CMC, which should ensure an homogeneous spreading of the surfactant at the interface of the forming droplets.

2.2 Set up

Each liquid combination ($\mathcal {S}_{\rm{o}}$, $\mathcal {S}_{\rm{w}}$) required channel walls with a different coating to ensure appropriate wetting. So two identical chips were fabricated in PDMS by soft-lithography. First the channel geometry was drawn in AutoCAD (AutoDesk), then printed on a foil mask with a photoplotter (Bungard, resolution 8192 dpi). The geometry is chosen as simple as possible, in order to focus on the droplet formation without introducing any additional influence from other parts of the chip. The lengths of the water inlet, the oil inlets and the emulsion outlet are 10, 5 and 10 mm, respectively, to provide sufficient channel resistance and observation length for the droplets in the outlet. The cross-junction is symmetrical and all channels have the same theoretical width $W=155\,{\upmu}$m (Fig. 1—CAD mask available in SI). We fabricated a master with SU-8 negative photoresist (SU-8 2050, MicroChem, MicroResist Technology) on a silicon wafer. The targeted thickness was $50\,{\upmu}$m. We silanized the master for 3 h in a desiccator in order to prevent the replica from sticking to the master. We poured a degassed 10:1 mixture of Sylgard 184 PDMS (Dow Corning) onto the master and then baked it for one hour at $85\,^{\circ }$C. We carefully peeled the cured PDMS and punched inlets/outlet holes. In parallel, we spin-coated some glass slides with a very thin layer of PDMS that we cured at $85\,^{\circ }$C for 30 min. Finally, we bonded the PDMS chip to these PDMS-coated glass slides after plasma activation (air plasma, Diener, 120 s). The assembly was strengthened by baking for one additional hour at $85\,^{\circ }$C. Afterward, we coated the channel walls to ensure hydrophobicity and oleophilicity. The silicone-oil chip ($\mathcal {S}_{\rm{o}}$) was flushed first with rain-X water-repellent (Auto5) then with air, and finally dried overnight. The FC$-40$ chip ($\mathcal {S}_{\rm{w}}$) was flushed first with Aquapel (PPG) Mazutis et al. (2013), then air. It was rinsed with pure FC-40, and finally flushed again with air. Liquids were pushed inside the chip at constant flow rate using two syringe pumps (Nemesys 290N, Cetoni) connected with PVC tubing (Thermo Scientific) with inner diameter $r_{\rm{i}}=1$ mm, outer diameter $r_{\rm{o}}=2$ mm, length $L_{\rm{t}}=0.1$ m, and Young’s Modulus $E_{\rm{t}}=6.1$ MPa. After calibration (detailed procedure available in SI), the flow-rate accuracy was 5 %. Experiments were performed at controlled temperature 20 $\,\pm\,0.5\, ^{\circ }$C.

Microscopy measurements on dry chips indicated channel width of 151 and $166\,{\upmu}{\rm{m}}$ for chips ($\mathcal {S}_{\rm{o}}$) and ($\mathcal {S}_{\rm{w}}$), respectively. This difference was already present on the corresponding SU-8 masters. The channel height was measured to $56\,{\upmu}{\rm{m}}$ by optical profilometry. Unfortunately, these dimensions could be significantly altered by the swelling of the PDMS. The channel width was therefore measured a second time after having flushed the oil phase for 40 min. After this complete swelling, the mean channel width was 116 and $166\,{\upmu}{\rm{m}}$ for ($\mathcal {S}_{\rm{o}}$) and ($\mathcal {S}_{\rm{w}}$), respectively. The PDMS did not swell significantly with the FC-40 + surfactant mixture; thus, its height was expected to be about $56\,{\upmu}{\rm{m}}$. In contrast, the PDMS swelled considerably with silicone oil. In these conditions, the resulting channel height had to be determined a posteriori. The corresponding calibration procedure (detailed in SI) yields $H=62.9\,{\upmu}{\rm{m}}$ for ($\mathcal {S}_{\rm{o}}$) and $H=51.8\,{\upmu}{\rm{m}}$ for ($\mathcal {S}_{\rm{w}}$). The aspect ratio of each device is therefore $W^*=\frac{W}{H} = 1.8$ and 3.2, respectively.

2.3 Acquisition

The capillary number Ca was varied over two orders of magnitude (from $8\times 10^{-4}$ to 0.3) by changing the oil flow rate. For each Ca, at least ten values of $\phi$ were considered, by changing the water flow rate. These values ranged from the lower limit at which squeezing was sporadic to the upper limit of continuous dripping. Experimental data points are all represented in the phase diagram of Fig. 2. The range of Ca and $\phi$ was significantly larger than the range considered in previous studies of droplet formation in cross-junctions Chen et al. (2014); Tan et al. (2008).

The chips were observed with a stereo-microscope (Zeiss SteREO Discovery.V12) combined with a high-speed camera (Photron Fastcam MINI UX100). Its frame rate was adapted to the production frequency. We waited at least two minutes before recording every time flow rates were changed, in order to ensure that both flow rates were stabilized. About 100 successive droplets (on average) were recorded for every combination of Ca and $\phi$. For each, the position of the interface was tracked over time (image processing with Matlab). The production frequency was determined from the number of droplets produced divided by the duration of the experiment. In subsequent figures, random errors (e.g., the standard deviation of the statistical ensemble) are always included in the error bars, whereas systematic errors (e.g., the pixel-to-metric conversion <1 %) are not represented.

3 Results

3.1 Phase diagrams

Fig. 2

Phase diagram of droplet production regimes as a function of the Capillary number Ca and the flow-rate ratio $\phi$. a Without surfactant ($\mathcal {S}_{\rm{o}}$), and b with surfactant ($\mathcal {S}_{\rm{w}}$). Symbols correspond to different regimes: filled circle = periodic squeezing, open circle = aperiodic squeezing, open triangle = dripping, x $=$ secondary droplets. The gray shade indicates the area where periodic squeezing was observed experimentally. The dashed contour in a represents the zone investigated experimentally by Chen et al. (2014). The line in a and b represents the lower limit of periodic squeezing predicted by Eq. (16). c Snapshots of droplet production for ($\mathcal {S}_w$), illustrating some experimental data points selected in (b). filled circle: periodic squeezing $(Ca=0.013, \phi =0.2)$. open circle: aperiodic squeezing $(Ca=0.007, \phi =0.05)$. open triangle: dripping $(Ca=0.021, \phi = 1.21)$. x: secondary droplets $(Ca=0.097, \phi =0.04)$

The various droplet formation regimes observed in our experiments are illustrated in the diagrams of Fig. 2. In the squeezing regime, the pinching of the water–oil interface occurs in the immediate vicinity of the junction Anna and Mayer (2006); Cubaud and Mason (2008); Derzsi et al. (2013); Fu et al. (2012). Stable periodic squeezing is within a range that spans several decades of Ca and $\phi$. This range is reduced by the addition of surfactant. At low Ca and/or low $\phi$, squeezing becomes aperiodic and even strongly sporadic. The experimental origin of this unexpected behavior will be detailed in the discussion.

At $Ca \simeq 0.1$ and moderate $\phi$, the periodic monodisperse squeezing becomes unstable. After pinch-off, the interface does not fully recede owing to important viscous stress. It then pinches and emits one or two secondary droplets before finally receding and starting a new squeezing cycle. At high $\phi$, the droplet does not fully fill the outlet channel; instead it forms a stream entrained by the continuous phase, that pinches into droplets farther downstream. Dripping occurs as soon as the interface does not recede anymore after pinch-off Utada et al. (2007); Derzsi et al. (2013); Fu et al. (2012); Guillot et al. (2007). The radius of the produced droplets is significantly smaller than the channel width. The transition from squeezing to dripping has been extensively studied in many configurations Utada (2005); Fu et al. (2012); Derzsi et al. (2013); Cramer et al. (2004); Cubaud and Mason (2008). Our data indicate that surfactant can significantly shift this transition.

3.2 Satellite droplets

Fig. 3

a Top-view of a satellite droplet looping in the vertical plane between two main droplets ($\mathcal {S}_{\rm{o}}$, $Ca = 0.007$ and $\phi = 1.5$). The speed of the satellite droplet oscillates between 47 and 233 mm/s, whereas the speed of the main droplets is 131 mm/s, so the speed ratio $\chi = 233/131 = 1.78$. Scale bar 150 ${\upmu}{\rm{m}}$. b Spatio-temporal diagram of the sequence (a), obtained by vertically combining successive horizontal slices from the symmetry axis of the channel. c Top-view of a satellite droplet looping in the horizontal plane between two main droplets ($\mathcal {S}_{\rm{o}}$, $Ca = 0.012$ and $\phi = 1.5$). The speed of the satellite droplet oscillates between 73 and 313 mm/s, whereas the speed of the main droplets is 226 mm/s, so $\chi = 1.38$

Satellite droplets are often formed when a liquid interface pinches off. They have been frequently observed in the wake of droplets produced by squeezing, for oil-in-water emulsions at $\eta > 1$ Carrier et al. (2013, 2015); Fu et al. (2012); Derzsi et al. (2013); Cramer et al. (2004); Funfschilling et al. (2009). We here show that this phenomenon also exists for water-in-oil emulsions at $\eta <1$. Depending on the regime, the size of satellite droplets can vary from a few percent of the main droplet width (almost not visible), to a size comparable to the main droplet. In this latter case, the production is usually irregular and has been here referred as “secondary droplets”.

Satellite droplets are not strongly confined by the channel walls; they are therefore free to move in a space delimited by the former drop, the next drop and the walls (Fig. 3). Owing to their small size, they are purely advected by the flow, they behave as tracers. A satellite droplet is always formed approximately at the center of the outlet channel cross-section, so it initially moves with a local velocity larger than the preceding drop, and it quickly catches this latter. Then, most of the time, both droplets merge. Occasionally the satellite droplet bounces on the main droplet without merging. It is then pushed away from the central line, toward one of the walls, where the local oil velocity is now less than the velocity of the main droplet. The satellite droplet strongly decelerates and gets caught up by the following main droplet. Again, it can bounce on the latter and be pushed back to the central line, where it accelerates and repeats this cycle (Fig. 3).

The satellite droplet reveals some crucial information about the flow in the continuous phase. ${\upmu}$-PIV experiments in rectangular Sarrazin et al. (2006) and cylindrical microchannels (Khodaparast et al. 2014) have shown that the flow is almost Poiseuille-like (parabolic flow profile) at a distance from each drop equal to at least the channel diameter. We found (as detailed in SI) an approximate analytical solution to this flow that yields the same conclusion for rectangular channels. It moreover allows a prediction of the ratio $\chi$ between the maximum speed in the continuous phase and the speed of the main droplets. This velocity ratio strongly depends on the channel aspect ratio $W^*$, and weakly on the spacing between the main droplets. Consequently, $W^*$ can be estimated a posteriori from the tracking of satellite droplets. 40 satellite droplets from seven different experimental conditions were tracked over time. For $\mathcal {S}_{\rm{o}}$, the obtained velocity ratio is $\chi = 1.78\pm 0.09$, which corresponds to an aspect ratio $W^* = 1.84\pm 0.025$ and so to a channel heigth $H=63.7\pm 0.9\,{\upmu}{\rm{m}}$. Similarly, for $\mathcal {S}_{\rm{w}}$, $\chi = 1.57\pm 0.05$, so $W^* = 3.17\pm 0.1$ and $H=52.3\pm 1.7\,{\upmu}{\rm{m}}$.

These estimations of H from the motion of satellite droplets are backed up by two other methods (Table 1). First, the droplet volume calculated from Eq. 4 can be compared to the volume estimated by the geometrical approximation Chen et al. (2014)

$$\begin{aligned} V_{\rm{d}} = HA -\frac{H^2}{2}\left(1-\frac{\pi }{4}\right) \ell , \end{aligned}$$

(5)

where A and $\ell$ are the measured droplet area and perimeter (from top-view). Second, the measured spacing $\lambda$ between successive droplets should correspond to

$$\begin{aligned} \lambda = \frac{Q_{\rm{C}}}{F_{\rm{d}} WH}, \end{aligned}$$

(6)

in a first approximation.

Table 1 Different estimations of H [${\upmu}{\rm{m}}$] after swelling

3.3 The squeezing regime: decomposition in two steps

Fig. 4

a Squeezing in a cross-junction happens in two successive steps: filling (duration $T_1$) and pinching (duration $T_2$). Snapshots are taken at $Ca = 0.0026$ and $\phi = 0.5$ (configuration $\mathcal {S}_{\rm{o}}$). b Position of the front interface during the formation of 10 successive droplets, as a function of time (here made dimensionless and modulo with the droplet production frequency). The average speed is $\simeq\!\!4.4$ mm/s during filling, and $\simeq\!\!25.5$ mm/s during pinching. It corresponds to $0.5 Q_{\rm{D}}/(WH)$ and $0.97 (Q_{\rm{C}}+Q_{\rm{D}})/(WH)$ respectively. The transition from filling to pinching corresponds to the intersection of extrapolated constant-speed trajectories (red lines) (color figure online)

The evolution of the water–oil interface during squeezing is shown in Fig. 4. Its rightmost position is represented for ten successive droplets (Fig. 4b). The collapsed curves confirm periodic squeezing at frequency $F_{\rm{d}}$. The dynamics of the front interface reveals two distinct steps, invariantly present across the whole squeezing regime . The first is the filling of the dispersed phase inside the cross-junction, which starts just after the previous droplet detached. The front interface first quickly recoils from the previous detachment; then, it moves forward again at a relatively constant speed, slightly lower than the average speed in the water channel $Q_{\rm{D}} / (WH)$. The flow of the continuous phase into the outlet channel is not strongly affected. The first step lasts $T_1$, until the dispersed phase reaches the end of the junction. Then, in a second step called pinching, the dispersed phase enters the outlet channel and partially blocks the continuous phase. The incoming flow of the latter forces the front interface to quickly accelerate to an average speed close to $(Q_{\rm{C}} + Q_{\rm{D}})/(WH)$. The dispersed phase is then stretched and pinched, which results in the formation of a new droplet convected downstream at approximately the same speed Jakiela et al. (2011). The duration from blocking to pinch-off is $T_2$. These two steps have already been identified by several authors van Steijn et al. (2010); Fu et al. (2012); Wu et al. (2008), and they formed the cornerstone of the recent model of Chen et al. (2014). The dimensionless droplet volume $\varOmega$ (normalized by the volume of the cross-junction $W^2H$) can be expressed as a function of $T_1$ and $T_2$:

$$\begin{aligned} \varOmega = \frac{Q_{\rm{D}}}{F_{\rm{d}} W^2H} = (T_1+T_2) \frac{Q_{\rm{D}}}{W^2H}= \varOmega _1 + \varOmega _2 \phi , \end{aligned}$$

(7)

where

$$\begin{aligned} \varOmega _1 = \frac{T_1Q_{\rm{D}}}{W^2H} \text{ and } \varOmega _2 = \frac{T_2Q_{\rm{D}}}{W^2H} \end{aligned}$$

(8)

represent the volume of dispersed phase dispensed at step 1 (filling) and the volume of continuous phase dispensed at step 2 (pinching), respectively.

Fig. 5

a–c Dimensionless volume $\varOmega _1$ of the dispersed phase dispensed during $T_1$ (measured): a as a function of Ca for $\phi =0.2$, b as a function of $\phi$ for $Ca=0.007$, c as a function of the prediction $\varOmega _1^*$ of Eq. (9). d–f Dimensionless volume $\varOmega _2$ of the continuous phase dispensed during $T_2$ (measured): d as a function of Ca for $\phi =0.2$, e as a function of $\phi$ for $Ca=0.007$, f as a function of the prediction $\varOmega _2^*$ of Eq. (9). In a–f, black (resp. red) symbols and lines correspond to droplets without surfactant—$\mathcal {S}_o$ (resp. with surfactant—$\mathcal {S}_w$). Symbols represent the experiments. In a–b, d–e, the black and red solid lines correspond to the prediction of Eq. (9) with coefficients from Table 3, while the dashed line represents the model of Chen et al. (2014). In c and f, the horizontal error bar results from the estimated uncertainty on coefficients in Eq. 9 (color figure online)

Dimensionless volumes $\varOmega _1$ and $\varOmega _2$ are represented as functions of both Ca and $\phi$ in Fig. 5a–b, d–e. Both $\varOmega _i$ constantly remain of the order of unity, and they decrease when either Ca or $\phi$ is increased over more than one decade. The decrease in $\varOmega _1$ is more pronounced with surfactant ($\mathcal {S}_{\rm{w}}$, $W^*=3.2$). By contrast, neither surfactant nor aspect ratio does have any significant effect on $\varOmega _2$. Both $\varOmega _{\rm{i}}$ seem to diverge when $Ca \rightarrow 0$, while they remain finite when $\phi \rightarrow 0$, although stable squeezing cannot be observed in either of these limits (Fig. 2).

Fig. 6

Superposition of two snapshots from the same experiment right after pinch-off and initial retraction (orange), and after $T_1$ at the end of the filling step (blue). a $\mathcal {S}_{\rm{o}}$, $\phi = 0.2$, top $Ca = 0.0044$, bottom $Ca = 0.034$. b $\mathcal {S}_{\rm{w}}$, $\phi = 0.2$, top $Ca = 0.0045$, bottom $Ca = 0.035$. c $\mathcal {S}_o$, $Ca = 0.0073$, top $\phi = 0.1$, bottom $\phi = 1$. d $\mathcal {S}_w$, $Ca = 0.0075$, top $\phi = 0.1$, bottom $\phi = 1$. Colors are added by image processing to highlight the movement of the interface (color figure online)

More insight about the influence of each parameter on $\varOmega _1$ can be obtained from a direct comparison of snapshots taken at the same dimensionless time in different conditions. The interface motion during the filling step is highlighted in Fig. 6, where Ca, $\phi$ and $\mathcal {S}$ are changed one by one. The decrease in $\varOmega _1$ with either increasing Ca or $\phi$ is much more pronounced with surfactant than without. It is partly attributed to an earlier transition to the second step (pinching) and to a thinner water thread, both being induced by the shear stress from the oil flow. In addition, surfactant induces a strong dependence to Ca of the initial interface retraction after the previous pinch-off (orange line in Fig. 6). A similar analysis of $\varOmega _2$ is less straightforward, as this volume of oil around the water thread is less easily quantified from a top-view.

4 Discussion

4.1 Droplet volume in periodic squeezing

The experimental validation of the analytical model proposed by Chen et al. (2014) for the squeezing of droplets in cross-junctions included several aspect ratio $W^*$ and viscosity ratio $\eta$. Nevertheless, it did not consider the addition of surfactant, and the range of Ca and $\phi$ was limited to a small region of the squeezing regime (dashed frame in Fig. 2a). We here evaluate this model against our experimental data. We have solved the equations in Chen et al. (2014) with our experimental input parameters, and represented the solutions $\varOmega _1$ and $\varOmega _2$ in Fig. 5a–b, d–e. The model reproduces the finite value of both $\varOmega _{\rm{i}}$ as $\phi \rightarrow 0$, as well as their decrease with increasing Ca. It also confirms that the change in aspect ratio (from 1.8 to 3.2) does not influence significantly $\varOmega _{\rm{i}}$, so any significant difference between our two configurations is likely due to the presence of surfactant mostly. However, there are several discrepancies between our data and the model of Chen et al. First, the latter predicts a saturation at large Ca which is not observed in experiments. More importantly, it fails at capturing the slight decrease in $\varOmega _2$ with increasing $\phi$ (their validation extends up to $\phi \approx 0.5$). Instead, the prediction diverges at $\phi \simeq 1$. The discrepancy between the model and experiments is significantly stronger for $\mathcal {S}_{\rm{w}}$. This divergence is actually implicit to the model. Indeed, the volume $\varOmega _2$ is assumed to contain a positive contribution from the gutters alongside the forming drop, which is proportional to the drop volume $\varOmega = \varOmega _1 + \phi \varOmega _2$. Owing to such positive feedback, there is always a value of $\phi$ at which $\varOmega _2$ diverges because $Q_{\rm{C}}$ is not sufficiently important with respect to $Q_{\rm{D}}$ to fill-up the gutters. Another hypothesis of this model can be contested on experimental grounds: the interface position at the end of the filling step is observed to vary significantly with $\phi$, although it was assumed to be a function of Ca only. Consequently, our data do not entirely support the model of Chen et al. and another model has to be proposed that encompasses the full regime of periodic squeezing.

The empirical relation (2) proposed by Liu and Zhang (2011) cannot be directly adjusted to our data since it provides the droplet length instead of its volume. Moreover, their range of Ca and $\phi$ was also reduced, similar to the range of Chen et al. (2014). Nevertheless, several observations can be made as far as the droplet volume $\varOmega$ is assumed roughly proportional to its length $L_{\rm{d}}$. Then, both predicted $\varOmega _{\rm{i}}$ should scale as $Ca^{-m}$, with the same value of m, independently of $\phi$. This increase and divergence of both $\varOmega _{\rm{i}}$ as $Ca \rightarrow 0$ is observed in our experiments. However, our data reveal a dependence of m to the presence of surfactant, as well as a dependence of $\varOmega _{\rm{i}}$ on $\phi$ that Eq. (2) does not consider. The model of Liu et al. should therefore be augmented to take these observations into account.

In order to develop a more robust empirical relation, we have first checked that, in good approximation in the periodic squeezing regime, $\varOmega _i (Ca_1, \phi ) / \varOmega _i (Ca_2, \phi )$ is independent of $\phi$ and $\varOmega _{\rm{i}} (Ca, \phi _1) / \varOmega _{\rm{i}} (Ca, \phi _2)$ is independent of Ca. Consequently, each $\varOmega _{\rm{i}}$ can be expressed as the product of a function of Ca and a function of $\phi$. The sharp increase in both $\varOmega _{\rm{i}}$ with decreasing Ca suggests a power law of negative exponent (Fig. 5a, d), similarly to Eq. (2). Such divergence is not observed when $\phi$ tends to zero, which suggests a linear decrease in $\varOmega _{\rm{i}}$ with $\phi$ in first approximation. The following relation is therefore proposed:

$$\begin{aligned} \varOmega _{\rm{i}}^* = Ca^{-A_{\rm{i}}}(C_{\rm{i}} - B_{\rm{i}}\phi ), \quad i \in \{1,2\}. \end{aligned}$$

(9)

The positive coefficients $A_{\rm{i}}$, $B_{\rm{i}}$ and $C_{\rm{i}}$ are determined by least-square fitting of all data points in the dripping regime. They are summarized in Table 2, for both configurations without and with surfactant. The uncertainty on these coefficients is estimated as the interval in which the fitting residual is less than 10 % higher than its minimum value. Parity plots in Fig. 5c, f confirm the validity of Eq. 9 in the entire squeezing regime.

Table 2 Coefficients of Eq. (9) determined by least-square fitting of all the data points in the squeezing regime

Some of these coefficients are very similar to each other and their difference is within their respective error bars. In particular, as already observed in Figs. 5 and 6, the addition of surfactant and related change in aspect ratio do not significantly influence $\varOmega _2$, so the corresponding coefficients are approximately the same for both configurations. The coefficient $B_1$ seems equally unaffected by surfactant. Without surfactant, coefficients $A_1$ and $A_2$ are close to each other, so they could be assumed equal, as suggested in Liu’s relation Eq. (2). These assumptions reduce the number of coefficients from 12 to 7 for both $\mathcal {S}_{\rm{o}}$ and $\mathcal {S}_{\rm{w}}$ together. They are again determined by least-square fitting (Table 3).

Table 3 Coefficients of Eq. (9) determined by least-square fitting of all the data points in the squeezing regime.

Fig. 7

Parity plot of the measured dimensionless droplet volume $\varOmega = Q_{\rm{D}}/W^2HF_{\rm d}$ vs. the prediction based on Eqs. (7) and (9) with coefficients from Table 3, for the entire squeezing regime. Black symbols (resp. red) represent experiments from configuration $\mathcal {S}_{\rm{o}}$ (resp. $\mathcal {S}_{\rm{w}}$). (Inset) Probability distribution function of the relative difference (absolute value) between measured and predicted values. The solid line (resp. dash-dot) represents the prediction with coefficients from Table 3 (resp. Table 2) (color figure online)

The prediction $\varOmega ^* = \varOmega _1^* + \varOmega _2^* \phi$ of the dimensionless droplet volume $\varOmega$ is directly inferred from Eq. (9). Parity plot of Fig. 7 indicates that this estimation performs well for the entire range of periodic squeezing . For most measurements, the relative error (Fig. 7-inset) remains less than $20\,\%$ without surfactant and less than $10\,\%$ with surfactant, independently of the reduction in fitting coefficients from Table 2 to 3. The error was actually more important on parity plots of $\varOmega _1$ and $\varOmega _2$ (Fig. 5c, f), owing to the uncertainty in estimating $T_1$ and $T_2$ independently, i.e., in separating the filling and the pinching steps. By contrast, the squeezing period $(T_1 + T_2) = 1/F_d$ is measured with an accuracy of less than 5 %. The parity plot (Fig. 7) also reveals that in a given geometry, the droplet volume generated by squeezing can only vary by a factor of 10 in the full range of flow rates (and corresponding parameters Ca and $\phi$). Nevertheless, the production frequency here varies from 3 Hz to 5 kHz.

Several studies have already examined the effect of surfactants on droplet production in microchannels Glawdel and Ren (2012); Baret et al. (2009); Baret (2012). They are summarized in a recent review paper (Anna (2016). The surfactant PFO used in our experiments is highly soluble in FC-40, since its CMC is around 10 % in volume. Its transfer from the bulk to any newly created interface is dictated by molecular diffusion at the scale of H. Since the diffusion coefficient D is usually smaller than $10^-9\, {\rm{m}}^2/{\rm{s}}$, the associated timescale $H^2/D \sim 2.5$ is much larger than the squeezing period. Consequently, one should expect concentration gradients of surfactant and depletion zones in the bulk and at the interface. The resulting Marangoni stresses may also influence the droplet formation Baret et al. (2009).

4.2 Limitations from channel compliance

In many experimental studies of droplet microfluidics (including the present one), the chip and interconnecting tubes are often made of flexible material such as PVC or PTFE for the tubings, and PDMS for the chip. Consequently, each channel/tube may significantly deform in response to the local pressure. The related increase in channel volume corresponds to some liquid storage, similarly to a capacitance in an electrical circuit. In which conditions could this compliance influence droplet formation?

To address this question, we first calculate the equivalent resistance and capacitance of both tubings and microchannels. The resistance $\mathcal {R}$ is defined as the ratio between the pressure drop $\Delta p_L$ along the channel and the flow rate Q. The capacitance $\mathcal {C}$ is defined as the ratio between the volume increment $\Delta V$ inside the channel and the pressure difference $\Delta p_{\rm{C}}$ across the channel wall. For a thick-walled cylindrical tube of length $L_{\rm{t}}$, inner radius $r_{\rm{i}}$ and outer radius $r_{\rm{o}}$, according to Lamé equations, the variation $\varDelta r_{\rm{i}}$ of inner radius induced by a pressure difference $\varDelta p_{\rm{C}}$ is given by:

$$\begin{aligned} \varDelta r_{\rm{i}} = \frac{r_{\rm{i}}}{E_{\rm{t}}} \left[ \frac{r_{\rm{o}}^2 + r_{\rm{i}}^2}{r_{\rm{o}}^2 - r_{\rm{i}}^2} + \nu _{\rm{t}} \right] \varDelta p_{\rm{C}} \end{aligned}$$

(10)

where $E_{\rm{t}}$ and $\nu _{\rm{t}}$ are the Young’s modulus and the Poisson ratio of the tube material. The corresponding capacitance is then

$$\begin{aligned} \mathcal {C}_{\rm{t}} = \frac{2 \pi L_{\rm{t}} r_{\rm{i}} \varDelta r_{\rm{i}}}{\varDelta p_{\rm{C}}} \sim 6 \cdot 10^{-14} \frac{\text {m}^3}{\text {Pa}} \end{aligned}$$

(11)

The hydraulic resistance $\mathcal {R}_{\rm{t}}$ of the tube is given by Poiseuille law:

$$\begin{aligned} \mathcal {R}_{\rm{t}} = \frac{8 \mu L_{\rm{t}}}{\pi r_{\rm{i}}^4} \sim 4\cdot 10^9 \frac{\text {Pa.s}}{\text {m}^3} \end{aligned}$$

(12)

for water. In a microchannel (of the chip) of dimensions $L_{\rm{c}} \times W \times H$ (where $L_{\rm{c}}$ is the water inlet length $\sim\!\!0.01$ m), the elasticity equations are significantly more involved. Nevertheless, the increase in thickness $\varDelta H$ would scale as $H \varDelta p_{\rm{C}} / E_c$, where $E_{\rm{c}}$ is here the Young’s modulus of the PDMS chip. Consequently, the related capacitance $\mathcal {C}_{\rm{c}}$ would be of the order of:

$$\begin{aligned} \mathcal {C}_{\rm{c}} \sim \frac{H^2 L_{\rm{c}}}{E_{\rm{c}}} \sim 10^{-17} \frac{\text {m}^3}{\text {Pa}}, \end{aligned}$$

(13)

which is much smaller than the capacitance of the tube. The hydraulic resistance scales as

$$\begin{aligned} \mathcal {R}_{\rm{c}} \sim \frac{12 \mu L_{\rm{c}}}{H^3 W} \sim 6\cdot 10^{12} \frac{\text {Pa s}}{\text {m}^3} \end{aligned}$$

(14)

for water, which is much larger than the resistance of the tube. Therefore, only the resistance of the chip and the capacitance of the tube need to be taken into account.

The local pressure at the junction does vary during the formation of a drop. Since both Ca are smaller than unity, this variation of pressure should be of the order of the Laplace pressure $2 \sigma / H$. If this variation were instantaneously communicated to the tube, its volume would vary by $2 \sigma \mathcal {C}_{\rm{t}}/H$, which is here about 40 times more than the volume of a droplet ($\sim\!\!2$ nl), independently of the flow rates. In such conditions, tubes would be expected to strongly affect the production of droplets.

However, the tube cannot respond immediately to these pressure variations. As in a RC circuit, its time constant is given by

$$\begin{aligned} \tau \simeq \mathcal {R}_{\rm{c}} \mathcal {C}_{\rm{t}} \sim 0.4\,{\rm{s}} \end{aligned}$$

(15)

The tube compliance could therefore strongly influence the droplet formation when $F_{\rm{d}} \tau \lesssim 1$, i.e., when the drop production timescale gets comparable to, or larger than, the time to deform the tube.

The lowest formation frequencies $F_{\rm{d}}$ are observed when both Ca and $\phi$ are small, namely in the lower left bound of the phase diagram (Fig. 2) where squeezing is aperiodic. The loss of periodicity and the sporadic droplet release in this regime could therefore result from an effective coupling between the droplet formation and the deformation of the tubings upstream. To test this hypothesis, we have calculated an estimation of $F_{\rm{d}}$ for every Ca and $\phi$, based on the model prediction (Eq. (9)):

$$\begin{aligned} F_{\rm{d}} = \frac{Q_{\rm{D}}}{V_{\rm{d}}} = \frac{\sigma }{\mu W} \frac{\phi Ca}{\varOmega ^*} \end{aligned}$$

(16)

The contour $F_{\rm{d}} \tau = 2.2$ is represented in the phase diagrams of (Fig. 2). It captures well the transition from periodic to aperiodic squeezing, both with and without surfactant. In conclusion, compliance can interfere with droplet formation and lead to aperiodicity when the volume variations of the circuit (tube + chip) in response to the Laplace pressure are larger than the volume of one droplet, and when the corresponding response time is smaller than $2.2/F_{\rm{d}}$.

If the tubes were chosen significantly more rigid (and possibly with a smaller inner diameter), the capacitance of the tube could become negligible compared to the chip capacitance. In this case, the compliance time would be $\mathcal {R}_{\rm{c}} \mathcal {C}_{\rm{c}} \sim 10^{-4}\,{\rm{s}}$, which is much less than the formation period $1/F_{\rm{d}}$. However, the variation of volume in the microchannels would be of the order of $\sim\!2\sigma \mathcal {C}_{\rm{c}}/H$, which is here 200 times less than the droplet volume. So, the effects of compliance would be marginal.

4.3 Design rules

The approximate determination of droplet frequency and droplet volume comes at the early design stage of any droplet-microfluidic chip. Nevertheless, no robust model based on first principles has emerged yet to describe the entire squeezing regime of an arbitrary liquid in a cross-junction, owing to the complexity of the underlying fluid mechanics. This complexity is possibly augmented by the influence of surfactant transport, the microfluidic circuit downstream, and the compliance of both tubings and microchannels. From a practical point of view, the empirical relations (9) can provide a good estimation of the droplet volume (with less than 20 % error), as soon as the corresponding coefficients $A_{\rm{i}}$, $B_{\rm{i}}$ and $C_{\rm{i}}$ are determined for a given liquid pair and microchannel geometry. A methodology is therefore proposed to obtain these coefficients with a minimum of experiments.

• 1. Estimate the compliance time $\tau$ of the interconnected microfluidic system. Then, estimate the minimum capillary number $Ca_m$ for periodic squeezing at $\phi = 0.2$, from Eq. (16):

  $$\begin{aligned} Ca_{\rm{m}} = \frac{2.2}{\tau } \frac{\mu _{\rm{C}} W}{\sigma } \frac{1+2 \phi }{\phi } \end{aligned}$$

  (17)

  where in first approximation $\varOmega _1^* \sim 1$ and $\varOmega _2^* \sim 2$. Then, consider a reference capillary number $Ca_{\rm{r}} = \sqrt{0.1 Ca_{\rm{m}}}$, where 0.1 is an estimation of the maximum Ca for the squeezing to dripping transition.

• 2. Once the chip is connected, impose the flow rates $Q_{\rm{C}}$ and $Q_{\rm{D}}$ which correspond to $Ca_{\rm{r}}$ and $\phi \,=\,0.2$. Periodic squeezing should be observed. Record the droplet production with high-speed microscopy. Track the most forward position of the interface (on the central line of the output channel). Check that the dripping frequency is stable, then determine $F_{\rm{d}}$, $T_1$ and $T_2$, then calculate $\varOmega _1$ and $\varOmega _2$.

• 3. Repeat the previous step for two distinct values of $\phi$ at $Ca_r$, then for two distinct values of Ca at $\phi \,=\,0.2$.

• 4. From these five pairs $(\varOmega _1,\varOmega _2)$, determine coefficients $A_{\rm{i}}$, $B_{\rm{i}}$ and $C_{\rm{i}}$ by least-square fitting. An initial guess $A_i = 0.2$ shall be considered.

5 Conclusions

In droplet microfluidics, the cross-junction is a geometry that offers many advantages. First, the droplet production is stable and monodisperse in the periodic squeezing regime, which extends over one order of magnitude in volume and three orders of magnitude in frequency. Second, the number of geometrical parameters is reduced to one, which simplifies the design process of this functional unit.

We have here reported several regimes of droplet formation in cross-junctions; then, we focused our analysis on the squeezing regime. Based on a decomposition of the phenomenon in two steps, we have proposed an empirical relation that predicts the droplet volume as a function of both Ca and $\phi$. We have shown that this relation is valid within 20 % in the whole regime of periodic squeezing. Surfactant can significantly modify the droplet frequency and volume, especially at high Ca and high $\phi$ where the frequency is also the highest. Surfactant influences more the filling step than the pinching step. We have finally identified the minimum production frequency, below which tubing compliance starts to interfere and to destabilize the droplet formation. While an accurate physical description of squeezing in cross-junctions based on first principles is still missing, it is hoped that the proposed empirical relation and corresponding methodology will provide a good first-order estimation of droplet production characteristics for preliminary chip design.