1 Introduction

The inadequacy of the classical no-slip boundary condition even within the continuum assumption-based Navier–Stokes framework is well known in areas such as rarefied gas flows (Karniadakis et al. 2006), flow of polymer melts and solutions (Denn 2001) and spreading of liquid droplets over a surface (Dussan 1979). Only in the recent past has evidence from experiments, and molecular simulations confirmed the same for simple liquids (Cieplak et al. 2001; Tretheway and Meinhart 2002; Spikes and Granick 2003; Neto et al. 2005; Majumder et al. 2005; Lauga et al. 2007; Vinogradova et al. 2009). A common measure of slippage at a solid boundary is the distance behind the solid boundary at which fluid velocity vanishes if linearly extrapolated; this has been known as slip length. This slip length, possibly arising from low viscosity depletion zones near hydrophobic/solvophobic surfaces or trapped vapour bubbles near rough surfaces of any material (Lauga et al. 2007) can be of the order of 10 nm–10 μm (Vinogradova et al. 2009; Zhu et al. 2011). Therefore, with respect to confined viscous flows of significance to recent progress in microfluidics and nanofluidics (Whitesides 2006; Lee et al. 2014), a considerable degree of slippage-dependent flow rate enhancement has become observable (see, e.g. Choi et al. 2003), ever since microchannels and nanochannels have begun to be fabricated with at least one cross-dimension comparable in size to the aforesaid range of slip lengths.

The typical driving forces (see, e.g. Van der Heyden et al. 2006) used in the slippage-sensitive viscous flows through microfluidic/nanofluidic device include a pressure differential applied via mechanical pumping and/or a voltage differential set up to engender electro-osmotic flow. Interestingly and to technological convenience (Sparreboom et al. 2010), in electro-osmotic flow, slippage effects on the net flow rate through a channel do not deteriorate appreciably with increasing channel size. This is because the factor by which net flow is enhanced due to slippage in electro-osmotic flow is controlled by the ratio of the slip length to an electrostatic length scale (Debye screening length) rather than by the ratio of slip length to channel size, as in pressure-driven flow (Muller et al. 1986; Sparreboom et al. 2010; Datta and Choudhary 2013).

It is simplistic to ascribe a single slip length to a finite span of a surface, since the surface may have roughness elements or intentionally engineered nanostructures such as grooves and pillars (Ybert et al. 2007; Maali et al. 2012) leading to patterns of wetted and de-wetted regions where the liquid contacts the solid and trapped bubbles of air, respectively. In principle, local variations in slip length can also arise as a consequence of chemical patterning (Chaudhury and Whitesides 1992) of the wettability of a smooth surface (Hendy et al. 2005; Cieplak et al. 2006). Therefore, interest often lies in a macroscopic (pattern-averaged) description of a (microscopically) slip-patterned surface through an effective slip length, which is, in general, a rank 2 tensor (Bazant and Vinogradova 2008; Kamrin et al. 2010), implying that the velocity vector on the wall is not directed along the direction of the shear force on the wall (and therefore the force driving the flow such as electric field and pressure gradients). Among various engineered anisotropic patterns of slippage in thin channels, striped patterns of slip length are expected to lead to the largest degree of effective slippage (Feuillebois et al. 2009). Anisotropy as well as flow features arising from patterning of slip and charge can facilitate better solution-phase mixing of samples (Bazant and Vinogradova 2008), which is usually a difficult task to achieve in microfluidic devices (Stone et al. 2004). Micro-/nanochannels with patterned slip length on its walls can be experimentally realizable, given the recent progress in the technology of hydrophobic coatings (Vayssade et al. 2014), engineering of superhydrophobic surfaces (Lee and Choi 2008), flow visualization (see, e.g. Schmitz et al. 2011) and microfabrication technologies (Sparreboom et al. 2010).

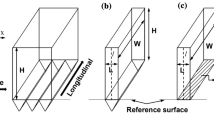
In this study on channels with patterned slip length, as in other works (e.g. Lauga and Stone 2003; Belyaev and Vinogradova 2010), boundary conditions corresponding to spatially varying liquid slippage will be applied to smooth planar surfaces corresponding to channel walls. This is a reasonable representation of not only smooth surfaces with chemically patterned wettability but also of the de-wetted (Cassie) state of a topologically patterned “super-hydrophobic” surface (Vinogradova and Belyaev 2011) barring meniscus curvature (cf. Steinberger et al. 2007) and gas phase dissipation effects. Using terminology reminiscent of topological patterning, a pattern varying along the co-ordinate perpendicular/parallel to the direction of the applied electric field in electro-osmotic flow (or applied pressure gradient in pressure-driven flow) will be termed as longitudinal/transverse pattern.

The literature on the effect of slippage patterning can be classified into studies that do or do not address flow confinement. In the former category, free shear flow over a single patterned surface has been considered by Hocking (1976), Kamrin et al. (2010), Belyaev and Vinogradova (2010), Asmolov and Vinogradova (2012) and Asmolov et al. (2013a, b). Of these studies, Asmolov et al. (2013b) are of special relevance to the current work, since it deals with continuous rather than discontinuous patterns of wall slip. Electro-osmotic flow over a single surface is studied by Squires (2008), Belyaev and Vinogradova (2011) and Bahga et al. (2010).

Among studies that address effect of flow confinement, Philip (1972) considers alternating transverse stick-perfect slip zones on wall(s) of a plane channel as well as circular pipe in pressure-driven flow through techniques of conformal mapping. Stroock et al. (2002) addresses liquid-filled periodic roughness elements, which is actually the opposite of de-wetted topological features that may correspond to the patterned slip investigated in this study. Lauga and Stone (2003) solve the longitudinal analogue of Philips’ circular pipe problem through a dual series-based approach. Hendy et al. (2005) investigate pressure-driven flow, and Ghosh and Chakraborty (2012) investigate electro-osmotic flow through channels with transverse-patterned slip. Feuillebois et al. (2009, 2010) and Ng and Zhou (2012) address flow through thin channels with the help of the lubrication approximation, which can spectrally resolve only the long waves (compared to channel height) in the local flow response. Schmieschek et al. (2012) consider discontinuous longitudinal and transverse patterns of alternating partial-slip/no-slip stripes in a plane channel through a dual series-based semi-analytical approach as well as through direct simulations using the Lattice Boltzmann method.

It is noteworthy that with the exceptions of Asmolov et al. (2013a, b), Hendy et al. (2005), Feuillebois et al. (2009, 2010), Ng and Zhou (2012), Zhao and Yang (2012) and Ghosh and Chakraborty (2012), the studies in the literature have focussed specifically on discontinuous patterns of alternating stick–slip zones. However, as noted by Asmolov et al. (2013b), a continuous pattern of slip length variation has the advantage of smaller viscous dissipation which may lead to more flow per unit driving force in comparison with discontinuous patterns; or in other words, a larger effective slip length.

This study focuses attention on a continuous periodic pattern of slip length on the surface(s) and the effect of flow confinement on the effective slip length and the local flow. A periodic (cosine) distribution of slippage is chosen on the solid surfaces to serve as a spectral basis for more complex slip length distribution. The geometry chosen is a plane channel with dissimilar patterns of slippage on each wall; the periodic distribution of slip lengths on the walls differs by a phase angle. A nonzero phase angle can represent an experimental situation where misalignment exists between the patterned surfaces that constitute opposite walls. To the knowledge of the authors, the only other study which investigates the effect of phase difference with respect to slippage patterns is Ng and Zhou (2012) with a lubrication theory approach, though a similar phase lag parameter has an history with respect to studies on the effects of surface charge patterning in electro-osmotic flow (Ajdari 1996; Ng and Zhou 2012; Datta and Choudhary 2013). In this study, instead of the “slow variations” (van Dyke 1987) or lubrication theory approach (as adopted by Feuillebois et al. 2009, 2010; Ng and Zhou 2012), a “slight or small amplitude variations” approach in the spirit of the analysis of grooved wetted channels performed in Stroock et al. (2002) will be adopted. In addition to not being limited to long wave patterns, this approach has the potential advantage of being capable of representing both the effective slip length and the local flow field in terms of simple closed-form expressions containing parameters such as the average slip length, height of the channel, amplitude and period of the patterning. This advantage is not available (except in specialized limits) from alternative approaches that have been applied elsewhere to flow problems of patterned slippage such as Fourier expansion followed by numerical solution of either dual trigonometric series (Bahga et al. 2010; Belyaev and Vinogradova 2010; Schmieschek et al. 2012) or algebraic equation systems arising from point collocation (Ng and Chu 2011; Ng and Wang 2010) and of course, direct numerical solution of equations representing the governing phenomena (see, e.g. Zhou et al. 2012). However, numerical solution of the Navier–Stokes equations will be employed even in this study to ascertain the range of applicability of the small amplitude theory developed in the next section.

Examples of perturbative approaches towards patterned slippage of similar nature to this work, as applied to transverse (but not longitudinal) stripes, can be found in Hendy et al. (2005) for pressure-driven flow and Zhao and Yang (2012) for electro-osmotic flow; however, none of this perturbative approaches is carried to order high enough to reflect the difference between effective slip and average slip, though the “effective slip length” is not calculated explicitly. Asmolov et al. (2013a) employ a perturbative approach to study a free shear flow over a surface which has a slip length magnitude much smaller than the patterning wavelength. Ghosh and Chakraborty (2012) study transverse patterns in electro-osmotic flows with no phase difference between the walls; their analysis is consistent with effective slip differing from average slip. Since longitudinal stripes are expected to lead to higher degree of effective slippage (see, e.g. Belyaev and Vinogradova 2011) than transverse stripes, attention is focused in this study to longitudinal stripes.

In comparison with pressure-driven flow, electro-osmotic flow is considered to be more sensitive to the flow enhancing effect of slippage (Muller et al. 1986; Joly et al. 2006; Bocquet and Barrat 2007; Audry et al. 2010; Datta and Choudhary 2013) with the flow enhancement nearly independent of the channel characteristic dimension. Further, the electro-osmotic flow is more amenable to miniaturization in microfluidics because of its better scaling of the flow rate characteristics to the driving force than pressure-driven flow (Stone et al. 2004). Such factors have led to considerable attention in studies of slip in microfluidics to be devoted to electro-osmotic flows. In this study, a large part of the analysis in the next section is therefore devoted to the development of an asymptotic (a regular perturbation approach based) theory for periodic patterned slippage in electro-osmotic flow valid in the limit when the amplitude of the slip patterning is much smaller than the average slip on the surface. Later in the same section, the asymptotic results are generalized for application to any kind of steady incompressible flow that forms parallel streamlines outside the end-effect (or flow development) zones, be it pressure-driven, shear-driven, electro-osmotically driven or surface tension driven. The key results and numerical comparisons required for evaluating the performance of the asymptotic theory are reported in the section that follows the mathematical model development. Finally, salient conclusions are presented and the scope for future work is discussed.

2 Theoretical formulation

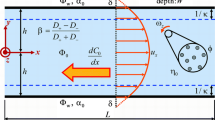
A rectangular micro-/nanochannel (Fig. 1) of height 2h and width 2W(≫2h) is considered in this study, on which the surface charge (σ) on the walls \((y = \pm h)\) is a constant. The channel wall surface is hydrophobic with hydrodynamic slip length b varying with the widthwise co-ordinate “x” given by the relation \(b(x) = b_{o} + a\cos (k_{s} x + \theta )\) for the top wall, and \(b(x) = b_{o} + a\cos (k_{s} x)\) for the bottom wall, thus taking a difference of phase angle θ between the slip waves on the two walls. The electric field is applied along the axial (z) direction. Under the effect of a constant applied electric field \((E\hat{k})\) along the z direction with unit vector \((\hat{k})\), the ions in the liquid are set into motion, leading to bulk motion of the liquid with viscosity μ and electrical permittivity ϵ. In general, a topological/chemical heterogeneity on the channel wall is anticipated to locally alter the wettability as well as the surface charge. Surface charge heterogeneities alone can have an effect on electro-osmotic flow fields (Ajdari 1996). However, in this study, attention will be focused to the interplay of confinement and heterogeneous wettability. So, the surface charge on each wall will be taken as spatially invariant.

Fig. 1
figure 1

Rectangular parallel plate micro-/nanochannel with constant surface charge density σ and patterned slip length b(x)

Full size image

In microfluidic applications, viscous forces on the liquid dominate over inertial forces, and as a result excluding entrance and exit zones, the flow arising from the patterning shown in Fig. 1 will have parallel streamlines, with a single nonzero velocity component V z . Since liquid flows are incompressible, V z should be independent of the co-ordinate z in order to satisfy conservation of mass. The following equations represent momentum conservation in z direction and the electrolyte-screened electrostatics in the channel.

$$\mu \nabla^{2} V_{z} + \rho E = 0$$
(1)
$${\text{Electrostatics:}}\,\rho = - \int {\frac{{{\text{d}}^{2} \phi }}{{{\text{d}}y^{2} }}dy}$$
(2)

In these equations, ρ is the net charge density due to the ions in the liquid, ϕ is the electrostatic potential due to the constant surface charge σ that governs the layering of ions in the electrolyte, and ∇ is the two-dimensional gradient operator in the x − y plane.

The following boundary conditions are appropriate for the channel walls.

$${\hbox{Liquid slip at channel's wall:}} \left( {V_{z} } \right)_{y = \pm h} = \mp b(x)\left( {\frac{{\partial V_{z} }}{\partial y}} \right)_{ \pm h}$$
(3)
$${\text{Wall surface charge:}}\,\left( {\frac{\partial \phi }{\partial y}} \right)_{ \pm h} = \pm \sigma$$
(4)

These equations can be cast into dimensionless forms by using the following rescaling scheme \(\bar{x} = (x/h);\bar{y} = (y/h);\bar{\phi } = (\phi /\zeta_{0} );\bar{V} = (V/V_{\text{HS}} )\). Here, V HS is Helmholtz–Smoluchowski velocity given by \(V_{\text{HS}} = - \smallint \zeta_{0} E/\mu\), where \(\zeta_{0}\) is the wall zeta potential. Note that given a surface charge density σ, \(\zeta_{0}\) can be calculated from the equations of screened electrostatics in the electrical double layer and vice versa. In terms of these dimensionless variables, Eqs. (1) and (2) can be combined to take the form

$$\nabla^{2} \bar{V}_{z} + \frac{{{\text{d}}^{2} \bar{\phi }}}{{{\text{d}}y^{2} }}\hat{e}_{z} = 0$$
(5)

The boundary conditions in terms of dimensionless variables become:

$$\left( {\bar{V}_{z} } \right)_{{\bar{y} = \pm 1}} = \mp \bar{b}(\bar{x})\left( {\frac{{\partial \bar{V}_{z} }}{{\partial \bar{y}}}} \right)_{{\bar{y} = \pm 1}}$$
(6)
$$\left( {\frac{{\partial \bar{\phi }}}{{\partial \bar{y}}}} \right)_{{\bar{y} = \pm 1}} = \pm \frac{\sigma h}{{\int {\zeta_{0} } }} = \frac{\sigma hE}{{\mu V_{HS} }} = \pm \kappa$$
(7)

The dimensionless slip length \(\bar{b}(\bar{x}) = b(x)/h\) has the forms \(b_{o} \{ 1 + \alpha \cos (\bar{k}_{s} \cdot \bar{x} + \theta )\}\) and \(b_{o} \{ 1 + \alpha \cos (\bar{k}_{s} .\bar{x})\},\) on the top and bottom walls, respectively. Here, b 0 and \(\alpha = a/b_{0}\) are the average slip length and the dimensionless amplitude of the pattern on either walls. Note that, to overrule the possibility of unphysical negative slippage, α ≤ 1 has to be imposed. The parameter on the right-hand side of Eq. (7) has been named κ. Interestingly, only in the limit of infinitely thin double layers and small electrostatic to thermal potential ratios of the ions, this notation can be reconciled with its more common usage in the literature to signify the “Debye–Huckel parameter” or the inverse of the dimensionless Debye length (H/λ).

It can be noted that with α = 0, slip length becomes constant, and with \(\alpha \ne 0\), slip length depends upon x. To understand its effect in more depth, α will be treated as a small perturbation parameter and \(\bar{V}_{{\bar{z}}}\) will be expanded in the asymptotic series:

$$\bar{V}_{{\bar{z}}} = \bar{V}_{{\bar{z}}}^{o} + \alpha \bar{V}_{{\bar{z}}}^{1} + \alpha^{2} \bar{V}_{{\bar{z}}}^{2} + O(\alpha^{3} )$$
(8)

Inserting this expansion in Eqs. (5)–(7), a sequence of problems arise for various orders of α.

2.1 Leading-order solution

At leading order, there is no dependence on x, so the momentum equation takes the form

$$\frac{{d^{2} }}{{d\bar{y}^{2} }}\left( {\bar{V}_{z}^{0} + \bar{\phi }} \right) = 0$$
(9)

Equation (9) is required to be solved subject to the following boundary conditions:

$$\left[ \begin{gathered} \left\{ {\bar{V}_{{\bar{z}}}^{o} } \right\}_{{\bar{y} = \pm 1}} = \mp \bar{b}_{o} \left( {\frac{{\partial \bar{V}_{{\bar{z}}}^{o} }}{{\partial \bar{y}}}} \right)_{{\bar{y} = \pm 1}} \hfill \\ \left( {\frac{{\partial \bar{\phi }}}{{\partial \bar{y}}}} \right)_{{\bar{y} = \pm 1}} = \pm \bar{\kappa } \hfill \\ \end{gathered} \right]$$
(10)

Solving Eqs. (9) and (10), the following expression is obtained for the velocity:

$$\bar{V}_{{_{{\bar{z}}} }}^{0} = \left\{ {1 - \bar{\phi } + \bar{b}_{o} \cdot \bar{\kappa }} \right\}$$
(11)

The function \(\bar{\phi }(y)\) describing the electrostatic potential distribution between two flat plates can be obtained through the solution of the Poisson–Boltzmann equation (Levine et al. 1975) and has an explicit but approximate form \(\bar{\phi }(\bar{y}) = \frac{{\cosh (\bar{\kappa }\bar{y})}}{{\sinh (\bar{\kappa })}}\) in the low electrostatic potential (Debye–Huckel) limit.

Integration of Eq. (9) over the channel cross-section reveals that the parameter \(\kappa = \pm \left( {\frac{{\partial \bar{\phi }}}{{\partial \bar{y}}}} \right)_{{\bar{y} = \pm 1}} = \mp \left( {\frac{{\partial \bar{V}_{Z}^{0} }}{{\partial \bar{y}}}} \right)_{{\bar{y} = \pm 1}}\) can also be interpreted as the magnitude of the dimensionless wall shear stress of a Newtonian fluid with slip length b 0. This observation will be referenced later in this study.

2.2 First-order solution

The governing equation is:

$$\left( {\frac{{\partial^{2} \bar{V}_{{\bar{z}}}^{1} }}{{\partial \bar{x}^{2} }} + \frac{{\partial^{2} \bar{V}_{{\bar{z}}}^{1} }}{{\partial \bar{y}^{2} }}} \right) = 0$$
(12)

Equation (12) is required to be solved subject to the following boundary conditions.

$$\left[ \begin{gathered} \left\{ {\bar{V}_{{\bar{z}}}^{1} + \bar{b}_{o} \left( {\frac{{\partial \bar{V}_{{\bar{z}}}^{1} }}{{\partial \bar{y}}}} \right)} \right\}_{{\bar{y} = 1}} = - \bar{b}_{o} \cos (\bar{k}_{s} .\bar{x} + \theta )\left( {\frac{{\partial \bar{V}_{{\bar{z}}}^{o} }}{{\partial \bar{y}}}} \right)_{{\bar{y} = 1}} \hfill \\ \left\{ {\bar{V}_{{\bar{z}}}^{1} - \bar{b}_{o} \left( {\frac{{\partial \bar{V}_{{\bar{z}}}^{1} }}{{\partial \bar{y}}}} \right)} \right\}_{{\bar{y} = - 1}} = \bar{b}_{o} \cos (\bar{k}_{s} .\bar{x})\left( {\frac{{\partial \bar{V}_{{\bar{z}}}^{o} }}{{\partial \bar{y}}}} \right)_{{\bar{y} = - 1}} \hfill \\ \end{gathered} \right]$$
(13)

Noticing the slip boundary condition for the first-order velocity, \(\bar{V}_{{\bar{z}}}^{1} = \cos (\bar{k}_{s} .\bar{x})\bar{f}(\bar{y}) + \sin (\bar{k}_{s} .\bar{x})\bar{g}(\bar{y})\) is taken as the trial solution of Eq. (12). Substitution of the assumed solution in Eqs. (12) and (13) followed by separation of variables and solution of the corresponding boundary value problem results in

$$\left\{ \begin{gathered} \bar{f}(\bar{y}) = B_{1} \cosh (\bar{k}_{s} .\bar{y}) + B_{2} \sinh (\bar{k}_{s} .\bar{y}) \hfill \\ \bar{g}(\bar{y}) = B_{3} \cosh (\bar{k}_{s} .\bar{y}) + B_{4} \sinh (\bar{k}_{s} .\bar{y}) \hfill \\ \end{gathered} \right\}$$
(14)

with the following values for the constants appearing in the right-hand side of Eq. (14):

$$\left[ \begin{gathered} B_{1} = \frac{{\bar{b}_{0} \cdot \bar{\kappa }(1 + \cos \theta )}}{{2\left\{ {\cosh (\bar{k}_{s} ) + \bar{b}_{0} \cdot \bar{k}_{s} \sinh (\bar{k}_{s} )} \right\}}};B_{2} = - \frac{{\bar{b}_{0} \cdot \bar{\kappa }(1 - \cos \theta )}}{{2\left\{ {\sinh (\bar{k}_{s} ) + \bar{b}_{0} \cdot \bar{k}_{s} \cosh (\bar{k}_{s} )} \right\}}} \hfill \\ B_{3} = - \frac{{\bar{b}_{0} \cdot \bar{\kappa }\sin \theta }}{{2\left\{ {\cosh (\bar{k}_{s} ) + \bar{b}_{0} \cdot k_{s} \sinh (\bar{k}_{s} )} \right\}}};B_{4} = - \frac{{\bar{b}_{0} \cdot \bar{\kappa }\sin \theta }}{{2\left\{ {\sinh (\bar{k}_{s} ) + \bar{b}_{0} \cdot \bar{k}_{s} \cosh (\bar{k}_{s} )} \right\}}} \hfill \\ \end{gathered} \right]$$
(15)

2.3 Second-order solution

The governing equation is:

$$\left( {\frac{{\partial^{2} \bar{V}_{{\bar{z}}}^{2} }}{{\partial \bar{x}^{2} }} + \frac{{\partial^{2} \bar{V}_{{\bar{z}}}^{2} }}{{\partial \bar{y}^{2} }}} \right) = 0$$
(16)

Equation (16) is required to be solved subject to the following boundary conditions.

$$\left[ \begin{gathered} \left\{ {\bar{V}_{{\bar{z}}}^{2} + \bar{b}_{o} \left( {\frac{{\partial \bar{V}_{{\bar{z}}}^{2} }}{{\partial \bar{y}}}} \right)} \right\}_{{\bar{y} = 1}} = - \bar{b}_{o} \cos (\bar{k}_{s} .\bar{x} + \theta )\left( {\frac{{\partial \bar{V}_{{\bar{z}}}^{1} }}{{\partial \bar{y}}}} \right)_{{\bar{y} = 1}} \hfill \\ \left\{ {\bar{V}_{{\bar{z}}}^{2} - \bar{b}_{o} \left( {\frac{{\partial \bar{V}_{{\bar{z}}}^{2} }}{{\partial \bar{y}}}} \right)} \right\}_{{\bar{y} = - 1}} = \bar{b}_{o} \cos (\bar{k}_{s} .\bar{x})\left( {\frac{{\partial \bar{V}_{{\bar{z}}}^{1} }}{{\partial \bar{y}}}} \right)_{{\bar{y} = - 1}} \hfill \\ \end{gathered} \right]$$
(17)

Noticing the form of the slip boundary condition given by Eq. (17), \(\bar{V}_{{\bar{z}}}^{2} = c_{o} + \cos (2\bar{k}_{s} \cdot \bar{x})\bar{F}(\bar{y}) + \sin (2\bar{k}_{s} \cdot \bar{x})\bar{G}(\bar{y})\) is taken as the trial solution of Eq. (16). Substitution of the assumed solution in Eqs. (16) and (17) followed by separation of variables and solution of the corresponding boundary value problem results in

$$\left\{ \begin{gathered} \bar{F}(\bar{y}) = c_{1} \cosh (2\bar{k}_{s} \cdot \bar{y}) + c_{2} \sinh (2\bar{k}_{s} \cdot \bar{y}) \hfill \\ \bar{G}(\bar{y}) = c_{3} \cosh (2\bar{k}_{s} \cdot \bar{y}) + c_{4} \sinh (2\bar{k}_{s} \cdot \bar{y}) \hfill \\ \end{gathered} \right\}$$
(18)

with the following value for the constants:

$$c_{o} = - \frac{{(\bar{b}_{0} )^{2} \cdot \bar{\kappa } \cdot \bar{k}_{s} }}{2}\left[ {\frac{{\sinh (\bar{k}_{s} )(1 + \cos \theta )}}{{2\left\{ {\cosh (\bar{k}_{s} ) + \bar{b}_{0} \cdot \bar{k}_{s} \sinh (\bar{k}_{s} )} \right\}}} + \frac{{\cosh (\bar{k}_{s} )(1 - \cos \theta )}}{{2\left\{ {\sinh (\bar{k}_{s} ) + \bar{b}_{0} \cdot \bar{k}_{s} \cosh (\bar{k}_{s} )} \right\}}}} \right]$$
(19a)
$$c_{1} = - \frac{{(\bar{b}_{0} )^{2} \cdot \bar{\kappa } \cdot \bar{k}_{s} }}{{8\left\{ {\cosh (2\bar{k}_{s} ) + 2\bar{b}_{0} \cdot \bar{k}_{s} \sinh (2\bar{k}_{s} )} \right\}}}\left[ {\frac{{\sinh (\bar{k}_{s} )(1 + \cos 2\theta + 2\cos \theta )}}{{\left\{ {\cosh (\bar{k}_{s} ) + \bar{b}_{0} \cdot \bar{k}_{s} \sinh (\bar{k}_{s} )} \right\}}} + \frac{{\cosh (\bar{k}_{s} )(1 + \cos 2\theta - 2\cos \theta )}}{{\left\{ {\sinh (\bar{k}_{s} ) + \bar{b}_{0} \cdot \bar{k}_{s} \cosh (\bar{k}_{s} )} \right\}}}} \right]$$
(19b)
$$c_{2} = \frac{{(\bar{b}_{0} )^{2} \cdot \bar{\kappa } \cdot \bar{k}_{s} (1 - \cos 2\theta )}}{{8\left\{ {\sinh (2\bar{k}_{s} ) + 2\bar{b}_{0} \cdot \bar{k}_{s} \cosh (2\bar{k}_{s} )} \right\}}}\left[ {\frac{{\sinh (\bar{k}_{s} )}}{{\left\{ {\cosh (\bar{k}_{s} ) + \bar{b}_{0} \cdot \bar{k}_{s} \sinh (\bar{k}_{s} )} \right\}}} + \frac{{\cosh (\bar{k}_{s} )}}{{\left\{ {\sinh (\bar{k}_{s} ) + \bar{b}_{0} \cdot \bar{k}_{s} \cosh (\bar{k}_{s} )} \right\}}}} \right]$$
(19c)
$$c_{3} = \frac{{(\bar{b}_{0} )^{2} .\bar{\kappa }.\bar{k}_{s} }}{{8\left\{ {\cosh (2\bar{k}_{s} ) + 2\bar{b}_{0} .\bar{k}_{s} \sinh (2\bar{k}_{s} )} \right\}}}\left[ {\frac{{\sinh (\bar{k}_{s} )(\sin 2\theta + 2\sin \theta )}}{{\left\{ {\cosh (\bar{k}_{s} ) + \bar{b}_{0} .\bar{k}_{s} \sinh (\bar{k}_{s} )} \right\}}} + \frac{{\cosh (\bar{k}_{s} )(\sin 2\theta - 2\sin \theta )}}{{\left\{ {\sinh (\bar{k}_{s} ) + \bar{b}_{0} .\bar{k}_{s} \cosh (\bar{k}_{s} )} \right\}}}} \right]$$
(19d)
$$c_{4} = \frac{{(\bar{b}_{0} )^{2} \cdot \bar{\kappa } \cdot \bar{k}_{s} \sin 2\theta }}{{8\left\{ {\sinh (2\bar{k}_{s} ) + 2\bar{b}_{0} \cdot \bar{k}_{s} \cosh (2\bar{k}_{s} )} \right\}}}\left[ {\frac{{\sinh (\bar{k}_{s} )}}{{\left\{ {\cosh (\bar{k}_{s} ) + \bar{b}_{0} \cdot \bar{k}_{s} \sinh (\bar{k}_{s} )} \right\}}} + \frac{{\cosh (\bar{k}_{s} )}}{{\left\{ {\sinh (\bar{k}_{s} ) + \bar{b}_{0} \cdot \bar{k}_{s} \cosh (\bar{k}_{s} )} \right\}}}} \right]$$
(19e)

2.4 Effective slip length

The dimensionless volume flow rate (\(Q\)) can be calculated by integrating \(V_{z} = V_{\bar{z}}^{0} + \alpha V_{\bar{z}}^{1} + \alpha^{2} V_{\bar{z}}^{2}\) over the periodic cell \(( - 1 \le y \le 1) \cup ( - \pi \le x \le \pi):\)

$$\bar{Q} = \frac{4\pi }{{k_{s} }}(V_{ns} + \bar{b}_{\text{eff}} \kappa )$$
(20)
$$\bar{b}_{\text{eff}} = \bar{b}_{o} - \alpha^{2} \frac{{\bar{b}_{0}^{2} \bar{k}_{s} }}{2}\left[ {\frac{{\sinh (\bar{k}_{s} )(1 + \cos \theta )}}{{2\left\{ {\cosh (\bar{k}_{s} ) + \bar{b}_{0} \cdot \bar{k}_{s} \sinh (\bar{k}_{s} )} \right\}}} + \frac{{\cosh (\bar{k}_{s} )(1 - \cos \theta )}}{{2\left\{ {\sinh (\bar{k}_{s} ) + \bar{b}_{0} \cdot \bar{k}_{s} \cosh (\bar{k}_{s} )} \right\}}}} \right]$$
(21)

Here, \(V_{ns} = 1 - \bar{\phi }_{av}\) is the depth-averaged value of the fully developed axial velocity in the same channel, had its walls been non-slipping (ns). Here, \(\bar{\phi }_{av}\) denotes the depth-averaged value of electrostatic potential \((\bar{\phi }(y))\). Equation (20) serves as a definition for a quantity called effective slip length \((\bar{b}_{\text{eff}} )\). This definition is very useful for internal flows (see also Lauga and Stone 2003) and relies on the analogy with the case of un-patterned slip (α = 0), in which case \(Q_{\alpha = 0} = \bar{Q} = \frac{4\pi }{{k_{s} }}(V_{ns} + b\kappa )\) (see for example, Muller et al. 1986; Datta and Choudhary 2013), as can be verified also by integration of Eq. (11). Another equivalent way (Squires 2008) to calculate the effective slip length, which leads to the same expression as Eq. (21), is through the expression \(\langle \left. V \right|_{y = \pm 1} \rangle = \mp \bar{b}_{eff} \langle \left. {\frac{\partial V}{\partial y}} \right|_{y = \pm 1} \rangle\),Footnote 1 where the angular brackets denote an average over one wavelength of the pattern. It is clear from Eq. (21) that flow rate enhancement due to patterned slip is less than that due to un-patterned slip. This can be attributed to the action of friction (viscosity) when the patterning of slip lengths causes the layers of liquid contacting on the y − z planes (Fig. 1) to slide against each other.

The analysis shown here can be replicated for a fully developed flow driven by a pressure differential ΔP in an uncharged channel with patterned walls. In this case, it is convenient to non-dimensionalize velocity by the scale \(\frac{{\Delta Ph^{2} }}{\mu L}\), rather than the velocity scale used before, giving a flow profile \(V_{p}^{{}} (x,y)\). Here, the zeroth-order problem will be different being governed by the balance of viscous force with the pressure-gradient force and will give rise to a wall shear stress \(\frac{{\partial V_{p}^{0} }}{\partial y}\hat{ \cup }_{y = \pm 1} = \mp 1\), rather than \(\frac{{\partial \bar{V}_{0}^{z} }}{\partial y}\hat{ \cup }_{y = \pm 1} = \mp \kappa\) as in the case of electro-osmotic flow [refer to the discussion under Eq. (7)]. The problem for the first- and second-order velocities will be same as in Eqs. (12), (13) and Eqs. (16), (17). Consequently, the first- and second-order velocities will have the same expressions as above, except for the absence of a multiplicative factor κ.

Interestingly, the expression for \(\bar{b}_{\text{eff}}\) in pressure-driven flow, as given by \(\langle \left. V \right|_{y = \pm 1} \rangle = \mp \bar{b}_{eff} \langle \left. {\frac{\partial V}{\partial y}} \right|_{y = \pm 1} \rangle\) or by the expression \(\bar{Q} = \frac{4\pi }{{k_{s} }}(V_{ns} + \bar{b}_{eff} )\) (Lauga and Stone 2003) in analogy with the uniformly slipping flow, is given by the same function as in Eq. (21). However, this conclusion is more general in the sense that it is true regardless of the amplitude α of the slippage pattern. This can be reasoned as follows. It can be noted Eq. (20) applies also to pressure-driven flow, since here \(\frac{{\partial V_{p}^{0} }}{\partial y}\hat{ \cup }_{y = \pm 1} = \mp 1 = \mp \kappa\). Further, since the right-hand side of the first equation in Eq. (10) is a constant, Eq. (20) will hold even if Eq. (9) is replaced by a linear boundary value problem in y co-ordinate characteristic of a general fully developed flow pattern.

Let \(\bar{V}_{\bar{z},\langle b(x)\rangle }\) denote the flow field that would exist in the channel had there been a uniform slip equal to the average slip \(\left\langle {b(x)} \right\rangle\) over the pattern. It can be noted that \(\bar{V}_{\bar{z},\langle b(x)\rangle } = \bar{V}_{z}^{0}\) in this study. Regardless of the amplitude of the slippage pattern, the “defect flow field” \(V^{\prime } = \bar{V}_{\bar{z}} - \bar{V}_{\bar{z},\langle b(x)\rangle }\), in either a pressure-driven flow with pressure differential ΔP or an electro-osmotic problem, is governed by the same equations, provided κ in any of the previous results is interpreted as the magnitude of the corresponding dimensionless wall shear stress \(\Delta Ph^{2} /(\mu LV_{HS} )\). In this context, the observation on interpretation of κ in the paragraph after Eq. (11) may also be referred to. These equations are:

$$\left( {\frac{{\partial^{2} V^{\prime }}}{{\partial \bar{x}^{2} }} + \frac{{\partial^{2} V^{\prime }}}{{\partial \bar{y}^{2} }}} \right) = 0$$
(22)
$$\left[ \begin{gathered} \left\{ {V^{\prime } + \bar{b}(x)\left( {\frac{{\partial V^{\prime } }}{{\partial \bar{y}}}} \right)} \right\}_{{\bar{y} = 1}} = - \left( {\bar{b}(x) - \langle \bar{b}(x)\rangle } \right)\left( {\frac{{\partial \bar{V}_{\bar{z},\langle b(x)\rangle } }}{{\partial \bar{y}}}} \right)_{{\bar{y} = 1}} \hfill \\ \left\{ {V^{\prime } - \bar{b}(x)\left( {\frac{{\partial V^{\prime } }}{{\partial \bar{y}}}} \right)} \right\}_{{\bar{y} = - 1}} = \left( {\bar{b}(x) - \langle \bar{b}(x)\rangle } \right)\left( {\frac{{\partial \bar{V}_{\bar{z},\langle b(x)\rangle } }}{{\partial \bar{y}}}} \right)_{{\bar{y} = - 1}} \hfill \\ \end{gathered} \right]$$
(23)

The driving force of the flow enters the problem only indirectly through the dimensionless wall shear stress \(\left( {\frac{{\partial \bar{V}_{\bar{z},\langle b(x)\rangle } }}{{\partial \bar{y}}}} \right)_{{\bar{y} = \pm 1}} = \mp \kappa\) on the right-hand side of Eq. (23). If flows with different driving forces are made to maintain the same dimensionless wall shear stress κ, the resultant \(V^{{\prime }}\) field will be same. Consequently, the effective slip length given by \(b_{0} + V_{\text{av}}^{{\prime }} /\kappa\) (where the subscript “av” denotes depth averaging) will be the same. Note that Eq. (23) is merely another form of the slip boundary condition given by Eq. (6), obtained by the substitution \(V^{\prime} = \bar{V}_{\bar{z}} - \bar{V}_{\bar{z},\langle b(x)\rangle }\). Its similarity in form with of Eqs. (13) and (17) can also be noted. The observation that \(\bar{b}_{\text{eff}}\) is same for an electro-osmotic flow with constant charge and a pressure-driven flow is also in consonance with the conclusions of Squires (2008), arising out of considerations based on the Lorentz reciprocity theorem. As a consequence of the linearity of the problem, Eq. (21) will also remain same for a flow driven by a combination of external pressure and voltage differentials. Further, based on the discussion above, Eq. (21) can be argued to hold true for any steady incompressible fully developed flow pattern in the plane channel geometry, with κ designating the dimensionless wall shear stress. It can also be noted that the factor 1/κ (which also equals the Debye length for weak electrostatic potentials) does not affect the effective slip length of uniformly charged channels even in electro-osmotic flow, or in other words, from Eq. (20), the effect of slip on electro-osmotic flow rate is fully governed by the ratio of effective slip length given by Eq. (21) to the Debye length. If the surface charge is patterned, the literature for electro-osmotic flow near a single surface (Bahga et al. 2010) points towards an effect of the Debye length on the effective slip length.

Given that the ratio of the average slip length (b 0) to the wavelength \(\lambda = 2\pi /k_{s}\) of the pattern is an intrinsic quality of the prepared patterned surface, and to facilitate understanding of the effect of channel size, it is convenient to re-express Eq. (21) in terms of dimensional variables in the following manner.

$$\frac{{b_{\text{eff}} }}{{b_{0} }} = 1 - \alpha^{2} \frac{{\frac{{2\pi b_{0} }}{\lambda }}}{2}\left[ {\frac{{\sinh \left( {\frac{2\pi h}{\lambda }} \right)(1 + \cos \theta )}}{{2\left\{ {\cosh \left( {\frac{2\pi h}{\lambda }} \right) + \frac{{2\pi b_{0} }}{\lambda }\sinh \left( {\frac{2\pi h}{\lambda }} \right)} \right\}}} + \frac{{\cosh \left( {\frac{2\pi h}{\lambda }} \right)(1 - \cos \theta )}}{{2\left\{ {\sinh \left( {\frac{2\pi h}{\lambda }} \right) + \frac{{2\pi b_{0} }}{\lambda }\cosh \left( {\frac{2\pi h}{\lambda }} \right)} \right\}}}} \right]$$
(24)

In the limit of channel size much larger than wavelength \((\frac{{h_{s} }}{\lambda } \to \infty )\), Eq. (23) takes the θ − independent form

$$b_{\text{eff}} /b_{0} = 1 - \alpha^{2} \frac{{2\pi b_{0} /\lambda }}{{2(1 + 2\pi b_{0} /\lambda )}}$$
(25)

Further, if the average slip length is also much larger than the pattern wavelength, then this expression simplifies to b eff/b 0 = 1 − α 2/2, which, expectedly, is the low α limit of Eq. (28) of Asmolov et al. (2013b). The referred equation of Asmolov et al. (2013b) provides in a different notation, an expression valid in the limit \(2\pi b_{0} /\lambda \to \infty\) for b eff in a shear flow over a single surface with the same periodic slippage pattern as in the current study (but for any value of α less than unity), obtained through a dual trigonometric series-based formulation of the problem.

3 Results and discussion

In this section, local results pertaining to the flow field calculated with the help of Eqs. (15) and (19), and the global effective slip length calculated by Eq. (21) will be shown. However, the asymptotic results of the previous section are subject to the assumption that α be “small enough” (see for example Murdock 1987), but provide no information on “how small” α need to be for the theory to be useful. Comparison with an alternative approach that does not formally depend on α being “small enough” is necessary. For this purpose, in this study, numerical solution of the defect velocity field V′ governed by Eqs. (22) and (23) has been performed. The simulations have been performed using the “Partial Differential Equations Module” of the finite-element method-based software COMSOL Multiphysics® on a uniform rectangular finite-element grid. To ensure that the numerical results are accurate, grid independence was checked. For example, seven decimal-place agreement was found between the flow rate through a periodic cell (obtained via fourth order quadrature) calculated using the grid size to be used in the subsequent results and a grid coarsened twofold for α = 0.3, θ = π, \(\bar{b}_{0} = 1\), \(\bar{k}_{s} = 3\).

The total velocity can be considered a synthesis of an x independent part which contributes to the overall flow \(\bar{V}_{\text{mean}} = \bar{V}^{0}_{\bar{z}} + \alpha^{2} c_{0}\) and a secondary part which does not contribute to net flow, viz. \(\bar{V}_{\text{secondary}} = \alpha \overline{{V^1_{\bar{z}} }} + \alpha^{2} \left( {\bar{V}^2_{\bar{z}} - c_{0} } \right).\) Figure 2 shows the contours of this secondary velocity calculated by the asymptotic theory when the slip length patterns on the two walls are in phase, e.g. \(\bar{k}_{s} = 1,\:\alpha = 0.1,\:\kappa = 3\).

Fig. 2
figure 2

Contours of the theoretically calculated secondary velocity \(\left[ {\alpha \overline{{V_{1} }} + \alpha^{2} \left( {\bar{V}_{2} - c_{0} } \right)} \right]\) for \(\bar{k}_{s} = 1,\) \(\alpha = 0.1\), \(\bar{b}_{0} = 1,\) \(\theta = 0\), \(\bar{\kappa } = 3\)

Full size image

Figure 3 shows the effective slip length versus the amplitude of wall slip waves calculated using Eq. (21) at a given wavenumber \(\overline{{k_{s} }} = 1\) for the two cases of wall patterns perfectly in phase (θ = 0) and perfectly out of phase (θ = π) and compares the same with numerical results. The decreasing trend of effective slip with amplitude indicates that there is less slippage in a patterned channel compared to an un-patterned channel of the same x-averaged slip length. This can be attributed to the action of additional viscous stresses (τ xz ) created due to the transverse patterning. Further, the slippage decreases at a progressively faster rate as the pattern amplitude is increased. Slip length is smaller when the patterns are out of phase (θ = π). This can be attributed to the dissimilarity in slip length between the top and bottom walls that exists in the x–y plane for θ = π, which engenders additional viscous stresses (τ xy ) compared to the θ = 0 case. The perturbation theory solution overpredicts the slip length, but only with a very slight error of 1.6 % or lower between the asymptotic and numerical solutions. As expected for an asymptotic theory, this error (not shown) for the case studied in Fig. 3 rose monotonically with α for a given θ and was largest (1.6 %) for the largest α, namely α = 0.8 for the θ = π case.

Fig. 3
figure 3

Effective slip length versus pattern amplitude α calculated using Eq. (21) compared with numerical results (symbols) for \(\theta = [0,\pi ]\), \(\bar{k}_{s} = 1\) and \(\bar{b}_{0} = 1\)

Full size image

The top pane of Fig. 4 shows that the effective slip length decreases with increasing wavenumber of the pattern for various phase angles and α = 0.3. This is because a short-wavelength (high wavenumber) pattern engenders more viscous stresses than a long-wavelength pattern. However, the effect of phase difference between the top and bottom walls is more pronounced at lower wavenumbers being maximum for an un-patterned channel. At high wavenumbers, the dissimilarity between the walls in terms of phase lead/lag has much less effect, as seen from the numerical results (symbols) as well as the asymptotic results; see also Eq. (25). This means that the effect of misalignment of the wall patterns can be rectified by choosing smaller pattern wavenumbers, which, however, compromise on the effective slip and, hence, the net flow rate. The asymptotic results are in good agreement with the numerical results. There is a trend of increasing (but small) deterioration in the agreement as the wavenumber increases; the maximum overprediction for α = 0.3 of only 0.073 % occurs at the highest wavenumber studied \((\bar{k}_{s} = 2\pi ,\theta = \pi )\). This is expected, since the asymptotically predicted α-dependent patterning effect correction [second term of Eq. (21)] is an increasing function of wavenumber, as also corroborated numerically. The bottom pane of Fig. 4 considers α = 0.6 a dimensionless amplitude, which may be considered to be not “small enough” for the formal validity of the asymptotic theory. Expectedly, the quality of agreement deteriorates in comparison with the top pane (α = 0.3), with the deterioration being more evident at large wave numbers. Even then, the largest disagreement between the numerical and asymptotic prediction calculable from this figure is about 1.6 %. By observing the curve slopes in Fig. 4, it can be concluded that the effective slip length is more sensitive to changes in wavenumber at intermediate wave numbers than at either small or large wavenumbers.

Fig. 4
figure 4

Effective slip length versus pattern wave number for various phase-angle differences between the top and bottom patterns. Here, \(\bar{b}_{0} = 1.\) The top and bottom panes are for α = 0.3 and α = 0.6. The solid lines are obtained using Eq. (21). Symbols denote results from numerical simulations

Full size image

In addition to the predicted flow rates (or effective slip lengths), good agreement between numerical and asymptotic predictions of the local velocity fields was also observed. As per expectations, this agreement deteriorated with increasing patterning amplitude (α) and increasing wavenumber \((\bar{k}_{s} )\). As an example, the four panes of Fig. 5 explore different \(\bar{k}_{s}\) and α combinations and compare the cross-channel velocity variation at x = 0 predicted by the asymptotic theory to that predicted numerically for α = 0.3, for the two cases of the top and bottom wall patterns being perfectly in phase and out of phase. From the pane combinations 1–3 and 2–4 of Fig. 5, it can be observed larger the pattern wave number, larger are the local flow velocity disturbances created by patterning. It should be noted that the accuracy of asymptotic predictions of local velocity is somewhat inferior to the corresponding global predictions of effective slip length, still being of the order of 6 % or less in Fig. 5.

Fig. 5
figure 5

Cross-channel variation of defect velocity \(\bar{V}_{\bar{z}} - \bar{V}_{\bar{z},\langle b(x)\rangle }\) at x = 0 for symmetrically (solid lines) and anti-symmetrically (dashed lines) patterned walls (\(\theta = [0,\pi ]\)). Here, \(\bar{b}_{0} = 1\) and κ = 1. The four panes show the effect of different values of the parameters \(\bar{k}_{s}\) and α. The solid lines are obtained using Eqs. (15) and (19). Symbols denote results from numerical simulations

Full size image

The top and bottom panes of Fig. 6 show the effect of channel size on the ratio of effective slip to average slip for dimensionless pattern amplitude of α = 0.3 and α = 0.6, respectively. With increasing channel size, the effective slip length decreases for every value of slip length to pattern wavelength ratio. For α = 0.3, the asymptotic prediction of Eq. (25) agrees quite well with numerical predictions with a trend of slight deterioration in agreement with increase in channel size and decrease in the pattern wavelength. Expectedly, the deviation from numerical predictions is worse (still of the order of 2 % or less) in the bottom pane, which is for a larger amplitude (α = 0.6) outside the formal limits of validity of the asymptotic theory in this study. In small enough channels, the effective slip is nearly equal to the average slip, which can be expected on the ground that stresses \(\tau_{xz}\) become much less significant than the stresses τ yz , which dominate viscous dissipation in that limit. b 0 The large channel limit theoretically given by Eq. (25) in the previous section is reached fairly fast. In fact, Fig. 6 reveals that the prediction of this equation is accurate (and quantitatively consistent with the shear flow results of Asmolov et al. 2013b) even for a channel size 2 h which just about equals the pattern wavelength λ. The curves on each pane of Fig. 6 also show that larger the ratio b 0/λ of average slip length to wavelength, lower is the b eff/b 0 value at each channel height as well as the saturation level that is reached for large channel sizes. The latter behaviour has also been predicted for free shear flow in Asmolov et al. (2013b). So, Fig. 6 suggests confinement and slowly varying patterns are both desirable, if the objective is to increase apparent slip.

Fig. 6
figure 6

The effect of channel height on the effective slip to average slip ratio for different values of slip length to wavelength ratio. Here, θ = 0. The solid lines are obtained using Eq. (24). Symbols denote numerical results

Full size image

4 Conclusions

The flow field and effective slip length of liquid flows through thin channels with widthwise sinusoidal patterning of wall wettability have been calculated through an asymptotic theory and compared with numerical results. In the context of the literature dealing with modelling of continuous wall slippage patterns, the numerically validated asymptotic theory developed in this work describes a regime that connects the limiting situations of thin channels addressed in Feuillebois et al. (2009) and thick channels (free shear flow) addressed in Asmolov et al. (2013b). The local velocities and effective slip due to arbitrary values of pattern-averaged slip length to pattern period ratios are also analytically tractable, complementing and reducing to asymptotic forms available in Asmolov et al. (2013b). Although the analytical development in this study uses electro-osmotic flow as a starting point, arguments have been presented to generalize the result for other types of flow. Equation (21), for the effective slip length, the main result of this work, is valid for both electro-osmotic and pressure-driven flows, and in general for any flow field, which, under uniform and identical slip on the walls, develops fully into a profile with only depthwise variation. Further, it is shown that in such flows, effective slip of the channel is fully determined by the wall stress that develops under uniform slip even if the small amplitude assumption used to obtain analytical expressions is relaxed.

The effective slip length (and hence, the hydraulic permeability) of a channel with sinusoidally slip-patterned walls is always smaller than that of an un-patterned channel with the same average slip length indicating the role of viscous stresses set forth by the patterning. The effective slip length decreases with patterning amplitude as well as the patterning spatial frequency. For a channel of given size, mismatch between the wall patterns in terms of a phase difference lowers the channel permeability. This effect can be made to disappear by using a sufficiently small pattern wavelength, which will, however, lower the permeability. The effect of phase mismatch also decreases with increasing separation between the microchannel walls. Confinement favours a larger degree of slippage, with the effective slip approaching the average of local slip on either walls, for narrow channels with matched wall patterns (see also Feuillebois et al. 2010). The decrease of effective slip with channel size flattens to asymptotic values consistent with Asmolov et al. (2013b) as channel size increases. The hydraulic permeability of a channel is more sensitive to changes in wavenumber at intermediate wave numbers than at either small or large wavenumbers. Larger the average slip length of the wall pattern, more depressed is the effective slip length of a channel, as measured in units of the average slip length. Larger the pattern wave number, larger are the local flow velocity disturbances created by patterning.

Although the formal requirement for any asymptotic theory is that the dimensionless pattern amplitude parameter α “approach zero”, agreement with numerical predictions to good quantitative accuracy is observed for the effective slip length as well as local velocity profiles even for moderate values of α. For example, with α = 0.6, \(\bar{k}_{s} = 2\pi\), θ = π (Fig. 4, bottom pane), when the effective slip is about 18 % lower than the average slip, the error in the dimensionless effective slip length relative to numerical predictions is of the order of 1.6 %. The relative error between the asymptotic and computed effective slip increased with amplitude (α) and wavenumber \((\bar{k}_{s} )\), consistent with the relative significance of friction in the planes aligned with the stripes. For a given value of amplitude, the large wavenumber behaviour of this error was one of progressively decreasing slope, suggesting uniform validity of Eq. (21) in \(\bar{k}_{s}\) space. The asymptotic theory slightly overpredicts the numerical prediction of effective slip length. The accuracy of the theory has a slight trend of decline with the degree of phase mismatch. The local values of velocity are predicted with a slightly lower accuracy than the effective slip length.

The results concerning electro-osmotic flow (but not pressure-driven flow) need to be generalized in the future to account for surface charge variation. This is anticipated to give the Debye layer thickness a more significant role than seen in the current work. In addition, the case of channel with transverse stripes can be studied which enable determination of the entire slip length tensor (Kamrin et al. 2010; Asmolov and Vinogradova 2012). Finally, it may be useful in the future to remove the assumption of “small α” for the current problem through a semi-analytical rather than grid-based numerical approach, as has been done, for example, in the corresponding free shear flow problem (Asmolov et al. 2013b).