Introduction

High-frame-rate ultrasound, which was introduced to ultrasound imaging in the 1980s [1], was used as the first practical application for visualization of shear wave propagation in tissue [2]. It was followed by cardiovascular applications for measurement of tissue dynamics [3–10].

The use of unfocused transmit beams, such as plane and diverging waves, and parallel receive beamforming enables the creation of scan lines, which are required to construct an ultrasound image, with a much smaller number of transmissions. On the other hand, lateral spatial resolution is degraded due to the low directivity of the transmit beam. The lateral spatial resolution can be improved by coherent compounding of multiple steered beams [11–14], but the coherent compounding requires multiple transmissions, resulting in the degradation of the imaging frame rate, i.e., temporal resolution. Therefore, it is preferable to improve the lateral spatial resolution without an increase in the number of transmissions.

There have been various studies on improvement of the spatial resolution of ultrasonic imaging, such as coherence-based imaging [15–17] and minimum variance beamforming [18–21]. In minimum variance beamforming, the spatial covariance matrix, which is obtained from echoes received by individual transducer elements, is required to determine the adaptive weights used in the beamforming procedure. To ensure the performance of the adaptive beamformer, the desired signal, i.e., the echo from the receiving focal point, contained in the spatial covariance matrix should be suppressed. In the conventional minimum variance beamforming, the desired signal is suppressed by sub-array averaging [19]. Blomberg et al. proposed the amplitude and phase estimation (APES) beamformer [22], which estimates the desired signal based on the conventional delay-and-sum (DAS) beamforming, and removed it from the covariance matrix. However, their method still requires sub-array averaging, because the directivity of each transducer element is not considered, and the desired signal in the spatial covariance matrix cannot be suppressed sufficiently. In our previous study, a modified APES beamformer was developed to remove the desired signal contained in the spatial covariance matrix more accurately by considering the directivity of each transducer element [23]. As a result, the computational complexity could be reduced by excluding sub-array averaging. Furthermore, our method was combined with sub-aperture beamforming, and the computational complexity was significantly lowered by reducing the dimension of the spatial covariance matrix. In addition, it was shown that the penetration of the modified APES beamformer could be controlled easily by diagonal loading at the expense of the spatial resolution [24].

In minimum variance beamforming including APES beamforming, it is important to obtain a statistically stable estimate of a spatial covariance matrix, which is obtained from ultrasonic echoes received by individual transducer elements. For such a purpose, a conventional minimum variance beamformer utilizes sub-array averaging [19], but it increases the computational complexity. Our modified APES beamformer can omit sub-array averaging and the computational complexity is further reduced when used with sub-aperture delay-and-sum beamforming. However, the condition of the spatial covariance matrix may be degraded in modified APES beamforming by omitting sub-array averaging. Therefore, the first purpose of this study was to evaluate the condition of the spatial covariance matrix quantitatively. In the previous studies, it was reported that the condition of the spatial covariance matrix was important, but the condition of the spatial covariance matrix has not been evaluated quantitatively. Therefore, in the present study, the condition of the spatial covariance matrix was evaluated quantitatively using the condition number. In addition, sub-aperture beamforming and sub-array averaging were combined to improve the condition of the spatial covariance matrix in the modified APES beamformer.

In the conventional DAS beamforming, the performance of the beamformer is also controlled by apodization. However, in minimum variance beamforming, only rectangular apodization was used in the previous studies. The second objective of this study was to examine the effect of apodization in APES beamforming. In this study, a strategy was proposed for implementing apodization in minimum variance beamforming together with sub-aperture beamforming. Sub-aperture beamforming was used together for reduction of the dimension of the covariance matrix corresponding to the computational complexity. By implementing apodization, the transverse oscillation [25], which is often used for measurement of tissue motion, can be used with adaptive beamforming. The feasibility of apodization in APES beamforming was evaluated by basic experiments using a phantom.

Materials and methods

APES beamforming

Let us define the complex signal of the ultrasonic echo received by the mth transducer element of an ultrasonic probe by \(s_m~(m=0, 1, 2,\ldots , M-1)\), where M is the total number of elements in the aperture. The M signals are ordered in a vector as follows:

$$\begin{aligned} \mathbf{S}=\left( s_0 \; s_1 \cdots s_{M-1}\right) ^\mathrm{T}, \end{aligned}$$
(1)

where \(^\mathrm{T}\) denotes the transpose. The lateral position of the mth transducer element is defined by \(x_m\) and the range position z of every transducer element is zero.

The output u of a beamformer is expressed as follows:

$$\begin{aligned} u=\mathbf{w^\mathrm{H}}{} \mathbf{S}, \end{aligned}$$
(2)

where \(\mathbf{w}\) and \(^\mathrm{H}\) are the weight vector applied to the received signal vector \(\mathbf{S}\) and the Hermitian operator, respectively.

The output of the conventional DAS beamformer with rectangular apodization is obtained by simply replacing the weight vector \(\mathbf{w}\) by the steering vector \(\mathbf{a}\), which indicates the position of the receiving focal point \((x_\mathrm{f}, z_\mathrm{f})\), expressed as follows:

$$\begin{aligned} \mathbf{a}=\left( \begin{array}{c} a_0\\ a_1\\ \vdots \\ a_{M-1} \end{array} \right) =\left( \begin{array}{c} \exp \left( -j\frac{\displaystyle 2\pi f_0\sqrt{(x_0-x_\mathrm{f})^2+z_\mathrm{f}^2}}{\displaystyle c_0}\right) \\ \exp \left( -j\frac{\displaystyle 2\pi f_0\sqrt{(x_1-x_\mathrm{f})^2+z_\mathrm{f}^2}}{\displaystyle c_0}\right) \\ \vdots \\ \exp \left( -j\frac{\displaystyle 2\pi f_0\sqrt{(x_{M-1}-x_\mathrm{f})^2+z_\mathrm{f}^2}}{\displaystyle c_0}\right) \end{array} \right) , \end{aligned}$$
(3)

where \(f_0\) is the ultrasonic center frequency, and \(c_0\) is the speed of sound.

On the other hand, in this study, the output of a beamformer with arbitrary apodization is expressed as follows:

$$\begin{aligned} u=\mathbf{w^\mathrm{H}}{} \mathbf{Z}, \end{aligned}$$
(4)

where \(\mathbf{Z}\) is the apodized received signal expressed as follows:

$$\begin{aligned} \mathbf{Z}= & {} \left( \begin{array}{c} Z_0\\ Z_1\\ \vdots \\ Z_{M-1} \end{array} \right) =\left( \begin{array}{cccccc} \alpha _0 &{} 0 &{} 0 &{} 0 &{} \cdots &{} 0\\ 0 &{} \alpha _1 &{} 0 &{} 0 &{} \cdots &{} 0\\ 0 &{} 0 &{} \alpha _2 &{} 0 &{} \cdots &{} 0\\ &{} &{} \vdots &{} &{} \ddots &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} \cdots &{} \alpha _{M-1} \end{array} \right) \mathbf{S}, \end{aligned}$$
(5)

where \(\alpha _i~~(i=0, 1, 2, \ldots , M-1)\) is the apodization weight.

In the conventional minimum variance beamforming, including APES beamforming, the spatial covariance matrix \(\mathbf{R}\) is obtained from the received ultrasonic echoes \(\mathbf{S}\) [19]. However, in this study, the covariance matrix \(\mathbf{R}\) is obtained from the apodized received signal \(\mathbf{Z}\) as follows:

$$\begin{aligned} \mathbf{R}=\mathrm{E}\left[ \mathbf{Z}{} \mathbf{Z}^\mathrm{H}\right] . \end{aligned}$$
(6)

The adaptive weight vector \(\mathbf{w}\) is estimated as follows [22]:

$$\begin{aligned} \mathbf{w}=\frac{\mathbf{Q^\mathrm{-1}a}}{\mathbf{a^\mathrm{H}Q^\mathrm{-1}a}}, \end{aligned}$$
(7)

where

$$\begin{aligned} \mathbf{Q}=\mathbf{R}-\mathbf{G}{} \mathbf{G^\mathrm{H}}, \end{aligned}$$
(8)

and \(\mathbf{G}=[g_0~~g_1~~g_2~~\cdots ~~g_{M-1}]^\mathrm{T}\). The vector \(\mathbf{G}\) corresponds to the desired signal from the receiving focal point, and in [22], all of the elements \(g_m~(m=0, 1, \ldots , M-1)\) of vector \(\mathbf{G}\) are estimated as follows:

$$\begin{aligned} g_m=\frac{\displaystyle \mathbf{a}^\mathrm{H}{} \mathbf{S}}{\displaystyle M}. \end{aligned}$$
(9)

In the conventional APES beamforming, the desired signal vector \(\mathbf{G}\) is estimated by Eq. (9), in which the element directivity and receive apodization are not considered. The modified APES beamformer proposed in our previous study [23] considers the element directivity. In addition, in this study, the apodized received signal \(\mathbf{Z}\) was used to estimate the desired signal \(\mathbf{G}\) instead of the non-apodized received signal \(\mathbf{S}\) as follows:

$$\begin{aligned} g_m=\frac{\displaystyle D(\theta _m)\mathbf{a}^\mathrm{H}\mathbf{Z}}{\sum \nolimits _{i=0}^{M-1}D(\theta _i)}, \end{aligned}$$
(10)

where

$$\begin{aligned} D(\theta _m)=\frac{\sin \left( \frac{\displaystyle \pi d}{\displaystyle \lambda }\sin \theta _m\right) }{\displaystyle \frac{\displaystyle \pi d}{\lambda }\sin \theta _m}, \end{aligned}$$
(11)
$$\begin{aligned} \theta _m=\tan ^{-1}\left( \frac{\displaystyle x_\mathrm{f}-x_{m}}{\displaystyle z_\mathrm{f}}\right) , \end{aligned}$$
(12)

d is the width of each transducer element, and \(\lambda\) is the ultrasonic wavelength. In the actual data processing, the delays among the received signals \(s_m\) are compensated before estimation of the weight \(\mathbf{w}\). In such a situation, the steering vector \(\mathbf{a}\) becomes a vector of ones.

APES beamforming with sub-aperture beamforming and sub-array averaging

In this study, sub-array averaging was also included in the modified APES beamformer with sub-aperture beamforming [23] to improve the condition of the spatial covariance matrix. The total receiving aperture was divided into K sub-apertures. Each sub-aperture consists of \(M_\mathrm{s}=M/K\) elements. In our previous study, the modified APES beamformer was applied to the output from the sub-apertures [23], as shown in Fig. 1a. In this study, \(L\,(<\!K)\) sub-arrays were also assigned in each sub-aperture, as illustrated in Fig. 1b. The output \(y_{k,l}\) from the l-th sub-array (\(l=0, 1, 2, \ldots , L-1\)) in the k-th sub-aperture (\(k=0, 1, 2, \ldots , K-1\)) is expressed as follows:

$$\begin{aligned} y_{k,l}&= \left( a_{M_\mathrm{s}\cdot k+l}^*~~a_{M_\mathrm{s}\cdot k+l+1}^*~~a_{M_\mathrm{s}\cdot k+l+2}^*~~\cdots ~~a_{M_\mathrm{s}\cdot k+l+(M_\mathrm{s}-L)-1}^*\right) \times \left( \begin{array}{c} Z_{M_\mathrm{s}\cdot k+l}\\ Z_{M_\mathrm{s}\cdot k+l+1}\\ Z_{M_\mathrm{s}\cdot k+l+2}\\ \vdots \\ Z_{M_\mathrm{s}\cdot k+l+(M_\mathrm{s}-L)-1} \end{array} \right) \nonumber \\ &= \mathbf{a}_{k,l}^\mathrm{H}{} \mathbf{Z}_{k,l}. \end{aligned}$$
(13)
Fig. 1
figure 1

Illustration of implementation of sub-aperture beamforming and sub-array averaging. a Estimation of covariance matrix with sub-aperture beamforming only [23]. b Estimation of covariance matrix with sub-aperture beamforming and sub-array averaging

Full size image

The spatial covariance matrix \(\mathbf{C}_l\) obtained from the output of the lth sub-array in the respective sub-aperture is expressed as follows:

$$\begin{aligned} \mathbf{C}_l=\mathbf{Y}_l\mathbf{Y}_l^\mathrm{H}-\mathbf{V}_l\mathbf{V}_l^\mathrm{H}, \end{aligned}$$
(14)

where \(\mathbf{Y}_l=(y_{0,l}~~y_{1,l}~~y_{2,l}~~\ldots ~~y_{K-1,l})^\mathrm{T}\) is the output signal vector from the l-th sub-array. The desired signal vector \(\mathbf{V}=(v_{0,l} v_{1,l} v_{2,l} \ldots v_{K-1,l})^\mathrm{T}\) is obtained as follows:

$$\begin{aligned} v_{k,l}=\frac{b_{k,l}\cdot \sum \nolimits _{i=0}^{K-1}y_{i,l}}{\sum \nolimits _{i=0}^{K-1}b_{i,l}}, \end{aligned}$$
(15)

where \(b_{k,l}\) is the directivity of the lth sub-array in the kth sub-aperture defined as follows:

$$\begin{aligned} b_{k,l}=\frac{\displaystyle 1}{\displaystyle M_\mathrm{s}-L}\sum _{i=0}^{M_\mathrm{s}-L-1}D(\theta _{M_\mathrm{s}\cdot k+l+i}). \end{aligned}$$
(16)

The covariance matrix \(\widehat{\mathbf{C}}\) estimated with sub-array averaging is expressed as follows:

$$\begin{aligned} \widehat{\mathbf{C}}=\frac{\displaystyle 1}{\displaystyle L+1}\sum _{l=0}^{L}{} \mathbf{C}_l+\beta \mathbf{I}. \end{aligned}$$
(17)

where \(\beta\) is a parameter determining the magnitude of diagonal loading.

Using the estimated covariance matrix \(\widehat{\mathbf{C}}\), the weight vector \(\mathbf{w}_\mathrm{s}\) is obtained as follows:

$$ \begin{aligned}{\mathbf{w}}=\frac{\widehat{\mathbf{C}}^{\mathrm{-1}}{\rm J}}{{\mathbf{J}^{\mathrm{H}} {\widehat{{\rm C}}}^{\mathrm{-1}}{\rm J}}}, \end{aligned}$$
(18)

where \(\mathbf{J}\) is a K-dimensional vector of ones. The output \(u_\mathrm{s}\) of the modified APES beamformer with sub-array averaging is expressed as follows:

$$\begin{aligned} u_\mathrm{s}=\mathbf{w}_\mathrm{s}^\mathrm{H}{} \mathbf{Y}, \end{aligned}$$
(19)

where

$$\begin{aligned} \mathbf{Y}=\frac{1}{L+1}\sum _{l=0}^{L}{} \mathbf{Y}_l. \end{aligned}$$
(20)

In this study, the condition of the spatial covariance matrix was evaluated using the condition number. The change in the condition number of the spatial covariance matrix depending on the number of sub-array averaging and diagonal loading was examined in the subsequent experimental section. In addition, the effects of the apodization weight \(\alpha _i~~(i=0, 1, 2, \ldots , M-1)\) on the modified APES beamformer were examined.

Evaluation of image quality

In this study, the quality of a B-mode image was evaluated by methods described in [26, 27].

Spatial resolution

The spatial resolution was defined as the lateral full width at half maximum of the amplitude profile of an echo from a point scatterer (fine wire in a phantom).

Contrast

Contrast C was evaluated as follows:

$$\begin{aligned} C=\frac{\displaystyle |\mu _\mathrm{b}-\mu _\mathrm{l}|}{\frac{\mu _\mathrm{b}+\mu _\mathrm{l}}{2}}, \end{aligned}$$
(21)

where \(\mu _\mathrm{b}\) and \(\mu _\mathrm{l}\) are mean gray levels in background and lesion, respectively. An anechoic cyst phantom was adopted as the lesion, and a diffuse scattering medium was adopted as the background.

Experimental setup

An ultrasound imaging phantom (model 040GSE, CIRS) was used for evaluation of the improvement in image quality. A linear array ultrasonic probe at a nominal center frequency of 7.5 MHz (PU-0558, Ueda Japan Radio) was used, and ultrasonic echo signals received by individual transducer elements were acquired by a custom-made ultrasound scanner (RSYS0002, Microsonic) at a sampling frequency of 31.25 MHz. The beamforming procedure was performed off-line on the ultrasound echo signals received by the individual elements using in-house software based on MATLAB (The MathWorks Inc., Natick, MA). The element pitch of the linear array was 0.1 mm, but the width d of each transducer element was not known. Therefore, the width d was assumed to be 0.08 mm. The high-frame-rate transmit–receive sequence is described in [23].

Experimental Results

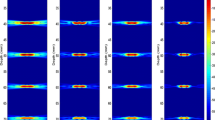
Figure 2a, b shows B-mode images of the string phantom obtained by the conventional DAS and APES beamforming, respectively. In this study, the conventional APES beamformer was used with sub-array averaging and diagonal loading under the condition recommended in [22]. As can be seen in Fig. 2, the lateral spatial resolution of the APES beamformer, 0.36 mm, is significantly better than that of the DAS beamformer, 0.67 mm. The condition number of the spatial covariance matrix in the conventional APES beamforming is 42.8. The computation time of the conventional APES beamformer was \((1.9\times 10^4)\)% of the DAS beamformer.

Fig. 2
figure 2

B-mode images of string phantom obtained by a conventional DAS beamforming and b conventional APES beamforming

Full size image

To reduce the computational complexity, sub-aperture beamforming was incorporated into APES beamforming in our previous study [23]. Figure 3a shows a B-mode image obtained by our modified APES beamformer with four sub-apertures. In Fig. 3a, diagonal loading corresponding to 0.05 / K of the received power was used, where K is the number of sub-apertures. In Fig. 3a, the lateral resolution of 0.34 mm, which is very similar to that obtained by the conventional APES beamforming (0.36 mm), can be achieved with much less computation time, i.e., \((3.5\times 10^2)\)% of the conventional DAS beamformer. The condition number of the spatial covariance matrix was 64.

Fig. 3
figure 3

B-mode images of string phantom obtained by modified APES beamforming with a no sub-array averaging, b sub-array averaging of \(L=4\), and c sub-array averaging of \(L=8\). Modified APES beamformer was used with four sub-apertures and diagonal loading corresponding to 0.05 / K of the received power

Full size image

To improve the condition number, the modified APES beamformer was used with sub-array averaging. Figure 3b, c shows B-mode images of the string phantom obtained by the modified APES beamformer with the numbers of sub-array averaging L of 4 and 8, respectively. The condition numbers of the covariance matrices in Fig. 3b and c were improved to 14 and 8, respectively. However, the point spread function was significantly broadened in the lateral direction, resulting in the spatial resolutions of 0.47 mm and 0.51 mm in Fig. 3b, c, respectively. In addition, the computation time increased to \((1.1\times 10^3)\) and \((1.4\times 10^3)\)% of the conventional DAS beamformer.

The condition number can also be improved by simply increasing the magnitude of diagonal loading. Figure 4a–c shows B-mode images of the string phantom obtained by modified APES beamforming without sub-array averaging but with four-sub-aperture beamforming and diagonal loading corresponding to 0.1 / K, 0.25 / K, and 0.5 / K of the received power, respectively. The condition numbers in Fig. 4a–c were improved to 33, 14, and 7, respectively, with less broadening of the point spread function than in Fig. 3 obtained with sub-array averaging. The lateral spatial resolutions in Fig. 4a–c were 0.38, 0.43, and 0.46 mm, respectively. There was no increase in computation time.

Fig. 4
figure 4

B-mode images of string phantom obtained by modified APES beamforming with four-sub-aperture beamforming and diagonal loadings corresponding to a 0.1 / K, b 0.25 / K, and c 0.5 / K of the received power. Sub-array averaging is not used

Full size image

The image contrast was also evaluated using a cyst phantom. Figure 5a, b shows B-mode images obtained by the conventional DAS and APES beamformers, respectively. The image contrast obtained by the conventional APES beamforming (3.8 dB) was better than that obtained by the conventional DAS beamforming (2.9 dB). The condition number of the covariance matrix in the APES beamformer was 49, which was worse than that obtained for the string phantom due to the lower intensity [lower signal-to-noise ratio (SNR)] of the scattered echo.

Fig. 5
figure 5

B-mode images of cyst phantom obtained by a conventional DAS beamforming and b conventional APES beamforming

Full size image

Figure 6a–c shows B-mode images of the cyst phantom obtained by the modified APES beamformer used with four-sub-aperture beamforming and sub-array averaging of \(L=0\) (no sub-array averaging), \(L=4\), and \(L=8\), respectively. Diagonal loading corresponding to 0.05 / K of the received power was used. By increasing the number of sub-array averaging, artifacts were generated in the cystic region, resulting in the image contrasts in Figs. 6a–c of 4.4, −3.6, and −5.1 dB, respectively. The condition numbers in Fig. 6a–c were 75, 15, and 9, respectively.

Fig. 6
figure 6

B-mode images of cyst phantom obtained by modified APES beamforming with a no sub-array averaging, b sub-array averaging of \(L=4\), and c sub-array averaging of \(L=8\). Modified APES beamformer was used with four sub-apertures and diagonal loading corresponding to 0.05 / K of the received power

Full size image

Figure 7a–c shows B-mode images obtained by the modified APES beamformer without sub-array averaging but with four-sub-aperture beamforming and diagonal loadings corresponding to 0.1 / K, 0.25 / K, and 0.5 / K of the received power, respectively. The B-mode images could be obtained without significant artifacts. The image contrast in Fig. 7a–c were 4.3, 4.2, and 4.1 dB, respectively, and the condition numbers in Fig. 7a–c were 38, 16, and 11, respectively. All the results described above are summarized in Table 1 and graphically summarized in Fig. 8. As can be seen in Fig. 8, the modified APES beamformer with sub-aperture beamforming without sub-array averaging realized better lateral resolution and contrast than that with sub-aperture beamforming and sub-array averaging. Therefore, in the subsequent examinations on the effect of apodization, the modified APES beamformer was used with sub-aperture beamforming, but sub-array averaging was not used.

Fig. 7
figure 7

B-mode images of cyst phantom obtained by modified APES beamforming with four-sub-aperture beamforming and diagonal loadings corresponding to a 0.1 / K, b 0.25 / K, and c 0.5 / K of the received power. Sub-array averaging is not used

Full size image
Fig. 8
figure 8

a Lateral spatial resolution and b image contrast are plotted as functions of condition number

Full size image
Table 1 Condition numbers of spatial covariance matrices, lateral resolutions corresponding to lateral full widths at half maxima (FWHM), contrast, and computation time obtained by delay-and-sum (DAS), amplitude and phase estimation (APES), and modified amplitude and phase estimation (mAPES) beamforming with different conditions of sub-array averaging (SA) and diagonal loading (DL)
Full size table

To obtain the B-mode images in Figs. 2, 3, 4, 5, 6, and 7, a rectangular function was used for the apodization weight \(\alpha _m~~(m=0, 1, 2, \ldots , M-1)\). In this study, tapered apodization was also examined. In many of previous studies, tapered apodization, such as Gaussian and Hanning apodization, was reported to reduce the side lobe level. Figure 9a, b shows a B-mode image of the string and cyst phantoms, respectively, obtained by the modified APES beamformer with four-sub-aperture beamforming, diagonal loading of 0.1 / K of the received power, and Gaussian apodization. The Gaussian weight \(\alpha _m\) is expressed as follows:

$$\begin{aligned} \alpha _m=\exp \left\{ -\left( \frac{m-\frac{\displaystyle M-1}{2}}{\eta \cdot M}\right) ^2\right\} \quad (m=0, 1, 2, \ldots , M-1), \end{aligned}$$
(22)

where \(\eta\) is a parameter controlling the width of the Gaussian function. In Fig. 9, \(\eta\) was set at 0.4.

Fig. 9
figure 9

B-mode image of the string and cyst phantoms, respectively, obtained by the modified APES beamformer with four-sub-aperture beamforming, diagonal loading of 0.1 / K of the received power, and Gaussian apodization (\(\eta =0.4\))

Full size image
Fig. 10
figure 10

Lateral echo amplitude profiles at peak of string target obtained by respective methods

Full size image

By comparing the echoes from the string targets in Figs. 4a and 9a, the side lobes, which are obviously seen in Fig. 4a, were suppressed by Gaussian apodization, as can be seen in Fig. 9a, at the same magnitude of diagonal loading of 0.1 / K of the received power. Figure 10 shows the lateral echo amplitude profiles at the peak of the string target obtained by the respective methods. The side lobe level could be reduced by Gaussian apodization, and the lateral spatial resolution obtained with Gaussian apodization (0.34 mm at \(\eta =0.4\)) was better than that (0.38 mm) with rectangular apodization. Furthermore, owing to the reduction of the side lobe level, the undesired echoes in the anechoic cyst phantom in Fig. 7a could be reduced significantly, as shown in Fig. 9b. The image contrast in Fig. 9b (5.1 dB) was better than that in Fig. 7a (4.3 dB).

Finally, the transverse oscillation [25] method was incorporated into the modified APES beamformer. In this study, lateral modulation was realized by Hanning apodization expressed as follows:

$$\begin{aligned} \alpha _m=0.5-0.5\cos \left\{ \frac{\displaystyle 4\pi (m+0.5)}{\displaystyle M}\right\} \quad (m=0, 1, 2, \ldots , M-1). \end{aligned}$$
(23)

Figure 11a shows a B-mode image of the string phantom obtained by the conventional DAS beamformer with apodization consisting of two Hanning functions, as defined by Eq. (23). Compared with Fig. 2a obtained with rectangular apodization, it was found from Fig. 11a that the point spread function (PSF) was modulated in the lateral direction. Figure 11b shows a B-mode image of the string phantom obtained with the modified APES beamformer with apodization defined by Eq. (23). As can be seen in Fig. 11b obtained by the modified APES beamformer, the string phantom was more “tagged” than in Fig. 11b obtained by the conventional DAS beamformer. Figure 12 shows the lateral echo amplitude profiles at the peak of the echo from the string target in Fig. 11 obtained by the respective methods. In Fig. 12, the modified APES beamformer realized the steepest (narrowest) peak among the three methods.

Fig. 11
figure 11

B-mode images of string phantom obtained by transverse oscillation method with a conventional DAS beamforming and b modified APES beamformer with four-sub-aperture beamforming and diagonal loading of 0.5 / K of the received power

Full size image
Fig. 12
figure 12

Lateral echo amplitude profiles at peak of string target obtained by respective methods

Full size image

Discussion and conclusion

In minimum variance beamforming including APES beamforming, the spatial covariance matrix needs to be obtained from the sampled ultrasonic echoes. To determine the weight in the beamforming process adaptively, the estimated spatial covariance matrix needs to be inverted. Therefore, the condition of the spatial covariance matrix is very important. In the previous studies, sub-array averaging was introduced to minimum variance beamforming for suppression of the components, which are correlated with the desired signal from the receiving focal point and, also, for improvement of the condition of the spatial covariance matrix. In our previous study, a modified APES beamformer was proposed with sub-aperture beamforming, but it was not used with sub-array averaging. In this study, therefore, sub-array averaging was also incorporated into the modified APES beamformer, and the effect of sub-array averaging was compared with that of diagonal loading, which is another strategy for improvement of the condition of the spatial covariance matrix. To evaluate the effect of sub-array averaging on the condition of the spatial covariance matrix quantitatively, the condition number was used in this study. At a similar condition number of the spatial covariance matrix, the performance, i.e., the lateral spatial resolution and image contrast, realized with diagonal loading was better than that with sub-array averaging. In the previous studies on minimum variance beamforming, the condition of the spatial covariance matrix has not been discussed quantitatively. By introducing the quantitative evaluation of the condition of the spatial covariance matrix, it could be confirmed that the modified APES beamforming achieved a better performance with diagonal loading than with sub-array averaging at a similar condition of the spatial covariance matrix.

In addition, a strategy to incorporate apodization into the modified APES beamforming was introduced in this study. With rectangular apodization, the conventional APES beamformer realized slightly better spatial resolution but slightly worse image contrast than the modified APES beamformer. The image contrast of the modified APES beamformer was further improved with Gaussian apodization. It is common knowledge that the side lobe level is reduced by tapered apodization, i.e., Gaussian apodization. The spatial resolution of the modified APES beamformer becomes better than that of the conventional APES beamformer when used with Gaussian apodization. It is also the common knowledge that tapered apodization reduces the side lobe level but degrades the spatial resolution. In this study, however, the tapered apodization, i.e., Gaussian apodization, also improved the spatial resolution when used with the modified APES beamformer. Other apodization methods, such as apodization, consisting of two Hanning functions, could also be used. It is very preferable that the performance of the modified APES beamformer be further improved, and other capabilities, such as transverse oscillation, can also be realized by introducing apodization to the modified APES beamformer. The computational complexity of the modified APES beamformer is significantly lower than that of the conventional APES beamformer, and it has potential to be used as a practical application.