Numerical and analytical analyses of the impact of monodisperse and bidisperse granular flows on a baffle structure

Abstract

Baffle structure, a promising countermeasure in reducing the destruction power of rapid granular flows, needs more investigation especially with focus on the physically based design strategy. To contribute to this point, we conduct a series of numerical modeling tests to investigate the impact dynamics of monodisperse and bidisperse granular flows against the baffle array, based on which a jet-based model for estimation of the peak impact force and run-up height is proposed for baffle design. The results show that the energy loss due to interparticle interaction increases with the Froude number; the hard contact of larger particles and the arching effect of debris–baffle interaction are important to the impact dynamics on baffle structure; the baffle design could ignore the static force component, at least for rapid granular flow with the smaller ratio of the baffle slit size to the particle size; and for the bidisperse granular flow impact, the effect of larger particles is only dominant when the percentage of larger particles is large because fine debris could provide a cushioning effect. A jet-based model considering conservation equations for momentum and energy is then proposed for baffle design with the introduction of jamming-related momentum and energy discharge process. The model is verified using numerical data in terms of the run-up height and impact force. On the basis of the proposed model, baffle design is further discussed considering flow material inhomogeneity and unsteady flow dynamics.

Introduction

Granular-flow-related geo-disasters have received much attention in the scientific and engineering domains because of their resulting human death tolls and economic losses (Dowling and Santi 2014; Wang 2013). With there being a great demand for disaster prevention measures, the impact dynamics of granular flow on barriers have recently become a hot topic as they serve as a basis for the engineering design of protection structures (Ho et al. 2021; Huang and Zhang 2020). This topic requires consideration of the debris–structure interaction mechanism and impact models for determining key design parameters, such as the impact force and structure height.

The debris–structure interaction mechanism describes the pattern or morphology of a granular flow impacting on barriers and is important to the development of an impact model based on reasonable assumptions. In the case of dry granular flows, a mechanism dominated by a dead zone and pile up has already been identified (Jiang and Towhata 2013; Ng et al. 2016; Shen et al. 2018) based on which an impact model considering momentum attenuation was proposed by Koo et al. (2016). In the case of two-phase granular flows, the mobility is much greater because of the fluid–solid interaction and the impact process exhibits run-up behavior (Choi et al. 2015; Ng et al. 2016). Armanini et al. (2019) described such impact behavior as a vertical jet and developed an impact model based on the mass, momentum, and energy conversation of the jet. In addition, another impact mechanism, referred to as the momentum jump describing an impact-induced shock wave propagating upstream, has been observed for both dry (Pudasaini et al. 2007) and two-phase granular flow (Song et al. 2021), and impact models based on the momentum jump have been developed (Albaba et al. 2018; Faug 2021; Iverson et al. 2016; Li et al. 2020).

Considering the superspeed nature and destructive power of granular flow, it is preferred to build baffle arrays behind engineering structures including main protection barriers and buildings to assist in the dissipation of the granular flow energy and thus improve the safety of a structure. Such a strategy has been demonstrated to be effective (Bi et al. 2018; Goodwin et al. 2020; Ng et al. 2014; Wang et al. 2020; Yang et al. 2021). The design of a baffle structure remains challenging because most guidelines (Kwan 2012) and impact models have been developed for closed-type barriers (Ahmadipur et al. 2019; Albaba et al. 2018; Faug 2021; Li et al. 2020; Song et al. 2021). Additionally, until recently, sophisticated impact models have been developed for slit dams (Rossi and Armanini 2019; Zhou et al. 2019) and permeable flexible barriers (Tan et al. 2019), whereas for the baffle structure, it seems more popular to investigate the configuration effect aiming at adjusting the baffle layout to maximize the energy dissipation potential (Bi et al. 2018; Goodwin et al. 2020; Huang et al. 2020; Jianbo et al. 2020; Wang et al. 2020; Zhang et al. 2021). A physical impact model for the debris–baffle interaction is still lacking.

Granular flow material is often inhomogeneous with the particle size ranging from millimeters to tens of meters, which complicates the granular impact dynamics (Song et al. 2018). The situation is even more complex for the debris–baffle interaction because the arching effect becomes important when granules pass narrow slits. The particle size of non-monodisperse granular flow that dominates the arching effect has not been identified, and the impact dynamics on baffle structures has thus not been well elucidated. In addition, granular flow surging downslopes is often characterized by unsteady development with spatiotemporal variability of the flow properties, such as the velocity and depth, which makes the selection of the design parameters challenging. As a result, the design of baffle in terms of resisting the impact effect needs to be better elucidated considering the material homogeneity and unsteady dynamics of granular flow.

This paper reports on a series of numerical simulations conducted using a three-dimensional (3D) discrete element method (DEM). According to an understanding of the debris–baffle interaction mechanism and the impact response of the baffles, we present an impact model that can be used to calculate the run-up height and impact force against the first baffle array impacted by granular flows with different particle sizes and Froude numbers (${N}_{Fr}$). The model is verified using numerical data.

Numerical model based on the DEM.

The DEM simulations are conducted using commercial software named EDEM, which calculates the particle contact force using the Hertz–Mindlin (no slip) model. Details of the contact model are given in the Appendix. The DEM simulation parameters are summarized in Table 1. The DEM model used in this paper is the same with that we have used in our previously published papers (Zhang and Huang 2022a), where the detailed calibration process also can be found.

Table 1 DEM input parameters

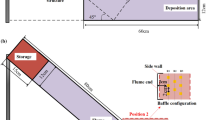
The configuration of the baffle model established using the DEM is presented in Fig. 1. We use a 4-m-long flume. The baffle R1 is placed 1.9 m downstream of the trigger gate. Two arrays of baffles are considered for simplicity. The baffle array spacing (${L}_{B}$) is 210 mm, the slit spacing (${S}_{B}$) is 70 mm, and the baffle dimensions are 30 mm $\times$ 30 mm. The baffle configuration is determined based on the suggestions of Ng et al. (2014) (${L}_{B}/{S}_{B}$ equals 3). The baffle height is large enough to avoid overflow. Because overflow could deteriorate the baffle performance (Ng et al. 2014), and also make it more difficult to mathematical description of debris–baffle interaction as the particles passing from baffle slits and crest would undergo different process characterized by distinct energy dissipation manner.

Fig. 1

DEM model of debris–baffle interaction

The simulation includes two stages: material preparation and simulation of the debris–baffle interaction. In the material simulation stage, gravity (1 g) is directed along the negative direction of the z-axis, and the flume has two sidewalls that limit its width (${W}_{F}$= 300 mm). A total quantity of 40 kg of spherical particles with different sizes (7, 8, 10, 12.5, 14, and 16 mm in diameter, which are determined based on ${S}_{B}/\delta$ reported by Goodwin et al. (2021)) and distributions (Table 2) are generated within a virtual box and driven by gravity to freely settle under the restrictions of the sidewalls and trigger gate. A rectangular granular assembly with dimensions of $0.4 \mathrm{m }\times 0.3 \mathrm{m }\times 0.23 \mathrm{m}$ has been formed once all of the particles have completely settled. Before activating the debris–baffle interaction simulation, the sidewalls are removed and the direction of gravity is instantaneously redirected ($\theta$= 25°, 30°, 35°, 40°, and 45°) to simulate the flume inclination while periodic boundaries are introduced respectively at 15 cm to the left and 15 cm to the right of the main axis to remove the effect of the sidewalls. A periodic boundary condition means that any particle leaving the domain on that side will instantly re-enter the domain from the opposite side. As a result, the simulation is laterally infinite. The trigger gate is then opened to produce granular flow, which interacts with the baffles. During the debris–baffle interaction, the impact force and granular run-up height are measured. In addition, simulations of free flows without baffles are conducted to quantify the flow properties. It is noted that the distal end of the flume is open, which means that the particles passing the flume distal end are removed from the domain to reduce the computation time. A total of 96 cases are simulated.

Table 2 Particle size distribution used to account for the material inhomogeneity effect

Interpretation of the DEM simulation results.

Free-flow properties

Flow properties including the flow depth (${h}_{f}=\frac{2}{{N}_{p}}\sum_{i=1}^{{N}_{p}}{Z}_{i}$, where ${N}_{p}$ is the total number of particles encompassed in the measuring region M1 and ${Z}_{i}$ is the coordinate of particle i in the z-direction), flow velocity (${u}_{f}=\frac{\sum_{i=1}^{{N}_{p}}{u}_{i}}{{N}_{p}}$, where ${u}_{i}$ is the single-particle velocity), and volume fraction (${\phi }_{f}=\frac{\sum_{i=1}^{{N}_{p}}{m}_{i}}{{\rho }_{s}{h}_{f}{W}_{F}\Delta l}$, where ${m}_{i}$ is the particle density, ${\rho }_{s}$ is the particle density, and $\Delta l$ is the length of the monitor section) are measured under free-flow conditions in M1, whose length is 4 $\delta$ and height and width are sufficiently large (Fig. 1). M1 is fixed on the flume, and the measured flow properties thus describe the behavior of granular flow passing the position of M1, which is immediately behind the baffle R1.

The Froude number (${N}_{Fr}={u}_{f}/\sqrt{g{h}_{f}\cos\theta }$) is used to characterize the flow dynamics. Table 3 summarizes the Froude number calculated from the maximum flow velocity and flow depth. The granular flow is highly unsteady and exhibits a wedge-shaped front and variable profile. Ng et al. (2019) indicated that the frontmost 5% of such flow dominates the granular impact dynamics, and the Froude number ${N}_{Fr}^{^{\prime}}$ should thus be calculated using the maximum velocity and depth of this critical zone. For comparison, we summarize ${N}_{Fr}^{^{\prime}}$ in Table 4. Additionally, Table 5 gives the Froude characteristics of bidisperse granular flow. The Froude number is an important input parameter of the analytical model presented later.

Table 3 Maximum velocity and flow depth of monodisperse granular flows. Length unit: m; velocity unit: m/s

Table 4 Maximum velocity and frontal depth of monodisperse granular flows. ${h}_{f\_fro}$ is determined following Ng et al. (2019). Length unit: m; velocity unit: m/s

Table 5 Maximum velocity and flow depth of bidisperse granular flows. Length unit: m; velocity unit: m/s

Energy consumption analysis

The mechanism of the debris–baffle interaction involves the formation of granular arches across the baffle slits, and with the breaking and reconstruction of the granular arches, the granular flow energy is dissipated continuously, as shown in Fig. 2b and discussed in depth in our previous work (Huang et al. 2020; Zhang et al. 2021). However, a detailed analysis based on energy consumption and considering the coupled effect of the particle size and Froude number is still lacking.

Fig. 2

Energy evolution for the flow of 10-mm particles under a slope angle of 35°: a free-flow condition and b two arrays of baffles

The energy components of the granular system in this study are the potential energy (${E}_{p}$), kinetic energy (${E}_{k}$), dissipated energy (${E}_{d}$), energy loss due to particle removal (because we have used an open flume, the particles passing flume end would be deleted for saving computational time, and thus a portion of system energy is lost, which is termed as ${E}_{r}$), and elastic strain energy (${E}_{s}$). The total energy (${E}_{0}$) should be the sum of ${E}_{p}$, ${E}_{k}$, ${E}_{d}$, ${E}_{r}$, and ${E}_{s}$ and can also be regarded as the potential energy of the granular system at the initial time defined as the time of the activation of the trigger gate. For simplicity, ${E}_{s}$ is neglected because it only accounts for a small portion of the total energy (Shen et al. 2018). ${E}_{d}$ can be further divided into three sources of energy loss due to inter-particle interaction (${E}_{d}^{p-p}$), particle–flume base interaction (${E}_{d}^{p-f}$), and particle–baffle interaction (${E}_{d}^{p-b}$). ${E}_{d}$ is generated mainly through normal contact damping, tangential contact damping or friction and rolling friction. Therefore,

$$\begin{array}{c}{E}_{d}={\sum }_{0}^{t}{\sum }_{i=1}^{N}{\overrightarrow{F}}_{i}^{t}\cdot \frac{{\overrightarrow{v}}_{i}^{t}+{\overrightarrow{v}}_{i}^{t-1}}{2}\cdot \Delta t+{\sum }_{0}^{t}{\sum }_{i=1}^{N}{\overrightarrow{M}}_{i}^{t}\cdot \frac{{\overrightarrow{\omega }}_{i}^{t}+{\overrightarrow{\omega }}_{i}^{t-1}}{2}\cdot \Delta t,\end{array}$$

(1)

$$\begin{array}{c}{E}_{k}=\frac{1}{2}{\sum }_{i=1}^{N}({m}_{i}{\left|{\overrightarrow{v}}_{i}^{t}\right|}^{2}+{I}_{i}{\left|{\overrightarrow{\omega }}_{i}^{t}\right|}^{2}),\end{array}$$

(2)

$$\begin{array}{c}{E}_{p}={\sum }_{i=1}^{N}({m}_{i}\overrightarrow{g}\cdot \left(-{\overrightarrow{P}}_{i}^{t}\right)).\end{array}$$

(3)

Here, t is the given time (t > 0 when calculating ${E}_{d}$); $N$ is the total particle number within the domain; ${\overrightarrow{F}}_{i}^{t}$ is the contact force vector; ${\overrightarrow{M}}_{i}^{t}$ is the rolling torque; ${\overrightarrow{v}}_{i}^{t}$ and ${\overrightarrow{v}}_{i}^{t-1}$ are respectively the particle translational velocity at times t and t − 1; ${\overrightarrow{\omega }}_{i}^{t}$ and ${\overrightarrow{\omega }}_{i}^{t-1}$ are respectively the particle rotation angular velocity at times t and t − 1; ${m}_{i}$ is the particle mass; ${I}_{i}$ is the moment of inertia; $\overrightarrow{g}$ is gravity; ${\overrightarrow{P}}_{i}^{t}$ is the position vector of the particle. Equation (3) expresses that the distal end of the flume (x = 0 and z = 0, Fig. 1) is taken as a reference to calculate the potential energy.

Figure 2 gives the time history of the energy evolution of the free flow and debris–baffle interaction. Each energy component is normalized by the total energy (${E}_{0}$). Under the free-flow condition, granular flow quickly develops until no particles remain within the computational domain, corresponding to ${E}_{p}$ equaling zero. The kinetic energy of the whole granular mass reaches approximately 30% of ${E}_{o}$. During the free flow, energy is mainly dissipated by the interparticle interaction (${E}_{d}^{p-p}$) and particle–flume interaction (${E}_{d}^{p-f}$), which respectively accounts for 12% and 39% of ${E}_{0}$. With the impediment of baffles, the residence time of particles within the computational domain is enlarged, and the energy consumption is thus enhanced with the deceleration of granular flow, which decreases approximately 12% of ${E}_{0}$. However, at the end time, ${E}_{d}^{p-p}$/${E}_{0}$ reaches 43%, which is an increase of 31%; ${E}_{d}^{p-f}$/${E}_{0}$ reaches 31%, which is a decrease of 8%; and ${E}_{d}^{p-b}$/${E}_{0}$ accounts for less than 2% of ${E}_{0}$.

Figure 3a presents the variation in the peak values of ${E}_{d}^{p-p}$/${E}_{0}$ and ${E}_{d}^{p-f}$/${E}_{0}$, indicating the discrepancy between baffle cases and free flow cases, and Fig. 3b presents the peak values of ${E}_{d}^{p-b}$/${E}_{0}$. It is concluded that the energy consumed by the baffles is negligible, only accounting for approximately 0.5–2.5% of ${E}_{0}$ (at least for the values of ${S}_{B}/\delta$ and ${N}_{Fr}$ considered here), whereas ${E}_{d}^{p-b}$/${E}_{0}$ depends on ${S}_{B}/\delta$ and ${N}_{Fr}$. Additionally, the baffles fundamentally decrease ${E}_{d}^{p-f}$/${E}_{0}$ by as much as 30% and increase ${E}_{d}^{p-p}$/${E}_{0}$ by 5–40%. Thus, the energy loss due to interparticle interaction is the main energy consumption, which is consistent with the debris–baffle interaction mechanism dominated by granular arches as shown in the inset of Fig. 2b. The enhanced energy loss (${E}_{d}^{p-p}$/${E}_{0}$) has a linear relation with ${N}_{Fr}$ but does not vary appreciably with ${S}_{B}/\delta$. This is because we calculate the energy loss of the whole granular mass during the entire simulation rather than focusing on the energy loss of the flow passing the baffles. The effect of ${S}_{B}/\delta$ on the flow behavior is greater close to the region of the baffles.

Fig. 3

a The different values of ${E}_{d}^{p-p}$/${E}_{0}$ and ${E}_{d}^{p-f}$/${E}_{0}$ between baffle cases and free flow cases; b peak value of ${E}_{d}^{p-b}$/${E}_{0}$

Impact force of monodisperse granular flows

The impact force is an important design parameter of the baffle structure. Figure 4 shows the time history of the impact force acting on baffle R1 and exerted by the flow of 7-mm particles under a slope of 35°, and the inset gives the impact force of the flow of 16-mm particles under the same conditions. It is observed that the larger particles generate a greater force impulse and stronger peak force. The fluctuation of the impact force may be attributed to the unsteady flow dynamics of the granular flow and the hard impact of a single boulder on the structure (discrete impact due to single particles (Goodwin and Choi 2021)). To compute the force impulse, we need to address the Hertzian contact mechanics (Goodwin and Choi 2021; Song et al. 2018), but this is not the main purpose of the present paper. We want to address the non-fluctuated impact force, which could give fundamental information of the effect of ${S}_{B}/\delta$ on the impact force acting on the baffle array and is also useful for verifying the steady-based impact model. To this end, the impact force is smoothed using 5 pts FFT Smooth method (Shen et al. 2018), and the peak values of the smoothed impact force acting on baffles R1 and R2 are respectively summarized in Fig. 5a and b.

Fig. 4

Time history of the impact force exerted on baffle R1 by a flow of 7-mm particles under a slope angle of 35°. The inset gives the impact force exerted on baffle R1 by a flow of 16-mm particles under a slope angle of 35°. The smoothed data are obtained using 5 pts FFT Smooth method (where pts refers to the number of points in the window)

Fig. 5

Peak impact forces (smoothed data) acting on a baffle R1 and b baffle R2

It is not surprising that the impact force acting on R1 increases almost linearly with ${N}_{Fr}$ (Faug 2021), but larger particles exhibit an appreciably stronger peak force on the baffle array; e.g., for a slope of 25°, the force exerted by 16-mm particles is almost twice that exerted by 7-mm particles (Fig. 5a). Besides the hard contact causing larger force for larger particles, the reason may also include the granular arches dominate debris–baffle interaction mechanism (Fig. 2b), because with smaller ${S}_{B}/\delta$ (larger particles), the granular arches could be more stable resulting more material accumulated behind baffle array, which results in larger run-up height and impact force. Thus, for the impact model, both ${N}_{Fr}$ and ${S}_{B}/\delta$ should be better considered, which has not been achieved. Because of the deceleration of the flow by baffle R1, the force acting on R2 is reduced by more than 50% (Fig. 5b), which highlights that the strength design of baffles should take the first baffle array as a reference.

According to their kinetic energy, the particles in contact with the baffles at a given time point can be divided into dead-zone particles and moving particles (Zhang and Huang 2022a, 2022b). In this paper, we decompose the total impact force (${F}_{n}$) acting on baffle R1 into the static force (${F}_{n}^{s}$) exerted by dead-zone particles and the dynamic force (${F}_{n}^{d}$) exerted by moving particles. The results for 7- and 16-mm particle flows under a slope of 25° are respectively shown in Fig. 6a and b, and the insets give the corresponding results for a slope of 45°. It is seen that the dynamic force is dominant during the debris–baffle interaction, and with increases in the particle size and ${N}_{Fr}$, the static force component becomes much less important. The calculation of the dead-zone exerted force on the barrier is often challengeable (Albaba et al. 2018; Jiang and Towhata 2013), and baffle design can thus ignore the static force component, at least for rapid granular flow with smaller ${S}_{B}/\delta$.

Fig. 6

Decomposition of the impact force on baffle array R1: a 7-mm particle flow and a slope angle of 25°, with the inset giving the force exerted by 7-mm particle flow for a slope angle of 45° and b 16-mm particle flow for a slope angle of 25°, with the inset giving the force exerted by 16-mm particle flow for a slope angle of 45°

Impact force of bidisperse granular flows

When considering the impact on the baffle structure of granular flows with different particle size distributions, the main problem lies in the velocity alteration due to particle-size segregation; different arching effects due to different values of ${S}_{B}/\delta$, and the different force components exerted by the different particle sizes.

Tables 3 and 5 show that the particle-size segregation did not appreciably change the bulk flow velocity, and we thus believe that the variation in the impact force acting on the baffle arrays is not attributed to the segregation-altered flow behavior.

Figure 7 shows the total impact force of the bidisperse granular flow acting on the baffle array. As shown in the inset of Fig. 7a, the time-history curve of the raw data of the impact force acting on the baffle R1 has a greater force impulse when the percentage of 16-mm particles is increased. The peak of smoothed data shows that the impact force of bidisperse granular flows is bound by the force of 8- and 16-mm particle flows, and for larger ${N}_{Fr}$, the force discrepancy also becomes notable. With an increase in the percentage of 16-mm particles, the peak in smoothed impact force data does not have a monotonous development trend, but roughly larger values are observed, which indicates that the impact force of bidisperse granular flow is much more complex than that of monodisperse granular flows. This is because the impact effect is also altered by the discharge process, which is controlled by the arching effect of the debris–baffle interaction. With the change in particle percentage, it is difficult to determine which particle size dominates the arching behavior. This problem is later discussed in depth.

Fig. 7

Impact force of bidisperse granular flows on a baffle R1 and b baffle R2. The inset gives the time history of the raw data of the impact force showing an appreciable force impulse. The impact force is normalized

The impact effect on baffle R2 is complex because the boulder filtration effect of baffle R1, in addition to the particle-size segregation effect and arching effect, is important. The inset of Fig. 7b shows that the force impulse acting on baffle R2 is negligible compared with that acting on baffle R1, and the peak value of the smoothed impact force shows that with an increase in ${N}_{Fr}$, bidisperse granular flow with a larger percentage of 16-mm particles exerts a weaker impact force on baffle R2, indicating that the filtration effect of the baffle array is stronger for larger ${N}_{Fr}$.

Figure 8 compares the impact force of smaller particles and larger particles acting on an array. The comparison reveals which particle size dominates the impact effect of the bidisperse granular flow. For the impact force of PSD2 (i.e., the percentage of 16-mm particles is 20%) shown in Fig. 8a, the force generated by the 16-mm particles is weaker and the total impact effect is dominated by the 8-mm particles, indicating that smaller particles exert a cushioning effect that reduces the impact force of larger particles. When the percentage of 16-mm particles is increased to 60% (PSD4, Fig. 8b), the force of 16-mm particles is increased but the impact of smaller particles still dominates, and until 80% (PSD5, Fig. 8c), the impact of 16-mm particles dominates. For the impact force of PSD6, the force generated by 8-mm particles is still considerable (Fig. 8d). This may be because the smaller particles more easily fall into the voids of larger particles and make contacts with the barrier. The inset of Fig. 8 shows the force acting on baffle R2, and similar characteristics have been observed.

Fig. 8

Comparison of the impact forces of smaller particles and larger particles on the array. The results for cases a PSD2, b PSD4, c PSD5, and d PSD6 under a slope angle of 45° are presented. The inset presents the impact force acting on baffle R2

Analytical model and verification.

Model derivation

Figure 9a1 and b1 respectively show the moment of the beginning of the run-up of the granular flow against the baffle array (t = 0.86) and the moment that the run-up height reaches peaks (t = 1.25). It is observed that the granular flow front undergoes an upward deviation against the baffle array, which resembles the jet-like impact model described by Armanini et al. (2019) for a debris-flow impact on a closed-type barrier. The conceptual model of the jet impact for baffle R1 is shown in Fig. 9. For development of the debris–baffle interaction model, we set a control volume encompassing the climbing flow material, and we assume that (1) the incoming flow is steady and uniform with streamlines strictly parallel to the longitudinal direction (x-axis), which means a plug-like flow behavior; (2) the flow density is constant and the variation in the flow density during run-up and outflow is neglected; (3) the run-up height is transversely uniform; (4) the outflow process is steady and can be described by a linear function; (5) the length (along the x-direction) of the control volume is sufficiently short and thus the normal (${p}_{b}$) and tangential stress (${\tau }_{b}$) applied at the base of the control volume can be negligible; (6) the temperature change is negligible; and (7) the baffle surface friction stress (${\tau }_{s}$) and granular internal shear stress are negligible. We emphasize that the model is mainly developed for baffle R1, which should be taken as a reference in baffle design.

Fig. 9

DEM results of the debris–baffle interaction model: a1 moment of the start of the run-up of granular flow against the baffle array (t = 0.86) and b1 moment when the run-up height reaches peak (t = 1.25). a2 and b2 respectively show the corresponding conceptual model based on the vertical-jet assumption. The results for 10-mm particle flow and a slope angle of 35° are presented as an example

The debris–baffle interaction can be described by the conversation equations of mass, momentum, and energy, which are respectively written as:

$$\begin{array}{c}\underset{cv}{\overset{}{\iiint }}\frac{\partial }{\partial t}\rho \overrightarrow{V}dB+\underset{cs}{\overset{}{\iint }}(\rho \overrightarrow{V})\left(\overrightarrow{V}\cdot \overrightarrow{n}\right)dA=\underset{cv}{\overset{}{\iiint }}\rho \overrightarrow{f}dB+\underset{cs}{\overset{}{\iint }}\overrightarrow{F}dA,\end{array}$$

(4)

$$\begin{array}{c}\underset{cv}{\overset{}{\iiint }}\frac{\partial }{\partial t}{(\rho e}_{t})dB+\underset{cs}{\overset{}{\iint }}\left(\rho {e}_{t}\right)\left(\overrightarrow{V}\cdot \overrightarrow{n}\right)dA=\underset{cs}{\overset{}{\iint }}\overrightarrow{F}\cdot \overrightarrow{V}dA-\frac{\partial \mathcal{H}}{\partial t},\end{array}$$

(5)

where $\rho$ is the flow density, $\overrightarrow{V}$ is the velocity vector, $\overrightarrow{f}$ is the mass force, $\overrightarrow{F}$ is the surface force, ${e}_{t}$ is the mechanical energy of flow per unit mass, and $\frac{\partial \mathcal{H}}{\partial t}$ represents the involved heat energy and is neglected in this paper.

The momentum conversation in the longitudinal direction (along the x-axis) can be expressed as (assuming the velocity of materials within the control volume is zero along the x-axis):

$$\begin{array}{c}-{\rho }_{f}{{u}_{f}}^{2}{h}_{f}+{\rho }_{0}{{u}_{0}}^{2}{h}_{0}B={\int }_{0}^{{h}_{f}}{p}_{f}dz-B{\int }_{0}^{{h}_{o}}{p}_{o}dz-\left(1-B\right){\int }_{0}^{{h}_{r}}{p}_{n}dz,\end{array}$$

(6)

where B is the opening ratio ($\sum {S}_{B}/{W}_{F}$), ${p}_{f}$ is the stress on the control volume exerted by the incoming flow, ${p}_{o}$ is the stress on the control volume exerted by the outflow, and ${p}_{n}$ is the stress on the control volume exerted by the baffle, as shown in Fig. 9. Considering the linear distribution of the earth pressure (Armanini et al. 2019; Faug 2021; Li et al. 2020; Zhou et al. 2019), Eq. (6) can be rewritten as

$$\begin{array}{c}-{\rho }_{f}{{u}_{f}}^{2}{h}_{f}+{\rho }_{0}{{u}_{0}}^{2}{h}_{0}B=\frac{1}{2}{\kappa }_{f}{\rho }_{f}g{{h}_{f}}^{2}\cos\theta -\frac{1}{2}B{\kappa }_{o}{\rho }_{o}g{{h}_{o}}^{2}\cos\theta -\stackrel{\sim }{{F}_{n}},\end{array}$$

(7)

where $\stackrel{\sim }{{F}_{n}}$ is the total impact force per unit chute width, ${\rho }_{0}{{u}_{0}}^{2}{h}_{0}B$ is the momentum discharge, and for simplicity, we introduce a reduction coefficient ${\Psi }_{m}$ that describes the momentum discharge according to

$$\begin{array}{c}{\rho }_{0}{{u}_{0}}^{2}{h}_{0}B={\Psi }_{m}\left({\rho }_{f}{{u}_{f}}^{2}{h}_{f}\right).\end{array}$$

(8)

The substitution of Eq. (9) into Eq. (8) yields

$$\begin{array}{c}{\alpha }_{dyn}=\frac{{F}_{n}}{{\rho }_{f}{{u}_{f}}^{2}{h}_{f}}=\left(1-{\Psi }_{m}\right)+\frac{1}{2{{N}_{Fr}}^{2}}\left({\kappa }_{f}-{\gamma }_{r}B{\kappa }_{o}{\left(\frac{{h}_{r}}{{h}_{f}}\right)}^{2}\right)+{\alpha }_{0},\end{array}$$

(9)

where ${\kappa }_{f}$ and ${\kappa }_{o}$ represent the ratio of the longitudinal-to-vertical normal stress. We have introduced an empirical coefficient ${\gamma }_{r}$ in Eq. (10) for compensation of the overestimation of ${h}_{r}$, as will be discussed later. ${\alpha }_{0}$ is an additional coefficient, which will also be discussed later. And in Eq. (10), we have used the assumption: ${\rho }_{0}={\rho }_{f}$ and ${h}_{o}={h}_{r}$, where ${\rho }_{f}$ and ${\rho }_{0}$ are the density of incoming flow and the outflow, respectively; and ${h}_{o}$ is the granular run-up height at the position of baffle slits.

${e}_{t}$ in Eq. (5) can be expressed as

$$\begin{array}{c}{e}_{t}={e}_{k}+{e}_{p}=\frac{1}{2}{u}^{2}+gz\cos\theta ,\end{array}$$

(10)

where $\frac{1}{2}{u}^{2}$ is the kinetic energy per unit flow mass and $gz\mathrm{cos}\theta$ is the potential energy per unit flow mass.

The first term on the left-hand side of Eq. (5) can be written, under the assumption that the energy per unit flow mass is constant for the run-up material (Armanini et al. 2019), as

$$\begin{array}{c}\underset{cv}{\overset{}{\iiint }}\frac{\partial }{\partial t}{(\rho e}_{t})dB={\rho }_{r}{\left(\frac{1}{2}{u}^{2}+gz\cos\theta \right)}_{r}\frac{\partial {h}_{r}}{\partial t}{b}_{r}={\rho }_{r}{\left(\frac{1}{2}{u}^{2}+gz\cos\theta \right)}_{r}{u}_{r}{b}_{r}.\end{array}$$

(11)

When the run-up reaches its peak, ${u}_{r}$ becomes zero, resulting in the expression in Eq. (11) equaling zero. The second term on the left-hand side of Eq. (5) describes the flux of the energy across the surface of the control volume and can be written along the longitudinal direction (along the x-axis) as

$$\begin{array}{c}\underset{cs}{\overset{}{\iint }}\left(\rho {e}_{t}\right)\left(\overrightarrow{V}\cdot \overrightarrow{n}\right)dA={\int }_{0}^{{h}_{f}}{\rho }_{f}{\left(\frac{1}{2}{u}^{2}+gz\cos\theta \right)}_{f}\left(-{u}_{f}\right)dz\\ +B{\int }_{0}^{{h}_{o}}{\rho }_{o}{\left(\frac{1}{2}{u}^{2}+gz\cos\theta \right)}_{o}\left({u}_{o}\right)dz\end{array}$$

(12)

For simplicity, we introduce a reduction coefficient ${\Psi }_{e}$ to express the energy discharge as

$$\begin{array}{c}B{\int }_{0}^{{h}_{o}}{\rho }_{o}{\left(\frac{1}{2}{u}^{2}+gz\cos\theta \right)}_{f}\left({u}_{o}\right)dz={\Psi }_{e}{\int }_{0}^{{h}_{f}}{\rho }_{f}{\left(\frac{1}{2}{u}^{2}+gz\cos\theta \right)}_{o}\left({u}_{f}\right)dz,\end{array}$$

(13)

and Eq. (12) thus reduces to

$$\begin{array}{c}\underset{cs}{\overset{}{\iint }}\left(\rho {e}_{t}\right)\left(\overrightarrow{V}\cdot \overrightarrow{n}\right)dA=\left({\Psi }_{e}-1\right){\int }_{0}^{{h}_{f}}{\rho }_{f}{\left(\frac{1}{2}{u}^{2}+gz\cos\theta \right)}_{f}\left({u}_{f}\right)dz\\ =\left({\Psi }_{e}-1\right){\rho }_{f}{u}_{f}{h}_{f}{\left(\frac{1}{2}{u}^{2}+gz\cos\theta \right)}_{f},\end{array}$$

(14)

where the energy density $\frac{1}{2}{u}^{2}+gz\cos\theta$ is assumed to be constant along the incoming flow depth.

The first term on the right-hand side of Eq. (5) describes the work done by the surface force applied to the surface of the control volume and can be formulated as

$$\begin{array}{c}\underset{cs}{\overset{}{\iint }}\overrightarrow{F}\cdot \overrightarrow{V}dA={\int }_{0}^{{h}_{f}}{p}_{f}{u}_{f}dz-B{\int }_{0}^{{h}_{o}}{p}_{o}{u}_{o}dz\\ =\frac{1}{2}{\kappa }_{f}{\rho }_{f}g{{h}_{f}}^{2}{u}_{f}\cos\theta -\frac{1}{2}B{\kappa }_{o}{\rho }_{f}g{{h}_{r}}^{2}{u}_{o}\cos\theta .\end{array}$$

(15)

It is assumed that the outflow velocity can be described by the linear formula

$$\begin{array}{c}{u}_{o}={\Psi }_{u}{u}_{f}.\end{array}$$

(16)

Combining Eqs. (11) and (14)–(16) yields

$$\begin{array}{c}{\rho }_{r}{\left(\frac{1}{2}{u}^{2}+gz\cos\theta \right)}_{r}{u}_{r}{b}_{r}+\left({\Psi }_{e}-1\right){\rho }_{f}{u}_{f}{h}_{f}{\left(\frac{1}{2}{u}^{2}+gz\cos\theta \right)}_{f}\\ =\frac{1}{2}{\kappa }_{f}{\rho }_{f}g{{h}_{f}}^{2}{u}_{f}\cos\theta -\frac{1}{2}B{\Psi }_{u}{\kappa }_{o}{\rho }_{f}g{{h}_{r}}^{2}{u}_{f}\cos\theta .\end{array}$$

(17)

We solve Eq. (17) for the period during which the run-up reaches and remains at its peak; i.e., the solved ${h}_{r}$ is regarded as the maximum value. When the energy per unit flow mass ($\frac{1}{2}{u}^{2}+gz\cos\theta$) is adopted as ( $\frac{1}{2}{{u}_{f}}^{2}+g{h}_{f}\cos\theta$), we obtain

$$\begin{array}{c}\frac{{\left({h}_{r}\right)}_{max}}{{h}_{f}}={\left[\frac{{\kappa }_{f}+\left(1-{\Psi }_{e}\right)\left({{N}_{Fr}}^{2}+2\right)}{{\Psi }_{u}B{\kappa }_{o}}\right]}^\frac{1}{2}.\end{array}$$

(18)

Equations (9) and (18) are jointly used for predicting the peak impact force and peak run-up height of the granular flow against the baffle structures. It is noted that the computed impact force is the total force exerted on the baffle array and not that exerted on a single baffle.

Determination of empirical coefficients

${\Psi }_{e}$, ${\Psi }_{m}$, and ${\Psi }_{u}$ are important coefficients for a slit structure and but have no widely accepted models. Assuming that the outflow process is steady and can be described by a linear relation, we analyze the DEM data and obtain ${\Psi }_{m}$ and ${\Psi }_{e}$. It is difficult to characterize the average velocity of the outflow as the flow front is discrete and agitated, and ${\Psi }_{u}$ is thus roughly obtained from ${\Psi }_{e}/{\Psi }_{m}$ for simplicity (here ${\Psi }_{e}$ is mainly estimated using the data of kinetic energy). The energy data are more convergent with less dependence on the Froude number (${N}_{Fr}$) than the momentum data, and we thus use data averaged for the same slope angle to obtain Eq. (19) by linear fitting and the error in Eq. (19) is within $\pm$ 10% as shown in Fig. 10a. ${\Psi }_{m}$ is a more complex function of both ${N}_{Fr}$ and ${S}_{B}/\delta$, as shown by Eq. (20) obtained through the linear fitting of the data of 16-mm particle flows (orange line in Fig. 10b) and empirical linear interpolation considering different values of ${S}_{B}/\delta$. It is noted that the coefficient of 0.11 in Eq. (21) is subjectively given with consideration of whether the calculated ${\Psi }_{m}$ for 7-mm particle flows (black line in Fig. 10b) can bind the numerical data. The equations are

Fig. 10

Determination of empirical coefficients: a the kinetic energy reduction coefficient ${\psi }_{e}$ and b the momentum reduction coefficient ${\psi }_{m}$. The details of data analysis are presented in Zhang and Huang (2022c)

$$\begin{array}{c}{\Psi }_{e}=0.116+0.0281\frac{{S}_{B}}{\delta },\end{array}$$

(19)

$$\begin{array}{c}{\Psi }_{m}=\left(0.26+0.0388{N}_{Fr}\right)\left[1+0.11*\left(\frac{{S}_{B}}{\delta }-4.375\right)\right].\end{array}$$

(20)

Equation (18) does not consider the energy loss due to friction, which can be implicitly encompassed in the coefficients ${\kappa }_{f}$ and ${\kappa }_{o}$. The longitudinal stress coefficient depends on the deformation stage of the granular material (Faug 2021) and ranges 0.2–5.0 for debris flow (Iverson et al. 2016). We conducted a sensitivity analysis of the impact force and run-up height of granular flow against the baffle array to ${\kappa }_{f}$ and ${\kappa }_{o}$ as shown in Fig. 11. It is observed that ${\kappa }_{f}$ has less effect on ${h}_{r}$/${h}_{f}$ than ${\kappa }_{o}$, indicating that the behavior of the outflow material is much more important. ${\alpha }_{dyn}$ is much more dependent on ${\kappa }_{f}$ for smaller ${N}_{Fr}$ (< 4). ${\alpha }_{dyn}$ is not affected by ${\kappa }_{o}$ because a value of zero is adopted for ${\gamma }_{r}$.

Fig. 11

Analysis of the sensitivity of the normalized impact force ${\alpha }_{dyn}$ and ${h}_{r}$/${h}_{f}$ to a ${\kappa }_{f}$ (${\Psi }_{e}$= 0.3, ${\Psi }_{m}$= 0.6, ${\kappa }_{o}$= 1.0, and ${\gamma }_{r}$= 0) and b ${\kappa }_{o}$ (${\Psi }_{e}$ = 0.3, ${\Psi }_{m}$= 0.6, ${\kappa }_{f}$= 1.0 and ${\gamma }_{r}$= 0)

It is noted that Eq. (18) is valid only when the run-up of the granular flow reaches its peak and remains at the peak for a while, and at this time, the Froude number of the incoming flow has been largely attenuated because of the energy dissipation of the barrier structure, whereas when feeding the run-up model, it is challenging to obtain sophisticated incoming flow properties (Albaba et al. 2018) and the free-flow properties are thus often used for simplicity, which may result in the overestimation of the run-up height. Additionally, the inappropriate consideration of the energy consumption during debris–baffle interaction may result in the overestimation of the run-up height. However, Eq. (9) is generally true despite the fact that we ignore some factors that are less important. Inputting a run-up height that is too high into Eq. (10) may lead to a negative value of ${\alpha }_{dyn}$, which is physically meaningless, as shown in Fig. 12. We thus introduce ${\gamma }_{r}$ to compensate for the overestimation of ${h}_{r}$/${h}_{f}$. ${\gamma }_{r}$ has a notable effect on ${\alpha }_{dyn}$ for smaller ${N}_{Fr}$ (< 4). In addition, the introduction of ${\gamma }_{r}$ has another benefit.

Fig. 12

Analysis of the sensitivity to ${\gamma }_{r}$ (${\Psi }_{e}$= 0.3, ${\Psi }_{m}$= 0.6, ${\kappa }_{f}$= 1.0, and ${\kappa }_{o}$= 1.0)

Comparison of the numerical results and analytical results

The data of monodisperse granular flows acting against baffle R1 are used to verify the proposed debris–baffle interaction model as summarized in Tables 3, 6, and 7. ${h}_{r}$ obtained by DEM simulation is normalized by the maximum flow depth of free flow (${h}_{f\_max}$), and the simulation-generated force (${F}_{n}$, total impact force per unit chute width) is normalized by the maximum flow velocity (${u}_{f\_max}$), maximum flow depth (${h}_{f\_max}$), and maximum flow density (${\rho }_{f\_max}$) of the free flows.

Table 6 Peak values of the impact force of monodisperse granular flows acting on baffles R1 and R2. Force unit: N

Table 7 Peak values of the run-up height of monodisperse granular flows against baffles R1 and R2. Length unit: m

Figure 13a compares the measured ${h}_{r\_max}/{h}_{f\_max}$ and ${h}_{r\_max}/{h}_{f\_max}$ calculated by feeding Eq. (19) with ${N}_{Fr}$ from Table 3 and the longitudinal pressure coefficients (${\kappa }_{f}$= 1.0 and ${\kappa }_{o}$ = 2.5). It is observed that Eq. (18) performs well as it generally captures the magnitude and evolution trend of the peak run-up height of monogranular flows against the baffle structure. Larger errors are observed for flows with larger (16- and 14-mm) particles, especially at lower ${N}_{Fr}$.

Fig. 13

Model verification. a Comparison of the run-up height between numerical data and model calculated data, where ${h}_{r}$ obtained in DEM simulation is normalized using the maximum flow depth of free flows (${h}_{f\_max}$). b Comparison of the impact force between numerical data and model calculated data, where the measured ${\alpha }_{dyn}$ is obtained by normalizing the simulation-generated force (${F}_{n}$, total impact force per unit chute width) using the maximum flow velocity (${u}_{f\_max}$), maximum flow depth (${h}_{f\_max}$), and maximum flow density (${\rho }_{f\_max}$) of free flows. The feeding parameters (${N}_{Fr}$) for empirical models are summarized in Table 3. ${\kappa }_{f}$ = 1.0, ${\kappa }_{o}$ = 2.5, and ${\gamma }_{r}$ = 0. ${\alpha }_{0}$ is set at 0 and $9.3{{N}_{Fr}}^{-1.9}$

Figure 13b compares the measured ${\alpha }_{dyn}$ and ${\alpha }_{dyn}$ calculated (data with gray background) by feeding Eq. (10) with ${N}_{Fr}$ from Table 3 and the longitudinal pressure coefficient (${\kappa }_{f}$= 1.0, ${\kappa }_{o}$ = 2.5, ${\gamma }_{r}$= 0 and ${\alpha }_{0}=0$). It is seen that the performance of Eq. (10) is not satisfying, especially for flows with larger ${N}_{Fr}$ with the largest error even reaching nearly 50%, although we have fed Eq. (10) with ${\gamma }_{r}$ = 0, which is the lowest correction coefficient as discussed in Fig. 12.

Discussion

Model improvement

Figure 13 demonstrates that the proposed model does not perform satisfactorily for monodisperse granular flows with lower ${N}_{Fr}$ (approximately 4–5). The reason for the poor performance may be the assumption that the granular impact against the baffles follows a vertical-jet model no matter the range of ${N}_{Fr}$, and this assumption may not be true for granular flows with lower ${N}_{Fr}$. For debris flow, Armanini et al. (2019) indicated that if the velocity of the incoming flow is not sufficiently high, the impact process would undergo another distinct pattern. Song et al. (2021) further demonstrated that the jet model is more appropriate for debris flows with ${N}_{Fr}$ higher than 3–4. As a result, the Froude effect is an important consideration in the development of the impact model. The particle size effect may be attributed to the overestimation of the effect of energy discharge on the granular flow run-up and the linear discharge assumption not being strictly true. However, although not perfect, Eq. (18) for the run-up height prediction is acceptable for engineering design purposes.

The estimation of the impact force for the granular impact is much more complex and difficult (Faug 2021; Li et al. 2020; Song et al. 2021). The error in Eq. (9) for predicting the impact force cannot be ignored or tolerated in engineering design because the underestimation of the impact force may lead to the destruction of the baffle structures. Revisiting the momentum balance (Eq. (7)), we see that besides the error due to the overestimation of ${h}_{r}$/${h}_{f}$ as ${\gamma }_{r}$ is set at zero, the reasons may include four aspects. (1) The momentum discharge is not strictly linear as assumed and cannot be perfectly described by Eq. (20), which may lead to errors in the prediction. However, we hold this is not the main source of error. (2) In Eq. (9), we have largely ignored the contribution of the static force of the climbed material on the baffle array, which may important especially for flows with lower ${N}_{Fr}$ as indicated by Fig. 6a (where the static force component can account for more than 50% for 7-mm particle flow under a slope of 25°) and as demonstrated by Jiang and Towhata (2013). Again, this is not the main source of error because the maximum prediction error is observed for larger particles (12.5–16 mm) as depicted by Fig. 13b, whereas in the inset of Fig. 6b, the static force component for 16-mm particle flow under a slope of 25° is small (< 5%). (3) Eq. (9) implies that the impact force exerted by the incoming flow is transmitted by the retarding material between the front and the baffle array, while the granular material accumulating behind structures can serve as a cushioning layer assisting the dissipation of the momentum of the subsequent flow (Koo et al. 2016; Zhang et al. 2020), and the direct impact of granular flow on the baffle is thus not properly considered. (4) Eq. (9) is established on the basis of the flow mechanics of commonly found fluid but without consideration of the granular impact characteristics; the particle size is an important consideration for granular impacts (Cui et al. 2018; Goodwin and Choi 2021; Jiang et al. 2015; Song et al. 2018), as is true for our results. For example, ignoring both ${\Psi }_{m}$ and ${\gamma }_{r}$ in Eq. (9) yields the expression ($1+1/2{{N}_{Fr}}^{2}$), which is the typical expression for debris flow proposed by Armanini et al. (2019), but ${\alpha }_{dyn}$ for 16-mm particle flow (and also 12.5- and 14-mm particle flow) at a slope angle of 25° in Fig. 13b exceeds the prediction of ($1+1/2{{N}_{Fr}}^{2}$) by a factor exceeding 1.2. We believe that error sources (3) and (4) are dominant but difficult to mathematically model. As a result, we introduce ${\alpha }_{0}$, another empirical coefficient, to improve the performance of Eq. (9) in the estimation of the impact force. ${\alpha }_{0}$, as formulated by Eq. (21), is obtained through the nonlinear fitting of the error data (Fig. 14), namely the discrepancy between the measurements and values calculated using Eq. (9). By introducing ${\alpha }_{0}$, the modification is much improved, as shown by the data with the pale-yellow background in Fig. 13b. The formulation of ${\alpha }_{0}$ is

Fig. 14

Analysis of the prediction error of the impact force

$$\begin{array}{c}{\alpha }_{0}=9.3{{N}_{Fr}}^{-1.9}.\end{array}$$

(21)

Baffle design considering the inhomogeneity of the flow material

Tables 5 and 8 summarize the absolute values of the run-up height and impact force of bidisperse granular flows. ${h}_{r\_max}/{h}_{f\_max}$ and ${\alpha }_{dyn}$ for bidisperse granular flows against baffle R1 are presented against ${N}_{Fr}$ (scattered points) in Fig. 15, and the model calculations (solid lines) are obtained by feeding Eqs. (18) and (19) with ${N}_{Fr}$ listed in Table 5 and particle sizes of 8, 12, and 16 mm, respectively, as the bidisperse granular flows considered in this paper mainly contain 8- and 16-mm particles. Additionally, empirical coefficients are set the same as for monodisperse granular flows. Figure 15 shows that if the largest particle size of the monodisperse granular flow is used, ${h}_{r\_max}/{h}_{f\_max}$ and ${\alpha }_{dyn}$ are overestimated but with the predicted values falling on the safer side considering the engineering design purpose. However, for smaller prediction error, it seems that the averaged particle size is more appropriate, while it is noted that we consider only bidisperse granular flows with particle percentage no less than 10%.

Table 8 Peak values of the impact force and run-up height of bidisperse granular flows against baffles R1 and R2. Length unit: m. Force unit: N

Fig. 15

Baffle design considering the material homogeneity of granular flow. ${\kappa }_{f}$ = 1.0, ${\kappa }_{o}$ = 2.5, ${\gamma }_{r}$ = 0, and ${\alpha }_{0} = 9.3{{N}_{Fr}}^{-1.9}$

Baffle design considering unsteady flow dynamics

The selection of design parameters, especially the flow depth, is important when using the proposed impact models because the flow depth varies along the flow length. Although the flow velocity also varies, the maximum velocity is commonly suggested in design guidelines (Kwan 2012) and the literature (Faug 2021; Jiang et al. 2015; Koo et al. 2016; Song et al. 2021), whereas the selection of the flow depth remains obscure. The flow front depth (Ng et al. 2016) and maximum flow depth (Kwan 2012) are always adopted, but no study has made a detailed investigation of the effects of these parameters. Another problem is the definition of the flow front, which is challenging because the flow front is often wedge-shaped. Ng et al. (2019) suggested the maximum depth of the frontmost 5% of a flow should be selected in calculations of the impact force and pile-up height for dry granular flows. Table 4 summarizes the frontal depth (${h}_{f\_fro}$) and corresponding Froude number (${N}_{Fr}^{^{\prime}}$). It is noted that ${N}_{Fr}^{^{\prime}}$ is larger than ${N}_{Fr}$, which is calculated using the maximum flow depth (${h}_{f\_max}$).

The adoption of different strategies of Froude characterization could affect the empirical coefficients (${\Psi }_{m}$ and ${\alpha }_{0}$), making it meaningless to compare the performances of impact models when feeding different Froude numbers. Therefore, we only present a comparison of the run-up height prediction, because ${\Psi }_{e}$ in the run-up height prediction model (Eq. (19)) is independent of the Froude number. ${h}_{r}$ obtained in DEM simulation is normalized by the frontal flow depth of the free flows (${h}_{f\_fro}$). The results are presented in Fig. 16. It is seen that the model performance performs unsatisfactorily especially for a larger Froude number, as ${h}_{r\_max}/{h}_{f\_fro}$ is largely underestimated. A comparison with the results presented in Fig. 13a suggests that the maximum flow depth and maximum flow velocity should be used in baffle design.

Fig. 16

Baffle design considering the unsteady dynamics of granular flow. The feeding parameters (${N}_{Fr}^{^{\prime}}$) for the empirical models are summarized in Table 4. ${\kappa }_{f}$ = 1.0, ${\kappa }_{o}$ = 2.5, and ${\gamma }_{r}$ = 0. The straight line represents a reference line depicting the ideal agreement between the measured and calculated value

Limitations and perspectives

The limitations of this paper lie in two aspects. One the one hand, we have only considered limited cases. At current stage, researches about baffles mostly focused on dry granular avalanches under reduced stress level. Although it is demonstrated that granular mobility is independent with stress level when the flow moves en mass (Cagnoli 2021), the sensitivity of arching effect of slit structure to stress level has not been fully investigated. In addition, with the influence of interstitial fluid, the energy dissipation of debris–baffle interaction could be distinct. And thus, the results presented in this paper are more relevant to situations having similar conditions (flow types, ${N}_{Fr}$ and ${S}_{B}/\delta$). On the other hand, the proposed model was verified using a limited dataset. It should be noted that the empirical coefficients like ${\Psi }_{e}$ and ${\Psi }_{m}$ are highly dependent on friction properties of granular soils. Our model verification only can justify the credibility of the jet model, but for the determination of empirical coefficients needs further investigation. Thus, for safer engineering design, the proposed model should be tested using more data obtained under various debris–barrier interaction conditions and especially field data, although field data are scarce and difficult to obtain. Another important issue is the boulder impact force of the granular flow, which is important to barrier design (Goodwin and Choi 2021; Song et al. 2018), whereas our models only address the debris impact load. The calculation of the boulder-generated impulse load thus needs to be discussed in detail and encompassed into the design model for baffle structures.

Conclusion

This paper aims to improve the baffle design strategy by understanding the impact dynamics of granular flows with different particle size distribution and Froude characteristics against baffle array and developing a physically based model to estimate the peak values of impact force and run-up height. For such a purpose, a series of DEM simulations was conducted, and the following conclusions are drawn from the results of the study:

• 1. The interparticle energy loss is enhanced while particle–flume energy loss is reduced because of the function of baffle structure, and with the increase of Froude number of granular flow, the difference values of interparticle energy loss between baffle cases and free flow cases are increased but of the particle–flume energy loss are reduced. Besides, the energy loss due to particle–baffle interaction is negligible.

• 2. For monodisperse granular flow, larger particles have a higher force impulse and larger values of the smoothed data of the force acting on the baffle array. For bidisperse granular flow, with an increasing percentage of larger particles, the force impulse becomes appreciable, and the peak of smoothed force data does not change monotonously but roughly larger. This difference between monodisperse and bidisperse granular flow impact is attributed to the hard contact inducing stronger force for larger particles and arching effect of the debris–baffle interaction, and the former is dominant.

• 3. The dynamic force generated by moving particles is dominant during debris–baffle interaction, and with the increase of particle size and ${N}_{Fr}$, the static force component generated by the dead zone behind the baffles becomes much less important. It is suggested that baffle design could ignore the static force component, at least for rapid granular flow with a smaller ratio of the baffle slit size to particle size.

• 4. For the impact of bidisperse granular flow, the effect of larger particles is only dominant when the percentage of larger particles is larger because fine debris provides a cushioning effect for the boulder impact, and the fine debris impact is considerable even at a lower percentage of fine debris and should not be ignored.

• 5. The impact force is largely attenuated after passing the first baffle array (by more than 50%), and baffle design can take the performance of the first baffle array as a reference. A jet-based impact model was proposed to calculate the peak value of total impact force and the run-up height against the first baffle array considering the Froude number and the ratio of the baffle slit size to particle size, and the model was verified using numerical data.

• 6. Based on the proposed model, we further suggest that when considering flow material inhomogeneity in baffle design, the largest particle size with a percentage no less than 10% should be used as the characterized particle size; and when considering the unsteady flow dynamics, the maximum flow depth and velocity be used as design parameters.

Appendix. DEM contact model

The DEM simulations in this paper are conducted using EDEM software, which offers an efficient contact model referred to as a Hertz–Mindlin (no-slip) contact model combined with an anti-rolling model to compensate for the simplification of the real particle shape in DEM simulation:

$$\begin{array}{c}{F}_{n}^{c}=-{K}_{n}{\lambda }_{n}+{D}_{n}{v}_{n}^{rel},\end{array}$$

(22)

$$\begin{array}{c}{F}_{t}^{c}=min\left\{{K}_{t}{\lambda }_{t}+{D}_{t}{v}_{t}^{rel}, {\mu }_{s}{F}_{n}^{c}\right\},\end{array}$$

(23)

$$\begin{array}{c}{M}_{r}={-\mu }_{r}{F}_{n}^{c}{d}_{i}{\widehat{\omega }}_{i}.\end{array}$$

(24)

Here, the subscripts n and t respectively indicate the normal and tangential directions. And the definitions of variables are presented in Nomenclature.

Nomenclature
DEM contact model	${F}_{n}^{c}$, ${F}_{t}^{c}$: normal and tangential contact force; K: elastic stiffness constant; D: damping coefficient; $\lambda$: overlap; ${v}^{rel}:$ relative velocity; ${\mu }_{s}:$coefficient of Coulomb friction; ${\mu }_{r}$: rolling friction coefficient; ${d}_{i}$: distance between the contact point and center of mass; ${\widehat{\omega }}_{i}$: unit angular velocity.
Baffle layout	${L}_{B}$: baffle array spacing; ${S}_{B}$: slit spacing; ${W}_{F}$: flume width; ${h}_{B}$: baffle height; ${W}_{B}$: baffle width; B: opening ratio.
Flow properties	${h}_{f}$: flow depth; ${u}_{f}$: flow velocity; $\delta$: particle diameter; ${u}_{f}$: flow velocity; ${\phi }_{f}$: solid volume fraction; ${\rho }_{s}$: particle density: ${N}_{Fr}$: Froude number; ${E}_{k}$: kinetic energy: ${E}_{p}$: potential energy; ${E}_{d}$: dissipated energy; ${E}_{r}$: energy loss due to particle removal; ${E}_{s}$: elastic strain energy.
Design Parameters	${F}_{n}$: total impact force; ${F}_{n}^{s}$: static force component; ${F}_{n}^{d}$: dynamic force component; ${\Psi }_{m}$: momentum reduction coefficient; ${\Psi }_{u}$: velocity reduction coefficient; ${h}_{r}$: run-up height; ${\Psi }_{e}$: energy reduction coefficient; ${\kappa }_{f}$: longitudinal pressure coefficient; ${\gamma }_{r}$: empirical coefficient for compensation of the overestimation of run-up height; ${\alpha }_{0}$: force correction coefficient.