Key message

  • Wolbachia has been widely used to control arboviruses, but how fecundity variation of the vector impacts Wolbachia establishment remains unknown.

  • Fecundity overdispersion was observed in most studied insects, and it may help Wolbachia to establish from low frequencies but reduce the certainty of fixation at high frequencies.

  • Fecundity variation should be considered in Wolbachia-based vector replacement strategies, and more transfected individuals may need to be released across a longer period than is currently used.

Introduction

Ubiquitous arthropod-borne viruses (arboviruses) have been posing threats to human health for a long time. The pandemic of dengue virus infection has spread to five continents at an unprecedentedly high rate of 390 million cases per year, placing over 3 billion people at risk of the disease (Bhatt et al. 2013; Brady and Hay 2020). Since the first noteworthy epidemic on Yap Island in Micronesia in 2007, Zika virus has caused massive outbreaks throughout South America, Central America, and the Caribbean (Cugola et al. 2016; Fauci and Morens 2016). Besides the developments of effective vaccines and therapeutics against pathogenic arboviruses, control of their vector populations also plays a critical role in epidemic prevention (Ritchie et al. 2018). However, suppressing the vectors through chemical insecticides is challenged by the evolution of resistance (Moyes et al. 2017) and criticism on the damages to ecosystems caused by the chemicals (Pance 2018). Recently, more effective, natural, and self-sustaining biocontrol strategies using endosymbionts have been proposed and developed (Dorigatti et al. 2018; Ghosh et al. 2018; Ross et al. 2019).

Wolbachia spp. are probably the most abundant endosymbiotic intracellular bacteria infecting more than half of the million-plus species of insects (Hilgenboecker et al. 2008; Zug et al. 2012). Some Wolbachia strains have been recognized to effectively inhibit the proliferation and transmission of various RNA arboviruses in their host insects (Hedges et al. 2008; Teixeira et al. 2008), probably through competition over resources and innate immune priming (Terradas and McGraw 2017). However, Wolbachia do not naturally occur in some arboviral vectors including the primary vector of Zika, dengue, malaria, and chikungunya (i.e. the Aedes aegypti mosquito). A promising avenue for tackling this issue is release of transinfected vectors, which aims at population replacement with virus-blocking Wolbachia. So far, introduction of wMel Wolbachia strains from Drosophila melanogaster into A. aegypti is the leading transinfection mode, with operational releases in ten countries by the World Mosquito Program (Ritchie et al. 2018). These wMel-releases have resulted in a dramatic reduction (up to 97%) of dengue incidence in the project sites where Wolbachia have established at high frequency, in contrast to only a moderate reduction (c. 50%) in hot areas such as Brazil (https://www.worldmosquitoprogram.org/). In the light of large reduction in invasiveness and virus-blocking capacities for wMel at high temperatures in contrast to wAlbB from A. albopictus which is much less susceptible to similar temperatures (Ant et al. 2018; Ross et al. 2017), wAlbB may be well suited for population replacement in hot tropical environments. Recently, A. aegypti mosquitoes carrying wAlbB were released at six sites in Kuala Lumpur, Malaysia (Nazni et al. 2019). The strain has been successfully established and maintained at high frequency at some sites, but large fluctuations of Wolbachia frequency were also observed (Nazni et al. 2019).

A key driver for Wolbachia replacement is the induction of cytoplasmic incompatibility (CI), which elevates the mortality of embryos of matings between infected males and uninfected females or females carrying an incompatible Wolbachia strain (Hoffmann and Turelli 1997; Laven 1956). Because of maternal transmission of Wolbachia, CI provides infected females with a frequency-dependent fitness advantage (Caspari and Watson 1959). Successful establishment of Wolbachia then depends on CI outweighing possible fitness cost on infected hosts and outweighing incomplete maternal transmission of infection (Hancock et al. 2011; Turelli 1994). This creates bistable frequency dynamics under which the infection frequency must exceed a threshold for Wolbachia to spread rather than to be lost from a population (Caspari and Watson 1959). Other dynamics, such as Fisherian dynamics under which Wolbachia will always spread throughout the host populations even with very low initial numbers in the absence of CI (Barton and Turelli 2011), are seldom reported or utilized in arbovirus control (but see Kriesner et al. 2013).

However, large fluctuations in infection frequency and thereby obstructions of Wolbachia invasion confronting field replacement releases are beyond the prediction of the model. In the A. aegypti population of Nogotirto, Indonesia, wMel frequency was raised to more than 80% at the end of field release period, but then oscillated strongly between 50 and 100% (Tantowijoyo et al. 2020). Collapse of wMel introduction has also been observed in Westcourt, Australia (Schmidt et al. 2017) and Rio de Janeiro, Brazil (Garcia et al. 2019). Following the releases of wAlbB-carrying A. aegypti in Malaysia, the Wolbachia frequency once exceeded 95% but subsequently fluctuated and even decreased to 20% at two of four primary intervention sites (Nazni et al. 2019). Temperature susceptibility of Wolbachia strain or lack of insecticide resistance in released mosquitoes may account for some unavailing releases (Ant et al. 2018; Garcia et al. 2019), but was proved to have minor effect in some other cases (e.g. Nazni et al. 2019).

An alternative and probably more general factor that underlies large fluctuations and thereby collapse of Wolbachia introduction is stochastic processes (Engelstadter and Telschow 2009). Previous drift models showed weak impacts of stochasticity on Wolbachia dynamics in large host populations, leading to a conclusion that employment of Wolbachia as a driving element in pest control normally does not need to consider stochastic effects (Egas et al. 2002; Jansen et al. 2008). However, those models invoked the population genetic parameter ‘effective population size’, i.e. the size of an idealized panmictic population that experiences the same strength of genetic drift as the actual population (Fisher 1930; Wright 1931). This parameter facilitates modelling but can hardly assist Wolbachia-based epidemic management, because effective population size is usually unknown for most vector populations and is difficult to estimate accurately (Wang 2016). In contrast, more variation in fecundity than expected by the Poisson distribution (termed ‘overdispersion’), the latter assumed in the Wright–Fisher idealized population (Kimura and Crow 1963), has been observed in many insect species including mosquitoes (Blackmore and Lord 2000; Ferguson et al. 2003; Vezilier et al. 2012). It should be expected that such overdispersion generates more stochasticity to the invasion dynamics of Wolbachia and, importantly, that the degree of the overdispersion can be easily estimated in the laboratory or in the field. Overdispersion may also provide an explanation for the paradox between the model prediction of poor performance of Wolbachia in a novel host from few infections and the reality that Wolbachia have successfully infected millions of arthropod species (Fenton et al. 2011). Nevertheless, fecundity overdispersion has rarely been evaluated empirically in insect populations, nor is it understood how fecundity overdispersion impacts the fates of Wolbachia in a local host population.

Here we present evidence of fecundity overdispersion in insects through reanalyzing empirical data sets and construct a general Wolbachia frequency-dynamic model explicitly considering host fecundity variation. Based on the empirical estimates of overdispersion, we performed a general analysis using the model. We then further used the model to estimate the number of infected vectors required for successful population replacement, to offer some operational suggestions for optimum release strategies in Wolbachia-based biocontrol. Additionally, we also explore how and how often Wolbachia succeed to invade a novel host population starting from a single infection, which may provide mechanistic insights into the ubiquity of those endosymbionts.

Materials and method

Literature search

We conducted a literature search using ‘TI = (fecundity) and TS = (insect*)' on the ISI Web of Knowledge database (http://apps.webofknowledge.com) in April 2020 to identify experimental data of insect fecundity, yielding a total of 1914 records. We also searched for the fecundity of A. aegypti using ‘TS = (A. aegypti and fecundity)', yielding 672 records. We then screened these records according to the following criteria: (i) realized fecundity (not potential fecundity) was measured, (ii) insect fecundity was counted at the individual level, and (iii) there was at least one group of studied insects free of the experimental treatments that are unlikely to occur in natural conditions (e.g. pesticides and RNA interference). After screening, we retained 56 studies for estimation of fecundity dispersion (Appendix S1, Supporting Information).

Estimation of fecundity dispersion

For each species examined in each retained study, we calculated the sample size (n), the mean (\(\stackrel{-}{x}\)), and variance (S2) of fecundity from the deposited data. If original data were not available, these statistics were extracted from main texts or graphs only concerning the insect individuals that met the third criterion. When multiple groups were needed to be combined together (the conditions could occur in the same population, e.g. treatments with different hosts), but the statistics were reported separately for those groups, the total statistics were calculated as \(\stackrel{-}{x}=\sum {n}_{i}{\stackrel{-}{x}}_{i}/\sum {n}_{i}\) and \({S}^{2}=\sum {n}_{i}\left({S}_{i}^{2}+{\stackrel{-}{x}}_{i}^{2}\right)/\sum {n}_{i}-{\left(\sum {n}_{i}{\stackrel{-}{x}}_{i}/\sum {n}_{i}\right)}^{2}\) (see Appendix S2). In the cases where only the ranges of fecundity were reported for each group, we randomly sampled ni values from the corresponding uniform distribution. We then pooled all groups together and calculated the summary statistics based on 10,000 simulations for each species. The Kolmogorov–Smirnov test was used to examine whether the fecundity data were Poisson distributed in each species. If not, overdispersion parameter θ was estimated by \(\theta ={\stackrel{-}{x}}^{2}/\left({S}^{2}-\stackrel{-}{x}\right)\). Zero inflation is a source of overdispersion (Linden and Mantyniemi 2011), but zeros might have been eliminated in data analyses, leading to an underestimation of overdispersion. Hence, we recorded whether zero values were included in each data set.

The model of Wolbachia dynamics

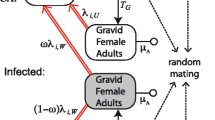
We construct a general dynamic model of infection frequency to describe how host fecundity variation together with CI and infection cost impact the fate of Wolbachia in a host population. We focus on CI because it is the most frequently found Wolbachia-induced reproductive effect (Werren et al. 2008) and most relevant to Wolbachia invasion for pest management (Ritchie et al. 2018).

We denote the fecundity of the ith infected female and that of the jth uninfected female using FI(i) and FU(j) (both can be zero), which have expected values of λ1 and λ2, respectively. The fecundity cost due to Wolbachia parasitism is thus given by sf = 1–λ1/λ2. We let H < 1 represent the hatch rate from a CI cross relative to other crosses, and let μ ≤ 1 denote the probability for an infected female to transmit Wolbachia to its eggs. Thus, sh = 1–H quantifies the intensity of CI, and 1–μ quantifies imperfect maternal transmission. We assume discrete generations of the host population, but generation overlap and age structure may be incorporated into our model like Turelli (2010) and Hancock et al. (2011). Panmixia is assumed for the host population, and more realistic nonrandom mating may be reconciled by partitioning the population into several panmictic subpopulations linked via gene flow.

The population dynamics of Wolbachia can be modelled by tracking changes in the frequency of infected hosts across generations. If the frequency of hosts being infected at generation t is pt, and the total number of reproductive females within the population is N, the numbers of crosses are then expected to be Npt2, Npt(1–pt), Npt(1–pt), and N(1–pt)2, for IF × IM, IF × UM, UF × IM, and UF × UM, respectively (I: infected, U: uninfected; F: female, M: male). Multiplying them by the corresponding fecundity and hatch rate, we obtain the recursion equation

$${p}_{{t}+1}=\frac{\mu {\sum }_{i=1}^{{\rm {Np}}_{t}}{F}_{\rm {I}(i)}}{{\sum }_{i=1}^{N{p}_{\rm {t}}}{F}_{\rm {I}(i)}+{\sum }_{j=1}^{N[1-\left(1+{s}_{\rm {h}}\right){p}_{\rm {t}}+{s}_{\rm {h}}{p}_{\rm {t}}^{2}]}{F}_{\rm {U}(j)}}$$
(1)

Stochastic deviation of the numbers of crosses from the expectations may exist due to finite population size, but we argue that the variation can be regarded as a source of dispersion in fecundity (FI and FU). Therefore, Eq. (1) holds in such cases. For investigating the role of host fecundity variation in the dynamics of Wolbachia, we characterize FI and FU in the following three cases.

Case 1: No variation of fecundity

We first assume constant fecundity, that is, FI = λ1 and FU = λ2. Then, Eq. (1) reduces to

$${p}_{t+1}=\frac{(1-{s}_{f})\mu }{1+{s}_{h}{p}_{t}^{2}-\left({s}_{f}+{s}_{h}\right){p}_{t}}\bullet {p}_{t}$$
(2)

and yields three equilibria by setting \({p}_{\mathrm{t}+1}={p}_{\mathrm{t}}\):

$$p = 0,\,p = \frac{{{s_f} + {s_h} - \sqrt {{{\left( {{s_f} - {s_h}} \right)}^2} - 4{s_h}\left( {1 - \mu } \right)\left( {1 - {s_f}} \right)} }}{{2{s_h}}},\,{\rm and}\,p = \frac{{{s_f} + {s_h} + \sqrt {{{\left( {{s_f} - {s_h}} \right)}^2} - 4{s_h}\left( {1 - \mu } \right)\left( {1 - {s_f}} \right)} }}{{2{s_h}}}$$

For a simple example, if we assume perfect maternal transmission (i.e. μ = 1), there will be two stable equilibria (p = 0 and p = 1) and one unstable equilibrium (\(\widehat{p}={s}_{\rm {f}}/{s}_{\rm {h}}\)) for the infection frequency. When the initial frequency (p0) is above the establishment threshold \(\widehat{p}\), Wolbachia will spread throughout the whole population, but when p0 < \(\widehat{p}\), Wolbachia will ultimately be lost in this population. Thus, this case corresponds to those deterministic models that predict bistable dynamics (Barton and Turelli 2011; Caspari and Watson 1959; Turelli and Barton 2017; Turelli and Hoffmann 1991).

Case 2: Poisson distribution for dispersed fecundity

We use the Poisson distribution to model moderate variation of host fecundity: FI ~ Poisson (λ1) and FU ~ Poisson (λ2), where the expected variances of FI and FU equal to their means (λ1 and λ2), respectively. This case corresponds to stochastic models that test for the effects of drift (Jansen et al. 2008; Rigaud and Rousset 1996).

Case 3: Negative binomial distribution for overdispersed fecundity

We take the negative binomial distribution to model FI and FU to include the overdispersion of host fecundity, because this distribution has a good performance in characterizing overdispersion of biological count data (Linden and Mantyniemi 2011; Warton et al. 2016). Specifically, the probability functions of FI and FU are defined by

$$f\left({F}_{\rm {I}}=k\right)=\frac{\Gamma \left(\theta +k\right)}{k!\Gamma \left(\theta \right)}{\left(\frac{{\lambda }_{1}}{\theta +{\lambda }_{1}}\right)}^{k}{\left(\frac{\theta }{\theta +{\lambda }_{1}}\right)}^{\theta }$$
(3)

and

$$f\left({F}_{\rm {U}}=k\right)=\frac{\Gamma \left(\theta +k\right)}{k!\Gamma \left(\theta \right)}{\left(\frac{{\lambda }_{2}}{\theta +{\lambda }_{2}}\right)}^{k}{\left(\frac{\theta }{\theta +{\lambda }_{2}}\right)}^{\theta }$$
(4)

with the variances \({\lambda }_{1}+{\lambda }_{1}^{2}/\theta\) and \({\lambda }_{2}+{\lambda }_{2}^{2}/\theta\), respectively, where θ > 0 is the dispersion parameter with smaller values representing stronger overdispersion. When θ approaches infinity, the distribution converges to the Poisson distribution.

To illustrate how variation of host fecundity affects the fates of Wolbachia, we perform numerical simulations for a total of 60 scenarios over the three cases, setting four levels of fecundity cost (sf = 0, 0.01, 0.1, and 0.25), three levels of host population size (N = 102, 103, and 104), and six distributions of fecundity (constant, Poisson, and four negative binomials with θ = 0.01, 0.1, 1, and 10 according to the empirical results). Perfect maternal transmission (i.e. μ = 1) and complete CI (i.e. sh = 1) are assumed in all scenarios, which is reasonable for a variety of Wolbachia strains in A. aegypti (Ant et al. 2018; Hoffmann et al. 2014). For each scenario, we set the initial infection frequency (p0) from 0.01 to 0.99 with an increase of 0.01 each time and then calculated p1, p2, using Eq. (1) until pt = 0 or 1. In the scenarios with fecundity variation, values of FI(i) and FU(j) are sampled from the Poisson distribution or using Eqs. (3) and (4). One thousand simulations are run for each p0 of each scenario to determine the probability of Wolbachia fixation.

Applications of the model

We used the model to address two specific issues. First, we estimated the number of infected A. aegypti mosquitoes that need to be released in order to ensure a high probability (say, ≥ 0.95) for successful Wolbachia invasion, when there is overdispersion in host fecundity. The fecundity cost on Wolbachia-infected A. aegypti was estimated at c. 20% for wMel infection (Hoffmann et al. 2011) and 10–15% for wAlbB infection (Axford et al. 2016; Xi et al. 2005). We thus assumed fecundity cost at sf= 0.15. The dispersion parameter θ was set to vary over the range 0.01–10, according to the empirical estimates. The number of reproductive female mosquitoes N was set at 102, 103, and 104. For comparison, simulations with the same settings except for θ were also performed in cases where host fecundity is fixed or Poisson distributed.

Second, the model was used to estimate the probability of Wolbachia’s fixation following the introduction of a single infected female into a population (i.e. p0 = 1/N) through interspecific horizontal transfers. For comparison, we used the same settings of fecundity cost as Jansen et al. (2008). Given the empirical results of fecundity overdispersion in insects, we considered four plausible scenarios of overdispersion, i.e. θ = 10, 1, 0.1, and 0.01, and use Poisson-distributed fecundity as the control. We ran the model one million times for each combination of parameters to get the probability of fixation of Wolbachia.

Results

Fecundity overdispersion

We obtained a total of 56 articles that met the three criteria, involving 47 species and 79 data sets. Only one of them (grain aphid Sitobion avenae) showed a Poisson-type distribution of fecundity, with the variance close to the mean (23.74 vs. 26.09, P = 0.58). Overdispersion was found in all other cases, with estimates of overdispersion parameter θ 0.01 − 20.29 (median: 2.6). The largest overdispersion (θ = 0.01) was found in the eusocial red ant Myrmica rubra. Besides S. avenae, 57 data sets did not include zero values, which produced significantly larger θ (i.e. less overdispersion) than the 21 data sets with zeros (5.04 ± SE 0.58 vs. 0.80 ± SE 0.11, Mann–Whitney U = 1121, P < 0.001; Fig. 1). For the same species, parameter θ was overestimated by approximately one order of magnitude (median: 4.08-fold) when zero values were overlooked (Fig. 1). Summary statistics of all studies are provided in Table S1.

Fig. 1
figure 1

Empirical estimates of overdispersion in realized fecundity for 47 insect species. Smaller values of θ represent stronger overdispersion. The estimate for Sitobion avenae is not given, because the species showed Poisson-distributed fecundity. Each estimate is derived from one study except in A. aegypti and A. albopictus, and the numbers of studies used for the two species are shown. The difference of estimates between with- and without-zero data sets for the same species is denoted by solid line when the same study is used in both cases, or by dash line when using different studies. All estimates from with- and without-zero data sets, respectively, are summarized by boxplots. Insert shows the estimates for A. aegypti from each study

Full size image

Among the data sets involving A. aegypti (n = 14), six studies reported zero values and displayed substantial fecundity overdispersion, with θ ranging 0.55–1.57 (median 1.05). The remaining eight data sets that did not include zero values showed much weaker overdispersion, where θ varied between 1.97 and 7.39 (median 4.50). When zero values were deliberately excluded from the with-zero data sets, the increases in the estimate of θ were large in two of three cases (Fig. 1).

Wolbachia fixation from different initial frequencies

The fixation probability displays a step function of initial infection frequency (p0) if assuming no variation for host fecundity (case 1), but turns to a sigmoid function when fecundity is Poisson-distributed (case 2) or overdispersed (case 3). Compared to Poisson-distributed fecundity, overdispersed fecundity produces smoother curves for the fixation probability function (Fig. 2). More generally, when the overdispersion in fecundity becomes larger (with a smaller θ), the model provides smoother curves for the fixation probability function at all levels of fecundity cost (Fig. 2).

Fig. 2
figure 2

Probability of local fixation of Wolbachia as a function of initial infection frequency, with varying levels of parasitism cost (sf), host population size (N), and host fecundity variation. The variation of fecundity increases from no dispersion (black lines), dispersion (green lines), to overdispersion (purple, blue, yellow and red lines). For each p0 under each parameter setting, the model is conducted 1000 times to estimate the fixation probability. Scenarios with sf = 0 are very similar to those with sf = 0.01, and thus not shown here

Full size image

When p0 is smaller than the threshold (\(\widehat{p}\)) predicted by the deterministic model, the model predicts nonzero fixation probabilities when there are some variations in fecundity, and these probabilities generally increase with larger extent of fecundity dispersion (Fig. 2). For example, a Wolbachia strain causing fecundity cost of 25% is always unable to fix itself in a host population of 1000 reproductive females, when the initial infection frequency is 0.17 and host fecundity is Poisson distributed (Fig. 2f). In contrast, the strain has a 9.2% chance to achieve fixation if host fecundity shows a negative binomial distribution with θ = 0.1. When p0 > \(\widehat{p}\), however, overdispersion can introduce larger variation to Wolbachia fixation, and the uncertainty of fixation increases with stronger overdispersion (e.g. p0 > 0.25 in Fig. 2f). This trend is extremely strong when population size is relatively small (e.g. comparing Fig. 2c , f).

Application 1: replacement releases of Wolbachia-infected vectors

In the vector population replacement with Wolbachia, fecundity variation significantly elevates the number of infected vectors that should be released to ensure the successful invasion of Wolbachia (Fig. 3). For a vector population of 1000 reproductive females, 27% more Wolbachia-carrying vectors are required than predicted by the deterministic model when accounting for Poisson-distributed fecundity. This proportion increases to 33%, 40%, 80% and 220% when fecundity is overdispersed with θ of 10, 1, 0.1, and 0.01, respectively. The strength of such effect of fecundity variation depends negatively on population size. The required initial infection frequency increases at an astonishing rate in a population of 100 reproductive females when fecundity variation becomes larger, whereas the impacts of overdispersion are much weaker in a very large population (e.g. 10,000 reproductive females) (Fig. 3). Nevertheless, there is still a substantial effect that needs to be considered in such large populations if fecundity overdispersion is of the order of θ = 0.1 (Fig. 3).

Fig. 3
figure 3

Initial frequencies for ensuring a probability of 95% for successful establishment of Wolbachia in relation to host fecundity overdispersion. Smaller θ values represent larger overdispersion. Three population sizes (N) are considered, and we assume sf= 0.15, sh = 1, and μ = 1. The predictions from the deterministic and stochastic models are also shown (dash lines). Grey area denotes the estimation for A. aegypti

Full size image

When regarding the primary vector of Zika and dengue fever, A. aegypti, based on the empirical estimates of fecundity overdispersion of θ = 0.55–1.57 (Fig. 1), our model predicts that the numbers of released mosquitoes into a population of 100, 1000, and 10,000 reproductive females need to exceed the expectations from the deterministic model by 107–130%, 33–40%, and 13%, and exceed those from the stochastic model by 11–23%, 5–11%, and 0%, respectively (Fig. 3).

Application 2: spread of Wolbachia from a single infection

When assuming Poisson-distributed host fecundity, the fixation probability declines with population size in an approximately linear manner on the log–log plot if the Wolbachia strains are neutral to their hosts (Fig. 4a). When population size is small, the fixation probability of a weakly deleterious Wolbachia strain is close to the neutral one, but the discrepancy enlarges rapidly as the deleterious effect of Wolbachia and/or population size increases (Fig. 3a). Note that a strain with cost sf = 0.125 is still unable to establish itself in any population of N > 600 following one million events of lateral introduction of a single infection.

Fig. 4
figure 4

Fixation probability of Wolbachia following the introduction of a single infected female into a host population of size N with different distributions of fecundity. A range of parasitism costs (sf) is plotted

Full size image

Overdispersion of host fecundity increases the probability of Wolbachia spreading to fixation from a single infection in a host population, and this effect becomes stronger when population size, the deleterious effect of Wolbachia, and the magnitude of overdispersion increase (Fig. 3b − d). In contrast to the Poisson scenario, a strain with cost sf = 0.125 achieves fixation in a host population of N = 631 every 550 events of introducing a single infection if host fecundity is overdispersed with θ = 0.1.

Discussion

This study provides to our knowledge the first assessment of overdispersion in insect fecundity and its effect on the invasion dynamics of Wolbachia. Empirical data present compelling evidence for overdispersion of fecundity in most studied insect species. Furthermore, our model demonstrates that the overdispersion may help in CI-inducing Wolbachia spread in novel hosts from few infections, but can also undermine vector population replacement with Wolbachia in epidemic management.

Our analysis may provide an underestimate for fecundity overdispersion in many insect species due to several reasons. First, the conspecific insects used here to estimate fecundity variation were reared under almost the same condition in each data set. However, environmental heterogeneity, variation in the availability and quality of food and mates, and other biotic factors may augment the overdispersion of fecundity in field populations (Awmack and Leather 2002; Borer et al. 2009; Reigada et al. 2018; Zanchi et al. 2012). Second, zero inflation is an important source of overdispersion (Linden and Mantyniemi 2011), as shown by the large overdispersion of the eusocial species Myrmica rubra (θ = 0.01). Most studies reviewed here were not designed to test the variation of fecundity, and therefore some oviposition failures might be treated as noise and excluded artificially. However, null fecundity has a close relevance to the invasion of Wolbachia, because it may directly lead to the loss of Wolbachia. Additionally, copious oviposition sites were supplied for each adult in those studies, whereas competition for oviposition sites may occur in field populations of some species, resulting in lower or even null fecundity of some adults. This is likely the case in two populations of A. aegypti with wAlbB-releases in Malaysia, where the population sizes decreased considerably following the cessation of releases (Nazni et al. 2019).

Consistent with the results of previous stochastic models (Egas et al. 2002; Jansen et al. 2008), our model suggests it is usually difficult for a deleterious Wolbachia strain to spread from few initial infections if host fecundity is Poisson distributed. Repeated Wolbachia transfers can compensate for the extremely low fixation probability of a single transfer event (Jansen et al. 2008), but in this situation it is unclear whether the waiting time for fixation is biologically relevant. In our study, the estimated probabilities of Wolbachia reaching fixation from a single infection in host populations of overdispersed fecundity appear to relax the assumptions of Jansen et al. (2008) on transfer rate and waiting time, and may reconcile the contradictions among occasional and probably rare interspecific transfer events (Turelli et al. 2018), bistable population dynamics (Barton and Turelli 2011), and the remarkable prevalence of Wolbachia (Werren et al. 2008).

The uncertainty in the fixation of Wolbachia caused by overdispersion of host fecundity (see Figs. 2 and 3) may to some extent explain the large fluctuations of Wolbachia frequency in some A. aegypti populations after replacement releases (Nazni et al. 2019; Schmidt et al. 2017; Tantowijoyo et al. 2020). Especially for the releases of A. aegypti in Malaysia, lack of wAlbB invasion was found in low-density sites where oviposition sites might be rare (Nazni et al. 2019). This phenomenon is consistent with the expectations of large overdispersion of fecundity. Although we illustrate a special case of sf = 0.15, the need for increasing released individuals is prevalent across diverse fecundity costs of Wolbachia infection and becomes even more critical when the cost is smaller (see Fig. 2). In the light of great efforts being made to search for Wolbachia strains of low fecundity costs (Ant et al. 2018; Pance 2018), the significance of considering fecundity overdispersion in successful vector control is likely to increase further.

Nevertheless, the effects of fecundity overdispersion may be counterbalanced by other factors that have not been included in the model. An important factor particularly for A. aegypti is larval density-dependent competition (Hancock et al. 2016a). This density effect is likely to weaken the overdispersion effects, due to the trade-off between adult fecundity and larval fitness. Yet, the outcomes of density dependence for Wolbachia-based biocontrol strategies are very similar to those of overdispersion, i.e. greater numbers of released mosquitoes and longer time of Wolbachia establishment following releases (Hancock et al. 2016a, 2016b). While increased mortality due to Wolbachia infection, imperfect maternal transmission (e.g. at high temperatures), or occurrence of adverse conditions, may augment the effects of overdispersion (Jansen et al. 2008).

Our model focuses on CI-inducing Wolbachia strains especially wMel and wAlbB. However, the wAu strain which does not induce CI shows more efficient virus blocking and greater temperature stability than the two strains (Ant et al. 2018). Hence, a superinfection wAu-wAlbB was created to combine strong viral inhibition and CI and has been proposed as a novel biocontrol agent (Ant et al. 2018). Intriguingly, our model can also apply for the superinfection, but if wAu and wAlbB decoupled over time in the field, only the dynamics of wAlbB would be described by our model.

Our model assumes a panmictic population, but mating is often nonrandom in the field populations, especially when it routinely takes place at breeding sites before individuals disperse (Macke et al. 2011). After an initial phase of local establishment, Wolbachia may spread to other areas in a wave of colonization (Barton and Turelli 2011; Schmidt et al. 2017) or via stepping stone subpopulations (Engelstadter and Telschow 2009). In both cases, spatial spread can be slowed or even stopped if the host density is much higher in surrounding uninfected areas, because there are insufficient migrants transporting Wolbachia. These areas are analogous to the ‘tension zones’ where transitions occur between alternative genetic equilibria. Local fluctuations in population density and dispersal rate can drive development and movement of these tension zones (Barton 1979; Barton and Hewitt 1989). Nonetheless, the increased probabilities of fixation caused by overdispersion in host fecundity should help Wolbachia to pass through such tension zones via few migrants.

In conclusion, fecundity overdispersion is ubiquitous in insect populations, placing large stochasticity on the dynamics of Wolbachia. The significance of this stochasticity has been underestimated in both explaining the pandemic distribution of Wolbachia and formulating strategies for sustainable biocontrol of insect-borne diseases with Wolbachia. Our study address that efforts should be made to understand the dispersion of fecundity in the target vector populations before decision on the nature of the Wolbachia releases and also that the stochasticity brought by fecundity overdispersion greatly contributes to the local establishment and spatial spread of Wolbachia after the releases.

Author contributions

XYC and XT conceived and designed research. XT and JJ constructed models. XT, XYC, SGC, YC, YYD, RW, and JJ analysed data. XT wrote the manuscript. All authors read and approved the manuscript.