1 Introduction

Micro-electro-mechanical system/nano-electro-mechanical system (MEMS/NEMS) devices play a significant role in the field of high precision, showing unprecedented application prospects in medical equipment, consumer electronics, aerospace, and other fields [1,2,3]. MEMS/NEMS devices have many thin film-substrate structures [4,5,6]. Wrinkling, fracture, and buckling delamination are the main failures of thin film-substrate systems [7]. Parry et al. [8] investigated the effect of the substrate on the buckling height and critical stress. Abdallah et al. [9] proposed a new analytical model to evaluate the energy release rate of film-substrate systems. Xue et al. [10] used a 3D model to simulate the whole process of film buckling, interfacial cracking, and film fracture, and compared the results with experiments. Thanh-Tam et al. [11] studied biaxial loading effects on critical strain energy release rate in elastic hydrogels. The results showed that critical strain energy release rate significantly relies on the type of biaxial loading. Cui et al. [12] researched the problem of buckling and delamination of thermo-electric pn-junctions. It was shown that the greater the temperature difference, the greater the energy release rate. Zhou et al. [13] researched the influence of the nonlinear piezoelectric effect and size effect on the static deformation of a piezoelectric multilayer circular micro-diaphragm. Wang et al. [14] established an electro-mechanical model to investigate flexo-electricity in freestanding buckling films. Shabanijafroudi et al. [15] developed a new methodology for modeling the post-buckling behavior of composite plates with through-the-width delamination. Hou et al. [16] developed a mesh-free MK interpolation method to investigate the vibration of SGPs described by a sixth-order partial differential equation.

The main structural units of MEMS-/-NEMS micro-sensor devices are micro-scale structures such as micro-plates, micro-beams, micro-shells, and micro-film-substrate systems. Experiments [17,18,19] showed that when the structural size of the material reaches the micro-nano level, the mechanical properties change significantly compared to the macroscopic size, and the classical theory fails. The traditional couple stress theory [20,21,22] considers both displacement and rotation of point particles to analyze the size effect of materials. However, the material parameters are more complicated and are not suitable for practical engineering. In 2002, Yang et al. [23] put forward a modified couple stress theory containing only one scale parameter, which simplifies the material parameters and facilitates practical engineering applications. Recently, Richa et al. [24] investigated the stability and free vibration characteristics of microlaminates under different axial loads based on MCST. It was found that beams with high buckling loads and high intrinsic frequencies have more significant scaling effects under clamped–clamped (C–C) support conditions. The applicability of the modified coupled stress theory to web sandwich panels was verified by Romanoff et al. [25] Li et al. [26] devised a standard experimental methodology for determining the parameters of scaling effects for the MCST. Tang et al. [27, 28] analyzed the bending, buckling, post-buckling, and vibration properties of micro-thin plates based on MCST. It was concluded that the microstructural effect is negligible when the thickness of the thin plate is greater than 10 times the micro-structurale ffect parameter. Zhou et al. [29] explained the necessity of including more than one length-scale parameters in the strain gradient theory to consider size effects in the micron scale. Zhang et al. [30,31,32] developed a surface energy-enriched gradient elastic Kirchhoff plate model to examine the combined effects of strain gradient, inertia gradient, and surface energy on the static bending and free vibration behavior of micro-plates. Duan et al. [33, 34] developed an elastic buckling model for thick skew microplates under in-plane axial and shear loads based on TVRSDT and MCST, and proposed a four-node 32-DOF differential quadrature finite element to solve the related buckling boundary value problem.

Critical strain energy release rate is an important criterion established by Le et al. [35] to study crack propagation. In addition, the stress intensity factor and J-integral are also important criteria for crack propagation. Shin et al. [36, 37] analyzed the transient response problem of inverse plane motion cracks and cracks in functionally graded piezoelectric materials using the integral transform method. The direction and magnitude of the electrical load and increasing thickness of the functionally graded piezoelectric layer can affect the crack extension in the functionally graded piezoelectric interface layer. The energy release rate increases with the increase of the material property grade of the functionally graded piezoelectric layer. Santos et al. [38] studied and analyzed the effect of temperature on the crack growth rate and critical energy release rate of polyurethane (PU) adhesives. The results showed that the critical energy release rate decreases with increasing temperature, while the crack growth rate increases for a given critical strain energy release rate. A finite crack growth energy release rate method was proposed by Xu et al. [39], where the effect of plastic dissipation on crack growth was considered as the driving force,and the stabilized crack growth and residual strength of plates under different types of loads were well predicted.

Currently, no direct evidence has been found regarding the influence of the micro-structural effect on interface crack propagation in micro-electro-mechanical systems (MEMS). However, numerous experiments have shown that when the size of the material reaches the micro- or nanoscale, its mechanical properties undergo significant changes. Therefore, the micro-structural effect has an important impact on interface mechanics in MEMS. This paper focuses on studying the influence of micro-structural effect on interface crack propagation. There are many studies on critical strain energy release rates, but the authors have not seen a crack extension research based on MCST. In this article, the phenomenon of ultra-thin film-substrate delamination is investigated based on MCST. Equivalent elastic modulus (EEM) and equivalent flexural rigidity (EFR) are derived and substituted into the classical Kirchhoff plate theory to obtain the governing equations for the ultra-thin film-substrate system with the micro-structural effect. The effects of stress ratio \(\frac{\sigma }{{\sigma_{c} }}\), initial crack length, film thickness, and micro-structural effect parameters on crack extension were analyzed. The critical strain energy release rates at different film thicknesses and different initial crack lengths are investigated using the finite element method (FEM). The differences between the three theoretical approaches, i.e.,MCST, classical theory (CT), and FEM, are comparatively analyzed. The MEMS/NEMS stability in small-scale physical field environments remains a challenge [40,41,42,43,44]. The contents of this paper are important for the design and stability analysis of MEMS/NEMS.

2 Formulations and Theories of Ultra-Thin Film-Substrate System

2.1 Classical Kirchhoff-Thin Plate Theory [45,46,47]

The classical Kirchhoff plate theory is used to consider the instability and crack extension in thin-film substrate systems.When the ratio of the thickness of the film to the minimum in-plane size of the film is lower than 0.05, the displacement field based on the Kirchhoff theory can be given by

$$ \begin{gathered} u(x,y,z)\,{ = }\,u(x,y,t) - z\frac{\partial w}{{\partial x}} \hfill \\ v(x,y,z)\,{ = }\,v(x,y,t) - z\frac{\partial w}{{\partial y}} \hfill \\ w(x,y,z,t)\,{ = }\,w(x,y,t) \hfill \\ \end{gathered} $$
(1)

where (u, v, w) denote the displacements of a point on the midplane of the plate in the direction of the (x, y, z) coordinates. The Kirchhoff strain associated with the displacement field of Eq. (1) can be derived as

$$ \begin{gathered} \varepsilon_{xx} = \frac{\partial u}{{\partial x}} + \frac{1}{2}\left( {\frac{\partial w}{{\partial x}}} \right)^{2} - z\frac{{\partial^{2} w}}{{\partial x^{2} }} \hfill \\ \varepsilon_{yy} = \frac{\partial v}{{\partial y}} + \frac{{1}}{{2}}\left( {\frac{\partial w}{{\partial y}}} \right)^{{2}} - z\frac{{\partial^{2} w}}{{\partial y^{2} }} \hfill \\ \gamma_{xy} = \frac{\partial u}{{\partial y}} + \frac{\partial v}{{\partial x}} + \frac{\partial w}{{\partial x}}\frac{\partial w}{{\partial y}} - 2z\frac{{\partial^{2} w}}{\partial x\partial y} \hfill \\ \gamma_{xz} = \gamma_{yz} = \varepsilon_{zz} = 0 \hfill \\ \end{gathered} $$
(2)

The components of the rotation vector and curvature tensor associated with the displacement field can be expressed as

$$ \theta_{x} = \frac{\partial w}{{\partial y}},\theta_{y} = - \frac{\partial w}{{\partial x}},\theta_{z} = \frac{1}{2}\left( {\frac{\partial v}{{\partial x}} - \frac{\partial u}{{\partial y}}} \right) $$
(3)
$$ \begin{gathered} \chi_{xx} = \frac{{\partial^{2} w}}{\partial x\partial y},\chi_{yy} = - \frac{{\partial^{2} w}}{\partial x\partial y} \hfill \\ \chi_{xy} = \chi_{yx} = \frac{1}{2}\left( {\frac{{\partial^{2} w}}{{\partial y^{2} }} - \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)\hfill \\\chi_{xz} = \chi_{zx} = \frac{1}{4}\left( {\frac{{\partial^{2} v}}{{\partial x^{2} }} - \frac{{\partial^{2} u}}{\partial x\partial y}} \right) \hfill \\ \chi_{yz} = \chi_{zy} = \frac{1}{4}\left( {\frac{{\partial^{2} v}}{\partial x\partial y} - \frac{{\partial^{2} u}}{{\partial x^{2} }}} \right),\chi_{zz} = 0 \hfill \\ \end{gathered} $$
(4)

2.2 The Kirchhoff Theory Coupled with MCST

The constitutive equation of ultra-thin plates can be expressed as follows based on MCST:

$$ \begin{gathered} \sigma_{ij} = \lambda \varepsilon_{kk} \delta_{ij} + 2\mu \varepsilon_{ij} \hfill \\ \varepsilon_{ij} = \frac{1}{2}\left( {u_{i,j} + u_{j,i} } \right) \hfill \\ \chi_{ij} = \frac{1}{2}\left( {\theta_{i,j} + \theta_{j,i} } \right) \hfill \\ \theta_{i} = \frac{1}{2}e_{ijk} u_{k,j} \hfill \\ m_{ij} = 2l^{2} \mu \chi_{ij} \hfill \\ \end{gathered} $$
(5)

where σij, εij, χij, and mij are expressed stress tensor, strain tensor, symmetric curvature tensor, and couple stress tensor, respectively, l is the scale parameter of material that is related to the size effect, θi is the rotation vector, eijk is the permutation symbol, E is elastic modulus, and υ is Poisson’s ratio.

$$\mu =S=\frac{E}{2\left(1+\upsilon \right)}$$
(6)
$$ \lambda = \frac{E\upsilon }{{\left( {1 + \upsilon } \right)\left( {1 - 2\upsilon } \right)}} $$
(7)

where μ and λ are Lame constants. The bending moment and shear force according to MCST can be expressed as

$${M}_{x}={\int}_{h}{\sigma }_{xx}z\text{d}z+{\int }_{h}{m}_{xy}\text{d}z=\frac{-E{h}^{3}}{12(1-{\upsilon }^{2})}\left(\frac{{\partial }^{2}w}{\partial {x}^{2}}+\upsilon \frac{{\partial }^{2}w}{\partial {y}^{2}}\right)-{l}^{2}Sh\left(\frac{{\partial }^{2}w}{\partial {x}^{2}}-\frac{{\partial }^{2}w}{\partial {y}^{2}}\right)$$
(8)
$${M}_{y}={\int}_{h}{\sigma }_{xx}z\text{d}z-{\int }_{h}{m}_{yx}\text{d}z=\frac{-E{h}^{3}}{12(1-{\upsilon }^{2})}\left(\frac{{\partial }^{2}w}{\partial {y}^{2}}+\upsilon \frac{{\partial }^{2}w}{\partial {x}^{2}}\right)-{l}^{2}Sh\left(\frac{{\partial }^{2}w}{\partial {y}^{2}}-\frac{{\partial }^{2}w}{\partial {x}^{2}}\right)$$
(9)
$${M}_{xy}={M}_{yx}={\int}_{h}{\sigma }_{xy}z\text{d}z-{\int }_{h}{m}_{xx}\text{d}z={\int }_{h}{\sigma }_{yx}z\text{d}z+{\int }_{h}{m}_{yy}\text{d}z =\frac{-E{h}^{3}}{12(1-{\upsilon }^{2})}\frac{{\partial }^{2}w}{\partial x\partial y}-2{l}^{2}Sh\frac{{\partial }^{2}w}{\partial x\partial y}$$
(10)
$${Q}_{x}={\int }_{h}{\sigma }_{xz}\text{d}z$$
(11)
$${Q}_{y}={\int }_{h}{\sigma }_{yz}\text{d}z$$
(12)

The equilibrium equation can be expressed as follows

$$ \frac{{\partial M_{x} }}{\partial x} + \frac{{\partial M_{yx} }}{\partial y} = Q_{x} $$
(13)
$$ \frac{{\partial M_{y} }}{\partial y} + \frac{{\partial M_{xy} }}{\partial x} = Q_{y} $$
(14)
$$ \frac{{\partial Q_{x} }}{\partial x} + \frac{{\partial Q_{y} }}{\partial y} + q = 0 $$
(15)

where q refers to the load in the z-direction. By using Eqs. (13)–(15), the ultra-thin plate governing equation can be expressed as

$$(D+{l}^{2}Sh){\nabla }^{4}w=q$$
(16)

where

$$ D = \frac{{Eh^{3} }}{{12\left( {1 - \upsilon^{2} } \right)}} $$
(17)

Compared with classical governing equations [48,49,50], the flexural rigidity and elastic modulus of ultra-thin plate based on MCST are

$${D}^{\prime}=D+{l}^{2}Sh$$
(18)
$$ E^{\prime} = E + E\frac{{6l^{2} \left( {1 - \upsilon } \right)}}{{h^{2} }} $$
(19)

Actually, \(D^{\prime}\) is equivalent to flexural rigidity (EFR), and \(E^{\prime}\) is equivalent to elastic modulus (EEM) based on MCST. In the special case of l = 0, EFR and EEM are reduced to classical flexural rigidity and classical elastic modulus.

3 Critical Strain Energy Release Rate for the Ultra-Thin Film-Substrate System with Micro-Structural Effect Based on MCST

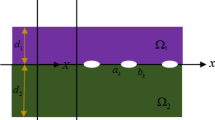
Considering the geometry and force diagram of a film-substrate system with an interface crack, as shown in Fig. 1, the film-substrate system with an initial cracks of length 2b and initial deflection w0 absorbs the load P, resulting in buckling deflection w. The local loading of the interface crack is shown on the right side of Fig. 1. The isotropic and linear elastic film with thickness h is subjected to the change of axial force ∆N and bending moment M. The film-substrate interface is regarded as the x-axis, the buckling direction of the film is the w-axis, and the middle position of the crack is taken as the coordinate origin.

Fig. 1
figure 1

Loading and geometry of interface crack in the film-substrate system

Full size image

According to Hutchinson et al.[51] and in conjunction with MCST [23], the calculation formula for the critical strain energy release rate of an ultra-thin film-substrate system with micro-structural effect is derived as

$$ G = \frac{{6\left( {1 - \upsilon_{1}^{2} } \right)}}{{E_{1} h^{3} + 6E_{1} l^{2} \left( {1 - \upsilon_{1} } \right)h}}\left( {M^{2} + \frac{{h^{2} \Delta N^{2} }}{12}} \right) $$
(20)

where G is the critical strain energy release rate, υ1 is Poisson’s ratio of the film, \(E^{\prime}_{1}\) is the equivalent elastic modulus of the film based on MCST, h is the thickness of the film, and ∆N and M denote the change in axial force and the bending moment, respectively. It is worth noting that the flexural rigidity and elastic modulus are only relevant to material properties, and independent of the plate theory. Although EFR and EEM are derived from the small-deflection theory of thin plates, they are independent of the plate theory and therefore equally applicable to the large-deflection theory. So the ultra-thin film buckling problem governing equations based on MCST become

$$(D+{l}^{2}Sh){\nabla }^{4}w+{N}_{x}\frac{{\partial }^{2}w}{\partial {x}^{2}}=0$$
(21)

The buckling junction is in a fixed state and can be regarded as a fully clamped boundary condition, expressed as

$$ N_{x} = - P,w = 0\;{\text{and}}\;\frac{\partial w}{{\partial x}} = 0\;{\text{at}}\;x = - b,b $$
(22)

where P is the axial force at the junction of membrane debonding and unbonding. To satisfy the boundary conditions, the deflection function can be expressed as

$$ w\left( x \right) = \frac{1}{2}w_{0} \left( {1 + \cos \frac{\pi x}{b}} \right) $$
(23)

where \(w_{0}\) is the amplitude of the film buckling deflection. Substituting Eq. (23) into Eq. (21), we have

$$\left[(D+{l}^{2}Sh){\left(\frac{\pi }{b}\right)}^{2}-P\right]{w}_{0}=0$$
(24)

The critical buckling load \({P}_{\text{cr}}\) can be obtained as

$${P}_{\text{cr}}=(D+{l}^{2}Sh){\left(\frac{\pi }{b}\right)}^{2}$$
(25)

According to Hutchinson et al. [51], a parameter \(\xi\), defined as \(w_{0} = \xi h\), is created and related to the residual stress as

$$ \xi = \left[ {\frac{4}{3}\left( {\frac{\sigma }{{\sigma_{c} }} - 1} \right)} \right]^{\frac{1}{2}} $$
(26)

where

$${\sigma }_{c}=\frac{{\pi }^{2}(D+{l}^{2}Sh)}{h{b}^{2}}$$
(27)

The bending moment M and the change in axial force ∆N are expressed as

$$M=\frac{{\pi }^{2}}{2}\frac{(D+{l}^{2}Sh)h}{{b}^{2}}\xi $$
(28)
$$\Delta N=\frac{3{\pi }^{2}}{4}\frac{(D+{l}^{2}Sh)}{{b}^{2}}{\xi }^{2}$$
(29)

Substituting Eqs. (28) and (29) into Eq. (20), we have

$$ G = \frac{{\left( {1 - \upsilon_{1}^{2} } \right)h^{3} }}{{2E_{1} h^{2} + 12E_{1} l^{2} \left( {1 - \upsilon_{1} } \right)}}\sigma_{c}^{2} \left( {\frac{\sigma }{{\sigma_{c} }} - 1} \right)\left( {\frac{\sigma }{{\sigma_{c} }} + 3} \right) $$
(30)

4 Results and Discussion

4.1 Approximate Analytical Solution Results and Discussion

This section investigates numerical examples of buckling delamination energy release problems for film-substrate systems. The film-substrate system consists of a Cu film of thickness h and a Si substrate of thickness H, assuming that \(h \ll H\). The material properties of this film-substrate system are described as follows [26, 52]:

$$ E_{{{\text{cu}}}} = 110\;{\text{GPa}},\;\upsilon_{{{\text{cu}}}} = 0.35,\;h = 10 \, \upmu{\text{m}}$$
$$ E_{{{\text{Si}}}} = 107{\text{ GPa}},\upsilon_{{{\text{Si}}}} = 0.33,b = 30\, \upmu{\text{m}}$$

By considering various scale parameters, the relationship between critical buckling load Ncr and initial interface crack length b is plotted in Fig. 2 based on CT and MCST. Equation (16) shows that the MCST can be converted into CT when the scaling effect parameter l = 0. It can be seen from Fig. 2 that the micro-structural effect shows significant roles. Figure 2 shows that with the same film thickness, as the micro-structural effect parameter l increases, the critical buckling load Ncr tends to increase. Comparing Fig. 2a, b, and c, the initial interface crack length b plays a major role in the magnitude of the critical buckling load Ncr. When the initial crack length b is at the micron level, the critical buckling force Ncr is very high and the film-substrate system is not susceptible to buckling. While the initial crack length b is in the millimeter range, the critical buckling force Ncr shows an exponential decrease. According to Eq. (25), considering initial interface crack length b = 30 μm, the change of critical buckling force Ncr with Cu plate thickness is shown in Fig. 3. An increase in thickness h leads to an increase in modulus of elasticity, ultimately leading to an increase in critical buckling force Ncr. With the increase of micro-structural effect parameter l, the critical buckling force Ncr also increases, and more importantly, micro-structural effects make buckling harder to occur.

Fig. 2
figure 2

Influence of micro-structural effect parameters on critical buckling load with different initial interface crack lengths b when thickness h = 10 μm

Full size image
Fig. 3
figure 3

Influence of micro-structural effect parameters on critical buckling load with different thicknesses when initial interface crack length b = 30 μm

Full size image

Equation (27) shows the relationship between the thickness h, the initial interface crack length b, and the critical buckling stress \(\sigma_{c}\). Figure 4 shows the trend of critical buckling stress \(\sigma_{c}\) versus initial interface crack length b. Figure 4a, b, and c illustrate the significant impact of initial interface crack length b on critical buckling stress \(\sigma_{c}\). When the length b is multiplied, the stress decays exponentially. Both Figs. 4 and 5 show that the critical buckling stress increases with the increase of the micro-structural effect parameter l under the same conditions.

Fig. 4
figure 4

Influence of micro-structural effect parameters on critical buckling stress with different initial interface crack lengths b when thickness h = 10 μm

Full size image
Fig. 5
figure 5

Influence of micro-structural effect parameters on critical buckling stress with different thicknesses when initial interface crack length b = 30 μm

Full size image

Figure 6 shows the effect of micro-structural effect parameters on the variation of axial force at different stress ratios. As the stress ratio increases, the variation of axial force also increases. Under the same circumstances, an increase in the micro-structural effect parameter l leads to an increase in the axial force variation.

Fig. 6
figure 6

Influence of micro-structural effect parameters on axial force variation with different stress ratios

Full size image

Figure 7 shows the nonlinear trend of bending moment with different stress ratios. An increase in the stress ratio and the scaling parameter l leads to an increase in the bending moment. When the stress ratio is greater than 2, the slope of the curve decreases, causing the increase in bending moment to slow.

Fig. 7
figure 7

Influence of micro-structural effect parameters on bending moment with different stress ratios

Full size image

The relationship between the critical strain energy release rate and stress ratio is shown in Fig. 8. The critical strain energy release rate increases with the increase of stress ratio. Micro-structural effects play an important role in the critical strain energy release rate. With the increase of micro-structural effect parameter l, the critical strain energy release rate increases.

Fig. 8
figure 8

Influence of micro-structural effect parameters on critical strain energy release rate with different stress ratios

Full size image

Figures 9 and 10 illustrate the effects of stress ratio \(\frac{\sigma }{{\sigma_{c} }}\), initial interface crack length b, and micro-structural effect parameter l on critical strain energy release rate based on a modified couple stress theory. As can be seen, the micro-structural effect gradually plays an essential role in the critical strain energy release rate with the increase of stress ratio \(\frac{\sigma }{{\sigma_{c} }}\) and decrease of initial interface crack length b. The energy release rate increases as the stress ratio increases or the initial interface crack length b decreases. As the stress ratio increases, the energy release rate also increases. It is worth noting that, in the same case, an increase in the stress ratio and the scaling micro-structural effect parameter l leads to an increase in the critical strain energy release rate G. When G > Gc, according to Griffith’s theory, the energy release rate G of crack extension is greater than the critical energy release rate Gc, and crack extension occurs. So the micro-structural effects tend to make crack propagation easier. Figure 10 displays the contour line of the critical strain energy release rate, which reflects the trend of the energy release rate.

Fig. 9
figure 9

Influence of micro-structural effect parameters on critical strain energy release rate with different stress ratios and different initial interface crack lengths

Full size image
Fig. 10
figure 10

Contour line of critical strain energy release rate with different stress ratios and different initial interface crack lengths when l = 0

Full size image

Figures 11 and 12 illustrate the effect of stress ratio \(\frac{\sigma }{{\sigma_{c} }}\), ultra-thin plate thickness h, and micro-structural effect parameter l on critical strain energy release rate based on a modified couple stress theory. As can be seen, the micro-structural effect gradually plays an essential role in the critical strain energy release rate with the increase of stress ratio \(\frac{\sigma }{{\sigma_{c} }}\) and thickness h. The energy release rate increases as the stress ratio increases. As the stress ratio increases or the thickness increases, the energy release rate also increases. In the same case, an increase in the micro-structural effect parameter l leads to an increase in the critical strain energy release rate G. When G > Gc, according to Griffith’s theory, the energy release rate G of crack extension is greater than the critical energy release rate Gc,and crack extension occurs. So the micro-structural effects tend to make crack propagation easier. Figure 12 illustrates the contour line of the critical strain energy release rate, which reflects the trend of energy release rate.

Fig. 11
figure 11

Influence of micro-structural effect parameters on critical strain energy release rate with different stress ratios and different thicknesses

Full size image
Fig. 12
figure 12

Contour line of critical strain energy release rate with different stress ratios and different thicknesses when l = 0

Full size image

4.2 FEM Results and Discussion

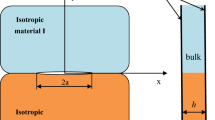
Finite element modeling is conducted using the Abaqus software. The model is divided into two parts: the substrate and the thin film. The material of the thin film is Cu, with a Young’s modulus of 110 GPa and a Poisson’s ratio of 0.35. The substrate is made of Si, with a Young’s modulus of 107 GPa and a Poisson’s ratio of 0.35. The two-dimensional model size is 200 × 40 μm. Meshing is carried out under structured conditions, with a CPE4R grid type and 8000 units. Pre-fabricated cracks are inserted between the film and the substrate and the extended finite element method (XFEM) is used for crack extension simulation. The virtual crack closure technique (VCCT) is used to calculate the energy release rate of crack extension. The lower surface is set to be fully constrained and the model is illustrated in Fig. 13.

Fig. 13
figure 13

Schematic of Abaqus model of thin plate-substrate system with initial interfacial cracks

Full size image

Figure 14 shows the variation of critical strain energy release rate with crack width, comparing CT, MCST, and FEM under the same thickness h = 10 μm. The specific values are shown in Table 1, and Fig. 16 shows a portion of the FEM results. It can be seen that the energy release rate decreases as the crack width increases, which indicates that larger initial cracks promote crack extension. When b > 10 μm, the results of CT theory are in good agreement with those of FEM. When b < 10 μm, the finite element results tend to be constant, but the CT results are significantly larger than the FEM results. The calculated values of MCST exceed those of CT, with the critical strain energy release rate increasing alongside the micro- structural effect parameter.

Fig. 14
figure 14

Variation of critical strain energy release rate with crack width comparison of scaling effect and finite element method

Full size image
Table 1 The values of critical strain energy release rate for different crack lengths under different theories
Full size table

Figure 15 shows the variation of critical strain energy release rate with film thickness for CT, MCST, and FEM calculations under the same crack width b = 30 μm (Fig. 16). The specific values are shown in Table 2, and Fig. 17 shows a portion of the FEM results. It can be seen that the energy release rate increases with thickness, which is in agreement with [53, 54]. It indicates that higher film thickness makes crack extension more difficult. The values of energy release rate for CT and FEM are similar, while the critical strain energy release rate values for MCST are larger than those of CT and FEM, progressively increasing with micro-structural effect parameters. This suggests that micro-structural effects hinder crack extension.

Fig. 15
figure 15

Variation of critical strain energy release rate with thickness comparison of scaling effect and finite element method

Full size image
Fig. 16
figure 16

FEM simulation of the critical strain energy release rate at different crack widths when film thickness h = 10 μm

Full size image
Table 2 The values of critical strain energy release rate for different film thicknesses under different theories
Full size table
Fig. 17
figure 17

FEM simulation of the critical strain energy release rate at different film thicknesses when crack length b = 30 μm

Full size image

Table 3 shows the values of critical strain energy release rate for different film thicknesses under different theories. Ostrowicki et al. [55] studied the strain energy release rate of copper films on silicon substrates. The energy release rates of 1.4 J/m2 and 0.8 J/m2 obtained from the experimental tests are essentially the same as the results of 1.39 J/m2 (for \(\frac{\sigma }{{\sigma_{c} }}{ = 5}\)) and 0.81 J/m2 (for \(\frac{\sigma }{{\sigma_{c} }}{ = 3}\)) obtained in this paper at l = 1.422 μm. The results in this paper also verify the correctness of the experimentally measured micro-structural effect of 1.422 μm for Cu by Li et al. [56] based on MCST. The strain energy release rates of Cu and epoxy are larger than those of Cu and Si in this paper, probably because the surface of Si is smoother than that of epoxy.

Table 3 The values of critical strain energy release rate for different film thicknesses under different theories
Full size table

5 Concluding Remarks

Based on a modified coupled stress theory, the buckling delamination of an ultra-thin film-substrate system is analyzed. An equivalent elastic modulus (EEM) parameter is presented for the analysis to incorporate the micro-structural effect. Substituting EEM and EFR into the classical Kirchhoff plate theory, the governing equations of the ultra-thin film-substrate system with micro-structural effect can be obtained. Analytical solutions of critical buckling stress and critical strain energy release rate based on micro-structural effect are obtained. The influence of the micro-structural effect on critical buckling stress and critical strain energy release rate is investigated in detail. The critical strain energy release rate is calculated using FEM. Moreover, the effects of stress ratio \(\frac{\sigma }{{\sigma_{c} }}\), initial interface crack length b, ultra-thin plate thickness h, and micro-structural effect parameter l on thecritical strain energy release rate are discussed. This clarifies how microstructural effects impact the crack extension energy release rate criterion and validates the correctness of the theory through comparative finite element analysis. These findings hold substantial theoretical significance for addressing common interface problems in micro-electro-mechanical systems. The most significant conclusions are summarized as follows:

  • The initial interface crack length b significantly influences the critical buckling load Ncr and critical buckling stress \(\sigma_{c}\). When the length b is multiplied, both the critical buckling load and stress decay exponentially. Once the crack length reaches a certain size, failure becomes difficult to control, dramatically reducing the load capacity of the device or structure, eventually leading to failure. This phenomenon is consistent with engineering practice. Under the same circumstances, the micro- structural effect can increase critical buckling load and stress, thus making buckling difficult.

  • With the increase of stress ratio \(\frac{\sigma }{{\sigma_{c} }}\), the axial force variation ∆N and bending moment M increases, leading to an increase in the energy release rate.

  • The initial interface crack length 2b and film thickness h have a more significant impact on the energy release rate than the stress ratio \(\frac{\sigma }{{\sigma_{c} }}\); smaller crack sizes and large film thicknesses can dramatically increase the energy release rate. Micro-structural effects can also increase the energy release rate.

  • Micro-structural effects also influence rack extension. A larger micro-structural effect parameter increases the difficulty of crack extension, indicating that greater film thicknesses and smaller crack lengths lead to increased difficulty in extension. The energy release rate considering the micro-structural effects exceeds that of the classical theory (CT). The FEM simulation results are in agreement with the CT calculations. The presence of scale effects in microelectronic devices makes failure less likely to occur, thereby enhancing device reliability and extending the device’s lifespan.