Dynamic Impact of High-Density Aluminum Foam

Abstract

High-density aluminum foam can provide higher stiffness and absorb more energy during the impact Obtaining the constitutive law of such foam requires tri-axial tests with very high pressure, where difficulty may arise because the hydrostatic pressure can reach more than 30 MPa. In this paper, instead of using tri-axial tests, we proposed three easier tests—tension, compression and shear to obtain the parameters of constitutive model (the Deshpande–Fleck model). To verify the constitutive model both statically and dynamically, we carried out additional triaxial tests and direct impact tests, respectively. Based on the derived model, we performed finite element simulation to study the impact response of the present foam. By dimensional analysis, we proposed an empirical equation for a non-dimensional impact time  ${\bar{t}}_{\mathrm {d}}$, the impact time divided by the time required for plastic wave travelling from the impact surface to the bottom surface, to determine the deformation characteristic of the aluminum foam after impact. For the case with ${\bar{t}}_{\mathrm {d}}\le 1$, the deformation tends to exhibit a shock-type characteristic, while for the case with ${\bar{t}}_{\mathrm {d}}>5$, the deformation tends to exhibit an upsetting-type characteristic.

1 Introduction

Metallic foams [1] are widely used for energy absorption in cases such as nuclear waste container, anti-blast armor [2], building structure [3], orbital debris shielding [4], etc. To describe the ability of energy absorption, some phenomenological constitutive models were proposed for the dynamic behavior of the foam. Deshpande and Fleck [5] developed an isotropic hardening model for metallic foams suggesting symmetric behavior in tension and compression. However, this symmetric behavior is always violated by experiments, which show different yield strengths between compression and tension for the foam. As a result, the constitutive model was improved to the volumetric hardening model in the commercial software ABAQUS. This volumetric hardening model assumes perfectly plastic behavior for the stress states of pure shear and tension, while hardening takes place for the stress states of positive hydrostatic pressure. The physical differences are due to the fact that the cell wall tends to buckle in compression [6, 7] and break in tension [7]. Recently, Zhu et al. [8] carried out simulations with various loading scenarios and obtained the ellipticity by fitting the numerical simulations with different equivalent plastic strains. With this fact, they thus proposed a modified Deshpande–Fleck model.

For constitutive relation of the aluminum foam, a key point is the failure surface, which can be determined by designed tests. Reyes et al. [9] used combined shear–tensile test to obtain the failure surface of closed-cell aluminum alloy foam under complex multi-axial loading conditions, the apparatus was similar to the setup by Hanssen et al. [10], which used a circular pure-shear sample to produce a homogeneous state of pure shear. Reyes et al. [9] measured the failure surface of the aluminum foam under biaxial and axisymmetric triaxial loading. Their experimental results provided support for the investigated phenomenological models. They concluded that both the Miller [11] and Deshpande–Fleck [12] criteria could provide a good description for the multiaxial failure. However, the yield strengths in all previous experiments discussed here were very low less than 6 MPa.

The failure surface of another type of low-strength foam—polyvinylchloride (PVC)—was also studied by experimentalists. Hanssen et al. [13] developed two apparatus to measure the yield behavior of ductile PVC foam. Under combinations of axial and radial tension and compression, the two systems they developed can be used to investigate the yield behavior of the foam. The difference between plasticity models (associated flow and non-associated flow models) was discussed in their work. Other studies [14, 15] developed custom-built multi-axial testing apparatus to probe the yield surface of isotropic Divinycell H-100 PVC foam. Their results revealed that yielding in foams exhibited linear pressure dependence. The yield strength for PVC was normally less than 5 MPa, so these phenomenological models discussed were only suitable for low strength.

Because foam structure is widely used for energy absorption, the dynamic behavior of foams has drawn much attention [16]. Shen et al. [17] and Xu et al. [18] showed that the energy dissipation capacity of ALPORAS foam was dependent on the strain rate. The density of the foam they used was about $0.23 \hbox { g/cm}^{\mathrm {3}}$ and the yield strength about 1.9 MPa. Deshpande and Fleck [12] studied the dynamic behavior of closed-cell foams under high-velocity impact. They discovered that shock wave speed was strongly dependent on the impact velocity, as well as the plastic hardening. To test the response of Alulight and Duocel foam, they used SHPB and direct impact techniques, and found little effect of strain rate on plateau stress for strain rates of up to $5000\hbox { s}^{\mathrm {-1}}$ [12]. The yield strength of their foam was close to 4 MPa. The ‘shock-type’ (a term often used to describe the deformation characteristics of cellular materials under high-velocity impact [19]) response of an open-cell foam was examined by Barnes et al. [20]. Impacting at velocities lower than 40 m/s exhibited response and deformation patterns similar to quasi-static crushing. However, impacting with velocities above 60 m/s provided nearly planar shocks which propagated at well-defined velocities over the specimen. Still, the yield strength of the foam was quite low, about 3 MPa. Gaitanaros and Kyriakides later modeled the crushing behavior using the beam elements in LS-DYNA, focusing on how the initial speed changed the crushing behavior [21]. Tan et al. [22, 23] estimated that a transition to a ‘shock-type’ deformation occurs at an impact velocity of approximately 108 m/s for large cell foam and 42 m/s for small cell foam. The prediction for the dynamic behavior of closed-cell foams is highly dependent on the selection of constitutive law. Hanssen et al. [10] performed numerical validations of various published constitutive models for aluminum foam for failure analyses. They compared different foam’s models with extensive experimental results and concluded that most of the models are unable to predict fracture of the foam. The yield strength of foam they studied was 4.88 MPa. Wang et al. obtained a stress–strain relation for the closed-cell foams taking into account the cellular density, the hardening behavior of the cell material, and the gas trapped within cells [24].

To conclude, previous studies have provided methods for determining both the initial yield surface and impact behaviors, but only for the foam with low yield strength—mostly less than 6 MPa. High-density aluminum foam has high stiffness and high yield strength, thus it is more suitable for structural applications compared with low-density aluminum foam [25]. However, the constitutive model for high-density aluminum foam is rarely studied. To the authors’ knowledge, very few studies for aluminum foam with density higher than $0.6\hbox { g/mm}^{\mathrm {3}}$ can be found in the literature, and which constitutive model is valid remains a question.

In this study, we firstly proposed three tests tension, shear and compression, to obtain the parameters of the Deshpande–Fleck model. Further, we carried out triaxial tests with two hydraulic pressure levels to verify the model, and direct impact tests to check the strain rate effect of the high-density foam. With the derived constitutive model, we carried out finite element simulations to study the shock response of the foam. Results show that: two types of deformation the shock-type deformation and the upsettingtype deformation (bulging in the middle) are controlled by a non-dimensional impact time, which is in turn determined by two non-dimensional variables—impact energy and velocity.

2 Sample, Experiments, and Constitutive Model

2.1 Sample Properties

The high-density aluminum foam was purchased from Sichuan Yuantaida Non-ferrous Metals Co,. Ltd, China. Compared with the aluminum foam commonly used by researchers, such as the ALPORAS, Alulight and Duocel foams, this type of aluminum foam had higher density and greater initial strength. The density was $0.910\pm 0.022\hbox { g/cm}^{\mathrm {3}}$, and the initial compressive yield strength was about 27 MPa.

The optical approach was used to measure the cellular size $D_{V}$. Multiple cross-sectional planes (with three orthogonal directions N, T, R) were scanned and analyzed. Figure 1 shows a typical optical image of a cross-sectional plane, of which the inset shows the N-, T-, and R-directions. The cellular dimensions along the N-, T- and R-directions were $2.31\pm 1.16\hbox { mm}$, $2.46\pm 1.18\hbox { mm}$ and $2.49\pm 1.19\hbox { mm}$ respectively.

Fig. 1

Cross section of the aluminum foam sample (inset)

2.2 Experiments

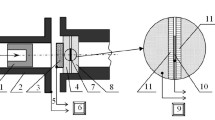
To derive the constitutive model, we carried out the uniaxial tension/compression test and shear test. The uniaxial tension/compression testing (Fig. 2a) and the shear testing (Fig. 2b) were conducted using the MTS Landmark Servo-hydraulic Test System at room temperature. All tests were carried out under displacement control mode to keep the engineering strain rate at about $5\times 10^{\mathrm {-4}}\hbox { s}^{\mathrm {-1}}$. The specimens for tension test were of a dog-bone shape with a gauge length of 100 mm and a section size of $40\hbox { mm}\times 40\hbox { mm}$. An extensometer with 40-mm gauge length was used for tensile strain measurement. The specimens for compression test were of a cuboid shape with 40-mm edge length. According to the ASTM C273 standard, the shear region of the specimen was designed with a thickness of 10 mm, a width of 20 mm and a length of 120 mm. For measurement of engineering shear strain, a COD extensometer (Extensometer 634.31F-24) was used to measure the displacement between the two sides of the shear area. With the uniaxial tension, uniaxial compression, and shear tests, we can obtain the yield surface for the present aluminum foam.

Fig. 2

Experimental setups for a uniaxial tension/compression test, b shear test, c tri-axial compression test, d direct impact test, and e schematic for tri-axial compression test. Uniaxial tension/compression and shear test were used for deriving the constitutive model. Tri-axial compression test was used for validation. Impact test was used to validate the model under dynamic condition as well as to study the strain rate effect

Fig. 3

Yield surface of metal foam

2.3 Constitutive Model

According to the Deshpande–Fleck constitutive model, the initial yield surface of metal foam is shown in Fig. 3. The abscissa (the p axis) is the hydrostatic stress and the ordinate (the q axis) is the Mises equivalent stress. The hydrostatic stress and the Mises equivalent stress can be expressed with the following equations.

$$\begin{aligned} \left\{ {\begin{array}{cc} p&{}=\frac{\sigma _{11}+\sigma _{22}+\sigma _{33}}{3} \\ q&{}=\sqrt{\frac{3}{2}s_{ij}s_{ij}} \\ s_{ij}&{}=\sigma _{ij}-p\delta _{ij} \\ \end{array}}\right. \end{aligned}$$

(1)

where $\sigma _{ij}$ is the stress tensor, $s_{ij}$ the deviatoric stress tensor and $\delta _{ij}$ the Kronecker tensor. Then the yield surface equation can be obtained by the following equation.

$$\begin{aligned} f=\left( q^{2}+\alpha ^{2}\left( p-p_{0} \right) ^{2} \right) ^{\frac{1}{2}}-\alpha A=0 \end{aligned}$$

(2)

where $\alpha$, $p_{0}$ and A are coefficients to be determined. Equation (2) can also be written as:

$$\begin{aligned} \frac{\left( p-p_{0} \right) ^{2}}{A^{2}}+\frac{q^{2}}{\alpha ^{2}A^{2}}=1 \end{aligned}$$

(3)

In fact, the yield surface of aluminum foam can be too complicated to be determined by only the von Mises stress and the mean stress [26]. By creative designs, Wu et al. suggested using both multi-axial and uniaxial experiments to determine the measured point on the failure or yield surface [27, 28]. The yield point determined by the multi-axial test should follow the rule that the plastic dissipation of multi-axial loading is equal to that of uniaxial loading. However, in the present study, because the Fleck–Deshpande model was commonly adopted for aluminum foam, the parameters that define the Fleck–Deshpande model for the current high-density aluminum foam needed to be determined. To do this, we only needed to identify three variables: $p_{0}, A,$ and $\alpha$, and use four types of experiment: tension, compression, shear and tri-axial compression to provide sufficient data.

Fig. 4

Typical stress–strain curves for a uniaxial tensile tests and b uniaxial compression tests

Fig. 5

Experimental data and derived yield surfaces

Yang and Kyriakides [29] studied the continuum modeling of low-density foam, and showed that the crushable foam behavior dictated the adoption of a non-associated flow rule. In our approach, a volumetric hardening model was adopted. The plastic strain rate for the volumetric hardening model was assumed to be:

$$\begin{aligned} {\dot{\varepsilon }}^{p}={\dot{\varepsilon }}_{\mathrm {eq}}\frac{\partial G}{\partial \mathbf {\sigma }} \end{aligned}$$

(4)

where G is the flow potential and the non-associative flow rule was adopted by choosing:

$$\begin{aligned} G=\sqrt{q^{2}+\frac{9}{2}p^{2}} \end{aligned}$$

(5)

To identify these three coefficients, $p_{0}$, $\alpha$ and A with uniaxial tension, uniaxial compression and shear tests the yield strengths including $\sigma _{c0}$ for compression $\sigma _{t0}$ for tension, and $\tau _{c0}$ for shear were obtained by experiments in advance, as shown in Tables 1, 2 and 3, respectively. Figure 4 plots typical stress–strain curves for uniaxial tensile test and uniaxial compression test as an example. On the one hand, for a general foam material, because there could exists a nonlinear elastic regime and a distinguishable yield point was not observed in the macroscope like common homogenous metallic material does, we selected the first peak value of the loading curve as the yield point. On the other hand, the samples hardly showed anisotropy under compression, whilst the modules in the R-direction was slightly larger (4.6%) than that in the T-direction for tension and shear tests. Further, using the strain-stress curve obtained by the compression test, we calculated the hardening parameters, as shown in Table 4.

Fig. 6

Hardening properties of the aluminum foam

Fig. 7

Mesh dependency for the present FEM model (inset)

The points on the yield surface corresponding to uniaxial compression, tension and shear can be determined as:

$$\begin{aligned} \left( p, q \right) =\left\{ {\begin{array}{ll} \left( \frac{\sigma _{c0}}{3},\sigma _{c0} \right) &{} \mathrm {for\,uniaxial\,compression\,test} \\ \left( 0,\sqrt{3 \tau _{c0} }\right) &{}\mathrm {for shear test} \\ \left( -\frac{\sigma _{t0}}{3},\sigma _{t0} \right) &{} \mathrm {for\,uniaxial\,tension test} \\ \end{array}} \right. \end{aligned}$$

(6)

Table 1 Experimental results for compression tests

Table 2 Experimental results for tensile tests

Table 3 Experimental results for shear tests

Substituting Eqs. (4) into (3), the undetermined coefficients for the Fleck–Deshpande model can be obtained as follows

$$\begin{aligned} \left\{ {\begin{array}{ll} p_{0}&{}=\frac{\tau _{c0}^{2}\left( \sigma _{c0}-\sigma _{t0} \right) }{2\left( 3\tau _{c0}^{2}-\sigma _{c0}\sigma _{t0} \right) } \\ A&{}=\left| \frac{\tau _{c0}\sqrt{3\left( \sigma _{c0}+\sigma _{t0} \right) ^{2}\tau _{c0}^{2}-4\sigma _{c0}^{2}\sigma _{t0}^{2}} }{2\sqrt{3 \left( 3\tau _{c0}^{2}-\sigma _{c0}\sigma _{t0} \right) }} \right| \\ \alpha &{}=\left| \sqrt{\frac{9\left( 3\tau _{c0}^{2}-\sigma _{c0}\sigma _{t0} \right) }{\sigma _{c0}\sigma _{t0}}}\right| \\ \end{array}} \right. \end{aligned}$$

(7)

Further, the coordinates of the intersection points of the ellipse and the abscissa, namely $(-p_{t},0)$ and $(p_{c},0)$ as illustrated by Fig. 3, can be calculated with the following equations

$$\begin{aligned} \left\{ {\begin{array}{ll} p_{c}&{}=A+p_{0} \\ p_{t}&{}=A-p_{0} \\ \end{array}}\right. \end{aligned}$$

(8)

With Eq. (7), the derived values of parameters $p_{0}$, A, and $\alpha$ can be obtained:

$$\begin{aligned} \left\{ {\begin{array}{ll} p_{0}&{}=13.63\quad (\mathrm {MPa}) \\ A&{}=20.52\quad \left( \mathrm {MPa} \right) \\ \alpha &{}=1.386 \\ \end{array}} \right. \end{aligned}$$

(9)

Table 4 Hardening parameters obtained from compression tests

Figure 5 plots the derived data for the constitutive model. The mean yield surface is shown in the black solid line. The data from the tension test, the compression test, and the shear test are plotted as black, blue and red markers, respectively.

Fig. 8

Model validation with impact experiments

Fig. 9

Distribution of equivalent plastic strain under different impact conditions

Given Eq. (9), two constants, the compression yield stress ratio (k) and hydrostatic yield stress ratio ($k_{c})$ for the FEM constitutive model can be calculated by $k=\sigma _{c0}/p_{c}$ and $k_{t}=p_{t}/p_{c}$, where $\sigma _{c0}=\frac{1}{3}\left( 26.73+27.35+27.25 \right) \mathrm {MPa}$ is the averaged uniaxial compressive strength according to Table 1. In sum, Table 5 gathers the calculated results and these parameters were adopted in the FEM simulation.

Table 5 Calculated parameters for the aluminum foam

3 Validation

To validate the derived constitutive model, tri-axial compression tests were carried out. Furthermore, direct impact tests were also conducted to study the strain rate effect. An FEM model was built accordingly to compare the results and to check the feasibility of the derived model for dynamic analysis and mechanical behavior prediction.

Fig. 10

a Plastic wave propagation under various impact velocities ($E=600$ J), and b the corresponding distribution of plastic strain

Fig. 11

Surface plot of fitted function by Eq. (9)

Fig. 12

Transition map for deformation configuration

3.1 Tri-axial Compression Tests

To validate the derived model, we conducted 48 tri-axial compression tests using a high-pressure tri-axial testing system. A pressure chamber, as shown in Fig. 2c, was used to generate a hydraulic pressure. The schematic for the tri-axial compression is shown in Fig. 2e. The specimen, a cylinder with a diameter of 40 mm and a height of 40 mm, was encased in rubber membranes, sealed using a fixture with wedge surface, fixed in the pressure chamber, and compressed by the holders. The required high pressure was generated with hydraulic fluid and monitored by a pressure gauge. These tests were also carried out under displacement control mode to keep the strain rate at about $5\times 10^{\mathrm {-4}}\,\hbox {s}^{\mathrm {-1}}$. To investigate the effect of hydraulic pressure on the yield surface of the aluminum foam, tests at two hydraulic pressures, 5 MPa and 10 MPa, were conducted. For the tests under the hydraulic pressure of 5 MPa, tests were ceased when the strain reached 15%. For the tests under the hydraulic pressure of 10 MPa, to prevent the rubber membranes from tearing, tests were ceased when the strain reached 10%. To sum up, two conditions were adopted for the tri-axial tests:

• Condition 1: the hydraulic pressure was 5 MPa, and the strain was less than 15%;

• Condition 2: the hydraulic pressure was 10 MPa, and the strain was less than 10%.

Table 6 lists the results for the tri-axial compression tests. Under the hydraulic pressure of both 5 MPa and 10 MPa, the mechanical performance of the sample is not sensitive to the choice of direction. Figure 5 also plots the experimental data of tri-axial compression tests, which fit well on the derived yield surface, and thus the derived model is validated by the tri-axial tests.

In addition, to verify the feasibility of the present method, we performed fitting with all experimental data including those of the tri-axial compression tests. The corresponding parameters were fitted as: $p_{0}=13.71$ MPa, $A=20.45$ MPa, and $\alpha =1.386$, which are very close to Eq. (9)—with the differences less than 0.6%. It can be concluded that the uniaxial tension tests, uniaxial compression tests and shear tests are sufficient for deriving the constitutive model for present aluminum foam.

Table 6 Experimental results for tri-axial compression tests

3.2 Verification of Dynamic Response

3.2.1 Direct Impact Tests

The impact compression tests were conducted using an INSTRON CEAST 9350 drop hammer testing machine (Fig. 2d). The impact energy was set at 996 J in these tests, about the same level as the energy absorption during the uniaxial compression tests. Two impact velocities of 8 m/s and 14 m/s were used to set the initiate strain rates at $200\hbox { s}^{\mathrm {-1}}$ and $350\hbox { s}^{\mathrm {-1}}$, respectively. The specimens for impacting test are the same as those for tri-axial compression. For each direction, i.e., N, R, or T, we performed eight experiments with two initial impact velocities (48 tests in total). To avoid surface damage in specimen preparation, all specimens were cut from one large aluminum foam plate by electrical discharge machining (EDM).

Table 7 lists the results of impact tests. The present aluminum foam exhibits very little anisotropy under impact. In addition, strain rate dependency can be hardly found.

Table 7 Experimental results of impact tests

3.2.2 FEM Simulation of Direct Impact

The FEM simulation was performed with the commercial software ABAQUS. The model was based on the constitutive model for crushable foam. Table 5 lists the material constants for the FEM model Table 4 lists the hardening parameters, and Fig. 6 plots the hardening behavior (the red line with circular markers) obtained by uniaxial compression. By interpolating and fitting the yield strength $\sigma _{\mathrm {Y}}$ with the plastic strain $\varepsilon ^{\mathrm {p}}$, the yield strength in our case can be specifically approximated by a quadratic polynomial of the plastic strain. Differentiating $\sigma _{\mathrm {Y}}$ with $\varepsilon ^{\mathrm {p}}$ yields the tangent modulus $E^{\mathrm {t}}$, which is in turn a linear form of $\varepsilon ^{\mathrm {p}}$ and is shown by the blue dotted line. The plastic wave speed can be determined by $c_{\mathrm {p}}=\sqrt{E^{\mathrm {t}}/\rho }$ represented by the magenta dash line. The average plastic wave speed can be estimated to be  $\left\langle c_{\mathrm {p}} \right\rangle =128\,\mathrm {m/s}$.

The aluminum sample was cylindrical, with radius $R=20\, \mathrm {mm}$ and length $L=40\,\mathrm {mm}$. The cylindrical axis was in coincidence with the global z-axis and the bottom cap surface lay on the global xy-plane. Two analytical rigid surface bodies were used to model the impactor and the holder. The movement of the impactor was confined along the z-axis and the holder was fixed. Contact pairs were established between the impactor/holder and the top/bottom cap face respectively. The friction coefficient of contact was assumed to be 0.1. An initial field of velocity and an inertial property were imposed on the impactor according to the experimental conditions Two cases were investigated: case 1 with the initial velocity at 8 m/s and case 2 with the initial velocity at 14 m/s. The mass of the impactor was set to be 30.94 kg for case 1 and 10.10 kg for case 2, so that the impact kinetic energy was 990 J in both cases. The sample was meshed with linear hexahedral elements of type C3D8R. To check the mesh dependency, models with different element counts were compared. Figure 7 shows the relationship between the initial peak force of contact and the element count of the model. The simulation results indicate that the mesh choice of $N_{e}=38000$ can describe the impact process reasonably and efficiently. The feasibility of checking mesh dependency by initial peak force is also proven valid by Liu et al. [30] and Rawat et al. [31].

Figure 8 shows the results for model validation. The blue and green lines are the time series of the contact forces during impact under the impact velocities of 14m/s and 8m/s, respectively. The yellow and magenta lines are the simulation results by the present model. With the present constitutive relation, trends of the simulated contact forces with time agree with those by experiments. However, in comparison with the computational results, the experimental contact forces undulate severely. Those harsh bumps in the experimental curves are due to clashing of closed cells during compression, which is unable to be modeled with a continuous model. Nevertheless, the experimental data of the total impulse by the contact force were $279.91\pm 2.84\hbox { N}\cdot \hbox { s}$ under the impact velocity of 14 m/s, and $145.36\pm 2.38\hbox { N}\cdot \hbox { s}$ under the impact velocity of 8 m/s, while the simulated results of total impulse are $258.69\hbox { N}\cdot \hbox { s}$ and $147.91 \hbox { N}\cdot \hbox { s}$, respectively. The difference between simulated results and experimental data is within 8%, which verifies the validity of the present FEM model Such a model can be used to study the dynamic response of the aluminum foam under the condition of various impact parameters. On the other hand, the deformed state of the specimen after impact is similar to that obtained by FEM simulation, as shown by the insets in Fig. 8.

3.3 Discussion of Material Models for Porous Metal

For porous metal, the Gurson model is also widely applied for the cases with high relative density. In the original work of Gurson [32], the yield surface of porous ductile metal was examined with the relative density from 0.7 to 0.995. In another pioneer work by Tvergaard [33], a continuum model for porous solid was built, and the relative density in the simulation was from 0.89 to 0.99. In another pioneer work by Koplik and Needleman [34], by using the finite element method, the deformations of porous metal were simulated with the relative densities of 0.99 and 0.999 respectively, and a phenomenological model was used to describe the void growth. They suggested that the Gurson model is valid for porous metal with high relative density, for instance, even with large void under large plastic deformation, the relative density should be higher than 0.75.

Also, in a very nice review by Benzerga and Leblond [35], they showed that the porosity for Gurson type material is mostly less than 30%; in other words, the relative density should be higher than 0.7. The unsuccessful use of Gurson model in our study is that the Gurson model assumes the unit cell consists of one spherical void with very thick wall. For a recent study by Lacroix [36], the initial porosity was 0.001, so that the relative density was higher than 0.9.

Unlike the Gurson model, the Deshpande–Fleck model is a phenomenological model which does not have the micromechanical physics based on the cellular solid [5]. However, with few parameters experimentally calibrated, this model is widely applied and can even simulate crushable materials other than foam, such as balsa wood. In a recent paper by Zhu et al [8], they proposed a modified Deshpande–Fleck model with variable ellipticity to predict the uni/multi-axial compression of the cell foam One example they used had a relative density of 0.41. This fact also suggests that our approach is valid in present work for the relative density from 0.3 to 0.4. In this work, we did not use the original Deshpande–Fleck model with isotropic hardening. Instead, we used the volume hardening model (mixed hardening) to represent the asymmetry of compression and tension [37].

4 Shock Response

To study the shock response of the aluminum foam under impact via FEM simulation, various values of impact kinetic energy $E_{\mathrm {k}}$ (10 J, 30 J, 60 J, 100 J, 300 J, 600 J, and 900 J) and impact velocity $V_{0}$ (6 m/s, 8 m/s, 10 m/s, 12 m/s, 14 m/s, 20 m/s, 40 m/s, 80 m/s, 120 m/s, 160 m/s, and 200 m/s) were adopted. Figure 9 shows contours of the equivalent plastic strain of typical cases. Generally, there are two distinct types of deformation: the upsetting-type and the shock-type. On the one hand, the higher the impact energy is, the severer the foam deforms. On the other hand, a high impact velocity leads to an evident shock-type deformation, while a low-speed impact results in an upsettingtype deformation similar to quasi-static compression. This result is in accordance with the result by Barnes et al. [20]

The factor accounting for the difference of deformation is the impact time $t_{\mathrm {d}}$, which can be defined as the time when the contact force vanishes. Figure 10a illustrates the plastic wave propagations under the impact energy of 600 J and the velocities of 20 m/s, 80 m/s as well as 200 m/s. In Fig. 10a, the non-dimensional ordinate ${\bar{t}}_{\mathrm {d}}$ is defined as

$$\begin{aligned} {\bar{t}}_{\mathrm {d}}=\frac{t_{\mathrm {d}}}{t_{\mathrm {ref}}} \end{aligned}$$

(10)

where $t_{\mathrm {ref}}$ is the time for the plastic wave to travel from the top surface to the bottom surface, namely

$$\begin{aligned} t_{\mathrm {ref}}=\frac{L}{\left\langle c_{\mathrm {p}} \right\rangle } \end{aligned}$$

(11)

For a high-speed impact at 200 m/s, ${\bar{t}}_{\mathrm {d}}$ is about 0.7. Since the elastic wave travels much faster than the plastic wave, the plastic wave is unloaded by the unloading wave before it hits the bottom surface. This mechanism in turn exhibits a typical shock-type deformation, which is severe at the top (${\bar{z}}\equiv z/L=0)$ and limited at the bottom (${\bar{z}}=1)$. The red line representing the distribution of the equivalent plastic strain in Fig. 10b clearly shows such a configuration. The slight rise near ${\bar{z}}=1$ is caused by the superposition of incident elastic wave and the reflective elastic wave. For a low-speed impact (20 m/s), the plastic wave is unloaded after it reflects 5 times. The deformation is more evenly distributed compared with the high-speed case. The black line in Fig. 10b indicates the upsettingtype configuration in the middle (${\bar{z}}=0.5)$. The plastic strain is slightly higher at both ends due to superposition of elastic waves. For an in-between mid-speed impact (80 m/s), plastic wave is unloaded before it reaches the top surface. Compared with the high-speed scenario, the plastic strain in the interval $0.5\le {\bar{z}}\le 1$ is evidently higher, yet it does not exhibit an upsettingtype characteristic The blue line in Fig. 10b shows a convex distribution of the equivalent plastic strain, which indicates a transition from shock-type characteristic to upsettingtype characteristic.

Deformation characteristic is a direct result of the distribution of plastic strain, which is controlled by the absorbed energy and the impact time. The level of absorbed energy determines the total plastic strain energy. The impact time determines the distribution of the plastic strain. Generally, the relation of the impact time $t_{\mathrm {d}}$ with other parameters can be expressed with the following equation.

$$\begin{aligned} f_{1}\left( t_{\mathrm {d}},E_{\mathrm {k}}, V_{0},E,E^{\mathrm {t}},\sigma _{\mathrm {Y}},\rho ,L,A_{s} \right) =0 \end{aligned}$$

(12)

where $A_{s}$ is the area of the cross-section of the aluminum foam. A dimension analysis shows that there are only 6 independent variables in Eq. (12). The choice of such independent variables is rather arbitrary. A possible choice can be done as follows.

$$\begin{aligned} f_{2}\left( \frac{t_{\mathrm {d}}}{L}\sqrt{\frac{E^{\mathrm {t}}}{\rho }} ,\frac{E_{\mathrm {k}}}{\sigma _{\mathrm {Y}}A_{s}L},\frac{\sigma _{\mathrm {Y}}}{V_{0}\sqrt{E\rho } },\frac{E^{\mathrm {t}}}{E},\frac{\sigma _{\mathrm {Y}}}{E},\frac{L}{\sqrt{A_{s}}}\,\right) =0 \end{aligned}$$

(13)

where the first three variables are related to external loading conditions and the last three variables are related to material properties and geometry only. It can be easily verified that these six variables are independent. Given an object with a certain set of material properties and geometry dimensions, we could write the following relation for impact time.

$$\begin{aligned} {\bar{t}}_{\mathrm {d}}=\frac{t_{\mathrm {d}}}{L}\sqrt{\frac{E^{\mathrm {t}}}{\rho }} =g\left( \frac{E_{\mathrm {k}}}{\sigma _{\mathrm {Y}}A_{s}L},\frac{\sigma _{\mathrm {Y}}}{V_{0}\sqrt{E\rho } } \right) \end{aligned}$$

(14)

Using the FEM simulation results to fit Eq. (14) with polynomials, we have the following explicit form of the relation between $\frac{t_{\mathrm {d}}}{L}\sqrt{\frac{E^{\mathrm {t}}}{\rho }}$, $\frac{E_{\mathrm {k}}}{\sigma _{\mathrm {Y}}A_{s}L}$ and $\frac{\sigma _{\mathrm {Y}}}{V_{0}\sqrt{E\rho } }$ for $\frac{E_{\mathrm {k}}}{\sigma _{\mathrm {Y}}A_{s}L}\in [0.007,\,0.726]$ and $\frac{\sigma _{\mathrm {Y}}}{V_{0}\sqrt{E\rho } }\in [0.047,1.562]$

$$\begin{aligned} \frac{t_{\mathrm {d}}}{L}\sqrt{\frac{E^{\mathrm {t}}}{\rho }} =\left( -16.42\left( \frac{E_{\mathrm {k}}}{\sigma _{\mathrm {Y}}A_{s}L} \right) ^{2}+34.95\frac{E_{\mathrm {k}}}{\sigma _{\mathrm {Y}}A_{s}L} \right) \cdot \frac{\sigma _{\mathrm {Y}}}{V_{0}\sqrt{E\rho } } \end{aligned}$$

(15)

where the constant coefficients of the polynomial of $\frac{E_{\mathrm {k}}}{\sigma _{\mathrm {Y}}A_{s}L}$ may vary accordingly with the values of material properties and geometry. In the present study, Fig. 11 shows the fitted surface expressed by Eq. (15) and the FEM data, which is marked with red dots.

With Eq. (15), a contour of ${\bar{t}}_{\mathrm {d}}=\frac{t_{\mathrm {d}}}{L}\sqrt{\frac{E^{\mathrm {t}}}{\rho }}$ can be drawn to differentiate the deformation characteristics. For ${\bar{t}}_{\mathrm {d}}<1$ the plastic wave does not reach the bottom surface, and in turn, the deformation shows shock-type characteristic; for ${\bar{t}}_{\mathrm {d}}>5$, the plastic wave travels back and forth for several times, and in turn, the deformation shows upsetting-type characteristic, as shown in Fig. 12. For those values in-between, as ${\bar{t}}_{\mathrm {d}}$ increases from 1 to 5, the deformation shows a continuous transition from the shock-type to the upsettingtype since the variation of $\frac{t_{\mathrm {d}}}{L}\sqrt{\frac{E^{\mathrm {t}}}{\rho }}$ is continuous with respect to both $\frac{E_{\mathrm {k}}}{\sigma _{\mathrm {Y}}A_{s}L}$ and $\frac{\sigma _{\mathrm {Y}}}{V_{0}\sqrt{E\rho } }$ We also put our experimental situations in Fig. 12 (red dot), the upsetting configuration found in the experiment is consistent with our prediction using Eq. (15).

It is worth noticing that Zheng et al. [38] pointed out three types of deformation mode: homogenous mode, transitional mode, and shock mode. In the shock mode, foams are crashed layer-by-layer. In the homogenous mode, shear bands are randomly distributed. In the transitional mode, shear band are more likely to initiate near the proximal end. In the present study, we distinguish the type of deformation based on the final deformed shape, which links to the distribution of plastic deformation, and in turn, links to how many times the plastic wave travels back and forth before it is unloaded. Thus, we have three distinct areas in Fig. 12: shock-type, upsetting-type, and the area in-between, as shown by Fig. 12. The shock-type indicates that the plastic wave is unloaded before it hits the bottom surface, corresponding to the shock mode. The upsetting type exhibits a more homogenous distribution of plastic deformation, thus corresponding to the homogenous mode. The transitional area indicates that the plastic wave travels back and forth for several but not many times, so that the plastic strain is evenly distributed, which corresponds to the transitional mode.

5 Conclusion

To study the dynamic impact behavior of the high-density aluminum foam, we firstly obtained the constitutive parameters by three simple tests and then validated the model by tri-axial tests and direct impact tests. Further, with the developed constitutive relation, we performed FEM simulation to study the shock response of high-density aluminum foam. The conclusions are as follows:

• 1. For high-density aluminum foam, the yield surface of Deshpande–Fleck’s constitutive model can be determined by three tests: tension, compression and shear. The validation with triaxial compression test shows good agreement. With three tests, the yield surface can be determined by Eq. (5). With the volumetric hardening law the Deshpande–Fleck model can adequately simulate the dynamic behavior of high-density aluminum foam.

• 2. A numerical model (FEM) is built with Deshpande–Fleck’s constitutive model concerning the mechanical behavior of aluminum foam under impact. Impact tests are carried out validating the FEM model with good agreement. The undulation of impact force due to the clash of closed cells is beyond the capacity of a continuous model.

• 3. A model for a non-dimensional impact time  ${\bar{t}}_{\mathrm {d}}$, as shown in Eq. (14), is proposed to study the relationship between deformation configuration and impact time. Results show that: for ${\bar{t}}_{\mathrm {d}}<1$ the deformation of the aluminum foam is shock-type, with high plastic strain found at the impact surface, because plastic wave could not hit the bottom surface; for ${\bar{t}}_{\mathrm {d}}>5$ the deformed sample is upsettingtype, similar to the deformation due to quasi-static compression.