1 Introduction

NiTi shape memory alloy (SMA) is widely applied in the fields of aerospace, civil engineering, automobile and biomedicine because of its excellent superelasticity, shape memory effect (SME) and biological compatibility. It is known that NiTi SMA can be used in many fields to produce commercial actuators, especially in biomedical sectors due to its shape memory effect [1]. The recovery force or recovery strain occurring in NiTi-based SMA actuators is an important indicator of shape memory effect. However, the residual strain induced by reorientation and reorientation-induced plasticity can result in the degeneration of shape memory effect, and further reduce the recovery capacity of actuators.

Over the past few decades, many experiments were carried out to investigate the degeneration of NiTi SMA due to residual strain [2,3,4,5,6,7,8,9]. They discussed the influences of different factors on the superelastic degeneration of NiTi SMA, including the applied peak strain level [2,3,4,5], loading path [7], loading rate [8] and grain size [9]. For the SME, the researchers explored the thermo-mechanical coupling response of NiTi SMA under temperature cycles with constant stress [4, 10,11,12,13,14,15], and the influence of transformation-induced plasticity on the driving force of transformation. However, the degeneration of shape memory effect still keeps unrevealed. Recently, experimental observations on the degeneration of SME at different peak strains were carried out [16]. It can be seen from the stress–strain curves that: (1) nonlinear hardening can be observed during mechanical loading; (2) the temperature–strain curve shows that the strain after mechanical unloading cannot be fully recovered during the heating process, i.e., residual strain exists; (3) residual strain further increases during the cooling process; (4) residual strain remarkably depends on the loading level.

Based on the above-mentioned experimental observations on the SME of NiTi SMA, many macroscopic phenomenological models [17,18,19,20,21,22,23,24,25] were established to simulate the thermo-mechanical responses of NiTi SMA because of their fewer parameters comparing with the microscopic ones. Brinson [22] proposed an uniaxial phase diagram in temperature-stress space to describe the arbitrary transformations among twinned martensite, detwinned martensite and austenite under different thermo-mechanical loading paths. Based on the phase diagram, Leclercq and Lexcellent [23] established a three-dimensional model using two scalar volume fractions of twinned and detwinned martensites as internal variables; Juhasz et al. [24], however, selected transformation strain tensor as an internal variable. Both models focused on the thermo-mechanical responses of NiTi SMA under complex thermo-mechanical loading paths. In their models, the linear evolution equations of internal variables were adopted during the transformation from the twinned martensite to the detwinned martensite, and the residual strain induced by plastic strain was neglected. And then, Lagoudas and Shu [25] proposed a model to capture the residual strain in the two-way shape memory of NiTi SMA, where the residual strain consists of the martensitic detwinning strain, martensitic reorientation strain and plastic strain at high peak strain. Recently, Yu et al. [16] proposed a macro-phenomenological model to capture the cyclic responses of NiTi SMA including the residual strain after cooling, where the martensitic reorientation during the mechanical loading was addressed and the evolution equations of the martensite volume fractions were assumed to be linear. However, there are two mechanisms for the phase transformation from twinned martensite to detwinned martensite, i.e., the movement of interfaces/twin boundaries between habit plane variants (martensitic reorientation), and the movement of interfaces/twin boundaries between lattice correspondence variants (martensitic detwinning) [26]. Therefore, it is necessary to construct a multi-mechanism model for reasonably describing the peak strain-dependent degeneration of SME.

The work is organized as below, in Sect. 2, the outline of experimental observations of the degeneration of SME is presented, and a macroscopic constitutive model is established in Sect. 3. Then in Sect. 4, the calibration of material parameters is introduced, and the capability of the proposed model is verified by comparing the simulated results with the experimental ones.

2 Experimental Observations

2.1 Experimental Procedures and Results

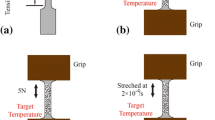
As reported by Yu et al. [16], experimental observations on the degeneration of SME were carried out. For the integrity of the content in this work, the typical features of SME are outlined briefly. The NiTi SMA (Ni, 50.9 at%, from Jiangyin Lumenous Peiertech Co., Ltd., China), whose initial phase at test temperature was twinned martensite, was employed in the thermo-mechanical experiments to investigate the degeneration of SME. The tubular specimens were uniaxially stretched to different strain amplitudes at room temperature (298 K). The strain rate was prescribed to be 0.2%/s. After unloading, the specimens were heated to 393 K (over the austenite finish temperature \(A_\mathrm{f} \)), and then cooled to 298 K.

Figure 1 shows the typical stress–strain and strain–temperature curves of NiTi SMA with the peak strain of 10%. It can be seen that:

(1) When NiTi SMA undergoes the SME process, the initial phase is twinned martensite. During the mechanical loading, the inelastic deformation can be divided into two stages (b to c in Fig. 1a), where the modulus of stage II is significantly higher than that of stage I. After elastic unloading, the inelastic deformation can be observed at point d. As shown in Fig. 1b, once the specimen is heated to \(A_\mathrm{f} \), the inelastic deformation can be partly recovered from point e to point f (the temperatures corresponding to points e and f are the start temperature \(A_\mathrm{s} \) and finish temperature \(A_\mathrm{f} \) of austenitic transformation, respectively). The strain tends to be stable and there remains irreversible strain \(\varepsilon _\mathrm{rh} \) at point f.

(2) During the subsequent cooling (i.e., from point g to point h in Fig. 1b), the residual strain increases (the temperatures correspond to points g and h are the start temperature \(M_\mathrm{s} \) and finish temperature \(M_\mathrm{f} \) of martensitic transformation, respectively), and \(\varepsilon _\mathrm{rl} \) indicates the strain increment during cooling. The recovery strain can be represented by \(\varepsilon _\mathrm{ru} \), it means that the final residual strain consists of \(\varepsilon _\mathrm{rh} \) and \(\varepsilon _\mathrm{rl} \).

(3) It is seen from Fig. 1c that these residual strains strongly depend on the peak strain, i.e., the residual strain increases with the increase in peak strain.

Fig. 1
figure 1

Results of the SME with the peak strain of 10%: a stress–strain curve; b temperature–strain curve; c experimental and simulated stress–strain–temperature curves

Full size image

2.2 Summary of Physical Mechanism

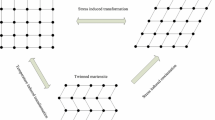
Based on the experimental observations in Sect. 2.1, Fig. 2 shows the illustration of the transformations among austenite, twinned martensite and detwinned martensite of NiTi SMA. During the mechanical loading, the martensitic reorientation only occurs in stage I (i.e., from point b to point c in Fig. 2), and further martensitic detwinning emerges in stage II once the stress reaches the value at point c. It is known that the resistance of martensitic detwinning is much higher than that of martensitic reorientation [16, 26], and thus, the slope of stage II is greater than that of stage I. Meanwhile, the dislocation slipping can be activated with the help of the local stress near the interfaces between martensite variants during the martensitic reorientation, even if the applied stress is lower than the plastic yield stress of martensite [27]; and such an inelastic deformation mechanism is named reorientation-induced plasticity [28]. It is noted that the reorientation-induced plastic deformation is accompanied with the martensitic reorientation.

After elastic unloading, if the applied stress is sufficiently high, all twinned martensites can become detwinned martensites, then the phases of SMA consist of detwinned martensites and some dislocation slippings. After heating, the reverse transformation from detwinned martensite to austenite (from point f to point g) occurs once the temperature reaches a critical value \(A_\mathrm{s} \). During this process, a new plastic deformation named transformation-induced plasticity [29] emerges during the reverse transformation. However, it is very difficult to distinguish the proportions of reorientation-induced and transformation-induced plastic strains. Therefore, all plastic deformations can be assumed as the reorientation-induced plasticity. Although the reverse transformation induced by temperature can be pinned by dislocation slipping [6], all martensite variants can transform into austenite ones (see point g) as long as the temperature is sufficiently high [30].

When the strain remains stable, i.e., at point g, the SMA consists of austenite phase with more dislocation slippings. During the subsequent cooling, when the temperature reaches the critical value \(M_\mathrm{s} \), the transformation from austenite to twinned martensite (from point h to point i) occurs, and the strain increment \(\varepsilon _\mathrm{rl} \) increases. If the SMA is heated again, the strain will be recovered again (showing the two-way shape memory effect) [31, 32]. Therefore, the strain increment \(\varepsilon _\mathrm{rl} \) can be assumed as the residual reorientation strain induced by partial detwinned martensites. When the specimen is cooled to room temperature (point j), the SMA consists of the mixed phases of twinned and detwinned martensites with some dislocation slippings.

Fig. 2
figure 2

Illustration of the transformations among austenite, twinned martensite and detwinned martensite in NiTi SMA

Full size image

3 Constitutive Model

Based on the Liang and Rogers model [22, 33], Brinson [22] proposed a one-dimensional constitutive model to describe the thermo-mechanical deformation behavior of NiTi SMA. The internal variable, i.e., the martensite volume fraction, is divided into the stress-induced and the temperature-induced ones. Considering the transformations among different phases under different thermo-mechanical loading paths based on the phase diagram, the SME and superelasticity can be reproduced. Based on the phase diagram and experimental observations, a new multi-mechanism constitutive model is established to accurately describe the reorientation and reorientation-induced plasticity of NiTi SMA.

3.1 Constitutive Equations

It is known that NiTi SMA can undergo a large transformation strain (about \(8-10\%\)) under uniaxial tension, which is at the boundary between small and large strains. In the meantime, the strain remains small since the mechanical loading often induces a large displacement with a small strain in structures, and thus the assumption of small deformation holds for NiTi SMA [23]. A macroscopic formulation based on large deformation should be developed in future work to capture the SME more accurately.

With the assumption of small deformation, the total strain \({\varvec{\varepsilon }}\) can be decomposed into four parts, i.e., elastic strain \({\varvec{\varepsilon }}^\mathrm{e}\), reorientation strain \({\varvec{\varepsilon }}^{\mathrm{reo}}\), thermal expansion strain \({\varvec{\varepsilon }}^\mathrm{th}\) and reorientation-induced plastic strain \({\varvec{\varepsilon }}^{\mathrm{reop}}\).

The rate form of strain decomposition can be written as:

$$\begin{aligned} {\dot{\varvec{\varepsilon }}}={\dot{\varvec{\varepsilon }}}^\mathrm{e}+{\dot{\varvec{\varepsilon }}}^{\mathrm{reo}}+{\dot{\varvec{\varepsilon }}}^{\mathrm{reop}}+{\dot{\varvec{\varepsilon }}}^\mathrm{th} \end{aligned}$$
(1)

The elastic stress–strain relationship can be expressed as:

$$\begin{aligned} {\dot{\varvec{\sigma }}}={{\varvec{D}}}:\left( {{\dot{\varvec{\varepsilon }}}-{\dot{\varvec{\varepsilon }}}^{\mathrm{reo}}-{\dot{\varvec{\varepsilon }}}^\mathrm{{reop}}-{\dot{\varvec{\varepsilon }}}^\mathrm{th}} \right) \end{aligned}$$
(2)

where \({\varvec{\sigma }}\) and \({{\varvec{D}}}\) are the stress tensor and elastic tensor, respectively.

The total martensite volume fraction \(\xi \) is divided into the stress-induced martensite volume fraction \(\xi _\mathrm{s} \) and the temperature-induced martensite volume fraction \(\xi _\mathrm{t} \), i.e.,

$$\begin{aligned} \xi =\xi _\mathrm{s} +\xi _\mathrm{t} \end{aligned}$$
(3)

It should be noted that the total martensite volume fraction is limited within \(0\le \xi \le 1\).

The reorientation strain produces during mechanical loading and recovers during heating. Therefore, the stress-induced martensite volume fraction should be related to temperature and stress simultaneously. The rate of martensitic reorientation strain \({\dot{\varvec{\varepsilon }}}^\mathrm{{reo}}\) can be written as:

$$\begin{aligned} {\dot{\varvec{\varepsilon }}}^\mathrm{{reo}}\left( {{\dot{\varvec{\sigma }}},\dot{T}} \right)= & {} \varepsilon _l {\varvec{\varLambda }}_\mathrm{{reo}} \dot{\xi }_\mathrm{s} \left( {{\dot{\varvec{\sigma }}},\dot{T}} \right) \end{aligned}$$
(4a)
$$\begin{aligned} {\varvec{\varLambda }}_\mathrm{{reo}}= & {} \left\{ {\begin{array}{l} \sqrt{\frac{3}{2}}\frac{\varvec{s}}{\left\| {\varvec{s}} \right\| },\quad \dot{\xi }_\mathrm{s} \left( {{\dot{\varvec{\sigma }}},\dot{T}} \right) >0 \\ \sqrt{\frac{2}{3}}\frac{{\varvec{e}}^\mathrm{{reo}}}{\left\| {{\varvec{e}}^\mathrm{{reo}}} \right\| },\quad \dot{\xi }_\mathrm{s} \left( {{\dot{\varvec{\sigma }}},\dot{T}} \right) <0 \\ \end{array}} \right. \end{aligned}$$
(4b)

where \(\varepsilon _l \) is the maximum reorientation strain during the transformation from twinned martensite to detwinned martensite, the value of which can be determined from experiments directly; \({\varvec{\varLambda }}_\mathrm{{reo}} \) is the direction tensor of stress-induced martensitic reorientation (\(\dot{\xi }_\mathrm{s} >0\)) and temperature-induced martensitic transformation (\(\dot{\xi }_\mathrm{s} <0\), corresponding to the stress-free state), respectively; \(\left\| \cdot \right\| \) is the usual Euclidean norm; \({\varvec{s}}\) and \({\varvec{e}}^\mathrm{{reo}}\) are the deviatoric parts of stress \({\varvec{\sigma }}\) and reorientation strain \({\varvec{\varepsilon }}^\mathrm{{reo}}\), respectively; and \(\dot{\xi }_\mathrm{s}~({{\dot{\varvec{\sigma }}},\dot{T}})\) is the function of stress and temperature rates, the specific form of which is described in Sect. 3.2.

Thermal strain only occurs during heating and cooling, that is, \(\dot{T}=0\) during mechanical loading. Therefore, the thermal strain rate can be calculated as follows:

$$\begin{aligned} {\dot{\varvec{\varepsilon }}}^\mathrm{th}=\alpha {{\varvec{I}}}\dot{T} \end{aligned}$$
(5)

where \(\alpha \) is the coefficient of thermal expansion, \(\dot{T}\) is temperature rate, and \({\varvec{I}}\) is the second unit tensor.

As commented in Sect. 2.2, the reorientation-induced and transformation-induced plastic deformations occur during the transformations from twinned martensite to detwinned martensite and from detwinned martensite to austenite, respectively. All plastic strains can be assumed as the reorientation-induced plastic strain, and their directions are consistent with that of reorientation. Thus, the reorientation-induced plastic strain rate can be expressed as:

$$\begin{aligned} {\dot{\varvec{\varepsilon }}}^\mathrm{{reop}}={\varvec{\varLambda }}_\mathrm{{reo}} f(\dot{\xi }_\mathrm{s} ) \end{aligned}$$
(6)

where \(f(\dot{\xi }_\mathrm{s} )\) is a function of the stress-induced martensite volume fraction \(\dot{\xi }_\mathrm{s} \), the specific form of which is described in Sect. 3.3.

3.2 Evolution Law of Reorientation Strain

3.2.1 Transformation Surface

Different from the plastic yield surface of general metals, the reorientation strain depends on stress and temperature simultaneously. The stress-dependent and temperature-dependent reorientation strains can be captured by using the specific stress-dependent transformation surface and temperature-dependent transformation surface, respectively:

$$\begin{aligned} F_\mathrm{s}^\alpha \left( {{\varvec{\sigma }},\bar{{\xi }},T_0 } \right)= & {} {\varvec{\sigma }}:{\varvec{\varLambda }}_\mathrm{{reo}} -\sigma _\mathrm{s}^\alpha \left( {\bar{{\xi }},T_0 } \right) =0 \end{aligned}$$
(7a)
$$\begin{aligned} F_T^\alpha \left( {{\varvec{\sigma }}_0 ,\bar{{\xi }},T} \right)= & {} T-T_T^\alpha \left( {\bar{{\xi }},{\varvec{\sigma }}_0 } \right) =0 \end{aligned}$$
(7b)

where \({\varvec{\sigma }}_0 \) and \(T_0 \) are the initial stress and temperature related to previous loading history, respectively; \(\sigma _\mathrm{s}^\alpha \left( {\bar{{\xi }},T_0 } \right) \) and \(T_T^\alpha \left( {\bar{{\xi }},{\varvec{\sigma }}_0 } \right) \) are the critical stress and temperature of reorientation, respectively; the superscript \(\alpha \) takes I, II and III in turn, representing the transformations at different stress and temperature states, as shown in Fig. 3; and \(\bar{{\xi }}\) represents \(\xi _\mathrm{s} \) or \(\xi \) for different transformations, as shown in Table 1.

Fig. 3
figure 3

Illustrated stress-dependent and temperature-dependent transformations of NiTi SMA in the stress–temperature diagram. a stress-induced transformation; b temperature-induced transformation

Full size image
Table 1 The statements of \(\varvec{\alpha } \) and \(\bar{{\varvec{\xi }}}\) based on the phase diagram
Full size table

3.2.2 Evolution of Reorientation Strain

(1) Stress-dependent transformations

For the transformation from austenite to detwinned martensite shown in Table 1, the critical stress of transformation and martensitic volume fractions can be calculated as:

when \(T_0 >M_\mathrm{s}\) and \(\sigma _\mathrm{s} +C_M \left( {T_0 -M_\mathrm{s} } \right)<\sigma _\mathrm{eq} <\sigma _\mathrm{f} +C_M \left( {T_0 -M_\mathrm{s} } \right) \):

$$\begin{aligned} \sigma _\mathrm{s}^\mathrm{{I}} \left( {\xi _\mathrm{s},T_0 } \right)= & {} \frac{\sigma _\mathrm{s} -\sigma _\mathrm{f} }{\pi }\arccos \left[ {\frac{2}{1-\xi _{s0} }\left( {\xi _\mathrm{s} -\frac{1+\xi _{s0} }{2}} \right) } \right] +C_M \left( {T_0 -M_\mathrm{s} } \right) +\sigma _\mathrm{f} \end{aligned}$$
(8a)
$$\begin{aligned} \dot{\xi }_\mathrm{t}= & {} -\frac{\xi _{t0} }{1-\xi _{s0} }\dot{\xi }_\mathrm{s} \end{aligned}$$
(8b)
$$\begin{aligned} \dot{\xi }= & {} \dot{\xi }_\mathrm{s} +\dot{\xi }_\mathrm{t} \end{aligned}$$
(8c)

where \(\xi _{s0} \) and \(\xi _{t0} \) represent the initial values of stress-induced and temperature-induced martensite volume fractions at the beginning of the transformation, respectively; \(\sigma _\mathrm{eq} \) is the von Mises equivalent stress; material constants \(C_A \) and \(C_M \) are the slopes of the critical stress–temperature curves; \(\sigma _\mathrm{s} \) and \(\sigma _\mathrm{f} \) are start and finish stresses of martensitic reorientation, respectively, as shown in Fig. 3a.

As discussed in Sect. 2.2, the martensitic reorientation (from twinned martensite to detwinned martensite) can be divided into martensitic reorientation (stage I) and martensitic detwinning with further reorientation (stage II). The slope of stage II is greater than that of stage I. Thus, the detwinned stress \({\varvec{\sigma }}_\mathrm{t} \) is introduced to reflect the additional hardening mechanism, and a sine function is adopted to describe the nonlinear hardening at stage II:

when \(T_0 <M_\mathrm{s} \) and \(\sigma _\mathrm{s}<\sigma _\mathrm{eq} <\sigma _\mathrm{f} \):

$$\begin{aligned} \sigma _\mathrm{s}^\mathrm{{II}} \left( {\xi _\mathrm{s},T_0 } \right)= & {} \frac{\sigma _\mathrm{s} -\sigma _\mathrm{f} }{\pi }\arccos \left[ {\frac{2}{1-\xi _{s0} }\left( {\xi _\mathrm{s} -\frac{1+\xi _{s0} }{2}} \right) } \right] +\sigma _\mathrm{f} +{\varvec{\sigma }}_\mathrm{t} :{\varvec{\varLambda }}_\mathrm{{reo}} \end{aligned}$$
(9a)
$$\begin{aligned} {\varvec{\sigma }}_\mathrm{t}= & {} \sigma _\mathrm{t} {\varvec{\varLambda }}_\mathrm{{reo}} \end{aligned}$$
(9b)
$$\begin{aligned} \sigma _\mathrm{t}= & {} \left\{ {\begin{array}{ll} 0&{}\quad (\sigma _\mathrm{s} \le \sigma _\mathrm{eq}<\sigma _m )\\ \sigma _0 +\sigma _h \sin \left[ {\frac{\pi \left( {\xi _\mathrm{s} -\xi _c } \right) }{\omega }} \right] &{}\quad (\sigma _m \le \sigma _\mathrm{eq} <\sigma _\mathrm{f} ) \\ \end{array}} \right. \end{aligned}$$
(9c)
$$\begin{aligned} \dot{\xi }_\mathrm{t}= & {} -\frac{\xi _{t0} }{1-\xi _{s0} }\dot{\xi }_\mathrm{s} \end{aligned}$$
(9d)
$$\begin{aligned} \dot{\xi }= & {} \dot{\xi }_\mathrm{s} +\dot{\xi }_\mathrm{t} \end{aligned}$$
(9e)

where \(\sigma _0 \), \(\sigma _h \), \(\xi _c \) and \(\omega \) are material parameters and \(\sigma _m \) is the stress related to the turning point between stage I and stage II.

For the transformation from martensite to austenite, the critical stress of transformation and martensitic volume fractions can be expressed as:

when \(T_0 >A_\mathrm{s}\) and \(C_A \left( {T_0 -A_\mathrm{f} } \right)<\sigma _\mathrm{eq} <C_A \left( {T_0 -A_\mathrm{s} } \right) \):

$$\begin{aligned} \sigma _\mathrm{s}^\mathrm{{III}} \left( {\xi _\mathrm{s} ,T_0 } \right)= & {} C_A \left\{ {T_0 -A_\mathrm{s} -\frac{A_\mathrm{f} -A_\mathrm{s} }{\pi }\arccos \left[ {\frac{2}{\xi _0 }\left( {\xi -\frac{\xi _0 }{2}} \right) } \right] } \right\} \end{aligned}$$
(10a)
$$\begin{aligned} \dot{\xi }_\mathrm{s}= & {} \frac{\xi _{s0} }{\xi _0 }\dot{\xi } \end{aligned}$$
(10b)
$$\begin{aligned} \dot{\xi }_\mathrm{t}= & {} \frac{\xi _{t0} }{\xi _0 }\dot{\xi } \end{aligned}$$
(10c)

where \(\xi _0 \) represent the initial value of total martensite volume fraction at the beginning of transformation.

(2) Temperature-dependent transformations

The evolution equation of temperature during transformation from austenite to detwinned martensite is adopted as below:

when \(T>M_\mathrm{s}\) and \(\sigma _\mathrm{s} +C_M \left( {T-M_\mathrm{s} } \right)<\sigma _{0 \mathrm{eq}} <\sigma _\mathrm{f} +C_M \left( {T-M_\mathrm{s} } \right) \):

$$\begin{aligned} T_T^\mathrm{{I}} \left( {\xi _\mathrm{s} ,{\varvec{\sigma }}_0 } \right)= & {} \frac{1}{C_M }\left\{ {\sigma _{0\mathrm{eq}} -\sigma _\mathrm{f} -\frac{\sigma _\mathrm{s} -\sigma _\mathrm{f} }{\pi }\arccos \left[ {\frac{2}{1-\xi _{s0} }\left( {\xi _\mathrm{s} -\frac{1+\xi _{s0} }{2}} \right) } \right] } \right\} +M_\mathrm{s} \end{aligned}$$
(11a)
$$\begin{aligned} \dot{\xi }_\mathrm{t}= & {} -\frac{\xi _{t0} }{1-\xi _{s0} }\dot{\xi }_\mathrm{s} \end{aligned}$$
(11b)
$$\begin{aligned} \dot{\xi }= & {} \dot{\xi }_\mathrm{s} +\dot{\xi }_\mathrm{t} \end{aligned}$$
(11c)

where \(\sigma _{0\mathrm{eq}} \) is the equivalent stress of the initial stress tensor \({\varvec{\sigma }}_0 \).

For transformation from martensite to austenite induced by temperature, the below evolution equations of temperature are adopted:

when \(T>A_\mathrm{s}\) and \(C_A \left( {T-A_\mathrm{f} } \right)<\sigma _{0\mathrm{eq}} <C_A \left( {T-A_\mathrm{s} } \right) \):

$$\begin{aligned} T_T^{{\mathrm{II}}} \left( {\xi ,{\varvec{\sigma }}_0 } \right)= & {} \frac{A_\mathrm{f} -A_\mathrm{s} }{\pi }\arccos \left[ {\frac{2}{\xi _0 }\left( {\xi -\frac{\xi _0 }{2}} \right) } \right] +A_\mathrm{s} +\frac{\sigma _{0\mathrm{eq}} }{C_A } \end{aligned}$$
(12a)
$$\begin{aligned} \dot{\xi }_\mathrm{s}= & {} \frac{\xi _{s0} }{\xi _0 }\dot{\xi } \end{aligned}$$
(12b)
$$\begin{aligned} \dot{\xi }_\mathrm{t}= & {} \frac{\xi _{t0} }{\xi _0 }\dot{\xi } \end{aligned}$$
(12c)

According to the discussion in Sect. 2.2, the evolution of martensite volume fraction during the transformation from austenite to twinned martensite depends on the ratio of the residual reorientation strain to the maximum reorientation strain. Thus, the evolution of martensite volume fraction during the transformation from austenite to twinned martensite can be written as:

when \(T<M_\mathrm{s}\) and \(0\le \sigma _{0\mathrm{eq}} <\sigma _\mathrm{f} \):

$$\begin{aligned} T_T^\mathrm{{III}} \left( {\xi ,{\varvec{\sigma }}_0 } \right)= & {} \frac{1}{C_M }\arccos \left[ {\frac{2}{1-\xi _0 }\left( {\xi -\frac{1+\xi _0 }{2}} \right) } \right] +M_\mathrm{s} +\frac{\sigma _{0\mathrm{eq}} }{C_M } \end{aligned}$$
(13a)
$$\begin{aligned} \dot{\xi }_\mathrm{s}= & {} \frac{\varepsilon _\mathrm{rl}\dot{\xi }}{\varepsilon _l } \end{aligned}$$
(13b)
$$\begin{aligned} \dot{\xi }_\mathrm{t}= & {} \dot{\xi }-\dot{\xi }_\mathrm{s} \end{aligned}$$
(13c)

It can be seen from Eq. (13b) that the rate of the stress-induced martensite volume fraction \(\dot{\xi }_\mathrm{s} \) is proportional to the residual reorientation strain \(\varepsilon _\mathrm{rl} \). Based on the experimental observations shown in Fig. 5a, the residual reorientation strain depends on the peak strain level, and thus an exponential function is adopted to describe the evolution of residual reorientation strain in uniaxial case:

$$\begin{aligned} \varepsilon _\mathrm{rl} =\varepsilon _\mathrm{rl}^\mathrm{sat} \exp \left[ {-\,b_1 \cdot \left( {1-\int {\left| {\dot{\xi }_\mathrm{s} } \right| } \hbox {d}t} \right) } \right] \end{aligned}$$
(14)

where \(\varepsilon _\mathrm{rl}^\mathrm{sat} \) represents the residual reorientation strain corresponding to the full transformation from twinned martensite to detwinned martensite in uniaxial case; the parameter \(b_1 \) is used to characterize the accumulated rate of residual reorientation strain; and the specific expression of \(\varepsilon _\mathrm{rl}^\mathrm{sat} \) is shown in Sect. 3.4.

3.2.3 The Solution of \(\dot{\bar{{\xi }}}\)

According to the transformation surfaces shown in Eqs. (7a) and (7b), the martensite volume fraction under different paths of the phase diagram can be solved by the consistent condition, for stress-induced and temperature-induced transformations, respectively.

(1) Stress-induced transformation

The stress-induced \(\dot{\bar{{\xi }}}\) can be derived from Eq. (7a):

$$\begin{aligned} \dot{F}_\mathrm{s}^\alpha \left( {{\varvec{\sigma }},\bar{{\xi }},T_0 } \right)= & {} \frac{\partial \dot{F}_\mathrm{s}^\alpha \left( {{\varvec{\sigma }},\bar{{\xi }},T_0 } \right) }{\partial {\varvec{\sigma }}}{\dot{\varvec{\sigma }}}+\frac{\partial \dot{F}_\mathrm{s}^\alpha \left( {{\varvec{\sigma }},\bar{{\xi }},T_0 } \right) }{\partial \bar{{\xi }}}\dot{\bar{{\xi }}}=0 \end{aligned}$$
(15a)
$$\begin{aligned} \dot{\bar{{\xi }}}= & {} -\frac{\partial \dot{F}_\mathrm{s}^\alpha \left( {{\varvec{\sigma }},\bar{{\xi }},T_0 } \right) }{\partial {\varvec{\sigma }}}{\dot{\varvec{\sigma }}}/\frac{\partial \dot{F}_\mathrm{s}^\alpha \left( {{\varvec{\sigma }},\bar{{\xi }},T_0 } \right) }{\partial \bar{{\xi }}} \end{aligned}$$
(15b)

(2) Temperature-induced transformation

The temperature-dependent \(\dot{\bar{{\xi }}}\) can be derived from Eq. (7b):

$$\begin{aligned} \dot{F}_T^\alpha \left( {{\varvec{\sigma }}_0 ,\bar{{\xi }},T} \right)= & {} \frac{\partial \dot{F}_T^\alpha \left( {{\varvec{\sigma }}_0 ,\bar{{\xi }},T} \right) }{\partial T}\dot{T}+\frac{\partial \dot{F}_T^\alpha \left( {{\varvec{\sigma }}_0 ,\bar{{\xi }},T} \right) }{\partial \bar{{\xi }}}\dot{\bar{{\xi }}}=0 \end{aligned}$$
(16a)
$$\begin{aligned} \dot{\bar{{\xi }}}= & {} -\frac{\partial \dot{F}_T^\alpha \left( {{\varvec{\sigma }}_0 ,\bar{{\xi }},T} \right) }{\partial T}\dot{T}/\frac{\partial \dot{F}_T^\alpha \left( {{\varvec{\sigma }}_0 ,\bar{{\xi }},T} \right) }{\partial \bar{{\xi }}} \end{aligned}$$
(16b)

From Eqs. (15) and (16), the rate of martensite volume fraction can be determined, and then the stress, strain and temperature can be solved in turn.

3.3 Evolution of Reorientation-Induced Plastic Strain

Since the reorientation-induced plasticity is accompanied with the process of martensitic reorientation, the reorientation-induced plastic strain rate \({\dot{\varvec{\varepsilon }}}^\mathrm{{reop}}\) depends on the volume fraction of stress-induced martensitic reorientation, and can be written as:

$$\begin{aligned} {\dot{\varvec{\varepsilon }}}^\mathrm{{reop}}=b_2 \varepsilon _p^\mathrm{sat} {\varvec{\varLambda }}_\mathrm{{reo}} \exp \left( {-b_2 \cdot \left( {1-\int {\left| {\dot{\xi }_\mathrm{s} } \right| } \mathrm{d}t} \right) } \right) \left| {\dot{\xi }_\mathrm{s} } \right| \end{aligned}$$
(17)

where \(\varepsilon _p^\mathrm{sat} \) represents the maximum plastic strain corresponding to the full transformation from twinned martensite to detwinned martensite in uniaxial case, and the parameter \(b_2 \) controls the accumulated rate of reorientation-induced plastic strain.

3.4 Evolutions of Transformation Temperatures

According to the experimental curves of peak strain versus transformation temperatures shown in Fig. 5b, the transformation temperatures have an approximately linear correlation with the peak strain. In the meantime, the accumulated detwinned martensite volume fraction also increases with the increase in peak strain. Thus, it can be assumed that the transformation temperatures are proportional to the accumulated detwinned martensite volume fraction. Thus, the below equations can be obtained:

$$\begin{aligned} A_\mathrm{s}= & {} A_\mathrm{s}^0 +k_1 \int {\left| {\dot{\xi }_\mathrm{s} } \right| } \hbox {d}t \end{aligned}$$
(18a)
$$\begin{aligned} A_\mathrm{f}= & {} A_\mathrm{f}^0 +k_2 \int {\left| {\dot{\xi }_\mathrm{s} } \right| } \hbox {d}t \end{aligned}$$
(18b)
$$\begin{aligned} M_\mathrm{s}= & {} M_\mathrm{s}^0 +k_3 \int {\left| {\dot{\xi }_\mathrm{s} } \right| } \hbox {d}t \end{aligned}$$
(18c)
$$\begin{aligned} M_\mathrm{f}= & {} M_\mathrm{f}^0 +k_4 \int {\left| {\dot{\xi }_\mathrm{s} } \right| } \hbox {d}t \end{aligned}$$
(18d)

where \(A_\mathrm{s}^0 \), \(A_\mathrm{f}^0 \), \(M_\mathrm{s}^0 \) and \(M_\mathrm{f}^0 \) represent the transformation temperatures of austenite start, austenite finish, martensite start and martensite finish in the stress-free state, respectively; and the parameters \(k_1 \), \(k_2 \), \(k_3 \), and \(k_4 \) are linear correlation coefficients.

4 Verification and Discussion

4.1 Parameter Calibrations

The parameters used in the proposed model can be determined by the below procedures:

(1) The thermal expansion coefficient of NiTi SMA varies from \(6.6\times 10^{-6}\) to \(11\times 10^{-6 }~\hbox {K}^{-1 }\) [34], and the thermal strain changes from 0.05 to 0.09% when the temperature varies from 304 K to 394 K. Considering that the thermal strain is very small and makes little contribution to the overall deformation, the thermal expansion coefficient is taken as \(10\times 10^{-6}~\hbox {K}^{-1}\) for simplicity. The values of E,\(\sigma _\mathrm{s} ,\sigma _\mathrm{f} \), and \(\sigma _m \) can be directly obtained from the experimental results, as shown in Fig. 4a.

Fig. 4
figure 4

Stress–strain–temperature curves used to determine the material parameters for the proposed model: a stress–strain curves; b strain–temperature curves

Full size image

Equation (9b) is a sine function with stress versus stress-induced martensite volume fraction, as shown in Fig. 4a, and the half period \(\omega \) can be calculated as follows:

$$\begin{aligned} \omega =\frac{\varepsilon _{0.1} -\varepsilon _m }{\varepsilon _{0.1} } \end{aligned}$$
(19)

where \(\varepsilon _{0.1} \) is the total inelastic strain after mechanical unloading with the peak strain of 10%, and \(\varepsilon _m \) is the strain at the turning point between martensitic reorientation and detwinning. It is noted that according to Eq. (9c), the maximum and minimum values of \(\sigma _\mathrm{t} \) can be calculated from \(\sigma _\mathrm{t}^{\max } =\sigma _0 +\sigma _h \) and \(\sigma _\mathrm{t}^{\min } =\sigma _0 -\sigma _h =0\), respectively. Then \(\sigma _0 \) and \(\sigma _h \) can be obtained approximately by:

$$\begin{aligned} \sigma _0 =\sigma _h =\frac{\sigma _{0.1} -\sigma _\mathrm{f} }{2} \end{aligned}$$
(20)

The parameter \(\xi _c \) shown in Eq. (9c) is used to adjust the hardening modulus of stage II, which can be evaluated by fitting the curve of stress versus strain with the peak strain of 10%.

(2) Material constants \(C_A \) and \(C_M \) are the slopes of the critical stress–temperature curves, which can be determined by fitting the experimental data [16]. The value of \(T_0 \) is set as room temperature. According to the assumptions in Sect. 3.4, taking \(A_\mathrm{s}^0 \) as an example, \(k_1 \) can be determined by

$$\begin{aligned} \left\{ {\begin{array}{l} A_\mathrm{s}^{0.1} =A_\mathrm{s}^0 +k_1 \\ A_\mathrm{s}^{0.042} =A_\mathrm{s}^0 +k_1 \frac{\varepsilon _{0.042} }{\varepsilon _{0.1} } \\ \end{array}} \right. \end{aligned}$$
(21)

where \(\varepsilon _{0.042} \) and \(A_\mathrm{s}^{0.042} \) are, respectively, the total inelastic strain and austenitic transformation temperature obtained from the experiment with a peak strain of 4.2%. The other parameters \(M_\mathrm{f}^0 \), \(M_\mathrm{s}^0 \), \(A_\mathrm{f}^0 \), \(k_2 \), \(k_3 \) and \(k_4 \) can be determined using the same method. Since \(M_\mathrm{s} \) remains almost unchanged at different peak strains, i.e., \(M_\mathrm{s}^0 =M_\mathrm{s}^{0.1} \), the value of \(M_\mathrm{s}^0 \) can be determined directly from the critical temperature \(M_\mathrm{s}^{0.1} \), and \(k_3 \) is equal to 0.

(3) The parameters \(\varepsilon _p^\mathrm{sat} \) and \(\varepsilon _\mathrm{rl}^\mathrm{sat} \) are related to the reorientation-induced plastic strain and the residual reorientation strain with a maximum peak strain, and can be determined by Eqs. (22) and (23), respectively. The values of \(b_1 \) and \(b_2 \) can be evaluated by fitting the curve shown in Fig. 4b.

$$\begin{aligned} \varepsilon _p^\mathrm{sat} =\varepsilon _\mathrm{rh} -\alpha \Delta T \end{aligned}$$
(22)
$$\begin{aligned} \varepsilon _\mathrm{rl}^\mathrm{sat} =\varepsilon _\mathrm{rl} -\alpha \Delta T \end{aligned}$$
(23)

where \(\Delta T\) is temperature increment; and \(\varepsilon _\mathrm{rh} \) and \(\varepsilon _\mathrm{rl} \) are strains after heating and cooling, respectively, as shown in Fig. 4b.

Finally, all material parameters used in the proposed model are listed in Table 2.

Table 2 Material parameters used in the proposed model
Full size table

4.2 Verification and Discussion

Since the initial phase is twinned martensite, the parameters \(\xi _{s0} \), \(\xi _{t0} \) and \(\xi _0 \) are set as 0, 1 and 1, respectively. By using the parameters shown in Table 2, the proposed model is numerically implemented to describe the SME of NiTi SMA. The simulated and experimental stress–strain–temperature curves with the peak strains of 4.2, 6, 8 and 10% are shown in Fig. 1c. It is seen that: (1) the nonlinear evolution of inelastic deformation at different peak strains can be described reasonably; (2) the proposed model can reasonably capture the responses of partially recovered inelastic deformation during the transformation from detwinned martensite to austenite and the increased residual strain during the transformation from austenite to twinned martensite.

Fig. 5
figure 5

Evolution curves of a inelastic strain; b transformation temperature versus peak strain

Full size image

The simulated and experimental evolution curves of inelastic strains (i.e., \(\varepsilon _\mathrm{ru} \), \(\varepsilon _\mathrm{rl} \) and \(\varepsilon _\mathrm{rh}\)) and critical transformation temperatures are shown in Fig. 5a and b, respectively. It is found that the evolution of the recovery strain, plastic strain, residual reorientation strain and critical transformation temperatures at different peak strains are well predicted. This means that the proposed model can capture the peak strain-dependent degeneration of SME.

The evolution curves of \(\varepsilon ^\mathrm{{reo}}\), \(\varepsilon ^\mathrm{{reop}}\) and \(\varepsilon ^\mathrm{th}\) during the uniaxial mechanical loading-unloading and heating-cooling with peak strain of 10% are shown in Fig. 6a and b, respectively.

Fig. 6
figure 6

Evolution curves of inelastic strain (\(\varepsilon ^\mathrm{th}\), \(\varepsilon ^\mathrm{{reo}}\) and \(\varepsilon ^\mathrm{{reop}}\)) with a peak strain of 10%: a the mechanical loading–unloading process; b the heating–cooling process

Full size image

It can be seen from Fig. 6a that each strain in the initial state is zero, and the initial temperature keeps constant as 303 K. Then the total elastic strain increases while the inelastic strains (include \(\varepsilon ^\mathrm{{reo}}\) and \(\varepsilon ^\mathrm{{reop}}\)) and thermal strain \(\varepsilon ^\mathrm{th}\) remain zero during elastic loading (from point a to point b). The reorientation strain \(\varepsilon ^\mathrm{{reo}}\) starts to increase while the plastic strain \(\varepsilon ^\mathrm{{reop}}\) slowly increases from point b to point c, which corresponds to stage I (i.e., martensitic reorientation). And then, the growth of reorientation strain \(\varepsilon ^\mathrm{{reo}}\) gradually slows down, while the reorientation-induced plastic strain \(\varepsilon ^\mathrm{{reop}}\) increases faster and faster in stage II from point c to point d. The inelastic strains remain unchanged during the elastic unloading process from point d to point e. It is also seen that, from point a to point d, the thermal strain \(\varepsilon ^\mathrm{th}\) is always zero since the temperature keeps unchanged.

As shown in Fig. 6b, during heating (i.e., from point f to point i), when the temperature reaches point g, the transformation from detwinned martensite to austenite occurs, and then finishes at point h, i.e., period I. The reorientation strain \(\varepsilon ^\mathrm{{reo}}\) drastically decreases while the thermal expansion strain \(\varepsilon ^{th}\) increases slightly. During the process of cooling (i.e., from point i to point l), when the temperature reaches point j, the transformation from austenite to twinned martensite occurs, and finishes at point l, i.e., period II. Taking into account, the twinned martensite generated by the local residual stress, a part of reorientation strain \(\varepsilon ^\mathrm{{reo}}\) can also be produced, which is consistent with the experimental observations [16]. Meanwhile, the reorientation-induced plastic strain \(\varepsilon ^\mathrm{{reop}}\) keeps constant and the thermal strain \(\varepsilon ^\mathrm{th}\) changes with temperature.

5 Conclusions

In this work, based on experimental observations of the SME with different peak strains, a new multi-mechanism model describing reorientation and reorientation-induced plasticity of NiTi SMA is constructed by using the phase diagram. The transformations among twinned martensite, detwinned martensite and austenite are considered to capture the SME. As a new internal variable, the detwinned stress and its evolution equation are introduced to describe the nonlinear hardening of transformation from twinned martensite to detwinned martensite. The reorientation-induced plasticity is considered to capture the residual strain after heating, and the residual reorientation strain is introduced to describe the growth of strain under stress-free state during cooling. The evolution equations of inelastic strain and transformation temperatures are assumed to be dependent on the accumulated detwinned martensite volume fraction, which can describe the peak strain-dependent degeneration of SME. Finally, the proposed model is validated by comparing the simulated curves of stress, strain and temperature at different peak strains with the experimental results.