1 Introduction

Shape memory polymers (SMPs) are a type of stimuli-responsive smart materials [1,2,3]. The shape of such materials can be changed through external stimuli, such as thermal [4], electrical [5], magnetic [6], photic [7, 8], watery [9], chemical [10, 11] stimuli, etc., to reach a pre-set shape. SMPs are also called programmable smart materials. During the process of shape changing, the shape memory and complex self-assembly behaviors can be carried out without any external power supplies. Comparing with other shape memory materials, such as shape memory alloys, SMPs have many advantages, such as lightweight, low cost, large recoverable deformation, biocompatibility, biodegradability, printability, colorability, and so on [1]. Therefore, they have been widely applied in many fields, such as those of bio-medical materials [12, 13], aerospace [14, 15], and functional textiles [3, 16, 17].

At present, one of the most popular shape memory polymers is the thermo-induced shape memory polyurethane (TSMPU). The TSMPU presents a glassy state below the glass transition temperature (\(\theta _\mathrm{g}\)) and a rubbery state above \(\theta _\mathrm{g}\) [18]. According to the applications and applied loads, the shape memory behavior of TSMPU can be categorized into two types: one is that the deformation above \(\theta _\mathrm{g}\) is fixed, when the temperature decreases below \(\theta _\mathrm{g}\), it can return to its initial shape by heating above \(\theta _\mathrm{g}\) [1], e.g., the one demonstrated in the process of vascular stent implantation [12]; the other is that the visco-plastic deformation occurring at low temperature can be recovered by heating above \(\theta _\mathrm{g}\) [19], e.g., the one shown in the shape memory textiles [3]. The thermo-mechanically coupled deformation behavior of TSMPU also includes mainly two types: one is that the change of ambient temperature results in the change in mechanical properties and induces the transition between the glassy and rubbery states; the other is that the mechanical deformation causes internal heat production and further affects the mechanical properties and shape memory effect.

Most existing thermo-mechanically coupled experiments focused on the shape memory behavior of TSMPU at different temperatures [19,20,21,22,23,24,25,26,27], while the internal heat production below \(\theta _\mathrm{g}\) was often neglected. Recently, Pieczyska et al. [28,29,30,31] performed some experimental observations on the internal heat production of SMP at different strain rates and found that the drop in temperature is related to the thermo-elastic effect and the increased temperature is accompanied by the visco-plastic deformation of TSMPU. However, further studies are necessary to investigate the influence of internal heat production on the mechanical properties and shape memory effect of TSMPU.

It is known that the mechanical properties of polymers are very sensitive to the variation of temperature. A temperature increase can improve the thermal motion of molecules, reduce the strength, expand the volume and change the viscosity of polymers, etc. Whether caused by the internal heat production or the ambient temperature, the thermo-mechanical coupling deformation of TSMPU can be reasonably described by a thermo-mechanically coupled constitutive model. In past decades, many constitutive models of polymers were established at finite deformation, but most of them mainly focused on the thermo-elastic effect [32,33,34], which did not consider the influence of visco-plastic deformation on the internal heat production. A thermo-mechanically coupled model proposed by Pieczyska et al. [31] could simulate the temperature-dependent mechanical behavior of TSMPU through introducing a classical thermo-elastic formula to calculate the temperature drop; however, the predicted temperature variations did not match with the experimental data well. Recently, the thermo-mechanically coupled models at finite deformation were derived by Anand et al. [35,36,37] for amorphous polymers through rigorous thermodynamic validation. These models could reasonably describe the influence of ambient temperature on the mechanical properties of polymers under uniaxial tension over a wide temperature range. Billon [38] constructed a physical mechanism-based constitutive model by considering the deformation constraint caused by permanent nodes and slip links, which was further extended to describe the thermo-mechanically coupled behavior of a semicrystalline polyamide 66 [39]. Pouriayevali et al. [40] proposed a constitutive model to simulate the rate-sensitive response of semicrystalline Nylon 6 based on an elastic–visco-elastic–visco-plastic framework. Based on irreversible thermodynamics, Yu et al. [41] proposed a visco-elasticity–visco-plasticity model at small deformation to describe the thermo-mechanically coupled cyclic deformation of polymers. By introducing the influences of temperature and humidity on glass transition temperature, the model was extended to a hygro-thermo-mechanical coupled version to describe the multi-field-coupled cyclic deformation of polymer [42]. According to the above reviews, the thermo-mechanically coupled constitutive models for general polymers have been constructed to reasonably predict their rate-dependent tensile deformations and temperature variations. For TSMPU, a thermal-mechanically coupled model needs to be constructed based on detailed thermal-mechanical coupled experiments.

The organization of this paper is as follows: in Sect. 2, the experimental observations are firstly presented to investigate the thermo-mechanical coupling effect at different strain rates. In Sect. 3, a thermo-mechanically coupled constitutive model at finite deformation is proposed based on the irreversible thermodynamics framework. In Sect. 4, the rate-dependent stress–strain curves and temperature variations are predicted using the proposed model. Conclusions are summarized in Sect. 5.

2 Experimental Observations

2.1 Material

The TSMPU, numbered as MM-4520, was purchased from SMP Technologies Inc., Japan. Its glass transition temperature (\(\theta _\mathrm{g}\)) is 323 K, and its transition region is from 300 to 343 K. The density of TSMPU is \(1.25~\hbox {g/cm}^{3}\). Before molding specimens, the pellet was baked at 353 K in a vacuum oven for 2 h. Then the pellet was injected as a dumbbell-type flat specimen for uniaxial tension, as shown in Fig. 1. The sample was machined as a rectangular solid with the size of \(20~\hbox {mm}\times 1.5~\hbox {mm}\times 3~\hbox {mm}\) for dynamic mechanical analysis (DMA). All prepared samples were stored in a dry vessel for testing purpose.

Fig. 1
figure 1

Diagram of specimen (unit: mm)

Full size image

2.2 Experimental Results

The DMA was conducted by a machine of DMA-Q800 in a tensile mode. The experiments were carried out by increasing the temperature in a ramp mode by 2 K/min at 1 Hz from 273 to 413 K. The results are shown in Fig. 2. Parameters \(E'\) and \(E''\) denote the storage modulus and loss modulus, characterizing the stiffness and viscosity of TSMPU, respectively. Parameter tan \(\delta \) denotes the loss angle, representing the ratio of \(E'\) to \(E''\). It is shown that the difference between moduli at the high and low temperatures has three orders of magnitude, and moduli \(E'\) and \(E''\) are almost constant outside the glass transition region. When the temperature is higher than its glass transition temperature \(\theta _\mathrm{g}\), the TSMPU exhibits rubber-like visco-elastic properties, whereas at the temperature below \(\theta _\mathrm{g}\), it is in the glassy state.

Fig. 2
figure 2

Results of dynamic mechanical analysis

Full size image

The shape memory effect of TSMPU is induced by heating above \(\theta _\mathrm{g}\) [1], which can be simulated based on the time-temperature superposition principle [19, 43]. The thermo-mechanically coupled responses of TSMPU can be directly observed during mechanical loading. Therefore, tensile experiments were carried out by using a MTS Bionix858 machine at 295 K with four nominal strain rates of 1.4, 0.7, 0.35 and 0.14%/s, respectively. The true stress–strain curves at different strain rates are shown in Fig. 3. It is found that the loading strain rate only has an obvious effect on the yield peak, i.e., the yield peak increases with the increase of strain rate, which is consistent with the existed observation in [44]. However, an unexpected rate-independence is observed at the post-yield stage. It is caused by the competition between the strain hardening induced by the increase of strain rate and the thermo-softening caused by the gradually increasing internal heat production, which weakens the effect of strain rate. Such characteristics should be addressed in constitutive modeling by reasonably considering the interaction between the mechanical deformation and the temperature change.

Fig. 3
figure 3

True stress–strain curves at different strain rates

Full size image

The average temperature variation was obtained by a fast and sensitive non-contract infrared camera, FLIR-A655sc. The curves of temperature variation versus true strain are shown in Fig. 4. An obvious thermo-elastic effect is observed, i.e., the temperature variation decreases with the increase of elastic deformation, but the strain rate has little effect on the temperature variation at the elastic deformation stage. At the visco-plastic deformation stage, the temperature variation strongly depends on the loading strain rate, i.e., the higher the strain rate is, the higher the temperature rises. This implies that the internal heat production induced mainly by the visco-plastic deformation should be considered in constitutive modeling.

Fig. 4
figure 4

Curves of temperature variation versus true strain at different strain rates

Full size image

3 Thermo-Mechanically Coupled Constitutive Model

3.1 Thermodynamic Framework

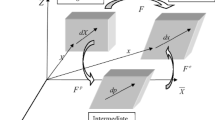
Owing to the capability of large deformation of TSMPU, the model should be constructed at finite deformation. As shown in Fig. 5, let \(\varvec{X}_0\) denote the reference configuration of an undeformed and unheated continuum body at time \(t_{0}\) and temperature \(\theta _0\). \(\varvec{X}^{\uptheta }\) denotes the thermal stress-free configuration of a heated continuum body, which is a changeable equilibrium state with temperature change. \({\varvec{x}}\) is the current configuration after a series of mechanical deformations. An unloading stress-free configuration can be obtained after removing the external mechanical load, and it varies with time due to the viscosity of TSMPU. The mapping of a given material point \(\varvec{X}\) in the reference configuration to its position \({\varvec{x}}\) in the current configuration is given by the deformation gradient: \(\varvec{F}=\partial {\varvec{x}}/{\partial \varvec{X}}\). Considering the coupling between the thermal expansion and the mechanical behavior of a continuum body, the thermo-mechanical response can be described by multiplicatively decomposing the deformation gradient \({\varvec{F}}\) into a thermal part \(\varvec{F}^{\uptheta }\) and a time-dependent mechanical part \(\varvec{F}^\mathrm{M}\), as done by Lion [45]. The time-dependent mechanical deformation gradient can be decomposed into an elastic component \(\varvec{F}^\mathrm{e}\) and a visco-plastic component \(\varvec{F}^{\mathrm{vp}}\) further [43, 45,46,47].

$$\begin{aligned} {\varvec{F}}= & {} {\varvec{F}}^{\mathrm{M}}{\varvec{F}}^{\uptheta } \end{aligned}$$
(1)
$$\begin{aligned} {\varvec{F}}^{\mathrm{M}}= & {} {\varvec{F}}^{\mathrm{e}}{\varvec{F}}^{\mathrm{vp}} \end{aligned}$$
(2)

where \({\varvec{F}}^{\mathrm{M}}, {\varvec{F}}^{\uptheta }, {\varvec{F}}^{\mathrm{e}}, {\varvec{F}}^{\mathrm{vp}}\) represent the mechanical, thermal, elastic and visco-plastic parts of the deformation gradient, respectively.

Fig. 5
figure 5

Illustration of multiplicative decomposition of the deformation gradient of TSMPU

Full size image

Polar decomposition of the mechanical deformation gradient is shown as,

$$\begin{aligned} {\varvec{F}}^{\mathrm{i}} = {\varvec{R}}^{\mathrm{i}} {\varvec{U}}^{\mathrm{i}} = {\varvec{V}}^{\mathrm{i}} {\varvec{R}}^{\mathrm{i}} \end{aligned}$$
(3)

where \({\varvec{R}}\) is the rotation tensor, \({\varvec{U}}\) and \({\varvec{V}}\) define unique, positive definite, symmetric tensors, called the right (or material) and left (or spatial) stretch tensors, respectively. The subscript \(\hbox {i}\) represents \(\hbox {M}\), \(\hbox {e}\), and \(\hbox {vp}\) in turn.

As shown in Fig. 6, it is assumed that the thermal part of the deformation gradient only causes the change of volume and does not generate thermal stress. However, the temperature change can vary the thermal deformation gradient, which results in a change in the mechanical deformation directly and a change in stress indirectly with the deformation constraint. Therefore, the total stress is only derived from the elastic strain, and the thermal and visco-plastic strains provide the volume change and the plastic flow, respectively.

Fig. 6
figure 6

Illustration of a linear rheological model

Full size image

Assuming that the TSMPU is isotropic, the thermal deformation gradient can be expressed as:

$$\begin{aligned} {\varvec{F}}^{{\uptheta }}=J_{\uptheta }^{1/3}{{\varvec{1}}} \end{aligned}$$
(4)

where \(J_{\uptheta } =\det ({\varvec{F}}^{{\uptheta }})\) is the volume ratio caused by the thermal deformation, and \({{\varvec{1}}}\) is a second-order identity tensor. The volume ratio can be calculated by \(J_{\uptheta } =\left( {1+\alpha \Delta \theta } \right) ^{3}\), in which \(\alpha \) and \(\Delta \theta \) represent the coefficient of thermal expansion and the change in temperature, respectively.

Therefore, the thermal deformation gradient can be expressed as:

$$\begin{aligned} {\varvec{F}}^{{\uptheta }}=\left( {1+\alpha \Delta \theta } \right) {{\varvec{1}}} \end{aligned}$$
(5)

The velocity gradient of the mechanical part consists of the elastic and visco-plastic velocity gradients, i.e.,

$$\begin{aligned} \varvec{L}^{\mathrm{M}}=\dot{\varvec{F}}^{\mathrm{M}}\varvec{F}^{\mathrm{M}-1},\quad \varvec{L}^{\mathrm{e}}=\dot{\varvec{F}}^{\mathrm{e}}\varvec{F}^{\mathrm{e}-1},\quad \varvec{L}^{\mathrm{vp}}=\dot{\varvec{F}}^{\mathrm{vp}}\varvec{F}^{{\mathrm{vp}}-1} \end{aligned}$$
(6)

The velocity gradient contains the deformation stretching and spin tensors, as \({\varvec{L}} = {\varvec{D}} + {\varvec{W}}\), and it is assumed that the flow is irrotational, i.e., \({\varvec{W}}=0\). Then,

$$\begin{aligned} \varvec{D}^{\mathrm{M}}=\dot{\varvec{F}}^{\mathrm{M}}\varvec{F}^{\mathrm{M}-1},\quad \varvec{D}^{\mathrm{e}}=\dot{\varvec{F}}^{\mathrm{e}}\varvec{F}^{\mathrm{e}-1},\quad \varvec{D}^{\mathrm{vp}}=\dot{\varvec{F}}^{\mathrm{vp}}\varvec{F}^{{\mathrm{vp}}-1} \end{aligned}$$
(7)

The right and left Cauchy–Green tensors are given as:

$$\begin{aligned} \varvec{C}^{\mathrm{i}}=\varvec{F}^{\mathrm{iT}}\varvec{F}^{\mathrm{i}}=\varvec{U}^{\mathrm{i}2},\quad \varvec{B}^{\mathrm{i}}=\varvec{F}^{\mathrm{i}}\varvec{F}^{\mathrm{iT}}=\varvec{V}^{\mathrm{i}2} \end{aligned}$$
(8)

where the subscript \(\hbox {i}\) represents \(\hbox {M}\), \(\hbox {e}\), and \(\hbox {vp}\) in turn.

3.2 Constitutive Equations

According to the experimental results, it is shown that the elasticity of TSMPU is not remarkably sensitive to strain rate, and the deformation is contributed mainly by the visco-plastic part (see Fig. 3). Therefore, a thermo-elastic-visco-plastic model is constructed here. To consider the thermo-mechanical coupled characteristics of TSMPU, the Helmholtz free energy is decomposed into three parts, i.e., the instantaneous elastic free energy \(\psi ^{\mathrm{e}}\), the visco-plastic free energy \(\psi ^{\mathrm{vp}}\) and the heat free energy \(\psi ^{\theta }\).

$$\begin{aligned} \psi \left( {\varvec{C}^{\mathrm{e}},\varvec{B}^{\mathrm{vp}},\theta } \right) =\psi ^{\mathrm{e}}\left( {\varvec{C}^{\mathrm{e}},\theta } \right) +\psi ^{\mathrm{vp}}\left( {\varvec{B}^{\mathrm{vp}},\theta } \right) +\psi ^{\theta }\left( \theta \right) \end{aligned}$$
(9)

where \(\psi ^{\mathrm{e}}\) is related to the elastic right Cauchy–Green tensor \({\varvec{C}}^{\mathrm{e}}\) and the temperature \(\theta \) caused by the elastic deformation; \(\psi ^{\mathrm{vp}}\) is related to the visco-plastic left Cauchy–Green tensor \({\varvec{B}}^{\mathrm{vp}}\) and \(\theta \) caused by the visco-plastic deformation; and \(\psi ^{\theta }\) is related to \(\theta \) caused by temperature variation.

To describe the strain at finite deformation, Hencky’s logarithmic strain is adopted here:

$$\begin{aligned} {\varvec{E}}^{\mathrm{e}}= & {} \frac{1}{2}\ln \left( {{\varvec{C}}}^{\mathrm{e}} \right) \end{aligned}$$
(10)
$$\begin{aligned} {\varvec{E}}_{0}^\mathrm{e}= & {} {\varvec{E}}^{\mathrm{e}}-\frac{1}{3}\hbox {tr}({\varvec{E}}^{\mathrm{e}}){{\varvec{1}}} \end{aligned}$$
(11)

To describe the visco-plastic flow, an effective visco-plastic stretch is defined as:

$$\begin{aligned} \lambda ^{\mathrm{vp}}=\sqrt{\frac{\hbox {tr}\left( {{\varvec{B}}^{\mathrm{vp}}} \right) }{3}} \end{aligned}$$
(12)

Then, the visco-plastic free energy is rewritten as:

$$\begin{aligned} \psi \left( {{\varvec{B}}}^{\mathrm{vp}} \right) =\psi \left( {\lambda ^{\mathrm{vp}}} \right) \ge 0,\quad \psi \left( 1 \right) =0 \end{aligned}$$
(13)

Based on the continuum theory of Anand et al. [36,37,38, 41, 48, 49], the free energy equations are given as:

$$\begin{aligned} \psi ^{\mathrm{e}}\left( {\varvec{E}^{\mathrm{e}},\theta } \right)= & {} G\left( \theta \right) \left| {\varvec{E}_\mathrm{0}^\mathrm{e}} \right| ^{2}+\frac{1}{2}K\left( \theta \right) \left| {\hbox {tr}\left( {\varvec{E}^{\mathrm{e}}} \right) } \right| ^{2}-3K\left( \theta \right) \hbox {tr}\left( {\varvec{E}^{\mathrm{e}}} \right) \alpha \left( {\theta -\theta _0 } \right) \end{aligned}$$
(14)
$$\begin{aligned} \psi ^{\mathrm{vp}}\left( {\lambda ^{\mathrm{vp}},\theta } \right)= & {} \mu _\mathrm{R} \left( \theta \right) \lambda _\mathrm{L}^{2}\left[ {\left( {\frac{\lambda ^{\mathrm{vp}}}{\lambda _\mathrm{L} }} \right) x+\ln \left( {\frac{x}{\sinh x}} \right) } \right] ,\,\, x=\mathcal{L}^{-1}\left( {\frac{\lambda ^{\mathrm{vp}}}{\lambda _\mathrm{L} }} \right) \end{aligned}$$
(15)
$$\begin{aligned} \psi ^{\theta }\left( \theta \right)= & {} c\left[ {\left( {\theta -\theta _0 } \right) -\theta \ln \left( {\frac{\theta }{\theta _0 }} \right) } \right] +u_0 -\eta _0 \theta \end{aligned}$$
(16)

where \({\varvec{E}}^{\mathrm{e}}\), \(\theta _0\), \(\lambda _\mathrm{L}\), \(u_0\) and \(\eta _0\) denote the elastic strain tensor, initial temperature, limiting stretch, initial internal energy and initial entropy, respectively; \(\mu _\mathrm{R}\), G, K denote the temperature-dependent hardening modulus, shear modulus and bulk modulus, respectively; the parameter c denotes the specific heat; and the symbol \(\mathcal{L}^{-1}\) denotes the inverse of the Langevin function, which is approximately defined as:

$$\begin{aligned} \mathcal{L}^{-1}\left( a \right) =\frac{a\left( {3-a^{2}} \right) }{\left( {1-a^{2}} \right) } \end{aligned}$$
(17)

where a can be replaced by an arbitrary variable.

Assuming that the change in temperature does not directly contribute to the mechanical work, the stress power is constructed from the thermal stress-free configuration to the current configuration in Fig. 5. According to the principle of virtual work, the balance equation of macroscopic force and moment balance can be obtained [48]. According to the first law of thermodynamics, the relationship between the work and energy is expressed as:

$$\begin{aligned} \dot{U}=J_\mathrm{M} {\varvec{TF}}^{\mathrm{-T}}: \dot{{\varvec{F}}}-\nabla \cdot {\varvec{q}}+q \end{aligned}$$
(18)

where \({\varvec{q}}\) is heat flux, and q is heat supply which is neglected in this work. According to the assumption of the irrotational visco-plastic flow, Eq. (18) can be described by using the elastic stretching \({\varvec{D}}^{\mathrm{e}}\) and the visco-plastic stretching \({\varvec{D}}^{\mathrm{vp}}\), i.e.,

$$\begin{aligned} \dot{U}= & {} J_\mathrm{M} \varvec{TF}^{-T}:\varvec{\dot{F}}-\nabla \cdot \varvec{q} \nonumber \\= & {} J_\mathrm{M} \varvec{T}:\dot{\varvec{F}}{\varvec{F}}^{-1}-\nabla \cdot \varvec{q} \nonumber \\= & {} J_\mathrm{M} \varvec{T}:\varvec{L}-\nabla \cdot \varvec{q} \nonumber \\= & {} J_\mathrm{M} \varvec{T}:\left( {\varvec{L}^{\mathrm{e}}+\varvec{F}^{\mathrm{e}}\varvec{L}^{\mathrm{vp}}\left( {\varvec{F}^{\mathrm{e}}} \right) ^{-1}} \right) -\nabla \cdot \varvec{q} \nonumber \\= & {} J_\mathrm{M} \varvec{T}:\varvec{D}^{\mathrm{e}}+J_\mathrm{M} \left( {\varvec{F}^{\mathrm{e}}} \right) ^{\mathrm{T}}\varvec{T}\left( {\varvec{F}^{\mathrm{e}}} \right) ^{\mathrm{-T}}:\varvec{D}^{\mathrm{vp}}-\nabla \cdot \varvec{q} \nonumber \\= & {} J_\mathrm{M} \varvec{T}:\varvec{D}^{\mathrm{e}}+\varvec{T}^{\mathrm{vp}}:\varvec{D}^{\mathrm{vp}}-\nabla \cdot \varvec{q} \end{aligned}$$
(19)

where \(\nabla =\frac{\partial }{\partial x}\), \(J_\mathrm{M} =\det (\varvec{F}^{\mathrm{M}})=\det (\varvec{F}^{\mathrm{e}})\) due to \(\det (\varvec{F}^{\mathrm{vp}})=1\), and \(\varvec{T}^{\mathrm{vp}}\) is a symmetric and deviatoric tensor as :

$$\begin{aligned} \varvec{T}^{\mathrm{vp}}=J_\mathrm{M} \varvec{F}^{\mathrm{eT}}\varvec{TF}^{\mathrm{e-T}} \end{aligned}$$
(20)

The elastic stretching \(\varvec{D}^{\mathrm{e}}\) and the Cauchy stress \(\varvec{T}\) are conjugate; the visco-plastic stretching \(\varvec{D}^{\mathrm{vp}}\) and the internal force \(\varvec{T}^{\mathrm{vp}}\) are conjugate.

The relationship between the free energy and the internal energy is given as:

$$\begin{aligned} U=\psi +\eta \theta \end{aligned}$$
(21)

Combining Eq. (19) with Eq. (21), the nonnegative dissipation inequality is derived as:

$$\begin{aligned} \varGamma =\dot{\eta }\theta =J_\mathrm{M} \varvec{T}:\varvec{D}^{\varvec{e}}\varvec{+T}^{\mathrm{vp}}:\varvec{D}^{\mathrm{vp}}-\dot{\psi }-\eta \dot{\theta }-\nabla \cdot \varvec{q}\ge 0 \end{aligned}$$
(22)

The rate form of the Helmholtz free energy can be written as:

$$\begin{aligned} \dot{\psi }=\frac{\partial \psi ^{\mathrm{e}}}{\partial \varvec{E}^{\mathrm{e}}}:\dot{\varvec{E}}^{\mathrm{e}}+\frac{\partial \psi ^{\mathrm{e}}}{\partial \theta }\dot{\theta }+\frac{\partial \psi ^{\mathrm{vp}}}{\partial \varvec{B}^{\mathrm{vp}}}:\dot{\varvec{B}}^{\mathrm{vp}}+\frac{\partial \psi ^{\mathrm{vp}}}{\partial \theta }\dot{\theta }+\frac{\partial \psi ^{{\uptheta }}}{\partial \theta }\dot{\theta } \end{aligned}$$
(23)

It is assumed that the Kirchhoff stress, \({{\varvec{\tau }}}\), and the elastic Hencky strain, \({\varvec{E}}^{\mathrm{e}}\), are coaxial [50]. Thus, the following expression is obtained:

$$\begin{aligned} {\varvec{\tau }} :\dot{\varvec{E}}^{\mathrm{e}}= & {} \varvec{\tau }:\varvec{D}^{\mathrm{e}} \end{aligned}$$
(24)
$$\begin{aligned} \varvec{\tau }= & {} J_\mathrm{M} \varvec{T} \end{aligned}$$
(25)

Substituting Eqs. (23), (24) and (25) into Eq. (22) yields:

$$\begin{aligned} \underbrace{\left( \varvec{\tau }-\frac{\partial \psi ^{\mathrm{e}}}{\partial \varvec{E}^{\mathrm{e}}} \right) :\varvec{D}^{\mathrm{e}}}_{\mathrm{Elastic\,\,dissipation}}+\underbrace{\left( \varvec{T}^{\mathrm{vp}}-2\hbox {sym}_\mathrm{0} \left( {\frac{\partial \psi ^{\mathrm{vp}}}{\partial \varvec{B}^{\mathrm{vp}}}\varvec{B}^{\mathrm{vp}}} \right) \right) :\varvec{D}^{\mathrm{vp}}}_{{\begin{array}{ll} {\hbox {Visco-plastic}}&{} {\hbox {dissipation}} \\ \end{array} }}-\left( {\frac{\partial \psi }{\partial \theta }+\eta } \right) \dot{\theta }-\underbrace{\nabla \cdot \varvec{q}}_{{\begin{array}{ll} {{\begin{array}{ll} {\hbox {Heat}}&{} {\hbox {flux}} \\ \end{array} }}&{} {\hbox {dissipation}} \\ \end{array} }}\ge 0 \end{aligned}$$
(26)

where \(\hbox {sym}_{0} ({\bullet })\) denotes the symmetric and deviatoric part of tensor \(({\bullet })\). The elastic stretching tensor \({\varvec{D}}^{\mathrm{e}}\) is linear and does not depend on its coefficient. Therefore, its coefficient needs to be zero to guarantee that the elastic dissipation is not less than zero. As the temperature changes randomly, the coefficient of temperature rate needs to be zero. Therefore, the Cauchy stress and entropy can be obtained as follows.

$$\begin{aligned} \varvec{T}= & {} J_\mathrm{M}^{-1}\frac{\partial \psi ^{\mathrm{e}}}{\partial \varvec{E}^{\mathrm{e}}} \end{aligned}$$
(27)
$$\begin{aligned} \eta= & {} -\frac{\partial \psi }{\partial \theta } \end{aligned}$$
(28)

Substituting Eqs. (14) and (25) into Eq. (27), the Kirchhoff stress is obtained as:

$$\begin{aligned} \varvec{\tau }=\frac{\partial \psi ^{\mathrm{e}}}{\partial \varvec{E}^{\mathrm{e}}}=2G\left( \theta \right) \varvec{E}_\mathrm{0}^\mathrm{e} +K\left( \theta \right) \hbox {tr}\left( {\varvec{E}^{\mathrm{e}}} \right) {\varvec{1}}-3K\left( \theta \right) \alpha \left( {\theta -\theta _0 } \right) {\varvec{1}} \end{aligned}$$
(29)

According to Eq. (26), a flow stress \(\varvec{Y}^{\mathrm{vp}}\left( \varvec{E}^{\mathrm{e}}, \varvec{B}^{\mathrm{vp}},\theta , \xi \right) \) is defined as:

$$\begin{aligned} \varvec{Y}^{\mathrm{vp}}=\varvec{T}^{\mathrm{vp}}-2\hbox {sym}_{0} \left( {\frac{\partial \psi ^{\mathrm{vp}}}{\partial \varvec{B}^{\mathrm{vp}}}\varvec{B}^{\mathrm{vp}}} \right) \end{aligned}$$
(30)

The directions of the flow stress and visco-plastic flow are consistent, so the following formula is satisfied:

$$\begin{aligned} \varvec{Y}^{\mathrm{vp}}:\varvec{D}^{\mathrm{vp}}>0\,\, \hbox {for}\,\, \varvec{D}^{\mathrm{vp}}\ne 0 \end{aligned}$$
(31)

Eq. (30) can be rewritten as

$$\begin{aligned} \varvec{T}^{\mathrm{vp}}=\varvec{Y}^{\mathrm{vp}}+2\hbox {sym}_\mathrm{0} \left( {\frac{\partial \psi ^{\mathrm{vp}}}{\partial \varvec{B}^{\mathrm{vp}}}\varvec{B}^{\mathrm{vp}}} \right) \end{aligned}$$
(32)

Therefore, \(\varvec{T}^{\mathrm{vp}}\) and \(\varvec{Y}^{\mathrm{vp}}\) are symmetric.

Because \(\varvec{q}=-\,\varvec{k}\cdot \nabla \theta \), heat dissipation naturally satisfies nonnegativity, i.e.,

$$\begin{aligned} -J\frac{\varvec{q}\cdot \nabla \theta }{\theta }=J\frac{\varvec{k}:\left( {\nabla \theta \otimes \nabla \theta } \right) }{\theta }\ge 0 \end{aligned}$$
(33)

where \(\varvec{k}=k\varvec{I}\), \(J=\det \left( \varvec{F} \right) \), and k is the heat conductivity coefficient.

3.3 Flow Rule

The second Piola–Kirchhoff stress tensor \(\varvec{S}\) is obtained from the Cauchy stress \(\varvec{T}\) as:

$$\begin{aligned} \varvec{S}=J_\mathrm{M} \varvec{F}^{\mathrm{e}-1}\varvec{TF}^{\mathrm{e-T}} \end{aligned}$$
(34)

The Mandel stress \(\varvec{M}\) is obtained from the second Piola–Kirchhoff stress \(\varvec{S}\) as:

$$\begin{aligned} \varvec{M}=\varvec{C}^{\mathrm{e}}\varvec{S} \end{aligned}$$
(35)

Substituting Eqs. (34) and (35) into Eq. (20), \(\varvec{T}^{\mathrm{vp}}\) can be rewritten as:

$$\begin{aligned} \varvec{T}^{\mathrm{vp}}=\varvec{M} \end{aligned}$$
(36)

The Mandel stress is decomposed into the deviatoric and spherical parts,

$$\begin{aligned} \varvec{M}=\varvec{M}_{0} +\frac{1}{3}\hbox {tr}(\varvec{M}) \end{aligned}$$
(37)

A symmetric and deviatoric back stress \(\varvec{S}_{\mathrm{back}}\) is defined. Due to the symmetry, Eq. (30) is reduced as:

$$\begin{aligned} \varvec{Y}^{\mathrm{vp}}=\varvec{M}_0 -\varvec{S}_{\mathrm{back}} \end{aligned}$$
(38)

where

$$\begin{aligned} \varvec{S}_{\mathrm{back}} =2\hbox {sym}_\mathrm{0} \left( {\frac{\partial \psi ^{\mathrm{vp}}}{\partial \varvec{B}^{\mathrm{vp}}}\varvec{B}^{\mathrm{vp}}} \right) \end{aligned}$$
(39)

According to Eqs. (12), (13), (15) and (39), let’s take the derivative of the visco-plastic free energy \(\psi \left( {\varvec{B}^{\mathrm{vp}}} \right) \) with respect to the left Cauchy–Green tensor \(\varvec{B}^{\mathrm{vp}}\):

$$\begin{aligned} \frac{\partial \psi ^{\mathrm{vp}}}{\partial \varvec{B}^{\mathrm{vp}}}=\frac{\partial \psi ^{\mathrm{vp}}}{\partial \lambda ^{\mathrm{vp}}}\frac{\partial \lambda ^{\mathrm{vp}}}{\partial \varvec{B}^{\mathrm{vp}}}=\frac{\mu }{2}{\varvec{1}} \end{aligned}$$
(40)

where

$$\begin{aligned} \mu =\frac{1}{3}\mu _\mathrm{R} \left( \theta \right) \frac{\lambda _\mathrm{L} }{\lambda ^{\mathrm{vp}}}\mathcal{L}^{-1}\left( {\frac{\lambda ^{\mathrm{vp}}}{\lambda _\mathrm{L} }} \right) \end{aligned}$$
(41)

Therefore, the back stress in Eq. (39) is deduced as:

$$\begin{aligned} \varvec{S}_{\mathrm{back}} =\mu \varvec{B}_0^{\mathrm{vp}} \end{aligned}$$
(42)

where

$$\begin{aligned} \varvec{B}_0^{\mathrm{vp}} =\varvec{B}^{\mathrm{vp}}-\frac{1}{3}\left( {\hbox {tr}\varvec{B}^{\mathrm{vp}}} \right) {\varvec{1}} \end{aligned}$$
(43)

As proposed in literature [19], the molecular process of a viscous flow is to overcome the shear resistance of the material for local rearrangement. Therefore, the visco-plastic stretching rate \(\varvec{D}^{\mathrm{vp}}\) can be constitutively prescribed with the plastic shear strain rate \(\dot{\gamma }^{\mathrm{vp}}\) [19, 47] as follows:

$$\begin{aligned} \varvec{D}^{\mathrm{vp}}=\dot{\gamma }^{\mathrm{vp}}\varvec{N} \end{aligned}$$
(44)

where

$$\begin{aligned} \varvec{N}=\frac{\varvec{M}_0 -\mu \varvec{B}_0^{\mathrm{vp}} }{\sqrt{2}\bar{{\tau }}} \end{aligned}$$
(45)

The equivalent shear stress is defined as:

$$\begin{aligned} \bar{{\tau }}=\frac{1}{\sqrt{2}}\left| {\varvec{M}_0 -\mu \varvec{B}_0^{\mathrm{vp}} } \right| \end{aligned}$$
(46)

As done in literature [44, 48], the specific form of the shear plastic strain rate is given as:

$$\begin{aligned} \dot{\gamma }^{\mathrm{vp}}=\dot{\gamma }_0^{\mathrm{vp}} \left( {\frac{\bar{{\tau }}}{s\left( {1+a_\mathrm{p} p/s} \right) }} \right) ^{1/m} \end{aligned}$$
(47)

where \(\dot{\gamma }_{0}^{\mathrm{vp}} \) is the reference shear plastic strain rate, \(a_\mathrm{p}\) is a pressure sensitivity parameter, \(p=-\frac{1}{3}\hbox {tr}(\varvec{T})\) is hydrostatic pressure, the internal variable s represents the resistance to the visco-plastic flow, and m is a rate sensitivity parameter. As done in literature [48], the observed yield peak and strain softening after yielding can be captured by the following evolution equations:

$$\begin{aligned} \dot{s}= & {} h_0 \left( {1-\frac{s}{\tilde{s}_\mathrm{s} \left( \chi \right) }} \right) \dot{\gamma }^{\mathrm{vp}} \end{aligned}$$
(48)
$$\begin{aligned} \dot{\chi }= & {} g_0 \left( {\frac{s}{s_{\mathrm{sat}} }-1} \right) \dot{\gamma }^{\mathrm{vp}} \end{aligned}$$
(49)
$$\begin{aligned} \tilde{s}_\mathrm{s} \left( \chi \right)= & {} s_{\mathrm{sat}} \left[ {1+b\left( {\chi _{\mathrm{sat}} -\chi } \right) } \right] \end{aligned}$$
(50)

where the internal variable \(\chi \) represents a change in the free volume of TSMPU, \(s_{\mathrm{sat}}\) and \(\chi _{\mathrm{sat}}\) are the saturated values of s and \(\chi \), respectively, and parameters \(h_0\), \(g_0\) and b control the evolutions of s, \(\chi \) and \(\tilde{s}_\mathrm{s} \left( \chi \right) \), respectively.

Figure 7 shows how the material parameters in Eqs. (48)–(50) affect the yield peak and strain softening of the stress–strain curve. It is stated that only the discussed parameters are shown in Fig. 7, and other parameters can be found in Table 1. It is seen that the parameters \(h_0\) and \(g_0\) mainly change the slopes of pre-peak and post-peak of the stress–strain curve, respectively. Parameter \(s_{\mathrm{sat}}\) affects the post-yield behavior, and an increased \(s_{\mathrm{sat}}\) can elevate the whole stress–strain curve. An increase of b can raise the stress peak. Parameter \(\chi \) affects the size of the yield peak. Indeed, the change in the free volume of TSMPU is quite small [51], which is thus determined as a small value.

Fig. 7
figure 7

Influence of material parameters a \(h_0\); b \(g_0\); c b; d \(s_{\mathrm{sat}}\); e \(\chi _{\mathrm{sat}}\) on the true stress versus true strain curve at the strain rate of 0.7%. (Arrows indicate the increases in these parameters)

Full size image

3.4 Heat Equilibrium Equations

In this work, we only focus on the overall strain–stress curve and the average temperature of a specimen, rather than the detailed distributions of stress, strain and temperature fields. Thus, in this section, some simplifications are necessary.

Table 1 Material parameters used in the proposed model
Full size table

Combining Eqs. (19), (21) and (22), the energy conservation equation is written as:

$$\begin{aligned} \dot{\psi }-J_\mathrm{M} \varvec{T}:\varvec{D}^{\varvec{e}}-\varvec{T}^{\mathrm{vp}}:\varvec{D}^{\mathrm{vp}}+\eta \dot{\theta }+\dot{\eta }\theta +\nabla \cdot \varvec{q}=0 \end{aligned}$$
(51)

Combining Eqs. (9), (14)–(16) and (28), the expressions of entropy and its rate yield:

$$\begin{aligned} \eta= & {} -\frac{\partial G\left( \theta \right) }{\partial \theta }\left| {\varvec{E}_\mathrm{0}^\mathrm{e} } \right| ^{2}-\frac{1}{2}\frac{\partial K\left( \theta \right) }{\partial \theta }\left| {\hbox {tr}\left( {\varvec{E}^{\mathrm{e}}} \right) } \right| ^{2}+3\frac{\partial K\left( \theta \right) }{\partial \theta }\hbox {tr}\left( {\varvec{E}^{\mathrm{e}}} \right) \alpha \left( {\theta -\theta _0 } \right) \nonumber \\&+\,3K\left( \theta \right) \hbox {tr}\left( {\varvec{E}^{\mathrm{e}}} \right) \alpha -\frac{\partial \mu _\mathrm{R} \left( \theta \right) }{\partial \theta }\lambda _\mathrm{L}^{2}\left[ {\left( {\frac{\lambda ^{\mathrm{vp}}}{\lambda _\mathrm{L} }} \right) x+\ln \left( {\frac{x}{\sinh x}} \right) } \right] +c\ln \left( {\frac{\theta }{\theta _0 }} \right) +\eta _0 \end{aligned}$$
(52)
$$\begin{aligned} \dot{\eta }= & {} \left\{ {\begin{array}{l} c\frac{1}{\theta }-\frac{\partial ^{2}G\left( \theta \right) }{\partial \theta ^{2}}\left| {\varvec{E}_\mathrm{0}^\mathrm{e} } \right| ^{2}-\frac{1}{2}\frac{\partial ^{2}K\left( \theta \right) }{\partial \theta ^{2}}\left| {\hbox {tr}\left( {\varvec{E}^{\mathrm{e}}} \right) } \right| ^{2}+3\alpha \left( {\theta -\theta _0 } \right) \frac{\partial K^{2}\left( \theta \right) }{\partial \theta ^{2}}\hbox {tr}\left( {\varvec{E}^{\mathrm{e}}} \right) \\ +6\alpha \frac{\partial K\left( \theta \right) }{\partial \theta }\hbox {tr}\left( {\varvec{E}^{\mathrm{e}}} \right) -\frac{\partial ^{2}\mu _\mathrm{R} \left( \theta \right) }{\partial ^{2}\theta }\lambda _\mathrm{L}^{2}\left[ {\left( {\frac{\lambda ^{\mathrm{vp}}}{\lambda _\mathrm{L} }} \right) x+\ln \left( {\frac{x}{\sinh x}} \right) } \right] \\ \end{array}} \right\} \dot{\theta } \nonumber \\&+\left\{ {3\alpha K\left( \theta \right) -\frac{\partial K\left( \theta \right) }{\partial \theta }\hbox {tr}\left( {\varvec{E}^{\mathrm{e}}} \right) +3\alpha \left( {\theta -\theta _0 } \right) \frac{\partial K\left( \theta \right) }{\partial \theta }} \right\} \hbox {tr}\left( {\varvec{\dot{E}}^{\mathrm{e}}} \right) \nonumber \\&-2\frac{\partial G\left( \theta \right) }{\partial \theta }\left( {\varvec{E}_\mathrm{0}^\mathrm{e} :\varvec{\dot{E}}_\mathrm{0}^\mathrm{e} } \right) -\lambda _\mathrm{L} \frac{\partial \mu _\mathrm{R} \left( \theta \right) }{\partial \theta }\left[ {x+\frac{3+\left( {\frac{\lambda ^{\mathrm{vp}}}{\lambda _\mathrm{L} }} \right) ^{4}}{\left( {1-\left( {\frac{\lambda ^{\mathrm{vp}}}{\lambda _\mathrm{L} }} \right) ^{2}} \right) ^{2}}\left( {\frac{\lambda ^{\mathrm{vp}}}{\lambda _\mathrm{L} }+\frac{1}{x}-\frac{\cosh x}{\sinh x}} \right) } \right] \dot{\lambda }^{\mathrm{vp}} \end{aligned}$$
(53)

Substituting Eqs. (33), (40)–(42), (52) and (53) into Eq. (51), the heat equilibrium equation is deduced as:

$$\begin{aligned} c_{\mathrm{eff}} \dot{\theta }=\varGamma _{\mathrm{eff}} +\nabla \cdot \left( {\varvec{k}\cdot \nabla \theta } \right) \end{aligned}$$
(54)

where

$$\begin{aligned} c_{\mathrm{eff}}= & {} c-\theta \frac{\partial ^{2}G\left( \theta \right) }{\partial \theta ^{2}}\left| {\varvec{E}_\mathrm{0}^\mathrm{e} } \right| ^{2}-\frac{1}{2}\theta \frac{\partial ^{2}K\left( \theta \right) }{\partial \theta ^{2}}\left| {\hbox {tr}\left( {\varvec{E}^{\mathrm{e}}} \right) } \right| ^{2}+3\alpha \theta \left( {\theta -\theta _0 } \right) \frac{\partial K^{2}\left( \theta \right) }{\partial \theta ^{2}}\hbox {tr}\left( {\varvec{E}^{\mathrm{e}}} \right) \nonumber \\&+\,6\alpha \theta \frac{\partial K\left( \theta \right) }{\partial \theta }\hbox {tr}\left( {\varvec{E}^{\mathrm{e}}} \right) -\theta \frac{\partial ^{2}\mu _\mathrm{R} \left( \theta \right) }{\partial ^{2}\theta }\lambda _\mathrm{L}^{2}\left[ {\left( {\frac{\lambda ^{\mathrm{vp}}}{\lambda _\mathrm{L} }} \right) x+\ln \left( {\frac{x}{\sinh x}} \right) } \right] \end{aligned}$$
(55)
$$\begin{aligned} \varGamma _{\mathrm{eff}}= & {} \underbrace{\left( {\varvec{T}^{\mathrm{vp}}-\mu \varvec{B}_\mathrm{0}^{\mathrm{vp}} } \right) :\varvec{D}^{\mathrm{vp}}}_{{\begin{array}{ll} {\hbox {Visco-plastic}}&{} {\hbox {dissipation}} \\ \end{array} }} \nonumber \\&{\begin{array}{ll} &{} \\ \end{array} }\underbrace{+\,\lambda _\mathrm{L} \theta \frac{\partial \mu _\mathrm{R} \left( \theta \right) }{\partial \theta }\left[ {x+\frac{3+\left( {\frac{\lambda ^{\mathrm{vp}}}{\lambda _\mathrm{L} }} \right) ^{4}}{\left( {1-\left( {\frac{\lambda ^{\mathrm{vp}}}{\lambda _\mathrm{L} }} \right) ^{2}} \right) ^{2}}\left( {\frac{\lambda ^{\mathrm{vp}}}{\lambda _\mathrm{L} }+\frac{1}{x}-\frac{\cosh x}{\sinh x}} \right) } \right] \dot{\lambda }^{\mathrm{vp}}}_{\text {Thermo-plasticity}} \nonumber \\&{\begin{array}{ll} &{} \\ \end{array} }\underbrace{\begin{array}{lll} -\,\theta \left\{ {3\alpha K\left( \theta \right) -\frac{\partial K\left( \theta \right) }{\partial \theta }\hbox {tr}\left( {\varvec{E}^{\mathrm{e}}} \right) +3\alpha \left( {\theta -\theta _0 } \right) \frac{\partial K\left( \theta \right) }{\partial \theta }} \right\} \hbox {tr}\left( {\varvec{\dot{E}}^{\mathrm{e}}} \right) \nonumber \\ +\,2\theta \frac{\partial G\left( \theta \right) }{\partial \theta }\left( {\varvec{E}_\mathrm{0}^\mathrm{e} :\varvec{\dot{E}}_\mathrm{0}^\mathrm{e} } \right) \\ \end{array}}_{\text {Thermo-elasticity}} \\ \end{aligned}$$
(56)

It is assumed that the volume and surface of a specimen are V and S, respectively, the temperature field and internal heat are evenly distributed, and the heat conduction is isotropic in the entire space [41]. According to Ref. [40], only the dissipative part of the energy can convert into heat, and the remaining portion of the energy is stored in materials. Therefore, a proportional factor \(\omega \) is introduced to reflect the proportion of the work converting into heat. It is noted that the factor \(\omega \) must satisfy the limitation of \(0\le \omega \le 1\). Then, Eq. (55) is rewritten as:

$$\begin{aligned} c_{\mathrm{eff}} \dot{\theta }=\omega \varGamma _{\mathrm{eff}} +\frac{h\left( {\theta _{0} -\theta } \right) S}{V} \end{aligned}$$
(57)

where h is the heat exchange coefficient of ambient media, which is a constant if without forced convection. Temperature is assumed to be decomposed into two parts, i.e., the one caused by internal heat production and the ambient temperature. Whether it is caused by the internal heat production or the ambient temperature, the thermo-mechanical coupling deformation of TSMPU has influence on its material mechanical properties.

According to Eq. (55), the internal heat production and temperature variation can be calculated during the tensile deformation. At the same time, the increased temperature, in turn, acts on the material, changes the material properties, and promotes the material softening and molecular mobility. However, as shown in Figs. 3 and 4, the stress does not decrease obviously with the increase of temperature. The reason can be that the stress caused by the increase of strain rate is weakened by the heat softening due to the temperature rise.

The transformation between the glassy and rubbery states of TSMPU can be regarded as a type of phase transformation. The temperature change in SMA [52] and TSMPU [53] has a smaller effect on the initial phase transformation, but shows a greater effect on later phase transformation. It is assumed that the effect of temperature rise on the material properties of TSMPU is only related to the changes in volume and moduli, including elastic modulus, shear modulus, bulk modulus and hardening modulus. The change in volume can be expressed by Eq. (5). The elastic modulus varying with temperature is shown in Fig. 2. It is found that they show exponential evolutions with the increase of temperature. Therefore, the following temperature-dependent relations are used to describe the changes in elastic modulus with temperature [22]:

$$\begin{aligned} E\left( \theta \right)= & {} E_{\mathrm{ref}} \exp \left[ {-\alpha _\mathrm{E} \left( {\frac{\theta }{\theta _{\mathrm{ref}} }-1} \right) } \right] \end{aligned}$$
(58)
$$\begin{aligned} G\left( \theta \right)= & {} \frac{E\left( \theta \right) }{2\left( {1+\nu } \right) } \end{aligned}$$
(59)
$$\begin{aligned} K\left( \theta \right)= & {} \frac{E\left( \theta \right) }{3\left( {1-2\nu } \right) } \end{aligned}$$
(60)

where \(\alpha _\mathrm{E}\) denotes the factor, \(\theta _{\mathrm{ref}}\) and \(E_{\mathrm{ref}}\) denote the reference temperature and the reference elastic modulus, respectively, and \(\nu \) denotes Poisson’s ratio, which keeps unchanged with temperature here.

Due to internal heat production, the hardening modulus changes with the variation of strain rate, i.e., \(\mu _\mathrm{R}\) decreases with the increase of temperature. The hardening modulus can be described by a linear expression, i.e.,

$$\begin{aligned} \mu _\mathrm{R} \left( \theta \right) =\mu _{\mathrm{ref}} -h_\mu \left( {\frac{\theta }{\theta _{\mathrm{ref}} }-1} \right) \end{aligned}$$
(61)

where \(\mu _{\mathrm{ref}}\) is the reference hardening modulus at reference temperature \(\theta _{\mathrm{ref}}\), and \(h_\mu \) is the slope of \(\mu _\mathrm{R}\) changing with temperature.

3.5 Calibration of Parameters

3.5.1 Parameters Related to Mechanical Deformation

  1. (1)

    Referential elastic modulus

    According to Fig. 3, the elastic deformation has almost no rate dependence; the referential elastic modulus can be fitted at different strain rates below the linear stress segment.

  2. (2)

    Poisson’s ratio

    Through measuring the material deformation with the digital image correlation (DIC) method, the elastic strain field is obtained at room temperature. Then the strains in the stretching direction, \(\varepsilon _x\), and lateral direction, \(\varepsilon _y\), are computed. The Poisson’s ratio is obtained as 0.414 through the formula \(v={-\varepsilon _y}/{\varepsilon _x}\). The temperature dependence is neglected.

  3. (3)

    Referential shear plastic strain rate

    The referential shear plastic strain rate is considered equal to the loading rate; therefore, \(\dot{\gamma }_0^{\mathrm{vp}} =0.007\)/s.

  4. (4)

    Rate sensitivity coefficient m

    It is assumed that the plastic strain rate is related to the strain rate, and the ratio of \(\bar{{\tau }}\) to \(\tilde{s}\) is dimensionless. \(\bar{{\tau }}\) and \(\tilde{s}\) can be obtained from the peak stress of a stress–strain curve [51]. The logarithm of Eq. (47) yields:

    $$\begin{aligned} m\ln \left( {\frac{\dot{\gamma }^{\mathrm{p}}}{\dot{\gamma }_0^\mathrm{p} }} \right) =\ln \left( {\frac{\bar{{\tau }}}{\tilde{s}}} \right) \end{aligned}$$
    (62)

    Substituting the peak stress and strain rate into Eq. (62), the average value of m can be obtained as 0.09.

  5. (5)

    Visco-plastic flow parameters: \(s_0\), \(s_{\mathrm{sat}}\), \(\chi _0\) and \(\chi _{\mathrm{sat}}\)

    The material parameters \(s_0\) and \(s_{\mathrm{sat}}\) represent the initial and saturated resistances to the visco-plastic flow, respectively. \(\chi _0\) and \(\chi _{\mathrm{sat}}\) represent the initial and saturated values of free volume, respectively. These values can be obtained by fitting the tensile stress–strain curves at the referential strain rate according to the parameter analysis shown in Fig. 7.

  6. (6)

    Controlling parameters: \(g_0\), \(h_0\) and b

    Through the parameter analysis shown in Fig. 7, the controlling parameters, \(g_0\), \(h_0\) and b can be obtained by fitting the stress–strain curve at the reference rate.

  7. (7)

    Limiting stretch \(\lambda _\mathrm{L}\)

    The limiting stretch, \(\lambda _\mathrm{L}\), denotes the limit of stretch before fracture under tension. In this work, because there is no fracture, the limiting stretch is set with a large value.

3.5.2 Parameters Related to Temperature

  1. (1)

    Density \(\rho \) and specific heat c

    The density of TSMPU is approximated as \(1250~\hbox {kg}/\hbox {m}^{3}\), and the specific heat is \(2800~{\hbox {kJ}}/{( {\hbox {m}^{3}\,\hbox {K}})}\).

  2. (2)

    Heat exchange coefficient h

    The empirical values of heat exchange coefficient h in the natural environment without wind are 5–\(25~\hbox {W}/(\hbox {m}^{2}\,\hbox {K})\). Since the heat exchange of polymers is very slow and the experimental environment is indoor, the heat exchange coefficient is given as \(25~\hbox {W}/(\hbox {m}^{2}\,\hbox {K})\), as done in [41].

  3. (3)

    Thermal expansion coefficient

    According to [29, 53], the difference of thermal expansion coefficient between the glassy and rubbery states is not very large. In this work, all experiments were carried out at room temperature below the transition temperature, and the maximum temperature variation was limited within 5 K, as shown in Fig. 4. Therefore, the thermal expansion coefficient of the glassy state is adopted as \(1.48\times 10^{-4}\)/K according to [29].

  4. (5)

    Exponential factor \(\alpha _\mathrm{E}\)

    According to Eq. (58), the exponential factor is determined by fitting the experimental moduli shown in Fig. 2.

  5. (6)

    Hardening modulus and its coefficient

    The hardening modulus, \(\mu _{\mathrm{ref}}\), is obtained from the slope of flow stress at the reference temperature. The coefficient \(h_{\mu }\) denotes the slope of hardening modulus changing with temperature and can be obtained by fitting the moduli at different strain rates.

  6. (7)

    Proportional factor \(\omega \)

    The proportional factor \(\omega \) is determined by referring to the value in Ref. [40].

According to the above parameter calibration method, all material parameters used in the simulations are shown in Table 1.

4 Verification and Discussion

In this section, the proposed thermo-elasto-visco-plastic constitutive model is numerically implemented to simulate the tensile stress–strain curves and the internal heat production of TSMPU at different strain rates. The simulated results are shown in Figs. 8 and 9.

4.1 Stress–Strain Curves at Different Strain Rates

The simulated stress–strain curves are shown in Fig. 8. It is clear that the proposed model can predict the tensile stress–strain curves reasonably. Since the proposed model introduces the visco-plastic flow equation, it has the ability to simulate the rate-dependent yield peak. The introduced back stress in the visco-plastic flow equation can describe the hardening behavior after yielding. Since the internal heat production is introduced, the hardening behavior after yielding is restrained by the increase of internal heat production.

Fig. 8
figure 8

Simulated stress–strain curves at different strain rates: a 1.4%/s; b 0.7%/s; c 0.35%/s and d 0.14%/s

Full size image

4.2 Temperature Variation at Different Strain Rates

The simulated temperature variations induced by the internal heat production at different strain rates are shown in Fig. 9. It indicates that the proposed model can predict the temperature drop at the elastic deformation stage and temperature rise at the visco-plastic deformation stage. However, the predicted initial temperature variation after yielding is higher than the experimental ones, especially at lower loading rates. The reason is that the temperature variation is observed on the local surface of the specimen, where the heat exchange at a low strain rate becomes very easy, which results in a slow increase of temperature. However, the internal heat production induced by the visco-plastic deformation is simulated by the proposed model based on the average temperature field, where the temperature field is assumed to be uniformly distributed over the entire surface of the specimen.

Fig. 9
figure 9

Experimental and simulated results of temperature variation at different strain rates: a 1.4%/s; b 0.7%/s; c 0.35%/s and d 0.14%/s

Full size image
Fig. 10
figure 10

Axial stretch at different strain rates: a elastic stretch; b plastic stretch; c thermal stretch

Full size image
Fig. 11
figure 11

Temperature variation at different strain rates induced by a thermo-elasticity, b visco-plasticity and c heat exchange

Full size image

4.3 Discussion

To demonstrate how the proposed model simulates the thermo-mechanical coupling effect, Fig. 10 shows the evolutions of elastic, visco-plastic and thermal stretches at different strain rates. It is seen that the elastic deformation occurs accompanied by the decreased thermal stretch, and then, the elastic unloading occurs at the post-yield stage due to the disentanglement of molecular chains. As seen in Figs. 10a and 11a, due to the thermo-elastic effect, temperature decreases and increases during elastic loading and unloading, respectively. Comparing Fig. 9 with Fig. 11b, c, it is found that the temperature variation induced by the visco-plastic deformation is higher than the temperature variation due to thermo-elasticity and heat exchange, and the temperature variation is lower at a high strain rate than at a low strain rate, which is the reason why the heat exchange becomes easy at a low strain rate. As seen in Figs. 10b and 11b, the visco-plastic stretch is almost rate-independent since the temperature increases with the increase of strain rate.

The evolutions of internal variables \(\left\{ {s,s_\mathrm{s} ,\chi } \right\} \) with the increase of strain at different strain rates are shown in Figs. 12, 13 and 14. It is seen that the parameters only affect the visco-plastic deformation after the yield peak, which is consistent with Eqs. (48)–(50), where the internal variables only depend on the plastic shear strain rate.

Fig. 12
figure 12

Curves of flow resistance stress versus strain at different strain rates

Full size image
Fig. 13
figure 13

Curves of saturated flow resistance stress versus strain at different strain rates

Full size image
Fig. 14
figure 14

Curves of free volume versus strain at different strain rates

Full size image

The thermo-mechanically coupled model and the isothermal model are compared in Figs. 15 and 16 at different strain rates. As seen in Fig. 15, the elastic and hardening moduli decrease with the increase of strain rate due to the thermo-softening induced by the increase of temperature variation. In the isothermal model, the elastic and hardening moduli keep unchanged. Moreover, it is found from Fig. 16 that the thermo-mechanically coupled effect mainly exhibits during the visco-plastic flow due to the obvious temperature variation. Comparing the true stresses simulated by the thermo-mechanically coupled model and the isothermal model, it is seen that the simulated true stress at post-yield stage remarkably increases with the increase of strain rate for the isothermal model. However, the change in true stress at post-yield stage slows down with the increase of strain rate and strain, which results from the competition between strain hardening and thermo-softening, so the simulations are consistent with the experimental results shown in Fig. 3.

Fig. 15
figure 15

Influence of thermo-mechanically coupled effect on a elastic modulus and b hardening modulus

Full size image
Fig. 16
figure 16

Influence of thermo-mechanically coupled effect on stress–strain curve

Full size image

5 Conclusions

DMA and strain rate-dependent tensile experiments are carried out to investigate the thermo-mechanically coupled interaction of TSMPU at glassy state. It is found that the TSMPU is very sensitive to temperature, and an increase in strain rate can elevate the yield peak, but it only has a slight influence on the post-yield process. Obvious temperature variations induced by thermo-elasticity and visco-plasticity are observed. Based on the irreversible thermodynamic framework, the Helmholtz free energy is decomposed into three parts, i.e., the instantaneous elastic free energy, visco-plastic free energy and heat free energy, and a thermo-mechanically coupled elasto-visco-plastic constitutive model is established at finite deformation. Heat equilibrium equations considering internal heat production and heat exchange are derived in accordance with the first and second laws of thermodynamics. Comparing the simulated results with the experimental data, it indicates that the proposed model can predict the rate-dependent stress–strain responses and temperature variations, including the temperature drop due to thermo-elastic effect and temperature rise due to visco-plastic dissipation. It is noted that the present experiments and simulations are only limited to uniaxial tensile loading conditions. The investigation on the multi-axial thermo-mechanically coupled behavior of TSMPU will be performed in further work.