Investigating impact of converging training walls of the ogee spillways on hydraulic performance

Abstract

Due to their economical and structural aspects, ogee-crested spillways can be constructed and operated in a wide variety of situations. In this study, a three-dimensional physical model (1:50 scale) was planned and constructed to investigate the impact of converging training walls of the ogee spillways with a curve axis on flow characteristics such as the discharge coefficient, free surface profile, flow depth and pressure on the spillway. For this purpose, the spillway was constructed, tested and verified in both the symmetrical and asymmetrical convergence of training walls ranging from 0° to 120°. Observations from flow depth and piezometric pressure along the spillway in various convergence angles indicate that as θ increases, the flow depth and piezometric pressure increase at the bottom and the toe of the spillway model. Also, in convergence angles of 60° and 90° tested in both symmetric and asymmetric states, the angles with lower L_ch/L have larger flow depth and piezometric pressure. The results of the experiments indicated that in the converging ogee spillway, by increasing the total upstream head, the discharge coefficient shows increment for each of the convergence angles (θ’s) and eventually the downstream flow changes its condition to either supercritical or critical stages. It must be considered that the discharge coefficient is independent of symmetric or asymmetric situations. On the other hand, at the submergence stage for the spillway, the difference in the discharge coefficient can be due to tailwater submergence occurring in some convergence angles. Also, the flow depth and the piezometric pressure on the bottom and the toe of the spillway increased more in the symmetrical convergence angles in comparison with the asymmetrical convergence angles. Also, by decreasing the downstream channel width to the crest length (L_ch/L), the flow depth and piezometric pressure increase subsequently. Results approved that the 60° convergence is the most economic convergence angle due to its capability in passing the largest flow discharge in the maximum head. The reason for this choice is that the crest length of this angle is 33% lesser than that of 120° convergence.

Introduction

Due to their superior performance in measuring the flow as well as controlling flood and water level in hydraulic structures, spillways are one of the most crucial parts of hydraulic structures (Mansoori et al. 2017; Alavi et al. 2018; Razavi and Ahmadi 2017; Vayghan et al. 2019). One of the most typical kinds of spillways is the ogee spillway. Simplicity in design, steady flow pattern, straight forward flow passing system and lower construction costs are some of the advantages of this kind of spillways. The ogee-crested spillway’s efficient characteristics are due to its shape which is derived based on the low surface of an aerated nappe flowing above a sharp-crested spillway (USBR 1990; USACE 1987). The ogee form leads to almost atmospheric pressure on the crest area for a design head. Crest resistance causes discharge reduction at the heads less than the design head. For greater heads, the discharge is higher than an aerated sharp-crested spillway due to the more flow sucked by negative crest pressure. Even though a lot is known concerning the ogee shape and its flow properties, it can also be claimed that a change from the typical design parameters like a change in upstream head conditions, a change in crest shape, or modification of the approach channel owing to positional geometric qualities may change the flow characteristics. Some study has been carried out to determine the hydraulic properties of ogee spillway, and various approaches are available that mainly rely on the relative typical design parameters of the spillway (Maynord 1985). Chow (1959) conducted an extensive investigation and was the first ever to study the ogee shape. Following Chow (1959), the overwhelming majority of the present information comes from considerable data obtained from physical models performed by the USBR (1987) and the USACE (USBR 1990; USACE 1995). Since this paper is not planned to become a compendium of the literature and the design conditions, the readership is referred to the other references for more related details [i.e., Bradley (1954), Jansen (1957), Locher (1971), Johnson and Savage (2006), Hong et al. (2010), Khatsuria (2004), Ramamurthy and Tadayon (2009), Shabanlou and Khorami (2013) and Saneie et al. (2016)]. Due to the limitations in design instructions available for converging spillways, engineers have introduced spillway sidewalls design as a research topic. Due to some other limitations such as unequal total spillway width in upstream and downstream, converging ogee spillway is often proposed. Furthermore, change in season leads to alteration in weather which causes the high-intensity precipitation as well as floods in places where such problems have never taken place. The effect of this phenomenon on the reservoir is that water surface elevation rises faster. For such a condition, converging ogee spillway can keep down the accidental flooding situations and it can be used as an emergency spillway. The concept of ogee crest spillway with curve axis has been used in the research to increase capacity by providing added crest length for a given total spillway width even though the discharge is unknown. In recent years, many researchers have tried to solve similar problems using an overwhelming majority of physical and numerical models. Morales et al. (2012) implemented principally numerical simulations by volume of fluid (VOF) method so as to evaluate the free surface profile over the spillway and under the gate of a diversion dam located on the Ca${\tilde{\text{n}}}$ar, Ecuador. The numerical results were considerably closer to those obtained from the experiments.

In the present study, a physical model with a 1:50 scale was built and utilized to assess the impact of converging vertical training walls on the flow variation in the ogee spillway. Convergence training walls in both symmetrical and asymmetrical situations ranging from 0° to 120° were tested under a series of flow alteration, discharge coefficient, water surface profiles, crest pressures on the spillway and vertical distributions of pressure, considering that the effect of convergence angle was investigated and analyzed for each spillway configuration.

Materials and methods

Experimental setup

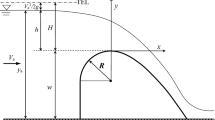
The experiments were conducted at the Soil Conservation and Watershed Management Research Institute (SCWMRI) in Tehran, Iran. The design parameters for models with a 1:50 scale (3-D) of a converging ogee spillway design as well as prototype design parameters for a particular proposed site are summarized in Table 1. In addition, this structure was tested in both symmetrical and asymmetrical convergence of training walls ranging from 0° to 120°. No specific pattern was used for fabricating asymmetrical angels. The only parameter considered in the construction of these angles was the created angle between the training walls. In order to test the angles of walls in both symmetrical and asymmetrical states, the non-dimensional parameter ($\frac{{L _{\text{ch}} }}{L}$) was used. In this way, at the same time the impact of both considered angle and symmetry/asymmetry state can be investigated. L_ch is the downstream channel width (m) and L is the crest length (m). A schematic of the ogee spillway with converging training walls and four samples of the convergence angles are shown in Figs. 1 and 2, respectively.

Table 1 Model and prototype design elements and dimensions

Fig. 1

Schematic of a typical converging ogee spillway with curve axis

Fig. 2

Photographs of the spillway with convergence angles of: a 0° symmetric, b 120° symmetric, c 60° symmetric and d 60° asymmetric

The spillway model with the downstream channel was located at the outlet of a rectangular flume 0.8 m wide, 0.4 m high and 3.00 m long. The ogee section was placed in the flume in a section with transparent PLEXIGLAS sides; hence, the flow could be detected. Before the test area, the flume was provided with a sufficient stilling procedure to obtain the uniform approach flow. Controlling the flow was conducted with two separate valves of two pumps providing the flow into the channel (Aminoroayaie Yamini et al. 2017). The discharge was measured using a sharp triangular weir with an apex angle of 90° in the output of channel throughout the experiment, and the channel was kept at a rough zero-slope. The water surface profile and flow depth were measured with a point gage. Measurement uncertainties of experiments for water elevation reading are ± 1 mm. Due to water-level fluctuation, average values of free surface elevations were taken based on many measurements, whereas for specific purpose flow depths along the training wall were recorded. To determine the pressure on the spillway, several taps were placed along the centerline of the spillway with the other two specific lines located on either side (Fig. 3) and were then connected to the piezometers board. This method was also used by Johnson and Savage (2006) and Naghavi et al. (2011. Connection tubes (PVC) with an internal diameter of 5 mm and a maximum length of 1.5 m were used to connect the piezometers to the piezometers board. The model and prototype were generally based on Froude (Fr) similarity in scale relationship as the impact of gravity was typically more important compared to the impact of viscosity and surface tension for this type of model. Froude similarity was utilized in the present model study. Generally, in hydraulic modeling Reynolds (R), the number of the model with more than 104, was agreed (USBR 1987; Aminoroayaie Yamini et al. 2017).

Fig. 3

Schematic of the position of picked lines data

In the fabrication of each angel (θ), in order to consider the constant downstream channel width, there was a changing spillway’s length of the crest for every θ. Therefore, flow rates were selected in varying θ’s based on the unit discharge flow rate (q) at the crest in order to maintain constant test conditions for all of the convergence angles (Table 2).

Table 2 Discharge in prototype and model flow

Research methodology

Discharge for an ogee-crested spillway can be expressed as follows:

$$Q = \frac{2}{3}C_{\text{d}} \sqrt {2g} LH^{3/2} ,$$

(1)

where Q = discharge (m³/s), C_d = the coefficient of discharge (−), g = the gravitational acceleration (m/s²), L = the width of the spillway (m), and H = the total upstream head on the spillway (m). The discharge capacity over an ogee spillway might be considered as a function of the geometric parameters and flow characteristics. Figure 1 demonstrates the hydraulic variables and the geometric form of the converging ogee spillway applied in this study.

Referring to Fig. 1, a functional relationship linking the main parameters of flow over the converging ogee spillway can be expressed as follows:

$$f \, (Q, \, H, \, L, \, P, \, H_{\text{d}} ,g,\rho ,\mu ,\sigma , \, h_{\text{d}} ,d,\alpha , \, \theta ) = 0,$$

(2)

where f is a functional symbol; P is the spillway height; H_d is the design head; ρ and μ are density and dynamic viscosity, respectively; d and h_d are the flow depth in the downstream channel and high difference between the water surface elevation in the crest and downstream flow depth, respectively; σ is the surface tension; α is the angle between the upstream face and the horizontal face; and θ is the convergence angle of training walls. Equation (2) represents a physical phenomenon. Centered on the Buckingham Π theorem, this equation may be expressed in a dimensionless form as follows:

$$\varPi_{1} = f\left( {\varPi_{2} ,\varPi_{3} ,\varPi_{4} ,\varPi_{5} ,\varPi_{6} ,\varPi_{7} ,\varPi_{8} ,\varPi_{9} ,\varPi_{10} } \right),$$

(3)

where $\varPi_{1} ,\varPi_{2} ,\varPi_{3} ,\varPi_{4} ,\varPi_{5} ,\varPi_{6} ,\varPi_{7} ,\varPi_{8} ,\varPi_{9}$ and $\varPi_{10}$ are the dimensionless. Considering Q, H and ρ as dimensional independent parameters, according to the procedure suggested by Mohammadzadeh-Habili et al. (2013), the non-dimensional groups were achieved as follows:

$$\varPi_{1} = \frac{{gH^{5} }}{{Q^{2} }},\varPi_{2} = \frac{H}{P},\varPi_{3} = \frac{H}{{H_{\text{d}} }},\varPi_{4} = \frac{{h_{d} }}{H},\varPi_{5} = \frac{L}{H},\varPi_{6} = \frac{{d + h_{\text{d}} }}{H},\varPi_{7} = \frac{\mu H}{\rho Q},\varPi_{8} = \frac{{\sigma H^{3} }}{{\rho Q^{2} }},\varPi_{9} = \theta , \varPi_{10} = \alpha .$$

(4)

Considering that some groups must be combined to deduce the dimensionless parameters commonly applied in hydraulics, Eq. (3) is expressed as follows:

$$\frac{3\sqrt 3 }{{2\varPi_{5} \left( {2\varPi_{1} } \right)^{0.5} }} = \phi \left( {\varPi_{2} ,\varPi_{3} ,\varPi_{4} ,\varPi_{5} ,\varPi_{6} ,\frac{1}{{\varPi_{7} }},\frac{{\varPi_{8} }}{{\varPi_{1} }},\varPi_{9} ,\varPi_{10} } \right),$$

(5)

where $\phi$ is a functional symbol. Substituting $\varPi_{1} ,\varPi_{2} ,\varPi_{3} ,\varPi_{4} ,\varPi_{5} ,\varPi_{6} ,\varPi_{7} ,\varPi_{8}$ and $\varPi_{9}$ from Eq. (4) into Eq. (5) gives:

$$\frac{Q}{{\frac{2}{3}LH\sqrt {\frac{2}{3}gH} }} = \phi \left( {\frac{H}{P},\frac{H}{{H_{\text{d}} }},\frac{{h_{\text{d }} }}{H},\frac{L}{H},\frac{{d + h_{\text{d}} }}{H} ,\frac{\rho Q}{\mu H},\frac{\sigma }{{\rho gH^{2} }}, \theta , \alpha } \right).$$

(6)

The left-hand side of Eq. (6) represents the spillway C_d. The sixth and the seventh terms on the right-hand side represent the Reynolds number (R) and the Weber number (W), respectively. The effects of the Reynolds number and the Weber number can be negligible except for very low values of the measured water head (h) over the spillway, so they were excluded from the analysis (Ranga Raju and Asawa 1977). Further, since P and H_d were kept fixed in this study, both ratios of H/H_d and H/P represented the variation of H; thus, the ratio H/P was neglected to avoid redundancy. Moreover, the ogee-shaped crest has a vertical upstream slope, so it has no significant effect on the C_d (USBR 1987). Besides, this structure was tested in both symmetrical and asymmetrical converging training walls (θ’s). Thus, the non-dimensional parameter ($\frac{{L _{\text{ch}} }}{L}$) was used. In this way, at the same time the impact of both considered angle and symmetry and asymmetry can be investigated. Consequently, Eq. (7) is expressed as follows:

$$C_{\text{d}} = \phi \left( {\frac{H}{{H_{\text{d}} }},\frac{{d + h_{\text{d}} }}{H},\frac{{h_{\text{d}} }}{H},\frac{{L _{\text{ch}} }}{L}} \right).$$

(7)

Results and discussion

In this study, an experimental model of Germi-Chay Mianeh dam spillway was used; this model with a curved axis was made in a 1:50 scale. It is important to consider the effect of scale on the constructed model in order to ensure the accuracy of obtained results and its agreement with the Germi-Chay Mianeh dam.

The scale effect on ogee spillway with an arc in plan and converging training walls was studied using model family and a laboratory approach developed by Saneie et al. (2016). Saneie et al. (2016) demonstrated that for condition having the minimum Reynolds and Weber numbers which are 3.1 × 10⁴ and 270, respectively, and W^0.6R^0.2 > 300, it is possible to neglect the effect of viscosity and surface tension in converging ogee spillway. As an example, Figs. 4 and 5 indicate Reynolds (R) and Weber (W) numbers, respectively, to water elevation on spillway crest divided by spillway elevation. Figures 4 and 5 show different convergence angles for the model in a 1:50 scale in which the conditions required by Saneie et al. (2016) to omit the scale effect were satisfied.

Fig. 4

Reynolds number diagram to water elevation on the spillway crest (H = discharge head on the spillway, P = is the spillway height)

Fig. 5

Weber number diagram to water elevation on the spillway crest (H = discharge head on the spillway, P = is the spillway height)

Free surface

Flow characteristics which include the discharge coefficient, free surface profile, flow depth and pressure on the spillway are used to compare the differences among all of the θ’s. Based on visual observation, in each of the convergence angles, before the submerged discharge, the flow over the spillway was at the supercritical stage and at the bottom of the spillway a rooster tail was observed due to convergence of training walls. Rooster tail is a descriptive term to identify the surface of waterspout of spray and/or the water generated either by interfering with oscillatory waves or by standing waves (Niedoroda and Tanner 1970). For discharges above this point, a supercritical flow over the spillway and a constant hydraulic jump at the toe of the spillway were observed. Figure 6a shows a rooster tail at the bottom of the spillway, and Fig. 6b shows the hydraulic jump below the overflow crest. In this model, in the convergence angle of 120° from 0.25 to 0.62 Q_d, a rooster tail occurred. For the flow above this point up to 1.13 Q_d, a hydraulic jump was observed, and gradually, as the discharge increased, a drowned jump occurred for θ’s of 90° symmetric and 120° in which the high-velocity jet can follow the face of the spillway and then remain in a fluctuating path for a noticeable distance under and through the slower water.

Fig. 6

Photograph of the hydraulic phenomena of the converging ogee spillway; a rooster tail and b hydraulic jump

That is to say, for each of the symmetrical convergence angles, flow characteristic was precisely similar on both sides of the physical model. Also, in asymmetrical angles, the fluctuation range of measured data was small among all of the obtained data lines. So, by comparison water surface and crest pressure in different discharges, average value of the normalized water surface elevation [(H/H_d) versus (X/H_d)] and crest pressure [(H_p/H_d) versus (X/H_d) where H_p is the hydrostatic pressure and X is the longitudinal distance from crest] were used and are depicted in Figs. 7 and 8.

Fig. 7

Water surface comparison in the centerline of the physical model with the other two determined lines placed on either side: a with a symmetrical convergence angle of 120°; b with an asymmetrical convergence angle of 60°

Fig. 8

Piezometric pressure comparison in the centerline of the physical model with the other determined lines placed on either side: a with a symmetrical convergence angle of 120°; b with an asymmetrical convergence angle of 60°

Flow depth

Data collected during testing containing average water surface profiles along the spillway for a single unit discharge flow rate $\left( {{\text{l}}/{\text{s}}\;{\text{m}}} \right)$, varying θ’s, are compared in Fig. 9. Water surface elevation increased as θ increased or $\frac{{L_{\text{ch}} }}{L}$ reduced. For each of the θ’s in a symmetric situation, the highest flow elevation was observed along the centerline at the bottom and the toe of the spillway model, due to flow convergence. In contrast, the highest water surface elevation in asymmetric angels was generated along the wall having a lower deviation angle from the centerline of the model. The normalized flow depths data along the walls [(y/y_c) versus (X/y_c), where y and y_c are depth and critical depth, respectively, and X is the longitudinal distance from crest] for the highest common discharge are plotted in Fig. 10. For instance, the flow depth along the convergence angle of 120° at station 4.72 was nearly 9.5 times greater than the flow depth generated along the 0° convergence. Conclusions are drawn from Fig. 10 which allows designers to use this result as an indicator in order to estimate the minimum sidewall height requirements to prevent overtopping for identified critical depth.

Fig. 9

Water surface over the ogee spillway with varying convergence angles and q = 40.52 l/m s (H = discharge head on the spillway, H_d = design head, X = longitudinal distance from crest)

Fig. 10

Flow depth near the training wall versus distance from crest normalized by critical depth for varying convergence angles and q = 40.52 l/m s (y = depth, y_c = critical depth and X = longitudinal distance from crest)

Piezometric pressure

The pressure heads (H_p) on the spillways evaluated have been non-dimensionalized by dividing them by the design head (H_d) for each of the tested θ’s. Figure 11 provides a comparison of average spillway pressures for different convergence angles on the model. As indicated in this figure for all of the convergence angles in both symmetrical and asymmetrical situations, piezometric pressure profiles decreased in the spillway crest, whereas it increased at the end of the straight portion of the model face and the toe. It should be noted that the ratio of $\frac{{L_{\text{ch}} }}{L}$ in symmetrical convergence angles is smaller than that in asymmetric angles, which led to more flow convergence, and it causes the larger piezometric pressure. For example, the pressure distribution along the 60° convergence for both symmetric and asymmetric situations was reported H_p/H_d = 2.42 and H_p/H_d = 2.22, respectively. Figure 12 shows the Froude number changes for unit discharge flow rate for varying θ’s. It can be resulted from Figs. 11 and 12 that where the downstream flow is at the subcritical stage (Fr < 1) or where the drowned jump occurs, the increase in the static pressure was observed.

Fig. 11

Crest pressure on the ogee spillway with varying convergence angles and q = 40.52 l/m s (H_p = hydrostatic pressure, H_d = design head and X = longitudinal distance from crest)

Fig. 12

Froude number on the ogee spillway with varying convergence angles and q = 40.52 l/m s (Fr = Froude, H_p = hydrostatic pressure, H_d = design head and X = longitudinal distance from crest)

Dynamic pressure

The assumption of hydrostatic pressure distribution over the canal bed is logical, but in channels with concave or convex curvature in the bed as the current lines diverse in the moving direction under the effect of the bed deflection, the pressure distribution is not hydrostatic because of the centrifugal force. In flows in which the current lines’ curvature is concave, the pressure in each point is more than the hydrostatic pressure because of the similar direction of the centrifugal and gravity force (Aminoroayaie Yamini et al. 2015).

In order to determine the dynamic pressure distribution on the spillway surface and the effects of this pressure on the chute of the spillway, the normalized parameter of the pressure (H_p) could be defined as follows:

$$H_{\text{p}} = \left( {h_{\text{p}} - h_{0} } \right)/\left( {h_{\text{PM}} - h_{0} } \right),$$

where h_p is the total pressure head recorded in spillway surface or the chute bottom, h₀ is the depth of the input flow in spillway surface before the bottom curve of the spillway and h_PM is the maximum pressure recorded in the longitudinal direction from the input upstream of the bottom curve to the ending of the bottom curve of the spillway ($1.05 < \frac{X}{{H_{\text{d}} }} < 4$) (Fig. 13).

Fig. 13

Schematic of spillway body with a determined bottom curve

Figure 14 demonstrates the piezometric pressure of spillways longitudinal direction with a convergence angle of 120°. As it can be seen, an increase in discharge and decrease in Froude number lead to an increase in piezometric pressure, whereas the highest piezometric pressure was observed in $\frac{X}{{H_{\text{d}} }} = 3.$

Fig. 14

Piezometric pressure head distribution on the bed of the spillway in central axis for various flow rates

The effect of the bottom curve on dynamic pressure for $1.05 < {\text{Fr}} < 4.97$ was investigated, and the results are demonstrated in Fig. 15. As it can be seen from Fig. 13, the effect of this curve on pressure dynamic is obvious from $\frac{X}{{H_{\text{d}} }} = 1.6$, which has reached its maximum value in $\frac{X}{{H_{\text{d}} }} = 3$. The dynamic pressure rate starts to decrease afterward. The reason for this event could be related to the geometry of the spillway. Therefore, an increase in the kinetic energy, due to the high velocity caused by spillways’ slope, leads to an increase in dynamic pressure. Afterward, a decrease in the bottom curve slope causes a reduction in dynamic pressure.

Fig. 15

Normal distribution of dynamic pressure head (H_p) on the bed of spillway in the central axis of the buckets

Discharge coefficient

Figure 16 indicates the ratio of the discharge coefficient which was affected by the ratio of tailwater conditions (C_s) to the discharge coefficient (C_d) for free flow conditions. Moreover, the experimental results of USBR (1987) are also illustrated for the comparison. As shown in the figure for the submerged stage, the variation of convergence angles between symmetrical and asymmetrical angles has a considerable effect on the discharge coefficient. It can be because of tailwater submergence that occurred in symmetrical convergence angles (i.e., θ’s of 60 and 120°) faster than that in asymmetrical convergence angles. Note that the ratio of coefficient (C_s/C_d) in a constant $\frac{{h_{\text{d}} }}{H}$ for the recent study is less than that for the USBR study data. It is just because of the interfering of the flow lines and a decrease in the suction of the present spillway.

Fig. 16

Ratio of discharge coefficients caused by tailwater effects

Figure 17 shows a plot of downstream floor conditions on the C_d. Also, the C_d interpolated from the USBR data is shown in this figure (USBR 1987). When the flow of downstream apron is at the supercritical stage or when the hydraulic jump occurs, the decrease in the coefficient of discharge is basically due to the backpressure influence of the downstream floor position and is not dependent of any submergence effect from the tailwater. By contrast, when the spillway is submerged, there is a considerable decline in the coefficient caused by the submergence effect from the tailwater occurring in some convergence angles, i.e., θ = 120°. Therefore, it is concluded that a decrease in the coefficient for (h_d + d)/H > 3.5 is due to the downstream apron for all convergence angles. In the submergence stage of the spillway, water-level elevation below an ogee spillway is high enough to affect the discharge. Submergence is defined as the ratio of the high difference between the crest and downstream flow depth to the headwater, both measured relative to the spillway crest.

Fig. 17

Ratio of discharge coefficients caused by the position of downstream apron effects

Figure 18 shows the variation of the coefficient as related to values of Q/Q_d for varying θ’s. As indicated in the figure, the discharge coefficient will go up by increasing Q/Q_d for various θ’s tested. The acquired results show that where the downstream flow is at the supercritical stage or where the hydraulic jump occurs, C/C_d is clearly indicated in one Q/Q_d and is independent of the symmetrical or asymmetrical convergence angles. Moreover, when the spillway was submerged, there is a decrease in the coefficient that can be caused by tailwater submergence and it causes the differences in the discharge coefficient for each of the θ’s. For instance, although the ratio of coefficient to the discharge coefficient (C/C_d) in 120° convergence went up remarkably to just over 1.0 in Q/Q_d = 1.3, that then significantly dropped in Q/Q_d > 1.3, as shown in Fig. 18.

Fig. 18

Comparison of discharge coefficients for varying convergence angles (C/C_d vs. Q/Q_d)

Figure 19 shows the discharge coefficient variations with H/H_d for varying θ’s. Furthermore, the experimental results of USBR (1987) are also depicted for the comparison. As shown in the figure, before the submergence stage, the convergence angles variations have no effect on the discharge coefficient considerably. The discharge coefficient starts with 0.78 in H/H_d = 0.45 and in H/H_d = 2.3. It will increase up to 1.99. It seems that for greater H/H_d, the increasing discharge coefficient could tend to continue if the spillway were not submerged. Moreover, as indicated in this figure, the discharge coefficient of the spillway model is lower than that of the USBR data. It can be concluded that before the submerged stage for spillway, flow convergence had a significant impact on the discharge coefficient which can be created by the axis curve case of the model and cannot be independent of the variation of convergence angles. In this model, the discharge coefficient decreased considerably for θ’s of 90° in both symmetric and asymmetric situations and 120° in the range of $\frac{H}{{H_{\text{d}} }}$  > 1.3, due to the submergence stage for the spillway. Total upstream head data of the spillway model for all of the tested θ’s are presented against Q in Fig. 20. From Fig. 20, it can be inferred that 60° convergence with the ability to pass the largest flow discharge in the maximum head (31 l/s) can be selected as the most economic convergence angle. This convergence angle was chosen because the crest length of it is 33% lesser than that in 120° convergence having maximum crest length among all of the convergence.

Fig. 19

Discharge coefficient against the total upstream head for various θ’s tested (C/C_d vs. H/H_d)

Fig. 20

Total upstream head against discharge coefficient for various θ’s tested

Conclusion

This study was aimed to evaluate the impact of converging training walls of the ogee spillway on flow characteristics for both symmetrical and asymmetrical convergence angles. The data obtained from flow depth and static pressure distribution along the spillway in various convergence angles indicate that as θ increases, the flow depth and static pressure increase at the bottom and the toe of the spillway model. Also, in convergence angles of 60° and 90° tested in both symmetric and asymmetric states, the angles with lower $\frac{{L_{\text{ch}} }}{L}$ have larger flow depth and static pressure. The range of flow depth changes with any increase in the total upstream head near the walls can be used to estimate the minimum sidewall height requirements to decrease overtopping for the future site utilizing similar design criteria.

The discharge coefficient for free flow conditions will increase in all of the compared convergence angles by increasing the upstream total head. In addition, it was observed that where the downstream flow is at the supercritical stage or where the hydraulic jump occurs, the convergence angles variations have no effect on the discharge coefficient considerably, but when the spillway is submerged, there is a decrease in the coefficient which could be caused by tailwater submergence.

The discharge coefficient of the spillway model is lower than that of the Bureau of Reclamation spillway. It can be principally caused by flow convergence which can be created by the axis curve case of the spillway and cannot be independent of the convergence angles variation.

The 60° convergence can be selected as the most economic convergence angle due to its ability to pass the largest flow discharge in the maximum head. The reason for this choice is that the crest length of this angle is 33% lesser than that of 120° convergence.