A unified model of GNSS phase/code bias calibration for PPP ambiguity resolution with GPS, BDS, Galileo and GLONASS multi-frequency observations

Abstract

The performance of high-precision Global Navigation Satellite System (GNSS) positioning in multi-frequency and multi-constellation environments strongly depends on the understanding and handling the biases that inevitably exist between the different systems and signals. The usage of observable-specific signal bias (OSB), allowing to map biases to each individual observation type involved, provides full flexibility for the multi-GNSS bias processing. In this contribution, the OSB estimation model is extended from the traditional dual-frequency model to multi-frequency and multi-GNSS one to provide GPS/GLONASS triple-frequency, Galileo five-frequency, BDS six-frequency phase/code bias products for precise point positioning (PPP) ambiguity resolution (AR). Results indicate that the code bias products exhibit high stability with average standard deviations (STDs) of 0.06–0.10 ns for GPS and 0.16–0.33 ns for BDS/Galileo/GLONASS. Likewise, the daily phase bias is extremely stable, with average STDs of 0.01–0.02 ns for GPS and Galileo, 0.03–0.05 ns for BDS and 0.05–0.07 ns for GLONASS. Particularly, for the modernized binary offset carrier signals of Galileo E5 and BDS-3 B2, their phase/code biases present relatively high consistency between the different tracking modes and different frequencies. In addition, obvious differences in the range of 10.92–28.58 ns can be noted between the receiver-specific code bias of BDS-2 and BDS-3 for their common frequency signals. Based on the observable-specific phase and code biases, a multi-frequency PPP cascade integer resolution model is developed to make full use of all available observations from different GNSSs. After applying these bias products, PPP AR with GPS, BDS, Galileo and GLONASS multi-frequency observations is achieved with an average convergence time of 4.44 min, showing remarkable improvements of 56.8% and 16.8% compared to dual-frequency PPP float and fixed solutions, respectively.

Introduction

With the rapid development of BDS and Galileo and the modernization of GPS and GLONASS, the current Global Navigation Satellite Systems (GNSS) world has evolved into multi-GNSS with multiple satellite constellations as well as a variety of frequencies and signals. More than 140 satellites are currently available for GNSS users, and each GNSS transmits at least three frequency signals. The combination of multi-GNSS constellation and signals is foreseen to bring promising insights to improve the accuracy, convergence and reliability of GNSS positioning (Montenbruck et al. 2017; Li et al. 2018, 2019).

The anticipated improvements strongly depend on the understanding and handling of the biases that inevitably exist between the different systems and signals. The biases of the code and phase measurements generally result from the systematic delays related to the signal generating and processing chain. The common way to deal with code and phase biases is to estimate their combined form, such as differential code bias (DCB, Montenbruck et al. 2013) and uncalibrated phase delay (UPD, Li et al. 2018; Wang et al. 2021), and correct them in the subsequent process. Nowadays, the wide range of GNSS signals results in a large number of phase- and code-specific bias types in the combined form. Considering the number of possible combined forms, applying the combined corrections becomes difficult. Moreover, it also causes inflexibility in the traditional differential signal bias parametrization since the differential form is changeable concerning observation types that participated in the positioning process.

In response to this circumstance, the approach called observable-specific signal bias (OSB) parametrization has been proposed and implemented recently (Villiger et al. 2019; Wang et al. 2020; Deng et al. 2021). The OSB parametrization specifies an absolute bias for each observable involved in bias processing without numerous combinations. In this case, bias corrections can be straightforwardly applied to the corresponding observations. Thanks to its high flexibility and expandability for bias handling, the usage of OSB parametrization is well suited for the multi-GNSS and multi-frequency PPP processing. In fact, similar use such as pseudo-absolute code biases has been defined in the standard of Radio Technical Commission for Maritime Service (RTCM-SC 2016) and is widely used in the real-time GNSS community. In recent years, the acquisition methods and characteristics of OSBs for the post-processing of GNSS data have been investigated. Villiger et al. (2019) explained the relationship between the traditional DCB and code OSB parameters, thereby proposing an approach for multi-GNSS code OSB estimation for the first time. The long-term stability of GPS, GLONASS, Galileo and BDS-2 satellite OSBs was also analyzed. Later, Wang et al. (2020) and Deng et al. (2021) conducted more comprehensive research on multi-GNSS code OSB estimation with all possible OSBs estimated for the latest GNSS. Results indicate that the RMS of GPS and Galileo code OSB is at the level of 0.2–0.3 ns, while that of GLONASS and BDS OSBs reaches 0.5–1.0 ns. As for the phase OSB, Geng et al. (2019) proposed a modified GPS phase clock/bias model to enable the undifferenced ambiguity resolution. This GPS daily OSB product is now released by Wuhan University. Schaer et al. (2021) in CODE further generalized the GPS and Galileo phase OSB for the PPP AR together with the integer clock products. However, the GLONASS and BDS phase OSBs are still unavailable, and the current GPS/Galileo phase OSB can only be employed for dual-frequency users. A unified observable-specific bias estimation and calibration model is urgently needed to make full use of the multi-frequency observations of GPS, BDS, Galileo and GLONASS systems. Moreover, the characteristic of the estimated OSBs of new GNSS signals and the performance of OSB-based multi-frequency and multi-GNSS PPP AR also needs further investigation.

The traditional dual-frequency OSB estimation model is expanded to derive four-system OSB products at all frequencies for achieving multi-GNSS and multi-frequency PPP AR. The proposed model is implemented and validated using one month of GPS, BDS, Galileo and GLONASS multi-frequency observations of 145 multi-GNSS Experiment (MGEX) stations. After this introduction, the detailed methods for estimating and calibrating code and phase biases are described. Then, the tracking stations and data processing strategies employed in bias estimation and PPP AR are introduced, respectively. Hereafter, the characteristics of phase/code biases are investigated and OSB-based PPP AR results are discussed. Finally, the conclusions of this study are summarized.

Methods

This section introduces the estimation method of multi-GNSS DCB and UPD products, which are important prerequisites for the OSB estimation. Hereafter, a detailed description of the code and phase OSB estimation of all types of GNSS signals is presented. The OSB-based multi-frequency and multi-GNSS PPP AR model is finally developed.

Multi-GNSS UPD and DCB estimation based on uncombined PPP model

The raw pseudorange $\left( {P_{r,\;n}^{s} } \right)$ and carrier phase $\left( {L_{r,\;n}^{s} } \right)$ observations from the satellite s to receiver $r$ at frequency $n$ can be expressed as:

$$P_{r,n}^{s} = \rho_{r}^{s} + t_{r,n} - t_{n}^{s} + \gamma_{n} I_{r,1}^{s} + T_{r}^{n} + b_{r,n} + b_{n}^{s} + \zeta_{r,n}^{s}$$

(1)

$$L_{r,n}^{s} = \rho_{r}^{s} + t_{r,n} - t_{n}^{s} - \gamma_{n} I_{r,1}^{s} + T_{r}^{n} + \lambda_{n} \cdot N_{r}^{n} + B_{r,n} + B_{n}^{s} + \varepsilon_{r,n}^{s}$$

(2)

where $\rho_{r}^{s}$ is the geometric distance from the GNSS satellite and receiver; $t$ indicates the clock offsets; $I$ and $T$ are ionospheric and tropospheric delays, respectively; $\lambda$ is the wavelength of carrier phase; $\gamma_{n}$ indicates frequency-dependent multiplier factor for the ionospheric delay, which can be expressed as $\gamma_{n} = {{\lambda_{n}^{2} } \mathord{\left/ {\vphantom {{\lambda_{n}^{2} } {\lambda_{1}^{2} }}} \right. \kern-\nulldelimiterspace} {\lambda_{1}^{2} }}$; $N$ stands for the integer ambiguity; $b$ and $B$ refer to hard- or software delays associated with code and phase measurements, respectively; $\zeta$ and $\varepsilon$ are the sum of errors including multipath and measurement noise. For the sake of clarity, other errors, including the satellite and receiver antenna phase center offsets (PCOs) and variations (PCVs), relativistic effects, Sagnac effect, tidal loadings and phase wind-up have been corrected according to the existing models.

In a multi-frequency and multi-GNSS environment, the general equations of the undifferenced and uncombined PPP model are written as (Li et al. 2021):

$$\left\{ \begin{gathered} p_{r,n}^{s,G} = \mu_{r}^{s,G} \cdot x + \hat{t}_{r} - \overline{t}_{ij}^{s,G} + \gamma_{n}^{G} \cdot \hat{I}_{r,1}^{s,G} + m_{r,w}^{s,G} \cdot Z_{r,w} + \kappa \cdot IFB_{n}^{s,G} + e_{r,n}^{s,G} \hfill \\ p_{r,n}^{{s,R_{{}} }} = \mu_{r}^{s,R} \cdot x + \hat{t}_{r} - \overline{t}_{{{\text{ij}}}}^{s,R} + \gamma_{n}^{s,R} \cdot \hat{I}_{r,1}^{s,R} + m_{r,w}^{s,R} \cdot Z_{r,w} + ISB_{{R_{s} - G}} + \kappa \cdot IFB_{n}^{s,R} + e_{r,n}^{s,R} \hfill \\ p_{r,n}^{s,E} = \mu_{r}^{s,E} \cdot x + \hat{t}_{r} - \overline{t}_{{{\text{ij}}}}^{s,E} + \gamma_{n}^{E} \cdot \hat{I}_{r,1}^{s,E} + m_{r,w}^{s,E} \cdot Z_{r,w} + ISB_{E - G} + \kappa \cdot IFB_{n}^{s,E} + e_{r,n}^{s,E} \hfill \\ p_{r,n}^{s,C} = \mu_{r}^{s,C} \cdot x + \hat{t}_{r} - \overline{t}_{{{\text{ij}}}}^{s,C} + \gamma_{n}^{C} \cdot \hat{I}_{r,1}^{s,C} + m_{r,w}^{s,C} \cdot Z_{r,w} + ISB_{C - G} + \kappa \cdot IFB_{n}^{s,C} + e_{r,n}^{s,C} \hfill \\ \end{gathered} \right.$$

(3)

$$\left\{ \begin{gathered} l_{r,n}^{s,G} = \mu_{r}^{s,G} \cdot x + \hat{t}_{r} - \overline{t}_{{{\text{ij}}}}^{s,G} - \gamma_{n}^{G} \cdot \hat{I}_{r,1}^{s,G} + m_{r,w}^{s,G} \cdot Z_{r,w} + \lambda_{n}^{G} \hat{N}_{r,n}^{s,G} + \varepsilon_{r,n}^{s,G} \hfill \\ l_{r,n}^{s,R} = \mu_{r}^{s,R} \cdot x + \hat{t}_{r} - \overline{t}_{{{\text{ij}}}}^{s,R} - \gamma_{n}^{s,R} \cdot \hat{I}_{r,1}^{s,R} + m_{r,w}^{s,R} \cdot Z_{r,w} + \lambda_{n}^{s,R} \hat{N}_{r,n}^{{s,R_{{}} }} + \varepsilon_{r,n}^{s,R} \hfill \\ l_{r,n}^{s,E} = \mu_{r}^{s,E} \cdot x + \hat{t}_{r} - \overline{t}_{{{\text{ij}}}}^{s,E} - \gamma_{n}^{E} \cdot \hat{I}_{r,1}^{s,E} + m_{r,w}^{s,E} \cdot Z_{r,w} + \lambda_{n}^{E} \hat{N}_{r,n}^{s,E} + \varepsilon_{r,n}^{s,E} \hfill \\ l_{r,n}^{s,C} = \mu_{r}^{s,C} \cdot x + \hat{t}_{r} - \overline{t}_{{{\text{ij}}}}^{s,C} - \gamma_{n}^{C} \cdot \hat{I}_{r,1}^{s,C} + m_{r,w}^{s,C} \cdot Z_{r,w} + \lambda_{n}^{C} \hat{N}_{r,n}^{s,C} + \varepsilon_{r,n}^{s,C} \hfill \\ \end{gathered} \right.$$

(4)

with

$$\kappa = \left\{ \begin{gathered} 0\;\;\;n = i\;{\text{or}}\;n = j \, \hfill \\ 1\;\;\;n \ne i\;{\text{and}}\;n \ne j \, \hfill \\ \end{gathered} \right. \,$$

(5)

$$\left\{ \begin{gathered} \overline{t}_{{{\text{ij}}}}^{{s,{\text{sys}}}} = t^{{s,{\text{sys}}}} + \left( {\alpha_{ij}^{{{\text{sys}}}} b_{i}^{{s,{\text{sys}}}} + \beta_{{{\text{ij}}}}^{{{\text{sys}}}} b_{j}^{{s,{\text{sys}}}} } \right) \hfill \\ \hat{t}_{r} = t_{r} + \left( {\alpha_{{{\text{ij}}}}^{G} b_{r,i}^{G} + \beta_{{{\text{ij}}}}^{G} b_{r,j}^{G} } \right) \hfill \\ \hat{I}_{r,i}^{s} = I_{r,i}^{s} + \beta_{{{\text{ij}}}}^{{{\text{sys}}}} \left( {b_{r,i}^{{{\text{sys}}}} - b_{r,j}^{{{\text{sys}}}} } \right) - \beta_{{{\text{ij}}}}^{{{\text{sys}}}} \left( {b_{i}^{{s,{\text{sys}}}} - b_{j}^{{s,{\text{sys}}}} } \right) \hfill \\ {\text{ISB}}_{{R_{s} - G}} = \left( {\alpha_{{{\text{ij}}}}^{{R_{s} }} b_{r,i}^{{R_{s} }} + \beta_{{{\text{ij}}}}^{{R_{s} }} b_{r,j}^{{R_{s} }} } \right) - \left( {\alpha_{{{\text{ij}}}}^{G} b_{r,i}^{G} + \beta_{{{\text{ij}}}}^{G} b_{r,j}^{G} } \right) \hfill \\ {\text{ISB}}_{E - G} = \left( {\alpha_{{{\text{ij}}}}^{E} b_{r,i}^{E} + \beta_{{{\text{ij}}}}^{E} b_{r,j}^{E} } \right) - \left( {\alpha_{{{\text{ij}}}}^{G} b_{r,i}^{G} + \beta_{{{\text{ij}}}}^{G} b_{r,j}^{G} } \right) \hfill \\ {\text{ISB}}_{C - G} = \left( {\alpha_{{{\text{ij}}}}^{C} b_{r,i}^{C} + \beta_{{{\text{ij}}}}^{C} b_{r,j}^{C} } \right) - \left( {\alpha_{{{\text{ij}}}}^{G} b_{r,i}^{G} + \beta_{{{\text{ij}}}}^{G} b_{r,j}^{G} } \right) \hfill \\ {\text{IFB}}_{k}^{{{\text{sys}}}} = \left[ {\left( {b_{r,k}^{{{\text{sys}}}} - b_{k}^{{s,{\text{sys}}}} } \right) - \left( {b_{r,i}^{{{\text{sys}}}} - b_{i}^{{s,{\text{sys}}}} } \right)} \right] + \frac{{\beta_{{{\text{ij}}}}^{{{\text{sys}}}} }}{{\beta_{{{\text{ik}}}}^{{{\text{sys}}}} }}\left[ {\left( {b_{r,i}^{{{\text{sys}}}} - b_{i}^{{s,{\text{sys}}}} } \right) - \left( {b_{r,j}^{{{\text{sys}}}} - b_{j}^{{s,{\text{sys}}}} } \right)} \right] \hfill \\ \hat{N}_{r,i}^{{s,{\text{sys}}}} = N_{r,i}^{{s,{\text{sys}}}} + \left( {B_{r,i}^{{{\text{sys}}}} - B_{i}^{{s,{\text{sys}}}} } \right) + {{\left[ {b_{{{\text{ij}}}}^{{s,{\text{sys}}}} - b_{{r,{\text{ij}}}}^{{{\text{sys}}}} + \beta_{{{\text{ij}}}} \left( {b_{r,i} - b_{r,j} } \right) - \beta_{{{\text{ij}}}} \left( {b_{i}^{s} - b_{j}^{s} } \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {b_{{{\text{ij}}}}^{{s,{\text{sys}}}} - b_{{r,{\text{ij}}}}^{{{\text{sys}}}} + \beta_{{{\text{ij}}}} \left( {b_{r,i} - b_{r,j} } \right) - \beta_{{{\text{ij}}}} \left( {b_{i}^{s} - b_{j}^{s} } \right)} \right]} {\lambda_{i} }}} \right. \kern-\nulldelimiterspace} {\lambda_{i} }} \hfill \\ \hat{N}_{r,j}^{{s,{\text{sys}}}} = N_{r,j}^{{s,{\text{sys}}}} + \left( {B_{r,j}^{{{\text{sys}}}} - B_{j}^{{s,{\text{sys}}}} } \right) + {{\left[ {b_{ij}^{{s,{\text{sys}}}} - b_{{r,{\text{ij}}}}^{{{\text{sys}}}} + \gamma_{j}^{{{\text{sys}}}} \beta_{{{\text{ij}}}} \left( {b_{r,i} - b_{r,j} } \right) - \gamma_{j}^{{{\text{sys}}}} \beta_{{{\text{ij}}}} \left( {b_{i}^{s} - b_{j}^{s} } \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {b_{ij}^{{s,{\text{sys}}}} - b_{{r,{\text{ij}}}}^{{{\text{sys}}}} + \gamma_{j}^{{{\text{sys}}}} \beta_{{{\text{ij}}}} \left( {b_{r,i} - b_{r,j} } \right) - \gamma_{j}^{{{\text{sys}}}} \beta_{{{\text{ij}}}} \left( {b_{i}^{s} - b_{j}^{s} } \right)} \right]} {\lambda_{i} }}} \right. \kern-\nulldelimiterspace} {\lambda_{i} }} \hfill \\ \hat{N}_{r,k}^{{s,{\text{sys}}}} = N_{r,k}^{{s,{\text{sys}}}} + \left( {B_{r,k}^{{{\text{sys}}}} - B_{k}^{{s,{\text{sys}}}} } \right) + {{\left[ {b_{{{\text{ij}}}}^{{s,{\text{sys}}}} - b_{{r,{\text{ij}}}}^{{{\text{sys}}}} + \gamma_{k}^{{{\text{sys}}}} \beta_{{{\text{ij}}}} \left( {b_{r,i} - b_{r,j} } \right) - \gamma_{k}^{{{\text{sys}}}} \beta_{{{\text{ij}}}} \left( {b_{i}^{s} - b_{j}^{s} } \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {b_{{{\text{ij}}}}^{{s,{\text{sys}}}} - b_{{r,{\text{ij}}}}^{{{\text{sys}}}} + \gamma_{k}^{{{\text{sys}}}} \beta_{{{\text{ij}}}} \left( {b_{r,i} - b_{r,j} } \right) - \gamma_{k}^{{{\text{sys}}}} \beta_{{{\text{ij}}}} \left( {b_{i}^{s} - b_{j}^{s} } \right)} \right]} {\lambda_{k} }}} \right. \kern-\nulldelimiterspace} {\lambda_{k} }} \hfill \\ \end{gathered} \right.$$

(6)

where the superscript ${\text{sys}}$ indicates GNSS system; $p_{r,j}^{s}$ and $l_{r,j}^{s}$ denote the observed minus computed values of the code and carrier phase observations, respectively; ${\mathbf{x}}$ (${\mathbf{x}} = [dx,dy,dz]$) is the vector of the receiver position increments relative to the a priori position, and ${{\varvec{\upmu}}}$ is the unit vector of the component from the receiver to the satellite;$Z_{r,w}$ represents the tropospheric zenith wet delay and $m_{r,w}^{s}$ is the corresponding mapping function; $\alpha_{{{\text{ij}}}}$ and $\beta_{{{\text{ij}}}}$ are the coefficients of the IF combinations with $\alpha_{{{\text{ij}}}} = \frac{{f_{i}^{2} }}{{f_{i}^{2} - f_{j}^{2} }},\beta_{{{\text{ij}}}} = \frac{{ - f_{j}^{2} }}{{f_{i}^{2} - f_{j}^{2} }}$. The code-specific inter-system bias (${\text{ISB}}_{r}$) is introduced for each system except for GPS under the assumption that the multi-GNSS code observations share the same receiver clock. Similarly, the inter-frequency bias (${\text{IFB}}$) is introduced to the additional frequency ($n \ne i\;{\text{and}}\;n \ne j$) for each satellite. To eliminate the rank deficiency in the linear system and get the full-rank model and detailed forms of the estimable parameters, a re-parameterization is carried out based on S-system theory (Odijk et al. 2016; Zhang et al. 2018; Ren et al. 2021). In this way, the combined forms of code and phase biases are absorbed by ionospheric delays, IFB and phase ambiguities, as shown in (4).

These re-parameterized parameters provide the basic observables for code and phase bias estimation (Liu et al. 2019). For example, the DCBs are estimable once the re-parameterized ionospheric delay and IFB parameters are obtained in the undifferenced PPP processing. The re-parameterized ionospheric delay and IFB parameters are expressed as:

$$\left\{ \begin{gathered} \hat{I}_{r,i}^{s} = I_{r,i}^{s} + \beta_{{{\text{ij}}}} \left( {D{\text{CB}}_{r,ij} - {\text{DCB}}_{{{\text{ij}}}}^{s} } \right) = \left( {\frac{40.31}{{f_{i}^{2} }}} \right) \cdot {\text{STEC}} + \beta_{{{\text{ij}}}} \left( {{\text{DCB}}_{{r,{\text{ij}}}} - {\text{DCB}}_{{{\text{ij}}}}^{s} } \right) \hfill \\ {\text{IFB}}_{k} = \left[ {{\text{DCB}}_{{{\text{ik}}}}^{s} - {\text{DCB}}_{{r,{\text{ik}}}} } \right] + \frac{{\beta_{{{\text{ij}}}} }}{{\beta_{{{\text{ik}}}} }}\left[ {{\text{DCB}}_{{r,{\text{ik}}}} - DCB_{{{\text{ij}}}}^{s} } \right] \hfill \\ \end{gathered} \right.$$

(7)

with

$$\left\{ \begin{gathered} {\text{DCB}}_{{{\text{ij}}}} = b_{i} - b_{j} \hfill \\ {\text{DCB}}_{{{\text{ik}}}} = b_{i} - b_{k} \hfill \\ \end{gathered} \right.$$

(8)

where ${\text{STEC}}$ is the slant total electron content, which can be precisely calculated with the auxiliary of global ionosphere maps (GIMs). With the ionospheric delay and IFB parameters available, the precise determination of multi-frequency DCB can be divided into two steps. Firstly, the DCB between two reference codes (${\text{DCB}}_{{{\text{ij}}}}$) is estimated with the PPP-derived slant ionospheric delay. Under the assumption that the DCB is constant over the period in a long arc, e.g. 24 h, the sum of satellite and receiver DCB can be obtained:

$${\text{DCB}}_{{r,{\text{ij}}}} + {\text{DCB}}_{{{\text{ij}}}}^{s} = \frac{1}{{N \cdot \beta_{{{\text{ij}}}} }}\sum\limits_{m = 1}^{N} {\left[ {\hat{I}_{r,i}^{s} - \frac{40.31}{{f_{i}^{2} }} \cdot {\text{STEC}}} \right]}$$

(9)

where $m$ is the epoch number and $N$ indicates the total number of epochs. To separate the satellite DCB, a least-square solution with zero-constellation-mean constraint is implemented (Montenbruck and Hauschild 2013). Later, when the IFB parameters and the ${\text{DCB}}_{{{\text{ij}}}}$ values are available, the DCBs between the reference code and additional code (${\text{DCB}}_{{{\text{ik}}}}$) can be determined based on a similar processing strategy.

Likewise, the combined bias absorbed by ambiguities, which is known as the UPD, is estimable when float ambiguities are available. The calibration of UPD is an important prerequisite for achieving PPP AR. In a multi-frequency and multi-GNSS environment, the extra-wide-lane (EWL), wide-lane (WL) and narrow-lane (NL) UPDs are required for users to conduct AR in a step-by-step way (Geng and Bock 2013). In an undifferenced and uncombined PPP model, the EWL, WL and NL ambiguities are formulated as:

$$\left\{ \begin{gathered} \hat{N}_{{r,\;{\text{ewl}}}}^{s} = \hat{N}_{r,\;j}^{s} - \hat{N}_{r,\;k}^{s} = N_{{r,\;{\text{ewl}}}}^{s} + d_{{r,\;{\text{ewl}}}} - d_{{{\text{ewl}}}}^{s} \hfill \\ \hat{N}_{{r,\;{\text{wl}}}}^{s} = \hat{N}_{r,\;i}^{s} - \hat{N}_{r,\;j}^{s} = N_{{r,\;{\text{wl}}}}^{s} + d_{{r,\;{\text{wl}}}} - d_{{{\text{wl}}}}^{s} \hfill \\ \hat{N}_{{r,\;{\text{nl}}}}^{s} = \left( {\alpha_{{{\text{ij}}}} \lambda_{i} \hat{N}_{r,\;i}^{s} + \beta_{{{\text{ij}}}} \lambda_{j} \hat{N}_{r,\;j}^{s} } \right)/\lambda_{{{\text{nl}}}} - \lambda_{i} N_{{r,\;{\text{wl}}}}^{s} /\left( {\lambda_{j} - \lambda_{i} } \right) = N_{{r,\;{\text{nl}}}}^{s} + d_{{r,\;{\text{nl}}}} - d_{{{\text{nl}}}}^{s} \hfill \\ \end{gathered} \right.$$

(10)

where the subscripts ${\text{ewl}}$, ${\text{wl}}$ and ${\text{nl}}$ refer to the combinations of EWL, WL and NL; $d_{r}$ and $d_{{}}^{s}$ denote the UPDs at the receiver and satellite sides, respectively. When there are plenty of ambiguities available from the reference stations, the satellite- and receiver-specific UPDs can be estimated by the least-square method. To avoid rank deficiency, we select one receiver or satellite as a reference with the corresponding UPD set as zero (Zhao et al. 2021).

Whether the DCB or UPD estimation, some important issues should be taken into account for different systems and frequencies: (1) For GLONASS frequency division multiple access (FDMA) signals, the GLONASS inter-frequency bias (GIFB) should be carefully considered (Liu et al. 2017). To avoid the effect of GIFB, the stations equipped with the same types of receivers are selected for UPD estimation. In this way, the GIFB will be absorbed by the satellite UPDs and enable the GLONASS PPP AR (Li et al. 2018). However, the GIFB is ignored in the DCB estimation because of its minimal effect on the estimation (Zhang et al. 2017). (2) The inter-frequency clock bias (IFCB) introduced by the phase observations of the third frequency should be corrected in the PPP processing and UPD estimation for GPS, BDS-2 and GLONASS in advance (Pan et al. 2017). In addition, the satellite-induced code bias of BDS-2 satellites also needs to be calibrated with the existing models (Wanninger and Beer 2015). (3) The receiver-specific code bias between the BDS-2 and BDS-3 should be noted. The code bias difference between BDS-2 and BDS-3 varies in a range of about 30 ns, which is also demonstrated in this study (Figure 6 and Table 3). Therefore, it would be better if we treat BDS-2 and BDS-3 as two individual systems for the bias estimation.

OSB estimation of code and phase measurement

Once the DCB correction is obtained, the OSB of individual code observation can be easily determined when an additional constraint is employed. Generally, this constraint should ensure that the estimated OSB corrections are compatible with the IGS clock products. As a convention, the clock products provided by IGS analysis centers use the IF combination with two code observations as reference signals (Banville et al. 2020). Assuming that $i$ and $j$ are the reference signals, the clock bias product can be modeled as follows:

$$\overline{t}^{s} = t^{s} - \left( {\alpha_{{{\text{ij}}}} b_{i}^{s} + \beta_{{{\text{ij}}}} b_{j}^{s} } \right)$$

(11)

where $\overline{t}$ is the satellite clock bias to be corrected in the precise positioning, and $t$ denotes the real clock offset concerning the reference time system.

Considering ${\text{DCB}}_{{{\text{ij}}}}^{s} = b_{i}^{s} - b_{j}^{s}$, the above equation can be rewritten as:

$$\overline{t}^{s} - \beta_{{{\text{ij}}}} {\text{DCB}}_{{{\text{ij}}}}^{s} = t^{s} - b_{i}^{s}$$

(12)

$$\overline{t}^{s} + \alpha_{{{\text{ij}}}} {\text{DCB}}_{{{\text{ij}}}}^{s} = t^{s} - b_{j}^{s}$$

(13)

with which the clock bias and code bias can be simultaneously corrected for users tracking code $i$ or code $j$.

Furthermore, for the code $k$ not used in the clock bias estimation, the corresponding correction model can be expressed as:

$$\overline{t}^{s} - \beta_{{{\text{ij}}}} {\text{DCB}}_{{{\text{ij}}}}^{s} + {\text{DCB}}_{{{\text{ik}}}}^{s} = t^{s} - b_{k}^{s}$$

(14)

then, the OSBs on the code $i$, $j$ and $k$ can be defined as:

$$\left\{ \begin{gathered} \overline{b}_{i}^{s} = \beta_{{{\text{ij}}}} {\text{DCB}}_{{{\text{ij}}}}^{s} \hfill \\ \overline{b}_{j}^{s} = - \alpha_{{{\text{ij}}}} {\text{DCB}}_{{{\text{ij}}}}^{s} \hfill \\ \overline{b}_{k}^{s} = \beta_{{{\text{ij}}}} {\text{DCB}}_{{{\text{ij}}}}^{s} - {\text{DCB}}_{1,k}^{s} = \overline{b}_{i}^{s} - {\text{DCB}}_{{{\text{ik}}}}^{s} \hfill \\ \end{gathered} \right.$$

(15)

where $\overline{b}$ is the so-called code OSB, which can be obtained by (15) directly when the DCB corrections are available. Additionally, it can be noticed that $\overline{b}_{{1}}^{s}$ and $\overline{b}_{2}^{s}$ satisfy the IF constraint:

$$f_{i}^{2} \overline{b}_{i}^{s} - f_{j}^{2} \overline{b}_{j}^{s} = 0$$

(16)

It demonstrates that the DCB can be converted to the “absolute” bias at each code observation when employing this IF constraint, and the derived code OSB maintains consistency with the IGS clock products. Note that the code “absolute” bias $\overline{b}$ is not equivalent to hardware delay $b$; rather, it is an observable-specific code bias released to the user instead of DCB.

Based on (10), we find that the satellite EWL, WL and NL UPDs can be expressed as the combination of code and phase OSBs as follows:

$$\left\{ \begin{gathered} d_{{{\text{ewl}}\_{\text{jk}}}}^{s} = \left( {\overline{B}_{j} - \overline{B}_{k} } \right) + \frac{{(1 - \eta )\overline{b}_{i} + \eta \overline{b}_{j} }}{{\lambda_{{{\text{ewl}}\_{\text{jk}}}} }} \hfill \\ d_{{{\text{wl}}\_{\text{ij}}}}^{s} = \left( {\overline{B}_{i} - \overline{B}_{j} } \right) - \frac{{\lambda_{j} \overline{b}_{j} + \lambda_{i} \overline{b}_{j} }}{{\left( {\lambda_{i} + \lambda_{j} } \right)\lambda_{{{\text{wl}}\_{\text{ij}}}} }} \hfill \\ d_{{{\text{nl}}}}^{s} = \frac{{\lambda_{j} }}{{\lambda_{j} - \lambda_{i} }}\left( {\overline{B}_{i} - \frac{{\overline{b}_{i} }}{{\lambda_{i} }}} \right) - \frac{{\lambda_{i} }}{{\lambda_{j} - \lambda_{i} }}\left( {\overline{B}_{j} - \frac{{\overline{b}_{j} }}{{\lambda_{j} }}} \right) \hfill \\ \end{gathered} \right.$$

(17)

with

$$\eta = \frac{{\lambda_{j} \lambda_{k} - \lambda_{i}^{2} }}{{\lambda_{j}^{2} - \lambda_{i}^{2} }}$$

(18)

where $\overline{b}$ and $\overline{B}$ refer to the code and phase OSBs, respectively. Therefore, once the code OSBs and phase UPDs are obtained, the phase OSBs can be calculated as follows:

$$\left\{ \begin{gathered} \overline{B}_{i} = \tfrac{{ - \lambda_{j} }}{{\left( {\gamma \lambda_{i} - \lambda_{j} } \right)\lambda_{i} }}\left[ {d_{{{\text{wl}}\_{\text{ij}}}}^{s} - \left( {\alpha_{{{\text{wl}}\_{\text{ij}}}} \overline{b}_{i} + \beta_{{{\text{wl}}\_{\text{ij}}}} \overline{b}_{j} } \right)} \right] + (\gamma - 1)\lambda_{{{\text{nl}}}} d_{{{\text{nl}}}}^{s} \hfill \\ \overline{B}_{j} = \tfrac{{ - \gamma \lambda_{i} }}{{\gamma \lambda_{i} - \lambda_{j} }}\left[ {d_{{{\text{wl}}\_{\text{ij}}}}^{s} - \left( {\alpha_{{{\text{wl}}\_{\text{ij}}}} \overline{b}_{i} + \beta_{wl\_ij} \overline{b}_{j} } \right)} \right] + (\gamma - 1)\lambda_{{{\text{nl}}}} d_{{{\text{nl}}}}^{s} \hfill \\ B_{k} = - \left[ {d_{{{\text{ewl}}\_{\text{jk}}}}^{s} - \left( {\alpha_{{{\text{wl}}\_{\text{ij}}}} \overline{b}_{i} + \beta_{{{\text{wl}}\_{\text{ij}}}} \overline{b}_{j} } \right) - B_{j}^{{}} } \right] \hfill \\ \end{gathered} \right.$$

(19)

with

$$\left\{ \begin{gathered} \alpha_{{{\text{nl}}\_{\text{ij}}}} = \frac{{\lambda_{j} }}{{\lambda_{i} (\lambda_{j} - \lambda_{i} )}};\;\beta_{{{\text{nl}}\_{\text{ij}}}} = \frac{{\lambda_{j} }}{{\lambda_{j} (\lambda_{j} - \lambda_{i} )}} \hfill \\ \alpha_{{{\text{wl}}\_{\text{ij}}}} = \frac{{\lambda_{i} - \lambda_{j} }}{{\lambda_{i} (\lambda_{j} + \lambda_{i} )}};\;\beta_{{{\text{wl}}\_{\text{ij}}}} = \frac{{\lambda_{i} - \lambda_{j} }}{{\lambda_{j} (\lambda_{j} + \lambda_{i} )}} \hfill \\ \alpha_{{{\text{ewl}}\_{\text{jk}}}} = \frac{1 - \eta }{{\lambda_{{{\text{ewl}}\_{\text{jk}}}} }};\;\beta_{{{\text{ewl}}\_{\text{jk}}}} = \frac{\eta }{{\lambda_{{{\text{ewl}}\_{\text{jk}}}} }} \hfill \\ \end{gathered} \right.$$

(20)

It can be seen from the equations that phase OSB is a linear combination of UPDs and code OSBs on corresponding frequencies. Likewise, the phase OSB $\overline{B}$ is not equivalent to phase delay $B$. It can be regarded as an “absolute” bias used to calibrate the phase observation for the recovery of the integer ambiguity.

Multi-frequency and multi-GNSS PPP AR with OSB corrections

After the phase and code OSBs are obtained, one can employ the OSB corrections to calibrate the corresponding measurements as follows:

$$\left\{ \begin{gathered} \tilde{P}_{r,n}^{s} { = }P_{r,n}^{s} - \overline{b}_{n} \hfill \\ \tilde{L}_{r,n}^{s} { = }L_{r,n}^{s} - \lambda_{n} \overline{B}_{n} \hfill \\ \end{gathered} \right.$$

(21)

where $\tilde{P}_{r,n}^{s}$ and $\tilde{L}_{r,n}^{s}$ are code and phase measurements after applying the OSB corrections. Then, multi-frequency and multi-GNSS PPP AR is implemented in three cascade steps with EWL, WL and L1 ambiguities resolved step by step. To make full use of the observations from all available signals and achieve the best positioning performance, when observations of more than three frequencies are used, a variety of EWL ambiguities can be formulated and used together to implement the PPP AR. The formulation of EWL ($\hat{N}_{{{\text{ewl}}\_{\text{jk}}}}^{s}$,…, $\hat{N}_{{{\text{ewl}}\_{\text{jn}}}}^{s}$), WL ($\hat{N}_{{{\text{wl}}\_{\text{ij}}}}^{s}$) and L1 ($\hat{N}_{r,i}^{s}$) ambiguities is shown as follows:

$$\left[ {\begin{array}{*{20}c} {\hat{N}_{r,i}^{s} } \\ {\hat{N}_{{{\text{wl}}\_{\text{ij}}}}^{s} } \\ {\hat{N}_{{{\text{ewl}}\_{\text{jk}}}}^{s} } \\ \vdots \\ {\hat{N}_{{{\text{ewl}}\_{\text{jn}}}}^{s} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 & 0 \\ 1 & { - 1} & 0 & 0 & 0 \\ 0 & 1 & { - 1} & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ 0 & 1 & 0 & 0 & { - 1} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\hat{N}_{r,i}^{s} } \\ {\hat{N}_{r,j}^{s} } \\ {\hat{N}_{r,k}^{s} } \\ \vdots \\ {\hat{N}_{r,n}^{s} } \\ \end{array} } \right]$$

(22)

With phase biases calibrated by the OSB products, these ambiguities keep their integer nature and can be easily fixed by the LAMBDA method (Teunissen 1995). In addition, the fixed ambiguities in the previous step will assist and accelerate the ambiguity resolution in the next steps. Moreover, the partial ambiguity resolution strategy is employed in the multi-GNSS PPP AR processing. These ambiguities whose fractional parts or elevation conditions cannot satisfy the given threshold are rejected for ambiguity resolution in advance. Then the valid ambiguities are removed one by one in the descending order according to their variance until the requirement of the ratio test has been satisfied (Teunissen et al.1999).

The whole process of code and phase OSB estimation is shown in Fig. 1. The bias estimation system starts from multi-frequency and multi-GNSS PPP processing, where GPS/GLONASS triple-frequency, Galileo five-frequency and BDS six-frequency observations are utilized in an uncombined data processing model. The PPP-derived ionospheric delay, IFB and ambiguity parameters provide the basic observables for the estimation of DCB and UPD. The estimated DCB can be converted to the code OSB based on an IF constraint, which also ensures the compatibility of the estimated code bias corrections with IGS clock products. Afterward, the phase bias of each observation is derived based on the linear relationship of absolute phase/code biases and UPDs. Finally, the general bias calibration model of all-types GNSS observations is developed to facilitate multi-GNSS and multi-frequency PPP AR.

Fig. 1

Flowchart of multi-frequency and multi-GNSS phase/code OSB estimation and calibration. The orange boxes denote data processing and the blue boxes present the specific procedure, while the white boxes denote observation data or products

Data set and processing strategy

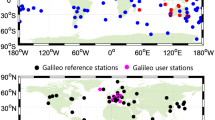
As mentioned in the Methods section, the estimation of DCB and UPD is an important prerequisite for the OSB estimation. Here, observations of GPS, Galileo, GLONASS and BDS from up to 145 MGEX stations during DOY 071-100 of 2021 are incorporated into the DCB and UPD estimation. The distribution of these stations is shown in Fig. 2. The stations selected are distributed evenly on a global scale for better estimation of code and phase biases. The multi-frequency and multi-GNSS UPD products are generated from GREAT-UPD software (https://geodesy.noaa.gov/gps-toolbox). It is worth noting that the UPD estimation of GLONASS satellites is performed for stations equipped with receiver SEPT POLARX5 to avoid the interference brought by the GIFB and these stations are marked by red dots in the figure.

Fig. 2

Distribution of MGEX stations used for DCB and UPD estimation in this study. The blue dots denote the reference stations employed for GPS, Galileo and BDS bias estimation, while the red dots refer to the ones for GLONASS bias estimation

To evaluate the estimated phase/code OSB products, we selected 30 MGEX stations as user stations to conduct multi-frequency and multi-GNSS PPP AR experiments. The distribution of user stations is shown in Fig. 3. The details of the processing strategy for multi-frequency and multi-GNSS PPP AR can be found in Table 1.

Fig. 3

Distribution of MGEX stations used for the multi-frequency and multi-GNSS PPP AR experiment in this study

Table 1 Processing strategies for multi-frequency and multi-GNSS PPP AR

Code and phase OSBs of GNSS signals

This section investigates the characteristics of phase and code OSBs of multiple GNSS signals. The day-to-day variations of code OSBs and the daily variations of phase OSBs are carefully analyzed. Our results indicate that GPS code and phase OSBs exhibit high stability with the average STDs of 0.06–0.10 ns and 0.01–0.02 ns, respectively, which is comparable to plenty of well-known investigations (Geng et al. 2019; Wang et al. 2020; Deng et al. 2021). Therefore, more attention is paid to the new-generation GNSS such as BDS, Galileo and GLONASS-K satellites. Table 2 lists some representative GNSS signals presented in this study with the reference signals of each system marked by ‘○’. Note that the current receivers utilize either a pure pilot-tracking mode (indicated by C1C and C5Q/C7Q/C8Q observation types) or a combined mode (indicated by C1X and C5X/C7X/C8X observation types) for Galileo signals; therefore, two sets of individual signals were selected as the reference.

Table 2 Some representative GNSS signals presented in this study

BDS OSBs

As of April 2021, 15 BDS-2 and 30 BDS-3 satellites provide a global positioning and navigation service. All BDS-2 satellites can transmit a total of three signals: B1I, B2I and B3I, while the BDS-3 satellites offer a variety of new signals, including B1C, B2a, B2b, B2a+b, besides the legacy signals of B1I and B3I. Moreover, different from BDS-2 satellites all manufactured by the China Academy of Space Technology (CAST), 19 BDS-3 satellites are manufactured by CAST and the others are manufactured by the Shanghai Engineering Center for Microsatellites (SECM).

Figure 4 presents the time series of BDS code OSBs on signals B1C (C1C, C1X), B1I (C2I, C2X), B2a (C5P, C5X), B3I (C6I), B2I (C7I), B2b (C7Z) and B2a+b (C8X) during the period of DOY 071 to 100, 2021. It shows that the range of OSB is roughly 200 ns across the BDS constellation, and the code biases of each signal and each satellite are rather stable over time. There are some gaps that span from DOY 72–75, 79–83, 97, 99 for C2X OSBs, which is attributed to the low availability of C2X code observations. Confronted with challenges of limited frequency resources, the BDS-3 satellites employ some modulations to broadcast a variety of signals on each frequency band. For example, the new B1C signal contains a data component and a pilot component, which provides measurements from data-tracking, pilot-tracking and pilot+data tracking. Particularly, in the B2 band, two signals, B2a and B2b, broadcast at two center frequencies, are combined into a constant envelope signal B2a+b with the dual-frequency constant envelope multiplexing (DCEM) technique (Liu et al. 2022). Our results indicate that differences between pilot-only tracking and combined tracking amount to less than 1 ns for B1C and B2a signals. Moreover, a close match of B2a-B2b and B2a-B2a+b code bias can be noted, which reflects a high correlation of code biases on two adjacent frequencies when using the DCEM method.

Fig. 4

Time series of daily code OSB for BDS satellites during the period of DOY 071-100, 2021. Different colors represent different satellites. The panels with types (C1P, C1X), (C2I, C2X), (C5P, C5X), C7I, C7Z, C6I and C8X show code OSB series on B1C, B1I, B2a, B2I, B2b, B3I and B2a+b signals, respectively

The mean values and monthly STDs of BDS OSBs on C2I and C6I are shown in Fig. 5. The satellite PRNs on the horizontal axis are re-aligned with respect to manufacturers. One can see that, for the BDS-3 satellites, the distribution ranges of C2I and C6I OSBs for SECM satellites are much smaller than CAST satellites. For SECM satellites, mean OSBs of C2I and C6I observations vary from − 3.47 ns to 15.69 ns and − 5.26 ns to 23.77 ns, respectively, while those for CAST satellites vary from − 48.65 ns to 82.02 ns and − 73.68 ns to 124.21 ns, respectively. It means that CAST satellites exhibit widely different code biases on frequencies B2I and B3I. In the case of stability, the STDs of OSBs are mostly less than 0.3 ns for all BDS satellites. The average STDs of BDS-2 and BDS-3 OSBs on B1I signal are 0.15 ns and 0.16 ns, respectively.

Fig. 5

Mean values (top) and STDs (bottom) of BDS C2I and C6I code OSBs during the period of DOY 071-100, 2021. The dashed line in the top panel divides the BDS satellite into two categories. One is manufactured by the CAST, while the other one is from the SECM. Similarly, the dashed line in the bottom panel divides the satellites into BDS-2 and BDS-3

The receiver code OSB is also estimated to investigate the code bias between BDS-3 and BDS-2 common frequency signals: B1I and B3I. Figure 6 presents the time series of BDS receiver code OSB for six MGEX stations: MGUE, ABMF, GANP, LPGS, GODN and KERG, which are equipped with SEPT POLARX5TR, SEPT POLARX5, Trimble ALLOY, Javad TRE_3, Javad TRE_3 DELTA and Trimble NETR9 receivers, respectively. The left and right panels show the OSB series of BDS-2 and BDS-3 signals, while the top and bottom panels show the results of B1I and B3I signals, respectively. Similar to the satellite code OSBs, the OSBs at the receiver side also exhibit high stability. It is worth noting that the receiver code OSB is quite different for the BDS-2 and BDS-3 common frequency signals. The average differences for the specific receiver types are listed in Table 3. The differences of receiver code bias between BDS-2 and BDS-3 range from 10.92 to 18.87 ns and 16.54–28.58 ns for the B1I and B3I signals, respectively. Moreover, the code biases of receivers from the same manufacturer are close to each other, such as Javad TRE_3 and Javad TRE_3 DELTA, SEPT POLARX5 and SEPT POLARX5TR. These results indicate that the code difference between BDS-2 and BDS-3 cannot be neglected, which needs to be carefully considered in high-precision GNSS applications.

Fig. 6

Receiver code OSB series of BDS B1I and B3I signals. The left and right panels indicate receiver OSB of BDS-2 and BDS-3, respectively. Different colors denote stations with different receiver types

Table 3 Receiver code OSBs of different receiver types on BDS signals B1I and B3I

The time series of phase OSBs on B1, B2 and B3 frequencies for BDS-2 and BDS-3 satellites with an update time interval of 30 s are presented in Fig. 7. Note that on the B2 frequency, phase OSBs of B2I and B2b signals are presented for BDS-2 and BDS-3 satellites, respectively. Similar to the code biases, the range of phase OSB series for BDS-3 CAST satellites is larger than SECM satellites. Also, it can be clearly seen from the figure that phase OSBs of BDS satellites are quite stable during a one-day period. The STDs of BDS phase OSBs are shown in Fig. 8. The STD values of BDS phase OSBs are generally less than 0.1 ns. The average STD values of BDS B1I, B2I, B3I and B2a OSBs are 0.07 ns, 0.04 ns, 0.09 ns and 0.14 ns, respectively. Taking B1I OSB as an example, the average STD of phase OSBs are 0.03ns and 0.05 ns for BDS-2 and BDS-3 satellites, respectively. This indicates that the BDS-3 phase OSB is not as stable as that of BDS-2 satellites. The possible reason may be that the current available BDS-3 observations are still less than BDS-2, and the error models of BDS-3 still need to be further refined.

Fig. 7

Time series of BDS-3 B1, B2 and B3 phase OSBs on DOY 071, 2021, with an update time interval of 30 s. Different colors represent different satellites. The left, middle and right panels depict the phase OSB series of BDS-2 satellites, BDS-3 CAST satellites and BDS-3 SECM satellites, respectively

Fig. 8

STDs of BDS B1I, B2I, B3I and B2a phase OSBs on DOY 071, 2021

Galileo OSBs

The current Galileo constellation comprises 26 satellites, including 4 In-Orbit-Validation (IOV) satellites and 22 Full Operational Capability (FOC) satellites. All Galileo satellites offer a total of five navigation signals, namely E1, E5a, E5b, E5ab and E6. Each signal contains a data and a pilot component, which are transmitted to users concurrently. The time series of code OSBs are plotted in Fig. 9. We can see from the figure that all these biases are generally stable and the code OSB of pilot-tracking signals agrees well with one of the combined-tracking signals. Besides, high consistency of code OSBs on E5a, E5b and E5ab can be noted. It may be attributed to the Alternative Binary Offset Carrier (Alt-BOC) modulation of the Galileo E5 signal, which also employs DECM technique to combine two Quadrature Phase Shift Keying (QPSK) signals on different frequencies into one integrated signal (Li et al. 2020).

Fig. 9

Time series of daily code OSBs for Galileo satellites during the period of DOY 071-100, 2021. Different colors represent different satellites. The panels from top to bottom show respectively code OSB series on E1, E6, E5a, E5b and E5ab signals. The left and right panels show the code OSBs of different code types on the same signal, respectively

The mean values and STDs of Galileo C1X, C6X, C5X, C7X and C8X OSBs during the 30-day period are shown in Fig. 10. The code OSBs of early launched two IOV satellites E11 and E12 exhibit a larger OSB value than other satellites. Difference between mean values of C5X, C7X and C8X OSBs range from 0.04 to 0.83 ns, which further demonstrates high agreement between C5X, C7X and C8X OSBs. The code OSBs for all Galileo satellites and all signals exhibit good stability with STD values less than 0.3 ns. The average STD values of Galileo C1X, C6X, C5X, C7X and C8X OSBs are 0.15 ns, 0.21 ns, 0.27 ns, 0.26 ns and 0.27 ns, respectively.

Fig. 10

Mean values (top) and STDs (bottom) of Galileo code OSBs during the period of DOY 071–100, 2021. The dashed line in the panels divides the Galileo satellites into IOV and FOC satellites

The time series of Galileo phase OSBs on E1, E5a and E5b are shown in the left panel of Fig. 11 with nine Galileo satellites selected for demonstration. The STDs of phase OSBs for all Galileo satellites are shown in the right panel. The Galileo phase OSBs are stable during a day with the average STD values of 0.017 ns, 0.025 ns and 0.024 ns for E1, E5a and E5b signals, respectively, which reflects a comparable performance as GPS phase OSBs.

Fig. 11

Time series of Galileo E1, E5a and E5b phase OSBs on DOY 071, 2021 with an update interval of 30 s (left panel), and the corresponding STDs of daily phase OSB series (right panel). In the left panel, nine Galileo satellites selected for demonstration are denoted by the different colors

GLONASS OSBs

The GLONASS constellation consists of 24 satellites with the capability of transmitting two FDMA signals. With the modernization of GLONASS, a new code-division-multiple-access (CDMA) signal L3 has been broadcasted by GLONASS-M satellites (for SVs 755–761) and new-generation GLONASS-K satellites in addition to the legacy FDMA signals. Currently, receivers can only track the L3 signal of one GLONASS-M satellite (R21) and two GLONASS-K satellites (R09 and R11) during the period of DOY 071-100, 2021. The time series of GLONASS code OSB on L1 (C1C, C1P), L2 (C2C, C2P) and L3 (C3Q, C3X) signals are shown in Fig. 12. The mean values and STDs of GLONASS triple-frequency OSBs are shown in Fig. 13. From the figures, it can be concluded that the triple-frequency code OSBs of GLONASS satellites are stable over time. The average STDs of GLONASS C1P, C2P and C3Q OSBs are 0.23 ns, 0.33 ns and 0.18 ns, respectively. Although only a few stations can currently track the third-frequency signal of GLONASS satellites, the code OSB of the third-frequency signal is still estimable. Its stability is even slightly better than the other frequency signals, which may be due to the CDMA strategy employed in the third-frequency signal.

Fig. 12

Time series of daily code OSBs for GLONASS satellites during the period of DOY 071–100, 2021. Different colors represent different satellites. The panels from top to bottom show, respectively, code OSB series on L1, L2 and L5 signals. The left and right panels show the code OSBs of different code types on the same signal, respectively

Fig. 13

Mean values and STDs of GLONASS code OSBs during the period of DOY 071-100, 2021. The blue, red and green bars denote code OSBs of C1P, C2P and C3Q

The time series of GLONASS L1, L2 and L3 phase OSBs are shown in the left panel of Fig. 14, and the STDs of all satellites are shown in the right panel. Note that the STD values are generally less than 0.1 ns, which proves that GLONASS phase OSBs are comparatively stable. The average STD values of GLONASS L1, L2 and L3 OSBs are 0.05 ns, 0.07 ns and 0.04 ns, respectively, which is slightly larger than GPS, BDS and Galileo phase OSBs. The possible reason may be attributable to the inter-frequency bias of FDMA signals, which cannot be completely eliminated even if we select the observations of the same receiver types for phase bias estimation.

Fig. 14

Time series of GLONASS L1, L2 and L3 phase OSBs on DOY 071, 2021, with an update interval of 30 s (left panel), and the corresponding STDs of daily phase OSB series (right panel). In the left panel, twelve GLONASS satellites selected for demonstration are denoted by the different colors

Multi-frequency and multi-GNSS PPP-AR with OSB products

To further assess the performance of estimated OSBs, the multi-frequency and multi-GNSS PPP AR is conducted based on these OSB products. Figure 15 shows positioning errors of OSB-based PPP float and fixed solutions at station DRAO in single- (GPS), dual- (GPS+BDS, GPS+Galileo) and four-system (GPS+BDS+Galileo+GLONASS) modes during 0–3 h on DOY 071, 2021. The dual-frequency PPP float solutions (DF-float), dual-frequency PPP fixed solutions (DF-fixed), multi-frequency PPP fixed solutions (MF-fixed) are indicated by green, blue and red lines, respectively. It can be clearly observed that PPP AR significantly shortens the convergence time and improves the position series compared to float PPP, whether in single-system or multi-system mode, which demonstrates the effectiveness of OSB corrections. Moreover, we also note that a better performance is achieved when multi-GNSS and multi-frequency observations are utilized.

Fig. 15

Positioning errors of OSB-based PPP at station DRAO in single-, dual- and four-system modes during 0–3 h on DOY 071, 2021. DF-float, DF-fixed and MF-fixed denote dual-frequency PPP float solutions, dual-frequency PPP fixed solutions and multi-frequency PPP fixed solutions, respectively

The convergence time of daily PPP float and fixed solutions for 30 user stations during the period in DOY 071–100 is computed and the average values are listed in Table 4. The convergence time is defined as the time taken for the horizontal positioning accuracy to be better than 5 cm and stay within 5 cm during ten consecutive epochs. As expected, the convergence time is significantly shortened by PPP AR. In four-system mode, the convergence time is shortened from 12.33 min to 4.44 min, with the improvement up to 63%. At the same time, the average time to first fix (TTFF) of PPP AR in dual- and multi-frequency modes is calculated and presented in Table 5. Here, the TTFF denotes the time taken for the first ambiguity to be successfully fixed and being fixed correctly during ten consecutive epochs. The average TTFF of dual-frequency PPP AR is 11.43 min, 11.17 min, 7.93 min and 7.85 min for G, GC, GE and GREC, respectively, which have been improved to 10.13 min, 9.20 min, 7.17 min and 6.85 min in multi-frequency mode, respectively.

Table 4 Average convergence time of float and fixed PPP solutions of 30 user stations (unit: min)

Table 5 Average TTFF of dual- and multi-frequency PPP fixed solutions of 30 user stations (unit: min)

A comparative experiment is executed between PPP AR using UPD products and OSB products. Figure 16 presents the float PPP, UPD- and OSB-based PPP AR solutions in single-, dual- and four-system modes at station ALGO on DOY 071, 2021. The green, blue and red lines indicate the float PPP, UPD-based and OSB-based PPP AR, respectively. For clarity, the positioning difference between two types of bias products are also demonstrated in Fig. 17. All the PPP solutions are processed in a multi-frequency mode. It can be noted that the OSB-applied PPP AR results are consistent with traditional ones using UPD corrections. It is reasonable since the OSB products are derived from the UPD and DCB products. The subtle difference between OSB- and UPD-based PPP AR can be attributed to different processing strategies, where UPD corrections in different combinations are selected to be applied to estimated ambiguities while the OSBs corrections are directly applied to raw GNSS observations before the parameter estimation.

Fig. 16

Positioning errors of multi-frequency PPP AR using UPD products (blue) and using OSB products (red) at station ALGO during 0-3 h on DOY 071, 2021

Fig. 17

Positioning difference between the UPD- and OSB-based multi-frequency PPP-AR in the horizontal components

Conclusion

This study expands the traditional OSB estimation model to more frequencies and more constellations. The phase and code OSBs of GPS/GLONASS triple-frequency, Galileo five-frequency, BDS six-frequency observations are estimated. The performance of OSB-based multi-frequency and multi-GNSS PPP AR is also investigated.

The proposed model is implemented and validated using a one-month period of 145 MGEX stations. The estimated code and phase biases exhibit high stability with time. The average STDs of code OSBs are within 0.06–0.1 ns for GPS and 0.16–0.33 ns for BDS/Galileo/GLONASS. It is worth noting that the code bias of GLONASS CDMA signals shows slightly better performance than FDMA signals, even though only a few stations can currently track the CDMA signal of GLONASS satellites. In the case of the phase OSBs, the daily biases of GPS and Galileo present the highest stability with the STD less than 0.02 ns, while those of BDS and GLONASS are slightly worse with the STDs of 0.03–0.05 ns and 0.05–0.07 ns, respectively. Especially for some modernized GNSS signals such as Galileo E5 and BDS-3 B2, we find that the code and phase biases have relatively high consistency between the different tracking modes and the different frequencies. In addition, the differences of receiver-specific code bias between BDS-2 and BDS-3 common frequency signals in the range of 10.92–28.58 ns can be noted, which needs to be carefully considered in the precise positioning and ambiguity resolution.

Multi-frequency and multi-GNSS PPP AR can be efficiently carried out when the code and phase OSB corrections are directly applied to GNSS raw observations. The positioning results show that the convergence time is significantly shortened by PPP AR using OSB corrections. The average convergence time of GREC multi-frequency PPP AR is 4.44 min, showing remarkable improvements of 56.8% and 16.8% compared to dual-frequency PPP float and fixed solutions, respectively. Moreover, the comparative tests show that OSB-based PPP AR results are consistent with traditional PPP AR using UPD corrections in single-, dual- and four-system modes, which further demonstrates the effectiveness of OSB products.