Introduction

With the development of global navigation satellite system (GNSS) which mainly includes GPS, GLONASS, BDS, and Galileo, more than 100 satellites will be available by 2020. Combining observations from multi-GNSS can significantly improve the positioning performance in terms of accuracy, integrity, continuity, and availability.

Many methods have been developed to combine observations from multi-GNSS for precise positioning, including real-time kinematic (RTK) positioning. Regarding the differential inter-system bias (DISB) issue resulting from the receiver hardware bias, Odolinski et al. (2015) proposed that the multi-GNSS combination methods can be divided into two modes. One is the DISB-float method to treat the DISB as a parameter to be estimated. Odijk and Teunissen (2013) have demonstrated that the DISB-float method cannot strengthen the positioning model when compared with the traditional double-difference (DD) RTK method, as represented by Teunissen et al. (2014), because the increasing redundancy is counterbalanced by the DISB parameter. When a priori DISB calibration value is available, the other method, denoted as the DISB-fixed method, was proposed to maximize the model redundancy and strengthen the positioning model. Gao et al. (2018), Julien et al. (2003), Li et al. (2017), and Odijk et al. (2017) have shown that the DISB-fixed method is of great significance for multi-GNSS positioning in challenging signal environments. The DISB-fixed method with overlapping frequencies has been widely used due to the absence of inter-frequency differential issue in Li et al. (2018), Odijk and Teunissen (2013), and Paziewski and Wielgosz (2014). Considering non-overlapping frequencies, referring to Kubo et al. (2018) and Lou et al. (2016), a differential inter-frequency bias (DIFB), which correlates with ambiguities, needs to be further corrected. Leick (1998), Li et al. (2017), and Wang (2000) have presented that the DIFB is a function of the inter-frequency difference and the pivot single-difference (SD) ambiguity. Therefore, the DIFB can be corrected by minimizing the inter-frequency difference and resolving the pivot SD ambiguity accurately. As for the minimization of inter-frequency difference, Tian et al. (2017) have presented all possible close-frequency sets with respect to currently available GNSS frequencies, e.g., GPS L1 and BDS B1 with an inter-frequency difference of 0.009 cycles, and GPS L1 and GLONASS L1 with an inter-frequency difference of 0.019 cycles. Li et al. (2017) utilized a triple-frequency combination technique to enrich the close-frequency sets by constructing virtual combination frequencies. Although the selected close-frequency set has minimal inter-frequency difference, the pivot SD ambiguity still needs to be resolved for the DIFB correction due to the presence of inter-frequency difference. Note that, with respect to overlapping frequencies, the pivot SD ambiguity resolution is not essential since its inter-frequency difference equals zero. Regarding the pivot SD ambiguity estimation, the traditional carrier-minus-code combination is utilized to approximately resolve the SD ambiguity by the integer rounding estimator, which can be found in Leick (1998) and Banville et al. (2018). However, due to the code multipath and the code–carrier inconsistency, Wang (2000) showed that the traditional SD ambiguity resolution method may result in a large SD ambiguity bias to undermine the DIFB correction. For instance, a code error of 5 m will result in a DIFB of above 0.2 cycles in the combination of the GPS L1 and BDS B1, which has an adverse impact on the ambiguity resolution. Gao et al. (2018) proposed a smoothing filter to reduce the effect of DIFB, but the irregular cycle slip issue will undermine the efficiency of the filter method in challenging signal environments. Therefore, Li et al. (2016) presented that a single-epoch/instantaneous ambiguity resolution method is a feasible solution to avoid this limitation because it is immune to the cycle slip issue.

A single-epoch SD ambiguity resolution is of crucial importance for the DIFB correction. Although the traditional carrier-minus-code combination method cannot accurately resolve the SD ambiguity due to the low precision of code observation, an SD ambiguity search space can be provided through this method. By applying the SD ambiguity search space, we will focus on developing a single-epoch SD ambiguity resolution method to correct the DIFB and subsequently improve the positioning performance of the DISB-fixed method with non-overlapping frequencies.

We describe the DISB-float and the DISB-fixed methods by using observations from multi-GNSS with non-overlapping frequencies. Then, by using the ambiguity search space, we propose a single-epoch SD ambiguity resolution method to correct the DIFB effectively. Finally, we present and analyze a real-time kinematic experiment in urban areas and summarize the research findings.

Methodology

In this section, the functional and stochastic models of the DISB-float and the DISB-fixed methods are described with focusing on the analysis of DISB and DIFB. Then, based on the ambiguity search space provided by the traditional carrier-minus-code combination method, an SD ambiguity resolution method is proposed to effectively correct the DIFB. The SD ambiguity resolution method can improve the ambiguity resolution and the positioning performance of the DISB-fixed method with non-overlapping frequencies.

Multi-GNSS combination functional models

We present the DISB-float and the DISB-fixed functional models based on single-frequency observations from GPS L1 and BDS B1. The base receiver and the rover receiver track GNSS satellites s* = 1*,…, m*, simultaneously, where m is the number of satellites. The symbol * denotes G for GPS and B for BDS. The between-receiver SD can eliminate satellite-dependent errors, and for short baselines, the atmospheric error can also be neglected. The SD observations can be expressed as

$$\begin{aligned} p^{{s_{*} }} & = \varvec{u}^{{s_{*} }} \cdot \varvec{x} + t + d^{*} + e^{s_{*}} \\ \phi^{{s_{*} }} & = \varvec{u}^{{s_{*} }} \cdot \varvec{x} + t + \delta^{*} + \lambda^{*} z^{{s_{*} }} + \varepsilon^{{s_{*} }} , \\ \end{aligned}$$
(1)

where \(p^{{s_{*} }}\) and \(\phi^{{s_{*} }}\) are the observed-minus-computed SD code and phase residual observations, respectively. \(\varvec{x}\) is a vector of incremental receiver positions, with its geometric vector \(\varvec{u}^{{s_{*} }}\), i.e., a normalized line-of-sight vector pointing from satellite s to the receiver. The three receiver-dependent terms involve receiver clock, receiver code, and phase bias, denoted as \(t\), \(d^{*}\), and \(\delta^{*}\), respectively. The wavelength and the ambiguity are denoted as \(\lambda^{*}\) and \(z^{{s_{*} }}\), respectively. The noises of code and phase observations are denoted as \(e^{{s_{*} }}\) and \(\varepsilon^{{s_{*} }}\), respectively. The \(z^{{s_{*} }}\) is expressed in cycles, and the remaining terms are all in meters. Note that an integer part of the receiver phase bias has been absorbed by the ambiguity so that \(\delta^{*}\) value is less than a wavelength.

It can be found that the positioning model (1) is rank-defective. One of the solutions for the rank-defective issue is the S-transformation proposed by Teunissen (1985). When the DISB is parametrized as an unknown, we can form a full-rank DISB-float model, shown as

$$\begin{aligned} p^{{s_{*} }} & = \varvec{u}^{{s_{*} }} \cdot \varvec{x} + \tilde{t}_{p} + d^{G*} + e^{{s_{*} }} \\ \phi^{{s_{*} }} & = \varvec{u}^{{s_{*} }} \cdot \varvec{x} + \tilde{t}_{\phi } + \tilde{\delta }^{G*} + \lambda^{*} z^{{1_{*} s_{*} }} + \varepsilon^{{s_{*} }} , \\ \end{aligned}$$
(2)

where GPS parameters are selected as the S-basis. The receiver code bias of GPS is assimilated into the reparametrized code receiver clock as \(\tilde{t}_{p} = t + d^{G}\). The code DISB parameter is formed as \(d^{G*} = d^{*} - d^{G}\). The phase receiver clock is rearranged by absorbing the receiver phase bias and the pivot SD ambiguity from GPS as \(\tilde{t}_{\phi } = t + \delta^{G} + \lambda^{G} z^{{1_{G} }}\). To ensure the integer nature of ambiguity, we also arrange the phase DISB parameter as \(\tilde{\delta }^{G*} = \delta^{*} - \delta^{G} + \lambda^{*} z^{{1_{G} 1_{*} }} + \left( {\lambda^{*} - \lambda^{G} } \right)z^{{1_{G} }}\). The corresponding ambiguity is reformed as \(z^{{1_{*} s_{*} }} = z^{{s_{*} }} - z^{{1_{*} }}\).

Håkansson et al. (2017) and Odijk and Teunissen (2013) have demonstrated that the DISBs can be calibrated based on their temporal stability. If the code and the phase DISB calibration values can be obtained, we can form a full-rank DISB-fixed model as

$$\begin{aligned} p^{{s_{*} }} - \bar{d}^{G*} & = \varvec{u}^{{s_{*} }} \cdot \varvec{x} + \tilde{t}_{p} + e^{{s_{*} }} \\ \phi^{{s_{*} }} - \bar{\delta }^{G*} & = \varvec{u}^{{s_{*} }} \cdot \varvec{x} + \tilde{t}_{\phi } + \lambda^{ *} \left( {z^{{1_{G} s_{*} }} + \frac{{\left( {\lambda^{*} - \lambda^{G} } \right)}}{{\lambda^{ *} }}z^{{1_{G} }} } \right) + \varepsilon^{{s_{*} }} , \\ \end{aligned}$$
(3)

where the code and the phase DISB calibration values are defined as \(\bar{d}^{G*} = d^{*} - d^{G}\) and \(\bar{\delta }^{G*} = \delta^{*} - \delta^{G}\), respectively. The term \(\frac{{\left( {\lambda^{*} - \lambda^{G} } \right)}}{{\lambda^{*} }}z^{{1_{G} }}\), i.e., the DIFB, is assimilated into the ambiguity and becomes a biased ambiguity parameter \(z^{{\text{b},1_{G} s_{*} }} = z^{{1_{G} s_{*} }} + \delta_{\text{DIFB}}\). If the frequencies from multi-GNSS are overlapping, e.g., GPS L1 and Galileo E1, the DIFB will be absent since the constant coefficient \(\frac{{\left( {\lambda^{*} - \lambda^{G} } \right)}}{{\lambda^{*} }}\) equals zero. However, for non-overlapping frequencies, the constant coefficient is not equal to zero, e.g., the constant coefficient corresponding to the BDS B1 and GPS L1 combination equals 0.009. Therefore, it is necessary to resolve the pivot SD ambiguity for the DIFB correction. Leick (1998) proposed a carrier-minus-code combination method to approximately resolve \(z^{{1_{G} }}\) as

$$\hat{z}^{{1_{G} }} = \left[ {\frac{1}{{\lambda^{G} }}\left( {\phi^{{1_{G} }} - p^{{1_{G} }} } \right)} \right]_{\text{round}} ,$$
(4)

where \(\left[ * \right]_{\text{round}}\) represents the integer rounding estimator. Due to the low precision of code observation, the SD ambiguity bias \(\Delta z^{{1_{G} }} = z^{{1_{G} }} - \hat{z}^{{1_{G} }}\) may be very large, especially in challenging signal environments. For instance, if the code error is 5 m, the SD ambiguity bias is larger than 25 cycles, which result in the DIFB of above 0.2 cycles. To accurately resolve \(z^{{1_{G} }}\), we have proposed a single-epoch SD ambiguity resolution method based on an ambiguity search space as presented in the following section.

Multi-GNSS combination stochastic models

The variance–covariance (VC) matrix for the SD code and phase observations from a single-system model is given as

$$\varvec{Q}_{yy}^{ * } = \varvec{C}^{ * } \otimes \varvec{R}_{{m_{ * } }} ,$$
(5)

where a priori standard deviations (STDs) for the SD code and phase observations are given \(C^{ * } = {\text{diag}} \left( {2\sigma_{p}^{2},\, 2\sigma_{\phi }^{2} } \right)\), in which “diag” denotes a diagonal matrix. We assume no cross-correlation between code and phase observations, otherwise the non-diagonal elements of \(C^{ * }\) will be occupied by considering the physical correlation between observations, which is demonstrated in Wang et al. (2002) and Schön and Brunner (2008). ⊗ denotes the Kronecker product of two matrices. \(\varvec{R}_{{m_{ * } }}\) is derived from the elevation-dependent weighting function. The VC matrix corresponding for the GPS L1 and BDS B1 combination model reads \(\varvec{Q}_{yy} = {\text{blk\, diag}}\left( {\varvec{Q}_{yy}^{G} ,\;\varvec{Q}_{yy}^{B} } \right)\), in which “blkdiag” denotes a block-diagonal matrix.

There are two differences between the DISB-float and the DISB-fixed models as shown by (2) and (3), respectively. One is observation redundancy. Table 1 gives the number of observations, the number of parameters, the observation redundancy, and the solvability condition, in which the solvability condition is the minimum number of required satellites to solve the positioning model. As seen from the table, since the increased observations are counterbalanced by the increased parameters, the DISB-float model cannot strengthen the positioning model when compared with the traditional DD model. When the code and phase DISBs are calibrated based on their temporal stability, the DISB-fixed model can obtain more observation redundancy and less solvability condition than the other models so that the DISB-fixed model is of great significance for improving the positioning performance in challenging signal environments. The other difference is the DIFB issue. As seen from the DISB-float model (2), the DIFB is absorbed by the phase DISB parameter to avoid affecting the integer nature of ambiguity. However, when the DISB is calibrated instead of estimated, it is necessary to correct the DIFB for the DISB-fixed model since the DIFB is absorbed by the ambiguity, as presented in (3).

Table 1 Redundancy and solvability conditions of single-frequency GPS and BDS combination model
Full size table

DIFB correction

The pivot SD ambiguity resolution is crucial for the DIFB correction. We proposed an SD ambiguity resolution method to resolve the pivot SD ambiguity accurately. Based on the DISB-float and the DISB-fixed multi-GNSS models in (2) and (3), a simplified model is given as

$$\varvec{E}\left[ \varvec{y} \right] = \left[ {\begin{array}{*{20}l} \varvec{H} \hfill & \varvec{G} \hfill \\ \end{array} } \right] \cdot \left[ {\begin{array}{*{20}c} \varvec{x} \\ \varvec{c} \\ \end{array} } \right] +\varvec{\varLambda}\cdot \varvec{z} = \varvec{B} \cdot \varvec{b} +\varvec{\varLambda}\cdot \varvec{z}\quad \varvec{D}\left[ y \right] = \varvec{Q}_{yy} ,$$
(6)

where E[*] and D[*] represent the expectation and the dispersion operators, respectively. y is a vector of SD code and phase observations in (2) or (3). The baseline vector is denoted as x, which is associated with the geometrical matrix H. c denotes receiver clocks; for the DISB-float model, the code and phase DISB parameters are also included, with design matrix G. z is the ambiguity vector and Λ is the wavelength matrix. For the DISB-fixed model, z is biased due to the presence of the DIFB. B denotes \(\left[ {\begin{array}{*{20}c} \varvec{H} & \varvec{G} \\ \end{array} } \right]\) and b denotes \(\left[ {\begin{array}{*{20}l} {\varvec{x}^{T} } \hfill & {\varvec{c}^{T} } \hfill \\ \end{array} } \right]^{T}\). We utilize the weighted least squares method to resolve the float baseline and ambiguity parameters based on (6):

$$\left[ {\begin{array}{*{20}c} {\hat{\varvec{b}}} \\ {\hat{\varvec{z}}} \\ \end{array} } \right] \sim {\rm N}\left\{ {\begin{array}{*{20}c} {\left[ {\begin{array}{*{20}c} \varvec{b} \\ {\varvec{z}\text{ + }\delta_{\text{DIFB}} } \\ \end{array} } \right]} & {,\left[ {\begin{array}{*{20}c} {\varvec{Q}_{{\varvec{\hat{b}\hat{b}}}} } & {\varvec{Q}_{{\varvec{\hat{b}\hat{z}}}} } \\ {\varvec{Q}_{{\varvec{\hat{z}\hat{b}}}} } & {\varvec{Q}_{{\varvec{\hat{z}\hat{z}}}} } \\ \end{array} } \right]} \\ \end{array} } \right\}$$
(7)

with the corresponding VC matrix

$$\left[ {\begin{array}{*{20}c} {\varvec{Q}_{{{\hat{\varvec{b}}\hat{b}}}} } & {\varvec{Q}_{{{\hat{\varvec{b}}\hat{z}}}} } \\ {\varvec{Q}_{{{\hat{\varvec{z}}\hat{\varvec{b}}}}} } & {\varvec{Q}_{{{\hat{\varvec{z}}\hat{\varvec{z}}}}} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\varvec{B}^{T} \varvec{Q}_{yy}^{ - 1} \varvec{B}} & {\varvec{B}^{T} \varvec{Q}_{yy}^{ - 1}\varvec{\varLambda}} \\ {\varvec{\varLambda}^{T} \varvec{Q}_{yy}^{ - 1} \varvec{B}} & {\varvec{\varLambda}^{T} \varvec{Q}_{yy}^{ - 1}\varvec{\varLambda}} \\ \end{array} } \right]^{ - 1} .$$
(8)

Since Teunissen (2010) has presented that the integer least squares (ILS) ambiguity estimator has the highest success rate among different integer estimators, the ILS ambiguity estimator is used as

$${\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varvec{z}} } = \mathop {\arg \,\hbox{min} }\limits_{{\varvec{z} \in {\mathbb{Z}}^{q} }} \left\| {\hat{\varvec{z}} - \varvec{z}} \right\|_{{\varvec{Q}_{{{\hat{\varvec{z}}\hat{\varvec{z}}}}} }} ,$$
(9)

where \({\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varvec{z}} } \in {\mathbb{Z}}^{q}\) denotes the fixed ambiguity vector. Due to the presence of DIFB, the float ambiguity vector \(\hat{\varvec{z}}\) is biased. Based on the carrier-minus-code combination method (4), an ambiguity search space can be provided as \(z_{{}}^{{1_{G} }} \in \left[ {z_{0} - N,\;z_{0} + N} \right]\; \cap \;{\mathbb{Z}}\), where the central ambiguity \(z_{0}\) is resolved by (4), \(N\) is an ambiguity search bound associated with the code accuracy level, and \({\mathbb{Z}}\) represents integer set. Due to the finiteness of the ambiguity search space, we can traverse the ambiguity search space to search the correct SD ambiguity value. It can be observed that the closer the SD ambiguity is to the correct one, the smaller the DIFB effect will be, which results in the quadratic form in (9) gradually approaching a minimum. When the correct SD ambiguity is found, the quadratic form should be minimal. Based on this, by traversing the ambiguity search space, a series of DIFB corrections \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\delta }_{\text{DIFB}}\) are used and the ILS ambiguity estimator (9) can be rearranged as

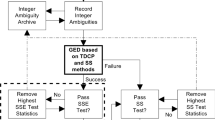
$$\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{z}^{{1_{G} }} ,{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varvec{z}} }} \right) = \mathop {\arg \,\hbox{min} }\limits_{{\mathop {z \in {\mathbb{Z}}^{q} }\limits_{{z^{{1_{G} }} \in \,\left[ {z_{0} - N,z_{0} + N} \right] \cap {\mathbb{Z}}}} }} \left\| {\hat{\varvec{z}} - \hat{\delta }_{\text{DIFB}} - \varvec{z}} \right\|_{{Q_{{\hat{z}\hat{z}}} }} ,\;\hat{\delta }_{\text{DIFB}} = \frac{{\left( {\lambda^{*} - \lambda^{G} } \right)}}{{\lambda^{*} }}z^{{1_{G} }} ,$$
(10)

where \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{z}^{{1_{G} }}\) is the correct SD ambiguity. To clarify the procedure of this method, the procedure is shown in Fig. 1, where Δz is an ambiguity search interval. In practice, the selection of Δz is dependent on the trade-off between the required success rate and computational issue. Meanwhile, referring to Li et al. (2017), Δz should be less than \(\left| {\frac{{0.1 \cdot \lambda^{*} }}{{\left( {\lambda^{*} - \lambda^{G} } \right)}}} \right|\), otherwise the search procedure will end in failure. When the correct SD ambiguity is obtained, the DISB-fixed model with non-overlapping frequencies will become unbiased by correcting the DIFB. In addition, referring to Teunissen (2010), the popular R-ratio test with a detection threshold of 3 is used to determine whether to accept the fixed results or not.

Fig. 1
figure 1

Procedure of SD ambiguity resolution for obtaining the DIFB correction

Full size image

When compared with the DISB-float method, the DISB-fixed method can bring increased redundancy to strengthen the multi-GNSS RTK model. Although the DISB-fixed method with overlapping frequencies has been widely used, the DIFB must be further corrected for the DISB-fixed method in case of non-overlapping frequencies. The proposed method provides a single-epoch SD ambiguity resolution method to accurately resolve the pivot SD ambiguity based on an ambiguity search space so that the DIFB can be effectively corrected. As a result, it can provide a better ambiguity resolution and positioning accuracy performance.

Experiment and analysis

A kinematic experiment with a duration of 110 min is carried out in the urban area of Yantai City, Shandong Province, China. The rover receiver is installed on a car. The location of the base station, the kinematic trajectory, and the velocity of the rover receiver are shown in Fig. 2. The maximum baseline distance during the kinematic experiment is 8.5 km, and the maximum velocity is greater than 40 km/h. The raw data are collected with a sampling interval of 1 s. The sky plot, the number of visible GPS and BDS satellites, and the corresponding PDOP values with a cutoff satellite elevation of 10ο are shown in Fig. 3. In addition, an elevation-dependent weighting model is applied, in which the STDs of observations are calculated by a function of the elevation angle θ as σ(θ) = σ0(1 + 1/sinθ), where σ0 is 30 cm for code and 3 mm for phase, respectively. Since a short-baseline dataset is used, the ionospheric error is disregarded. Due to the height difference between the base and the rover station, the hydrostatic part of the tropospheric error is compensated by the Saastamoinen model proposed by Saastamoinen (1973). The LAMBDA algorithm is used in our experiment to fix the ambiguity. Furthermore, the popular R-ratio test validation method with a detection threshold of 3 is applied for the ambiguity validation. The GPS and BDS dual-frequency post-processing results are used as reference solutions for the evaluation of ambiguity resolution and positioning performance.

Fig. 2
figure 2

Location of the base station, kinematic trajectory, and velocity [m/s] of the rover receiver

Full size image
Fig. 3
figure 3

PDOP values with a cutoff satellite elevation of 10°, January 04, 2017, and sky plot and number of the visible GPS and BDS satellites

Full size image

The epoch-wise code and phase DISBs are estimated by the DISB-float method (2). The corresponding results are shown in Fig. 4. As shown in the figure, the DISBs are very stable over the experimental duration, and the STDs of code and phase DISBs are less than 0.5 m and 0.04 cycles, respectively. Therefore, the DISBs can be calibrated based on their high temporal stability. For practical kinematic positioning environments, the rapid and precise DISB calibration is of significance for the applications of DISB-fixed method. In addition, Wang and Gao (2007) have confirmed that phase DISB will change when the receiver is restarted, which further demonstrates the importance of rapidly and precisely determining the DISB calibration values. Herein, the accuracy of the DISB calibration values associated with the short-period arcs of 10 s, 30 s, and 60 s is evaluated, respectively. The average values of short-period arcs are used to determine the DISB calibration values. The DISB calibration reference is averaged over all epochs. The DISB average values corresponding to different short-period arcs are shown in Fig. 5. It can be observed from the figure that the variation of code and phase DISBs around their calibration references is mostly restricted within 1.3 m and 0.07 cycles, respectively. When the duration of a short-period arc is increased, the variation becomes smaller. Therefore, the average values of short-period arcs are accurate enough to calibrate the DISB. In the next experiment, the code and phase DISB average values of 30 s are used as their calibration values for the DISB-fixed method.

Fig. 4
figure 4

Epoch-wise DISBs for code and phase, respectively. The cyan dotted line is the average values of the DISBs

Full size image
Fig. 5
figure 5

DISB average values of different short-period arcs for code and phase, respectively. The cyan dotted line is the average values of all epochs

Full size image

As seen from the DISB-fixed method (3), it is necessary to resolve the pivot SD ambiguity for the DIFB correction. The traditional DISB-fixed method uses the carrier-minus-code combination method (4) to obtain an approximate SD ambiguity, which is denoted as T-DISB-fixed method. The modified DISB-fixed method uses the proposed SD ambiguity resolution method (10), which is denoted as M-DSIB-fixed method. Regarding the M-DISB-fixed method, we assume that the code error is 10 m. Thus, the ambiguity search bound is set as N = 50. The ambiguity search space can be expressed as \(\left[ {z_{ 0} - 50,\;z_{ 0} + 50} \right] \cap {\mathbb{Z}}\), in which the central ambiguity \(z_{ 0}\) is obtained by the method (4). In addition, the ambiguity search interval Δz is set as 1 to achieve the highest success rate, without considering the computational issue. Based on the procedure of Fig. 1, the optimal SD ambiguity with minimum quadratic form is obtained by traversing the ambiguity search space.

Figure 6 shows the traversing results of two epochs from the pivot satellite G18 and G10, respectively. It can be found from the figure that the difference between the optimal SD ambiguity and the traditional ambiguity is larger than 10 cycles. As seen from the results of the pivot satellite G10, the quadratic form and the ratio value corresponding to the optimal ambiguity have a 3.5 reduction and 17.7 improvement, respectively, when compared with the traditional ambiguity. It can be demonstrated that using the optimal ambiguity can reduce the effect of DIFB on the ambiguity resolution more than the traditional ambiguity, which implies that using the optimal ambiguity is of great significance for improving the ambiguity resolution performance.

Fig. 6
figure 6

Traversing results of two epochs from the pivot satellite G18 and G10, respectively, in which Ω represents the quadratic form. Note that the x-axis denotes the difference between the traversed ambiguity and the traditional ambiguity

Full size image

Figure 7 presents the optimal ambiguities and the traditional ambiguities at all epochs, in which the optimal ambiguities will be used by M-DISB-fixed method, and the traditional ambiguities will be used by T-DISB-fixed method. Note that in our experiment the pivot GPS satellite is changed from G18 to G10 at the instant 50 min. As shown in the figure, the variation of traditional ambiguities is larger than 30 cycles, but the variation of optimal ambiguities is effectively restricted within 6 cycles, which indicates that the proposed SD ambiguity resolution method (10) can obtain more accurate SD ambiguity than the traditional method (4).

Fig. 7
figure 7

Optimal and traditional SD ambiguities at all epochs, in which the optimal ambiguity will be used by the M-DISB-fixed method and the traditional ambiguity will be used by the T-DISB-fixed method

Full size image

The left panel of Fig. 8 shows a comparison of ratio values for different methods, and the right panel gives the percentage of ratio values larger than the threshold values. Note that the ratio value is the ratio between the second-best ambiguity quadratic form and the best ambiguity quadratic form. Therefore, the larger the ratio value, the higher the reliability of ambiguity solution, which is demonstrated in Han et al. (2017). As shown in the figure, in case of the same threshold value, the M-DISB-fixed method has the largest percentage of the ratio values larger than the threshold values, while the DISB-float method is the second largest, and the T-DISB-fixed method is the smallest. The results demonstrate that although the DISB calibration can strengthen the DISB-fixed model, the inaccurate DIFB correction will undermine its ambiguity resolution performance, which reflects the necessity of the DIFB correction for the DISB-fixed method in case of non-overlapping frequencies.

Fig. 8
figure 8

Ratio values comparisons between different methods. The cyan dotted line denotes the detection threshold of 3

Full size image

The ambiguity dilution of precision (ADOP) and the success probability of ambiguity bootstrapping for different methods are shown in Fig. 9, in which the ADOP and the bootstrapped probability are as given in Teunissen (1998). As shown in the figure, when compared with the DISB-float method, the ADOP is reduced and the bootstrapped probability is increased by using the DISB-fixed method. This is because the DISB-fixed method benefits from the DISB calibration to strengthen the positioning models. It can be found from the figure that the two DISB-fixed methods have the same ADOP and the bootstrapped probability because the two DISB-fixed methods have the same functional and stochastic models.

Fig. 9
figure 9

ADOP and bootstrapped probability value comparisons between different methods

Full size image

The positioning errors of the three different methods are shown in Fig. 10. It should be noted that values are given for those epochs that pass the R-ratio test validation. The quantitative statistics of ambiguity resolution and positioning are shown in Table 2, in which fixing rate Pfix is defined as the ratio between the number of ambiguity-fixed epochs and the number of total epochs. Success rate Ps denoted the ratio between the number of correct ambiguity-fixed epochs and the number of ambiguity-fixed epochs. The root mean squares (RMSs) of the horizontal and the vertical positioning errors are also given in the table. In addition, due to the constraints of the solvability condition and the ambiguity R-ratio test validation, some epochs cannot provide the fixed position results, which results in the positioning discontinuity. Therefore, the maximum discontinuity interval between two consecutive fixed epochs is shown to reflect the positioning continuity of different methods. As shown in the table, the fixing rate Pfix of the T-DISB-fixed method is 3% smaller than the DISB-float method. Although increased redundancy strengthens the positioning model by the DISB calibration, the inaccurate DIFB correction prevents the DISB-fixed method from improving the ambiguity resolution performance. The M-DISB-fixed method shows the best fixing rate when compared with the other methods, showing an 8% and 6% improvement for the T-DISB-fixed method and the DISB-float method, respectively. This demonstrates that combining the DIFB correction and the DISB calibration together can achieve a better ambiguity resolution performance. Because the detection threshold of 3 is relatively stringent, the success rates of the three methods are similar and close to 100%. By comparing the positioning accuracy, the T-DISB-fixed method has slightly large errors due to the inaccuracy of the DIFB correction, which has also reflected the necessity of the DIFB correction. In addition, it can be observed from the statistics of the maximum discontinuity interval in the table that the maximum discontinuity interval between two consecutive fixed epochs was reduced from 25 s to 15 s when using the M-DISB-fixed method instead of the DISB-float method, which reflects that increasing the model redundancy resulting from the DISB calibration and the accurate DIFB correction is of great significance for improving the positioning continuity.

Fig. 10
figure 10

Positioning errors of different methods. The panels from the top and bottom represent the DISB-float, the T-DISB-fixed, and the M-DISB-fixed methods

Full size image
Table 2 Ambiguity resolution and positioning performance comparisons between different methods
Full size table

Conclusions

The DIFB correction is a challenge for the traditional DISB-fixed method with non-overlapping frequencies, especially in challenging signal environments. This is because the pivot SD ambiguity cannot be resolved accurately. Thus, an improved SD ambiguity resolution is proposed based on the ILS ambiguity estimator, by using an ambiguity search space provided by the traditional carrier-minus-code combination method. The effectiveness of the proposed method has been tested and compared with both the traditional DISB-fixed method and the DISB-float method in the urban areas. The kinematic experiment test demonstrated that, although the traditional DISB-fixed method provided more redundancy than the DISB-float method, its performance of positioning and ambiguity resolution is worse than the DISB-float method, which indicated the necessity of the DIFB correction. The proposed method can provide the best performance, using the improved SD ambiguity resolution method to effectively correct the DIFB. In addition, the results of positioning continuity indicated that the proposed DISB-fixed method is more suitable in challenging signal environments when compared with the DISB-float method and the traditional DISB-fixed method. Future work includes the evaluation of other multi-GNSS combinations and the consideration of atmospheric errors for medium- or long-baseline applications.