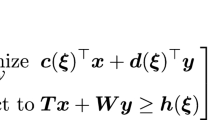Decomposition for adjustable robust linear optimization subject to uncertainty polytope

Abstract

We present in this paper a general decomposition framework to solve exactly adjustable robust linear optimization problems subject to polytope uncertainty. Our approach is based on replacing the polytope by the set of its extreme points and generating the extreme points on the fly within row generation or column-and-row generation algorithms. The novelty of our approach lies in formulating the separation problem as a feasibility problem instead of a max–min problem as done in recent works. Applying the Farkas lemma, we can reformulate the separation problem as a bilinear program, which is then linearized to obtained a mixed-integer linear programming formulation. We compare the two algorithms on a robust telecommunications network design under demand uncertainty and budgeted uncertainty polytope. Our results show that the relative performance of the algorithms depend on whether the budget is integer or fractional.

1 Introduction

Robust optimization is now a well-developed paradigm to tackle optimization problems under uncertainty. The framework has experienced its revival in the late nineties independently by Ben-Tal and Nemirovski (1998), El Ghaoui et al. (1998), Kouvelis and Yu (1997), and has witnessed an increasing attention in the past twenty years. Its essence lies in the use of convex sets to model uncertainty that can arise when solving optimization problems. In the robust counterpart of an optimization problem, the constraints involving uncertain parameters must be feasible for all values of the uncertain parameters in the convex sets. In particular, the optimization variables are fixed independently of the values taken by the uncertain parameters; it is not possible to adjust them after the uncertainty is known. When the problem constraints are linear, this approach leads to tractable optimization problems. For instance, the robust counterparts of linear constraints subject to polyhedral uncertainty are still linear constraints.

The framework can fail to model design problems that involve actions that are delayed in time, such as network design problems or facility location problems, among many others. In each of these optimization problem, we must take part of the decisions today, e.g. implantation of new links or building facilities. Then, when the new links or facilities are operational, we must choose how to use them optimally to provide a service to the customers. In these problems, the demand of the customers is usually not known with precision until the links or the facilities are constructed.

Adjustable robust optimization has been introduced by Ben-Tal et al. (2004) to improve over static robust optimization by allowing a subset of variables to account for the uncertainty. Namely, the framework partitions the optimization variables into two sets: part of them must fix their values before the uncertainty is revealed while the rest of them can adjust themselves according to the values taken by the uncertain parameters. These variables become functions defined on the uncertainty set. Ben-Tal et al. (2004) prove that adjustable robust optimization is untractable in general, so that they focus on approximations that restrict the adjustable variables to affine functions of the uncertainty, yielding the so-called affine decision rules. The main advantage of affine decision rules is their tractability, since they lead to robust optimization problems with the structure of classical robust counterparts. The properties of affine decision rules have been studied in subsequent papers: Bertsimas et al. (2011b) and Iancu et al. (2013) study conditions in which affine decision rules are optimal, while Bertsimas and Goyal (2012) study the suboptimality of affine decision rules from a worst-case perspective. Authors have also studied more complex decision rules that offer more flexibility than affine decision rules while providing tractable optimization problems. Among others, Chen et al. (2008) introduce deflected linear and segregated linear decision rules, Chen and Zhang (2009) propose to define affine decision rules on extended descriptions of the uncertainty set, Goh and Sim (2010) introduce complex piece-wise linear decision rules defined through liftings and projections, and Bertsimas and Georghiou (2015) propose piece-wise affine decision rules having fixed number of affine pieces. Alternatively, Bertsimas and Caramanis (2010) dynamically partition the uncertainty set and use constant decision rules in each set of the partition. The performance guarantee of the latter scheme is studied theoretically by Bertsimas et al. (2011a). This idea has been revived recently by Bertsimas and Dunning (2014) and Postek and Den Hertog (2014) who extend it to multi-stage linear mixed-integer linear programs and test it numerically on different problems.

To assess numerically the quality of the aforementioned approximations, one needs to compute the (exact) optimal solutions, at least on small instances. Hence, in contrast with approximations approaches, some authors have tried to solve exactly the adjustable problems. Indeed, when the robust constraints are linear and the uncertainty set is a polytope, we know that the latter can be replaced by the finite set of its extreme points. This reformulation as such is not very useful because the number of extreme points is usually prohibitive. However, recent works have proposed decomposition algorithms that generate the extreme points on the fly. The first work in that line of research was carried out by Bienstock and Özbay (2008) who propose cutting plane algorithms (denoted RG in the following) for computing optimal base-stock levels in a supply chain. Similar approaches have been used subsequently by Mattia (2013) who study a network design problem with integer link capacities under demand uncertainty, by Gabrel et al. (2014) who study a facility location problem under demand uncertainty, and by Bertsimas et al. (2013) who study a unit commitment problem under nodal injection uncertainty. In these four papers, the uncertainty is limited to the right-hand side of the constraints and problem specific algorithms are proposed. Zeng and Zhao (2013) improved over the previous papers by proposing a row-and-column generation algorithm (denoted RCG in the following) and comparing the latter numerically to RG. Their results show that RCG can be up to three order of magnitudes faster than RG. The idea behind RCG has also been combined with RG heuristically by Bertsimas et al. (2013). More general problems (based on algorithm RG) have also been considered by Billionnet et al. (2014).

This papers contributes to this line of research, proposing an alternative approach to solve exactly two-stage robust linear programs with continuous second stage variables. We implement cutting plane algorithms and row-and-column generation algorithms very close to those proposed by Zeng and Zhao (2013), with the difference that we consider the separation problem as a feasibility problem instead of a min-max problem as done by Zeng and Zhao (2013). Using the Farkas’ lemma, we can reformulate the feasibility problem into a bilinear program. Whenever the uncertainty set can be obtained as a mapping projection of a 0–1 polytope of reasonable dimension, which is the case for the budgeted uncertainty polytope from Bertsimas and Sim (2004), the bilinear program can be linearized to obtain a mixed-integer linear program. We assess our algorithms on a difficult telecommunication network design problem that has previously been studied in the literature by Poss and Raack (2013), comparing our results with the affine decision rules.

2 Problem overview

We consider in this paper the following type of two-stage robust optimization problems:

(1)

$$\begin{aligned} \begin{array}{llllllllll} (P)\quad&\,&\,&T(\xi )x + W y(\xi ) \ge h,&\quad&\xi \in \Xi \end{array} \end{aligned}$$

(2)

where $u\cdot v$ denotes the scalar product between any pair of vectors u and v, $c\in \mathbb {R}^{{\vert I\vert }}$, $W\in \mathbb {R}^{{\vert M\vert }\times {\vert J\vert }}$, $h\in \mathbb {R}^{{\vert M\vert }}$, $\mathcal {S}\subset \mathbb {R}^{{\vert I\vert }}$ denotes the first-stage feasibility polyhedron, $\Xi \subset \mathbb {R}^{{\vert K\vert }}$ denotes the uncertainty polytope, $T(\xi )\in \mathbb {R}^{{\vert M\vert }\times {\vert I\vert }}$ denotes the realization of the uncertain first-stage coefficient matrix, and $y(\xi )$ denotes the second-stage decision vector. We follow a classical assumption from the robust optimization literature and suppose that T depends affinely on uncertain parameter $\xi$. Hence, there exists matrices $T^0$ and $T^{1k}$ with the same dimensions as T such that

$$\begin{aligned} T(\xi ):=T^0+\sum _kT^{1k} \xi ^k. \end{aligned}$$

One readily sees that $(P)$ encompasses more general problems where (i) h depends affinely on $\xi$ and (ii) second stage variables y have fixed costs given by vector k. Similarly, the approaches presented in this paper can be applied (with minor modifications) to problems where set $\mathcal {S}$ is the intersection of $\mathbb {Z}^{{\vert I_1\vert }}\times \mathbb {R}^{{\vert I_2\vert }}$ and a polyhedron.

When $\Xi$ is not a singleton, problem $(P)$  is a linear program that contains an infinite number of variables, since y is defined for each $\xi \in \Xi$, as well as an infinite number of constraints (2). The ideas presented in this paper rely on considering only the extreme points of $\Xi$, which is formalized in the result below (whose proof can be found in Ben-Tal and Nemirovski 2002, among others).

Lemma 1

Let ${{\mathrm{vert}}}(\Xi )$ be the set of extreme points of $\Xi$ and $x\in \mathbb {R}^{\vert I\vert }$ a given vector. Vector x can be extended to an optimal solution (x, y) to $(P)$  if and only if it can be extended to an optimal solution $(x,y')$ to

(3)

We provide next an example showing that Lemma 1 may not hold if the recourse matrix W depends on the uncertainty parameters $\xi$, which implies that our approach cannot handle problems with random recourse. Consider a unique robust constraint defined by $W(\xi )=-1+2\xi$, $T(\xi )=-2+3\xi$, $h=0$, and $\Xi =[0,1]$, and consider $x^*=1$. The constraint becomes:

$$\begin{aligned} \xi =0&\quad \Rightarrow \quad -2-y(0)\ge 0\end{aligned}$$

(4)

$$\begin{aligned} \xi =0.5&\quad \Rightarrow \quad -0.5\ge 0\end{aligned}$$

(5)

$$\begin{aligned} \xi =1&\quad \Rightarrow \quad 1+y(1)\ge 0. \end{aligned}$$

(6)

Constraints (4) and (6) are feasible while constraint (5) is infeasible. Hence, $x^*$ is feasible for the constraints induced by each $\xi \in {{\mathrm{vert}}}([0,1])$ but infeasible for $\xi =0.5$, providing a counter-example to Lemma 1 when W is an affine function of $\xi$.

Let $\mathcal {K}$ denote the projection of the set defined by (3) on variables x. Set $\mathcal {K}$ is a polyhedron. Hence, if a vector x does not belong to $\mathcal {K}$, there exists a separating hyperplane between x and $\mathcal {K}$. We study in the following section how to find such a hyperplane and how to use it to solve $(P')$.

3 Solution approach

We propose in this section an algorithmic framework to solve $(P')$  by generating scenarios in ${{\mathrm{vert}}}(\Xi )$ on the fly. First, we provide in Sect. 3.1 a mathematical program for the following separation problem: does x belong to $\mathcal {K}$? Then, assuming that the separation problem can be solved adequately, we describe in Sect. 3.2 two algorithms for addressing $(P')$.

3.1 Separation

A naive approach to the separation problem would enumerate all elements of ${{\mathrm{vert}}}(\Xi )$. This is not suitable for practical problems since $\Xi$ is likely to have a very large number of extreme points. We propose instead to address the problem by solving a mathematical program. The next result is based on Farka’s lemma.

Theorem 1

Let $x^*\in \mathbb {R}^n$ be given. Vector $x^*$ belongs to $\mathcal {K}$ if and only if the optimal solution of the following optimization problem is non-positive

(7)

Before proving the Theorem, we introduce without proof a well-known property of bilinear optimization.

Lemma 2

Let $\mathcal {P}$ be a polytope, $\mathcal {Q}$ a closed and bounded set, and f(p, q) a bilinear function. It holds that

$$\begin{aligned} \{\max f(p,q) \text{ s.t. } p\in \mathcal {P}, q\in \mathcal {Q}\}= \{\max f(p,q) \text{ s.t. } p\in {{\mathrm{vert}}}(\mathcal {P}), q\in \mathcal {Q}\}. \end{aligned}$$

Proof (Proof of Theorem 1)

Consider a given vector $x^*\in \mathbb {R}^n$. Because $x^*$ is fixed, constraints (3) become separable for each $\xi \in {{\mathrm{vert}}}(\Xi )$. Hence, for each $\xi \in {{\mathrm{vert}}}(\Xi )$, vector $y(\xi )$ must satisfy

$$\begin{aligned} Wy(\xi ) \ge h-T(\xi )x^*. \end{aligned}$$

(8)

Let $\pi (\xi )$ be the dual multipliers associated to constraints (8). Using Farkas’ Lemma, we know that constraints (8) have a solution if and only if

$$\begin{aligned} (h-T(\xi )x^*)\cdot \pi (\xi ) \le 0 \end{aligned}$$

for all $\pi (\xi )$ that satisfy

$$\begin{aligned}&W^T\pi (\xi ) = 0 \end{aligned}$$

(9)

$$\begin{aligned}&\pi (\xi )\ge 0. \end{aligned}$$

(10)

Notice that the coefficients of constraints (9) and (10) do not depend on $\xi$. Hence, considering Farkas’ conditions for all $\xi \in {{\mathrm{vert}}}(\Xi )$ simultaneously, we obtain that constraints (8) for each $\xi \in {{\mathrm{vert}}}(\Xi )$ are consistent if and only if the optimal solution of

$$\begin{aligned}&\max \quad (h-T(\xi )x^*)\cdot \pi \end{aligned}$$

(11)

$$\begin{aligned} \text{ s.t. }\quad&\xi \in {{\mathrm{vert}}}(\Xi ) \\&W^T\pi =0 \nonumber \\&\pi \ge 0\nonumber \end{aligned}$$

(12)

is non-positive. Adding normalization constraint

$$\begin{aligned} \mathbf {1}\cdot \pi = 1 \end{aligned}$$

to the problem above does not impact the sign of its optimal solution. Finally, we can replace (12) by $\xi \in \Xi$ because objective (11) is bilinear in $\xi$ and $\pi$ and the constraints of $\xi$ and $\pi$ are independent from each other, so that Lemma 2 holds. $\square$

The objective function of $(SP)$  is bilinear so that $(SP)$  belongs to a class of problems NP-hard to solve exactly (Matsui 1996). Unreported results show that algorithms based on spatial branching (Ryoo and Sahinidis 2003) are unable to cope with $(SP)$  even for small instances. Hence, we propose to address $(SP)$  through mixed-integer linear reformulations, see Sect. 4.

3.2 Algorithms

We propose in this section two solution algorithms for $(P')$, denoted by $RG$  and $RCG$,  assuming that we can solve $(SP)$  through a black-box method. The algorithms are both based on generating dynamically a subset $\hat{\Xi }\subset {{\mathrm{vert}}}(\Xi )$. Both algorithms start by solving the following master problem

Given an optimal solution to $(MP)$, the algorithms solve the separation problem $(SP)$, yielding an optimal solution $(\xi ^*,\pi ^*)$. The two algorithms differ then by the way they include more information to $(MP)$ when the solution cost of $(SP)$  is positive. Algorithm $RG$  is a classical Benders’ decomposition approach that adds a violated Benders’ cut to the master problem

$$\begin{aligned} (h-T(\xi ^*)x)\cdot \pi ^* \le 0. \end{aligned}$$

(13)

The drawback of $RG$is that a single cut is added to the master problem at each iteration, facing the risk that many iterations may be required before obtaining a feasible solution for $(P')$. To incorporate more information to the master problem at each iteration, Algorithm $RCG$adds to $(MP)$  all constraints and variables associated to $\xi ^*$

$$\begin{aligned} T(\xi ^*)x + W y(\xi ^*) \ge h. \end{aligned}$$

(14)

For completeness, both algorithms are described formally in Algorithm 1.

Fig. 1

Example of affine mapping such that $\Omega =a(\Xi )$ and $\Omega$ is a 0–1 polytope. a $\Xi$. b $\Omega =a(\Xi )$

4 Mixed-integer programming reformulations

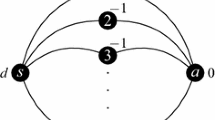
In this section, we propose two mixed-integer linear reformulations for $(SP)$. Recall that a polytope $\Omega$ is called a 0–1 polytope if each of its extreme points is a binary vector. Our first mixed-integer linear formulation for $(SP)$  is based on reformulating $\Xi$ as the affine mapping of a 0–1 polytope $\Omega \subset \mathbb {R}^{{\vert K'\vert }}$ of reasonable dimension ${\vert K'\vert }$. Notice that such a mapping always exists since we can represent $\Xi$ as the set of all convex combinations of the vectors in ${{\mathrm{vert}}}(\Xi )$. This example is useless, however, because the associated polytope $\Omega$ would be the unit simplex of dimension ${\vert {{\mathrm{vert}}}(\Xi )\vert }$. A more useful example of pair of polytopes $\Xi$ and $\Omega$ is given in Fig. 1.

Theorem 2

Let $x^*\in \mathbb {R}^{{\vert I\vert }}$ be given and suppose that we know a 0–1 polytope $\Omega \subset \mathbb {R}^{{\vert K'\vert }}$ and an affine mapping $a(\omega )= A\omega + b$ such that $\Xi =a(\Omega )$. Vector $x^*$ belongs to $\mathcal {K}$ if and only if the optimal solution of the following optimization problem is non-positive

$$\begin{aligned} \max \quad&(h-\tilde{T}^{0}_{}x^*)\cdot \pi -\sum _{k\in K}(\tilde{T}^{1k}_{}x^*)\cdot v^{k}\nonumber \\ (SPL)\quad \text{ s.t. }\quad&\omega \in \Omega \nonumber \\&W^T\pi =0\nonumber \\&\mathbf {1}\cdot \pi = 1\nonumber \\&v_{m}^k \ge \pi _m -(1-\omega ^k) \qquad k\in K', m\in M \end{aligned}$$

(15)

$$\begin{aligned}&v_{m}^k \le \omega ^k \qquad k\in K', m\in M \\&\pi ,v_{m}^k\ge 0, \nonumber \\&\omega \in \{0,1\}^{{\vert K'\vert }}\nonumber \end{aligned}$$

(16)

where $\tilde{T}^{1k}=\sum \nolimits _{h\in K}T^{1h}A_{hk}$  for each $k \in K$ and $\tilde{T}^0=T^0+\sum \nolimits _{k\in K}T^{1k}\sum \nolimits _{h\in K}A_{kh}b^k$.

Proof

The proof consists of two steps. First, we take $(SP)$  and make the change of variable $\xi =a(\omega )$:

$$\begin{aligned} \max \quad&(h-\tilde{T}(\omega )x^*)\cdot \pi \end{aligned}$$

(17)

$$\begin{aligned} \text{ s.t. }\quad&\omega \in \Omega \\&W^T\pi =0 \nonumber \\&\mathbf {1}\cdot \pi = 1\nonumber \\&\pi \ge 0\nonumber . \end{aligned}$$

(18)

Then, using Lemma 2, we replace constraint (17) by $\omega \in {{\mathrm{vert}}}(\Omega )$. Because $\Omega$ is a 0–1 polytope, we can add binary restrictions $\omega \in \{0,1\}^{{\vert K'\vert }}$ to the problem. Hence, each product $\omega ^k\pi _m$ involved in objective function (17) can be reformulated by introducing auxiliary variables $v_{m}^k$ and using big-M coefficients. Finally, the big-M coefficients can be set to 1, because $0\le \pi _m\le 1$, which yields constraints (15) and (16). $\square$

An interesting example of non-bijective affine mapping arises with the budgeted uncertainty set introduced in Bertsimas and Sim (2004):

$$\begin{aligned} \Xi ^\Gamma \equiv \left\{ \xi \in [0,1]^{\vert K\vert } \text{ s.t. } \sum _{k\in K}\xi ^k\le \Gamma \right\} . \end{aligned}$$

Polytope $\Xi ^\Gamma$ is a $0-1$ polytope only when $\Gamma$ is integer. Nevertheless, $\Xi ^\Gamma$ for fractional values of $\Gamma$ can be obtained as the affine transformation of the following polytope

$$\begin{aligned} \Omega ^\Gamma \equiv \left\{ (\omega ^1,\omega ^2){\in }[0,1]^{2{\vert K\vert }} \text{ s.t. } \omega ^{1k}+\omega ^{2k} \le 1, k{\in } K, \sum _{k\in K}\omega ^{1k}\le \lfloor \Gamma \rfloor , \sum _{k\in K}\omega ^{2k}\le 1 \right\} , \end{aligned}$$

using mapping $a(\omega )=\omega ^1+(\Gamma -\lfloor \Gamma \rfloor )\omega ^2$. One readily sees that $\Omega ^\Gamma$ is a 0–1 polytope.

A different approach has been used by Mattia (2013) for a specific network design problem. The result below generalizes the one of Mattia (2013) in two aspects: we do not assume that $\mathcal {S}$ has a specific form, and we allow the first-stage constraint matrix to depend on the uncertainties (while Mattia 2013 only considers right-hand-side uncertainty).

Theorem 3

Let $x^*\in \mathbb {R}^n$ be given and let $\Xi =\{\xi \in \mathbb {R}^{\vert K\vert } \text{ s.t. } B\xi \le b, \xi \ge 0\}$. Vector $x^*$ belongs to $\mathcal {K}$ if and only if the optimal solution of the following optimization problem is non-positive

Proof

Introducing notations $\tau ^0(x^*):=h^0-T^0x^*$ and $\tau ^{1k}(\pi , x^*):=(T^{1k}x^*)\cdot \pi$ for each $k\in K$, $(h-T(\xi )x^*)$ can be rewritten as

$$\begin{aligned} \tau ^0(x^*)\cdot \pi + \tau ^1(\pi , x^*)\cdot \xi , \end{aligned}$$

(19)

where only the second term of (19) depends on $\xi$. Hence, for any polyhedron $\Pi$, we have that

$$\begin{aligned} \max _{\pi \in \Pi , \xi \in \Xi } \tau ^0(x^*)\cdot \pi + \tau ^1(\pi , x^*)\cdot \xi = \max _{\pi \in \Pi }\left( \tau ^0(x^*)\cdot \pi + \max _{\xi \in \Xi }\tau ^1(\pi , x^*)\cdot \xi \right) \end{aligned}$$

so that we can rewrite $(SP)$ as a bilevel program sending $\xi$ to the follower’s decisions:

(20)

Recall that $\Xi$ is described by $\{\xi :B\xi \le b, \xi \ge 0\}$. Because $\Xi$ is bounded and non-empty, we know by linear programming duality that

$$\begin{aligned} \{\max \tau ^1(\pi , x^*)\cdot \xi : B\xi \le b, \xi \ge 0\} = \{\min b\cdot \gamma : B^T\gamma \ge \tau ^1(\pi , x^*), \gamma \ge 0\}. \end{aligned}$$

Then, replacing the follower’s problem by its dual and substituting the bilinear term $\tau ^1(\pi , x^*)\cdot \xi$ in the objective function (20) with the objective function of the dual, $b\cdot \gamma$, we obtain:

(21)

The result finally follows from applying the mixed-integer reformulation from (Audet et al. 1997, Corollary3.2) to the bilevel problem above. $\square$

Notice that in spite of its generality, the reformulation from Theorem 3 can be very hard to solve to optimality Mattia (2014). Hence, it should be combined with heuristic separation of violated extreme points as done by Mattia (2013) for a network loading problem.

5 Application to telecommunications network design

We illustrate in this section the performance of Algorithm 1 on an adjustable robust optimization problem previously studied in the literature.

5.1 Problem description

Telecommunications networks have evolved quickly, especially in the last two decades. This is due to the expansion of the Internet, on-line gaming, instant messaging, file sharing and plenty of other applications requiring fast and reliable communication technologies. This has resulted in increasing demands for higher bit-rates. Network operators are then under constant pressure to design high speed networks with larger capacities such as to satisfy the growing need for fast connections with no interruptions and latency. However, network operators also tend to design networks while minimizing capital costs and taking into account that resources are limited. Given a directed graph (V, A) and a set of point-to-point commodities K, network design can be defined as a planning process that involves setting up link capacities $x_a$ for each $a\in A$ and traffic routing $y^k_a$ for each $a\in A$ and $k\in K$ in order to route data packets for each commodity $k\in K$ from its source $s^k$ to its destination $t^k$. Its goal is to minimize the total capacity cost $\sum _{a\in A}c_a x_a$ while satisfying all traffic demands $d^k$ for $k\in K$.

Traditional models for network design ignored demand uncertainty and overestimated demand values to avoid blockages. This led to a waste in network capacities and investments. In order to obtain a more robust and efficient network, demand fluctuation has to be taken into consideration throughout the design procedure. As a result, the idea of demand uncertainty must be included in the mathematical program that models the planning process of the network.

Robust network design considers that the vector of demands d is uncertain and depends affinely on the uncertain parameters $\xi$ that can take any value in a predetermined uncertainty polytope. The problem becomes an adjustable robust optimization problem: capacities x are first-stage decision variables while routings y are second-stage decision variables. Let $\delta _v^+$ and $\delta _v^-$ be the sets of outgoing arcs and incoming arcs, respectively, for each $v\in V$. The mathematical program for the problem is given below.

$$\begin{aligned}&\min \quad&\sum _{a\in A}c_a x_a \end{aligned}$$

(22)

$$\begin{aligned} (RND)&\text{ s.t. }\quad&\sum _{a\in \delta ^-_v}y^k_a(\xi ) - \sum _{a\in \delta ^+_v}y^k_a(\xi ) = \left\{ \begin{array}{l} -d^k(\xi )\quad \text{ if } v=s^k\\ d^k(\xi )\quad \quad \text{ if } v=t^k\\ 0\qquad \quad \quad \text{ otherwise } \\ \end{array} \right. \quad v\in V, k\in K \end{aligned}$$

(23)

$$\begin{aligned}&\sum _{k\in K} y^k_a(\xi ) \le x_a \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad a\in A \\&x\ge 0, y\ge 0. \nonumber \end{aligned}$$

(24)

Objective function (22) minimizes the total capacity installation cost subject to flow balance constraints (23) and capacity constraints (24).

The above optimization problem has been studied previously by Poss and Raack (2013). Poss and Raack (2013) solves $(RND)$  by enumerating the extreme points of $\Xi$ using Lemma 1. This approach is of course restricted to uncertainty polytopes having limited number of extreme points and they address larger problems by applying affine decision rules to routing variables y:

$$\begin{aligned} y^k(\xi )=f^{0k}+\sum _{h\in K}f^{hk}\xi ^h, \quad k\in K. \end{aligned}$$

(25)

Other approximations of $(RND)$  have been considered in the literature, see Poss (2014) and the references therein. Among them, static routing which enforces $y^k$ to depend linearly on $\xi ^k$ by adding constraints

$$\begin{aligned} y^k(\xi )=f^k\xi ^k, \quad k\in K \end{aligned}$$

(26)

to $(RND)$, where f are non-negative optimization variables. It must be said that $(RND)$  with static or affine routing is much easier to solve than $(RND)$  because the problem can then be reformulated as a static robust optimization problem, which can be solved by dualizing the robust constraints.

In the next section, we apply the two versions of Algorithm 1 to the instances studied by Poss and Raack (2013).

5.2 Numerical results

We consider three realistic networks from SNDlib Orlowski et al. (2010): janos-us, sun, and giul-39. These networks have 26/27/39 nodes and 84/102/172 arcs, respectively. The networks are originally undirected and we direct them by replacing each edge by two arcs with opposite directions. To reduce the size of the formulations and to be able to do a series of runs, we considered the largest 20–50 commodities with respect to the mean value of $\overline{d}^k$. Our uncertainty set is based on the budgeted uncertainty polytope from Bertsimas and Sim (2004). Namely, $d^k(\xi )=\overline{d}^k+\xi ^k\hat{d}^k$ where the deviation $\hat{d}^k$ is set to $0.4\overline{d}^k$, and $\Xi \equiv \{\xi \in \mathbb {R}^{{\vert K\vert }} \text{ s.t. } \sum _{k\in K}\xi ^k\le \Gamma , 0\le \xi ^k\le 1 \text{ for } \text{ each } k\in K\}$. Polytope $\Xi$ is a 0–1 polytope so that we can reformulate the subproblem as $(SPL)$  from Theorem 2. Notice that our

Fig. 2

Performance profiles comparing the solution times of RG, RCG, and aff. a Integer values of $\Gamma$. b Fractional values of $\Gamma$

uncertainty set does not consider downward deviations. Hence, $\Xi$ corresponds to $\mathcal {D}_+^\sigma$ used in Poss and Raack (2013). We consider two sets of instances. In the first set, $\Gamma$ is integer and belongs to $\{1,2,\ldots ,6\}$. In the second set, $\Gamma$ is fractional and belongs to $\{1.5,2.5,\ldots ,5.5\}$. Our algorithms have been coded using the Concert Technology library for JAVA from CPLEX 12.6 IBM-ILOG (2015) on a 64-bit 2.53Ghz Quad-Core CPU with 6GB of memory and 16 threads. CPLEX is called with its default parameters and we have set a time limit of T seconds of CPU time for every individual run and our computing times are presented in seconds.

Figure 2 shows performance profiles Dolan and Moré (2002) that compare the solution times of algorithms RG and RCG as well as affine routing (denoted aff). Figure 2a reports the profile for $\Gamma \in \{1,2,\ldots ,6\}$ while Fig. 2b reports the profile for $\Gamma \in \{1.5,2.5,\ldots ,5.5\}$. Notice that the solution times of unsolved instances have been set to T seconds, so that the right part of the profiles should be considered as approximations of the true relative performance of the algorithms. Despite this, one can observe from the profiles that RG and RCG behave differently on the two sets of instances. Namely, when $\Gamma$ is integer, RCG clearly outperforms RG, and the performance of RCG is close to the one of affine routing. In contrast, when $\Gamma$ is fractional, RCG is outperformed by RG and both algorithms behave much worse than affine routing. This behavior can be explained by the following observations. First, the solution times of $(SPL)$ is usually higher when $\Gamma$ is fracional (see below). Second, algorithm RCG generates much more extreme points when $\Gamma$ is fractional. Hence, the time spent solving $(MP)$ increases, making it an important part of the total solution time. In contrast, the time spent solving $(MP)$ is insignificant for RG, which concentrates all of its effort on solving $(SPL)$.

Table 1 Results for $\Gamma$ integer

Table 2 Results for $\Gamma$ fractional

We present the extensive computational results on Tables 1 and 2. The columns of these tables report the number of commodities (K), the value of $\Gamma$, the optimal solution cost for static routing $(opt_{stat})$, the cost reduction $(gap_{aff})$ when using affine routing constraints (25) instead of static routing constraints (26), the cost reduction $(gap_{dyn})$ for the true optimal solution of $(RND)$, the time required by RCG ($t_{RCG}$) and RG ($t_{RG}$), the number of iterations of both algorithms (iter), and the time that they spent solving $(SPL)$ as a percentage of the total solution time ($t_{SPL}$ (%)). We also report the solution times spent to solve the problem with affine routing $(t_{aff})$ and to solve the problem that contains all extreme points $(t_{P'})$, although this last model very often consumes all memory available. Time and memory hits are denoted by T and M, respectively. Table 1 confirms the results summarized in Fig. 2a; that is, RCG is more efficient than RG on instances with integer values of $\Gamma$, solving the instances faster than the latter. In contrast Table 2 shows that RCG can solve only two instances with fractional values of $\Gamma$, while RG can solve roughly half of them. The tables also show that both algorithms spend most of their time in the solution of $(SPL)$  apart from RCG for the instances with high numbers of iterations. Figure 3 reports the arithmetic averages of the solution times for solving $(SPL)$  for each instance, which are based on the separations problems that were solved to optimality. Figure 3a, b show that for the instances janos-us and sun, the solution times of $(SPL)$  is much higher for fractional values of $\Gamma$ than for the integer ones. In contrast, Fig. 3b shows the opposite behavior for sun, particularly when $K=50$.

Fig. 3

Average solution times in seconds for $(SPL)$for each value of $K\in \{20,\ldots ,50\}$. Integer and fractional values of $\Gamma$ are reported in gray and black, respectively

6 Conclusion

We propose in this paper decomposition algorithms to solve adjustable robust linear programs under polytope uncertainty by generating the extreme points of the uncertainty polytope on the fly. We discuss algorithmic frameworks for decomposing the robust problem and solution algorithms to address the subproblem. Our numerical results show that the relative efficiency of row generation and row-and-column generation algorithms depends on the type of polytope considered. In any case, the bottleneck of these algorithms lies in finding the extreme point of the polytope that is mostly violated by the current solution, which amounts to solve a mixed-integer linear program (MIP).