1 Introduction

Scaffolds made of porous biomaterials can be implanted into the injured part of the human body to repair or replace the damaged tissue, such as bone defects. To this end, the scaffold must have porosity and mechanical properties similar to those of natural tissue (Chen 2019; Little et al. 2011). Due to differences in tissue type and implant location, it is required to have the ability to withstand different mechanical stresses and have appropriate fatigue life, while avoiding the occurrence of stress shielding (Dias et al. 2012; Han et al. 2018; Hollister 2005; Maskery et al. 2016; Melchels et al. 2010; Montazerian et al. 2017). Compared with polymer materials (Hallab et al. 2001), metal materials have greater advantages in strength, corrosion resistance and cell adhesion. However, the high stiffness of scaffolds will lead to a mismatch between the elastic properties of scaffolds and human tissue, resulting in mechanical loosening of the implant site (Hoyt et al. 2015). For example, the elastic modulus of titanium is 110 GPa, which is much higher than the elastic properties of human bones. TPMS units can be designed in different shapes and porosities by changing the parameters in the function expressions, which can achieve different mechanical properties and provide great convenience for the design of scaffold structures (Abueidda et al. 2016; Dalaq et al. 2016; Fantini et al. 2017; Garner et al. 2019; Liu and Wang 2015). For TPMS units, the low stiffness structures are greatly affected by the pore shapes (Montazerian et al. 2017). Also, TPMS porous structures can simulate the topological, mechanical and physical properties of bone trabeculae to a great extent (Bobbert et al. 2017).The TPMS structure has a higher elastic modulus and permeability under radial gradient pore distribution (Montazerian et al. 2019). However, previous studies have mostly considered the single mechanical properties of the structure and have not considered the mechanical properties of the scaffold structure in a complex mechanical environment. Due to the differences in the structures and design methods, it is difficult to unify these research results as the basis for comprehensively considering the various mechanical properties of the scaffold structure. Therefore, it is of great significance to systematically study and evaluate the various mechanical properties of the scaffold structure under a unified evaluation standard.

In terms of microscopic morphology, when the local curvature of the scaffold surface is larger than the range of cell size, the migration behavior of cells and local tissue formation will be affected by the curvature (Bidan et al. 2013; Park et al. 2009; Werner et al. 2016; Rumpler et al. 2008; Yin-Ping Lo et al. 2016). Scholars have carried out many researches on this topic. Through in vivo and in vitro experimental studies, Ripamonti and Graziano et al. found that, compared with the convex area, the concave area of ​​the scaffold structures will preferentially generate tissue, and the effect of tissue regeneration is better (Graziano et al. 2007; Ripamonti 2008). Rumpler et al. studied the growth process of bone tissue in vitro and found that the thickness of the tissue produced by osteoblasts depends on the local surface curvature of the scaffold structure (Rumpler et al. 2008), which indicates that the shape of tissue growth can be predicted by controlling the curvature. TPMS structures have the characteristics of hole interconnection and periodic surface curvature distribution, and each type of structure has a specific periodic surface curvature that can be tailored according to the target tissue needs. Maike Werner et al. selected eight different types of TPMS lattice structures with the same porosity but different curvatures. By studying the permeability properties, it was found that the curvature distribution would affect the shear stress generated by the fluid inside the TPMS structures and the uniformity of cell distribution (Blanquer et al. 2017). However, the effect of curvature on the mechanical properties of TPMS structures is still unclear. Importantly, external mechanical stimuli (such as local stress of the scaffold structure and shear stress generated by the fluid inside the scaffold) are important for promoting the proliferation and differentiation of tissue cells. It can be seen that it is necessary to study the relationship between the curvature and mechanical properties of the scaffold structures.

This paper presents our study on the influence of the spatial angle and surface curvature on the scaffold mechanical properties of the TPMS structures from the microscopic view, and the development of a novel model representative of the mechanical properties of TPMS scaffolds. The scaffolds were designed with varying structures of different spatial angles for given porosities. Using proportion transformation (geometric stretching and compression) and fusion transformation (multiple unit fusion) to change the curvature distribution of the structure surface, scaffolds were modified and designed with the same porosity but different curvatures. The effects of spatial angle and curvature on the static compression response, shear response and fatigue resistance of TPMS scaffold structures were investigated experimentally. The deformation and fracture mechanism of the scaffolds were analyzed through experiments and finite element simulation and compared with the literature data. Based on the entropy weight fuzzy comprehensive evaluation method, the mechanical performance evaluation model of the scaffold structure was developed, and the mechanical properties such as compression performance, shear performance and fatigue life of the scaffold structures under different curvatures were comprehensively evaluated.

2 Materials and methods

2.1 TPMS structures and modeling

TPMS structures can be generated by finding the \(\Psi = 0\) isosurface of TPMS equations (Cui et al. 2009; Maskery et al. 2016); primitive (P) and I-WP units are obtained by the following equation (Melchels et al. 2010):

$$ \begin{aligned} & \psi_{{\text{P}}} (x,y,z) = \cos \left( {k_{i} \cdot x} \right) + \cos \left( {k_{i} \cdot y} \right) + \cos \left( {k_{i} \cdot z} \right) + R_{{\text{P}}} = 0 \\ & \psi_{{\text{I - WP}}} (x,y,z) = 2 \cdot \left( {\cos \left( {k_{i} \cdot x} \right) \cdot \cos \left( {k_{i} \cdot y} \right) + \cos \left( {k_{i} \cdot y} \right) \cdot \cos \left( {k_{i} \cdot z} \right) + \cos \left( {k_{i} \cdot z} \right) \cdot \cos \left( {k_{i} \cdot x} \right)} \right) \\ \, & \quad \, - \cos \left( {k_{i} \cdot x} \right) + \cos \left( {k_{i} \cdot y} \right) + \cos \left( {k_{i} \cdot z} \right) + R_{{\text{I - WP}}} = 0 \\ \end{aligned} $$
(1)

where x, y, z are spatial coordinates; the isosurface \(\psi = 0\) is the boundary between solid and void material phases. \(R_{{\text{P}}} ,R_{{\text{I - WP}}}\) are the parameters that adjust the volume fraction. \(R_{{{\text{P\_I - WP}}}} ,R_{{{\text{P\_rot}}}} ,R_{{{\text{P\_scal}}}}\) in Eqs. (3) and (6) have the same meaning. For Eq. (1), \(k_{i}\) are the periodic functions of TPMS units, defined by

$$ k_{i} = 2\pi \frac{{n_{i} }}{{L_{i} }}\,\,\,\,(i = x,y,z) $$
(2)

where \(n_{i}\) are the numbers of TPMS lattices repetitions in the x, y and z directions, and \(L_{i}\) are the lengths of the lattices in those directions.

In order to obtain better-performing TPMS derivative structures, the P_IWP unit combining the structural characteristics of P and I-WP units is established, and the expression is as follows:

$$ \psi_{{{\text{P\_I - WP}}}} (x,y,z) = 0.1 \cdot \psi_{{\text{I - WP}}} (x,y,z) + 0.5 \cdot \psi_{{\text{P}}} (x,y,z) + R_{{{\text{P\_I - WP}}}} = 0 $$
(3)

Taking into account the sensitivity of the performance of TPMS structures to the change in coordinate parameters, the space rotation coordinate system and shape function are introduced, and the space rotation models of TPMS units around the x axis and the proportion transformation models along the z direction are established. The expression of the spatial rotation matrix is:

$$ \left[ {\begin{array}{*{20}c} {X_{{{\text{rot}}}} } \\ {Y_{{{\text{rot}}}} } \\ {Z_{{{\text{rot}}}} } \\ \end{array} } \right] = R_{x} \cdot \left[ {\begin{array}{*{20}c} x \\ y \\ z \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & {\cos (\theta )} & { - \sin (\theta )} \\ 0 & {\sin (\theta )} & {\cos (\theta )} \\ \end{array} } \right] \cdot \left[ {\begin{array}{*{20}c} x \\ y \\ z \\ \end{array} } \right] $$
(4)

where \(R_{x}\) is the spatial rotation matrix,\(\theta\) is the angle of rotation, and \(X_{{{\text{rot}}}} ,Y_{{{\text{rot}}}} ,Z_{{{\text{rot}}}}\) are the rotational coordinates. The expression of the proportional transformation matrix is:

$$ \left[ {\begin{array}{*{20}c} {X_{{{\text{scal}}}} } \\ {Y_{{{\text{scal}}}} } \\ {Z_{{{\text{scal}}}} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {N_{1} } \\ {N_{2} } \\ {N_{3} } \\ \end{array} } \right] \cdot \left[ {\begin{array}{*{20}c} x \\ y \\ z \\ \end{array} } \right] $$
(5)

where \(N_{1} ,N_{2} ,N_{3}\) are the scale factors and \(X_{{{\text{scal}}}} ,Y_{{{\text{scal}}}} ,Z_{{{\text{scal}}}}\) are the coordinates of the proportion transformation. Taking the P unit as an example, its spatial angle model and proportion transformation model are expressed as:

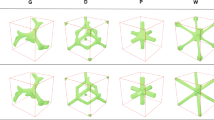
$$ \begin{aligned} & \psi_{{{\text{P\_rot}}}} (x,y,z) = \cos \left( {k_{i} \cdot X_{{{\text{rot}}}} } \right) + \cos \left( {k_{i} \cdot Y_{{{\text{rot}}}} } \right) + \cos \left( {k_{i} \cdot Z_{{{\text{rot}}}} } \right) + R_{{{\text{P\_rot}}}} = 0 \\ & \psi_{{{\text{P\_scal}}}} = \cos \left( {k_{i} \cdot X_{{{\text{scal}}}} } \right) + \cos \left( {k_{i} \cdot Y_{{{\text{scal}}}} } \right) + \cos \left( {k_{i} \cdot Z_{{{\text{scal}}}} } \right) + R_{{{\text{P\_scal}}}} = 0 \\ \end{aligned} $$
(6)

According to Eqs. (4), (5), (6), models of the P and I-WP units under different spatial angles (\(\theta = 0^{\circ } ,27^{\circ },45^{\circ }\)) and scale coefficients (\(N_{1} = N_{2} = 1,N_{3} = 2\) or \(N_{3} = 0.5\)) are established. The unit cell is cubic with a side length of 6 mm (if \(N_{3} = 2\), L = 3 mm; if \(N_{3} = 0.5\), L = 12 mm); each unit cell is repeatedly stacked in a three-dimensional space to form a 12-mm cubic scaffold. The structures studied in this paper are listed in Fig. 1.

Fig. 1
figure 1

Schematic diagram of TPMS structures under different structural transformation modes (porosities of spatial angle transformation structures, proportion transformation structures and fusion transformation structures are all 55%)

Full size image

2.2 Relative density

TPMS solid units can be obtained by defining two sides of the isosurface \(\Psi = 0\) as solid and void. The functional relationship between the volume fraction and the expression of TPMS units is calculated using triple integration (Yang et al. 2015, 2010):

$$ \begin{aligned} & \rho = \frac{{\int {\int {\int {_{\Omega } {\text{d}}v} } } }}{{(x_{\max } - x_{\min } ) \cdot (y_{\max } - y_{\min } ) \cdot (z_{\max } - z_{\min } )}} = 1 - p \\ & \Omega = \left\{ {(x,y,z)\left| {\psi (x,y,z) \le 0,x_{\min } \le x \le x_{\max } ,y_{\min } \le y \le y_{\max } ,} \right.z_{\min } \le z \le z_{\max } } \right\} \\ \end{aligned} $$
(7)

where ρ is the volume fraction and p is the porosity. The relationship between porosity and volume adjustment parameter R is shown in Fig. 2.

Fig. 2
figure 2

Relationship between volume adjustment parameter R (\(R_{{\text{P}}}\) or \(R_{{\text{I - WP}}}\),\(R_{{{\text{P\_I - WP}}}}\)) and porosity (p)

Full size image

2.3 Scaffold manufacturing

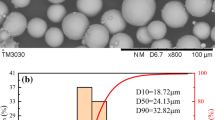
Three scaffold specimens of each model were fabricated using the SLM system (iSLM 280) equipped with a 500-W laser and a laser scanning speed of 1000 mm/s. AlSi10Mg powder with an average particle size of 15–53 μm and density of 1.45 g/cm3 is used as the printing material. The structures of the AlSi10Mg scaffolds are shown in Fig. 3.

Fig. 3
figure 3

TPMS structures made by SLM

Full size image

2.4 Surface curvature

The change of micro-curvature is of great significance to the performance of the structure. Gaussian curvature reflects the bending degree of the surface. Under the same mechanical environment, the bending degree of the surface is an important factor in determining the mechanical properties of structures. Therefore, exploring the relationship between the surface Gaussian curvature and mechanical properties is helpful for optimizing the scaffold structure. Figure 4 shows the Gaussian curvature on the geometric surface.

Fig. 4
figure 4

Displays curvature of a 1D line embedded in a 2D plane (a); mean (H) and Gaussian (Κ) surface curvatures as functions of the principal curvatures (b); some examples of intrinsically flat and intrinsically curved geometries (c)

Full size image

In this paper, the surface Gaussian curvature of TPMS units is obtained by the coordinate conversion method (Nan et al. 2010), and the local surface Gaussian curvatures of TPMS structures are shown in Fig. 5.

Fig. 5
figure 5

Contours of Gaussian curvature for different TPMS structures: a–c P units with different porosities; d–f I-WP units with different porosities; proportional transformation structures of P units with porosities of 55%: g Pte, h Pco; Proportional transformation structures of I-WP units with porosities of 55%: i I-WPte, j I-WPco; k P_I-WP structure with porosity of 55%

Full size image

2.5 Mechanical testing

The compression tests are performed with an SDS/M-20 tester with 25-KN load cell. Each test was performed under a displacement rate of 1 mm/min until mechanical failure. All samples were loaded in the same direction as the printing orientation. The elastic modulus is calculated from the slope of the first-line region of the stress–strain curve. The yield stress \((\sigma_{{\text{y}}} )\) is obtained by intersecting the stress–strain curve with a line parallel to the quasi-elastic gradient line with a strain offset of 0.2%. When the model is loaded and begins to deform, if the rate of strain is low enough, the heat loss caused by damping can be ignored. In this case, the energy loaded on the model is equal to the stored strain energy. This energy can be obtained by the following expression (Davis 2004):

$$ U_{{\text{total}}} \approx \left( {\frac{{\sigma_{\text{y}} + \sigma_{u} }}{2}} \right)\varepsilon_{f} $$
(8)

The modulus of resilience \(U_{{\text{resilience}}}\) can be expressed as follows (Davis 2004):

$$ U_{{\text{resilience}}} \approx \frac{{\sigma_{\text{y}}^{2} }}{2E} = \frac{1}{2}\varepsilon_{\text{y}} \sigma_{\text{y}} $$
(9)

The ratio of the modulus of resilience to the total energy is a standard to measure the relative toughness of the model (Davis 2004):

$$ U_{{{\text{relative}}}} \approx \frac{{U_{{{\text{resilience}}}} }}{{U_{{{\text{total}}}} }} $$
(10)

2.6 Morphology characterization

A scanning electron microscope (Gemini SEM-Germany) was used to study and observe the fracture surface morphology, and the deformation and failure mechanisms of different micro-curvature structures under compressive load were compared.

2.7 Finite element analysis

In order to simulate the deformation behavior and fatigue resistance of the TPMS structures under compressive load, finite element analysis (FEA) was performed. The material parameters of AlSi10Mg are shown in Table 1. The experimental test is reproduced by using similar boundary conditions. The boundary conditions of the FEA are shown in Fig. 6. The fatigue load is applied at a constant force ratio R = 0.1 (\(R = F_{\max } /F_{\min }\), where \(F_{\max }\) and \(F_{\min }\) are the maximum and minimum forces, respectively (Bobbert et al. 2017). The maximum force (\(F_{\max }\)) is determined based on the percentage of yield stress (\(\sigma_{{\text{y}}}\)). The fatigue life of the structure is regarded as infinite after 106 cycles.

Table 1 Material properties of AlSi10Mg
Full size table
Fig. 6
figure 6

Loading configuration considerations: a compressive load; b shear load

Full size image

2.8 Evaluation model of mechanical properties

2.8.1 Build factor set and evaluation set

In this study, the corresponding evaluation index system is determined according to the evaluation object, and then, the factor set and evaluation set are determined. The compression mechanical properties (\(U_{1}\)), shear mechanical properties (\(U_{2}\)) and fatigue resistance (\(U_{3}\)) are selected as the factor set to evaluate the mechanical properties of scaffolds. The evaluation results of the mechanical properties of scaffolds are divided into three levels, and the evaluation set is constructed as \(V = \left\{ {{\text{poor, }}\;{\text{medium, }}\;{\text{good}}} \right\}\).

2.8.2 Establish the fuzzy evaluation matrix and objective weights of evaluation indicators

Suppose the i-th factor Ui in the factor set U is judged, and the membership degree of the j-th element Vj in the evaluation set V is rij, then the judgment result of Ui can be expressed as a fuzzy set \(R_{i} = \left\{ {r_{i1} ,r_{i2} ,...,r_{in} } \right\}\). The membership degree of the evaluation set of each factor is formed into a fuzzy evaluation matrix R.

The entropy method is used to determine the weight of the evaluation index. The larger the value of entropy is, the smaller the indicator weight. In order to reflect the importance of each indicator, the corresponding weight \(w_{j}\) is assigned to each indicator, and the set \(W = \left\{ {w_{1} ,w_{2} ,...,w_{n} } \right\}\) is composed of each weight. Each weight \(w_{j}\) should meet the conditions of normalization and nonnegativity \(\sum\nolimits_{j = 1}^{n} {w_{j} = 1} ,w_{j} \ge 0\), which can be regarded as the degree of membership of each evaluation index \(U_{i}\) to the importance. Assuming that there are m objects and n evaluation parameters to be evaluated, the evaluation matrix of the evaluation model is (Wu et al. 2020):

$$ P^{\prime} = \left[ {\begin{array}{*{20}c} {p^{\prime}_{11} } & {p^{\prime}_{12} } & \cdots & {p^{\prime}_{1n} } \\ {p^{\prime}_{21} } & {p^{\prime}_{22} } & \cdots & {p^{\prime}_{2n} } \\ \vdots & \vdots & {} & \vdots \\ {p^{\prime}_{m1} } & {p^{\prime}_{m2} } & \cdots & {p^{\prime}_{mn} } \\ \end{array} } \right] $$
(11)
$$ p_{ij} = (\max p^{\prime}_{ij} - p^{\prime}_{ij} )/(\max p^{\prime}_{ij} - \min p^{\prime}_{ij} ) $$
(12)

where \(p_{ij}^{^{\prime}} (i = 1,2,...,m;j = 1,2,...,n)\) is the value of the j-th evaluation parameter for the i-th evaluation object. Use Eq. (12) to obtain the normalized evaluation matrix P. According to the basic principle of the entropy weight method, determining the entropy value \(H_{j}\) and entropy weight \(w_{j}\) of the j-th parameter, and the expression is (Wu et al. 2020):

$$ H_{j} = - \frac{1}{\ln m}\sum\limits_{i = 1}^{m} {\frac{{p_{ij} }}{{\sum\nolimits_{i = 1}^{m} {p_{ij} } }}\ln } \frac{{p_{ij} }}{{\sum\nolimits_{i = 1}^{m} {p_{ij} } }} $$
(13)
$$ w_{j} = \frac{{1 - H_{j} }}{{n - \sum\nolimits_{j = 1}^{n} {H_{j} } }} $$
(14)

In Eq. (13), \(0 \le H_{j} \le 1\), when \(p_{ij} /(\sum\nolimits_{i = 1}^{m} {p_{ij} } ) = 0\),\(\frac{{p_{ij} }}{{\sum\nolimits_{i = 1}^{m} {p_{ij} } }}\ln \frac{{p_{ij} }}{{\sum\nolimits_{i = 1}^{m} {p_{ij} } }} = 0\). In Eq. (14),\(0 \le w_{j} \le 1\), and \(\sum\nolimits_{j = 1}^{n} {w_{j} } = 1\).

2.8.3 Fuzzy comprehensive evaluation of the evaluation object

For the given evaluation matrix R, considering the importance of each factor, the fuzzy evaluation model is (Wu et al. 2020):

$$ B_{i} = W \circ R_{i} = [b_{i1} ,b_{i2} ,...,b_{ij} ] $$
(15)

where Bi is the comprehensive evaluation vector, W is the comprehensive weight matrix, and Ri is the membership of the i-th evaluation object relative to the j-th evaluation parameter.\(\circ\) represents fuzzy composition operator.

The operator \(M( \cdot , \oplus )\) can not only reflect the function of the weight, but also make full use of the information of the fuzzy evaluation matrix. This paper calculates the elements in the comprehensive evaluation vector according to this operator:

$$ b_{ij} = \sum\limits_{j = 1}^{n} {w_{j} r_{ij} } \quad (j = 1,2, \ldots ,n) $$
(16)

To facilitate analysis and comparison, it is necessary to normalize the comprehensive evaluation vector and then realize the grade evaluation of the evaluation object through the principle of maximum membership degree. The degree of good of the evaluation objects can also be evaluated according to their membership in the "good" grade based on the optimal evaluation principle.

3 Results

3.1 Mechanical behavior

After adjusting the spatial angle of TPMS structures, it can be seen from Fig. 7a that the elastic modulus of the P unit shows a decreasing trend with the increasing spatial angle. The higher the porosity is, the less the elastic modulus of the P unit is affected by the spatial angle. When the spatial angle \(\theta = 27^{\circ }\), the P units with different porosities all have the highest shear modulus. It can be seen from Fig. 7b that the variation of elastic modulus of the I-WP unit with spatial angle is the same as that of the P unit and is basically unaffected by the change of porosity. However, the shear modulus of the I-WP unit increases with the increasing spatial angle. Therefore, adjusting spatial angle can effectively improve the shear resistance of TPMS structures. It can be seen from Fig. 7c that when the porosity is the same, the elastic modulus and shear modulus of the stretched I-WP unit are significantly improved. The P unit also shows a higher elastic modulus value after stretching, but the shear modulus is lower than that of the original P structure. The mechanical properties of P and I-WP units after compression not only have not been significantly improved but have even become worse. Figure 7d shows that compared with P and I-WP units, the mechanical properties of the fusion model (P_I-WP) are significantly improved, its elastic modulus is 1.23 times that of the I-WP unit, and the shear modulus is 1.17 times that of the P unit. When \(\theta = 0^{\circ } ,p = 36\%\), the elastic modulus and yield strength of the P unit are higher than those of the I-WP unit. With the increase in porosity, the situation is opposite, which is consistent with the research results in the literature (Zhianmanesh et al. 2019).

Fig. 7
figure 7

The elastic modulus and shear modulus of TPMS lattice structures vary with the model coordinate parameters: primitive structures (a) and I-WP structures (b) under different porosities and spatial rotation angles; (c) comparison of mechanical properties between proportional transformation structures and original TPMS structures (d); comparison of mechanical properties between fusion structure and original TPMS structures

Full size image

3.2 Compressive fatigue behavior

In order to explore the influence of structural transformation methods on the fatigue life of TPMS structures, P and I-WP units after different transformations are selected to study their fatigue life. The magnitude of the applied force is determined according to the percentage of the yield stress to ensure that the load is in the elastic region of the structure (Yang et al. 2019b). The value of yield stress is shown in Table 2, ensuring that the porosity of each structure is 55%.

Table 2 Yield stress (MPa) of the TPMS lattice structures with a porosity of 55%
Full size table

In order to coordinate the differences in fatigue resistance between different structures, the fatigue performance of the TPMS units after the same structural transformation is grouped and compared. The applied load is determined according to the structure with the worst mechanical performance. The detailed grouping and load are shown in Table 3.

Table 3 Details of fatigue life analysis
Full size table

Figure 8 shows the minimum life of TPMS lattice structures. It can be seen from Fig. 8a that under the same stress, the minimum fatigue life of the tension models is the longest, while the compression models is the shortest. According to Fig. 8b, it can be seen that the spatial angle has a little effect on the fatigue life of the I-WP unit; when \(\theta = 45^{ \circ }\), the fatigue life of the P unit drops significantly. Figure 8c shows that compared with TPMS units, the fatigue life of the P_I-WP structure is significantly improved.

Fig. 8
figure 8

The minimum life of fatigue fracture of TPMS lattice structures: a TPMS structures before and after proportional transformation; b TPMS structures under different spatial rotation angles; c TPMS structures and fusion structure

Full size image

3.3 Influence of porosity and structure proportion on Gaussian curvature distribution

Microscopic curvature has a great influence on the local biomechanical properties of the structure, and mechanical stimulation can affect the proliferation of cells on the surface of scaffolds. Figure 9a, c, e shows the area proportion of the absolute value of the Gaussian curvature of TPMS structures. It can be seen from Fig. 9a, c that changing the porosity and structure proportion will have a certain impact on the curvature, but the absolute value of curvature corresponding to the peak value of area proportion is basically unchanged. However, it can be seen from Fig. 9e that the area proportion of Gaussian curvature of the fusion model changes greatly. Compared with P and I-WP units, the proportion of the area with a low absolute value is greatly increased. The area ratio of the Gaussian curvature illustrates the nonuniformity of the surface curvature distribution. Since the cell behavior is affected by the local curvature, the area proportion of curvature value is of great significance for the design of biomechanical friendly scaffolds.

Fig. 9
figure 9

Area proportion of the absolute value of Gaussian curvature |K| (a P structure under different structural parameters, c I-WP structure under different structural parameters, e P structure, I-WP structure and P_I-WP structure) and Gaussian curvature normal distribution (b, d, f) of different TPMS structures. (b, d, f the dense point clusters represent the centralized area of data distribution)

Full size image

The sign of the Gaussian curvature determines the type of local surface, which is already illustrated in Fig. 4. When the mechanical environment is the same, different local surfaces will produce different mechanical responses, resulting in different mechanical stimuli for cell growth. It can be seen from Figs. 9b and 5a, b, c, g, h that when the porosity is 36% and 74%, the negative curvature has a wide distribution range, and the median is higher and the mean value is lower, indicating that the gap between the positive and negative Gaussian curvatures is large, so a larger range of local spherical surfaces appears. The Gaussian curvature distribution range of the Pte structure is small and the value of curvature concentrates near zero, while the curvature of the Pco structure has a wide distribution range, and the negative Gaussian curvature has a large proportion. It can be seen from Figs. 9d and 5d, e, f, i, j that the Gaussian curvature distribution of the I-WP unit is similar to that of the P unit. When the porosity is 74%, the negative Gaussian curvature distribution range of the I-WP unit is the widest. After stretching, the Gaussian curvature distribution is the most concentrated. From Figs. 9f and 5(b)e, k, it can be seen that the curvature distribution of P_I-WP is wide and relatively scattered, but the upper quartile and median are high, so many local positive Gaussian curvature distribution areas appear in Fig. 5k.

3.4 Sample morphology and deformation under compression loading

Figure 10 shows the morphology comparison of the samples before and after compression. Figure 10a, b and e, f shows the morphological changes of the Pte and P_I-WP structures before and after compression. Although these two structures have no fracture failure, obvious compression folds appear and the direction is consistent with the curvature change trend of the structure surface. Figure 10c, d shows the fracture morphology of the Pco and I-WPte structures, respectively. It can be seen that some cleavage surfaces are distributed in the fracture, and there are obvious tearing edges and dimples, which are quasi-cleavage fractures.

Fig. 10
figure 10

SEM images of the compression samples: uncompressed model (a Pte, e P_I-WP); compression model (b Pte, c Pco, d I-WPte, f P_I-WP)

Full size image

The deformation and failure mechanism of the samples under axial compression are shown in Fig. 11. It can be seen from Fig. 11c, d that when the porosity is the same, the mechanical properties of the Pco structure and the I-WPte structure are relatively poor. Although the structural proportion has been changed, the P unit still has a global shear band at 45° to the loading direction. A similar shear band also appears in the I-WPte structure, which is different from previous conclusions (Li et al. 2021). This shows that changing structure proportion will affect the deformation mechanism of TPMS units, which may be due to the change in the local surface curvature. The curvature change causes the internal support topology to change, which changes the stress state and deformation mechanism of the structure. Comparing Fig. 11a, b, e, it is known that when the maximum load of the mechanical testing machine is reached, the P_I-WP structure has the smallest deformation, which indicates that the fusion structure not only has better elastic properties, but also has better resistance to plastic deformation.

Fig. 11
figure 11

Deformation and failure mechanism of samples with porosity of 55% under axial compression: a primitive structure; b Pte structure; c Pco structure; d I-WP structure; e P_I-WP structure

Full size image

4 Discussion

4.1 Dependence of mechanical behavior on coordinate parameters

In order to explore the sensitivity of the TPMS structures to coordinate parameters, models with different spatial angles and different curvature distributions are constructed, and the mechanical properties of these models under axial force and tangential force are analyzed. Table 4 shows that the elastic modulus of cancellous bone in various regions of the human body is generally 0.01–4.5 GPa. In this study, when the porosity is 74%, the elastic modulus of P and I-WP units obtained by changing the spatial angle is in the range of 2.31–6.5 GPa, which greatly overlaps the elastic modulus range of cancellous bone, which indicates that the elastic modulus of TPMS lattice structures under a specific size can be adjusted by the spatial angle on the premise of ensuring porosity, so as to effectively reduce the occurrence probability of stress shielding (Shimko et al. 2005). The important thing is that when the porosity is 55%, the I-WP unit is rotated from \(\theta = 0^{ \circ }\) to \(\theta = 45^{ \circ }\), the elastic modulus is reduced by 36%, while the yield strength is only reduced by 20.5%. This discovery provides a reference for us to establish scaffold models with high mechanical strength and low elastic modulus. The high mechanical strength provides sufficient support for the scaffold structure, while the low elastic modulus can effectively avoid stress shielding. When the porosity is 36%, by changing the space angle, the elastic modulus ranges of P and I-WP units are 22.7–35 GPa and 24.5–30.7 GPa, respectively, which are basically consistent with the elastic modulus of Tibia. The shear modulus ranges are 3.7GPa–7.1GPa and 6.2GPa–7.5GPa, respectively, including the shear modulus of compact bone in Table 4. This result provides a convenient method for us to adjust the scaffold structure according to the mechanical requirements.

Table 4 Mechanical properties of bones in different parts of the human body (Ali and Sen 2017; Olubamiji et al. 2016; Yang et al. 2019a)
Full size table

When the porosity is 55%, the elastic modulus and shear modulus of the Pco and I-WPco units both decrease, while the tension structures are the opposite. Among them, the elastic modulus and shear modulus of the Pte unit increased by 51% and 35%, respectively, compared with the P unit, while the elastic modulus and shear modulus of the I-WPte unit increased by 27.8% and 22.7%, respectively, compared with I-WP unit. The mechanical properties of the fusion structure are also significantly improved. Compared with the I-WP unit under the same porosity, elastic modulus and yield strength of the P_I-WP unit increased by 22.7% and 26.1%, respectively, and the shear modulus increased by 18.7%. The yield strength range of the model in this study is 65.8–146 MPa, which also has a large overlap with the yield strength in Table 4. The above analysis results show that it is very effective to design a scaffold structure that meets the requirements of different mechanical characteristics through the structure transformation method proposed in this paper.

4.2 Relationship between the curvature and the local mechanical properties

Mean curvature reflects the distribution of Gaussian curvature to a certain extent. By analyzing the relationship between the mean Gaussian curvature and the elastic modulus and shear modulus of the structure, the influence of curvature on the local mechanical response can be reflected. Taking P and I-WP units and their proportion transformation models as example, the porosities of these models are all 55%, the relationship between curvature and mechanical properties is explored in Fig. 12, which is fitted by a power function. It can be seen from Fig. 12a, b that the closer the average curvature is to 0, the better the mechanical properties are because the greater the proportion of the local surface is close to the cylindrical surface. Compared with spherical and hyperboloids, cylindrical surfaces have lower concentrated stress when subjected to external forces. Figure 12c shows that the mechanical properties of these three units have no obvious functional relationship with the mean value of curvature. When the porosity is the same, the surface curvature and mechanical properties of the same type of unit have a power function relationship.

Fig. 12
figure 12

Relationship between the mean Gaussian curvature of TPMS structures and elastic modulus and shear modulus: a primitive structures; b I-WP structures; c primitive structure, I-WP structure and fusion structure (P_I-WP)

Full size image

Figure 13 shows the relationship between the local surface curvature of the structure and the mechanical properties. The force states of the three different local surfaces depicted in Fig. 13a correspond to the three structures in Fig. 13b. When the same external load is applied and the curved surface is perpendicular to the load direction, the gentler the surface is, the greater the local stress and deformation are. Therefore, compared with the original structures, the performance of the compression structures is worse and the performance of the tension structures is better. This phenomenon can be explained by the force diagram in Fig. 13c; the resultant force F and the component force f have the following relationship:\(F = 2f\cos \theta\); when F is a fixed value, the larger the angle \(\theta\) is, the larger the component force f. Therefore, the gentler the curve of the force-bearing surface changes, the larger the local stress. The steeper the change is, the smaller the local stress is. When the force-bearing surface is parallel to the direction of the load, the gentler the force-bearing surface is, the better the mechanical properties, because it is equivalent to applying a load on the cylindrical surface, which does not easily produce stress concentration.

Fig. 13
figure 13

Relationship between the curvature of the structure and the stress and deformation during loading: a deformation and force state under different local surfaces; b surface curvature conditions under different structures; c force analysis on surfaces with different curvatures. Note a the length of the arrow represents the magnitude of the stress

Full size image

Figures 14 and 15 show the stress distribution contour and cross-sectional stress contour of the TPMS structures under axial force and tangential force; the porosity of all models is 55%. When an external force is applied, the P unit has a stress concentration near the necked part. There are two reasons for this phenomenon: one is that the local material density of the necked part is small, which is more prone to deformation and fracture; another reason is related to the local curvature of the structure at the necked part. Among these three different P structures, the curvature of the Pte structure near the necked part is closest to 0, which does not easily produce stress concentration areas, so the mechanical properties of the Pte structure are the best. The curvature of the Pco structure near the necked part is the smallest, and the local curved surface is a hyperboloid with large bending. Although the elastic modulus of the structure with more layers is larger (Maskery et al. 2018), the mechanical properties of the compression structure are still the worst, which shows that the local curvature has a greater influence on the mechanical properties of the P unit. For the I-WP unit, the compression resistance of the I-WPco structure is better than that of the I-WP structure, which may be caused by the large number of layers of the compression structure. This shows that the I-WP unit is more sensitive to the number of layers of the structure. When subjected to shear force, the hyperboloid surface under low curvature has a large degree of bending and has higher local stress when applying the force opposite to the surface bending radian direction (Buffiere et al. 2001; Mayer et al. 2003), which explains the poor shear resistance of the I-WPco structure. The local surface near the necking part of the I-WPte structure is close to the cylindrical surface, so the shear resistance of the tension structure is the best. Figure 9 shows that the Gaussian curvature distribution of Pco and I-WPco structures has become more dispersed, the negative Gaussian curvature has a large proportion, and the local curved surface is dominated by hyperboloids. The curvature distribution of the Pte and I-WPte structures is more concentrated in the range of 0 to − 0.3 and 0 to − 0.5, respectively, and the local curved surface is closer to a cylindrical surface. This result also reflects the overall state of force of the structure through the curvature distribution of the structure surface.

Fig. 14
figure 14

The stress distribution contour of TPMS structures at axial loading and the stress distribution contour of the X–Y section: a primitive structure; b Pte structure; c Pco structure; d I-WP structure; e I-WPte structure; f I-WPco structure; g P_I-WP structure

Full size image
Fig. 15
figure 15

The stress distribution contour of TPMS structures at tangential loading and the stress distribution contour of the Y–Z section: a’ primitive structure; b’ Pte structure; c’ Pco structure; d’ I-WP structure; e’ I-WPte structure; f’ I-WPco structure; g’ P_I-WP structure

Full size image

4.3 Influence of unit type and curvature on fatigue behavior

The fatigue mechanism of metal structures has been well studied, mainly focusing on aluminum and titanium alloys. The fatigue performance of the structure is affected not only by macroscopic factors such as loading stress amplitude, loading ratio, and macro-mechanical properties of the specimen (Li et al. 2012; Zhao et al. 2016), but also by the internal support topology of the structure. In order to analyze the influence of the transformation methods on the fatigue life of TPMS units, the stress loaded on the model is normalized, and the relationship between the normalized stress and fatigue life of different TPMS structures is shown in Fig. 16. It can be seen that the fatigue life of TPMS structures is basically greater than 106 at low stress levels. Under the same stress level, the fatigue resistance of the fusion model and the tension models are better than those of the original TPMS units, while the fatigue life of the compression models is reduced. This is because the proportion of the local hyperboloid of the compression structure increases, which leads to an increase in the number bending members. There are both tensile and compressive stresses in the struts. The bending rod has a higher local stress, which may significantly reduce the fatigue life of the scaffold structures (Buffiere et al. 2001; Mayer et al. 2003). The fatigue life of the P unit under high stress is longer than that of the I-WP unit under a low stress level. The fatigue resistance of the P unit is better than that of the I-WP unit, which is due to the large proportion of bending members in the I-WP unit and the high local maximum stress in the center of the inclined struts. This result is consistent with the conclusion of Zhao et al. (2016).

Fig. 16
figure 16

Relationship between the normalized stress and fatigue life of different TPMS structures with porosity of 55%. Note The Y-axis is a dimensionless normalized stress

Full size image

The local stress acting on the internal members of the structure varies with different unit types, which is mainly caused by topological effects (Smith et al. 2013; Yang et al. 2018). Taking into account the different stress distributions, the local maximum stress (von Mises stress) is used to analyze the fatigue life under cyclic damage. The finer stress distribution on the surface can not only delay the cyclic ratchet, but also effectively reduce the initiation and expansion of cracks, so that the structure can obtain higher axial compression performance and fatigue resistance (Yang et al. 2019b). From the axial stress contour shown in Fig. 14, it can be seen that for the same unit, the local maximum stress of the TPMS structure after tension decreases, while the compressed structures are the opposite. Through the above analysis and the results in Fig. 8, it can be seen that the conclusions of this article are consistent with the viewpoints put forward by Yang et al. (2019b). The above analysis can also be verified by the surface curvature. It can be seen from Fig. 9b, d, f that for both the P and I-WP units, when the porosity is the same, compared with the original structure, the negative curvature distribution range of the compression structure surface becomes wider, which shows that the proportion of the bent members of compression structures increases. It can also be inferred that the fatigue resistance of the compression structure is the worst, while the tension structures are the opposite. Interestingly, although the curvature distribution of the fusion unit is more dispersed, the fatigue resistance of the fusion unit is better than P unit, which shows that the relationship between the structure curvature and the fatigue performance is only applicable to the same type of unit.

4.4 Validation of finite element analysis results

The experimental results and finite element results are shown in Fig. 17. An image of the compression test is shown in Fig. 17a; the stress–strain curve of the compressed samples and the elastic modulus value obtained by the experiment and numerical simulation are shown in Fig. 17b, c, respectively. It can be seen from Fig. 17c that the experimental results are lower than the finite element results, which is caused by the manufacturing error of the samples. The mechanical properties of the samples are highly sensitive to the processing parameters (Montazerian et al. 2017). Figure 17b shows that within the maximum allowable load range, the stress–strain curve of the I-WPte structure fluctuates. This is due to the interlayer failure of the structure, which is consistent with the conclusion obtained from previous studies (Montazerian et al. 2017; Ning et al. 2018). The stress value of the Pco structure suddenly drops when the strain is approximately 0.11, which is due to the 45° shear fracture at the connection between layers, which is consistent with the deformation mechanism of the P unit dominated by bending deformation (Li et al. 2021). When the strain is approximately 0.13, the Pco structure reaches the dense zone, and the continuous compressive load at this time will cause the structure to be completely compacted. In the elastic region, the mechanical properties of the I-WPte structure and the P_I-WP structure are significantly higher than those of the P structure. This is consistent with the conclusion in Sect. 3.1, which proves that the simulation results in this paper are reliable.

Fig. 17
figure 17

Image of the compression test (a), compressive stress–strain curves of the experiment (b) and compression modulus for the experiment and FEA (c)

Full size image

Table 5 shows the energy absorption characteristics of the two samples with compression fracture during the experiment. It can be found that the energy absorbed by the Pco structure is higher than that absorbed by the I-WPte structure, which is due to the continuous absorption of energy after densification. However, the elastic storage energy of the I-WPte structure is higher than that of the Pco structure, which shows that the former has good mechanical properties in the elastic region, which is consistent with the simulation results.

Table 5 Energy absorption properties of TPMS structures
Full size table

4.5 Fuzzy evaluation of structural mechanics characteristics

In order to analyze the influence of surface curvature on the comprehensive mechanical properties of scaffolds, the P unit and its tension and compression structures, I-WP unit and its tension and compression structures, P and I-WP unit and their fusion structure are selected as three groups for mechanical performance evaluation, and the porosity is set to 55%. According to Eq. (12), the compressive elastic modulus, shear modulus and fatigue life of each group are normalized to obtain the normalized evaluation matrix. The mean entropy (Hj) and mean weight (wj) of the three evaluation indexes of compressive mechanical properties U1, shear mechanical properties U2 and fatigue resistance U3 are calculated according to Eqs. (13), (14) for further fuzzy evaluation. The mean values of entropy and weight are listed in Table 6.

Table 6 Entropy and weight of evaluation index
Full size table

We think that scaffold structures that perfectly match the mechanical properties required by the defect tissue have the best mechanical properties. According to the mechanical properties of implanted bone in the human body, the average compression elastic modulus of human cortical bone ranges from 15.4 to 35.3 GPa, the average shear modulus ranges from 0.05 to 9.87 GPa, and the specimen can be regarded as having unlimited fatigue life when the number of loading cycles before failure exceeds 106 cycles (Bobbert et al. 2017; Limmahakhun et al. 2017; Yang et al. 2019a). Therefore, when the mechanical properties of the scaffolds fall within the above range, we consider the mechanical properties of the scaffolds to be optimal”. Based on the above mechanical property range, we constructed that the membership functions of the compressive elastic modulus (GPa), shear modulus (GPa), and fatigue life (N) are established, and the expressions are as follows:

$$ {\text{bad}}:\mu (c) = \left\{ {\begin{array}{*{20}l} { \, 1 \, } \hfill & {(0,4]} \hfill & {} \hfill \\ {\frac{10 - c}{{10 - 4}}} \hfill & {(4,10)} \hfill & {} \hfill \\ 0 \hfill & {[10,\infty )} \hfill & {} \hfill \\ \end{array} } \right.{\text{medium}}:\mu (c) = \left\{ {\begin{array}{*{20}l} 0 \hfill & {(0,4]} \hfill & {} \hfill \\ {\frac{10 - c}{{10 - 4}}} \hfill & {(4,10)} \hfill & {} \hfill \\ 1 \hfill & {(c = 10)} \hfill & {} \hfill \\ {\frac{16 - c}{{16 - 10}}} \hfill & {(10,16)} \hfill & {} \hfill \\ 0 \hfill & {[16,\infty )} \hfill & {} \hfill \\ \end{array} } \right.{\text{good}}:\mu (c) = \left\{ {\begin{array}{*{20}l} 0 \hfill & {(c \le 10)} \hfill & {} \hfill \\ {\frac{c - 10}{{16 - 10}}} \hfill & {(10,16)} \hfill & {} \hfill \\ 1 \hfill & {[16,\infty )} \hfill & {} \hfill \\ \end{array} } \right. $$
(17)
$$ {\text{bad}}:\mu (c) = \left\{ {\begin{array}{*{20}l} { \, 1 \, } \hfill & {(0,0.75]} \hfill & {} \hfill \\ {\frac{1.5 - c}{{1.5 - 0.75}}} \hfill & {(0.75,1.5)} \hfill & {} \hfill \\ 0 \hfill & {[1.5,\infty )} \hfill & {} \hfill \\ \end{array} } \right.{\text{medium}}:\mu (c) = \left\{ {\begin{array}{*{20}l} 0 \hfill & {(0,0.75]} \hfill & {} \hfill \\ {\frac{c - 0.75}{{1.5 - 0.75}}} \hfill & {(0.75,1.5)} \hfill & {} \hfill \\ 1 \hfill & {(c = 1.5)} \hfill & {} \hfill \\ {\frac{2.25 - c}{{2.25 - 1.5}}} \hfill & {(1.5,2.25)} \hfill & {} \hfill \\ 0 \hfill & {[2.25,\infty )} \hfill & {} \hfill \\ \end{array} } \right.{\text{good}}:\mu (c) = \left\{ {\begin{array}{*{20}l} 0 \hfill & {(c \le 1.5)} \hfill & {} \hfill \\ {\frac{c - 1.5}{{2.25 - 1.5}}} \hfill & {(1.5,2.25)} \hfill & {} \hfill \\ 1 \hfill & {(2.25 \le c)} \hfill & {} \hfill \\ \end{array} } \right. $$
(18)
$$ {\text{bad}}:\mu (c) = \left\{ {\begin{array}{*{20}l} { \, 1 \, } \hfill & {(0,1{\text{e}}^{3} ]} \hfill & {} \hfill \\ {\frac{{5e^{4} - c}}{{5e^{4} - 1e^{3} }}} \hfill & {(1e^{3} ,5e^{4} )} \hfill & {} \hfill \\ 0 \hfill & {[5e^{4} ,\infty )} \hfill & {} \hfill \\ \end{array} } \right.{\text{medium}}:\mu (c) = \left\{ {\begin{array}{*{20}l} 0 \hfill & {(0,1e^{3} ]} \hfill & {} \hfill \\ {\frac{{c - 1e^{3} }}{{5e^{4} - 1e^{3} }}} \hfill & {(1e^{3} ,5e^{4} )} \hfill & {} \hfill \\ 1 \hfill & {(c = 5e^{4} )} \hfill & {} \hfill \\ {\frac{{1e^{6} - c}}{{1e^{6} - 5e^{4} }} \, } \hfill & {(5e^{4} ,1e^{6} )} \hfill & {} \hfill \\ 0 \hfill & {[1e^{6} ,\infty )} \hfill & {} \hfill \\ \end{array} } \right.{\text{good:}}\mu (c) = \left\{ {\begin{array}{*{20}l} 0 \hfill & {(c \le 5e^{4} )} \hfill & {} \hfill \\ {\frac{{c - 5e^{4} }}{{1e^{6} - 5e^{4} }}} \hfill & {(5e^{4} ,1e^{6} )} \hfill & {} \hfill \\ 1 \hfill & {[1e^{6} ,\infty )} \hfill & {} \hfill \\ \end{array} } \right. $$
(19)

Obtain the fuzzy evaluation matrix R of each unit according to Eqs. (17), (18) and (19), and obtain the fuzzy comprehensive evaluation matrix B of each group according to the operator \(M( \cdot , \oplus )\), as follows:

$$ \begin{gathered} {\text{Group 1:}}\;\; \, B_{{{\text{P55}}\% }} = \left[ {\begin{array}{*{20}c} 0 & {0.4196} & {0.5805} \\ \end{array} } \right], \, \quad \, B_{{{\text{Pco55}}\% }} = \left[ {\begin{array}{*{20}c} {0.1413} & {0.6477} & {0.2110} \\ \end{array} } \right]{, }\quad \, B_{{{\text{Pte55}}\% }} = \left[ {\begin{array}{*{20}c} 0 & {0.3632} & {0.6368} \\ \end{array} } \right] \hfill \\ {\text{Group 2:}}\;\; \, B_{{{\text{I - WP55}}\% }} = \left[ {\begin{array}{*{20}c} 0 & {0.0876} & {0.9124} \\ \end{array} } \right], \, \quad \, B_{{{\text{I - WPco55}}\% }} = \left[ {\begin{array}{*{20}c} 0 & {0.6636} & {0.3364} \\ \end{array} } \right], \, \quad \, B_{{{\text{I - WPte55}}\% }} = \left[ {\begin{array}{*{20}c} 0 & 0 & 1 \\ \end{array} } \right], \hfill \\ {\text{Group 3:}}\;\; \, B_{{{\text{P55}}\% }} = \left[ {\begin{array}{*{20}c} 0 & {0.0934} & {0.9066} \\ \end{array} } \right], \, \quad \, B_{{{\text{I - WP55}}\% }} = \left[ {\begin{array}{*{20}c} {0.1769} & {0.2894} & {0.5337} \\ \end{array} } \right], \, \quad \, B_{{{\text{P\_I - WP55}}\% }} = \left[ {\begin{array}{*{20}c} 0 & 0 & 1 \\ \end{array} } \right] \hfill \\ \end{gathered} $$

According to the principle of maximum membership degree, the performance of each group of structures is graded, and the results are shown in Table 7.

Table 7 Comprehensive performance evaluation level of each group
Full size table

According to the principle of optimal evaluation, the "good" grade membership of each group is compared, and it can be seen that: (a) in group 1 and group 2, the comprehensive performance of P and I-WP structures shows that the tension structures are the best and the compression structures are the worst; (b) in group 3, the order of comprehensive performance from good to poor is P_I-WP, P and I-WP. The above results show that improving the surface curvature distribution of the structure can effectively improve its comprehensive mechanical performance. The fusion structure can not only improve the performance of the structure but also expand the types of units, which provides more choices for the design of scaffolds.

The comprehensive mechanical performance evaluation model also provides an evaluation method for us to uniformly measure the performance of the scaffold structure. In a subsequent research, this evaluation model will consider the coupling effects of scaffold mechanics, fluid, porosity and other factors, so as to provide an effective means for preparing lightweight scaffold structures with excellent mechanical properties and good biocompatibility.

5 Conclusions

Mechanical properties are of importance to scaffolds applied in tissue engineering. This paper presents our study on the mechanical properties of scaffolds made from the P and I-WP units of the TPMS lattice structures by selective laser melting. Under the same porosity, the influence of the spatial angle and surface curvature on the static compression response, shear response and compression fatigue response of the scaffolds was studied and identified. The model representative of scaffold mechanical properties was developed based on the entropy weight fuzzy comprehensive evaluation method, and the mechanical properties and fatigue properties of TPMS units with different curvatures were analyzed and comprehensively evaluated. The main conclusions of this study are summarized as follows:

  1. 1.

    The surface curvature of the structure has a significant impact on the mechanical properties of scaffolds. For a given porosity, the structure with tensile transformation and fusion transformation has a higher elastic modulus, shear modulus and fatigue life. For a given type of unit, the more concentrated the surface Gaussian curvature is or the value of the curvature closer to zero, the stronger the mechanical properties and fatigue resistance of the structure are.

  2. 2.

    The spatial angle is a factor that effectively regulates mechanical properties of the scaffolds. Under compressive loading, the elastic modulus of both P and I-WP units decrease with the spatial angle. Furthermore, the porosity can significantly weaken the influence of the spatial angle on the elastic modulus of the P unit. Under shear loading, the shear modulus of the I-WP unit increases with the spatial angle, while the shear modulus of the P unit has its maximum value at the spatial angle θ = 27°. Under cyclic loading, the fatigue life of the P unit shows a downward trend with increasing spatial angle, while the fatigue life of the I-WP unit is barely affected by the spatial angle.

  3. 3.

    The results of the scaffold mechanical performance evaluation model show that for the same type of units at a given porosity, the tension structures have the best comprehensive mechanical performance, while the compression structures have the worst. In addition, the comprehensive mechanical properties of the P_I-WP structure are the best, followed by the P and I-WP units.