1 Introduction

Aortic dissection is typically characterized by an intramural tear of the aorta that communicates with the true lumen of the vessel and allows blood to enter and accumulate within the wall; such dissection can be a life-threatening event. Annual incidence rates of 3.5 to 15 per 100,000 persons have been reported in studies on different populations (Clouse et al. 2004; Howard et al. 2013; Landenhed et al. 2015). Determination of the exact incidence rate is difficult because aortic dissections can produce symptoms related to diseases of other organs, therefore giving aortic dissections the title “the great masquerader” (Elefteriades 2008). Dissection propensity varies tremendously along the aorta, being highest in the proximal thoracic region and lowest in the distal abdominal region. Dissection severity similarly varies by region, often requiring emergency surgery in the ascending thoracic aorta (Stanford Type A) but only medical surveillance in the descending thoracic aorta (Stanford Type B), which can be treated using an elective endovascular stent graft procedure (Evangelista et al. 2018). Regardless of type, it is widely accepted that intramural failure resulting in dissection occurs when wall stress exceeds wall strength (Wu et al. 2013; Tong et al. 2016). Nevertheless, there is a pressing need for a greater understanding of the mechanics underlying the differential presentation of dissection along the aorta.

Margot Roach and colleagues presented unique data in the 1980s–1990s that address the greater propensity of aortic dissection in the thoracic than in the abdominal region. Following earlier work (Robertson et al. 1948; Hirst et al. 1962), they inserted a fine needle into the wall of excised porcine aortas and injected measured volumes of India ink to visualize possible delamination of the wall. They found distinctly different behaviors in these two regions (Carson et al. 1990; Roach et al. 1994). In the thoracic aorta, the pressure–volume data for the injected ink revealed a rapid increase to a high pressure (525 mmHg, that is, 70 kPa) followed by a rapid monotonic decrease in pressure despite continued injection following the initial failure event; the response in the abdominal aorta showed more of a staircase increase in pressure starting at a lower value at initial failure with a subsequent series of mini-failures induced at successively higher pressures during continued volume injection. The authors suggested that the former arose because the lamellar elastic structure of the thoracic aorta includes only thin radially oriented connecting elastic fibers, whereas the latter arose because the lamellar elastic structure of the abdominal aorta includes copious radial interlamellar connections, similar to a honeycomb structure. They suggested further that although the abdominal segment can tear more easily, the tears in the thoracic segment can propagate more readily.

In this paper, we examine computationally the different failure characteristics of the thoracic and abdominal aorta reported by Roach and colleagues. We employ a phase-field finite-element model and compare predicted responses for an assumed homogenized aortic wall (nonlinear and anisotropic) versus a wall having a histologically motivated microstructure, namely structurally significant interlamellar struts. Computations reveal that these differential microstructural features give rise to the two distinctly different “pressure–volume responses” reported by Roach and colleagues and provide supporting evidence for the differential propensities to dissect exhibited by the thoracic and abdominal segments of the aorta. We conclude by describing possible tearing of the aortic wall by the interaction of multiple pools of injected intramural fluid, which is motivated by the presence of localized pools of mucoid material in the thoracic aorta in cases of increased dissection propensity.

2 Methods

Two separate phase-field finite-element models were employed to study the tearing of cut-open thoracic and abdominal aortic samples by the intramural injection of fluid. Consistent with dissections localizing to the medial layer in vivo and the focus on medial data in the experiments in vitro, we also focused on the media alone: first, a homogeneous model of the media of the thoracic aorta, which quantitatively reproduces the pressure of tearing and its decay, and second, a microstructural model, which qualitatively reproduces the stepwise increase in pressure in the media of the abdominal aorta.

2.1 Finite-element model

Tetrahedral elements were used to discretize select portions of the aortic wall. The displacement field \({\varvec{u}}\) was evaluated with the nearly incompressible behavior of the tissue enforced by a pressure-like field \(p\). Tissue damage, namely tearing, was represented by a phase field \(\phi \in [\mathrm{0,1}]\), with \(\phi =0\mathrm{ and }1\) corresponding to locally intact and fully torn states of the wall due to delamination. The volume of the pressurized fluid, introduced by injection, was prescribed incrementally and enforced using a global Lagrange multiplier, \(m\). The parameter \(m\) and the fields \({\varvec{u}}\), \(p\) and \(\phi\) were evaluated at each computational step defined by each injected volume, \({V}_{\mathrm{injection}}\). The solid deformed quasi-statically, and the fluid was treated as hydrostatic. The injection pressure was, therefore, uniform throughout the fluid subdomain. Tears were modeled as concentrated regions of damage surrounded by elastic material, similar to previous analysis of rubber-like elastomers (Rivlin and Thomas 1953; Gent 2012) and arterial tissue (Gültekin et al. 2019).

2.1.1 Phase-field model of tearing

A variational model of tearing using a phase field for damage (Bourdin et al. 2008) is motivated by a global minimization of energy similar to the approach of Griffith (1921) for fracture and thus by representing a crack (or tear) via a field of damage. The energy of tearing is formulated in terms of \(\phi\) and \(\nabla \phi\) such that its minimization leads to a concentrated field of damage that represents a sharp tear (Ambrosio et al. 1990). In modeling the delamination process, we prescribed each increment of the volume of injected fluid and computed \(m\) and the associated fields \({\varvec{u}},p\) and \(\phi\) by minimizing the total energy \({E}_{\mathrm{total}}\),

$${E}_{\mathrm{total}}={E}_{\mathrm{deform}}+{E}_{\mathrm{tear}}+{E}_{\mathrm{pressurized}-\mathrm{fluid}}+{E}_{\mathrm{damp}},$$
(1)

which comprises four contributions: deformation, tearing, injection of the fluid and viscous-like damping. That is, we sought

$$\left({{\varvec{u}}}_{j},{p}_{j},{m}_{j},{\phi }_{j}\right)=\underset{{\varvec{u}},p,m,\phi }{\mathrm{argmin}}\,{E}_{\mathrm{total}}({\varvec{u}},p,m,\phi )$$
(2)

for each \(j\)th increment of injection volume, with iterative minimization performed by finding roots of \({\nabla }_{\bar{u},\bar{p},\bar{m}} {E}_{\mathrm{total}}\) and \({\nabla }_{\bar{\phi }} {E}_{\mathrm{total}}\), where \({\nabla }_{\bar{u},\bar{p},\bar{m}}\) denotes a directional derivative in the direction of the test functions (Bonet et al. 2016) for \({\varvec{u}}\), \(p\) and \(m\) and \({\nabla }_{\bar{\phi }}\) denotes the directional derivative in the direction of the test function for \(\phi\). The solution to the damage problem was constrained between \(\phi\) at the previous increment of injected volume and its maximum value of 1, thus enforcing irreversible damage via tearing. The Bubnov–Galerkin method (Hughes 2012) was implemented within the FEniCS framework (Alnæs et al. 2015). FEniCS provides automatic differentiation and generation of parallel C++ code that corresponds to a weak form input by the user. It supplies an extensive set of routines that facilitate the solution of partial differential equations using the finite-element method. We utilized the interfaces provided by FEniCS to solve the deformation problem using the nonlinear solvers within PETSc and the constrained, damage problem using the TAO solver (Tanné et al. 2018).

2.1.2 Material models

The native vessel wall was modeled using a hyperelastic material model defined by a standard energy density function \({W}_{\mathrm{wall}}\) that accounts for structural contributions to the wall mainly by elastin, collagen and smooth muscle, augmented to enforce the incompressibility of the tissue. Specifically, the behavior of the elastin-dominated amorphous material was modeled as neo-Hookean, while the oriented collagen fibers and passive smooth muscle were modeled as Fung-type exponentially stiffening materials (Roccabianca et al. 2014b), namely

$${W}_{\mathrm{wall}}=\frac{c}{2}\left({\lambda }_{1}^{2}+{\lambda }_{2}^{2}+{\lambda }_{3}^{2}-3\right)+\sum_{i=1}^{4}\frac{{c}_{1}^{i}}{4{c}_{2}^{i}}\left(\mathrm{exp}\left({{c}_{2}^{i}\left({{(\lambda }^{i})}^{2}-1\right)}^{2}\right)-1\right),$$
(3)

where \(c\), \({c}_{1}^{i}\) and \({c}_{2}^{i}\) are material constants. Here, \({\lambda }_{1}\), \({\lambda }_{2}\) and \({\lambda }_{3}\) are principal stretch ratios and \({\lambda }^{i}\) are stretch ratios in one of the four main structural directions (\(i=1\), \(2\), \(3\) and \(4\) correspond to axial, circumferential and two diagonal directions, respectively). The diagonal directions are oriented at angles \(\pm \alpha\) with respect to the axial direction within the axial–circumferential plane. Values of the material parameters for the thoracic aorta were obtained from the data of Haskett et al. (2010) for the ascending aorta as modeled by Roccabianca et al. (2014b). Values of \(\alpha =\) 48.98 and 45.00 degrees were used in the models of the thoracic and abdominal aorta, respectively (Roccabianca et al., 2014b).

An approach similar to the perturbed Lagrangian method (Wriggers 2008) was used to ensure nearly isochoric deformations of the native arterial tissue (Li et al. 2020), with

$${W}_{\mathrm{vol}}=-{\left(1-\phi \right)}^{3} p \left({\lambda }_{1}{\lambda }_{2}{\lambda }_{3}-1\right)-\frac{{p}^{2}}{2\epsilon }.$$
(4)

The prefactor \({\left(1-\phi \right)}^{3}\) ensures relaxation of incompressibility in the fully damaged tissue, while the overall minimization of this contribution to the energy results in near incompressibility of the tissue in the intact region. \(\epsilon \gg 1\) is a perturbation parameter, with \({p}^{2}/(2\epsilon )\) regularizing the solution.

The total energy of deformation of the wall takes the form (Bourdin et al. 2008)

$${E}_{\mathrm{deform}}={\int }_{V}\left(\left({\left(1-\phi \right)}^{2}+\varepsilon \right){ W}_{\mathrm{wall}}+{W}_{\mathrm{vol}}\right) dV,$$
(5)

where the prefactor \({\left(1-\phi \right)}^{2}\) decreases the strain energy in the damaged region, with \(\varepsilon \ll 1\) a small number added to facilitate the computations. Sensitivity of the model to \(\epsilon\) and \(\varepsilon\) was determined via preliminary computations (supplementary figure S1).

The phase-field description of the energy of tearing, referred to as Ambrosio-Tortorelli I (Tanné et al. 2018), is

$${E}_{\mathrm{tear}}=\frac{3{G}_{c}}{8}\boldsymbol{ }{\int }_{V}\left(\frac{\phi }{l}+l{\left|\nabla \phi \right|}^{2}\right) dV,$$
(6)

where \({G}_{c}\) represents the critical energy release of tearing, that is, the energy required to advance a tear by 1 m2 in surface area. A value of 86 J/m2 was selected based on results of many preliminary simulations, which reproduced the pressure–volume behavior observed in the injection experiments. This value is comparable with the energy of delamination of arterial tissue evaluated in peeling and injection tests (Roach et al. 1994; Sommer et al. 2008; Pasta et al. 2012; Sherifova et al. 2019). The parameter \(l\) tunes the length scale of decay of the phase field from the tear to the intact material, chosen as 2\(h\) consistent with previous three-dimensional models (Borden et al. 2012), where \(h\) denotes the elemental size of the mesh. We chose \(h\) as the size of the elements in the finer regions of the mesh, where the tear progressed.

As the dissection front advances, prescribing the fluid pressure as a traction boundary condition presents a challenge. Thus, we replaced the boundary condition by a constraint over the total volume of the injected fluid. The volume of the fluid injected was prescribed using a global Lagrange multiplier \(m\), by adding to the total energy the expression

$${E}_{\mathrm{pressurized}-\mathrm{fluid}}=m\boldsymbol{ }\left(\boldsymbol{ }{\int }_{V}\phi {\lambda }_{1}{\lambda }_{2}{\lambda }_{3} dV-{V}_{\mathrm{injection}}\right).$$
(7)

The integral term in Eq. (7) represents the total damaged volume in the deformed configuration of the tissue, whereas \({V}_{\mathrm{injection}}\) was initially set as the volume of the initial ellipsoidal damaged region, \({V}_{0-\mathrm{injection}}\). At each increment, \({V}_{\mathrm{injection}}\) was increased in steps of 10–5 \({V}_{0-\mathrm{injection}}\). The viscous-like damping energy, \({E}_{\mathrm{damp}}\), was added to facilitate the numerical solution (Miehe et al. 2010).

2.1.3 Model geometry and mesh

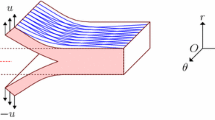
Motivated by the experiments of Roach and colleagues, the model geometry consisted of a 20 × 25 × 2 mm3 slab-shaped region that represents a quarter of a larger vessel wall, cut open, with the intima facing upwards (Fig. 1a). The initial damage zone (due to the introduction of a needle for injecting the fluid) was designated by prescribing \(\phi =1\). It consisted of the volume of a quarter of an ellipsoid of semi-axis lengths 0.3, 1.2 and 0.1 mm in the \(z\), \(\theta\) and \(r\) directions. These specific parameters were chosen to reproduce the resulting pressure–volume response reported by Carson et al. (1990) while maintaining an appearance comparable with the experimental images at the initial stages of injection. The subdomain, where the tear propagated with larger injection volumes, was meshed by elements of edge size \(h = 0.1\) mm. Coarser elements were used away from this region, where damage vanished and displacements were small. Tetrahedral elements, whose nodes resided on a rectangular grid, were generated using an in-house script.

Fig. 1
figure 1

Description of the model geometry as well as initial and boundary conditions. Geometric models of (a) the sudden tearing of the thoracic aorta and (b) the microstructure for the stepwise, progressive tearing of abdominal aorta, both by an intramural injection of fluid. Cartesian coordinates were used, but \(r\), \(z\) and \(\theta\) denote the radial, axial and circumferential directions before the cylindrical vessel was cut open and placed on a flat surface. A quarter of the symmetric model is shown, cut through the middle of the injection pool

Full size image

2.1.4 Microstructural model of progressive tearing of the abdominal aorta

To model the progressive intramural tearing observed in the abdominal aorta in response to the injected fluid, we further developed a minimal microstructural model, motivated by microscopy, which includes individual elastic lamellae and structurally significant radial struts that connect them (Fig. 1b). Material parameters, from data reported by Vande Geest et al. (2004) on the abdominal aorta and modeled by Roccabianca et al. (2014b), were used in this model. The model represents a miniature of the injection experiments by Roach et al. (1994). That is, to include the microscopic details, we modeled a smaller sample, and as a result, the volume of injection was orders of magnitude lower than the experimental value.

Five internal layers of the representative segment of the aortic wall were modeled by delineating the elastic lamellae, the radial struts connecting them and intralamellar media that filled the lamellar space. The tissue surrounding the detailed five layers was modeled as homogenous with averaged properties. The tangent stiffness and \({G}_{c}\) of the different subdomains differed according to their different mechanical behavior. The stiffness of the interlamellar struts and the intralamellar material were scaled by factors of 7.69 and 0.26 relative to the homogenized mean. The properties of these struts and intralamellar material thus differed by a factor of 30, whereas the lamellae and struts shared the same properties. The disparity in properties was motivated by two factors. First, the different behaviors of tissues torn by delamination versus tearing of individual lamellae (Purslow 1983; Sommer et al. 2016). Second, the power-law relations between stress and \({G}_{c}\) were discovered during preliminary simulations, as discussed in Results.

The \({G}_{c}\) of the struts, intralamellar material and surrounding media were set at 5.77, 0.20 and 0.75 J/m2, respectively. These values were chosen, based on many preliminary simulations, to reproduce the delamination at the small scale of the injection pool, which was feasible in the high-resolution microstructural model. The lamellae were 2 µm thick and separated by 10 µm; the interlamellar struts were 1 µm thick and occupied 10% of the intralamellar volume (Fig. 1b), noting that their positions within the \(\theta\)-\(z\) plane followed a uniform but random distribution. The mesh size was 1 µm in the subdomain representing microstructural details, whereas coarser elements were used away from this region where the damage and displacement fields vanished. \(l\) was equal to \(h\). An initial injection pool of 130 µm3 was placed in the middle of the topmost intralamellar space. Symmetric boundary conditions were used, similar to those in the thoracic model.

Two additional models were employed to test further whether the progressive, stepwise pressure–volume behavior is caused by the interlamellar struts. The radial struts were absent in these models. In the first model, the properties of the intralamellar media were unchanged. By contrast, a stronger and stiffer model was considered where the properties of the intralamellar media equaled that of the homogeneous surrounding medium. The tearing responses of these models were compared with the baseline model, which included the struts.

2.1.5 Model of multiple pools of injection

Motivated by the possibility of the existence of multiple pools of intramural mucoid material sequestering fluid (Ahmadzadeh et al. 2019), we modeled aortic samples with multiple injections. Over long periods, the fluid might permeate between the two pools: the pools may be separated by an impermeable barrier, or the pools may compete for the same reservoir of fluid. Motivated by these hypothetical scenarios, two sets of models were tested. In the first, the pools were connected to a shared reservoir; in the second, each pool was connected to its own reservoir.

In the case of a shared reservoir, the total change of volumes of the pools \({\Delta V}_{\mathrm{injection}}^{(1)}\) + \(\Delta {V}_{\mathrm{injection}}^{(2)}\) was prescribed, while they experienced the same pressure (note that superscripts (1) and (2) denote the separate pools). The description of \({E}_{\mathrm{pressurized}-\mathrm{fluid}}\) in Eq. (7) remained unchanged in the case of a shared reservoir. In the case with separate reservoirs, however, the volumes and pressures of the two pools could vary independently. In that case, the entire model was divided into two subdomains: \({V}^{(1)}\) and \({V}^{(2)}\). The points in \({V}^{(1)}\) were closer to the first pool and those in \({V}^{(2)}\) were closer to the other pool. In this case, \({E}_{\mathrm{pressurized}-\mathrm{fluid}}\) was replaced by

$${E}_{\mathrm{pressurized}-\mathrm{fluid}}=\sum_{k=\mathrm{1,2}}{m}^{(k)}\boldsymbol{ }\left(\boldsymbol{ }{\int }_{{V}^{(k)}}\phi {\lambda }_{1}{\lambda }_{2}{\lambda }_{3} dV-{V}_{\mathrm{injection}}^{\left(k\right)}\right),$$
(8)

where \(k\) denotes the subdomains and injection pools (1) or (2). Commonly, the initial volumes of the two pools in a model were slightly different. The difference was caused by the intersection of an ellipsoid, marking the locus of the initial injection pool, with the discrete mesh.

2.2 Sample preparation and in vivo imaging

The distinct microstructural features of the thoracic and abdominal aorta reported by Roach and colleagues in pigs were confirmed in aortic segments from mice. Specifically, aortas were harvested from three adult (3-month-old) female C57BL/6J mice using protocols approved by the Institutional Animal Care and Use Committee of Yale University. Descending thoracic aortic segments were excised between the first and the fourth pair of intercostal branches; suprarenal abdominal aorta segments were excised between the diaphragm and the first gonadal artery. Aortic samples were prepared by gently removing perivascular tissues and ligating all branches using nylon sutures. In all experimental steps, the sample was immersed in a Hanks’ buffered physiologic solution. Associated biomechanical analyses (cf. Ferruzzi et al. 2013) provided, among other biomechanical parameters, the in vivo axial stretch that was needed to define the state in which the sample was imaged. That is, the sample was maintained at a constant distending pressure (the ex vivo pressure equivalent to a diastolic pressure, that is, 80 mmHg) and at the in vivo axial stretch during microstructural investigation via multiphoton imaging, as described by Weiss et al. (2020). Briefly, the three-dimensional microstructure of the aortic wall—especially elastin structures—were captured in a stable in vivo equivalent mechanical configuration through the entire thickness using a Titanium-Sapphire Laser source at 840 nm and a water immersion 20 × objective lens. The auto-fluorescence signal of elastin structures was collected at a wavelength of 500–550 nm and resulted in 3D images with a numerical imaging resolution of 0.48 µm/pixel (in the circumferential–axial plane of the aorta) and an out-of-plane (in the radial axis of the aorta) step size of 1 µm/pixel.

3 Results

3.1 Intramural tears can propagate suddenly

As a first simulation, we modeled the tearing of a cut-open thoracic aortic sample subject to a single intramural injection experiment. Motivated by the reported experiments, the initially torn area (due to the insertion of the needle) was elongated along the circumferential direction. Prescribed increases in the injection volume resulted in two regimes of deformation: rising and tearing. In rising, the injected volume pushed up the portion of the wall above the pool, resulting in highly deformed tissue close to the edges of the pool. In this regime, the pressure of injection increased rapidly over a small range of the injection volume (Fig. 2a and b). Tearing started at a critical pressure, \({P}_{\mathrm{tear}}\)~ 67 kPa, close to the aforementioned value of 70 kPa reported by Roach and colleagues. After that, as the pool continued to cause tissue to rise, the intramural fluid also began to spread horizontally, tearing the tissue in the \(\theta\)-\(z\) plane (Fig. 2c). At first, the torn front progressed in the axial direction; at higher volumes, however, it spread both axially and circumferentially. Consequently, the torn region became larger and rounder as the volume of injection increased (supplementary figure S2). These patterns are similar to those reported in the experiments (Carson et al. 1990), as desired. The model revealed further that the tearing progressed in an opening mode, with the tear surface oriented normal to the directions of maximum stretch induced by the fluid pressure. Finally, the decay of pressure was slower during tearing (i.e., following \({P}_{\mathrm{tear}}\)) compared with its increase during rising. The decrease in pressure after \({P}_{\mathrm{tear}}\) suggests an unstable, sudden mode of tearing. In this mode, if the pressure \({P}_{\mathrm{tear}}\) was maintained, the pool would grow suddenly and indefinitely (unless interacting with other structures); that is, further increase in pressure was not required for the tear to continue to spread.

Fig. 2
figure 2

Model of the sudden delamination of a cut-open sample of the thoracic aortic wall by the injection of fluid. (a) The pressure of injection, \(P\), as a function of the volume of the injected fluid, \({V}_{\mathrm{injection}}\). The star symbol marks \({P}_{\mathrm{tear}}\), the pressure at which the arterial wall started tearing and the fluid began to propagate within the wall as it delaminated. The pressure decreased steadily after \({P}_{\mathrm{tear}}\), marking a sudden and unstable propagation of the tear at \({P}_{\mathrm{tear}}\). The experimental data (open circles) are reproduced from Carson and Roach (1990). The filled triangles, pointing upward, mark two volumes \({V}_{\mathrm{inject}}^{(1)}\) and \({V}_{\mathrm{inject}}^{(2)}\), corresponding to the same pressure \({P}_{0}\) (dashed line). Two pools that share the same reservoir may dilate to volumes \({V}_{\mathrm{inject}}^{(1)}\) and \({V}_{\mathrm{inject}}^{(2)}\) at pressure \({P}_{0}\) (see below). (b and c) Snapshots of the finite element model at the pressures 67 kPa and 25 kPa. Ink, shown in black, was modeled as a pressurized fluid, penetrating through the torn tissue. The process of tearing is shown in supplementary video S1

Full size image

3.2 Tearing pressure relates to tissue properties and the torn area

We then used the model of sudden tearing to characterize \({P}_{\mathrm{tear}}\) as a function of the geometry of the pool and surrounding tissue properties. The parameters of interest included \({G}_{c}\), the area of the torn tissue in the plane of tearing (\(\theta\)-\(z\)), \({A}_{\mathrm{torn}}\), the initial volume of the pool and the fold change of tangent stiffness of the tissue, \({K}_{t}/{K}_{t0}\). In the first set of simulations, computations of the tearing of thoracic tissue were repeated at various values of \({G}_{c}\), while all other parameters remained unchanged. The processes of rising and tearing were qualitatively similar to those in the original case, but we additionally found that \({P}_{\mathrm{tear}}\) increased monotonically with increasing \({G}_{c}\). The simulations indicated a power-law relation, namely \({P}_{\mathrm{tear}}^{2}\propto {G}_{c}\) (Fig. 3a).

Fig. 3
figure 3

Pressure of tearing as a function of the properties and geometry of the tissue. \({P}_{\mathrm{tear}}\) increases with both an increasing critical energy release rate of tearing (a) and tangent stiffness (c). In contrast, it decreases with increasing initial volume of the injection pool (inset of panel (a))) or the torn surface area of the arterial wall in the \(\theta\)-\(z\) plane, where it advances (b). \({P}_{\mathrm{tear}}\) relates to the tested parameters by power laws, which may be combined into a single expression, Eq. (9). The exponents of the power laws are shown on the plots by slopes of the solid lines, which are not curve fits to data. The inset in panel B shows the pressure of injection as a function of the torn area of the tissue as fluid was injected, corresponding to the tearing branch of Fig. 2a. (d) A comparison of the \({P}_{\mathrm{tear}}\) values obtained using the finite element model and Eq. (9) for various combinations of parameters, explained in the text. The diagonal dashed line indicates equal values of \({P}_{\mathrm{tear}}\) on the two axes. The plus sign in panel (b) denotes an initially circular torn area; the multiplication sign denotes an initial torn area in the shape of an ellipse oriented in the axial direction. All the other symbols correspond to elliptically shaped initial torn areas oriented in the circumferential direction. The pressure of tearing slightly increased in the case with a circular initial torn area, indicating that an elongated pool propagates at a slightly smaller pressure. All axes are plotted on the logarithmic scale, except those in panel d

Full size image

Next, we conducted a similar set of simulations where \({A}_{\mathrm{torn}}\) was varied by changing the dimensions of the injected pool in the circumferential and axial directions, while its semi-axis length in the radial direction remained unchanged. The tearing pressure \({P}_{\mathrm{tear}}\) decreased with increasing \({A}_{\mathrm{torn}}\), exhibiting a power-law behavior, \({P}_{\mathrm{tear}}^{2}\propto 1/\sqrt{{A}_{\mathrm{torn}}}\) (Fig. 3b). \({P}_{\mathrm{tear}}\) remained unchanged if the initial torn area was elongated in the axial direction instead of the circumferential direction and increased by 4% if the initial torn area was circular (Fig. 3b), indicating that an elongated pool propagates at a slightly lower pressure. Simulations demonstrated a decrease of \({P}_{\mathrm{tear}}\) with an increase in the initial volume of the pool, \({P}_{\mathrm{tear}}^{2}\propto 1/\sqrt{{V}_{0-\mathrm{injection}}}\), where \({V}_{0-\mathrm{injection}}\) was varied by isotropic scaling of the initially damaged volume (Fig. 3a, inset). Finally, the effect of tissue stiffness on \({P}_{\mathrm{tear}}\) was tested by uniform changes of the tangent stiffness at all states of strain. This change was prescribed by scaling the strain energy for the non-damaged tissue. \({P}_{\mathrm{tear}}\) increased with increasing \({K}_{t}/{K}_{t0}\), following the power law, \({P}_{\mathrm{tear}}^{2}\propto {K}_{t}/{K}_{t0}\) (Fig. 3c).

Numerical simulations indicated that within the vicinity of the baseline values, the power laws relating \({P}_{\mathrm{tear}}^{2}\) to \({G}_{c}\), \({A}_{\mathrm{torn}}\) and \({K}_{t}/{K}_{t0}\) may be combined to obtain

$${P}_{\mathrm{tear}}^{2}=5.55\times {10}^{4}\frac{{G}_{c}}{\sqrt{{A}_{\mathrm{torn}}}}\frac{{K}_{t}}{{K}_{t0}}.$$
(9)

In simulations using all combinations of the values \({G}_{c}=\{86, 112, 198\}\) J/m2, \({K}_{t}/{K}_{t0}=\{1, 1.3\}\) and \({A}_{\mathrm{torn}}=\{1.13, 2.26\}\) mm2, the largest relative difference between the computational values and Eq. (9) was 3% (Fig. 3d), indicating the accuracy of this expression in the vicinity of the tested parameters. Equation (9) relates the values in SI units. The constant in Eq. (9) accounts for other factors not tested.

3.3 Multiphoton microscopy of the structure of the arterial wall

To model the progressive, stepwise tearing observed by Roach and colleagues for a cut-open segment of abdominal aortic tissue in fluid injection experiments, we first confirmed their report of a differential arterial microstructure in the two aortic regions using multiphoton microscopy. Three-dimensional images of the aortic samples from mice revealed distinct differences characterizing the in vivo equivalent configuration of the descending thoracic aorta and the suprarenal abdominal aorta (representative images in Fig. 4). Elastin structures in the descending thoracic aorta exhibited large circular fenestrations recognizable on various circumferential–axial planes as thicker lines with a rounded shape lying within the elastic lamellae (Fig. 4a). Structures of this type were less frequent in the suprarenal abdominal aorta. In contrast, the elastin signal in the abdominal aorta revealed a large number of elongated and relatively thick radial elastin structures. They ran through the intralamellar space between the smooth muscle cells and connected the adjacent elastic lamellae (Fig. 4c). These thick struts were not seen in the descending thoracic aorta.

Fig. 4
figure 4

Representative multiphoton (two-photon fluorescence) microscopy images of elastin within the aortic wall in the (a and b) descending thoracic and (c and d) suprarenal abdominal aorta of mice. Each section of the aorta is shown in axial–circumferential (a and c) and axial–radial (b and d) planes. The axes indicate the circumferential (\(\theta\)), axial (\(z\)) and radial (\(r\)) directions. The yellow arrows point to thick elastin struts observed in the intralamellar space of the suprarenal abdominal samples. Many fewer radial struts and more fenestrations are present in the thoracic aorta. The scale bar is 100 µm

Full size image

3.4 Microstructural model of stepwise, progressive tearing of the abdominal aorta

Motivated by the report of Roach and colleagues and confirmed by microscopy, we use a microstructural model to investigate the stepwise mode of tearing in some samples of the abdominal aorta. In these simulations, the injected fluid first radially deformed the two adjacent elastic lamellae while stretching and bending the nearby radial struts that connected the lamellae (Fig. 5a). Increases in the injected volumes initiated tearing of the intralamellar media (0 in Fig. 5b), with the tear advancing in the axial–circumferential plane. At this stage, no struts were torn, except those originally disrupted when creating the initial injection pool consistent with the insertion of a needle (Fig. 5c). After a slight advance of the tear, the front of the tear appeared to be confined by the struts despite continued injection of fluid. Pressure thus built-up, which further deformed struts near the injection pool (Fig. 5a and c). At a critical pressure (I in Fig. 5b), one of the struts tore (I in Fig. 5c and d), followed by a sudden but small reduction in pressure that was followed by two more build-up and relief events, signified by S-shaped steps of the pressure–volume curve (Fig. 5b). The maximum pressure associated with each step corresponded to the tearing of a strut (II and III in Fig. 5b, c and d). The model thus suggested that it is the failure of the radial struts that causes the stepwise, progressive tearing with increasing \({G}_{c}\) serving as barriers to the advancement of the tearing front and increasing stiffness holding adjacent lamellae together.

Fig. 5
figure 5

Mechanism for a progressive, stepwise mode of tearing of the abdominal aortic wall. (a) Snapshot of the microstructural model of progressive tearing of the abdominal aorta. To aid visualization, the lamellae and interlamellar struts are brighter compared with the rest of the intralamellar space. The portion of the wall surrounding the struts was represented with homogeneous material properties. (b) The pressure of injection versus the volume of injection normalized by the initial volume of the pool. Three cases were considered: first, the microstructural model of panel a (solid curve), second, a model with no struts and a weak, less stiff intralamellar material (dashed curve) and, third, a model with no struts but the intralamellar material represented by a tangent stiffness and \({G}_{c}\) equal to those of the surrounding medium (dotted curve). The peaks marked by I, II and III correspond to the build-up of pressure and eventual tearing of radial struts marked by the same numbers in panels c and d. (c and d) Snapshots of the microstructural model in the vicinity of the pressurized fluid before and after tearing propagated. The arrows point to interlamellar struts, (c) stretched by the separated lamellae and bent by the fluid pressure or (d) eventually disrupted by the fluid. Pressure builds up as the front of the tear reaches the struts, with the fluid confined. The struts increase the pressure of propagation by two mechanisms. First, they increase the energy of tearing by forming barriers to the propagating fluid. Second, they increase the apparent stiffness of the tissue by acting as reinforcements, holding adjacent elastic lamella together. The process of tearing is shown in supplementary video S2

Full size image

To examine further whether progressive failure of the interlamellar struts causes the overall stepwise pressure–volume behavior, two additional simulations were performed in the absence of struts: first, for a sample having a weaker and less stiff intralamellar media and, second, for a sample with a stronger and stiffer intralamellar media. In the less stiff case, all materials had the same properties as those in the original simulation; only the struts had been replaced by the intralamellar media. In that case, the pressure–volume behavior exhibited a peak with a slow decay; steps and progressive increases of pressure vanished (Fig. 5b, dashed curve). A similar behavior was observed for a stronger intralamellar media. The decay of pressure after tearing is smaller here as compared with Fig. 2a because of the smaller volume of injection. These simulations further suggest a direct relationship between the presence of substantial radial struts and the stepwise increase in pressure as tearing advances.

3.5 Unequal growth and coalescence of multiple pools

Motivated by the possibility of the presence of multiple pools of native fluid (mucoid material with sequestered water) within a diseased aortic wall (Humphrey 2013; Roccabianca et al. 2014a; Ahmadzadeh et al. 2019), we tested cases with multiple injections of fluid. Noting further the possibilities of impermeable barriers, long-term permeation of injected fluid, or loss of fluid, we considered two cases with initially paired pools: one with a shared reservoir and one with separate reservoirs.

In the case of a shared reservoir of fluid, the two pools grew equally at small volumes of injection. If distant, one of the pools started to grow larger after tearing began, while the other pool seemingly arrested (Fig. 6a). This process was accompanied by a small reduction in the volume of a pool. The reduction in the volume of the smaller pool was accompanied by the fluid outflow. As the fluid moved out, the tissue above the pool was unloaded and moved downward. There was no change of the torn area as tearing was modeled as irreversible. At this stage, the volumes of the pools, \({V}_{\mathrm{inject}}^{(1)}\) and \({V}_{\mathrm{inject}}^{(2)}\), differed though their pressures were the same, \({P}_{0}\). One pool was larger than the critical volume of tearing, while the other one was smaller (Fig. 2a).

Fig. 6
figure 6

Unequal growth and coalescence of multiple intramural pools of fluid. (a) Snapshot of the unequal growth of a pair of pools. The pool on the right is growing and propagating, while the one on the left has come to an arrest. (b) The tearing pressure versus spacing of the pools, normalized by the size of the pools in the axial direction. In all simulations of multiple pools, the pools grew at an equal rate at small volumes. At higher volumes, closer pools coalesced, whereas pools farther apart grew unequally, with one pool growing and the other seemingly arresting. This effect led to a small reduction in the tearing pressure. In contrast, if the pools were connected to separate reservoirs, there was a reduced tearing pressure. (c) Snapshot of two nearby pools after coalescence. Panels a and c display half of the entire symmetric geometry, cut by a radial–axial plane through the middle section of both injection pools

Full size image

For large distances between the pools, more than 30 times the initial pool size in the axial direction \({P}_{\mathrm{tear}}\) decreased only slightly, by 6% (Fig. 6b). If the two pools were initially closer, however, they both started to spread and coalesce after an initial stage of equal growth (Fig. 6c). In this case, tearing started at a smaller pressure. For instance, for pools separated by a distance 3 times their initial size, \({P}_{\mathrm{tear}}\) was halved. In these simulations, the strain energies added at the section of the tissue between the two pools and overcame the cohesion of the tissue at a smaller pressure compared with that in the single injection.

In simulations where the pools were connected to separate reservoirs, the pools grew equally. In cases where the pools were distant, the two pools highly strained the tissue between them. The pressure of tearing was lower than that in simulations that included a shared reservoir (Fig. 6b).

4 Discussion

Aortic dissection is increasingly recognized as a significant health risk and more attention continues to be directed to the biomechanics (Wu et al. 2013; Nienaber et al. 2016; Tong et al. 2016). Diverse mechanical tests have been employed to examine the strength of the healthy and diseased aorta, including standard uniaxial and biaxial failure tests (Mohan et al. 1982, 1983; Shah et al. 2014). Multiple groups have also reported experimental and computational findings related to “tearing” and “peeling” tests wherein a cut is introduced within an excised strip of the wall that is then separated mechanically by exerting opposing normal forces on each side of the initial cut (Purslow 1983; Gasser et al. 2006; Pasta et al. 2012; Yu et al. 2020). Such studies have provided considerable information, particularly on wall strength and failure energies; for example, results reveal increasing fracture toughness from proximal to distal sites in the descending thoracic aorta (Purslow 1983). A nice quantitative review of findings from these and related studies can be found elsewhere (Table 1 in Sommer et al. 2008).

Whereas such uniaxial, biaxial and tearing tests do not preserve the in vivo cylindrical geometry, which affects dramatically the intramural stress field, others have introduced intramural swelling defects within cylindrical segments and connected these defects to the lumen with thin circumferential slits. Pressurization of the vessels propagates these defects, showing that propagation is possible at pressures slightly higher than normal resting values (Tam et al. 1998). A similar situation has been considered computationally, though without an initiating swelling defect (Wang et al. 2017). Although intramural swelling defects need not exist in all cases, a distinguishing histopathologic feature that appears to increase the propensity for dissection is localized accumulations of glycosaminoglycans, or GAGs (Humphrey 2013; Cikach et al. 2018; Shen et al. 2019). These GAGs are highly negatively charged; thus, they attract sodium ions to ensure local electroneutrality, which via osmosis results in local intramural Gibbs–Donnan pressures as water is sequestered. Computational models show that these swelling pressures can rise to values high enough to initiate the delamination of lamellar structures within the aortic wall (Ahmadzadeh et al. 2019; Roccabianca et al. 2014a), with calculated values of the associated radial stress concentrations reaching values found experimentally (~ 60 kPa) to delaminate the aorta (MacLean et al. 1999). Thus, the injection experiment of Roach and colleagues provides insight that is pathophysiologically relevant, especially when performed on cylindrical segments.

Despite the known strong regional differences, few investigators have compared dissection propensity directly between the thoracic and abdominal aorta. Given the relevance of their experimental approach and their direct comparison between the thoracic and abdominal aorta, we sought to use a state-of-the-art phase-field finite-element approach (Bourdin et al. 2008; Gültekin et al. 2019) to simulate the seminal studies of Roach et al. (1994). We found that an energetic analysis of tearing explains the observed differential pressure–volume responses. We also used our model to characterize the pressure of tearing as a function of the material stiffness, the critical energy release of tearing of the arterial wall and the geometry of the torn tissue, all of which revealed power-law relationships, combined into a single relation, Eq. (9). Importantly, a microstructural model that included structurally significant interlamellar struts also qualitatively reproduced the observed stepwise pressure–volume relation in the abdominal aorta; a local build-up of pressure resulted from confinement of fluid by radial struts, while pressure subsequently dropped as contained fluid was released by a tearing of the struts, which repeated as more struts gave way.

The computational approach, a variational phase-field model, is based on a minimization of energy inspired by the fracture approach of Griffith (1921), postulating \({G}_{c}\) as a material parameter. In peeling experiments, depending on specific artery and experimental conditions, the energy of dissection may be direction independent or may vary by up to 50% depending on the direction of peeling for the same tear surface (Tong et al. 2016; Sherifova et al. 2019; Yu et al. 2020). \({G}_{c}\) was isotropic in our model, and no anisotropy of critical tearing energy was included. We note, however, that the value of \({G}_{c}\) may be overestimated in peeling tests (Gent et al. 1987) and that the effective \({G}_{c}\) may differ slightly from the value input to the variational phase-field model (Tanné et al. 2018).

The expression for \({P}_{\mathrm{tear}}\), Eq. (9), characterizes tearing pressure as a function of tissue properties and tear geometry; it provides qualitative and quantitative insights into the tearing resistance of the arterial wall to the intramural pressurization. This relationship may be compared with expressions for critical pressure in the work of Gent et al. (1987) on the “blow-off pressure” of polymeric samples attached to a substrate. Both their analysis and the present work are based on an energetic approach. Yet, they tested an adhesive tape attached to a substrate, whereas we examined deforming tissue that was torn by an internal fluid pressure. Both studies nevertheless found positive correlations of the critical pressure with both material stiffness and the critical energy release of tearing as well as negative correlations with the deboned area. We expect that the overall trends suggested by Eq. (9) hold qualitatively in the case of a distended cylindrical artery.

More specifically, the previous works on the detachment of polymer films from stiff substrates demonstrated that the relationship between \({P}_{\mathrm{tear}}\), the material properties and the torn area for an idealized linear elastic material of modulus \(E\) and circular torn area of radius \(a\) can be supported by analytical reasoning. A variational argument can reveal an approximate expression for \({P}_{\mathrm{tear}}\). Considering the mode of propagation, the total energy \({E}_{\mathrm{total}}\), which in this case consists of elastic energy, fluid energy and tearing energy, can be expressed in terms of parameters such as \(a\), \(P\), \(E\) and \({G}_{c}\). Then, using a Griffith-type argument about the energy release rate, the tear starts to propagate when \(\partial {E}_{\mathrm{total}}/\partial a=0\), yielding \({P}_{\mathrm{tear}}\). Based on this analysis, a relation of the form \({P}_{\mathrm{tear}}=C\sqrt{E{G}_{c}/a}\) has been previously suggested in the context of the detachment of polymer films from stiff substrates, where \(C\) is a constant (Sneddon 1946; Williams 1969; Gent et al. 1987). In the special case of arterial tissue reported here, the tissue deformation was nonlinear and the torn area was not circular; therefore, we expressed the relation in terms of the torn area and the ratio of tangent stiffnesses instead of the radius and elastic modulus. Our numerical results similarly demonstrated that a power-law relation, Eq. (9), reasonably approximates \({P}_{\mathrm{tear}}\) in aortic tissue.

The trends suggested by Eq. (9) provide additional insight into the sudden and stepwise progressive modes of delamination. The negative correlation between the initially torn area and \({P}_{\mathrm{tear}}\) explains the sudden propagation of tears at a critical pressure, although as the fluid spreads the torn area does not advance equally in the circumferential and axial directions as in the tests of the variable initial torn area. The anisotropic advance of the tearing front causes a small deviation from the power-law relation \({P}_{\mathrm{tear}}^{2}\propto 1/\sqrt{{A}_{\mathrm{torn}}}\), while qualitatively maintaining the negative correlation (Fig. 3b, inset). The positive correlations of \({P}_{\mathrm{tear}}\) with stiffness and \({G}_{c}\) are consistent with a stepwise increase in pressure as the tearing front progressively encounters new interlamellar struts. The radially oriented struts increase fracture energy by forming obstacles to the tearing front and they increase stiffness by holding the adjacent elastic lamellae together, thus increasing \({P}_{\mathrm{tear}}\). The consistency of the homogeneous model and the sudden tearing experiments (Fig. 2a) suggests that lamellar structures are torn homogeneously in that case. In contrast, in the stepwise mode of tearing, weaker and stronger structures of the corresponding abdominal aortic samples tear at different times. Weaker materials tear first at a smaller fluid pressure, then stronger structures follow at larger pressures, signifying the structural consequences of microstructural heterogeneity of the arterial wall.

Notwithstanding the goodness of the results, there are challenges in modeling the stepwise tearing of the radial struts in the abdominal aortic tissue and there are limitations of the microstructural model. First, the sequential tearing of the non-uniformly distributed radial struts results in stochastic variations of pressure as injected volume increases, observed both in the model and the experiments (Roach et al. 1994). Moreover, in the previous experiments, the torn area was macroscopic, but the radial struts, suggested to cause the stepwise tearing, were microscopic. Including both length scales in one model proved challenging. Therefore, instead of quantitatively modeling the experimental setup, we resorted to a qualitative model by including a microscopic initial torn area and a weakened tissue response to tearing. We used Eq. (9) to tune the characteristic energy of tearing and produce tearing at roughly the same tissue strain and pressure as in the quantitative model, using a microscopic initial torn area. The microstructural model of the tearing of the radial struts is, therefore, limited by its qualitative nature. This model nonetheless demonstrates the possibility of the stepwise increase in pressure by the sequential tearing of the radial struts as the injection volume increases.

Our model accounted for the tearing of tissue by the pressurized injection of intramural fluid over the time scale of minutes. This choice was based on the in vitro experiments by the Roach group (Carson et al. 1990; Roach et al. 1994). In our model, tearing was irreversible and healing of the torn tissue was not considered, which was not considered experimentally and would occur over a longer period. Moreover, possible healing of dissected arteries likely involves thrombus resolution and inflammatory responses. Such healing responses merit attention in future studies.

In conclusion, aortic dissection is a complex clinical condition. Given that dissections present in patients having diverse risk factors, from younger individuals with particular genetic mutations to older individuals who are hypertensive (Wu et al. 2013; Nienaber et al. 2016), it is unlikely that all dissections arise from the same initiating biological or mechanical event. Rather dissections likely arise from many different types of initiators and diverse factors likely dictate whether the dissection will propagate, result in a re-entry site, or lead to complete transmural failure, that is, rupture. The reported relation for \({P}_{\mathrm{tear}}\) (Eq. (9)) implies that given the development of a large enough initial tear, the normal pressure of blood can propagate dissections even in healthy aortas. Furthermore, the present studies provide computational support for the seminal observations of Roach and colleagues that sites of intramural swelling can lead to propagating delaminations within the aortic wall and confirm the importance of the radially oriented structural constituents within the wall in allowing or arresting dissection (cf. Dingemans et al. 2006; Tsamis et al. 2014). In particular, elastic fibers within the wall that serve as radial struts can play important structural, not just instructional, roles (Dingemans et al. 2006; Humphrey et al. 2015; O’Connell et al. 2008) and must be considered in greater detail as we seek to understand the biomechanical mechanisms of aortic dissection.