Numerical investigation of biomechanically coupled growth in cortical folding

Abstract

Cortical folding—the process of forming the characteristic gyri (hills) and sulci (valleys) of the cortex—is a highly dynamic process that results from the interaction between gene expression, cellular mechanisms, and mechanical forces. Like many other cells, neurons are sensitive to their mechanical environment. Because of this, cortical growth may not happen uniformly throughout gyri and sulci after the onset of cortical folding, which is accompanied by patterns of tension and compression in the surrounding tissue. Here, as an extension of our previous work, we introduce a biomechanically coupled growth model to investigate the importance of interaction between biological growth and mechanical cues during brain development. Our earlier simulations of cortical growth consisted of a homogeneous growing cortex attached to an elastic subcortex. Here, we let the evolution of cortical growth depend on a geometrical quantity—the mean curvature of the cortex—to achieve preferential growth in either gyri or sulci. As opposed to the popular pre-patterning hypothesis, our model treats inhomogeneous cortical growth as the result of folding rather than the cause. The model is implemented numerically in a commercial finite element software Abaqus/Explicit in Abaqus reference manuals, Dassault Systemes Simulia, Providence (2019) by writing user-defined material subroutine (VUMAT). Our simulations show that gyral–sulcal thickness variations are a phenomenon particular to low stiffness ratios. In comparison with cortical thickness measurements of $N=28$ human brains via a consistent sampling scheme, our simulations with similar cortical and subcortical stiffnesses suggest that cortical growth is higher in gyri than in sulci.

1 Introduction

Cortical folding has been long studied by joint efforts of researchers from different backgrounds of neuroscience, biology, medical imaging, mechanics, etc. (Sejnowski et al. 1988; Sun and Hevner 2014; Fischl and Dale 2000; Tallinen et al. 2014). This process is associated with a dramatic increase in brain size and complexity, giving the folded, or gyrencephalic, brains of humans and other mammals a superior information processing capability compared to other species with smooth, or lissencephalic, brains. Deviation from typical development is correlated with many neurological disorders such as lissencephaly, polymicrogyria, and autism spectrum disorder (Walker 1942; Barkovich et al. 1999; Nordahl et al. 2007). Hence, a better understanding of the cortical folding could lead to improved diagnostics, treatments, and prevention for folding abnormalities in the diseased brain.

Over the past decade or so, the research on cortical folding has been growing exponentially, which has increased our understanding of key players such as gene expression, cellular, and mechanical mechanisms, but many questions remain. The debate as to whether biology or mechanics dominates cortical folding is ongoing (Borrell and Götz 2014; Kroenke and Bayly 2018). In reality, the interaction between the two is a promising area to be further explored.

From a biological point of view, neurons are created by neurogenesis within the subcortex at the early stage. Before cortical folding happens, newborn cortical neurons migrate radially along the radial glial fibers from the germinal layers to the cortical plate. It has been shown that inhomogeneous neurogenesis plays an important role in cortical folding (Kriegstein et al. 2006). Regions that undergo high neurogenesis have a greater expansion, and this inhomogeneous growth will eventually shape the brain’s morphology. Besides neurogenesis, the patterned expansion and folding of the cortex could also result from the tangential dispersion of neurons during their radial migration. In species with a folded cortex, the trajectory of radial glial fibers varies across regions, being dramatically divergent in areas where the cortical plate will later undergo the most significant expansion and folding (Reillo et al. 2011). This has been supported by genetic studies in ferrets, which found that the intentionally suppression of genes that correspond to the radial migration of neuron cells resulted in cortical malformations (Shinmyo et al. 2017).

From a mechanical perspective, early theories suggested that cortical folding could be a passive consequence of mechanical forces acting on the expanding brain, including cerebrospinal fluid pressure and the constraints from the cranium (Welker 1990). However, experiments by Barron (1950) showed that the forces primarily responsible for cortical folding are resident within the cortex. The hypothesis proposed by Van Essen (1997) states that the patterned axonal tension between specific cortical regions drives cortical folding, which is supported by axonal tracing evidence in the macaque. However, Xu et al. (2010) later showed that the tensile forces from axons do not act along the direction that would be required to bring the walls of developing gyri together. As an alternative hypothesis, the differential growth theory has become more convincing and popular (Bayly et al. 2013; Tallinen et al. 2014). The theory states that the outer layer of the brain undergoes faster tangential expansion than the inner core, which builds up compressive stresses and will trigger mechanical buckling after it reaches a critical threshold.

Neither biology nor mechanics is self-sufficient for capturing the whole picture of brain development when acting alone. Instead, they likely work together. Many cells are sensitive to their mechanical environment, with their proliferation and growth rate regulated by mechanical stresses (Shraiman 2005). Neurons are no exception. Their biomechanically coupled behaviors play an important role in shaping the neuronal morphology. For example, Pfister et al. (2004) reported that axons could be stretch-grown at rates of $8\hbox { mm/d}$ and reach lengths of $10\hbox { cm}$ without rupture. Accordingly, models that build upon the differential growth theory while taking into account axonal growth in the subcortex have provided more realistic results (Xu et al. 2010; Bayly et al. 2013; Budday et al. 2014; Holland et al. 2015). A recent study by Koser et al. (2016) reported that neuron cells grow faster when cultured in a relatively stiffer environment and that mechanical signals could act as the regulators for neuronal pathfinding. Furthermore, Anava et al. (2009) concluded that mechanical tension could regulate the axonal branch and the subsequent formation of synapses. By extension, it is reasonable to assume that cortical growth during cortical folding does not happen uniformly throughout the gyri and sulci, which are accompanied by patterns of tension and compression in the surrounding tissue.

Cortical thickness not only serves as an essential biomarker for diagnosing neurological disorders (Shaw et al. 2006) but also gives us a macroscopic assessment of brain morphologies. It is consistently found to be thicker in gyri and thinner in sulci. We have previously explained this fact using pure mechanical buckling theory, numerical simulations, and non-biological polymer experiments (Holland et al. 2018). However, the thickness ratio gap between non-biological analogues and human brains raises the question of how biological growth works alongside mechanics to affect cortical thickness.

The current work employs differential growth to trigger initial cortical folding and focuses on the interaction between biological growth and mechanics during the post-buckling process. More specifically, we use the mean curvature in the cortex as a macroscopic measure to represent the difference in the mechanical environment between gyri and sulci. We then link the cortical growth rate to the mechanics-induced mean curvature variations, achieving either gyral or sulcal growth by tuning a curvature-sensitive parameter. Our theory is implemented numerically in a finite element software. We further study the theory by running simulations in 2-D and 3-D settings, in which the brain is modeled as a bilayer system consisting of a growing cortical layer and an elastic subcortical substrate. Finally, we validate our model quantitatively by comparing the simulated results against measured cortical thicknesses from human brains.

2 Method

2.1 Cortical thickness measurements

We measured gyral and sulcal thicknesses ($t_{\mathrm{g}}, t_{\mathrm{s}}$) in humans by analyzing magnetic resonance images of $N = 28$ typically developing human brains (ages between 7 and 18) from Yale School of Medicine—a subset of a public database (Craddock et al. 2013). All images were analyzed using the open-source software FreeSurfer (Dale et al. 1999), which performs volumetric image segmentation, cortical reconstruction, and calculations of brain morphology, including cortical thickness (Fig. 1, top). We divided the cortex into sulcal and gyral regions by the mean curvature with gyral and sulcal regions bounded between [$-0.5,\,0$] and [$0,\, 0.5]\,\hbox {mm}^{-1}$ (Fig. 1, bottom), respectively.

Fig. 1

Patterns of cortical thickness and mean curvature in one of $N=28$ human brains studied. Top: cortical thickness. Bottom: mean curvature. Images to the left represent the anatomical cortical surfaces, while images on the right have been artificially inflated for improved visualization of sulcal values

The averaged gyral and sulcal thicknesses are susceptible to the sampling scheme we adopted here, as measurements obtained from only the most gyral and sulcal spots are different from the ones averaged from the larger area. (This is discussed further in Sect. 3.2.3). These results were later used to compare against our numerical simulations.

2.2 Mathematical model

2.2.1 Kinematics of finite growth

Consider a body $\mathcal {B}_\text {R}$ identified with the region of space it occupies in a fixed reference configuration, with arbitrary material points denoted as ${\mathbf{x}}_\text {R}$. The referential body $\mathcal {B}_\text {R}$ then undergoes a motion ${\mathbf{x}}= \chi ({\mathbf{x}}_\text {R},t)$ to the current deformed body $\mathcal {B}_{\mathrm{t}}$ with deformation gradient given by

$$\begin{aligned} {\mathbf{F}}= \nabla \chi , \quad \text {such that}\quad J=\det {\mathbf{F}}>0 \, , \end{aligned}$$

(1)

where $\nabla$ denotes the gradient with respect to the material point ${\mathbf{x}}_\text {R}$ in the reference configuration. Following Rodriguez et al. (1994), to take growth-related changes in volume within the region into account, we adopt the multiplicative decomposition of the total deformation gradient,

$$\begin{aligned} {\mathbf{F}}= {\mathbf{F}}^{\mathrm{e}} {\mathbf{F}}^{\mathrm{g}}, \end{aligned}$$

(2)

where ${\mathbf{F}}^{\mathrm{g}}$ is the irreversible growth part of the deformation measuring from reference configuration $\mathcal {B}_\text {R}$ to the intermediate stress-free configuration $\mathcal {B}_{\mathrm{g}}$ denoted by $\bar{{\mathbf{x}}}$, while ${\mathbf{F}}^{\mathrm{e}}$ is the reversible elastic part of the deformation measuring from the intermediate to the current configuration $\mathcal {B}_{\mathrm{t}}$. Similarly, the volumetric change can be decomposed into elastic and growth parts, i.e.,

$$\begin{aligned} J = \det {\mathbf{F}}= J^{\mathrm{e}} J^{\mathrm{g}} \, , \end{aligned}$$

(3)

where we consider the tissue to be slightly compressible, so $J^{\mathrm{e}}$ is not strictly 1. We model cortical growth as in-plane area growth and assume that the response normal to the cortical layer is purely elastic (Holland et al. 2015). The corresponding growth tensor is given by

$$\begin{aligned} {\mathbf{F}}^{\mathrm{g}} = \sqrt{\vartheta ^{\mathrm{g}}}\mathbf{1} + (1 - \sqrt{\vartheta ^{\mathrm{g}}}){\mathbf{n}}_\text {R}\otimes {\mathbf{n}}_\text {R}, \end{aligned}$$

(4)

where $\vartheta ^{\mathrm{g}}$ is a growth multiplier, ${\mathbf{n}}_\text {R}$ is the referential unit normal of the pial surface. It is worth noting that the growth parameter $\vartheta ^{\mathrm{g}}$ represents the increase in the cortical area,

$$\begin{aligned} \vartheta ^{\mathrm{g}} = ||J^{\mathrm{g}} {\mathbf{F}}^{\mathrm{g} -\scriptscriptstyle \top } \cdot {\mathbf{n}}_\text {R}|| = J^{\mathrm{g}}, \end{aligned}$$

(5)

which is identical to the increase in the cortical volume $J^{\mathrm{g}}$. We invert the growth tensor via Sherman–Morrison formula,

$$\begin{aligned} {\mathbf{F}}^{\mathrm{g-1}} = \frac{1}{\sqrt{\vartheta ^{\mathrm{g}}}} {\mathbf{1}}+ \frac{\sqrt{\vartheta ^{\mathrm{g}}} - 1}{\sqrt{\vartheta ^{\mathrm{g}}}} {\mathbf{n}}_\text {R}\otimes {\mathbf{n}}_\text {R}. \end{aligned}$$

(6)

The elastic deformation tensor is then calculated as

$$\begin{aligned} {\mathbf{F}}^{\mathrm{e}} = \frac{1}{\sqrt{\vartheta ^{\mathrm{g}}}}{\mathbf{F}}+ \dfrac{\sqrt{\vartheta ^{\mathrm{g}}} - 1}{\sqrt{\vartheta ^{\mathrm{g}}}} {\mathbf{n}}\otimes {\mathbf{n}}_\text {R}, \end{aligned}$$

(7)

where ${\mathbf{n}}= {\mathbf{F}}{\mathbf{n}}_\text {R}$ is the current unit normal of the pial surface. Finally, both elastic left and right Cauchy–Green tensors are given by

$$\begin{aligned} {\mathbf{B}}^{{\text{e}}} = {\mathbf{F}}^{{\text{e}}} {\mathbf{F}}^{{{\text{e}}{\top }}} \quad {\text{and}}\quad {\mathbf{C}}^{{\text{e}}} = {\mathbf{F}}^{{{\text{e}}{ \top }}} {\mathbf{F}}^{{\text{e}}} \end{aligned} .$$

(8)

2.2.2 Constitutive equations

We model both cortical and subcortical tissues as compressible neo-Hookean materials,

$$\begin{aligned} \psi _\text {R}({\mathbf{C}}^{\mathrm{e}}, J^{\mathrm{e}}) = \frac{\mu }{2} \big [\text {tr}\,({\mathbf{C}}^{\mathrm{e}}) - 3 - 2 \ln (J^{\mathrm{e}}) \big ] + \frac{L}{2} \ln ^2(J^{\mathrm{e}}), \end{aligned}$$

(9)

where $\mu$ and L denote Lamé constants and only elastic deformation induces stress. The Cauchy stress is thus given by

$${\mathbf{T}} = \frac{2}{{J^{e} }}{\mathbf{F}}^{e} \frac{{\partial \psi _{R} }}{{\partial C^{e} }}{\mathbf{F}}^{{e{ \top }}} = \frac{1}{{J^{e} }}\left[ {\mu {\mathbf{B}}^{e} + (L\ln (J^{e} ) - \mu ){\mathbf{1}}} \right].{\text{ }}$$

(10)

2.2.3 Growth kinetics

The evolution of the cortical growth parameter can correlate to several potential biological events: During the early stages of development, the increase in cortical volume is associated with migration of neurons to the cortex, which depends on symmetric and asymmetric division of neural progenitor cells (Sun and Hevner 2014; Rakic 2009). During the later stages of development, tangential expansion is associated with the maturation and dendritic arborization of the neuron cells (Garcia et al. 2018). Here we hypothesize that neurons are sensitive to mechanical forces, growing differently in sulci and gyri after the onset of cortical folding. Our hypothesis is contrary to the popular pre-patterning theory, which states that inhomogeneous growth determines the cortical folding (Gómez-Skarmeta et al. 2003). More specifically, we take the mean curvature as a macroscopic evaluation of the local mechanical environment that neurons are sensing. This is not intended to suggest that cells respond to surface curvature directly, but rather than surface curvature is a convenient proxy for the differing mechanical state between gyri and sulci. Thus, the mean curvature is linked to the cortical growth rate to model the preferential cortical growth in either gyri or sulci. The evolution equation is given by

$$\begin{aligned} \dot{\vartheta }^{\mathrm{g}} = \dot{\vartheta }^{\mathrm{g}}_{\mathrm{ctx}} + \dot{\vartheta }^{\mathrm{g}}_{\mathrm{cur}}, \end{aligned}$$

(11)

where

$$\begin{aligned} \dot{\vartheta }^{\mathrm{g}}_{\mathrm{ctx}} = G^{\mathrm{ctx}} \quad \text {and} \quad \dot{\vartheta }^{\mathrm{g}}_{\mathrm{cur}} = -G^{\mathrm{ctx}} r^{\mathrm{cur}} \tanh (\kappa ^{*}) \end{aligned}$$

(12)

are the homogeneous and curvature-dependent contributions, respectively, to the total growth rate, with $G^{\mathrm{ctx}}$ the homogeneous baseline cortical growth rate constant, $r^{\mathrm{cur}}$ a curvature-sensitive parameter, and $\kappa ^*= \kappa t_{\mathrm{i}}$ the dimensionless mean curvature normalized by the initial thickness of the cortex $t_{\mathrm{i}}$. We measure the mean curvature $\kappa$ at the centroid point of each cortical element instead of at the pial surface (further details can be found in Appendix 1), and its definition is given by

$$\begin{aligned} \kappa = -\frac{1}{2} \text {div}\,\hat{{\mathbf{n}}} \end{aligned}$$

(13)

where $\hat{{\mathbf{n}}}$ denotes the current unit normal of the cortical layer and $\text {div}\,$ is the divergence with respect to the point ${\mathbf{x}}=\chi ({\mathbf{x}}_\text {R},t)$ in the deformed configuration. With this evolution equation, varying the curvature-sensitive parameter $r^{\mathrm{cur}}$ from $-1$ to 1 results in a transition from sulcal to gyral growth (Fig. 2), with the case of uniform growth reproduced when $r^{\mathrm{cur}}=0$. As a preliminary study, we assume that the subcortex does not grow, i.e., $\dot{\vartheta }^{\mathrm{g}} = 0$.

Fig. 2

The cortical growth rate $\dot{\vartheta }^{\mathrm{g}}$ as a function of the normalized mean curvature $\kappa ^*$

2.2.4 Equilibrium equation

The balance of linear momentum is given by

$$\begin{aligned} \text {div}\,{\mathbf{T}}= \rho \ddot{{\mathbf{u}}} \quad \text {and} \quad {\mathbf{T}}= {\mathbf{T}}^{\scriptscriptstyle \top }, \end{aligned}$$

(14)

where $\rho$ is the mass density, $\ddot{{\mathbf{u}}}$ the acceleration, and ${\mathbf{T}}$ the Cauchy stress given by Eq. (10). The pial surface of the deformed body has outward unit normal ${\mathbf{n}}$, and the external surface traction on an element of the deformed pial surface is given by

$$\begin{aligned} {\mathbf{t}}= P_{\mathrm{v}}{\mathbf{n}}\end{aligned}$$

(15)

with the viscous pressure written as

$$\begin{aligned} P_{\mathrm{v}} = - c_{\mathrm{v}} {\mathbf{v}}\cdot {\mathbf{n}}, \end{aligned}$$

(16)

where $c_{\mathrm{v}}$ is the viscous coefficient and ${\mathbf{v}}$ the speed of the boundary. This surface traction acts to dampen inertial effects in order to achieve a quasi-static condition, i.e., $\ddot{{\mathbf{u}}} \approx 0$ in Eq. (14).

2.3 Computational model of growth

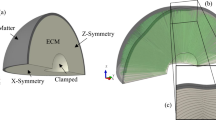
We have implemented our constitutive model in Abaqus by writing a user-defined material subroutine (VUMAT). In our numerical simulations, we model the developing brain as an idealized bilayer system consisting of a growing cortical layer with an initial thickness of $t_{\mathrm{i}}$ = $1.25\,\hbox {mm}$ and a pure elastic subcortical region. There are three different computational domains being considered: (1) 2-D rectangular brain slice with a dimension of $w \times h = 60\,\hbox {mm} \times 20\,\hbox {mm}$; (2) a quarter 2-D elliptical brain slice with a semi-major axis of $a = 36\hbox { mm}$ and a semi-minor axis of $b = 30\,\hbox {mm}$; (3) 3-D brain block with a dimension of $w \times w \times h = 30\,\hbox {mm} \times 30\,\hbox {mm} \times 10\,\hbox {mm}$. The computational domains are discretized into 2552 and 2329 four-noded quadrilateral plane-strain elements for the 2-D rectangle and quarter ellipse, respectively, and 9600 brick elements for 3-D block (Fig. 3).

In the 2-D rectangle simulation, we fix the bottom face CD and allow the nodes at faces of AD and BC to move only in the vertical direction. The top face AB is traction-free and allowed to make contact with itself and the rigid analytical surfaces (dashed-lines) without any friction. In the 2-D quarter ellipse simulation, we assign roller conditions to faces AB and AC to preserve symmetry. The curved face BC is traction-free and allowed to make contact with itself and two rigid analytical surfaces (dashed-lines). Finally, in the 3-D block simulation, its bottom face EFGH is fully fixed, and all four vertical faces are prescribed with roller conditions. The top face ABCD is again traction-free and allowed to make contact with itself, and four rigid analytical surfaces (not shown for clarity) extended from the vertical faces. To trigger instabilities, we introduce a geometric imperfection with a band of $1 \times 10^{-3}$ h in the vertical direction for both 2-D rectangle and 3-D block simulations. The results are essentially unaffected by sufficiently small imperfections (according to our simulations, imperfections less than roughly $8 \times 10^{-3}$ h). The 2-D ellipse simulation does not require an added imperfection because its curved pial surface serves as one.

Fig. 3

Geometry, finite element mesh, and boundary conditions used in the simulations of a 2-D rectangle, b 2-D quarter ellipse, and c 3-D block. Points E and C are not visible in c from the perspective depicted

3 Results

Here we demonstrate the new features of our proposed model by comparing the simulated results against the actual measurements from Sect. 2.1. Specifically, we consider two scenarios: (1) homogeneous cortical growth with various stiffness ratios and (2) inhomogeneous cortical growth with physiological stiffness ratios.

3.1 Homogeneous growth

We simulate homogeneous cortical growth by letting $r^{\mathrm{cur}} = 0$ in Eq. (12) and investigate brain morphologies for a range of cortical–subcortical stiffness ratios $\mu _{\mathrm{c}}/\mu _{\mathrm{s}} = 1 - 10$. For 2-D cases (Fig. 4), creases form when the cortex and subcortex have similar stiffnesses ($\mu _{\mathrm{c}}/\mu _{\mathrm{s}} = 1, 3$), as seen in experimental investigations (Kaster et al. 2011; Budday et al. 2015b). When using stiffness ratios of $\mu _{\mathrm{c}}/\mu _{\mathrm{s}} = 5,10$, which are much higher than those seen in the brain, the cortex buckles into more sinusoidal shapes. The amplitude of buckling, also referred to as the sulcal depth, also increases with the stiffness ratio.

Fig. 4

Simulated brain morphology in 2-D rectangle and ellipse considering homogeneous growth with four different stiffness ratios of $\mu _{\mathrm{c}}/\mu _{\mathrm{s}} = 1,3,5,$ and 10. The top images are shown at a cortical growth of $\vartheta ^{\mathrm{g}}_{\mathrm{ctx}} = 2.0$, while the bottom images are shown at a cortical growth of $\vartheta ^{\mathrm{g}}_{\mathrm{ctx}} = 2.5$

In the 3-D simulations of cortical folding, we use nine different combinations of stiffness ratio $\mu _{\mathrm{c}}/\mu _{\mathrm{s}} = [1,3,10]$ and initial thickness $t_{\mathrm{i}}/h = [0.05, 0.1, 0.2]$ (Fig. 5). Again, a transition in brain morphology from creases—or cusped sulci and smooth gyri—to smooth sinusoidal waves occurs as we increase the stiffness ratio, and the wavelength of wrinkles becomes larger as initial cortical thickness increases.

Fig. 5

Simulated brain morphology in a 3-D block with homogeneous growth at different combinations of thickness ratio $t_{\mathrm{i}}/h$ and stiffness ratio $\mu _{\mathrm{c}} / \mu _{\mathrm{s}}$. Images are shown at a cortical growth of $\vartheta ^{\mathrm{g}}_{\mathrm{ctx}} = 2.1$

Fig. 6

Effects of stiffness ratio $\mu _{\mathrm{c}}/\mu _{\mathrm{s}}$ on the gyral–sulcal thickness ratio $t_{\mathrm{g}}/t_{\mathrm{s}}$ in the case of homogeneous growth. a Evolution of gyral–sulcal thickness ratio for different stiffness ratios. b Gyral–sulcal thickness ratio as a function of stiffness ratio obtained at a cortical growth of $\vartheta ^{\mathrm{g}}_{\mathrm{ctx}} = 3$

We also investigate the effects of stiffness ratio $\mu _{\mathrm{c}}/\mu _{\mathrm{s}}$ on the gyral–sulcal thickness ratio $t_{\mathrm{g}}/t_{\mathrm{s}}$. The cortical thicknesses are measured at the apparent gyral peaks and sulcal fundi in the 2-D rectangular simulations (Fig. 4, top row). In agreement with the theoretical predictions in Holland et al. (2018), we find that the gyral–sulcal thickness ratio decreases with an increasing stiffness ratio (Fig. 6). This result suggests that gyral–sulcal thickness variations are a low-stiffness-ratio phenomenon that is less pronounced, or even absent, in large stiffness ratio systems.

3.2 Inhomogeneous growth

3.2.1 Effect of preferential cortical growth on final brain morphology

We simulate cortical folding with different combinations of curvature-dependent parameter and stiffness ratio. We vary curvature-sensitive parameter $r^{\mathrm{cur}}$ from $-2$ to 2 in Eq. (12) to achieve a transition from sulcal to gyral growth. Again, we let the cortical–subcortical stiffness ratio varying within the range of $1< \mu _{\mathrm{c}}/\mu _{\mathrm{s}} < 10$. It is worth noting that we only demonstrate 2-D quarter ellipse simulations here since the other geometries yield similar outcomes. For comparison, we use the gyrification index (GI)—the areal ratio between the entire pial surface and the convex hull—to parameterize the final brain morphology from each simulation at the cortical growth of $\vartheta ^{\mathrm{g}}_{\mathrm{ctx}} = 3$ (Fig. 7). Additionally, we demonstrate contour plots of growth parameter $\vartheta ^{\mathrm{g}}$ of nine representative cases indicated by markers in the gyrification index graph.

Interestingly, we see very little variation in brain morphology across growth modes at low stiffness ratios ($\mu _{\mathrm{c}}/\mu _{\mathrm{s}} = 1$). As the stiffness ratio increases, the variation becomes apparent, as indicated by the horizontal color gradient in Fig 7. When looking at the representative cases at the higher stiffness ratio $\mu _{\mathrm{c}}/\mu _{\mathrm{s}} = [5, 10]$, preferential gyral growth tends to yield creases, while preferential sulcal growth tends to maintain the smooth sinusoidal shape, as seen in the homogeneous growth mode. The physical insight is that the relatively thinner sulcal thickness has less bending rigidity, and therefore, crease formation is more energetically favorable at sulcal spots under the gyral growth mode. We also note that the preferential growth will not determine the exact locations of sulci and gyri, but rather serves to regulate brain morphology after the onset of mechanical buckling.

Fig. 7

Simulated brain morphology using different combinations of stiffness ratio $\mu _{\mathrm{c}}/\mu _{\mathrm{s}}$ and curvature-sensitive parameter $r^{\mathrm{cur}}$. In the gyrification index graph, markers indicate the corresponding contour plots of growth parameter $\vartheta ^{\mathrm{g}}$ from nine representative cases

3.2.2 Effect of preferential cortical growth on evolution of gyral and sulcal thicknesses

Next, we investigate the changes in gyral and sulcal thicknesses over time under a spectrum of growth modes of $r^\mathrm{cur} = [-2,-1,0,1,2]$. Based on the recent indentation tests on brains of porcine, ferret, and bovine (Van Dommelen et al. 2010; Xu et al. 2010; Budday et al. 2015b), we assume that the cortical layer has a similar stiffness as the subcortex region. Thus, we use stiffness ratio of $\mu _{\mathrm{c}}/\mu _{\mathrm{s}} = 1$ to mimic a physiological environment. We see that the gyri and sulci initially increase in thickness equally up to the point of bifurcation (Fig. 8a). This is because the roller boundary conditions constrain the lateral expansion and force the new volume to expand upward instead (I–II). After the initiation of wrinkles, gyri continue to thicken, while sulci experience a decrease from their thickness at the bifurcation (III). As growth continues, a second bifurcation may take place in which the period of the wrinkles doubles. Some folds deepen and thin, while alternating folds become shallower and regain some of their thickness (IV, Budday et al. (2015a); Holland et al. (2018)). Eventually, the folding pattern stabilizes, and the sulci keep deepening (V).

Throughout this folding process, gyral and sulcal thicknesses ($t_{\mathrm{g}}$, $t_{\mathrm{s}}$) are measured in the 2-D rectangle at the apparent gyral peaks and sulcal fundi (Fig. 8a). We find that the cortical thickness bifurcates at a volumetric change of $J^{\mathrm{g}} = \vartheta ^{\mathrm{g}}_{\mathrm{ctx}} \approx 1.85$, regardless of the type of preferential growth mode (Fig. 8b). Instead, the curvature-dependent parameter $r^{\mathrm{cur}}$ most affects the thickness gap between gyri and sulci, with the gap widening when $r^{\mathrm{cur}} > 0$ and closing when $r^{\mathrm{cur}} < 0$. We find that the thickness ratio in the uniform growth ($r^{\mathrm{cur}} = 0$) increases rapidly at the bifurcation and eventually reaches a plateau of around 2. The most gyral growth ($r^{\mathrm{cur}} = 2$) produces an even higher thickness ratio, up to 2.5, whereas in the case of most sulcal growth ($r^{\mathrm{cur}} = -2$) it decreases right after the bifurcation (Fig. 8c). Generally speaking, once gyri and sulci become stable, the curvature-sensitive parameter $r^{\mathrm{cur}}$ controls the amount of change in gyral–sulcal thickness ratio $t_{\mathrm{g}}/t_{\mathrm{s}}$ with respective to the cortical growth $\vartheta ^{\mathrm{g}}_{\mathrm{ctx}}$ (the slope in Fig. 8c). More intriguing, the slope variation on the gyral growth side is more dominant as we vary the curvature-sensitive parameter $r^{\mathrm{cur}}$. The theoretical insight is that the mean curvature is asymmetric in magnitude between gyri and sulci at the low stiffness ratio—the sulci are creases, while gyri are smooth wrinkles—accordingly, our model yields an asymmetric growth between gyral and sulcal spots.

3.2.3 Comparison between simulations and measurements

Finally, we compare our simulations in the 2-D rectangle domain against our measurements of cortical thickness in humans. Importantly, the calculated thickness ratio is highly dependent on the selection of gyral and sulcal points, and it is extremely important to be consistent in this selection for the meaningful comparison of thickness ratios across simulations, imaging, and other modalities. To demonstrate this quantitatively in our simulations, we use a piece of wrinkled cortical mesh consisting of a complete gyrus and sulcus (Fig. 9a). The apparent gyral peak and sulcal fundus are manually picked from the mesh (red and blue lines), and the gyral and sulcal regions are defined by increasing the area around the starting points until they meet (red and blue areas).

For comparison, we perform a similar analysis of $N=28$ human brains, using mean curvature as an indicator of which points are gyral ($\kappa < 0$) or sulcal ($\kappa > 0$). For consistency, we introduce a quantified measure of coverage—the number of nodes being picked for the comparison over the total number of nodes—to make the results from both simulations and measurements comparable. We consider the gyral peaks and sulcal fundi to correspond to the most-negative and most-positive mean curvature values, respectively, among the vertices. As the coverage increases, the range of mean curvature values considered increases, as points with less-negative and less-positive mean curvature are included in the analysis.

We plot the measured gyral–sulcal thickness ratio from the human brains alongside the simulations using a spectrum of curvature-dependent parameters of $r^{\mathrm{cur}} = [-2,1,0,1,2]$. Our measurements show that the mean cortical thickness of all gyral regions ($2.70\,\hbox {mm}$) is significantly higher than the one obtained from all sulcal regions ($2.02\,\hbox {mm}$), with an overall gyral–sulcal thickness ratio of $t_{\mathrm{g}}/t_{\mathrm{s}} = 1.33$. For the purpose of a robust comparison, we consider reasonable variations in our simulations, including 1) different stiffness ratios of $\mu _{\mathrm{c}}/\mu _{\mathrm{s}} = [1,3,5]$ at a fixed cortical growth of $\vartheta ^{\mathrm{g}}_{\mathrm{ctx}} = 3$ (Fig. 9b) and 2) a range of cortical growth of $\vartheta ^{\mathrm{g}}_{\mathrm{ctx}} = [2.3,2.5,2.7,3.0]$ at a fixed stiffness ratio of $\mu _{\mathrm{c}}/\mu _{\mathrm{s}} = 1$ (Fig. 9c).

We find that the gyral–sulcal thickness ratio generally decreases with the increasing coverage. Additionally, a lower variability, or a higher consistency, is achieved as coverage reaches $100\%$ in both simulations and measurements. Therefore, the comparison is most reliable at $100\%$ coverage. Our results suggest that mechanical forces alone do not produce enough thickness variation observed in the measurements under physiological condition ($\mu _{\mathrm{c}}/\mu _{\mathrm{s}}$ = 1). This supports the conclusion that increased gyral growth is partially responsible for the thickness variations seen in human brains. Gyral growth with $r^{\mathrm{cur}} \approx 1$ agrees reasonably well with our measurements at 100% coverage.

Fig. 8

Evolution of cortical thickness in 2-D rectangle considering a spectrum of cortical growth modes of $r^{\mathrm{cur}} = [-2,-1,0,1,2]$. a Contours of normalized mean curvature $\kappa ^*$ from the simulation of preferential uniform growth ($r^{\mathrm{cur}}=0$), with images shown at $\vartheta ^{\mathrm{g}}_{\mathrm{ctx}} = 1, 1.5, 2, 2.5,$ and 3, respectively. b Normalized sulcal and gyral thickness as a function of homogeneous growth parameter $\vartheta ^{\mathrm{g}}_{\mathrm{ctx}}$ with Roman numerals I–V corresponding to the contour plots in a. c Evolution of gyral–sulcal thickness ratio $t_{\mathrm{g}} / t_{\mathrm{s}}$

Fig. 9

Quantitative comparison between simulations and measurements. a Schematics of a wrinkled cortical mesh demonstrating different sampling schemes used for the comparison. Gyral–sulcal thickness ratio as a function of coverage using b the different stiffness ratios of $\mu _{\mathrm{c}}/\mu _{\mathrm{s}} = [1,3,5]$ at a fixed cortical growth of $\vartheta ^{\mathrm{g}}_{\mathrm{ctx}} = 3$ and c the different cortical growth of $\vartheta ^{\mathrm{g}}_{\mathrm{ctx}} = [2.3,2.5,2.7, 3.0]$ at a fixed stiffness ratio of $\mu _{\mathrm{c}}/\mu _{\mathrm{s}} = 1$. Simulations marked with a lighter color indicate a smaller value of stiffness ratio or cortical growth, while green bands denote the 20, 40, 60, 80, and 100 percentiles (from dark to light) of measured data from $N=28$ subjects

4 Limitations and potential improvements

Our work opens the door to investigating the role of preferential cortical growth during brain development. However, this is only a preliminary study, with several limitations and opportunities for potential improvement: First of all, while the observed thickness variation could be explained by our curvature feedback hypothesis, there are other underlying mechanisms that could yield the same observation. Thus, well-designed experiments are needed to refine our mathematical model. Secondly, in constitutive relations, we model the subcortex as a pure elastic and non-growing region. However, the subcortex consists of bundles of anisotropically oriented axons, and each axon grows in response to the physical stretch (Xu et al. 2010; Bayly et al. 2013; Holland et al. 2015). The anisotropic and viscoelastic response in the subcortex could be incorporated in the future to investigate their effects on the cortical thickness variations. Thirdly, we have used curvature as a macroscopic metric of the mechanical state of the tissue, but in reality neurons are sensitive to their surrounding mechanical environment. In the future, we will consider a more physics-based model that models this effect more directly.

5 Concluding remarks

In this work, we have developed and numerically implemented a growth theory that links the mechanics-induced curvature variations with the cortical growth rate to model preferential cortical growth in either gyri or sulci. Without any preference in cortical growth, our model suggests that the gyral–sulcal thickness variations are a low-stiffness-ratio phenomenon. We also made a meaningful comparison between simulations and measurements of $N = 28$ human brains in terms of the gyral–sulcal thickness via a consistent sampling scheme. Under a physiological stiffness ratio of $\mu _{\mathrm{c}}/\mu _{\mathrm{s}} =1$, our comparisons suggest that mechanics alone is able to predict cortical thickness patterns with some success. However, a small amount of gyral growth ($r^{\mathrm{cur}} \approx 1$) may contribute to the observed thickness difference, suggesting that the underlying biological mechanisms act to enlarge the thickness differences, with the increased cortical growth in gyri to make them thicker than they would be in the case of uniform growth. This work also implies that biological growth and mechanical forces closely interact in the process of cortical folding.

Appendix 1: Curvature calculation

In this section, we elaborate on the details of the curvature calculation in Eq. (13), starting with the 2-D case first and then extending it to a full 3-D case. The method we adopt here follows the work from Henann and Anand (2010), where they first utilized FORTRAN’s global module along with VUMAT to obtain the mean curvature, which requires non-local information.

Consider meshing the cortex into four-node quadrilateral plane-strain elements (shown in Fig. 10a). Unlike Henann and Anand (2010), we calculate the curvature at the centroid point of each element . The current coordinates of each centroid point are calculated based on the current coordinates of four integration points ($\times$) provided by Abaqus. To obtain the mean curvature at the centroid point A, we fit a parabola through point A and centroid points B and C from two adjacent elements, $y^\prime = a x^{\prime 2} + b x^\prime + c$. The fitting is based on a local coordinate $A x^\prime y^\prime$, where the outward normal $\hat{{\mathbf{n}}}$ is perpendicular to the dashed line connecting both points B and C. Note that both the slope and value of the parabola should be zero at the origin of the local coordinates, which makes the function reduce to $y^\prime = a x^{\prime 2}$ (in terms of the local coordinates). Finally, by definition, the mean curvature is $\kappa = - 1/2 (\partial ^2 y^\prime / \partial x^{\prime 2}) = - a$.

Given the global coordinates of the centroid point $A (x_0, y_0)$, and its two adjacent centroid points $B(x_1,y_1)$ and $C(x_2,y_2)$, the calculation of mean curvature at point A in 2-D is summarized as follows:

• 1. Obtain the local outward-normal $\hat{{\mathbf{n}}} = n_x {\mathbf{e}}_x + n_y {\mathbf{e}}_y$ in the global coordinate system, based on the coordinates of centroid points from two adjacent elements at $(x_1,y_1)$ and $(x_2,y_2)$, with components given by

  $$\begin{aligned} \left. \begin{aligned} n_x&= \dfrac{y_1 - y_2}{\sqrt{(y_2 - y_1)^2 + (x_2 - x_1)^2}}, \\ n_y&= \dfrac{x_2 - x_1}{\sqrt{(y_2 - y_1)^2 + (x_2 - x_1)^2}}. \end{aligned}\right. \end{aligned}$$

  (17)

• 2. Obtain the rotation matrix connecting global and local coordinates,

  $$\begin{aligned} \begin{bmatrix} {\mathbf{Q}}\end{bmatrix} = \begin{bmatrix} n_y &{} -n_x \\ n_x &{} n_y \\ \end{bmatrix}. \end{aligned}$$

  (18)

• 3. Obtain the coordinates of centroid points from adjacent elements in terms of local coordinates,

  $$\begin{aligned} \left. \begin{aligned} \begin{bmatrix} x^{\prime }_1 \\ y^{\prime }_1 \\ \end{bmatrix}&= \begin{bmatrix} {\mathbf{Q}}\end{bmatrix} \begin{bmatrix} x_1 - x_0 \\ y_1 - y_0 \end{bmatrix}, \\ \begin{bmatrix} x^{\prime }_2\\ y^{\prime }_2\\ \end{bmatrix}&= \begin{bmatrix} {\mathbf{Q}}\end{bmatrix} \begin{bmatrix} x_2 - x_0\\ y_2 - y_0 \end{bmatrix}. \end{aligned}\right. \end{aligned}$$

  (19)

• 4. Perform a linear least squares fit to the system of equations

  $$\begin{aligned} \begin{bmatrix} y^{\prime }_1\\ y^{\prime }_2\\ \end{bmatrix} = a \begin{bmatrix} x^{\prime 2}_1\\ x^{\prime 2}_2\\ \end{bmatrix}, \end{aligned}$$

  (20)

  , which yields

  $$\begin{aligned} a = \dfrac{x^{\prime 2}_1 y^{\prime }_1 + x^{\prime 2}_2 y^{\prime}_2}{x^{\prime 4}_1 + x^{\prime 4}_2}. \end{aligned}$$

  (21)

• 5. Calculate mean curvature as

  $$\begin{aligned} \kappa = -\dfrac{1}{2} \dfrac{\partial ^2 y^\prime }{\partial x^{\prime 2}} = -a. \end{aligned}$$

  (22)

The procedure for the 3-D case is similar but more tedious. Centroid point A again served as our point of interest. To calculate the mean curvature at point A, we fit a paraboloid through it and its eight nearest centroid points. The details are summarized as follows:

• 1. Find point A’s eight nearest neighbors by using the insertion sort algorithm.

• 2. Obtain the local outward-normal $\hat{{\mathbf{n}}} = n_x {\mathbf{e}}_x + n_y {\mathbf{e}}_y + n_z {\mathbf{e}}_z$ in the global coordinate system by fitting the surface equation $z = ax + by + c$ to the eight nearest centroid points. The components are given by

  $$\begin{aligned} \left. \begin{aligned} n_x&= \dfrac{-a}{\sqrt{a^2 + b^2 + 1}}, \quad n_y = \dfrac{-b}{\sqrt{a^2 + b^2 + 1}}, \\ n_z&= \dfrac{1}{\sqrt{a^2 + b^2 + 1}}. \end{aligned}\right. \end{aligned}$$

  (23)

• 2. Obtain the rotation matrix linking global to local coordinates,

  $$\begin{aligned} \begin{bmatrix} {\mathbf{Q}}\end{bmatrix} = \begin{bmatrix} \dfrac{n_x^2 n_z + n_y^2}{n_x^2 + n_y^2} &{} \dfrac{-n_x n_y (1 - n_z)}{n_x^2 + n_y^2} &{} -n_x\\ \dfrac{-n_x n_y (1 - n_z)}{n_x^2 + n_y^2} &{} \dfrac{n_x^2 + n_y^2 n_z}{n_x^2 + n_y^2} &{} -n_y\\ n_x &{} n_y &{} n_z \end{bmatrix}. \end{aligned}$$

  (24)

• 3. Obtain the position of the eight nearest centroid points in terms of local coordinates,

  $$\begin{aligned} \begin{bmatrix} x_i^\prime \\ y_i^\prime \\ z_i^\prime \end{bmatrix} = \begin{bmatrix} {\mathbf{Q}}\end{bmatrix} \begin{bmatrix} x_i - x_0\\ y_i - y_0 \\ z_i - z_0 \end{bmatrix} \quad \text {for} \quad i = 1 \,\,\text {to} \,\,8. \end{aligned}$$

  (25)

• 4. Perform a linear least squares fit to the system of equations

  $$\begin{aligned} z_i^\prime = \alpha x^{\prime 2}_i + \beta y^{\prime 2}_i + \gamma x_i^\prime y_i^\prime \quad \text {for} \quad i = 1 \,\,\text {to} \,\,8, \end{aligned}$$

  (26)

  which yields eight equations with three unknowns. Let $[d]^{\scriptscriptstyle \top }$ denote an array of the three unknowns ($\alpha$, $\beta$, $\gamma$) and $[z]^{\scriptscriptstyle \top }$ denote an array of the eight measured values of $z_i$, and [A] denote an 8-by-3 matrix storing the values $(x^{\prime 2}_i, y^{\prime 2}_i, x^\prime_i y^\prime_i )$ for $i=1$ to 8. Thus, equation (26) can be rewritten

  $$\begin{aligned} \begin{bmatrix} A \end{bmatrix} \begin{bmatrix} d \end{bmatrix}^{\scriptscriptstyle \top } = \begin{bmatrix} z \end{bmatrix}^{\scriptscriptstyle \top }, \end{aligned}$$

  (27)

  with the optimal solution given by

  $$\begin{aligned} \begin{bmatrix} d \end{bmatrix}^{\scriptscriptstyle \top } =\big (\begin{bmatrix} A \end{bmatrix}^{\scriptscriptstyle \top } \begin{bmatrix} A \end{bmatrix} \big )^{-1} \begin{bmatrix} A \end{bmatrix}^{\scriptscriptstyle \top } \begin{bmatrix} z \end{bmatrix}^{\scriptscriptstyle \top }. \end{aligned}$$

  (28)

• 6. Calculate mean curvature as

  $$\begin{aligned} \kappa = - \dfrac{1}{2} \bigg ( \dfrac{\partial ^2 z^\prime }{\partial {x^{\prime 2}}} + \dfrac{\partial ^2 z^\prime }{\partial {y^{\prime 2}}} \bigg ) = - (\alpha + \beta ). \end{aligned}$$

  (29)

The algorithm was implemented in both our user-defined subroutine (VUMAT) and MATLAB. We verified our implementations by comparing the calculated mean curvature values at the middle surface of the wrinkled cortex between the two programs (Fig. 11).

Fig. 10

Schematics of finite element mesh used in the cortex. a 2-D four-noded equilateral plane-strain elements and b 3-D brick elements. Note integration points are denoted as cross markers, and the centroid points are denoted as red circles

Fig. 11

Verification of our curvature calculation algorithm. a Profiles of wrinkled cortex with boundary and centroid points denoted as black symbol lines and red circles. b Comparison of mean curvatures at the centroid points between MATLAB and Abaqus