1 Introduction

Skeletal tissue engineering (TE) strategies hold a great promise for the regeneration of bone and cartilage based on the combination of bioreactors, 3D biomaterials and mesenchymal stem cells (MSCs). MSCs are progenitor cells crucial for skeletal TE applications due to their ability to undergo osteogenic and chondrogenic differentiation under the influence of various biochemical, biophysical and, importantly, biomechanical cues. Perfusion bioreactors have been extensively employed for the expansion and differentiation of MSCs providing sufficient mass transport for cell growth and differentiation (Sikavitsas et al. 2005; Grayson et al. 2011; Sonnaert et al. 2014). Furthermore, shear stress can determine early stem cell lineage commitment (Song et al. 2013) but also promote terminal osteogenic differentiation of bone marrow, periosteum and adipose-derived MSCs and enhance extracellular matrix (ECM) deposition (McCoy et al. 2010; Rauh et al. 2011; Papantoniou et al. 2013). There is a substantial body of the literature illustrating the osteogenic effect of mechanical stimulation either due to fluid flow or mechanical compression (or stretching) on the differentiation of MSCs when cultured in dynamic environments seeded on 3D scaffolds in vitro (Wang et al. 2013; Delaine-Smith et al. 2011).

In scaffold-based perfusion bioreactor culture, 3D cell growth and neotissue formation have been observed to begin with 2D cell proliferation on the scaffold strut surface. Subsequently, cells bridge scaffold struts and start growing toward the pore void followed by ECM deposition. Eventually, 3D cell growth will result in scaffold void filling, something that has been studied recently using computed tomography imaging techniques (Voronov et al. 2013; Papantoniou et al. 2014). The calculation of wall shear stress values in empty scaffold geometries are therefore indicative of the shear stress experienced by cells during early culture time (Truscello et al. 2011). A current challenge to further advance and utilize computational modeling strategies in the TE field is to comprise a domain composed of cells and ECM (a growing permeable neotissue) on real 3D scaffold geometries. There are intriguing 2D studies investigating this (Sacco et al. 2011; Hossain et al. 2014); however, it was recently shown that without the third dimension, model parameters were overestimated, losing accuracy in the representation of neotissue growth (Nava et al. 2013).

Computational fluid dynamics (CFD) modeling has been extensively used in the field of TE [for review, see Hutmacher et al. (2008), Hossain et al. (2012), Patrachari et al. (2012)]. The quantification of flow-associated shear stresses as well as their spatial distribution within various 3D scaffold geometries has been thoroughly investigated in perfused bioreactor setups (Raimondi et al. 2004; Porter et al. 2005; Boschetti et al. 2006; Cioffi et al. 2006; Jungreuthmayer et al. 2009; Maes et al. 2009; Voronov et al. 2010). In previous studies, local shear stresses were defined as a function of flow rate of the culture medium, bioreactor configuration, porosity and porous scaffold microarchitecture (Voronov et al. 2010; Pham et al. 2012). Most 3D CFD studies to date only use empty scaffold geometries to calculate shear stress magnitude and distribution across the empty scaffold surface, i.e., wall shear stress. The aforementioned studies do not take into account the transient nature of the 3D neotissue domain as a result of neotissue growth which has been observed experimentally (Papantoniou, Sonnaert et al. 2014). There have been few attempts to capture 3D neotissue growth on scaffolds, limited to gradually increasing scaffold struts (Lesman et al. 2010), representing the neotissue layer as an impermeable domain. A recent interesting study describes the growth of a ‘biomass’ domain (similar to what we term neotissue in this study) whose growth was coupled to oxygen concentration and shear stress (Nava et al. 2013).

In addition to flow-associated shear stress, neotissue growth kinetics have been also linked to the geometric features of scaffolds. Pore size (Zeltinger et al. 2001), pore shape (Knychala et al. 2013) and more specific features such as local curvature (Rumpler et al. 2008; Gamsjager et al. 2013) have been demonstrated to control cell fate for both in vitro (Rumpler et al. 2008; Guyot et al. 2014) and in vivo applications (Bidan et al. 2012).

Building on our previous studies where we investigated the effect of local curvature on in vitro 3D growth (Guyot et al. 2014) and where we used the evolving neotissue growth in a 3D scaffold to accurately determine the shear stress values in both the void space and the neotissue during the bioreactor culture process (Guyot et al. 2015), this study demonstrates the added value of using also the shear stress as a parameter that influences the neotissue growth. Hereto this study shows the development of a level-set-based computational tool able to capture the difference in growth of a microporous neotissue domain in a dynamic culture environment (perfusion bioreactor) under different flow rates. Capturing this difference is only possible by the explicit incorporation of flow-induced shear stresses as a parameter in the calculation of the neotissue growth velocity [alongside the scaffold geometry which was already present (Guyot et al. 2014)]. This tool provides the ability to steer fluid flow during long-term culture in order to provide given shear stress profiles and magnitudes across the whole scaffold volume.

2 Methods

In this section, the model describing the neotissue growth, the calculation of the flow-induced shear stresses and the influence of the latter on the former will be explained.

2.1 Neotissue growth via the level set method

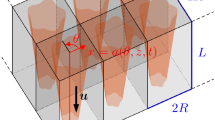
The growth-induced changes in the neotissue topology during the culture process can be seen as a moving interface between two different domains (Sethian 1999): In this study, one domain represents the neotissue volume \(\varOmega _\mathrm{nt} \), and the other one is the void \(\varOmega _\mathrm{v}\), separated by an interface \(\varGamma \), with a normal \({\varvec{n}}_{{\varvec{\Gamma }}}\) (see Fig. 1b). The level set method (LSM) is a technique that has been developed to deal with this kind of moving interfaces, and it is used in the context of this study to simulate the evolution of the frontline \(\varGamma \) between neotissue and void space in a mesh-free manner. The principle of the LSM consists in defining a signed distance function \(\varphi \) in \(\varOmega =\varOmega _\mathrm{nt} \cup \varOmega _\mathrm{v}\) with the following properties:

$$\begin{aligned} \left\{ {{\begin{array}{l} {\varphi >0\quad \textit{in }\varOmega _\mathrm{nt} } \\ {\varphi <0\quad \textit{in }\varOmega _\mathrm{v}} \\ {\varphi =0\quad \textit{on }\varGamma } \\ \end{array} }} \right. \end{aligned}$$
(1)

In order to capture the evolution of the moving interface \(\varGamma \), the following transient advection equation is solved with a given growth velocity \({\varvec{v_G}}\) and homogenous Neumann boundary condition (\(\partial \varphi /\partial {\varvec{n}} = 0\), with \({\varvec{n}}\) being the normal to the computational domain \(\varOmega )\).

$$\begin{aligned} \frac{\partial \varphi }{\partial t}+{\varvec{v_G}} \cdot \nabla \varphi =0\,\mathrm{in}\,\varOmega . \end{aligned}$$
(2)

With \({\varvec{v_G}} =V_{G}{*}{{{\mathbf {n}}}_{\varvec{\Gamma }}}\), and \({{\mathbf {n}}}_{\varvec{\Gamma }} =\frac{\nabla \varphi }{\left| {\nabla \varphi } \right| }.\) The expression of the growth velocity magnitude \(V_{G}\) will be described later. The initial configuration of the distance function \(\varphi \) corresponds to a homogenous single cell layer over the scaffold struts with a thickness equal to \(20\,\upmu \hbox {m}\) (Darling et al. 2008). The time discretization of Eq. (2) was done using the backward Euler method, and the advection term was treated with the method of characteristics. For more details about the implementation, please refer to (Guyot et al. 2014).

Fig. 1
figure 1

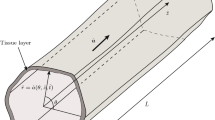
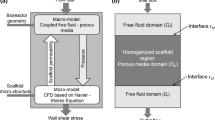
Model setup. a Representation of the scaffold and the bioreactor chamber; the region of interest is delimited by two yellow circles. The scaffold is then removed from a cylinder representing the delimited area. Finally, a mesh is created in the computational domain. b Schematic representation of curvature- driven neotissue growth using the level set method. c Schematic representation of the Brinkman approximation used in this study. d The influence of shear stress on the neotissue growth velocity in this study (right) is a combination of the continuous shape proposed by Nava et al. (2013) and the values by Chapman et al. (2014) (middle)

Full size image

2.2 Shear stress distribution

During dynamic culture, the neotissue grows, eventually filling up the whole scaffold void. These changes affect the flow patterns developed, depending on the presence (or not) of neotissue, and so the flow profile has to be treated differently in \(\varOmega _\mathrm{nt}\) and \(\varOmega _\mathrm{v}\) [as described in detail in Guyot et al. (2015)]. In \(\varOmega _\mathrm{v}\), due to a low Reynolds number (\(Re<1\)), the flow profile was approximated via the Stokes Eq. (3). In \(\varOmega _\mathrm{nt}\), the complex structure of the neotissue can be seen as a homogenous porous medium with a given permeability \(K_0 \), leading to the flow profile being calculated with the Darcy Eq. (4). According to the definition of the LSM, the interface \(\varGamma \) is never conforming to the computational mesh, resulting in difficulties to couple Eqs. (3) and (4) together with suitable boundary conditions at the interface. To overcome this, the Brinkman Eq. (5) was used to calculate the flow profile in the whole domain \(\varOmega \) (see Fig. 1c). A no-slip boundary condition was applied on the scaffold surface as well as on the chamber walls. The scaffold was placed at a sufficient distance from the inlet avoiding refluxes occurring at the entrance of the scaffold (Papantoniou et al. 2014), so the boundary condition for the inflow was set to a Poiseuille profile with a velocity u corresponding to the given flow rate Q.

$$\begin{aligned}&\left\{ {{\begin{array}{l} {-\mu \Delta {\varvec{u}}+\nabla p=0\quad \hbox {in }\varOmega _\mathrm{v} } \\ {\nabla \cdot {\varvec{u}}=0\quad \hbox {in }\varOmega _\mathrm{v} } \\ \end{array} }} \right. \end{aligned}$$
(3)
$$\begin{aligned}&\left\{ {{\begin{array}{l} {\frac{\mu }{K_0 }{\varvec{u}}+\nabla p=0\quad \hbox {in }\varOmega _\mathrm{nt} } \\ {\nabla \cdot {\varvec{u}}=0\quad \hbox {in}\,\varOmega _\mathrm{nt} } \\ \end{array} }} \right. \end{aligned}$$
(4)
$$\begin{aligned}&\left\{ {{\begin{array}{l} {-\mu \varDelta {\varvec{u}}+\nabla p+\frac{\mu }{K}{\varvec{u}}=0\quad \hbox {in }\varOmega } \\ {\nabla \cdot {\varvec{u}}=0\quad \hbox {in }\varOmega } \\ \end{array} }} \right. \end{aligned}$$
(5)

This technique can be seen as a penalization method; indeed, when K is equal to the neotissue permeability \((K\ll 1)\) in \(\varOmega _\mathrm{nt} \), it makes the Stokes term in (5) negligible. At the contrary, when K is set to a very high value \((K\gg 1)\) in \(\varOmega _\mathrm{v} \), it leads to the Darcy term to be close to zero. To avoid numerical problems, this switch between the two values was implemented using a space- and time-dependent smeared-out Heaviside function H (6), and K was updated according to this function (7) (\(\varepsilon =1.5\) h, with h the mesh size).

$$\begin{aligned} H(\varphi )= & {} \left\{ {{\begin{array}{l} {0,\quad \varphi <-\varepsilon } \\ {\frac{1}{2}+\frac{\varphi }{2\varepsilon }+\frac{1}{2\pi }\sin \left( {\frac{\pi \varphi }{\varepsilon }} \right) ,\quad -\varepsilon <\varphi <\varepsilon } \\ {1,\quad \varphi >-\varepsilon } \\ \end{array} }} \right. \end{aligned}$$
(6)
$$\begin{aligned} K({\varvec{x}})= & {} 10^{30}(1-H)+K_0 H \end{aligned}$$
(7)

The parameter \(K_0\) was estimated using the random fibers theory approximation. In Nabovati et al. (2009), the authors provide an approximation of the permeability of a porous media made of a random fiber web:

$$\begin{aligned} K_0 =0.491 \delta ^{2}\sqrt{\frac{1-\psi _\mathrm{c} }{1-\psi }-1}^{2.31}. \end{aligned}$$
(8)

In this equation, \(\psi \) represents the porosity of the media (neotissue, assumed to be equal to 90 % in this study, which is in the range of porosities of soft tissues and hydrogels) and \(\psi _\mathrm{c}\) corresponds to a percolation threshold or a threshold porosity where flow is permitted (set to zero in this study). Finally, \(\delta \) represents the micropore size of the neotissue and was set to \(50\,\upmu \hbox {m}\), assuming the pore size equal to half to one-third of the size of a fully spread cell of the type used in this study (Eyckmans et al. 2012).

In this study, we distinguished two different wall shear stresses acting on cells depending on their location. The first one \((SS_\mathrm{Surf} )\) is the shear stress acting on the interface \(\varGamma \) due to the different flow profiles from either side and is calculated with the usual definition:

$$\begin{aligned}&SS_\mathrm{surf} =\sqrt{\tau _{12} ^{2}+\tau _{23} ^{2}+\tau _{13}^{2}},\quad \mathrm{with}\nonumber \\&\tau _{ij} =\mu \left( {\frac{\partial u_i }{\partial x_j }+\frac{\partial u_j }{\partial x_i }} \right) . \end{aligned}$$
(9)

The second one \((SS_\mathrm{In})\) is the shear stress acting within the neotissue, and it is associated with the interstitial flow through the microporous neotissue and is approximated following the method presented in Whittaker et al. (2009). This method is based on the fact that the microporous neotissue is assumed to be composed of cylindrical ducts of diameter \(\delta \). Since the Darcy equation just gives the average (Darcy) velocity u, the interstitial velocity magnitude \(u_\mathrm{in}\) is calculated from results of Eq. (5) and is turned into a Poiseuille velocity profile \((u_\mathrm{p})\) in a cylindrical channel in order to have an analytical expression of local wall shear stress (on the wall of the cylindrical ducts, representing here the micropores), allowing for the estimation of \({SS}_\mathrm{in}\).

$$\begin{aligned} u_\mathrm{in}= & {} \left| {\varvec{u}} \right| /\psi \end{aligned}$$
(10)
$$\begin{aligned} u_\mathrm{p}\approx & {} 2u_\mathrm{in} \left( {1-\left( {\frac{2r}{\delta }} \right) ^{2}} \right) \end{aligned}$$
(11)
$$\begin{aligned} SS_\mathrm{In}= & {} \mu \left| {\frac{\partial u_\mathrm{p} }{\partial r}} \right| _{r=\delta /2} \approx \frac{8\mu u_\mathrm{in} }{\delta }\approx \frac{8\mu |{\varvec{u}}|}{\delta \psi } \end{aligned}$$
(12)

2.3 Neotissue growth velocity

A key parameter of the study is the local growth velocity of the neotissue. In Guyot et al. (2014), this space-dependent velocity was only depending on the local mean curvature of the interface as it has been shown in Bidan et al. (2012) or Rumpler et al. (2008). Another important growth-influencing factor is the local shear stress on cells. In Nava et al. (2013), authors present a biomass growth model for cartilage describing an interface moving in time in function of the fluid-induced shear stress, and in Chapman et al. (2014), the authors introduce a growth model for cell aggregates in hollow fiber bioreactors where cell population growth increased or decreased depending on wall shear stresses experienced by cells. In this study, a similar approach is used and the local neotissue growth velocity \(V_{G} \) is described as a function of both the mean curvature and the flow-induced shear stress:

$$\begin{aligned} V_{G} =A\cdot f({SS_\mathrm{surf}})\cdot g(\kappa ). \end{aligned}$$
(13)

The neotissue growth velocity parameter A was estimated from the experimental data obtained for the low-flow-rate results obtained in Papantoniou et al. (2014) using a trial-and-error approach and was set equal to \(4\times 10^{-14}\hbox { m}^{2}/\hbox {s}\). As described extensively in Guyot et al. (2014), the basis of the influence of curvature on the neotissue growth comes from the observation that neotissue grows faster where the curvature is higher and that it does not grow if the curvature is negative or equal to zero (Bidan et al. 2013). The mean curvature influence function \(g(\kappa )\) can therefore be expressed mathematically as follows:

$$\begin{aligned} g(k)=\left\{ {{\begin{array}{lll} -\kappa &{}\quad \mathrm{if}&{}\kappa >0 \\ 0&{}\quad \mathrm{if}&{}\kappa \le 0 \\ \end{array} }} \right. , \end{aligned}$$
(14)

where \(\kappa \) is the local mean curvature (\({\upkappa }=\nabla \cdot {{\mathbf {n}}}_{\varvec{\Gamma }}\)) and the second row of Eq. (14) depicts that there is no growth when the curvature is null or negative. The negative sign in Eq. (14) comes from the fact that according to our definition of \(\varphi \), the normal \({{\mathbf {n}}}_{\varvec{\Gamma }}\) points toward neotissue, so growth has to be toward the opposite of \(\nabla \varphi \). The surface shear stress influence function \(f({SS_\mathrm{surf}})\) (unit less) was inspired by Nava et al. (2013) (Fig. 1d) and defined as a continuous function

$$\begin{aligned} f\left( {SS_\mathrm{surf} } \right) =\left\{ {{\begin{array}{ll} 0.5+\frac{0.5\cdot SS_\mathrm{surf} }{a_1 }&{}\quad 0\le SS_\mathrm{surf} <a_1 \\ 1 &{}\quad a_1 \le SS_\mathrm{surf} <a_2 \\ \frac{SS_\mathrm{surf} -a_3 }{a_2 -a_3 }&{}\quad a_2 \le SS_\mathrm{surf} <a_3 \\ 0&{}\quad a_3 \le SS_\mathrm{surf} \\ \end{array} }} \right. \end{aligned}$$

This function was established in order to have an optimal shear stress influence that enhances the growth (\(a_1 <SS_\mathrm{surf} <a_2 )\) and a critical threshold (\(SS_\mathrm{surf} >a_3 )\) above which shear stress inhibits the cells and growth cannot occur anymore; in this study, \(a_1 ,a_2 and a_3 \) were, respectively, set to 0.01, 0.03 and 0.05 Pa (Chapman et al. 2014). Table 1 summarizes all the parameters used in the calculation of the neotissue growth velocity \(v_{G}\).

Table 1 Model parameters used for the calculation of the neotissue growth rate \(v_{G}\)
Full size table

2.4 Implementation

The full model was implemented with the free partial differential equation solver FreeFem++ (2012). The computational domain (see Fig. 1a) chosen consisted of the part of the perfusion bioreactor chamber comprising the entire scaffold including 2 mm of the chamber at each scaffold side. This was done in order to avoid numerical refluxes and was meshed with approximately 3 million tetrahedrons. The numerical problem was solved in parallel using a 12 core facility. In order to avoid unnecessary computational effort, the Brinkman equation was solved on only one quarter of the full mesh cut along the flow axis and with respect to symmetrical boundary condition.

2.5 Summary of experimental setup

In this study, results presented in Papantoniou et al. (2014) were used in a first calibration and validation setup. The setup of the experiment is briefly repeated below. Three-dimensional additive manufactured open porous Ti6Al4V scaffolds (Ø = 6 mm, h = 6 mm, \(\hbox {porosity} = 73\pm 1\) %, strut \(\hbox {diameter} = 245 \pm 2\) mm and pore \(\hbox {size} = 755 \pm 3\) mm), produced on an in-house developed selective laser melting machine (Van Bael et al. 2011) were used. Human periosteal-derived stem cells (hPDCs, one of the known sources of MSCs) were isolated from periosteal biopsies of different donors as described previously (Eyckmans et al. 2006) and expanded in culture flasks. When a sufficient amount of these cells was produced in this 2D culture (number of population doublings = 15), cells were harvested by trypsinization with Tryple Express (Invitrogen) and seeded on the scaffolds, which marked the start of the bioreactor experiment. The TE constructs were cultured in an in-house developed bioreactor for 14, 21 and 28 days under dynamic culture conditions (\(n = 9\) per flow rate—in triplicate per time point). Two different perfusion flow rates were used: 4 ml/min (\(Q_{1}\), high) and 0.04 ml/min (\(Q_{2}\), low). After culture, three constructs for each time point were prepared for contrast-enhanced nanofocus Computed Tomography (NanoCT) imaging (Kerckhofs et al. 2013) allowing for visualization and quantification of the neotissue volume formed inside the constructs.

3 Results

The model was run for different flow rates according to the experimental setup described in Papantoniou et al. (2014). Simulations show a significant difference between the two conditions regarding the total amount of neotissue that has been produced at different time points (Figs. 2, 3). Indeed, under the high flow rate, the local shear stress acting on the neotissue interface is higher than for the lowest flow rate, resulting in an acceleration of neotissue growth. Although differences can be observed between the simulations and experiments, the simulations are capable of capturing the experimentally observed differences between the two flow rates in terms of volume filling (Fig. 3b). The model was also able to compute quantitative data (shown in Fig. 4) regarding important culture variables during neotissue growth such as pressure drop across the scaffold along the flow axis, average surface and inner shear stresses, giving an overview of different mechanical stimuli acting on cells over culture time.

Fig. 2
figure 2

Neotissue growth (green) on scaffold (gray) at different time points for two different flow rates and two different views (direction of flow rate is from bottom to top in side view). Gradual scaffold pore closure can be observed. Scale bar represents 1 mm

Full size image
Fig. 3
figure 3

Comparison between simulations and experimental results (Papantoniou et al. 2014). a Evolution of volume filling over culture time for the two different flow rates used in this study. Experimental results are presented through the mean and standard deviation (\(n=3\)). b Quantitative differences in volume filling between the different flow rates, indicating that the simulated differences are similar to those experimentally observed

Full size image
Fig. 4
figure 4

Mechanical characterization of the predicted tissue growth for flow rates \({Q}_{1}\) (4 ml/min, left) and \({Q}_{2}\) (0.04 ml/min, right). a Pressure drop between the entrance and the exit of the scaffold. b Average neotissue surface shear stress. c Average inside neotissue shear stress. Notice the difference in scale on the vertical axes between left and right figures

Full size image

The pressure drop (Fig. 4a) across the scaffold varied from almost 4 Pa in the first days of culture to 11 Pa at day 28 for the high flow rate \(Q_{1}\), while it ranged from 0.03 to 0.08 Pa for the low flow rate \(Q_{2}\) in an equivalent period of time. The surface shear stresses (Fig. 4b) and inside shear stresses (Fig. 4c) differed by a factor of 100 between the two different flow rates. For both flow rates, the inner shear stress, the stress acting on cells embedded into the neotissue, can be around 3 (for early time points) to 20 (for late time points) times bigger than the interface shear stress acting on cells at interface in contact with the free flow. Figure 5 shows how the flow regime changes from when the scaffold is almost empty (Fig. 5a) to where it is partially filled (Fig. 5b). Figure 6 depicts the local growth velocity \(v_G\) showing the influence of the distributed shear stress as well as the local mean curvature of the surface. Maximal neotissue growth velocities of 3 and \(7\,\upmu \hbox {m}\)/day were obtained for the low and high flow rates, respectively.

Fig. 5
figure 5

Close-up view on a section of the scaffold illustrating the different flow profiles (u) at early (a) and late (b) time points (neotissue volume is indicated in pink). a The scaffold is almost empty, so the flow is mostly ruled by the Stokes equation leading to Poiseuille flow in the bottom part. b The bottom part of the scaffold is completely filled with neotissue, so the flow profile in this area is ruled by the Darcy equation. Plus scaffold, square neotissue, triangle void

Full size image
Fig. 6
figure 6

Local distribution of the neotissue growth velocity \({v}_{g}\) (m/s) at the neotissue–void interface at 28 days for flow rates \({Q}_{2}\) (0.04 ml/min, left) and \({Q}_{1}\) (4 ml/min, right). The neotissue is indicated in light gray)

Full size image

4 Discussion

Understanding spatiotemporal cell growth in dynamic cultures constitutes a challenge in TE, in particular the quantification, distribution and interplay between scaffold geometry, shear stress and neotissue growth. The present model provides a foundation that will allow the quantitative investigation of the effect of shear stresses on cell growth and ECM production, which today is still not well understood. The most important contribution of this study is the extension of a previously developed model of local curvature-dependent neotissue growth to incorporate the influence of the local shear stresses on the neotissue growth, on complete scaffolds in 3D. The importance of 3D models in comparison with 2D has been shown by Nava et al. (2013), the latter suffering from a lack of accurate representation which leads to loss of information and an incorrect parameter estimation.

Recent experimental observations have revealed that hPDCs (the MSC source used in this study) may grow in the third dimension by bridging scaffold struts, leading to complete filling of scaffold pores when cultured in perfusion bioreactors in glucose-based growth medium (Sonnaert et al. 2014) and in growth factor containing osteogenic medium (Papantoniou et al. 2013). NanoCT imaging has been employed to confirm that complete pore closure could be obtained depending on bioreactor operating conditions (Papantoniou et al. 2014). Similar 3D cell growth behavior upon seeding on scaffolds has been also observed for other cell types such as human bone marrow MSCs (Zhao et al. 2005; Li et al. 2009), primary fibroblasts (Joly et al. 2013) and cell lines such as MC3T3-E1 pre-osteoblast cells (Kommareddy et al. 2010). This opens the possibility to create 3D in vitro tissue-like structures where cells may grow independently of the initial scaffold surface allowing for the study of the interaction between cells and their own ECM and the culture environment. Additionally, this means that when simulating the experimentally observed void filling due to 3D neotissue growth, models should take into account the specificity of the experimentally used cell type (Chapman et al. 2014). In this work, we attempt to investigate this for adult stem cell types in particular for hPDCs.

Neotissue growth kinetics in 3D dynamic and scaffold-based culture setups has been linked with oxygen level (Zhao et al. 2005), shear stress (Nava et al. 2013) and scaffold geometry—in particular curvature (Bidan et al. 2013; Knychala et al. 2013). In our study, oxygen was not investigated since for the flow rate and scaffold dimensions used in this work, taking into account the oxygen consumption rate of hPDCs (Lambrechts et al. 2014), there is no significant oxygen drop detected from inlet to outlet. Therefore, the assumption that the whole cell population is exposed to the same level of dissolved oxygen tension (atmospheric) seems to be justified. When other flow regimes and/or other cell types will be studied, this assumption has to be re-evaluated. An additional assumption was the existence of an initial single cell layer at the start of the simulations. This layer was assumed to be \(20\,\upmu \hbox {m}\) based on 2D suspended MSC diameter values (Darling et al. 2008), leading to an initial filling percentage of 18 %. Provided that a high number of cells are used for cell seeding (Chen et al. 2011), a homogeneous distribution can indeed be achieved across the scaffold. This step has been studied in detail for regular geometry scaffolds (Melchels et al. 2011). The initial filling percentage is likely an overestimation of the real filling and is (in its current way of calculating) dependent on the available surface of the scaffold under study. With the currently used measurement technique (NanoCT), the experimental value for the initial filling cannot be obtained due to the absence of matrix produced by the cells immediately after seeding. This parameter therefore merits further study in future work. Neotissue shrinkage/loss due to cell death was not incorporated in the presented model; however, there is a possibility that this shrinkage/loss occurs for those cases where excessively harsh culture conditions are developed, i.e., very low dissolved oxygen tension (anoxia) and glucose concentration or high lactate concentration (Flaibani et al. 2010). Further efforts are required in order to incorporate the aforementioned physicochemical components in our model. However, this is out of the scope of the present study, where geometry and fluid dynamics are the main regulators of neotissue growth.

In this study, neotissue growth velocity was coupled to the local scaffold topography (curvature) (Guyot et al. 2014) and local fluid flow-induced shear stress. Shear stress was modeled to enhance increasingly neotissue growth from 0 to \(a_1 \) reaching a maximum value between \(a_1 \) and \(a_2 \) (equal to 0.01 and 0.03 Pa, respectively). The lower amount of neotissue observed at the periphery of the scaffolds is due to the low values of fluid flow- induced shear stresses at that location. This in turn is due to the flow demonstrating a Poiseuille profile when entering the scaffold, thereby positively influencing to a greater extent the neotissue formation at the center of the scaffold. When the shear stress reaches threshold \(a_3 \) equal to 0.05 Pa, its effect on neotissue growth was modeled to change into a prohibitive one with decreasing neotissue growth for increasing shear stresses beyond \(a_{3}\). Experimental observations of 0.015 Pa as an optimum shear stress level for human bone marrow MSCs cultured in perfusion bioreactors confirmed this hypothesis (Li et al. 2009). A similar range of shear stresses has been reported for human bone marrow MSCs by Grayson et al. (2010) although these values referred to empty scaffold geometries. We have recently experimentally observed the adverse effects of excessive shear stress on neotissue growth by hPDCs in perfusion bioreactors resulting in inhomogeneous tissue- engineered constructs (Papantoniou et al. 2014). This was observed for shear stress values in excess of 0.05 Pa which is the threshold value used in this study. Interestingly (McCoy et al. 2012) estimated a critical threshold for human bone MSC detachment from irregular scaffolds at 0.088 Pa closely matching the one used here, taking into account the differences in scaffold architecture and cell type.

The growth velocity term A was estimated in a trial-and-error fashion based on in-house experimental observations (Papantoniou et al. 2014) measuring neotissue growth on the simulated scaffold for the low flow rate \(Q_{2}\) . The prediction obtained for the high flow rate \(Q_{1}\) shows an increase in volume filling, similar to the experimental data (Fig. 3b). The discrepancy observed between experimental and computationally derived neotissue growth kinetics seen in Fig. 3 could be attributed to numerical and physical factors. For the former (numerical factor), we did not go through an objective and rigorous optimization process to find the value for A because of the insufficient quantity of experimental data available. In a follow-up study, dedicated experimental data will be generated to parametrize the model. As to the latter (physical factor), neotissue growth kinetics do not solely depend upon scaffold geometry and shear stress magnitude. The introduction in the model of additional physicochemical parameters that are well known for their influence on neotissue growth such as dissolved oxygen tension (Grayson et al. 2007; Santos et al. 2010), glucose concentration (Saki et al. 2013) and lactate concentrations (Schop et al. 2009) in the medium could help to improve the agreement between experimentally and computationally determined values. Even though for the experiments used in this study (Papantoniou et al. 2014) no global changes in oxygen tension were observed between the inlet and outlet for the flow rate and cell source used, the model allows to quantify these variable throughout the entire scaffold, potentially showing pockets of decreased oxygen tension (and neotissue growth) coming from improper perfusion due to local geometrical particularities. Additionally, the possibility that higher flow rates might lead to the secretion of more ECM could also explain to a certain extent the differences in volume filling patterns between simulations and experiments.

In a very interesting recent study, neotissue was modeled in 3D by Nava et al. (2013) using the arbitrary Lagrangian–Eulerian (ALE) method to implement mesh movement. However, the flow was only modeled in the void space, which is acceptable for the early growth phase, but is not suitable to simulate complete filling of the scaffold. In this study, we employed the level set method to represent neotissue growth as described previously in Guyot et al. (2014, 2015). This method, separating the movement of the interface from the definition of the mesh, allows tracking the neotissue kinetics until full scaffold pore filling is reached. A maximal neotissue growth velocity of 3 and \(7\,\upmu \hbox {m}\)/day was obtained for the low and high flow rates, respectively, as seen in Fig. 6. The average growth velocities from the present study are the same order of magnitude than the ones estimated in Nava et al. (2013) which were in the order of \(1\,\upmu \hbox {m}\)/day and higher than the values adopted in previous tissue growth models (Sacco et al. 2011). This could be due to the fact that chondrocytes modeled in that work are slow proliferating cells compared to hPDCs.

Numerical predictions obtained in this study (Figs. 4, 5) are in general agreement with published literature with regard to the range of shear stresses calculated at the neotissue interphase during neotissue growth (Boschetti et al. 2006; Cioffi et al. 2006; Lesman et al. 2010; Nava et al. 2013). However, shear stresses developed within the neotissue \((SS_\mathrm{in})\) were seen to be an order of magnitude higher than the surface shear stresses. It is interesting to note that the average values obtained for inner shear stress for the high flow rate in this work, reaching 0.7 Pa, compared closely to the ones determined for native bone (1–3 Pa) (Zeng et al. 1994), closer than what has been reported to date for tissue-engineered constructs. In this study, it was assumed that the pores within the neotissue had a size of \(50\,\upmu \hbox {m}\), and this was justified, for our case study, for large hPDC cells whose size has been shown to range between \(100{-}150\,\upmu \hbox {m}\) when fully spread (Eyckmans et al. 2012). This value could become smaller upon 3D confluency when cells ECM secretion might lead to fuller neotissue structures. Interestingly, the calculated inner neotissue (microporous) shear stress magnitude for the selected neotissue pore size matched closely to those determined via single cell simulations (Jungreuthmayer et al. 2009; Verbruggen et al. 2014; Zhao et al. 2014). Empty scaffold simulations may be useful for early time points and have been successfully used to determine stem cell lineage commitment (Song et al. 2013); however, for later culture time points, these models seem to be insufficient.

Using the whole scaffold geometry, it was also possible to determine changing pressure drop values during neotissue growth and subsequent scaffold pore closure. The maximum pressure drop values obtained for the high flow rate, for completely full scaffolds, equaled to 11 Pa for the parameters of this study (cylindrical scaffold dimensions d = 6 mm, h = 6 mm; neotissue porosity 90 %, \(\hbox {pore size} = 50\,\upmu \hbox {m}\)). This value is close to pressure drop measured computationally in microporous polyester scaffolds in flow-through perfusion bioreactors [\(\Delta P = 46\) Pa, scaffold h = 20 mm, d = 100 mm, flow rate 10 ml/min (Podichetty et al. 2014)] but also with experimentally measured pressure drop values for chitosan–gelatin scaffolds [with 80–92 % porosity and pore size \({\sim }100\,\upmu \hbox {m}\), d = 100 mm, h = 2 mm (Podichetty et al. 2012)]. Pressure drop is a parameter that can be measured online during bioreactor culture and, when linked to this whole scaffold model, could provide a noninvasive readout to monitor neotissue growth in perfusion bioreactors. The continuous secretion of ECM, in particular upon reaching 3D ‘confluency’, is expected to lead a decrease in neotissue permeability. This will occur mostly toward the later stages of perfusion culture. To achieve this in the present model, a time-dependent parameter could be coupled to the porosity parameter making it decrease over time, reflecting ECM deposition. This could be experimentally validated by measuring pressure drop across the tissue-engineered construct over time, for fixed flow rates.

Scaffold design in perfusion bioreactors can affect neotissue growth in two ways. First, due to their geometry, the scaffolds provide topographies that will enhance 3D cell growth and neotissue formation (Melchels et al. 2010; Van Bael et al. 2012). Second, their design will define fluid flow patterns throughout the entirety of the scaffold affecting the mechanical stimuli exerted on the cells (Hutmacher et al. 2008) and the resulting growth kinetics. The computational tool developed in this study could be used to assess biomechanical regimes that will develop in a particular scaffold during neotissue growth but also to evaluate the effect of specific geometries using scaffold CAD designs on these regimes. This model could also suggest ‘ideal’ geometries where shear stress variation exerted on cells across the scaffold could be minimized, resulting thus in a more homogeneous cell population phenotype. The spatiotemporal mapping of shear stress levels will allow to more accurately link phenotypic responses in bioreactors (Yu et al. 2013; Grayson et al. 2011) with the experienced biomechanical microenvironment. Moreover, already observed phenomena such as shear stress-dependent ECM secretion and mineralization (Sikavitsas et al. 2005; Papantoniou et al. 2013) could be also linked to the experienced microenvironment. For their validation, such models will require 3D tools of high resolution such as NanoCT as presented here or synchrotron X ray micro-CT as reported elsewhere (Voronov et al. 2013).

5 Conclusion

In this study, a 3D model of microporous neotissue growth in a dynamic culture environment was presented in which the neotissue growth velocity depends on scaffold geometry and fluid flow-induced shear stress. The obtained simulation results showed a correspondence with established experimental observations. Although the model can be extended to include additional determinants of the growth process, in its current state it is already able to act as a scaffold shape and bioprocess optimization tool, allowing for a control of the flow-induced mechanical stimulation and growth of the neotissue.