1 Introduction

Fluid mud is a high-concentration suspension of fine-grained sediment formed in the near bottom layer of the water column (McAnally et al. 2007). Fluid mud is primarily composed of water, clay-sized and silt-sized particles, organic matter, and contaminants. Fluid mud can be formed in a water body in which fine sediments are sufficiently supplied and the flow keeps stagnant or slow for long periods. Fluid mud can also occur in density flows near river mouths during fluidization from wave action. Once formed, fluid mud may be transported both vertically and horizontally. Fluid mud is resuspended vertically by entrainment and flows horizontally by shear flows, gravity, and streaming. At the same time, fluid mud consolidates to form bed materials. Different from the transport of water and sediment particles, fluid mud can flow down slopes due to gravity as a density current, with complicated rheological behaviors ranging from elastic to pseudo-plastic (McAnally et al. 2007).

Fluid mud has been observed in numerous estuaries and lakes worldwide, for example, the Mississippi River Delta in the United States (Corbett et al. 2007), the Amazon River Delta in Brazil (Kineke and Sternberg 1995), and the Changjiang Estuary (Li et al. 2001; Wan et al. 2014) and Lianyungang Harbor (Xie et al. 2010) in China. In many locations, accumulation of fluid mud can seriously impede navigation in harbors and channels. Moreover, the organic and contaminant content of fluid mud can cause environmental problems. The numerical investigation of fluid mud has both scientific and engineering significance.

A numerical model for fluid mud transport should solve both the dynamics of the overlying water body and the underlying fluid mud. The fluid mud layer and the above water flow can be solved by three-dimensional Navier–Stokes equations with the rheological behavior described by the apparent viscosity (Yan 1995; Le Hir et al. 2000; Watanabe et al. 2000; Guan et al. 2005; Knoch and Malcherec 2011). This method considers the water column and fluid mud as a whole body and can reflect the vertical distribution of velocity and density. However, the thickness of the fluid mud is usually small compared to the water depth, which is often tens to thousands of meters. The vertical resolution must be high enough because several layers near the bottom should be used to represent the fluid mud. As a result, a high computational cost will be required if the simulation is performed at field scale. For fluid mud flow in estuaries, the horizontal scale is usually larger than the vertical scale. A two-layer system with a three-dimensional hydrodynamic model simulating the overlying water column coupled with a two-dimensional shallow water model for the horizontal fluid mud model provides an alternative.

Efforts have been made to simulate the water column and fluid mud via a two-layer model (Odd and Cooper 1989; Le Normant 2000; Winterwerp et al. 2002; Wang et al. 2008; Canestrelli et al. 2012). As the main feature of fluid mud, the rheological behavior must be introduced into the model. Some studies simply increase the viscosity of the fluid mud (Le Normant 2000), while more studies reflect the rheological behaviors through the shear stress term between the fluid mud and the underlying bed (Odd and Cooper 1989; Winterwerp et al. 2002; Wang et al. 2008; Canestrelli et al. 2012). The shear stress term is expressed as a function of the yield stress, the vertical averaged velocity of the fluid mud, and the friction factor between the fluid mud and the bed, with the friction factor being determined empirically. For example, Odd and Cooper (1989) set the friction factor between the fluid mud and the bed the same as the friction factor between the water column and the fluid mud layer. Wang et al. (2008) set the friction factor between the fluid mud and the bed as a certain multiple of the friction factor between the water column and the fluid mud layer, empirically. To achieve a good result, many trials of the friction factor must be performed. Moreover, the actual friction factor will vary as flow condition changes. Therefore, development is lacking of a method to determine the actual friction factor to obtain a more realistic shear stress for the two-dimensional fluid mud simulation.

In the present study, a two-layer model for water and fluid mud to investigate fluid mud flow will be developed. The model is based on the finite volume coastal ocean model (FVCOM) (Chen et al. 2003). This model was chosen because of its flexible unstructured grid and good performance in coastal and estuarine studies. The hydrodynamics and sediment transport of the overlying water column are simulated by the original three-dimensional FVCOM model, which solved the primitive equations with a σ coordinate vertical system. A two-dimensional fluid mud model is introduced into the FVCOM model. The fluid mud interacts with the water through sediment flux, current, and shear stress.

The expression of the friction factor is derived with the assumption that the vertical distribution of shear stress below the yield surface of fluid mud is identical to that of uniform laminar flow of a Newtonian fluid in the open channel. Once the rheological parameters and vertical averaged velocity of fluid mud are known, the friction factor can be solved iteratively.

The two-layer model is validated by two experiments. The first experiment is the flow of viscoplastic fluid without overlying water. This experiment is selected to assess the capability of the model for reproducing the flow of a non-Newtonian fluid itself, which is the basis and kernel of a fluid mud model. The second experiment is an experiment of gravity flow of fluid mud in a flume filled with static water. The shear stress between the fluid mud and the water is included. Both the fluid mud flow and the interaction between fluid mud and water column are investigated in this case. For preliminary validation, only the flow of the fluid mud is focused on. The sediment flux exchange is neglected because it involves the process of cohesive sediment transport, which requires further validation of the sediment model. Furthermore, the two-layer model with a derived friction factor and with a friction factor set as a fixed value are established to discuss the necessity of the derivation of the friction factor.

The arrangement of this paper is as follows. The introduction of the two-layer model and the derivation of the friction factor are described in Section 2. The validation results of the two-layer model are presented in Section 3. The discussion of the simulation with the derived friction factor and with the friction factor given as fixed values is provided in Section 4. Finally, the summary is presented in Section 5.

2 Two-layer model

2.1 Basic equations

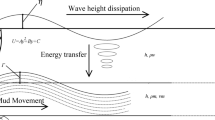
A flow field consisting of two layers is assumed, with water carrying low-concentration sediment as the upper layer and the high-concentration fluid mud layer flowing below the water layer. The fluxes are exchanged between the two layers. The suspended sediment in the water layer settles and deposits onto the bottom, becoming a main source for the formation of fluid mud. Once formed, the fluid mud may be entrained by the overlying flow and increase the concentration of the suspended sediment. The fluid mud will also consolidate to form the bed. If fluid mud flows quickly enough, it will erode the bed. At the surface and bottom interface of the fluid mud, there are shear stresses that reflect the interaction of fluid mud with the water column and the bed (Fig. 1). Because the fluid mud is much thinner than the water layer, the influence of the fluid mud thickness on the hydrodynamics of the water column is neglected in the present study.

Fig. 1
figure 1

Sketch of the two-layer model

Full size image

Three-dimensional transport of water column and suspended sediment in the upper layer is simulated using the FVCOM model, governed by the three-dimensional primitive equations and the sediment transport equation. For more details, refer to Chen et al. (2003). The fluid mud model integrated into the FVCOM model solves the two-dimensional mass balance equation and momentum equations as follows:

$$ \frac{\partial {d}_m}{\partial t}+\frac{\partial \left({u}_m{d}_m\right)}{\partial x}+\frac{\partial \left({v}_m{d}_m\right)}{\partial y}=\frac{1}{c_m}\frac{dM}{dt} $$
(1)
$$ \begin{array}{c}\frac{\partial {u}_m{d}_m}{\partial t}+{u}_m\frac{\partial {u}_m{d}_m}{\partial x}+{v}_m\frac{\partial {u}_m{d}_m}{\partial y}-f{v}_m{d}_m=\hfill \\ {}\hfill -g{d}_m\frac{\rho_m-\rho }{\rho_m}\frac{\partial {\eta}_m}{\partial x}-\frac{1}{\rho_m}\left({\tau}_{bx}-{\tau}_{sx}\right)-\frac{d_m}{\rho_m}\rho g\frac{\partial \eta }{\partial x}\end{array} $$
(2)
$$ \begin{array}{c}\frac{\partial {v}_m{d}_m}{\partial t}+{u}_m\frac{\partial {v}_m{d}_m}{\partial x}+{v}_m\frac{\partial {v}_m{d}_m}{\partial y}+f{u}_m{d}_m=\hfill \\ {}\hfill -g{d}_m\frac{\rho_m-\rho }{\rho_m}\frac{\partial {\eta}_m}{\partial y}-\frac{1}{\rho_m}\left({\tau}_{by}-{\tau}_{sy}\right)-\frac{d_m}{\rho_m}\rho g\frac{\partial \eta }{\partial y}\end{array} $$
(3)

where d m is the thickness of the fluid mud layer; u m and v m are the flow velocities of the fluid mud in the x and y directions, respectively; c m is the sediment concentration of the mud layer; dM/dt represents the mass exchange between the water column and the fluid mud layer; f is the parameter of the Coriolis acceleration; g is the gravitational acceleration; ρ m and ρ are the densities of the fluid mud layer and the water layer, respectively; η m  = Z b  + d m is the surface of the fluid mud layer, where Z b is the bottom level; η is the surface of the water layer provided by the upper layer model; τ sx and τ sy are the shear stresses at the water-fluid mud interface in the x and y directions, respectively; and τ bx and τ by are the shear stresses at the fluid mud-bed interface in the x and y directions, respectively. The shear stresses are given as:

$$ \left(\begin{array}{l}{\tau}_{sx}\\ {}{\tau}_{sy}\end{array}\right)=\left(\begin{array}{l}u-{u}_m\\ {}v-{v}_m\end{array}\right)\frac{f_s\rho }{8}\sqrt{{\left(u-{u}_m\right)}^2+{\left(v-{v}_m\right)}^2} $$
(4)
$$ \left(\begin{array}{l}{\tau}_{bx}\\ {}{\tau}_{by}\end{array}\right)=\left(\begin{array}{l}{u}_m\\ {}{v}_m\end{array}\right)\frac{f_m{\rho}_m}{8}\sqrt{u_m^2+{v}_m^2},\ \mathrm{with}\ \left|{\tau}_{bx}\right|\ge {\tau}_B\ \mathrm{and}\ \left|{\tau}_{by}\right|\ge {\tau}_B $$
(5)

where f s is the friction factor between the water layer and the fluid mud layer (refer to Traykovski et al. (2000) and Tang (2013) for relevant experiments); u and v are the velocities of the water column near the bottom in the x and y directions, respectively (here, the velocities of the lowest layer solved by the three-dimensional hydrodynamic model are taken as u and v); f m is the friction factor between the fluid mud layer and the underlying bed (the calculation of f m will be introduced in Section 2.2); and τ B is the yield stress.

The exchanged mass flux between the fluid mud layer and the water layer is described as:

$$ \frac{dM}{dt}=D+E-En-Dw $$
(6)

where D is the deposition flux from the overlying water column; E is the erosion flux from the underlying bed; En is the entrainment flux of the fluid mud; and Dw is the dewatering flux of the fluid mud layer.

The fluid mud at the same time has an influence on the overlying suspension layer. The shear stress at the fluid mud-water interface is taken as the acting force at the bottom boundary for solving the flow of the upper layer. The entrainment flux of the fluid mud layer is added into the upper layer to increase the suspended sediment concentration at the bottom of the water column. In the present work, the flux between the mud and water column is not included, so the details are not introduced here.

2.2 Friction factor derivation

Regarding the fluid with a yield stress similar to fluid mud, the vertical distribution of the velocity is shown in Fig. 2. There is a yield surface where the shear stress equals the yield stress. Beneath the yield surface, a shear flow region with sheared flow exists. Above the yield stress, there is a plug flow with no velocity gradient (Mei and Yuhi 2001). Here, it is assumed that the shear stress in the shear flow region follows the distribution of uniform flow in the open channel. The Herschel-Bulkley model is selected to describe the rheological behavior of fluid mud as an example in the following derivation. The rheological equation of the Herschel-Bulkley fluid is expressed as:

$$ \tau ={\tau}_B+K{\left(\frac{\partial {u}_m}{\partial z}\right)}^n $$
(7)

where τ is the shear stress at height z; ∂u m /∂z represents the shear rate; K is the consistency; and n is the index. The shear stress distribution in the uniform flow of the open channel is given as:

$$ \tau ={\rho}_mg\left({d}_m-z\right)J $$
(8)

where J is the hydraulic slope. The shear stresses at the bottom of the fluid and at the yield surface are presented as follows:

$$ {\tau}_0={\rho}_mg{d}_mJ,\;\mathrm{at}\;z=0 $$
(9)
$$ {\tau}_B={\rho}_mg\left({d}_m-{h}_B\right)J,\;\mathrm{at}\;z={h}_B $$
(10)

where h B is the height of the yield surface, so that the plug flow region is located in h B  < z ≤ d m and the shear flow region in 0 ≤ z ≤ h B . Following the assumption made above, Eq. (7) is set equal to Eq. (8), which leads to the vertical distribution of fluid velocity in the shear flow region being derived as:

$$ {u}_m=-{\left(\frac{\tau_B}{K\left({d}_m-{h}_B\right)}\right)}^{1/n}\frac{{\left({h}_B-z\right)}^{1/n+1}-{h}_B^{1/n+1}}{1/n+1}\begin{array}{cc}\hfill \hfill & \hfill 0\le z\le {h}_B\hfill \end{array} $$
(11)
Fig. 2
figure 2

Vertical distribution of the fluid mud velocity

Full size image

Without a velocity gradient, the plug flow region has a uniform velocity, which equals the velocity at the yield surface:

$$ {u}_{m,B}={\left(\frac{\tau_B}{K\left({d}_m-{h}_B\right)}\right)}^{1/n}\frac{h_B^{1/n+1}}{1/n+1}\begin{array}{cc}\hfill \hfill & \hfill z={h}_B\hfill \end{array} $$
(12)

The vertical distribution of velocity through the entire fluid is then summarized as:

$$ {u}_m=\left\{\begin{array}{ll}-{\left(\frac{\tau_B}{K\left({d}_m-{h}_B\right)}\right)}^{1/n}\frac{{\left({h}_B-z\right)}^{1/n+1}-{h}_B^{1/n+1}}{1/n+1}\hfill & 0\le z\le {h}_B\hfill \\ {}{\left(\frac{\tau_B}{K\left({d}_m-{h}_B\right)}\right)}^{1/n}\frac{h_B^{1/n+1}}{1/n+1}\hfill & {h}_B<z\le {d}_m\hfill \end{array}\right. $$
(13)

Integrating through the entire thickness of the fluid, the vertical averaged velocity can be obtained as:

$$ {U}_m=\frac{{\left({\rho}_mg\right)}^{1/n}{J}^{1/n}\left[{d}_m\left(1/n+2\right)-{h}_B\right]{h}_B^{1/n+1}}{K^{1/n}\left(1/n+1\right)\left(1/n+2\right){d}_m} $$
(14)

In addition to Eq. (9), the shear stress at the bottom can also be expressed as a function of the vertical averaged velocity and the friction factor:

$$ {\tau}_0={f}_m\frac{\rho_m{U}_m^2}{8} $$
(15)

Equations (9) and (15) are set to be equal to obtain the expression of the hydraulic slope:

$$ J={f}_m\frac{U_m^2}{8gh} $$
(16)

Substituting Eq. (16) into Eq. (14), the relationship between the vertical averaged velocity U m and the friction factor f m is established and the hydraulic slope J is eliminated. Next, some efforts are made to eliminate the remaining unknown variable h B . According to Eq. (15), the ratio of yield stress to the bottom shear stress can be expressed as:

$$ \frac{\tau_B}{\tau_0}=\frac{\left({d}_m-{h}_B\right)}{d_m}=\frac{8{\tau}_B}{f_m{\rho}_m{U}_m^2} $$
(17)

Equation (17) is substituted into Eq. (14) to eliminate h B and to obtain the final expression of f m :

$$ {f}_m=\frac{8K{\left(1/n+1\right)}^n{\left(1/n+2\right)}^n}{\rho_m{U}_m^{2-n}{d}_m^n{\left(1/n+1+\frac{8{\tau}_B}{f_m{\rho}_m{U}_m^2}\right)}^n{\left(1-\frac{8{\tau}_B}{f_m{\rho}_m{U}_m^2}\right)}^{1+n}} $$
(18)

The friction factor f m can be iteratively solved if given the rheological parameters τ B , K and n, the vertical averaged velocity of fluid mud U m , and the thickness of fluid mud d m .

Equation (18) is obtained based on the Herschel-Bulkley rheological model. When K is the viscosity of fluid mud η and n = 1, the fluid mud changes to a Bingham fluid. The friction factor of the Bingham fluid is presented as Eq. (19) and is consistent with Zhang (1990):

$$ {f}_m=\frac{24\eta }{\rho_m{U}_m{d}_m\left(1+\frac{4{\tau}_B}{f_m{\rho}_m{U}_m^2}\right){\left(1-\frac{8{\tau}_B}{f_m{\rho}_m{U}_m^2}\right)}^2} $$
(19)

Furthermore, when τ B  = 0, K is the viscosity μ and n = 1, the fluid degrades to the Newtonian fluid. The friction factor is then given as Eq. (20), which is consistent with Yen (2002):

$$ {f}_m=\frac{24\mu }{\rho_m{U}_m{d}_m} $$
(20)

2.3 Numerical scheme

The two-layer model based on the FVCOM model is discretized using the finite volume method. The horizontal computational domain is subdivided into unstructured triangular cells, as shown in Fig. 3. The scalar variables, such as water elevation, sediment concentration, and thickness of the fluid mud, are defined at the nodes (●). The velocity vectors of the water column and the fluid mud are defined at the center of the cells (⨁). A “mode splitting” method is used that divides the computation into external and internal modes. The method improves the computational efficiency by allowing two modes using distinct time steps. The external mode explicitly solves the elevation and vertical averaged velocity of the water column, as well as the thickness and vertical averaged velocity of fluid mud. Based on the results of the external mode, the three-dimensional velocity of the water column and the sediment transport are solved by internal mode using a combined explicit and implicit scheme. The time integration is performed using a modified fourth-order Runge–Kutta time stepping scheme. For more details regarding the numerical scheme, refer to the FVCOM model (Chen et al. 2003).

Fig. 3
figure 3

Illustration of unstructured girds

Full size image

3 Model validation

3.1 Viscoplastic fluid flow without overlying water

The dam break experiment conducted by Cochard and Ancey (2009) is selected to validate the ability of the model to accurately reproduce the flow of the non-Newtonian fluid when removing the overlying water. The layout of the experiment is shown in Fig. 4. The full facility is a 5.5-m-long and 1.8-m-wide plane, which can be inclined using a digital inclinometer from 0° to 45°, with a resolution of 0.1°. A reservoir with a length of 0.51 m and a width of 0.3 m is positioned at the top of the inclined plane. A gate wall, 1.6 m wide, 0.8 m high, and 0.04 m thick, composed of ultralight carbon is located before the reservoir. The experiment is performed using a 30 % Carbopol Ultrez 10 solution, which is a viscoplastic stable polymeric gel. The fluid density is 811 kg/m3. The behavior of the fluid is approximated by a Herschel-Bulkley model. The rheological properties are determined by a rheometer. The yield stress τ B is set as 89 ± 1 Pa according to the creep test. The consistency K = 47.68 ± 1.7 Pa/sn and the power-law index n = 0.415 ± 0.021 are set according to the flow curve determined by the rheological test. The test performed on a slope of α = 6° is selected to validate the fluid mud model. At the beginning of the experiment, a 43 kg mass of fluid is initially stored in the reservoir. During the experiment, the gate is opened by two pneumatic jacks to the desired height within 0.8 s, and then the fluid spreads on the slope. The measurement of the free surface shape of the fluid is conducted using an imaging system consisting of a high-speed digital camera and a synchronized micro-mirror projector. The flow-depth profile at the centerline and the contours of the mass are extracted in the experiment.

Fig. 4
figure 4

Schematic of the experimental setup after Cochard and Ancey (2009) (unit: m): a side view; b plane view

Full size image

To reproduce the above experiment, which is performed with no overlying water by our fluid mud model, the governing equations are modified by removing the terms regarding the water column. The Coriolis force term is also neglected. The basic Eqs. (1) to (3) are changed to:

$$ \frac{\partial {d}_m}{\partial t}+\frac{\partial \left({u}_m{d}_m\right)}{\partial x}+\frac{\partial \left({v}_m{d}_m\right)}{\partial y}=0 $$
(21)
$$ \frac{\partial {u}_m{d}_m}{\partial t}+{u}_m\frac{\partial {u}_m{d}_m}{\partial x}+{v}_m\frac{\partial {u}_m{d}_m}{\partial y}-f{v}_m{d}_m=-g{d}_m\frac{\partial {\eta}_m}{\partial x}-\frac{\tau_{bx}}{\rho_m} $$
(22)
$$ \frac{\partial {v}_m{d}_m}{\partial t}+{u}_m\frac{\partial {v}_m{d}_m}{\partial x}+{v}_m\frac{\partial {v}_m{d}_m}{\partial y}+f{u}_m{d}_m=-g{d}_m\frac{\partial {\eta}_m}{\partial y}-\frac{\tau_{by}}{\rho_m} $$
(23)

The computational domain is set to be the same as the experiment, with a 5.5 m length and 1.8 m width. The inclined plane is represented numerically using a mesh of 8986 triangular cells, with the minimum grid size of 0.05 m. The dam break process cannot be directly simulated by the current numerical scheme. Here, a time series of the inflow depth and the discharge are imposed at the dam gate (Table 1) as the inflow boundary conditions. The inflow depth at the boundary is taken from the measurement. The inflow discharge cannot be obtained directly from the measurement, so the inflow discharge is estimated through the change rate of the fluid volume calculated according to the measured data. The simulation is performed for 200 s with a time step of 0.002 s. The rheological behavior is described by the Herschel-Bulkley model, and the friction factor is estimated by Eq. (18) using the measured rheological parameters.

Table 1 Inflow boundary conditions of the flow depth and discharge at the dam gate
Full size table

The simulation results of the time variations of the flow-depth profile at the centerline and the contours of the mass are compared with the measured data in Figs. 5 and 6, with the relative errors presented in Table 2. The calculated friction factors at different times are presented in Fig. 7. The model reproduces the process of the viscoplastic fluid flowing down the slope. The inflow depth of the fluid decreases slowly during the entire process (Fig. 5). The mass propagates down along the slope due to gravity while simultaneously spreading out to its right and left sides because of the flow-depth difference (Fig. 6). As the mass propagetes, the flow becomes slower as a result of the decreasing of inflow discharge. From T = 2 s to T = 20 s, the fluid flows for a distance of approximately 0.05 m during the time period of 18 s, while for they next 180 s (from T = 20 s to T = 200 s), the fluid only propagates 0.05 m. The averaged propagating velocity of the fluid from T = 20 s to T = 200 s is nearly one-tenth of the velocity from T = 2 s to T = 20 s (Fig. 6). The velocity of the fluid is reduced due to its high yield stress and consistency, which increases the frictional resistance through the calculated friction factor and reduces the effect of gravity force. The maximum friction factor is approximately 80, which occurs near the edge of the fluid (Fig. 7). The simulated contours of the mass are generally consistent with the measured data, with a maximum relative error of 12.8 %. While less favorable agreement is found regarding the flow-depth profile, the predicted free surface flows obviously ahead of the experimental observations for a short distance (Fig. 5). The relative error of flow depth is greater than 30 % after T = 2 s, reaching a maximum value of 38.4 %. Several possible explanations may cause the discrepancies. The real dam break is reproduced by approximate inflow boundary conditions due to the limitation of the current numerical scheme. The inertial effect is not considered sufficiently for the numerical simulation. Furthermore, the surface tension is also neglected, which can influence the flow of the experimental fluid.

Fig. 5
figure 5

Comparison of the measured and the simulated flow-depth profiles for a T = 0.4 s, b T = 2 s, c T = 20 s, and d T = 200 s

Full size image
Fig. 6
figure 6

Comparison of the measured and simulated mass contours for a T = 0.4 s, b T = 2 s, c T = 20 s, and d T = 200 s

Full size image
Table 2 Relative errors of the flow depth and mass contour (%)
Full size table
Fig. 7
figure 7

Friction factor f m for a T = 0.4 s, b T = 2 s, c T = 20 s, and d T = 200 s

Full size image

3.2 Two-layer flow of the fluid mud and water

The gravity current experiment of fluid mud on an inclined bed with overlying water performed by van Kessel and Kranenburg (1996) is simulated by the two-layer model in this study. The experiment is conducted in a 13.75-m-long, 0.5-m-wide, and 0.72-m-high laboratory flume (Fig. 8). A sloping bottom is installed in the flume. The china clay and tap water are mixed by a rotating grid and a circulation pump in a 3.5 m3 mixing tank to produce the artificial muds with bulk density values ranging from 1050 to 1230 kg/m3. The suspension mixed in the tank is fed to the inflow compartment of the flume via the pump during the experiment. The flow rate is kept constant using a Foxboro electromagnetic flow meter. The main part of the flume is filled with tap water and separated by a movable dam gate from the inflow compartment. The gate is lifted up to the desired height to generate a density current for 300–600 s in the flume. At the end of the flume, the density current is caught and drained into a settling tank. The measurement of the velocities and the concentrations of both the water current and the density current are conducted at distances of both 1.27 m (P1) and 5.43 m (P2) from the gate. The velocities are measured using an electromagnetic velocity meter, and the concentrations are measured using an ultrasonic high-concentration meter.

Fig. 8
figure 8

Schematic of the experimental setup after van Kessel and Kranenburg (1996) (units: m)

Full size image

The experimental case performed on a slope of 1:42.6 and an 8.75-m-long sloping bottom is selected to validate the present two-layer model. The experimental conditions are presented in Table 3. A 13.75-m-long and 5-m-wide computation domain is established numerically using a mesh of 56,760 triangular cells, with a minimum grid size of 0.05 m. The depth of the upper layer water ranges from 0.51 m at the top of the slope to 0.72 m at the end of the slope. The water column is divided into 20 non-uniform σ layers in the vertical direction, with σ = 0.0025D (D is the water depth) near the bottom. The flow depth and flow rate are imposed at the inflow boundary, and a laminar density current is generated. The simulation is performed for 300 s with an external time step of 0.0005 s and an internal time step of 0.005 s for the upper layer three-dimensional hydrodynamic model and a time step of 0.0005 s for the underlying fluid mud model. The Coriolis force is neglected, and the friction factor between the water column and the mud is determined according to relevant experiments (Tang 2013). The rheological behavior of the fluid mud is described as a Bingham plastic body, and the friction factor between the fluid mud and the bottom is calculated using Eq. (19). The rheological properties are determined as (van Kessel and Kranenburg 1996):

$$ {\tau}_B={c}_1{C_V}^{c_2} $$
(24)
$$ \mu ={\mu}_w\left(1+{c}_3{C_V}^{c_4}\right) $$
(25)

where μ is the viscosity of the fluid mud and μ w is the viscosity of the water column. c 1 − c 4 are constants determined after van Kessel and Kranenburg (1996) (Table 2), and C V is the volumetric concentration calculated as:

$$ {C}_V=\frac{\rho_m-\rho }{\rho_s-\rho } $$
(26)

where ρ s is the density of sediment (ρ s  ≈ 2590 kg/m3 for china clay).

Table 3 Experimental conditions and simulation parameters
Full size table

The simulated density and velocity profiles in both the water layer and the fluid mud layer are compared with the experimental observations in Fig. 9. Uniform density and velocity are obtained from the two-dimensional fluid mud model in the fluid mud layer. The relative error of the velocity is presented in Table 4. The friction factors between the fluid mud and the bottom at different times are shown in Fig. 10. The time variation of the simulated free surface of the fluid mud flow is presented in Fig. 11. The flow is assumed to be uniform along the width direction of the flume. The fluid thickness calculated by the model is approximately 0.47 m at P1 position. A clear interface is observed between the water layer and the underlying fluid mud layer. The experiment results indicate that a step of density exists at the interface, with nearly no mass exchange between the two layers. The present simulation neglects the exchange process and regards the density of the water column as 1000 kg/m3 and the fluid mud as 1200 kg/m3. The observed velocity profile indicates that the water at the interface flows due to the drag force of the underlying fluid mud (Fig. 9). The relative errors of the velocities for the water layer and the fluid mud layer are most small, with one exception that velocity of the water column at the depth of 10 cm is 165.8 % larger than the observation. This is mainly because the measured velocity which is used as the denominator when calculating the relative error is so small. Actually, it can be found that the simulated velocity profile is similar to the observed profile from Fig. 9b. As a result, the simulated velocities of both the water layer and the fluid mud layer are acceptable comparing with the measured data. The maximum friction factor between the fluid mud and the bottom occurs near the edge of the fluid mud, with a value of approximately 2.2 (Fig. 10). The flowing process of the fluid mud is reproduced by the model. When released from the inflow, the fluid mud flows down the inclined plane due to gravity, and a small bank-up exists near the bottom of the slope (T = 50 s in Fig. 11). The inflow and outflow masses become balanced after T = 100 s (Fig. 11). The two-layer model reproduces the flow processes of both the water column and the underlying fluid mud.

Fig. 9
figure 9

Comparison of the measured and simulated profiles at P1 of a density and b velocity

Full size image
Table 4 Relative error of the velocities for the water layer and fluid mud layer (%)
Full size table
Fig. 10
figure 10

Friction factor f m for a T = 10 s, b T = 40 s, c T = 80 s, and d T = 300 s

Full size image
Fig. 11
figure 11

Simulated free surface of the fluid mud

Full size image

4 Discussion

The two-layer model with the derived friction factor was validated by the experimental data. In this section, the numerical results with the derived friction factor and with the friction factor given as fixed values are compared to determine the necessity of the derivation of the friction factor.

4.1 Case setup

The numerical test is performed based on the experiment of Cochard and Ancey (2009), which was already modeled in Section 3.1 to validate the two-layer model. In the validation, the friction factor f m is varied as the flow condition changes, having a value between 0 and 80 (Fig. 7). The friction factor is then set as three fixed values: f m  = 5, f m  = 60, and f m  = 80. The numerical results with different friction factors are compared with the experimental data.

4.2 Numerical results

The fluid mud flow with different friction factors is simulated by the developed two-layer model. The front positions and widths of the fluid at different times are compared with the measured data, as shown in Figs. 12 and 13. The relative errors of the front positions and the widths for different friction factors are presented in Table 5 and Table 6. For the case with the friction factor calculated using Eq. (18), the front position and width of the fluid mud exhibit reasonable agreement with the measured data. For the case with the friction factor set as a small value (f m  = 5), before T = 2 s, the front position is close to the measured position, with a relative error of less than 18 %, while the width is greater than the measurement by over 50 %. After T = 2 s, the simulated fluid moves much more rapidly than the measured fluid in the directions of both the length and the width, with a maximum relative error of 697.7 %. For the case with the friction factor set as a large value (f m  = 80), the simulated results of the front position are smaller than measured data for the entire process, with a mean relative error of 28.2 %. For f m  = 60, in the direction of the length, the simulated fluid continues to move more slowly compared to the measured fluid until T = 200 s. The simulated widths of the fluid mud of f m  = 60 and f m  = 80 are both close to the measured width, with a mean relative error of approximately 8 %. The variation of the friction factor has more influence on the flow in the direction of the length, along with a larger gradient of gravity. In general, the mean relative errors of the front position and the width for the calculated friction factor are both small, less than 9 %. It can be concluded that the case with the friction factor presented in Section 2.1 most closely agrees with the experimental data.

Fig. 12
figure 12

Comparison of the measured and simulated front positions of the fluid mud

Full size image
Fig. 13
figure 13

Comparison of the measured and simulated widths of the fluid mud

Full size image
Table 5 Relative error of the front position for different values of the friction factor (%)
Full size table
Table 6 Relative error of the width for different values of the friction factor (%)
Full size table

5 Summary

A two-layer model was developed based on the FVCOM model to investigate the dynamics of the fluid mud flow. In the model, the water layer is solved by the three-dimensional hydrodynamic model of the FVCOM model, and the underlying fluid mud is simulated by the horizontal two-dimensional fluid mud model, which is introduced into the FVCOM model in the present study. The interaction at the water-mud interface is through sediment flux, current parameters, and shear stress. The friction factor between the fluid mud and the bottom, which is traditionally determined empirically, is derived with the assumption that the shear stress profile below the yield surface of the fluid mud is identical to that of uniform laminar flow of a Newtonian fluid in the open channel. The two-layer model was validated by two experiments. The first experiment was the flow of viscoplastic fluid without overlying water, which was performed to demonstrate the capability of the model for simulating the flow of the underlying layer itself. The second was an experiment of density current with overlying water to investigate the dynamics of both fluid mud and water column. Our model reproduced the processes of both experiments. To demonstrate the necessity of the derivation of the friction factor, numerical results with the derived friction factor and with the friction factor given as fixed values are compared with the measured data. The results simulated with the derived friction factor exhibited the best agreement with the experiment. In general, the model is capable of reproducing the flow properties of the fluid mud. However, the derivation of the friction factor is based on the assumption of laminar flow, so the model is not suitable for turbulent flow. The current model can only be applied to the fluid mud flow on a gentle slope with slow velocity. More efforts should be made to extend the model into the turbulent range. Furthermore, in the present study, only the validation of the fluid mud flow is focused on and the mass exchange at the interface is neglected. Further validation of the suspended sediment model and the flux exchange must be made for the two-layer model and its future application to engineering.