1 Introduction

The importance of reinsurance is growing steadily due to its role in helping insurers mitigate their potential losses and, through stable earnings, it enables continued growth and innovation.

In recent years, the increasing severity and frequency of natural catastrophes, man-made catastrophic events or pandemics have highlighted the important role of reinsurance companies in supporting the non-life and life insurance industry in paying claims to their policyholders and enabling their financial investments.

The augmented interest in the problem is also witnessed by the number of academic studies which consider the problem under a variety of criteria and for different models of the claim arrivals and investment market. We refer to Cao et al. (2020) and Brachetta et al. (2022) for recent and concise surveys on the existing literature on the topic.

We consider a reinsurance-investment problem taking the side of the insurer that by transferring her risks reduces earnings volatility and optimizes the financial results. The motivation for buying reinsurance and the amount required vary depending on several factors and in particular on the exposure to different types of risk. We consider the model introduced by Dassios and Zhao (2011), which is a generalisation of the Cox process with shot noise intensity and the Hawkes process. This contagion model is extremely versatile, as it allows for the consideration of risks due to exogenous factors, such as earthquakes and natural disasters, as well as endogenous risks, and in the model the occurrence of these events increases the probability of future events. The simplest proportional reinsurance is the quota share, see e.g. Zeng and Li (2011), in which the primary insurer retains a fixed percentage of each policy’s premiums and cedes the remainder according to a ratio defined in their contract. Losses are apportioned at the same ratio.

This relatively simple form of reinsurance has the disadvantage that it is not flexible, as it does not protect against extreme losses and, moreover, depending on the quota, the insurer may be forced to cede too much at the expense of profits.

A possible solution to the latter drawback is to combine a quota share agreement with another popular form of reinsurance, the so-called excess of loss agreement, in which only claims exceeding a certain threshold are reinsured (see e.g. Li et al. (2017)). Thus, we consider here a proportional reinsurance where the reinsurance covers a quota share of the claim excess over a certain fixed retention level. This type of contract has two collateral advantages. The first is related to the practical need to keep the level of the deductible constant at least in a suitable time window (e.g. on an annual basis) and, in the contract we are considering, the level is fixed. The second is related to the advantages of the proportional contract. Within the time window, the insurer seeks the optimal proportion of losses exceeding the fixed threshold, and this proportion will assure the reinsurance counterparty that a portion of the higher risks will be shared by the insurance company.

Following the works of Li et al. (2017) and Cao et al. (2020), for this type of contract we provide in closed form the insurer’s optimal quota share when the insurer optimizes according to the mean-variance criterion, and discuss the results obtained over time and in terms of the retention level.

In Li et al. (2017) for a spectrally negative Lèvy model, it is shown that the optimal equilibrium contract is of the excess-of-loss type, where the optimal retention level can be computed in terms of the solution of an ordinary differential equation, while in Cao et al. (2020) a similar result is obtained for the same dynamic contagion model considered here. Therefore, as expected, the performance of the mixed contract we propose in this work lies between that of the classical proportional and the XL contract. This can be easily explained by the fact that in the mixed contract the insurance company offers to share part of the higher risks with the reinsurance counterparty. However, even if the proposed contract does not outperform the XL contracts of Li et al. (2017) and Cao et al. (2020) at every threshold level, it is important to note that numerical examples show there are levels where the value functions for the optimization problem are identical for both types of contracts. Moreover, the XL mixed contract, characterized by a constant retention level and proportional excess, is superior to the traditional proportional contract. The latter is a special case that occurs when the retention level is set to zero. By sharing only the risks above a fixed threshold, the primary insurer benefits from retaining more of the lower-risk portions, leading to improved risk management and potentially higher profitability compared to the classical proportional contract.

The paper is organized as follows. In Sect. 2, we introduce the dynamic contagion model, the surplus process and the mixed contract, and we formulate the reinsurance-investment problem. Section 3 contains the main result, as it provides the optimal portfolio strategy and the optimal retention proportion in closed form via an extended Hamilton–Jacobi–Bellman equation. The optimal retention proportion depends on the solution of an ordinary differential equation, whose behaviour is discussed over time and with respect to the threshold level. Section 4 is devoted to some numerical examples, which illustrate the theoretical results under the assumption that the claims are exponentially distributed. Finally, a conclusion is presented in Sect. 5.

2 Problem formulation

On a filtered probability space \((\Omega ,{{\mathscr {F}}},\mathbb {F}=\{{\mathcal {F}}_t, t\in [0,T]\},\mathbb {P})\) satisfying the usual conditions of completeness and right continuity with a fixed time horizon \(T<+\infty \), we model the insurer aggregate claim process by the compound process introduced in Dassios and Zhao (2011).

The claims arrivals

$$\begin{aligned} C_t=\underset{i\ge 1}{\sum }Y_i 1\!\!1_{T_i\le t}. \end{aligned}$$

follow a contagion model that generalizes the Hawkes process and the Cox process with shot noise intensity and includes a component depending on external events together with a self-exciting component. In particular, the point process describing the claims arrivals \(N=\{N_t, t\in [0,T]\}\), \(N_t=\sum _{i\ge 1} 1\!\!1_{T_i\le t}\) is characterized by the stochastic intensity \(\lambda \), whose self excited part has jumps \(R_i\) at the claims arrival times \(T_i\), whereas its externally excited part has jumps \(Z_i\) occurring at the jumps times \(T_i^{(1)}\) of a homogeneous Poisson process \(N^{1}\) with intensity \(\rho \). Mathematically, the process \(\lambda \) is written as

$$\begin{aligned} \lambda _t=\beta +(\lambda _0-\beta )e^{-\alpha t}+\underset{i\ge 1}{\sum }Z_i e^{-\alpha (t-T_i^{(1)})}1\!\!1_{T_i^{(1)}\le t}+\underset{i\ge 1}{\sum }R_i e^{-\alpha (t-T_i)}1\!\!1_{T_i\le t}, \end{aligned}$$

for constant reversion level \(\beta \ge 0\), initial value \(\lambda _0>0\) and rate of exponential decay \(\alpha >0\).

The claims \(Y_i\) are supposed to be positive i.i.d. (independent, identically distributed) random variables and, analogously, the externally excited jumps \(Z_i\) and the jumps \(R_i\) responsible for the self-excited effect are positive i.i.d.. Furthermore, \(Y_i\), \(R_i, Z_i\) and also \(T_i^{(1)}\) are considered independent of each other.

The dynamics of the intensity process \(\lambda \) can be rewritten in terms of the counting random measures \(\nu ^{(1),\lambda }\) and \(\nu ^{\lambda }\) associated, respectively, to the external and self-excited jumps of the intensity \(\lambda \),

$$\begin{aligned} & \nu ^{(1),\lambda }(dt,dz)=\underset{i\ge 1}{\sum }\delta _{(T_i^{(1)},Z_i)}(dt,dz)1\!\!1_{T_i^{(1)}<\infty } \ \ \text {and} \\ & \nu ^{\lambda }(dt,dr)=\underset{i\ge 1}{\sum }\delta _{(T_i,R_i)}(dt,dr)1\!\!1_{T_i<\infty } \end{aligned}$$

as

$$\begin{aligned} d\lambda _t=\alpha (\beta -\lambda _{t^-})dt+\int _0^{+\infty }z \nu ^{(1),\lambda }(dt,dz)+\int _0^{+\infty }r \nu ^{\lambda }(dt,dr). \end{aligned}$$

Note that the processes \(\lambda \) and \((N,\lambda )\) are Markovian.

We recall that the compensators of the measures \(\nu ^{(1),\lambda }(dt,dz)\) and \(\nu ^{\lambda }(dt,dr)\) can be respectively written as \(\rho F_Z(dz)dt\) and \(\lambda _{t^-} F_R(dr)dt\), where \(F_Z\), \(F_R\) denote the distribution of the external, respectively self-excited, jumps. Moreover, \(m_Z\), \(n_Z\), and \(m_R\), \(n_R\) will denote the finite first and second moments of the variables \(Z_i\) and \(R_i\). We assume \(m_R<\alpha \) to guarantee the stationarity of the intensity process.

With regard to the aggregate claim process, we introduce the associated counting measure \( \nu ^{C}(dt,dy)=\underset{i\ge 1}{\sum }\delta _{(T_i,Y_i)}(dt,dy)1\!\!1_{T_i<\infty }\). Let us observe that the two measures \(\nu ^{\lambda }\) and \(\nu ^C\) depend on the N’s jumps times and write \(dC_t=\int _0^{+\infty }y \nu ^{C}(dt,dy)\). Furthermore, recall that the compensator of the measure \(\nu ^C\) is \(\lambda _{t^-}F_Y(dy)dt\).

The reinsurance-investment problem of the insurer can be described as follows.

The insurer chooses her retention function \(\ell _p(t,y)\) on the base of the information available, and, once observed the claim \(Y=y\), she identifies the part covered by the insurer (and the part \(y-\ell _p(t,y)\) to be reinsured). Once \(\ell _p(t,y)\) is chosen, it will yield a surplus with a dynamics given by

$$\begin{aligned} {d\xi _t}=\lambda _{t^-} m_Y (\theta -\eta ) dt +\lambda _{t^-} {\mathbb {E}}[{\ell _p(t,Y)}|{\mathcal {F}}_{t^-}] (1+\eta ) dt -\int _0^\infty \ell _p(t,y) \nu ^{C}(dt,dy) \end{aligned}$$

where \(\theta \) and \(\eta \), \(0<\theta <\eta \), are respectively the insurer and reinsurer premium safety loadings. Moreover note that \({\mathbb {E}}[{\ell _p(t,Y)}|{\mathcal {F}}_{t^-}]=\int _0^\infty {\ell _p(t,y)}F_Y(dy)\), due to the independence of the claims \(Y_i\).

We assume the primary insurer considers a reinsurance contract characterized by the retention function

$$\begin{aligned} \ell _p(t,y) = {\left\{ \begin{array}{ll} p_t (y-l)+ l & \text {if } y>l\\ y & \text {if } 0\le y \le l, \end{array}\right. } \end{aligned}$$
(2.1)

where \(0\le p_t\le 1\) is the proportion which needs to be chosen optimally and \(l\ge 0\) is a given threshold level.

The insurer invests the surplus in a financial market and decides the dollar amount \(\pi _t\) of the surplus which will be invested in a risky asset, leaving the residual in a bank account paying interests at a constant rate r.

We describe the risky asset price S dynamics by

$$\begin{aligned} dS_t=S_{t}(\mu dt+\sigma dW_t),\quad S_0>0, \end{aligned}$$

with constant coefficients \(\mu ,\sigma \) and denote by \(X^\textbf{u}\) the surplus process, that represents the net value of the investment of the insurer after considering the reinsurance and the premiums paid and received. The controlled evolution of the surplus investment \(X^\textbf{u}\) can be written as follows

$$\begin{aligned} dX_t^\textbf{u}&=\left[ (\mu -r) \pi _t + r X_{t^-}^\textbf{u} + \lambda _{t^-} m_Y \left( \theta -\eta \right) +\lambda _{t^-} {\mathbb {E}}[{\ell _p(t,Y)}|{\mathcal {F}}_{t^-}] (1+\eta ) \right] dt \nonumber \\ &\quad +\sigma \pi _tdW_t -\int _0^\infty \ell _p(t,y) \nu ^{C}(dy,dt), \end{aligned}$$

where \(\textbf{u}=(p,\pi )\) belongs to the class of admissible controls \(\textbf{U}\), defined as the set of predictable processes satisfying the integrability condition

$$\begin{aligned} {\mathbb {E}}\big [\int _0^T \pi _t^2 dt\big ]<\infty \ \ \text{ and } \ \ p_t\in [0,1], \forall t\in [0,T]. \end{aligned}$$

The strategy will be chosen in order to maximize the mean-variance objective functional of the final wealth, i.e.

$$\begin{aligned} \sup _{\textbf{u} \in \textbf{U}}J^\textbf{u}(t,x,\lambda ), \end{aligned}$$
(2.2)

where \(J^\textbf{u}(t,x,\lambda )\) is the expected total reward at maturity with a penalization proportional to the variance

$$\begin{aligned} J^\textbf{u}(t,x,\lambda )= \mathbb {E}_{t,x,\lambda }[X_T^\textbf{u}]-\frac{\gamma }{2} Var_{t,x,\lambda }[X_T^\textbf{u}] \end{aligned}$$
(2.3)

for a fixed insurer risk aversion parameter \(\gamma >0\).

It is well known that the mean variance criterion has the issue of being time inconsistent, which implies that the dynamic programming principle does not apply. Therefore, following Björk and Murgoci (2010) (see also Björk et al. (2017)) we approach the decision problem as a non cooperative-game and look for the solution among the equilibrium strategies defined as follows (see also Landriault et al. (2018)).

Definition 2.1

An admissible strategy \(\hat{\textbf{u}}=({\hat{p}}, {\hat{\pi }})\) is called a (reinsurance-investment) equilibrium strategy for Problem (2.2)–(2.3) if for any \((t,x,\lambda )\) and any perturbed strategy \(\textbf{u}^\epsilon =(p^\epsilon , \pi ^\epsilon )\) with \(\epsilon >0\),

$$\begin{aligned} \underset{\epsilon \rightarrow 0}{\lim }\ \frac{J^{\hat{\textbf{u}}}(t,x,\lambda )-J^\mathbf{u^\epsilon }(t,x,\lambda )}{\epsilon }\ge 0, \end{aligned}$$

where \(\textbf{u}^\epsilon =(p^\epsilon , \pi ^\epsilon )\) is any admissible strategy equal to \(\hat{\textbf{u}}=({\hat{p}}, {\hat{\pi }})\) on the set \([t+\epsilon ,T].\)

3 Main results

For any \(\phi (t,x,\lambda )\in C^{1,2,1}([0,T]\times {\mathbb {R}} \times (0,+\infty ))\), the infinitesimal generator of the controlled surplus \(X_t^\textbf{u}\) is given by

$$\begin{aligned} {\mathcal {A}}^u \phi (t,x,\lambda )&= \left[ (\mu -r) \pi + r x + \lambda m_Y \left( \theta -\eta \right) +\lambda {\mathbb {E}}[{\ell _p(t,Y)}] (1+\eta )\right] \phi _x(t,x,\lambda ) \nonumber \\&\quad +\phi _t(t,x,\lambda )+ \alpha (\beta - \lambda )\phi _{\lambda }(t,x,\lambda )+\frac{1}{2} \sigma ^2\pi ^2 \phi _{xx}(t,x,\lambda ) \nonumber \\&\quad + \rho \mathbb {E}\left[ \phi (t,x,\lambda +Z)-\phi (t,x,\lambda )|{\mathcal {F}}_{t^-}\right] \end{aligned}$$
(3.1)
$$\begin{aligned}&\quad + \lambda \mathbb {E}\left[ \phi (t,x-\ell _p(t,Y),\lambda +R)-\phi (t,x,\lambda )|{\mathcal {F}}_{t^-}\right] , \end{aligned}$$
(3.2)

where the two conditional expected values in (3.1) and (3.2) are finite. It is worth noting that in (3.2) the jumps due to the measures \(\nu ^{(1),\lambda }\) and \(\nu ^C\) both depend on N’s jump times and, that the conditional expectations are respectively

$$\mathbb {E}\left[ \phi (t,x-\ell _p(t,Y),\lambda +R)|{\mathcal {F}}_{t^-}\right] =\int _0^\infty \int _0^\infty \phi (t,x-\ell _p(t,y),\lambda +r)F_Y(dy)F_R(dr),$$

and

$$\mathbb {E}\left[ \phi (t,x,\lambda +Z)|{\mathcal {F}}_{t^-}\right] =\int _0^\infty \phi (t,x,\lambda +z)F_Z(dz)$$

due to the independence hypotheses on the claims \(Y_i\) and on the jumps of the intensity \(Z_i\) and \(R_i\).

The next result is a verification theorem for an equilibrium reinsurance proportion and investment strategy. It is a particular case of Theorem 5.2 in Björk et al. (2017) (see also Cao et al. (2020)).

Theorem 3.1

Suppose there exist functions \(V(t,x,\lambda ), g(t,x,\lambda )\in C^{1,2,1}([0,T]\times {\mathbb {R}}\times (0,+\infty )\) satisfying the following conditions:

  1. 1.

    For all \((t,x,\lambda )\in [0,T]\times {\mathbb {R}}\times (0,+\infty )\),

    $$\begin{aligned} \sup _{u=(p,\pi )\in [0,1]\times {\mathbb {R}}}\left\{ {\mathcal {A}}^uV(t,x,\lambda ) \!-\!\frac{\gamma }{2} {\mathcal {A}}^ug^2(t,x,\lambda ) \!+\!\gamma g(t,x,\lambda ) {\mathcal {A}}^ug(t,x,\lambda ) \right\} =0.\nonumber \\ \end{aligned}$$
    (3.3)
  2. 2.

    For all \((t,x,\lambda )\in [0,T]\times {\mathbb {R}}\times (0,+\infty )\),

    $$\begin{aligned} {\mathcal {A}}^{\hat{\textbf{u}}}g(t,x,\lambda )=0, \end{aligned}$$
    (3.4)

    where \(\hat{\textbf{u}}=({\hat{p}}, {\hat{\pi }})\) is the strategy that attains the supremum in (3.3).

  3. 3.

    For all \((x,\lambda )\in {\mathbb {R}}\times (0,+\infty )\),

    $$\begin{aligned} V(T,x,\lambda )=g(T,x,\lambda )=x. \end{aligned}$$
    (3.5)

    Then \(\hat{\textbf{u}}=(\hat{p}, \hat{ \pi })\) is an equilibrium reinsurance-investment strategy for objective (2.2). Moreover, \(V(t,x,\lambda )=J^{\hat{\textbf{u}}}(t,x,\lambda )\) and \(g(t,x,\lambda )=\mathbb {E}_{t,x,\lambda }[X_T^{{\hat{\textbf{u}}}}]\).

Applying the previous verification theorem, we obtain our main result, which states the solution of our problem in explicit form.

In the following, we need the moments of \(\ell _p\), thus we introduce the notation

$$\begin{aligned} m_{\ell _p}(p_t)={\mathbb {E}}[{\ell _p(t,Y)}|{\mathcal {F}}_{t^-}], \quad n_{\ell _p}(p_t)={\mathbb {E}}[{\ell _p^2(t,Y)}|{\mathcal {F}}_{t^-}], \end{aligned}$$

and, taking into account the definition of the contract (2.1), we compute

$$\begin{aligned} m_{\ell _p}(p_t)=m_Y- \left( 1-p_t\right) {\mathbb {E}}\left( Y-l\right) ^+ \end{aligned}$$

and

$$\begin{aligned} n_{\ell _p}(p_t)&= n_Y +(p_t^2-1){\mathbb {E}}(Y^2 1\!\!1_{(Y>l)}) +l^2 \left( 1-p_t\right) ^2 {\mathbb {P}}(Y>l) \nonumber \\&\qquad + 2 \, l\, p_t\left( 1-p_t\right) {\mathbb {E}}(Y 1\!\!1_{(Y>l)})\nonumber \\&= n_Y-\left( 1-p_t^2\right) {\mathbb {E}}\left( \left( Y-l\right) ^+\right) ^2 - 2\, l\, \left( 1-p_t\right) {\mathbb {E}}\left( Y-l\right) ^+. \end{aligned}$$

Theorem 3.2

An equilibrium reinsurance-investment strategy \(\hat{\textbf{u}}=({\hat{p}}, {\hat{\pi }})\) for objective (2.2) is given by

$$\begin{aligned} {\hat{p}}_t=\min \left\{ \textrm{RP} (t, k(t)), 1\right\} , \quad {\hat{\pi }}_t=\frac{\mu -r}{\gamma \, \sigma ^2}e^{-r(T-t)}, \end{aligned}$$

where \(\textrm{RP}(t,\kappa )\) denotes the retention limit proportion function

$$\begin{aligned} \textrm{RP}(t,\kappa )=\frac{{\mathbb {E}}\left( Y-l\right) ^+}{{\mathbb {E}}\left( \left( Y-l\right) ^+ \right) ^2}\left( \frac{\eta }{\gamma }+ m_R \kappa - \, l\, e^{r(T-t)} \right) ^+ e^{-r(T-t)} \end{aligned}$$

and k(t) is the unique solution of the ODE

$$\begin{aligned} \dot{k}(t)+(m_R-\alpha ) k(t)+ \left( m_Y(\theta -\eta )+\eta \ m_{\ell _p}(\hat{p}_t)\right) e^{r(T-t)}=0, \quad k(T)=0.\qquad \end{aligned}$$
(3.6)

Moreover, the equilibrium value function is given by

$$\begin{aligned} V(t,x,\lambda )=J^{\hat{\textbf{u}}}(t,x,\lambda )=e^{r(T-t)} x+A(t)+K(t) \lambda , \end{aligned}$$
(3.7)

where

$$\begin{aligned} A(t)= \int _t^T \left( \left( \alpha \beta +\rho \ m_Z\right) K(s) -\frac{\gamma }{2}\rho \ n_Z k^2(s) +\frac{(\mu -r)^2}{2\gamma \sigma ^2}\right) \, ds \end{aligned}$$
(3.8)

and K(t) is the unique solution of the following ODE

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{K}(t)+ (m_R-\alpha ) K(t) + m_Y (\theta -\eta ) e^{r(T-t)}-\frac{\gamma }{2} n_R k^2(t) + P(t)=0\\ K(T)=0 \end{array}\right. } \end{aligned}$$
(3.9)

where

$$\begin{aligned} P(t)=\left( -\frac{\gamma }{2} e^{r(T-t)} n_{\ell _p}(\hat{p}_t) +\left( \eta +\gamma m_R k(t)\right) m_{\ell _p}(\hat{p}_t) \right) e^{r(T-t)}. \end{aligned}$$

Proof

Assume that V and g take the form

$$\begin{aligned} V(t,x,\lambda )=e^{r(T-t)} x+A(t)+K(t) \lambda , \quad g(t,x,\lambda )=e^{r(T-t)} x+a(t)+k(t) \lambda , \end{aligned}$$

for suitable functions A(t), K(t), a(t), k(t) to be determined. From (3.5) we deduce that \(A(T)=K(T)=a(T)=k(T)=0\).

The extended HJB equation (3.3) writes as

$$\begin{aligned} \sup _{p\in [0,1]} I_1(t,x,\lambda ,p)+ \sup _{\pi \in {\mathbb {R}}} I_2(t,x,\lambda ,\pi )+ I_3(t,x,\lambda )=0, \end{aligned}$$

where

$$\begin{aligned} I_1(t,x,\lambda ,p)= & \lambda e^{r(T-t)} \left( -\frac{\gamma }{2} e^{r(T-t)} n_{\ell _p}(p) +(\eta + \gamma m_R k(t)) m_{\ell _p}(p) \right) ,\qquad \end{aligned}$$
(3.10)
$$\begin{aligned} I_2(t,x,\lambda ,\pi )= & e^{r(T-t)} \left( -\frac{\gamma }{2} \sigma ^2 e^{r(T-t)} \pi ^2 +(\mu -r)\pi \right) , \end{aligned}$$
(3.11)

and

$$\begin{aligned} I_3(t,x,\lambda )&=\lambda \left[ \dot{K}(t)+\left( m_R-\alpha \right) K(t)+m_Y(\theta -\eta )e^{r(T-t)}-\frac{\gamma }{2} n_R k^2(t)\right] \\&\quad + \dot{A}(t) +\left( \alpha \beta +\rho m_Z\right) K(t) -\frac{\gamma }{2} \rho n_Z k^2(t). \end{aligned}$$

The optimal retention proportion and investment strategy follow immediately from (3.10) and (3.11), respectively.

Since for all \((t,x,\lambda )\in [0,T] \times {\mathbb {R}} \times (0,+\infty )\) it holds

$$\begin{aligned} 0&= I_1(t,x,\lambda ,\hat{p})+ I_2(t,x,\lambda ,\hat{\pi })+ I_3(t,x,\lambda ) \\&= \lambda \left[ \dot{K}(t)+\left( m_R-\alpha \right) K(t)+m_Y(\theta -\eta )e^{r(T-t)}-\frac{\gamma }{2} n_R k^2(t) +P(t)\right] \\&\quad + \dot{A}(t) +\left( \alpha \beta +\rho m_Z\right) K(t) -\frac{\gamma }{2} \rho n_Z k^2(t) + \frac{(\mu -r)^2}{2\gamma \sigma ^2}, \end{aligned}$$

we deduce (3.8) and (3.9).

Equation (3.4) becomes

$$\begin{aligned} 0= {\mathcal {A}}^{\hat{u}} g(t,x,\lambda )=&\lambda \left[ \dot{k}(t)+(m_R-\alpha ) k(t)+ \left( m_Y(\theta -\eta )+\eta m_{\ell _p}(\hat{p}(t))\right) e^{r(T-t)} \right] \\&\quad + \dot{a}(t) + (\alpha \beta + \rho m_Z ) k(t) + \frac{(\mu -r)^2}{\gamma \sigma ^2} \end{aligned}$$

which holds for all \((t,x,\lambda )\in [0,T] \times {\mathbb {R}} \times (0,+\infty )\). Taking into account that \(a(T)=k(T)=0\), we deduce (3.6) and that

$$\begin{aligned} a(t)=\int _t^T \left( \left( \alpha \beta +\rho m_Z\right) k(s) + \frac{(\mu -r)^2}{\gamma \sigma ^2} \right) \, ds. \end{aligned}$$

Finally, the uniqueness of the solutions k(t) and K(t) of (3.6) and, respectively, (3.9) is due to the fact that the generators of the ODEs satisfy the uniform Lipschitz condition. In fact, the generator of (3.6) can be written as

$$\begin{aligned} f(t,\kappa )&=(m_R-\alpha )\kappa +\left( m_Y \theta -\eta {\mathbb {E}}\left( Y-l\right) ^+ \right) e^{r(T-t)} \\&\quad +\eta {\mathbb {E}}\left( Y-l\right) ^+ e^{r(T-t)} \min \{\textrm{RP}(t,\kappa ), 1\} \end{aligned}$$

and satisfies

$$\begin{aligned}&|f(t,\kappa _1) -f(t,\kappa _2)| \le |m_R-\alpha | \, |\kappa _1 -\kappa _2| \\&+ \frac{\eta \left( {\mathbb {E}}\left( Y-l\right) ^+\right) ^2}{\gamma {\mathbb {E}}\left( \left( Y-l\right) ^+\right) ^2 } \left| \left( \eta +\gamma m_R \kappa _1 -\gamma \, l\, e^{r(T-t)} \right) ^+-\left( \eta +\gamma m_R \kappa _2 -\gamma \, l\, e^{r(T-t)} \right) ^+\right| \\&\quad \le |m_R-\alpha | \, |\kappa _1 -\kappa _2|+ \eta m_R |\kappa _1 -\kappa _2| \le \left( |m_R-\alpha | + \eta \right) |\kappa _1 -\kappa _2|. \end{aligned}$$

Similarly, we can prove that the generator of (3.9) satisfies the uniform Lipschitz condition. \(\square \)

Let us now discuss the results obtained and compare them with those of Cao et al. (2020) and Li et al. (2017). Both the equilibrium investment and the retention proportion strategies do not depend on the capital x, which is due to having considered a constant risk aversion \(\gamma \). In particular, the equilibrium investment strategy is identical to that found in the two papers above, because the investment market is the same and the price dynamics is independent of the aggregate claims process. The comparison for the equilibrium retention is more involved, as we consider a different contract than the excess of loss type and, moreover, a different model than Li et al. (2017), who have a Lèvy-type aggregate claim dynamics instead of our contagion model also used in Cao et al. (2020). In Li et al. (2017), the equilibrium excess of loss reinsurance strategy does not depend on the claim, whereas in Cao et al. (2020), due to the contagion effect, the reinsurance strategy depends on the distribution of the claim. It follows from Theorem 3.2 that the equilibrium reinsurance proportion \(\hat{p}\) depends on the distribution of the claim Y exceeding level l, either explicitly through the moments \({\mathbb {E}}\left( Y-l\right) ^+\) and \({\mathbb {E}} \left( \left( Y-l\right) ^+\right) ^2\), specifically related to the proportional type of strategies, or implicitly through the function k(t). Note that, as in Cao et al. (2020), the presence of the function k(t) is related to the internal and not external contagion effect. In fact, it does not depend on the externally excited jumps, i.e. on the distribution of Z and on the Poisson intensity \(\rho \). This suggests that the external effects are fully and implicitly hedged through the related change in the premium rate, while self-excited effects require more attention and management adjustments.

In the following proposition, we analyze the sign of k(t) to determine how the contagion and, as already noted, the internal clustering specifically, affect the insurer’s choice to retain more or less risk. We set the interest rate \(r=0\) for simplicity, so that the ODEs in Theorem 3.2 are autonomous functions and k(t) is monotone in t. When \(r\ne 0\) is small, similar results we expect can be written (see Cao et al. (2020)).

Let us preliminary observe that, with \(r=0\) the retention limit proportion function \(\textrm{RP}\) does not depend explicitly on time, that is

$$\begin{aligned} \textrm{RP}(\kappa )=\frac{{\mathbb {E}}\left( Y-l\right) ^+}{{\mathbb {E}} \left( \left( Y-l\right) ^+\right) ^2} \left( \frac{\eta }{\gamma }+ m_R \kappa -\, l \right) ^+. \end{aligned}$$

Proposition 3.1

Assume \(r=0\). Then

  1. 1.

    If \(\textrm{RP}(0) > 1-\frac{\theta }{\eta }\frac{m_Y}{{\mathbb {E}}\left( Y-l\right) ^+}\) then k(t) is decreasing in t and \(k(t)> 0\) for all \(t\in [0,T)\), \(k(T)=0\);

  2. 2.

    If \(\textrm{RP}(0)=1-\frac{\theta }{\eta }\frac{m_Y}{{\mathbb {E}}\left( Y-l\right) ^+}\) then \(k(t)=0\) for all \(t\in [0,T]\);

  3. 3.

    If \(\textrm{RP}(0)<1-\frac{\theta }{\eta }\frac{m_Y}{{\mathbb {E}}\left( Y-l\right) ^+}\) then k(t) is increasing in t and \(k(t) <0\) for all \(t\in [0,T)\), \(k(T)=0\).

Proof

Let \(\tilde{k}(t)=k(T-t)\), \(t\in [0,T]\). Then, the ODE (3.6) can be rewritten in forward time as \(\dot{\tilde{k}}(t)=f(\tilde{k}(t))\), \(\tilde{k}(0)=0\), where

$$\begin{aligned} f({{\tilde{\kappa }}})=(m_R-\alpha ) {\tilde{\kappa }}+ m_Y \theta -\eta \left( 1-\min \{\textrm{RP}({\tilde{\kappa }}), 1 \}\right) {\mathbb {E}}\left( Y-l\right) ^+. \end{aligned}$$

It is well known (see, e.g., Lemma 1.7 in Hale and Koçak (1991)) that solutions of an autonomous ODE are monotone in t, and the monotonicity depends on the sign of f(0). If \(\textrm{RP}(0)\ge 1\) then \(f(0)=m_Y \theta >0\), thus \(\tilde{k}(t)\) is positive and increasing or, equivalently, k(t) is positive and decreasing.

If \(\textrm{RP}(0)<1\) then

$$\begin{aligned} f(0)= m_Y \theta -\eta \left( 1-\textrm{RP}(0)\right) {\mathbb {E}}\left( Y-l\right) ^+ \end{aligned}$$

and the sign and the monotonicity of \(\tilde{k}(t)\) depend on the sign of f(0).

In particular, if \(f(0)=0\), equivalently \(\textrm{RP}(0)=1-\frac{\theta }{\eta }\frac{m_Y}{{\mathbb {E}}\left( Y-l\right) ^+}\), the unique solution the ODE (3.6) is \(\tilde{k}(t)=0\) for all \(t\in [0, T]\).

\(\square \)

From the previous proposition, we can see that we have one of the following cases.

If \(\textrm{RP}(0)\ge 1\), k(t) is decreasing in t and thus \(\textrm{RP}(k(t))\ge \textrm{RP}(k(T))=\textrm{RP}(0)\). This implies that the reinsurance equilibrium proportion strategy is \({\hat{p}}_t=1\) for all \(t\in [0, T]\), which means that nothing is reinsured. In this case, \(l < \frac{\eta }{\gamma }\) and the claim size Y is light-tail with \({\mathbb {E}}\left( Y-l\right) ^+\le \left( \frac{\eta }{\gamma }-\, l \right) ^+\).

When \( 1-\frac{\theta }{\eta }\frac{m_Y}{{\mathbb {E}}\left( Y-l\right) ^+}<\textrm{RP}(0)<1\), the optimal retention quota \(\hat{p}_T=\mathrm RP(0)\) exceeds the net relative cost of reinsurance assuming that all of the portion of the claim above the level is reinsured. In this case, k(t) is again decreasing in t and so are \(\textrm{RP}(k(t))\) and \(\hat{p}_t=\min \{\textrm{RP}(k(t)), 1 \}\). This implies that \(1-\hat{p}_T=1-\textrm{RP}(0)\) represents the maximum reinsurance quota.

In the special case when \(\textrm{RP}(0)=1-\frac{\theta }{\eta }\frac{m_Y}{{\mathbb {E}}\left( Y-l\right) ^+}\) it is \(k(t)=0\) for all \(t\in [0, T]\) and, therefore, the optimal strategy is not affected by the contagion. In this case, the equilibrium reinsurance proportion strategy is constant, precisely \(\hat{p}_t=\textrm{RP}(0)\). If, in addition, \(l\ge \frac{\eta }{\gamma }\) then the equilibrium proportion is null and the insurer reinsures all the claim exceeding l. Observe that, in the latter situation the insurer net cost for the reinsurance is null, i.e. \(\eta {\mathbb {E}}\left( Y-l\right) ^+-\theta m_Y=0\) .

Lastly, if \(\textrm{RP}(0)< 1-\frac{\theta }{\eta }\frac{m_Y}{{\mathbb {E}}\left( Y-l\right) ^+}\), which implies the inequality \(\theta m_Y<\eta {\mathbb {E}}\left( Y-l\right) ^+\) that would be required for reinsurance, we have that k(t) is increasing in t and so is \(\hat{p}_t=\textrm{RP}(k(t))\). This implies that \(1-\hat{p}_T=1-\textrm{RP}(0)\) represents the minimum proportion for reinsurance.

For l greater than \(\frac{\eta }{\gamma }\), different cases are possible as the following corollary shows.

Corollary 3.1

Assume \(r=0\) and \(l\ge \frac{\eta }{\gamma }\). Then

  1. 1.

    If \(\frac{m_Y}{{\mathbb {E}}\left( Y-l\right) ^+}> \frac{\eta }{\theta }\) then k(t) is decreasing in t and \(k(t)> 0\) for all \(t\in [0,T)\), \(k(T)=0\);

  2. 2.

    If \(\frac{m_Y}{{\mathbb {E}}\left( Y-l\right) ^+} = \frac{\eta }{\theta }\) then \(k(t)=0\) for all \(t\in [0,T]\);

  3. 3.

    If \(\frac{m_Y}{{\mathbb {E}}\left( Y-l\right) ^+}< \frac{\eta }{\theta }\) then then k(t) is increasing in t and \(k(t) <0\) for all \(t\in [0,T)\), \(k(T)=0\).

Proof

The result follows immediately from Proposition 3.1 since, for \(l\ge \frac{\eta }{\gamma }\), \(\textrm{RP}(0)=0\). \(\square \)

In the next proposition, we analyze the behaviour of k(t) in terms of the level parameter.

Proposition 3.2

Assume \(r=0\) and denote

$$\begin{aligned} k_l(t)=\displaystyle \frac{\partial }{\partial l}k(t), \quad m_{Y>l}={\mathbb {E}}\left( Y-l\right) ^+, \quad Q_{Y>l}=\frac{{\mathbb {E}}\left( Y-l\right) ^+}{{\mathbb {E}}\left( \left( Y-l\right) ^+\right) ^2}. \end{aligned}$$

Then

$$\begin{aligned} k_l(t) =&\,- \displaystyle \int _t^T I(u) \exp \Big \{-\int _t^u \left( \alpha -m_R -\eta m_R \left( m_{Y>l} \right) \right. \nonumber \\&\times \left. \left( Q_{Y>l}\right) 1_{\{0<(Q_{Y>l})\left( \frac{\eta }{\gamma }+m_Rk(s)-l\right) <1\}} \right) ds \Big \} du, \end{aligned}$$
(3.12)

where

$$\begin{aligned}&I(t)=\eta \left( 1-\hat{p}_t\right) \frac{\partial }{\partial l}\left( m_{Y>l}\right) -\eta \left( m_{Y>l} \right) 1_{\{0<(Q_{Y>l})\left( \frac{\eta }{\gamma }+m_Rk(t)-l\right) <1\}} \nonumber \\&\qquad \qquad \times \Bigg \{\left( \frac{\eta }{\gamma }+m_Rk(t)-l\right) \frac{\partial }{\partial l}\left( Q_{Y>l}\right) - \left( Q_{Y>l}\right) \Bigg \}. \end{aligned}$$
(3.13)

Proof

Differentiating equation (3.6) with respect to l yields

$$\begin{aligned} \dot{k_l}(t)&=(\alpha -m_R) k_l(t)- \eta \frac{\partial }{\partial l} \left( m_{\ell _p}(\hat{p}_t)\right) =(\alpha -m_R) k_l(t)+ \eta \frac{\partial }{\partial l}\left( \left( m_{Y>l}\right) \left( 1-\hat{p}_t\right) \right) \nonumber \\&= (\alpha -m_R) k_l(t)+ \eta \left( 1-\hat{p}_t\right) \frac{\partial }{\partial l}\left( m_{Y>l}\right) -\eta \left( m_{Y>l} \right) \frac{\partial }{\partial l}\hat{p}_t \nonumber \\&=(\alpha -m_R) k_l(t)+ \eta \left( 1-\hat{p}_t\right) \frac{\partial }{\partial l}\left( m_{Y>l}\right) \nonumber \\&\qquad -\eta \left( m_{Y>l} \right) 1_{\{0<Q_{Y>l}\left( \frac{\eta }{\gamma }+m_Rk(t)-l\right)<1\}}\frac{\partial }{\partial l}\left( Q_{Y>l}\left( \frac{\eta }{\gamma }+m_Rk(t)-l\right) \right) \nonumber \\&=(\alpha -m_R) k_l(t)+ \eta \left( 1-\hat{p}_t\right) \frac{\partial }{\partial l}\left( m_{Y>l}\right) \nonumber \\&\qquad -\eta \left( m_{Y>l} \right) 1_{\{0<Q_{Y>l}\left( \frac{\eta }{\gamma }+m_Rk(t)-l\right) <1\}} \nonumber \\&\qquad \qquad \times \Bigg \{\left( \frac{\eta }{\gamma }+m_Rk(t)-l\right) \frac{\partial }{\partial l}\left( Q_{Y>l}\right) + \left( Q_{Y>l}\right) \left( m_R k_l(t)-1\right) \Bigg \}. \end{aligned}$$

Therefore

$$\begin{aligned} \dot{k_l}(t)&=\left( \alpha -m_R -\eta m_R \left( m_{Y>l} \right) \left( Q_{Y>l}\right) 1_{\{0<Q_{Y>l}\left( \frac{\eta }{\gamma }+m_Rk(t)-l\right)<1\}} \right) k_l(t) \nonumber \\&\quad + \eta \left( 1-\hat{p}_t\right) \frac{\partial }{\partial l}\left( m_{Y>l}\right) -\eta \left( m_{Y>l} \right) 1_{\{0<Q_{Y>l}\left( \frac{\eta }{\gamma }+m_Rk(t)-l\right) <1\}} \nonumber \\&\quad \times \Bigg \{\left( \frac{\eta }{\gamma }+m_Rk(t)-l\right) \frac{\partial }{\partial l}\left( Q_{Y>l}\right) - \left( Q_{Y>l}\right) \Bigg \}, \end{aligned}$$

with boundary condition \(k_l(T)=0\) as \(k(T)=0\). The thesis follows immediately. \(\square \)

We observe that from the previous result it follows that the monotonicity of k(t) with respect to the level depends on the sign of I(u) in (3.13). This reflects on the mean of the controlled surplus investment \(X_T^{{\hat{\textbf{u}}}}\) since

$$\begin{aligned} \mathbb {E}_{t,x,\lambda }[X_T^{{\hat{\textbf{u}}}}]=g(t,x,\lambda )=x+a(t)+k(t) \lambda , \end{aligned}$$
(3.14)

with

$$\begin{aligned} a(t)=\int _t^T \left( \left( \alpha \beta +\rho m_Z\right) k(s) + \frac{\mu ^2}{\gamma \sigma ^2} \right) \, ds. \end{aligned}$$

The behaviour with respect to the level of the variance

$$\begin{aligned} Var_{t,x,\lambda }[X_T^{\hat{\textbf{u}}}]=\frac{2}{\gamma }\left( g(t,x,\lambda ) - V(t,x,\lambda ) \right) , \end{aligned}$$

where \(V(t,x,\lambda )\) is defined by (3.7), depends on the co-movement of k(t) and K(t).

In the next section we illustrate some examples and show the behaviour of the optimal proportion \(\hat{p}_t\) and of the value function for different choices of the threshold level l.

4 Numerical examples

Example 1: Proportional reinsurance

The proportional reinsurance, that means \(\ell _p(t,y)=p_ty\), is obtained setting \(l=0\). In this case, the equilibrium retention proportion reduces to

$$\begin{aligned} {\hat{p}}_t&=\min \Big \{ \textrm{RP}(t,k(t)), 1 \Big \}, \quad \textrm{RP}(t,\kappa )=\frac{m_Y}{ n_Y } \left( \frac{\eta }{\gamma }+ m_R\kappa \right) ^+ e^{-r(T-t)}, \end{aligned}$$

where k(t) solves the ODE

$$\begin{aligned} \dot{k}(t)+(m_R-\alpha ) k(t)+ m_Y \left( \theta -\eta +\eta \hat{p}_t\right) e^{r(T-t)}=0, \quad k(T)=0. \end{aligned}$$

Furthermore, K(t) solves the ODE (3.9) with

$$\begin{aligned} P(t)=\left( -\frac{\gamma }{2} e^{r(T-t)} n_Y\hat{p}_t^2 +\left( \eta +\gamma m_R k(t)\right) m_Y \hat{p}_t \right) e^{r(T-t)}. \end{aligned}$$

When additionally \(r=0\), Proposition 3.1 applies with \({RP}(0)=\frac{m_Y \eta }{n_Y \gamma }\).

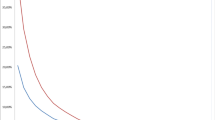
The time behaviour of k(t) and of the optimal proportion \(\hat{p}_t\) is represented in Figs. 2 and 3 (continuous lines), under the assumption that the claims are exponentially distributed. We observe that the optimal proportional retention \(\hat{p}_t\) has the same behaviour as k(t). In particular, for \(T=5\), \(m_R=1\), \(\alpha =3\), \(\theta =0.3\), \(\eta =0.4\), \(\gamma =0.05\), \(m_Y=5\), case 1 of Proposition 3.1 applies and k(t) is positive and decreasing, whereas if \(m_Y=18\), case 3 applies and k(t) is negative and increasing. In both cases, the optimal proportion is affected by contagion, retaining more for less risky claims and less for riskier ones. As expected, the self-exciting effect vanishes as time approaches the terminal horizon T. Finally, the value of the objective function for the proportional contract can be deduced from Fig. 4 and compared with our generalized proportional contract.

Example 2: Exponentially distributed claims

If \(Y\sim \text {Exp}\) then

$$\begin{aligned} {\mathbb {E}}\left( Y-l\right) ^+= m_Y e^{-\frac{l}{m_Y}}, \quad {\mathbb {E}}\left( \left( Y-l\right) ^+\right) ^2=n_Y e^{-\frac{l}{m_Y}}=2m^2_Y e^{-\frac{l}{m_Y}}, \end{aligned}$$

so that

$$\begin{aligned} {\hat{p}}_t&= \min \{\textrm{RP}(t,k(t)), 1\}, \quad \textrm{RP}(t,\kappa )=\frac{1}{2m_Y}\left( \frac{\eta }{\gamma }+ m_R \kappa - l\, e^{r(T-t)} \right) ^+ e^{-r(T-t)}, \end{aligned}$$

where k(t) solves the ODE

$$\begin{aligned} \dot{k}(t)+(m_R-\alpha ) k(t)+ m_Y \left( \theta -\eta (1- \hat{p}_t)e^{-\frac{l}{ m_Y}} \right) e^{r(T-t)}=0, \quad k(T)=0. \end{aligned}$$

Furthermore, K(t) solves the ODE (3.9) with

$$\begin{aligned} P(t)=\left( -\frac{\gamma }{2} e^{r(T-t)} n_{\ell _p}(\hat{p}_t) +\left( \eta +\gamma m_R k(t)\right) m_{\ell _p}(\hat{p}_t) \right) e^{r(T-t)}, \end{aligned}$$

where

$$\begin{aligned} n_{\ell _p}(\hat{p}_t)=n_Y-(1-\hat{p}_t^2)n_Ye^{-l/m_Y}- 2\, l (1-\hat{p}_t)m_Y e^{-l/m_Y} \end{aligned}$$

and

$$\begin{aligned} m_{\ell _p}(\hat{p}_t)=m_Y-(1-\hat{p}_t)m_Y e^{-l/m_Y}. \end{aligned}$$

When additionally \(r=0\), by Proposition 3.1 we deduce that if

$$\begin{aligned} \textrm{RP}(0)=\frac{1}{2m_Y}\left( \frac{\eta }{\gamma }- l\right) ^+ > 1-\frac{\theta }{\eta }e^{l/m_Y} \end{aligned}$$
(4.1)

then k(t) is decreasing in t and positive for all \(t\in [0,T)\) (and this happens at least for all \(l> l_0=m_Y\log (\frac{\eta }{\theta })\)), while it is increasing and negative if the inequality in (4.1) is the opposite. The equality in (4.1) corresponds to \(k(t)=0\) for all \(t\in [0,T]\), and thus to \(\hat{p}_t\) constant on [0, T].

Regarding the behaviour of k(t) with respect to the level, from

$$\begin{aligned} k(t)=-\int _t^T m_Y\left( - \theta + \eta \left( 1-\hat{p}_u\right) e^{-\frac{l}{m_Y}}\right) e^{-(\alpha -m_R)(u-t)} du \end{aligned}$$

we observe that it is a bounded function of l. Therefore, \(\textrm{RP}(\kappa (t))=\frac{1}{2m_Y}\left( \frac{\eta }{\gamma }+ m_R \kappa (t) - l \right) ^+\) vanishes for l above a certain level and \(\hat{p}_t=0\) \(\forall \, t\in [0,T]\), which means that all is reinsured. Below that level, \(\hat{p}_t\) may either be positive for all \(t\in [0,T]\), or it may vanish/become positive after a certain instant (respectively, if k(t) is positive and decreasing/negative and increasing).

Figure 1 illustrates some significant examples of the different situations that can occur depending on the values of the model parameters.

Figure 1a is one of the simplest cases. For \(\eta =0.4\), \(\gamma =0.05\), \(\theta =0.3\), \(m_Y=5\), (4.1) holds for any value of the threshold level l, so k(t) and consequently \(\hat{p}_t\) are positive and decreasing in t. By additionally fixing \(\alpha =3\), \(m_R=1\), \(T=5\), a plot of their time behaviour is reported in Fig. 2 for different values of l. As a consequence of Proposition 3.2, this plot also shows that the optimal proportion is decreasing with respect to l and vanishes over a suitable l.

In Fig. 1b, we set the same values of the model parameters except for \(m_Y=18\). In this case, we observe that there exists a level \(l=l_*\) for which the equality in (4.1) holds true. Therefore, for that level it results that \(k(t)=0\) for all \(t\in [0,T]\), which means that there is no contagion effect on the optimal proportion. Moreover, since \(l_*<\frac{\eta }{\gamma }\), we get \(\hat{p}_t=\frac{1}{2m_Y}\left( \frac{\eta }{\gamma }- l_*\right) \) for all \(t\in [0,T]\). Besides, if \(0\le l<l_*\), k(t) is negative and increasing in t, while it is positive and decreasing for \(l>l_*\). This situation is presented in Fig. 3.

In Fig. 1c, \(m_Y=30\) and, similarly to the previous case, there exists \(l_*\) such that \(k(t)=0\) for all \(t\in [0,T]\). Since \(l_*>\frac{\eta }{\gamma }\), for that level it results that \(\hat{p}_t=0\) for all \(t\in [0,T]\). Furthermore, since by Proposition 3.2 one can check that \(\hat{p}_t\) is decreasing with respect to l, the optimal proportion is null for all levels \(l>l_*\).

The situation in Fig. 1d is more involved, since there are two levels \(l_*<l<l^*\) for which the equality in (4.1) is fulfilled. Nevertheless, the monotonicity of k(t) and \(\hat{p}_t\) follows from similar arguments.

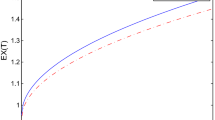
Figure 4a and b are devoted to the value function \(V(t,x,\lambda )\). Figure 4a studies the dependence of \(V(t,x,\lambda )\) on the level. The function is plotted for three different initial times \(t=0, \,2, \,4\) and for \(x=0\), \(\lambda =3\) when the model parameters are \(\eta =0.4\), \(\gamma =0.05\), \(\theta =0.3\), \(m_Y=5\), \(\alpha =3\), \(m_R=1\), \(T=5\) (see Fig. 2), and \(\beta =1\), \(\sigma =0.3\), \(\rho =2\), \(\mu =0.05\), \(\lambda =3\), \(n_R=2\), \(m_Z=1\), \(n_Z=2\). It can be seen that there is a level for which the value functions reaches a maximum. Whereas, in Fig. 4b the relative difference of the value function compared to that of Cao et al. (2020) is evaluated and from the result it can be deduced that the maximum reaches the optimal value obtained by Cao et al. (2020).

It is finally worth noting that, by applying Proposition 3.2 with \(m_{Y>l}=m_Y e^{-\frac{l}{m_Y}}\) and \(Q_{Y>l}=\frac{m_Y}{n_Y}=\frac{1}{2m_Y}\) we get

$$\begin{aligned} I(t)=\eta e^{-\frac{l}{m_Y}} \left( -(1 - \hat{p}_t) +\frac{1}{2} 1_{ \{0< \frac{1}{2m_Y} \left( \frac{\eta }{\gamma }+m_Rk(t)-l\right) <1\}} \right) . \end{aligned}$$
(4.2)

Since k(t) is a bounded function of level, the indicator function in (4.2) vanishes from a certain level upwards, and thus I(t) is negative from that level. This implies, by (3.12) and (3.14), that k(t), and thus \(\mathbb {E}_{t,x,\lambda }[X_T^{{\hat{\textbf{u}}}}]\), are increasing in l at least from a certain level upwards.

Fig. 1
figure 1

Proposition 3.1 under different choices of model parameters

Full size image
Fig. 2
figure 2

Time behaviour of k(t) and \(\hat{p}(t)\) for different levels. Model parameters are: \(\eta =0.4\), \(\gamma =0.05\), \(\theta =0.3\), \(m_Y=5\) (see Fig. 1a), and \(\alpha =3\), \(m_R=1\), \(T=5\)

Full size image
Fig. 3
figure 3

Time behaviour of k(t) and \(\hat{p}(t)\) for different levels. Model parameters are: \(\eta =0.4\), \(\gamma =0.05\), \(\theta =0.3\), \(m_Y=18\) (see Fig. 1b), and \(\alpha =3\), \(m_R=1\), \(T=5\)

Full size image
Fig. 4
figure 4

Behaviour of the value function V(t, x, t) with respect to the level and relative difference of the value functions with benchmark (Cao et al. 2020) for three different times \(t=0, \,2, \,4\) and for \(x=0\), \(\lambda =3\). Model parameters are: \(\eta =0.4\), \(\gamma =0.05\), \(\theta =0.3\), \(m_Y=5\), \(\alpha =3\), \(m_R=1\), \(T=5\) (see Fig. 2), and \(\beta =1\), \(\sigma =0.3\), \(\rho =2\), \(\mu =0.05\), \(\lambda =3\), \(n_R=2\), \(m_Z=1\), \(n_Z=2\)

Full size image

5 Conclusions

In this paper, we consider an optimal investment-reinsurance problem in a dynamic contagion model allowing for self and externally excited claim clustering effects. We find explicit mean-variance reinsurance-investment time consistent strategies for a proportional reinsurance contract where the reinsurance cover a quota share of the claim exceedance over a certain fixed retention level. The contract mitigates the possible drawback of the proportional resulting in the primary insurer ceding too much still guaranteeing to share higher risks to the reinsurance counterpart. The insurer’s retention proportion depends on the model contagion and on the tail heaviness of the claim distribution depending on the fixed threshold level.