Binary classifier calibration using an ensemble of piecewise linear regression models

Abstract

In this paper, we present a new nonparametric calibration method called ensemble of near-isotonic regression (ENIR). The method can be considered as an extension of BBQ (Naeini et al., in: Proceedings of twenty-ninth AAAI conference on artificial intelligence, 2015b), a recently proposed calibration method, as well as the commonly used calibration method based on isotonic regression (IsoRegC) (Zadrozny and Elkan, in: Proceedings of the ACM SIGKDD international conference on knowledge discovery and data mining 2002). ENIR is designed to address the key limitation of IsoRegC which is the monotonicity assumption of the predictions. Similar to BBQ, the method post-processes the output of a binary classifier to obtain calibrated probabilities. Thus, it can be used with many existing classification models to generate accurate probabilistic predictions. We demonstrate the performance of ENIR on synthetic and real datasets for commonly applied binary classification models. Experimental results show that the method outperforms several common binary classifier calibration methods. In particular, on the real data, we evaluated ENIR commonly performs statistically significantly better than the other methods, and never worse. It is able to improve the calibration power of classifiers, while retaining their discrimination power. The method is also computationally tractable for large-scale datasets, as it is $O(N \log N)$ time, where N is the number of samples.

1 Introduction

In many real-world data mining applications, intelligent agents often must make decisions under considerable uncertainty due to noisy observations, physical randomness, incomplete data, and incomplete knowledge. Decision theory provides a normative basis for intelligent agents to make rational decisions under such uncertainty. To do so, decision theory combines utilities and probabilities to determine the optimal actions that maximize expected utility [32]. The output in many of the machine learning models that are used in data mining applications is designed to discriminate the patterns in data. However, such output should also provide accurate (calibrated) probabilities in order to be practically useful for rational decision-making in many real-world applications [1, 9, 13, 36, 38].

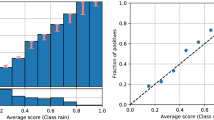
This paper focuses on developing a new nonparametric calibration method for post-processing the output of commonly used binary classification models to generate accurate probabilities. Informally, we say that a classification model is well-calibrated if events predicted to occur with probability p do occur about p fraction of the time, for all p. This concept applies to binary as well as multi-class classification problems [34]. Figure 1 illustrates the binary calibration problem using a reliability curve [7, 24]. The curve shows the probability predicted by the classification model versus the actual fraction of positive outcomes for a hypothetical binary classification problem, where Z is the binary event being predicted. The curve shows that when the model predicts $Z=1$ to have probability 0.2, the outcome $Z=1$ occurs in about 0.3 fraction of the time. The curve shows that the model is fairly well-calibrated, but it tends to underestimate the actual probabilities. In general, the straight dashed line connecting (0, 0) to (1, 1) represents a perfectly calibrated model. The closer a calibration curve is to this line, the better calibrated the associated prediction model. Deviations from perfect calibration are very common in practice and may vary widely depending on the binary classification model that is used [28].

Fig. 1

The solid line shows a calibration (reliability) curve for predicting $Z=1$. The dotted line is the ideal calibration curve

Producing well-calibrated probabilistic predictions is critical in many areas of science (e.g., determining which experiments to perform), medicine (e.g., deciding which therapy to give a patient), business (e.g., making investment decisions), and many others. In data mining problems, obtaining well-calibrated classification model is crucial not only for decision-making, but also for combining output of different classification models [3, 31, 37]. It is also useful when we aim to use the output of a classifier not only to discriminate the instances but also to rank them [14, 19, 41]. Research on learning well-calibrated models has not been explored in the data mining literature as extensively as, for example, learning models that have high discrimination (e.g., high accuracy).

There are two main approaches to obtaining well-calibrated classification models. The first approach is to build a classification model that is intrinsically well-calibrated ab initio. This approach will restrict the designer of the data mining model by requiring major changes in the objective function (e.g., using a different type of loss function) and could potentially increase the complexity and computational cost of the associated optimization program to learn the model. The other approach is to rely on the existing discriminative data mining models and then calibrate their output using post-processing methods. This approach has the advantage that it is general, flexible, and it frees the designer of a data mining algorithm from modifying the learning procedure and the associated optimization method [26]. However, this approach has the potential to decrease discrimination while increasing calibration, if care is not taken. The method we describe in this paper is shown empirically to improve calibration of different types of classifiers (e.g., LR, SVM, and NB) while maintaining their discrimination performance.

Existing post-processing binary classifier calibration methods include Platt scaling [29], histogram binning [39], isotonic regression [40], and a recently proposed method BBQ which is a Bayesian extension of histogram binning [28]. In all these methods, the post-processing step can be seen as a function that maps the outputs of a prediction model to probabilities that are intended to be well-calibrated. Figure 1 shows an example of such a mapping.

In general, there are two main applications of post-processing calibration methods. First, they can be used to convert the outputs of discriminative classification methods with no apparent probabilistic interpretation to posterior class probabilities [29, 31, 36]. An example is an SVM model that learns a discriminative model that does not have a direct probabilistic interpretation. In this paper, we show this use of calibration to map SVM outputs to well-calibrated probabilities. Second, calibration methods can be applied to improve the calibration of predictions of a probabilistic model that is miscalibrated. For example, a naïve Bayes (NB) model is a probabilistic model, but its class posteriors are often miscalibrated due to unrealistic independence assumptions [24]. The method we describe is shown empirically to improve the calibration of NB models without reducing their discrimination. The method can also work well on calibrating models that are less egregiously miscalibrated than are NB models.

2 Related work

Existing post-processing binary classifier calibration models can be divided into parametric and nonparametric methods. Platt’s method is an example of the former; it uses a sigmoid transformation to map the output of a classifier into a calibrated probability [29]. The two parameters of the sigmoid function are learned in a maximum-likelihood framework using a model-trust minimization algorithm [12]. The method was originally developed to transform the output of an SVM model into calibrated probabilities. It has also been used to calibrate other type of classifiers [24]. The method runs in O(1) at test time, and thus, it is fast. Its key disadvantage is the restrictive shape of sigmoid function that rarely fits the true distribution of the predictions [20].

A popular nonparametric calibration method is the equal frequency histogram binning model which is also known as quantile binning [39]. In quantile binning, predictions are partitioned into B equal frequency bins. For each new prediction y that falls into a specific bin, the associated frequency of observed positive instances will be used as the calibrated estimate for $P(z=1 | y)$, where z is the true label of an instance that is either 0 or 1. Histogram binning can be implemented in a way that allows it to be applied to large-scale data mining problems. Its limitations include (1) bins inherently pigeonhole calibrated probabilities into only B possibilities, (2) bin boundaries remain fixed over all predictions, and (3) there is uncertainty in the optimal number of the bins to use [40].

The most commonly used nonparametric classifier calibration method in machine learning and data mining applications is the isotonic regression-based calibration (IsoRegC) model [40]. To build a mapping from the uncalibrated output of a classifier to the calibrated probability, IsoRegC assumes the mapping is an isotonic (monotonic) mapping following the ranking imposed by the base classifier. The commonly used algorithm for isotonic regression is the pool adjacent violators algorithm (PAVA), which is linear in the number of training data [2]. An IsoRegC model based on PAVA can be viewed as a histogram binning model [40] where the position of the boundaries are selected by fitting the best monotone approximation to the train data according to the ordering imposed by the classifier. There is also a variation of the isotonic-regression-based calibration method for predicting accurate probabilities with a ranking loss [23]. In addition, an extension to IsoRegC combines the outputs generated by multiple binary classifiers to obtain calibrated probabilities [42]. While IsoRegC can perform well on some real datasets, the monotonicity assumption it makes can fail in real data mining applications. This can specifically occur when we encounter large-scale data mining problems in which we have to make simplifying assumptions to build the classification models. Thus, there is a need to relax the assumption, which is the focus of the current paper.

Adaptive calibration of predictions (ACP) is another extension to histogram binning [20]. ACP requires the derivation of a $95\%$ statistical confidence interval around each individual prediction to build the bins. It then sets the calibrated estimate to the observed frequency of the instances with positive class among all the predictions that fall within the bin. To date, ACP has been developed and evaluated using only logistic regression as the base classifier [20].

Recently, a new nonparametric calibration model called BBQ was proposed which is a refinement of the histogram binning calibration method [28]. BBQ addresses the main drawbacks of the histogram binning model by considering multiple different equal frequency histogram binning models and their combination using a Bayesian scoring function [15]. However, BBQ has two disadvantages. First, as a post-processing calibration method, it does not take advantage of the fact that in real-world applications a classifier with poor discrimination performance (e.g., low area under the ROC curve) will seldom be used. Thus, BBQ will usually be applied to calibrate classifiers with at least fair discrimination performance. Second, BBQ still selects the position and boundary of the bins by considering only equal frequency histogram binning models. A Bayesian nonparametric method called ABB addresses the latter problem by considering Bayesian averaging over all possible binning models induced by the training instances [27]. The main drawback of ABB is that it is computationally intractable for most real-world applications, as it requires $O(N^2)$ computations for learning the model as well as $O(N^2)$ computations for computing the calibrated estimate for each of the test instances.¹

This paper presents a new binary classifier calibration method called ensemble of near-isotonic regression (ENIR) that can post process the output generated by a wide variety of classification models. The essential idea in ENIR is to use prior knowledge that the scores to be calibrated are in fact generated by a well-performing classifier in terms of discrimination. IsoRegC also uses such prior knowledge; however, it is biased by constraining the calibrated scores to obey the ranking imposed by the classifier. In the limit, this is equivalent to presuming the classifier has AUC equal to 1, which rarely happens in real-world applications. In contrast, BBQ does not make any assumptions about the correctness of classifier rankings. ENIR provides a balanced approach that spans between IsoRegC and BBQ. In particular, ENIR assumes that the mapping from uncalibrated scores to calibrated probabilities is a near-isotonic (monotonic) mapping; it allows violations of the ordering imposed by the classifier and then penalizes them through the use of a regularization term. Figure 2 shows the calibration curve of three commonly used binary classifiers trained on the liver-disorder UCI dataset. The dataset consist of 345 total instances, and the final AUC is equal to 0.73. The figure shows that the isotonicity assumption made by IsoRegC is violated comparing the frequency of observations in the first and the second bins.

Fig. 2

Calibration curves based on using 5 equal frequency bins when we use logistic regression, SVM, and naïve Bayes classification models for the binary classification task in the liver-disorder UCI dataset. Considering the frequency of observations in the first and the second bin, we notice the violation of the isotonicity assumption that is made by IsoReg in all the classification models. a Logistic regression. b Linear kernel SVM. c Naïve Bayes

ENIR utilizes the path algorithm modified pool adjacent violators algorithm (mPAVA) that can find the solution path to a near-isotonic regression problem in $O(N \log N)$, where N is the number of training instances [35]. Finally, it uses the BIC scoring measure to combine the predictions made by these models to yield more robust calibrated predictions.

We perform an extensive set of experiments on a large suite of real datasets, to show that ENIR outperforms both IsoRegC and BBQ. Our experiments show that the near-isotonic assumption made by ENIR is a realistic assumption about the output of classifiers, and unlike the isotonicity assumption that is made by IsoReg, it is not biased. Moreover, our experiments show that by post-processing the output of classifiers using ENIR, we can gain high calibration improvement, without losing any statistically meaningful discrimination performance. Finally, we also compare the performance of ENIR with our other newly introduced binary classifier calibration method, ELiTE [25].

The remainder of this paper is organized as follows. Section 3 introduces the ENIR method. Section 4 describes a set of experiments that we performed to evaluate ENIR and other calibration methods. Section 5 describes briefly our other newly introduced calibration model based on using an ensemble of linear trend filtering models and compares its performance ENIR. Finally, Sect. 6 states conclusions and describes several areas for future work.

3 Method

In this section, we introduce the ensemble of near-isotonic regression (ENIR) calibration method. ENIR utilizes the near isotonic regression method that seeks a nearly monotone approximation for a sequence of data $y_1,\ldots ,y_n$ [35]. The proposed calibration method extends the commonly used isotonic regression-based calibration by an approximate selective Bayesian averaging of a set of nearly isotonic regression models. The set includes the isotonic regression model as an extreme member. From another viewpoint, ENIR can be considered as an extension to a recently introduced calibration model BBQ [28] by relaxing the assumption that probability estimates are independent inside the bins and finding the boundary of the bins automatically through an optimization algorithm.

Before getting into the details of the method, we define some notation. Let $y_i$ and $z_i$ define, respectively, an uncalibrated classifier prediction and the true class of the i’th instance. In this paper, we focus on calibrating a binary classifier’s output,² and thus, $z_i \in \{0,1\}$ and $y_i \in [0,1]$. Let $\mathcal {D}$ define the set of all training instances $(y_i , z _i)$. Without loss of generality, we can assume that the instances are sorted based on the classifier scores $y_i$, so we have $y_1 \le y_2 \le \cdots \le y_N$, where N is the total number of samples in the training data.

The standard isotonic regression-based calibration model finds the calibrated probability estimates by solving the following optimization problem:

$$\begin{aligned} \begin{aligned}&\hat{\varvec{p}}_\mathrm{iso} = \underset{\varvec{p} \in R^N}{\text {argmin}}&\frac{1}{2} \sum _{i=1}^{N} (p_i-z_i)^2 \\&\text {s.t.}&p_1 \le \cdots \le p_N \\&&0\le p_i \le 1 \quad \forall i \in \{1, \ldots , N\}, \\ \end{aligned} \end{aligned}$$

(1)

where $\hat{\varvec{p}}_\mathrm{iso}$ is the vector of calibrated probability estimates. The rationale behind this model is to assume that the base classifier ranks the instances correctly. To find the calibrated probability estimates, it seeks the best fit of the data that is consistent with the classifier’s ranking. A unique solution to the above convex optimization program exists and can be obtained by an iterative algorithm called pool adjacent violators algorithm (PAVA) that runs in O(N). Note, however, that isotonic regression calibration still needs $O(N \log N)$ computations due to the fact that instances are required to be sorted based on the classifier scores $y_i$. PAVA iteratively groups the consecutive instances that violate the ranking constraint and uses their average over z (frequency of positive instances) as the calibrated estimate for all the instances within the group. We define the set of these consecutive instances that are located in the same group and attain the same predicted calibrated estimate as a bin. Therefore, an isotonic regression-based calibration can be viewed as a histogram binning method [40] where the position of boundaries are selected by fitting the best monotone approximation to the training data according to the ranking imposed by the classifier.

One can show that the second constraint in the optimization given by Eq. 1 is redundant, and it is possible to rewrite the equation in the following equivalent form:

$$\begin{aligned} \begin{aligned}&\hat{\varvec{p}}_\mathrm{iso} = \underset{\varvec{p} \in R^N}{\text {argmin}}&\frac{1}{2} \sum _{i=1}^{N} (p_i-z_i)^2 + \lambda \sum _{i=1}^{N-1} (p_i - p_{i+1}) \nu _i\\&\text {s.t.}&\lambda = +\,\infty , \end{aligned} \end{aligned}$$

(2)

where $\nu _i = \mathbb {1}(p_i > p_{i+1})$ is the indicator function of ranking violation. Relaxing the equality constraint in the above optimization program leads to a new convex optimization program as follows:

$$\begin{aligned} \begin{aligned}&\hat{\varvec{p}}_{\lambda } = \underset{\varvec{p} \in R^N}{\text {argmin}}&\frac{1}{2} \sum _{i=1}^{N} (p_i-z_i)^2 + \lambda \sum _{i=1}^{N-1} (p_i - p_{i+1})\nu _i, \end{aligned} \end{aligned}$$

(3)

where $\lambda$ is a positive real number that regulates the trade-off between the monotonicity of the calibrated estimates with the goodness of fit by penalizing adjacent pairs that violate the ordering imposed by the base classifier. The above optimization problem is known as the near-isotonic regression problem [35]. It yields a unique solution $\hat{\varvec{p}_{\lambda }}$, where the use of the subscript $\lambda$ emphasizes the dependency of the final solution to the value of $\lambda$.

The entire path of solutions for any value of $\lambda$ of the near isotonic regression problem can be found using a similar algorithm to PAVA which is called modified pool adjacent violators algorithm (mPAVA) [35]. mPAVA finds the whole solution path in $O(N \log N)$, and needs O(N) memory space. Briefly, the algorithm works as follows: It starts by constructing N bins, each bin containing a single instance of the train data. Next, it finds the solution path by starting from the saturated fit $p_i = z_i$, that corresponds to setting $\lambda = 0$, and then increasing $\lambda$ iteratively. As the $\lambda$ increases the calibrated probability estimates $\hat{\varvec{p}}_{\lambda , i}$, for each bin, will change linearly with respect to $\lambda$ until the calibrated probability estimates of two consecutive bins attain equal value. At this stage, mPAVA merges the two bins that have the same calibrated estimate to build a larger bin, and it updates their corresponding estimate to a common value. The process continues until there is no change in the solution for a large enough value of $\lambda$ that corresponds to finding the standard isotonic regression solution. The essential idea of mPAVA is based on a theorem stating that if two adjacent bins are merged on some value of $\lambda$ to construct a larger bin, then the new bin will never split for all larger values of $\lambda$ [35].

mPAVA yields a collection of nearly isotonic calibration models, with the over fitted calibration model at one end ($\hat{\varvec{p}}_{\lambda =0} =\varvec{z}$) and the isotonic regression solution at the other ($\hat{\varvec{p}}_{\lambda = \lambda _\infty } = \hat{\varvec{p}}_{iso}$), where $\lambda _\infty$ is a large positive real number. Each of these models can be considered as a histogram binning model where the position of boundaries and the size of bins are selected according to how well the model trades off the goodness of fit with the preservation of the ranking generated by the classifier, which is governed by the value of $\lambda$, (as $\lambda$ increases the model is more concerned to preserving the original ranking of the classifier, while for the small $\lambda$ it prioritizes the goodness of fit).

ENIR employs the approach just described to generate a collection of models (one for each value of $\lambda$). It then uses the Bayesian Information Criterion (BIC) to score each of the models.³ Assume mPAVA yields the binning models $M_1, M_2, \ldots , M_T$, where T is the total number of models generated by mPAVA. For any new classifier output y, the calibrated prediction in the ENIR model is defined using selective Bayesian model averaging [16]:

$$\begin{aligned} \begin{aligned} P(z=1|y) =\sum _{i=1}^{T} \frac{ \mathrm{Score}(M_i)}{\sum _{j=1}^{T} \mathrm{Score}(M_j)} P(z=1|y,M_i) , \end{aligned} \end{aligned}$$

where $P(z=1|y,M_i)$ is the probability estimate obtained using the binning model $M_i$ for the uncalibrated classifier output y. Also, $\mathrm{Score}(M_i)$ is defined using the BIC scoring function⁴ [33].

Next, for the sake of completeness, we briefly describe the mPAVA algorithm; more detailed information about the algorithm and the derivations can be found in [35].

3.1 The modified PAV algorithm

Suppose at a value of $\lambda$ we have $N_\lambda$ bins, $B_1, B_2, \ldots ,B_{N_\lambda }$. We can represent the unconstrained optimization program given by Eq. 3 as the following loss function that we seek to minimize :

$$\begin{aligned} \begin{aligned}&\mathcal {L}_{B,\lambda }(\varvec{z}, \varvec{p}) =&\frac{1}{2} \sum _{i=1}^{N_\lambda } \sum _{j \in B_i} (p_{B_i} - z_j)^2 + \lambda \sum _{i=1}^{N_\lambda - 1} (p_{B_i} - p_{B_{i+1}}) \nu _i, \end{aligned} \end{aligned}$$

(4)

where $p_{B_i}$ defines the common estimated value for all the instances located at the bin $B_i$. The loss function $\mathcal {L}_{B,\lambda }$ is always differentiable with respect to $p_{B_i}$ unless two calibrated probabilities are just being joined (which only happens if $p_{B_i}=p_{B_{i+1}}$ for some i). Assuming that $\hat{p}_{B_i}(\lambda )$ is optimal, the partial derivative of $\mathcal {L}_{B,\lambda }$ has to be 0 at $\hat{p}_{B_i}(\lambda )$, which implies:

$$\begin{aligned} |B_i|\hat{p}_{B_i}(\lambda ) - \sum _{j \in B_i} z_j + \lambda (\nu _i - \nu _{i-1})=0 \quad \text { for } i = 1,\ldots , N_\lambda \end{aligned}$$

(5)

Rewriting the above equation, the optimum predicted value for each bin can be calculated as:

$$\begin{aligned} \hat{p}_{B_i}(\lambda )= \frac{\sum _{j \in B_i} z_j - \lambda \nu _i + \lambda \nu _{i-1}}{|B_i|} \quad \text { for } i = 1,\ldots , N_\lambda \end{aligned}$$

(6)

While PAVA uses the frequency of instances in each bin as the calibrated estimate, Eq. 6 shows that mPAVA uses a shrunken version of the frequencies by considering the estimates that are not following the ranking imposed by the base classifier. In Eq. 5, taking derivatives with respect to $\lambda$ yields:

$$\begin{aligned} \frac{\partial {\hat{p}_{B_i}}}{{\partial {\lambda }}} = \frac{\nu _{i-1}-\nu _i}{|B_i|}, \quad \text { for } i = 1,\ldots , N_\lambda , \end{aligned}$$

(7)

where we set $\nu _0 = \nu _N = 0$ for notational convenience. As we noted above, it has been proven that the optimal values of the instances located in the same bin are tied together and the only way that they can change is to merge two bins as they can never split apart as $\lambda$ increases [35]. Therefore, as we make changes in $\lambda$, the bins $B_i$, and hence the values $\nu _i$ remain constant. This implies the term $\frac{\partial {\hat{p}_{B_i}}}{{\partial {\lambda }}}$ is a constant in Eq. refeq:slope. Consequently, the solution path remains piecewise linear as $\lambda$ increases, and the breakpoints happen when two bins merge together. Now, using the piecewise linearity of the solution path and assuming that the two bins $B_i$ and $B_{i+1}$ are the first two bins to merge by increasing $\lambda$, the value of $\lambda _{i,i+1}$ at which the two bins $B_i$ and $B_{i+1}$ will merge is calculated as:

$$\begin{aligned} \lambda _{i,i+1} = \frac{\hat{p}_{B_i}(\lambda ) - \hat{p}_{B_{i+1}}(\lambda )}{a_{i+1}-a_{i}} + \lambda \quad \text { for } i= 1, \ldots N_\lambda -1 , \end{aligned}$$

(8)

where $a_{i} = \frac{\partial {\hat{p}_{B_i}}}{\partial {\lambda }}$ is the slope of the changes of $\hat{p}_{B_i}$ with respect to $\lambda$ according to Eq. 7. Using the above identity, the $\lambda$ at which the next breakpoint occurs is obtained using the following equation:

$$\begin{aligned} \begin{aligned}&\lambda ^* = \underset{i}{\text { min }} \lambda _{i,i+1}\\&\mathbb {I}^* = \left\{ i| \lambda _{i,i+1} = \lambda ^* \right\} , \end{aligned} \end{aligned}$$

(9)

where $\mathbb {I}^*$ indicates the set of the indexes of the bins that will be merged by their consecutive bins changing the $\lambda$.⁵ If $\lambda ^* \le \lambda$, then the algorithm will terminate since it has obtained the standard isotonic regression solution, and by increasing $\lambda$ none of the existing bins will ever merge. Having the solutions of the near-isotonic regression problem in Eq. 3 at the breakpoints, and using the piecewise linearity property of the solution path, it is possible to recover the solution for any value of $\lambda$ through interpolation. However, the current implementation of ENIR only uses the near-isotonic regression-based calibration models that corresponds to the value of $\lambda$ at the breakpoints. The sketch of the algorithm is shown as Algorithm 1.

4 Empirical results

This section describes the set of experiments that we performed to evaluate the performance of ENIR in comparison with isotonic regression-based calibration (IsoRegC) [40], and a recently introduced binary classifier calibration method called BBQ [28]. We use IsoRegC because it is one of the most commonly used calibration models showing promising performance on real-world applications [24, 40]. Moreover, ENIR is an extension of IsoRegC, and we are interested in evaluating whether it performs better than IsoRegC. We also include BBQ as a state-of-the-art binary classifier calibration model, which is a Bayesian extension of the simple histogram binning model [28]. We did not include Platt’s method since it is a simple and restricted parametric model and there are prior works showing that IsoRegC and BBQ perform superior to Platt’s method [24, 28, 40]. We also did not include the ACP method since it requires not only probabilistic predictions, but also a statistical confidence interval (CI) around each of those predictions, which makes it tailored to specific classifiers, such as LR [20]; this is counter to our goal of developing post-processing methods that can be used with any existing classification models. Finally, we did not include ABB in our experiments mainly because it is not computationally tractable for real datasets that have more than a couple of thousand instances. Moreover, even for small size datasets, we have observed that ABB performs similar to BBQ.

4.1 Evaluation measures

In order to evaluate the performance of the calibration models, we use 5 different evaluation measures. We use accuracy (ACC) and area under ROC curve (AUC) to evaluate how well the methods discriminate the positive and negative instances in the feature space. We also utilize three measures of calibration, namely root mean square error (RMSE),⁶ maximum calibration error (MCE), and expected calibration error (ECE) [27, 28]. MCE and ECE are two simple statistics of the reliability curve (Fig. 1 shows a hypothetical example of such curve) computed by partitioning the output space of the binary classifier, which is the interval [0, 1], into K fixed number of bins ($K = 10$ in our experiments). The estimated probability for each instance will be located in one of the bins. For each bin, we can define the associated calibration error as the absolute difference between the expected value of predictions and the actual observed frequency of positive instances. The MCE calculates the maximum calibration error among the bins, and ECE calculates expected calibration error over the bins, using empirical estimates as follows:

$$\begin{aligned} \mathrm{MCE}&= \max _{k=1}^K \left( \left| o_k-e_k \right| \right) \\ \mathrm{ECE}&= \sum _{k=1}^{K} P(k) \cdot \left| o_k-e_k \right| , \end{aligned}$$

where P(k) is the empirical probability or the fraction of all instances that fall into bin k, $e_k$ is the mean of the estimated probabilities for the instances in bin k, and $o_k$ is the observed fraction of positive instances in bin k. The lower the values of MCE and ECE, the better is the calibration of a model.

Fig. 3

Scatter plot of the simulated data. The two classes of the binary classification task are indicated by the red squares and blue stars. The black oval indicates the decision boundary found using SVM with a quadratic kernel (colour figure online)

4.2 Simulated data

For the simulated data experiments, we used a binary classification dataset in which the outcomes were not linearly separable. The scatter plot of the simulated dataset is shown in Fig. 3. We developed this classification problem to illustrate how IsoRegC can suffer from a violation of the isotonicity assumption, and to compare the performance of IsoRegC with our new calibration method that assumes approximate isotonicity. In our experiments, the data are divided into 1000 instances for training and calibrating the prediction model, and 1000 instances for testing the models. We report the average results of 10 random runs for the simulated dataset. To conduct the experiments with the simulated data, we used two extreme classifiers: support vector machines (SVM) with linear and quadratic kernels. The choice of SVM with a linear kernel allows us to see how ENIR perform when the classification model makes an over simplifying (linear) assumption. Also, to achieve good discrimination on the circular configuration data in Fig. 3, SVM with a quadratic kernel is a reasonable choice (as is also evidenced qualitatively in Fig. 3 and quantitatively in Table 1b). So, the experiment using quadratic kernel SVM allows us to see how well ENIR performs when we use models that should discriminate well.

As seen in Table 1, ENIR generally outperforms IsoRegC on the simulation dataset, especially when the linear SVM method is used as the base learner. This is due to the monotonicity assumption of IsoRegC which presumes the best-calibrated estimates will match the ordering imposed by the base classifier. When we use SVM with a linear kernel, this assumption is violated due to the non-linearity of the data. Consequently, IsoRegC only provides limited improvement of the calibration and discrimination performance of the base classifier. ENIR performs very well in this case since it is using the ranking information of the base classifier, but it is not anchored to it. The violation of the monotonicity assumption can happen in real data as well, especially in large-scale data mining problems in which we use simple classification models due to the computational constraints. As shown in Table 1b, even when we apply a highly appropriate SVM classifier to classify the instances for which IsoRegC is expected to perform well (and indeed does so), ENIR performs as well or better than IsoRegC.

Table 1 Experimental results on a simulated dataset

4.3 Real data

We ran two sets of experiments on 40 randomly selected baseline datasets from the UCI and LibSVM repositories⁷ [5, 22]. Five summary statistics of the size of the datasets and the percentage of the minority class are shown in Table 2. We used three common classifiers, logistic regression (LR), support vector machines (SVM), and naïve Bayes (NB) to evaluate the performance of the proposed calibration method. In both sets of experiments on real data, we used 10 random runs of 10-fold cross validation, and we always used the train data for calibrating the models.

Table 2 Summary statistics of the size of the real datasets and the percentage of the minority class. Q1 and Q3 defines the first quartile and thirds quartile, respectively

In the first set of experiments on real data, we were interested in evaluating whether there is experimental support for using ENIR as a post-processing calibration method. Table 3 shows the $95\%$ confidence interval for the mean of the random variable X, which is defined as the percentage of the gain (or loss) of ENIR with respect to the base classifier:

$$\begin{aligned} X = \frac{\mathrm{measure}_\mathrm{ENIR} - \mathrm{measure}_\mathrm{method}}{\mathrm{measure}_\mathrm{method}}, \end{aligned}$$

(10)

where measure is one of the evaluation measures AUC, ACC, ECE, MCE, or RMSE. Also, method denotes one of the choices of the base classifiers, namely, LR, SVM, or NB. For instance, Table 3 shows that by post-processing the output of SVM using ENIR, we are $95\%$ confident to gain anywhere from 17.6 to $31\%$ average improvement in terms of RMSE. This could be a significant improvement, depending on the application, considering the $95\%$ CI for the AUC which shows that by using ENIR we are $95\%$ confident not to lose more than $1\%$ of the SVM discrimination power in terms of AUC (note, however, that the CI includes zero, which indicates that there is not a statistically significant difference between the performance of SVM and ENIR in terms of AUC).

Overall, the results in Table 3 show that there is not a statistically meaningful difference between the performance of ENIR and the base classifiers in terms of AUC. The results support at a $95\%$ confidence level that ENIR improves the performance of LR and NB in terms of ACC. Furthermore, the results in Table 3 show that by post-processing the output of LR, SVM, and NB using ENIR, we can obtain dramatic improvements in terms of calibration measured by RMSE, ECE, and MCE. For instance, the results indicate that at a $95\%$ confidence level, ENIR improved the average performance of NB in terms of MCE anywhere from 30.5 to $55.2\%$, which could be practically significant in many decision-making and data mining applications.

Table 3 The $95\%$ confidence interval for the average percentage of improvement over the base classifiers (LR, SVM, NB) by using the ENIR method for post-processing

In the second set of experiments on real data, we were interested to evaluate the performance of ENIR compared with other calibration methods. To evaluate the performance of models, we used the recommended statistical test procedure by Janez Demsar [8]. More specifically, we used the nonparametric testing method based on the $F_F$ test statistic [18], which is an improved version of Freidman nonparametric hypothesis testing method [11], followed by Holm’s step-down procedure [17] to evaluate the performance of ENIR in comparison with other methods, across the 40 baseline datasets.

Tables 4, 5, and 6 show the results of the performance of ENIR in comparison with IsoRegC and BBQ. In these tables, we show the average rank of each method across the baseline datasets, where boldface indicates the best performing method. In these tables, the marker $*$/$\circledast$ indicates whether ENIR is statistically superior/inferior to the compared method using the improved Friedman test followed by Holm’s step-down procedure at a 0.05 significance level. For instance, Table 5 shows the performance of the calibration models when we use SVM as the base classifier; the results show that ENIR achieves the best performance in terms of RMSE by having an average rank of 1.675 across the 40 baseline datasets. The result indicates that in terms of RMSE, ENIR is statistically superior to BBQ; however, it is not performing statistically differently than IsoRegC.

Table 4 shows the results of comparison when we use LR as the base classifier. As shown, the performance of ENIR is always superior to BBQ and IsoRegC except for MCE in which BBQ is superior to ENIR; however, this difference is not statistically significant. The results show that in terms of discrimination based on AUC, there is not a statistically significant difference between the performance of ENIR compared with BBQ and IsoRegC. However, ENIR performs statistically better than BBQ in terms of ACC. In terms of calibration measures, ENIR is statistically superior to both IsoRegC and BBQ in terms of RMSE. In terms of MCE, ENIR is statistically superior to IsoRegC.

Table 4 Average rank of the calibration methods on the benchmark datasets using LR as the base classifier

Table 5 shows the results when we use SVM as the base classifier. As shown, the performance of ENIR is always superior to BBQ and IsoRegC except for MCE in which BBQ performs better than ENIR; however, the difference is not statistically significant for MCE. The results show that although ENIR is superior to IsoRegC and BBQ in terms of discrimination measures, AUC and ACC, the difference is not statistically significant. In terms of calibration measures, ENIR performs statistically superior to BBQ in terms of RMSE and it is statistically superior to IsoRegC in terms of MCE.

Table 5 Average rank of the calibration methods on the benchmark datasets using SVM as the base classifier

Table 6 Average rank of the calibration methods on the benchmark datasets using NB as the base classifier

Table 6 shows the results of comparison when we use NB as the base classifier. As shown, the performance of ENIR is always superior to BBQ and IsoRegC. In terms of discrimination, for AUC, there is not a statistically significant difference between the performance of ENIR compared with BBQ and IsoRegC; however, in terms of ACC, ENIR is statistically superior to BBQ. In terms of calibration measures, ENIR is always statistically superior to IsoRegC. ENIR is also statistically superior to BBQ in terms of ECE and RMSE.

Overall, in terms of discrimination measured by AUC and ACC, the results show that the proposed calibration method either outperforms IsoRegC and BBQ, or has a performance that is not statistically significantly different. In terms of calibration measured by ECE, MCE, and RMSE, ENIR either outperforms other calibration methods, or it has a statistically equivalent performance to IsoRegC and BBQ.

Finally, Table 7 shows a summary of the time complexity of different binary classifier calibration methods in learning for N training instances and the test time for only one instance.

Table 7 Note that N and B are the size of training sets and the number of bins found by the method, respectively. T is the number of iterations required for convergence of the Platt method, and M is defined as the total number of models used in the associated ensemble model

5 An extension to ENIR

This section briefly describes an extension to ENIR model which is called an ensemble of linear trend estimation (ELiTE) [25]. Figure 4 shows the main idea in developing ELiTE. As shown, in all of the histogram binning-based calibration models—including quantile binning (i.e., the equal frequency histogram binning), IsoRegC, Bayesian extensions to the histogram binning such as BBQ and ABB, and also ENIR—the generated mapping function is a piecewise constant function. The main idea of ELiTE is to extend ENIR and other binning-based calibration methods by using an ensemble of piecewise linear functions⁸ as it is shown in Fig. 4b.

Fig. 4

The figure shows how ELiTE extends binning-based calibration methods (e.g., ENIR) by using a piecewise linear calibration mapping instead of a piecewise constant mapping. a Calibration mapping generated by a binning-based calibration method (e.g., ENIR), b calibration mapping yield by ELiTE

Recall $z_i$ and $y_i$ are the true class of the i’th training instance and its corresponding classification score, respectively. Without loss of generality, we assume the training instances to be sorted in increasing order by their associate classification scores $y_i$. Borrowing the term “bin” from the histogram binning literature, we define each bin as the largest interval over the training data with a uniform slope of change (e.g., Fig. 4b indicates that there are 6 bins in the calibration mapping). ELiTE uses the $\ell _1$ (linear) trend filtering signal approximation method [21] and poses the problem of finding a piecewise calibration mapping as the following optimization program:

$$\begin{aligned} \begin{aligned}&\hat{\varvec{p}} = \underset{\varvec{p} \in R^N}{\text {argmin}}&\frac{1}{2} \sum _{i=1}^{N} (p_i-z_i)^2 + \lambda ||\mathbf {v}||_1 \end{aligned} \end{aligned}$$

(11)

where $\hat{\varvec{p}} = (\hat{p}_1,\ldots , \hat{p}_n)$ is the vector of calibrated probability estimates and the vector $\mathbf {v} \in R^{N-2}$ is defined as the second-order finite difference vector associated with the training data⁹ $\mathbf {v}_i = \frac{p_{i+2}-p_{i+1}}{y_{i+2}-y_{i+1}}-\frac{p_{i+1}-p_i}{y_{i+1}-y_i}$. Also, $\lambda$ is a penalization parameter that regulates the trade-off between the goodness of fit and the complexity of the model by penalizing the total variance over the slope of the resulting calibration mapping. Kim et al. used the shrinkage property of the $\ell _1$ norm and showed that the final solution to the above optimization program $\hat{\mathbf {p}}$ will be a continuous piecewise linear function with the kink points occurring on the training data [21].

ELiTE uses a specialized ADMM algorithm proposed by Ramdas and Tibshirani [30] and a warm start procedure that iterates over the values of lambda by ranging equally in the log space from $\lambda _\mathrm{max}$ to $\lambda _\mathrm{max}*10^{-4}$, where $\lambda _\mathrm{max}$ is the corresponding value of $\lambda$ that gives the best affine approximation of the calibration mapping that can be computed in O(N), where N is the number of training instances [21]. ELiTE uses the Akaike information criterion with a correction for finite sample sizes (AICc) [4] to score each of the piecewise linear calibration models associated with various values of the $\lambda$. Finally, for a new test instance, ELiTE uses the AICc scores to run a selective Bayesian averaging and estimate the final calibrated estimate [25].

Similar to ENIR, ELiTE is shown to perform superior to the commonly used binary classifier calibration methods including Platt’s method, isotonic regression, and BBQ [25]. In this section, we are interested to compare the performance of these two new calibration methods in terms of the discrimination and calibration capability. Table 8 shows the results of a comparison between the performance of ENIR and ELiTE over the 40 real datasets used in our previous experiments. A Wilcoxon signed rank test is used to statistically measure the significance of performance difference between ELiTE and ENIR. Median difference performance of ELiTE and ENIR over the baseline datasets is reported along with the corresponding p value of the test which is indicated in parentheses. The results show that there are some cases that ELiTE is statistically superior to ENIR. However, in terms of running time, ELiTE runs more than eight times slower, on a MacBook Pro with a 2.5 GHz Intel Core i7 CPU and a 16 GB RAM memory, in comparison to the ENIR even though its running time complexity is $O(N \log N)$ [25, 30]. Also, note that the median of the difference between the performance of ELiTE and ENIR is always very small (i.e., less than 0.01 in all cases).

Table 8 Median of the difference between the performance of ELiTE and ENIR on the 40 baseline datasets

6 Conclusion

In this paper, we presented a new nonparametric binary classifier calibration method called ensemble of near-isotonic regression (ENIR) to build accurate probabilistic prediction models. The method generalizes the isotonic regression-based calibration method (IsoRegC) [40] in two ways. First, ENIR makes a more realistic assumption compared to IsoRegC by assuming that the transformation from the uncalibrated output of a classifier to calibrated probability estimates is approximately (but not necessarily exactly) a monotonic function. Second, ENIR is an ensemble model that utilizes the BIC scoring function to perform selective model averaging over a set of near isotonic regression models that indeed includes IsoRegC as an extreme member. The method is computationally tractable, as it runs in $O(N \log N)$ for N training instances. It can be used to calibrate many different types of binary classifiers, including logistic regression, support vector machines, naïve Bayes, and others. Our experiments show that by post-processing the output of classifiers using ENIR, we can gain high calibration improvement in terms of RMSE, ECE, and MCE, without losing any statistically meaningful discrimination performance. Moreover, our experimental evaluation on a broad range of real datasets showed that ENIR outperforms IsoRegC and BBQ (i.e. a state-of-the-art binary classifier calibration method [28]).

We also evaluated the performance of ENIR in comparison with a newly introduced binary classifier calibration method called ELiTE.¹⁰ Our experiments show that even though ENIR is slightly inferior to ELiTE in terms of AUC and MCE measures, it runs overall (training + testing time) at least eight times faster than ELiTE over all of our experimental datasets. Note that, it is possible to combine the near-isotonicity constraints and the piecewise linear constraints of calibration mapping to build a calibration mapping that is both near-isotonic and piecewise linear. This can be easily done by simply adding the near-isotonic constraint to the ADMM constraint optimization program of ELiTE [25, 30]. We leave this extension as future work.

An important advantage of ENIR over Bayesian binning models (e.g., BBQ, and ABB) is that they can be extended to a multi-class and multi-label calibration models similar to what has done for the standard IsoRegC method [40]. This is an area of our current research. We also plan to investigate theoretical properties of ENIR. In particular, we are interested to investigate theoretical guarantees regarding the discrimination and calibration performance of these calibration methods, similar to what has been proved for the AUC guarantees of IsoRegC [10].