Efficient Monte Carlo clustering in subspaces

Abstract

Clustering of high-dimensional data is an important problem in many application areas, including image classification, genetic analysis, and collaborative filtering. However, it is common for clusters to form in different subsets of the dimensions. We present a randomized algorithm for subspace and projected clustering that is both simple and efficient. The complexity of the algorithm is linear in the number of data points and low-order polynomial in the number of dimensions. We present the results of a thorough evaluation of the algorithm using the OpenSubspace framework. Our algorithm outperforms competing subspace and projected clustering algorithms on both synthetic and real-world data sets.

1 Introduction

Clustering is used in many applications for the unsupervised classification of data points (objects) into subsets that are similar within each subset and dissimilar between subsets [18]. These applications increasingly rely on data points in high-dimensional spaces. Examples include image classification, genetic analysis, and collaborative filtering. When this is the case, clusters often form in a subset of the dimensions of the full space [3] and conventional algorithms, such as k-means clustering [14], perform poorly. This has led to the study of subspace clustering¹ (overlapping clusters) and projected clustering (disjoint clusters) [20]. Algorithms for these problems work in dimensional subsets.

The curse of dimensionality is a difficult problem to overcome. It has been shown that, under certain conditions, the ratio between the distance to the nearest neighbor and the distance to the farthest neighbor approaches one as the dimensionality of the space increases [7]. One solution is to use a dimensionality reduction technique, such as principal components analysis (PCA) [15]. This projects the entire data set into fewer dimensions, which might then be used for clustering using conventional techniques [9, 10]. However, this produces a single subspace, whereas in many applications the clusters exist in different subspaces of the full feature space. Thus, the use of PCA may prevent the detection of interesting clusters in the data set.

Subspace and projected clustering algorithms provide a more robust solution to this problem. These methods seek to determine both the clusters of similar objects and the associated subspaces in which they are similar. Unlike conventional clustering algorithms, some (or many) dimensions can be treated as irrelevant to each of the clusters. Unlike dimensionality reduction techniques, the clusters are not constrained to form in the same subset of dimensions.

Fig. 1

Example of two subspace clusters and projections onto subspaces. The blue cluster is visible when projected onto the x-y plane. The green cluster is visible when projected onto the y-z plane (color figure online)

The problem can be illustrated in three dimensions. See Fig. 1. Two subspace clusters are present, one in the x and y dimensions and one in the y and z dimensions. The projections of the points onto subspaces spanned by two axes are also shown, emphasizing the clusters present in the subspaces.

We formalize the subspace clustering problem as follows. Given a set of points P in a d-dimensional space, find all maximal sets of points $C_i \subset P$ and corresponding sets of dimensions $D_i \subset \left\{ 1,\ldots , d\right\}$ such that the point set is sufficiently close in each of the dimensions to form a cluster. We say that the points congregate in these dimensions; cluster will be used only as a noun. We also say that the dimensions in $D_i$ are the congregating dimensions of the cluster. We define this to be true if they are within a width w of each other:

$$\begin{aligned} \forall p,q\in C_i, \forall j\in D_i, |p_j-q_j| \le w. \end{aligned}$$

(1)

Furthermore, to be reported, each cluster must surpass some criteria with respect to the cardinalities of $C_i$ and $D_i$:

$$\begin{aligned} \mu (|C_i|,|D_i|) \ge \mu _0. \end{aligned}$$

(2)

The clusters reported are maximal sets to prevent all subsets of each cluster from being reported. Most algorithms relax the requirement of reporting all maximal sets, since there are typically many overlapping maximal sets that meet the above requirements. This is necessary for an efficient algorithm, since it is possible for the number of such maximal sets to be large.

We present a new algorithm to solve the subspace clustering problem that is simple, robust, and efficient. The algorithm is called SEPC, for Simple and Efficient Projected Clustering. Using a Monte Carlo algorithm, we find subspace clusters with high probability for most data sets. The complexity of the algorithm has a linear dependence on the number of data points and a polynomial dependence on the number of dimensions in the space. The algorithm does not require the number of output clusters as an input, it is able to operate with clusters of arbitrary size and dimensionality, and it is robust to outliers. No assumptions are made about the distribution of the clusters or outliers, except that the clusters must have a diameter no larger than a user-defined constant in any of the cluster dimensions. In addition, the algorithm can be used either to partition the data into disjoint clusters (with or without an outlier set) or generate overlapping dense regions in the subspaces. Our algorithm generates tighter clusters than previous Monte Carlo algorithms, such as FastDOC [32]. The computational complexity of our algorithm is also lower and less dependent on the cluster evaluation parameters.

We evaluate the algorithm using the OpenSubspace framework [25, 26]. A thorough evaluation with both synthetic and real-world data sets demonstrates the superiority of SEPC over competing approaches.

Our preliminary work on this algorithm has previously been presented in conferences [17, 28]. In this paper, we expand upon those works with new and improved explanation, discussion, and analysis of the algorithm, including a proof of the algorithm’s computational complexity.

In Sect. 2, we review related work on this problem. We then discuss our algorithm, including a detailed analysis, in Sect. 3. Experimental results on real and synthetic data are presented in Sect. 4. Finally, our conclusions are given in Sect. 5.

2 Related work

We are concerned with subspace clustering in the data mining and knowledge discovery usage of the term, where clusters of data points are detected that are mutually close to each other in a (still high-dimensional) subset of the dimensions of the full problem space [3, 5, 6, 8, 13, 19, 26, 30, 31]. These techniques often, but not always, require axis-parallel subspaces.

Extensive reviews of early work in subspace and projected clustering have been performed by Parsons, Haque and Liu [30] and Kriegel, Kröger, and Zimek [20]. We provide a brief overview of some historical algorithms and those closely related to our work.

The CLIQUE algorithm of Agrawal, Gehrke, Gunopulos and Raghavan [3, 4] was likely the first algorithm to address the subspace clustering problem. The algorithm uses a bottom-up strategy that initially finds clusters in projections onto single dimensions of the space (discretized into short intervals). Clusters previously found in k-dimensional spaces are used to find clusters in $(k+1)$-dimensional spaces. Clusters are built with one additional dimension at each step, until no more dimensions can be added. One drawback to the algorithm is that it is exponential in the number of dimensions in the output cluster. Other bottom-up algorithms include ENCLUS [8], MAFIA [13, 27], and P3C [24].

Aggarwal, Wolf, Yu, Procopiuc and Park [1] developed the PROCLUS algorithm for subspace clustering using a top-down strategy based on medoids. The medoids are individual points from the data set selected to serve as surrogate centers for the clusters. After initializing the medoids using sampling, an iterative hill-climbing approach is used to improve the set of points used as medoids. A refinement stage generates the final subspace clusters. This algorithm requires both the number of clusters and the average number of dimensions as inputs. Additional methods that use top-down strategies include ORCLUS [2] (which considers non-axis-parallel subspaces) and FINDIT [38].

Procopiuc, Jones, Agarwal and Murali [32] developed the DOC and FastDOC algorithms for subspace clustering. One of their contributions was a definition of an optimal subspace cluster (see Sect. 3). Procopiuc et al. developed a Monte Carlo algorithm for finding an optimal cluster. Their algorithm uses two loops, the outer loop selects a single seed point and the inner loop selects an additional set of points from the data called the discriminating set. The seed point and all of the discriminating set must belong to the optimal cluster for the trial to succeed. The dimensions in the cluster are determined by finding the dimensions in which all of the points in the discriminating set are within w of the seed point (allowing an overall cluster width of 2w). Given these dimensions, the cluster is estimated by finding all points in the data set within w of the seed point in these dimensions.

Yiu and Mamoulis describe the MineClus [39] and CFPC [40] algorithms. As in the DOC algorithm, an outer loop is used that samples individual points from the data set. However, they replace the inner loop from the DOC algorithm with a technique adapted from mining frequent itemsets to determine the cluster dimensions and points (assuming that the sample point is from the optimal cluster). No formal analysis of the computational complexity is given, but Yiu and Mamoulis reported improved speeds in comparison with PROCLUS and FastDOC. However, the speed of the method is dependent on subsampling the data set before processing.

Recent work on this problem includes development of the CartiClus algorithm [6] and the related CLON algorithm [5]. CartiClus transforms each data point into multiple sets consisting of its nearest neighbors in different views of the data. Performing frequent itemset mining on these sets and merging similar results yields the clustering algorithm. CLON uses ordered neighborhoods, also consisting of nearest neighbors in views of the data. Clusters are detected using a bottom-up strategy based on the fact that lower-dimensional projections of clusters are supersets of the clusters found in high-dimensional projections.

In the computer vision and machine learning communities, subspace clustering usually refers to a different, but related problem. This problem is the detection of points that belong to a union of low-dimensional linear or affine subspaces embedded in a high-dimensional space [11, 12, 35, 36]. These techniques generally require disjoint subspaces, but do not usually require axis-parallel subspaces. While this is related to the problem we solve, algorithms in one category do not generally solve problems in the other category. For example, the sparse subspace clustering work of Elhamifar and Vidal [12] is applied to the problem of motion segmentation, where each cluster of trajectories lies in a 3-D affine subspace. Recent work on this problem has examined subspaces with rank at least as high as 15 [16]. This is also an active area of current research [16, 29, 33, 34].

3 Simple and efficient subspace clustering

3.1 Preliminaries

We use the definition of an optimal cluster from Procopiuc, Jones, Agarwal and Murali [32]. An optimal cluster has the following properties:

• 1. It has a minimum density $\alpha$ (a fraction of the number of points in the data set).

• 2. It has a width of no more than w in each dimension in which it congregates.

• 3. It has a width larger than w in each dimension in which it does not congregate.

• 4. Among clusters that satisfy the above criteria, it maximizes a quality function $\mu (|C|,|D|)$, where |C| is the number of points in the cluster and |D| is the number of dimensions in which the cluster congregates.

While any function that is monotonically increasing in each variable can be used as the quality function, Procopiuc et al. use $\mu (|C|,|D|) = |C|\cdot (1/\beta )^{|D|}$, where $0< \beta < 1$ is a parameter that determines the trade-off between the number of points and the number of dimensions in the optimal cluster. If a cluster $C_1$ congregates in f fewer dimensions than $C_2$, it must have $|C_1| > |C_2|/\beta ^f$ points to surpass the score for $C_2$. An optimal cluster must have at least $1/\beta$ as many points as another cluster if it congregates in exactly one less dimension.

We solve the subspace clustering problem using a Monte Carlo algorithm. In each trial of the algorithm, a small set of data points is sampled. Following Procopiuc et al. [32], we call this the discriminating set. A trial can succeed only if all of the points in the discriminating set are from the same cluster, among other conditions. Many trials are performed in order to achieve a high likelihood of success. In Sect. 3.5, we examine the number of trials necessary.

Note that, in contrast to the DOC and FastDOC algorithms, we have no outer loop in which individual seed points are sampled. We use different methods to determine which points and dimensions are part of a cluster. The overall algorithm is similar in many ways to DOC, but yields large improvements in computational complexity and experimental results owing to the changes. The new algorithm analysis is also of interest. We point out complications that affect both algorithms that were not presented previously.

The base algorithm finds a single cluster. To find multiple clusters, it can be either iterated or modified to detect multiple clusters simultaneously (over multiple trials). The number of clusters in the data set is not assumed to be known in advance. The total number of clusters found is generally limited by a threshold on the scoring function, but the algorithm can be trivially modified to find the k best clusters if the number of clusters is known.

3.2 Approach

In each trial, the discriminating set is used to determine the set of congregating dimensions for a hypothetical subspace cluster by selecting the dimensions in which the span of the discriminating set is less than the desired cluster width w. This requires only finding the minimum and maximum value in each of the dimensions among the points in the discriminating set. Note that this is an improvement over the DOC algorithm, in which the width of the sheath used to determine the congregating dimensions is 2w. The narrower sheath is a key reason for the improvement in the algorithm. A sheath width that is half as wide is much less likely to capture all of the points in the discriminating set in any dimension that the full cluster does not congregate in and this likelihood is crucial to the analysis of the computational complexity of the algorithm. To use such a narrow sheath, the DOC algorithm would need to find a seed point that was in the middle of the cluster in each of the congregating dimensions. However, this is not known in advance.

The narrower sheath also allows us to use a larger value for $\beta$ (the fraction of points necessary to remain in a cluster to add another congregating dimension). The DOC algorithm is limited to using $\beta < 0.5$ because of the width of the sheath. With a sheath width of 2w, it is impossible to guarantee that the fraction of points in the full cluster that lies within the sheath in any non-congregating dimension is less than $2\beta$. (Otherwise, this dimension would need to be a congregating dimension.) When $\beta$ is 0.5 (or larger) the entire cluster can fit within the sheath in a non-congregating dimension. This would make the cluster impossible to find. In contrast, the SEPC algorithm is only restricted by the upper limit of $\beta < 1$.

Fig. 2

Comparison between the SEPC and DOC algorithms for determining cluster dimensions and cluster points using a discriminating set. Blue points are in the cluster. Red points are random. Light blue points form the discriminating set. The SEPC algorithm uses a sheath of width w to determine if a discriminating set congregates in a dimension. When the set congregates, a larger sheath with width $2w-\hat{w}_i$ is used to determine additional data points that are added to the cluster. Figure 3 shows a similar example for the DOC algorithm (color figure online)

Fig. 3

Comparison between the SEPC and DOC algorithms for determining cluster dimensions and cluster points using a discriminating set. Blue points are in the cluster. Red points are random. Light blue points form the discriminating set. The DOC seed point is brown. The DOC and FastDOC algorithms use a sheath with width 2w both to determine if the discriminating set congregates in a dimension and to find additional data points that are added to the cluster. Figure 2 shows a similar example for our algorithm (color figure online)

We next determine the points in the hypothetical cluster, given the congregating dimensions. Note that the cluster points will not necessarily fall within the bounds given by the discriminating set, since the discriminating set will not generally include the extremal points in all congregating dimensions of the cluster. If the width of the discriminating set in cluster dimension i is $\hat{w}_i$, the full cluster might extend beyond this sheath in either direction by $w-\hat{w}_i$, since the full cluster may have width w. Allowing this extra width on either side yields a larger sheath with width $2w-\hat{w}_i$. It may range from w for a discriminating set that spans the maximum possible width in the dimension to 2w for a discriminating set where every point has the same value in the dimension. See Fig. 2. In comparison, the DOC algorithm continues using a sheath with width 2w to determine which points are included in the cluster. See Fig. 3. The only consequence of a sheath larger than w in this step is that it allows clusters that are wider than w, since the sheath for adding points to the cluster is larger. However, few (if any) such outliers will be included, since they must congregate with the cluster in all of the congregating dimensions. Our narrower sheath width for finding the cluster points does not factor into the analysis for the computational complexity or optimal discriminating set cardinality (unlike the one used to determine the congregating dimensions) and results in only minor additional improvement over the DOC algorithm by reducing the possibility of outliers in the cluster.

The hypothetical cluster detected in each trial is given a score using the DOC metric and retained if the score is sufficiently high. When performing disjoint (projected) clustering, we retain only the top scoring cluster over all of the trials. This cluster is removed from the data, and further clusters are found using additional iterations of the algorithm.² The process continues until no more clusters surpassing some criteria are found. Any remaining points can be classified as outliers or added to the cluster to which they are closest. If overlapping clusters are desired, multiple clusters can be located in a single iteration of the algorithm with a simple modification. In this case, we store not just the best cluster found, but all clusters of sufficient quality that are qualitatively different.

If the highest scoring cluster found in an iteration has density less than $\alpha$, but meets the score criterion, we must report it, even if clusters exist with density larger than $\alpha$. If such clusters are discarded, then the algorithm analysis may fail. Consider a large cluster with a density of exactly $\alpha$. If a subcluster exists with one fewer point and one more dimension, then this subcluster will achieve a greater score, unless $\beta$ is set arbitrarily close to one. In addition, this subcluster will usually prevent the larger cluster from being found, since any discriminating set that does not contain the single additional point in the larger cluster will generate a set of congregating dimensions that includes the additional dimension and excludes the additional point from the detected cluster. If the subcluster is discarded owing to the density less than $\alpha$, then the larger cluster will be missed, even though it meets the necessary conditions, unless a discriminating set is chosen with the additional point. This can be made arbitrarily unlikely by increasing the size of the cluster and, thus, the analysis does not hold for this optimal cluster, unless we allow the higher scoring, yet smaller, cluster to supersede it. Note that this is true not just for our algorithm, but for all similar Monte Carlo algorithms.³ Instead of discarding the cluster, we allow the smaller cluster to supersede the larger cluster, since it has a higher score. Our objective will thus be to find an optimal cluster with density of at least $\alpha$ (if one exists) or a higher scoring cluster.

3.3 Algorithm details

The SEPC algorithm is given in Algorithm 1. The input to the algorithm includes the set of points P, the number of dimensions d, the maximum width of a cluster w, the number of trials $k_\mathrm{{trials}}$, the cardinality of each discriminating set s, and the cluster quality function $\mu ()$. In each trial, we randomly sample (without replacement) s points from the data. Within the discriminating set, the set of dimensions in which the points congregate is determined (line 4). For each dimension, bounds are determined on the span of the cluster (infinite bounds are used for dimensions in which the cluster does not congregate). The points in the cluster are determined (line 12) by finding the intersection of the point set with the Cartesian product of each of the dimension ranges $r_j$. Finally, the cluster is saved if it is the best found so far. This algorithm finds a single cluster and may be iterated after removing the cluster (for disjoint clustering). To detect non-disjoint clusters, multiple clusters can be found in a single iteration of the algorithm. In this case, all clusters of sufficient quality should be saved in lines 13–17, unless the clusters substantially overlap.

3.4 Overlapping clusters

Allowing overlapping clusters is problematic if we do not remove duplicate clusters. Since points are not removed from consideration when they are assigned to clusters, the algorithm needs to check that each newly found cluster is unique and has not been previously discovered. When a new cluster is discovered, it is compared to existing found clusters. However, using a strict test for equality will result in a large number of similar clusters being discovered. To address this problem, we loosen the criteria for equality between clusters.

Our test for cluster equality uses both the set of objects in each cluster and the subspaces that the clusters span. This allows us to differentiate clusters that overlap significantly in objects, but not in the subspace spanned. Formally, given two clusters $(C_i,D_i )$ and $(C_j,D_j )$, we say that they are equivalent if $|C_i \cap C_j |/ \min (|C_i|, |C_j|) \ge \gamma _c$ and $|D_i \cap D_j |/ \min (|D_i|, |D_j|) \ge \gamma _d$, where $\gamma _c$ and $\gamma _d$ are user-specified tolerances between zero and one.

Fig. 4

Flowchart for finding overlapping clusters with SEPC

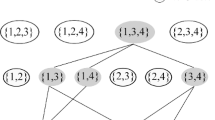
If a newly hypothesized cluster is determined to be redundant with respect to an existing cluster, then we discard it if its quality is lower than the existing cluster. If a newly hypothesized cluster is sufficiently unique (or of higher quality than redundant existing clusters), then we retain it. In this case, all existing clusters that are determined to be redundant with respect to the new cluster are removed from the clustering results. Figure 4 shows the process used by SEPC to discover overlapping clusters in a data set.

3.5 Number of trials

We want to set the number of trials in the SEPC algorithm such that it is highly likely that we find a subspace cluster should one exist. Theoretical guarantees are difficult to make, since it is possible to construct complex data sets with undesirable properties. For example, if all of the possible discriminating sets for a cluster congregate in at least one dimension in which the full cluster does not, then the sampling strategy will always detect the cluster with one or more extra dimension and find a smaller, suboptimal cluster. However, this can only happen if the probabilities of each cluster subset congregating in each extra dimension are negatively correlated; that is, knowing that a subset does not congregate in one dimension must make it more likely that it does in another dimension. This would be an unusual data set.

For the following analysis, we will assume that the probabilities are, at worst, independent; positive correlation would improve matters. However, this does mean that degenerate data sets exist where a suboptimal cluster would be detected instead of the optimal cluster. Furthermore, our randomized algorithm has a nonzero probability of never sampling a suitable discriminating set even when this is not the case. Of course, these issues also apply to other Monte Carlo algorithms, such as DOC and FastDOC. This independence is implicitly assumed by Procopiuc et al. [32]. Extensive testing (Sect. 4) indicates that our methodology outperforms other algorithms.

Assume that a cluster exists containing at least $m = \lceil \alpha n \rceil$ points, since we otherwise make no claims about the likelihood of a cluster being found. For a trial to succeed, we need for two conditions to hold. First, the trial must select only points within the subspace cluster (allowing us to find all of the dimensions in which the cluster is formed). Second, the trial must not select only points that randomly congregate in any dimension that is not a congregating dimension of the full subspace cluster, since this would result in an incorrect dimension being included in the trial. For any fixed s, a lower bound can be placed on the probability of both conditions holding:

$$\begin{aligned} P_\mathrm{{trial}} \ge \left( \frac{C^m_s}{C^n_s} \right) \left( 1 - \frac{C^l_s}{C^m_s} \right) ^d, \end{aligned}$$

(3)

where $l=\lfloor \beta m \rfloor$ and $C^j_k$ is the number of k-combinations that can be chosen from a set of cardinality j. The first term of (3) is a lower bound on probability of the first condition holding. The second term is a lower bound on the probability of the second condition holding, given that the first condition holds. This term is computed based on the fact that, for an optimal cluster of c points, no more than $\lfloor \beta c \rfloor$ points in the cluster can be within w of each other in any dimension that is not a congregating dimension of the cluster (otherwise, this subset would form a higher scoring subspace cluster that includes the dimension).⁴ The second term is taken to the dth power, since the random clustering could occur in any of the d dimensions (except for those that the subspace cluster does congregate in). This is where we make use of the assumption that the probabilities are independent (or positively correlated). The bound is not tight, since it includes all of the dimensions, rather than the (as yet unknown) dimensions in which the cluster does not congregate.

For large data sets, (3) is well approximated by:

$$\begin{aligned} P_{trial} \ge \alpha ^s(1-\beta ^s)^d. \end{aligned}$$

(4)

After $k_\mathrm{{trials}}$ iterations, we want the probability that none of the trials succeed to be below some small constant $\epsilon$ (e.g., $10^{-2}$). This is achieved with:

$$\begin{aligned} (1-P_\mathrm{{trial}})^{k_\mathrm{{trials}}} \le \epsilon , \end{aligned}$$

(5)

which yields:

$$\begin{aligned} k_\mathrm{{trials}} = \left\lceil \frac{\log \epsilon }{\log (1-P_\mathrm{{trial}})} \right\rceil . \end{aligned}$$

(6)

3.6 Discriminating set cardinality

The above analysis on the number of trials is valid for discriminating sets with arbitrary cardinality greater than one. However, the number of trials varies greatly depending on the cardinality of each discriminating set. If the cardinality is large, then it will be unlikely that the points in the set will all be in the desired cluster. If the cardinality is small, then it is likely that the points will congregate in (at least) one dimension in which the cluster does not. The optimal value for the cardinality of the discriminating set can be easily obtained by computing $k_{trials}$ for a small number of values and using the value that requires the fewest trials.

While the optimal value can be determined explicitly by testing values, we have also developed a heuristic to approximate the optimal value, which is useful in our analysis of the algorithm computational complexity. Our heuristic sets the cardinality such that the probability of the discriminating set congregating in even one of the incorrect dimensions is roughly 3/4. (The second term in (3) usually dominates the computation of $k_\mathrm{{trials}}$.)

With this heuristic we have:

$$\begin{aligned} \left( 1 - \frac{C^l_s}{C^m_s} \right) ^d \approx \frac{1}{4}, \end{aligned}$$

(7)

which yields:

$$\begin{aligned} \frac{l!(m-s)!}{m!(l-s)!} \approx 1-4^\frac{-1}{d} \end{aligned}$$

(8)

and

$$\begin{aligned}&\sum _{i=l-s+1}^{m-s} \log i - \sum _{i=l+1}^{m} \log i\approx \log (1-4^\frac{-1}{d}) . \end{aligned}$$

(9)

$$\begin{aligned}&\sum _{i=l-s+1}^{l} \log i - \sum _{i=m-s+1}^{m} \log i\approx \log (1-4^\frac{-1}{d}) . \end{aligned}$$

(10)

From this, we derive the following approximation to the optimal value of s:

$$\begin{aligned} s_\mathrm{{est}}\approx & {} \frac{\log (1-4^\frac{-1}{d})}{\log l - \log m} \end{aligned}$$

(11)

$$\begin{aligned}= & {} \frac{\log (1-4^\frac{-1}{d})}{ \log \lfloor \beta \lceil \alpha n \rceil \rfloor - \log \lceil \alpha n \rceil } \end{aligned}$$

(12)

$$\begin{aligned}\approx & {} \frac{\log (1-4^\frac{-1}{d})}{\log \beta } \end{aligned}$$

(13)

$$\begin{aligned}\approx & {} \frac{\log (d^{-1}\ln 4)}{\log \beta } = \frac{\log (d/\ln 4)}{\log (1/\beta )} \end{aligned}$$

(14)

This approximation (when rounded to the nearest whole number) overestimates the optimal cardinality in some cases [28], but the average percentage difference in the number of trials is less than 30% from the optimal value in all cases tested and the average percentage difference from the optimal number of trials is 4.42%. As expected, the cardinality of the discriminating set is logarithmic in the number of dimensions. It grows roughly linearly with $\beta$ for low values of $\beta$ before growing much faster as $\beta$ nears one.

Fig. 5

Scalability with number of dimensions and $\beta$. (a) Estimated values for discriminating set cardinality s with $\alpha = 0.1$, $n = 100{,}000$, and varying values for d and $\beta$. (b) Number of trials required with $\alpha = 0.1$, $\epsilon = 0.01$, $n = 100{,}000$, and varying values for d and $\beta$

Figure 5a shows the estimate for the optimal cardinality of the discriminating set with respect to the number of trials as specified by (6). For this comparison, $\alpha$ was held constant at 0.1 and n at 100,000. The levels of d and $\beta$ were varied (since these are the most influential in determining the optimal number of trials). Figure 5b shows the total number of trials necessary in the SEPC algorithm to detect a cluster with high probability. Here the growth is polynomial in both $\beta$ and the number of dimensions.

3.7 Computational complexity

For fixed $\alpha$, $\beta$, and d, the running time of the algorithm is O(n), since the number of trials does not depend on n. However, the running time has a more interesting relationship with $\alpha$, $\beta$, and d.

Lemma 1

With $s=\lceil \log (d / \ln 4)/\log (1/\beta ) \rceil$ and $d>3$, $(1-\beta ^s)^d \ge 1/10$.

Proof

This is equivalent to proving $d \ln (1-\beta ^s) \ge -\ln 10$. Using $\ln (1+x) \ge \frac{x}{1+x}$ for $x > -1$, we derive

$$\begin{aligned} d \ln (1-\beta ^s) \ge \frac{-d\beta ^s}{1-\beta ^s} \end{aligned}$$

(15)

Noting that $\beta ^{\log (d / \ln 4)/\log (1/\beta )} = (\ln 4) / d$, we arrive at

$$\begin{aligned} d \ln (1-\beta ^s) \ge \frac{d}{1-d/\ln 4}. \end{aligned}$$

(16)

Since $\frac{d}{1-d/\ln 4}$ is monotonically increasing with d (for $d>\ln 4$), the minimum value for an integer $d>3$ is obtained at $d=4$:

$$\begin{aligned} d \ln (1-\beta ^s) \ge \frac{4}{1-4/\ln 4}> -2.12 > -\ln 10 \end{aligned}$$

(17)

$\square$

Theorem 1

With $s=\lceil \log (d / \ln 4)/\log (1/\beta ) \rceil$ and $d>3$, the number of trials performed by SEPC satisfies:

$$\begin{aligned} k_\mathrm{{trials}} \le 1+\frac{10}{\alpha }\left( \frac{d}{\ln 4}\right) ^\frac{\log \alpha }{\log \beta }\ln \frac{1}{\epsilon } \end{aligned}$$

(18)

Proof

From (6), we have:

$$\begin{aligned} k_\mathrm{{trials}} = \left\lceil \frac{\log \epsilon }{\log (1 - \alpha ^s(1-\beta ^s)^d)} \right\rceil . \end{aligned}$$

(19)

Using the fact that $\ln (1+x) \le x$ for $x > -1$, we obtain:

$$\begin{aligned} k_\mathrm{{trials}} \le 1+\frac{\ln 1/\epsilon }{ \alpha ^s(1-\beta ^s)^d}. \end{aligned}$$

(20)

Using Lemma 1,

$$\begin{aligned}&k_\mathrm{{trials}} \le 1+\frac{10 \ln 1/\epsilon }{\alpha ^{\lceil \log (d / \ln 4)/\log (1/\beta ) \rceil }}. \end{aligned}$$

(21)

$$\begin{aligned}&k_\mathrm{{trials}} \le 1+10\alpha ^{-\log (d / \ln 4)/\log (1/\beta ) -1}\ln 1/\epsilon \end{aligned}$$

(22)

With some manipulation, this equation is equivalent to:

$$\begin{aligned} k_\mathrm{{trials}} \le 1+\frac{10}{\alpha }\left( \frac{d}{\ln 4}\right) ^\frac{\log \alpha }{\log \beta }\ln \frac{1}{\epsilon } \end{aligned}$$

(23)

$\square$

This proof implies that the number of trials required is $O(\frac{1}{\alpha }d^\frac{\log \alpha }{\log \beta }\log \frac{1}{\epsilon })$. The complexity of the overall algorithm is $O(\frac{1}{\alpha }nd^{1+\frac{\log \alpha }{\log \beta }}\log \frac{1}{\epsilon })$, since each trial in the algorithm requires O(nd) time.

The complexity of the SEPC algorithm can be contrasted with the DOC algorithm, which is $O(\frac{1}{\alpha }nd^{1+ \frac{\log (\alpha /2)}{\log 2\beta }}\log \frac{1}{\epsilon })$. With $\alpha = 0.1$, $\beta = 0.25$ and fixed $\epsilon$, our algorithm is $O(nd^{2.661})$, while the DOC algorithm is $O(nd^{5.322})$. SEPC has a lower computational complexity for any setting of the parameters. The difference between the exponents increases as the problem becomes more difficult (decreasing $\alpha$ and/or increasing $\beta$). SEPC requires three orders of magnitude less trials than DOC even for simple problems ($d=50$, $\alpha =0.1$, $\beta =0.15$) and over twenty orders of magnitude less trials for more complicated settings ($d=400$, $\alpha =0.1$, $\beta =0.35$) [28].

For many parameters, SEPC also has a lower computational complexity than the FastDOC algorithm, which is $O(nd^3)$ when the number of trials is limited to $d^2$. In cases where FastDOC has a lower computational complexity, it is because the number of trials is limited in such a way that clusters are often missed, as we have previously demonstrated [28].

3.8 Parameter setting

The SEPC algorithm has three important parameters, w, $\alpha$ and $\beta$. Less important is $\epsilon$, for which we use 0.01 in all cases. The values of $k_\mathrm{{trials}}$ and s are computed from these parameters (and the known number of dimensions in the data set). The maximum cluster width and minimum cluster cardinality (a function of $\alpha$) are common clustering algorithm parameters. These parameters can be chosen either using knowledge of the data set or empirically through testing on representative data. Techniques for automatic estimation of such parameters have also been examined [22].

The $\beta$ parameter is less intuitive, representing a trade-off between the number of points in the cluster and the number of dimensions in the cluster. However, every subspace clustering algorithm must (at least implicitly) estimate this trade-off. Given two clusters, A and B, with A congregating in $\delta$ more dimensions than B, A will score higher than B if $||A|| > \beta ^\delta ||B||$. We have found values between 0.2 and 0.35 to be most useful. Once again, prior knowledge and empirical testing can improve upon these estimates for a specific data set.

Given the increase in the number of trials necessary as $\beta$ increases, it might be questioned why a larger value is desirable. A larger value is necessary in some cases to prevent subsets of a cluster from producing a larger score than the “correct” cluster owing to random accumulation in one or more dimensions. Consider a subspace clustering problem in which each dimension ranges over [0, 1]. When determining the points in a cluster, we use a sheath of width $v \le 2w$ in the dimensions in which the discriminating set congregates. (The DOC and FastDOC algorithms use $v = 2w$.) A random outlier will fall within this sheath (in a single dimension) with probability v. When $\beta$ is less than v, the inclusion of an incorrect dimension usually leads to a cluster with a better score than the desired subspace cluster, since it will include an extra dimension (although fewer points). The fraction of points in the smaller cluster that are captured from the larger cluster is expected to be v (although it varies around this fraction given random data). If the larger cluster has score $\mu _1$, the smaller cluster is expected to have a score of approximately $\frac{v}{\beta }\mu _1$.

Procopiuc et al. [32] noticed this effect in their experiments. Their solution was to generate more output clusters than were present in the input data in order to find all of the cluster points, even though they are broken into multiple output clusters. This problem can be solved using other techniques. Two simple ones are increasing s and/or increasing $\beta$. The first would make it less likely that incorrect dimensions are included in each trial. The second would make incorrect dimensions less likely to matter, since the scoring function would weight the number of cluster points higher and the number of dimensions lower. However, both of these changes increase the number of trials necessary to find a subspace cluster.

3.9 Optimizations

One optimization that is useful is to limit the number of passes through the entire data set, particularly if it is too large to fit in memory and accessing it from a disk is time consuming. The idea here is to generate many discriminating sets $S_i$ during a single pass through the data. After the discriminating sets are constructed, they can be examined jointly in a single pass through the data (and further discriminating sets can be generated during this pass). An additional parameter is required with this optimization, $k_\mathrm{{sets}}$, which is the number of discriminating sets to consider simultaneously.

In the FastDOC algorithm, Procopiuc et al. [32] propose to consider only one discriminating set for each outer iteration of the algorithm. This discriminating set is chosen by finding the one that congregates in the largest number of dimensions. We can similarly consider only one of the $k_\mathrm{{sets}}$ discriminating sets each full pass through the data in the SEPC algorithm. This optimization reduces the likelihood of finding an optimal cluster, since not every trial is fully evaluated, but good results can be achieved since the discriminating sets yielding many cluster dimensions often yield high scoring clusters. The speedup achieved is roughly $k_\mathrm{{sets}}$, since scanning the data set for potential cluster points dominates the running time. We do not use this optimization in the following experiments.

Although we could use a heuristic to limit the number of trials as is done in FastDOC [32], we choose not to do this, since our algorithm is less computationally complex and can handle a much wider range of parameter values.

4 Experiments

In previous work, we demonstrated that SEPC has superior performance to DOC and FastDOC on both synthetic and real data sets [28]. Here, we describe a thorough evaluation of the SEPC algorithm using OpenSubspace [25, 26]. This open source framework contains implementations of several subspace clustering algorithms and tools for evaluating them. We have compared these implementations with our own implementation of the SEPC algorithm.

4.1 Metrics

Clustering metrics in OpenSubspace are divided into two classes [26]. The first class is purely object-based. These metrics ignore the congregating dimensions of clusters in evaluating cluster quality. Instead, they rely entirely on how objects have been allocated to clusters compared to the correct allocation. This approach works well when clusters are disjoint. However, in some instances, it is advantageous to allow points to belong to multiple clusters that span different subspaces. In such cases, this class of metrics will yield misleading results. For example, the synthetic data sets provided with OpenSubspace have clusters that are subsets of other clusters, but that congregate in additional dimensions. This causes problems for object-based metrics, since the assignment of points to clusters is not unique. The second class of metrics uses information on both the objects and the congregating dimensions. Metrics in this class, such as clustering error (CE) [31], yield more useful results when the clusters overlap.

Following the terminology of Müller et al. [26], we use found cluster to refer to a cluster returned as part of the results of running a clustering algorithm on a given data set. In contrast, a hidden cluster is known a priori (but not to the clustering algorithm). In the case of synthetic data sets, both the objects and subspace of hidden clusters are known; however, for real-world data, we are typically limited to information about object membership in hidden clusters.

4.1.1 Clustering error

Müller et al. [26] formulate the Clustering Error (CE) metric [31] such that it accounts for both cluster membership and cluster congregating dimensions. This allows clusters with the same points, but disjoint dimensions to be considered disjoint. Each object is partitioned into sub-objects (one for each dimension). An optimal one-to-one mapping is performed between found clusters and hidden clusters. If the number of found and hidden clusters is not the same, some clusters will not be matched. (This addresses a problem common to many subspace clustering quality metrics where many found clusters are allowed to match the same hidden cluster.)

The CE score then takes the ratio of the number sub-objects that are not in the correct found cluster to the total number of sub-objects in the hidden clusters. Let U be the number of sub-objects that are contained in the union of the found clusters and hidden clusters. Let I be the number of sub-objects in the hidden clusters that are correctly matched in the one-to-one mapping between found and hidden clusters. The CE score is:

$$\begin{aligned} CE = \frac{U-I}{U} \end{aligned}$$

(24)

A CE score of zero is ideal. Our plots show $1-$ CE so that the best scores are larger values. One drawback to using CE in this formulation is that the congregating dimensions are often unknown in real-world data sets. In these cases, we use the F1 score instead.

4.1.2 F1

The F1 score [26, 37] is an object-based metric computed with respect to each hidden cluster. Found clusters are matched to the best overlapping hidden cluster. The F1 score for each hidden cluster is computed as the harmonic mean of the recall (fraction of the hidden cluster contained in the matching found clusters) and precision (fraction of the matching found clusters contained in the hidden cluster). The overall F1 score is the average of the F1 scores for each hidden cluster. Let the n hidden clusters be $\left\{ H_1,\ldots ,H_n\right\}$. We then have:

$$\begin{aligned} F1 = \frac{1}{n} \sum _{i=1}^{n}\frac{2 \cdot \hbox {recall}(H_i) \cdot \hbox {precision}(H_i)}{\hbox {recall}(H_i) + \hbox {precision}(H_i)} \end{aligned}$$

(25)

Problems can arise with the F1 score when there are overlapping hidden clusters that span different subspaces. OpenSubspace maps each found cluster to the hidden cluster it contains the largest fraction of (not the hidden cluster that most overlaps it). This allows small hidden clusters to be matched with large found clusters, even though the found cluster is much larger than the hidden cluster (and may have more overlap with a different hidden cluster). This can result in a bias toward matching smaller hidden clusters. However, we use this metric only when the congregating dimensions for the data set are not available.

4.2 Comparison

We have performed experiments similar to those of Müller et al. [26] using the SEPC algorithm and several competing algorithms. Each experiment was conducted with many different parameter settings for each algorithm in an attempt to obtain the optimal performance. In addition, each run of an algorithm was limited to 30 min. The following algorithms, as implemented in OpenSubspace, were used in this comparison: CLIQUE [3], PROCLUS [1], FastDOC [32], MineClus [39], FIRES [19], P3C [24], and STATPC [23]. In addition, we compare against CLON [5], for which we wrote a wrapper to the code made available by its developers.⁵ The experiments were run on machines with 1.8GHz Dual-Core AMD Opteron 2210 processors and 2GB memory running Red Hat Linux 5.9 (except CLON, which was added later). With some parameter settings, algorithms did not finish within a 30-min time limit. Trials with these settings were discarded. Otherwise, the best performing trial was recorded. Note that DOC [32] is not included. In cases where it was able to finish within the time limit, the results were nearly the same as FastDOC.

4.2.1 Synthetic data

OpenSubspace is packaged with three synthetic data sets, each intended to explore a different aspect of algorithm performance. These data sets enable evaluation over increasing dimensionality (number of attributes), over increasing data set size (number of objects), and over increasing amounts of noise (irrelevant objects). Additionally, all of the data sets contain overlapping hidden clusters (clusters that share objects, but span different subspaces). We applied SEPC in non-disjoint mode.

We use clustering error (CE) to examine the relative quality of the clustering results generated on these synthetic data by each algorithm. This measure penalizes redundancy (multiple found clusters covering the same hidden cluster) and allows us to evaluate the ability to discover clusters with overlapping objects. Algorithms that generate disjoint clusters cannot achieve a perfect CE score when overlapping clusters are present.

Fig. 6

Algorithm performance under varying conditions. a Clustering error versus number of dimensions. b Clustering error versus number of object. c Clustering error versus percent outliers. d Run time versus number of dimensions

To evaluate the scalability of algorithms as the dimensionality of a data set increases, OpenSubspace includes data sets with dimensions varying from 5 to 75. Each data set includes ten subspace clusters that span 50, 60 and 80% of the full feature space. Figure 6a shows the results of our evaluations of each algorithm on the dimension-based data sets. Our results were similar to those of Müller et al. [26], who observed the best CE results for the cell-based approaches, particularly FastDOC and MineClus. In our evaluation, FastDOC and MineClus scored a CE value of approximately 0.8 across all dimensionalities. However, as can be seen in Fig. 6a, SEPC exceeded these results. CLON [5] did not fare well with respect to the CE measure. This is because large clusters were output as multiple smaller clusters for all parameter settings tested.

OpenSubspace also includes a set of synthetic data where the number of objects in each cluster varies, but the number of dimensions is constant. All of these data sets contain 20-dimensional objects, but they vary in size from roughly 1500 points up to 5500 points. We used these data sets to evaluate algorithm performance over increasing data set size. The best results for FastDOC and MineClus varied between CE values of 0.85 and 0.9. SEPC exceeded these results with a CE value of at least 0.95 and achieved a CE value of 0.99 for the data set containing 3500 data points. See Fig. 6b.

For noise-based experiments, OpenSubspace includes data sets where the percentage of noise objects increases from 10% noise up to 70% noise. These data sets were built by adding noise to the 20-dimensional data set from the scalability experiments. For noise-based experiments, Müller et al. reported CE results for FastDOC and MineClus of about 0.79 to 0.89 [26]. We saw similar results in our evaluation. It can be observed in Fig. 6c that the FastDOC and MineClus results exhibit a slight downward trend as the amount of noise in the data set increases. In contrast, the CE results for SEPC are consistent ranging from 0.95 to 0.97, with no degradation in performance with increasing amounts of noise. The high CE scores achieved by SEPC across all data sets indicate that the algorithm effectively discovers overlapping clusters.

We also examined the running times for the algorithm⁶ on each data set. For some algorithms, parameter settings significantly affect running time. We continued to use the parameter settings that yielded the optimal CE results. See Fig. 6d. We note that SEPC is faster than P3C, STATPC, FIRES, and FastDOC on all data sets. CLIQUE and PROCLUS are the fastest algorithms across all data sets. However, they also score among the lowest CE values. MineClus, which surpasses FastDOC for the second best cluster error performance, fairs relatively well here, with a lower run time than SEPC.

4.2.2 Real data

In addition to synthetic data, we used the real-world data packaged with OpenSubspace to evaluate SEPC against other subspace clustering algorithms. These publicly available data sets from the UCI archive [21] have typically been used in classification tasks and have class labels. The class labels are assumed to describe natural clusters in the data. However, no information about the subspaces of the clusters is known, so metrics that use the cluster subspace are not applicable. For these experiments, we use the F1 score. Since all of the clusters in the real-world data sets are disjoint, SEPC was run in disjoint mode for these experiments.

Fig. 7

Comparison of algorithms on real-world data sets using the F1 measure

Figure 7 summarizes the F1 results obtained by each algorithm for each of the seven real-world data sets. SEPC yielded the highest F1 score on four out of the seven data sets and the highest average score.

5 Conclusion

We have described a new algorithm called SEPC for locating subspace and projected clusters using Monte Carlo sampling. The algorithm is straightforward to implement and has low complexity (linear in the number of data points and low-order polynomial in the number of dimensions). In addition, the algorithm does not require the number of clusters or the number of cluster dimensions as input and does not make assumptions about the distribution of cluster points (other than that the clusters have bounded diameter). The algorithm is widely applicable to subspace clustering problems, including the ability to find both disjoint and non-disjoint clusters. The performance of the SEPC algorithm surpasses previous algorithms on both synthetic and real data.

Interesting future work exists in two areas. First, the detection of subspace clusters with arbitrarily oriented axes (rather than parallel to the attributes axes) is useful, since attributes may be correlated. Also, soft subspace clustering, where the cluster membership is probabilistic, may yield improvements over hard assignment.