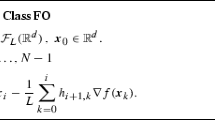Abstract
We consider the gradient method with variable step size for minimizing functions that are definable in o-minimal structures on the real field and differentiable with locally Lipschitz gradients. We prove that global convergence holds if continuous gradient trajectories are bounded, with the minimum gradient norm vanishing at the rate o(1/k) if the step sizes are greater than a positive constant. If additionally the gradient is continuously differentiable, all saddle points are strict, and the step sizes are constant, then convergence to a local minimum holds almost surely over any bounded set of initial points.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The gradient method for minimizing a differentiable function \(f: \mathbb {R}^n\rightarrow \mathbb {R}\) consists in choosing an initial point \(x_0 \in \mathbb {R}^n\) and generating a sequence of iterates according to the update rule \(x_{k+1} = x_k - \alpha _k \nabla f(x_k)\) for \(k=0,1,2,\ldots \) where \(\alpha _0,\alpha _1,\alpha _2,\ldots >0\) are called the step sizes. Many objective functions f of interest nowadays are not coercive and their gradient is not Lipschitz continuous, including those arising in nonconvex statistical estimation problems. Thus none of the convergence theorems regarding the gradient method apply, to the best of our knowledge. Merely showing that the iterates are bounded has remained elusive: it actually appears as an assumption in many recent works on the gradient method [1, Theorem 4.1], [7, Theorem 3.2], [55, Proposition 14], [70, Theorem 3], and [54, Assumption 7]. Even then, one needs to either choose the step sizes carefully or assume Lipschitz continuity of the gradient in order to obtain convergence results (see Sect. 2). The object of this paper is to take a first step towards filling this gap with Theorem 1. We next give some notations.
Let \(\mathbb {N}:= \{0,1,2,\ldots \}\) and let \(\Vert \cdot \Vert \) be the induced norm of an inner product \(\langle \cdot , \cdot \rangle \) on \(\mathbb {R}^n\). Throughout this paper, we fix an arbitrary o-minimal structure on the real field (see Definition 7), and say that sets or functions are definable if they are definable in this structure. For readers not familiar with o-minimal structures, note that seemingly all objective functions used in practice are definable in some o-minimal structure. Low-rank matrix recovery (for e.g., principal component analysis, matrix completion, and matrix sensing) and deep neural networks are no exception [20, Section 6.2].
Theorem 1
Let \(f:\mathbb {R}^n \rightarrow \mathbb {R}\) be a definable differentiable function whose gradient is locally Lipschitz. The following statements are equivalent:
-
1.
For all \(x_0 \in \mathbb {R}^n\), there exist \(\bar{\alpha }>0\) and \(c>0\) such that for all \(\alpha _0,\alpha _1,\alpha _2,\ldots \in (0,\bar{\alpha }]\), the sequence \(x_0,x_1,x_2,\ldots \in \mathbb {R}^n\) defined by
$$\begin{aligned} x_{k+1} = x_k - \alpha _k \nabla f(x_k), ~~~\forall k \in \mathbb {N}, \end{aligned}$$(1)satisfies \(\Vert x_k\Vert \leqslant c\) for all \(k \in \mathbb {N}\).
-
2.
For all \(0< T \leqslant \infty \) and any differentiable function \(x:[0,T)\rightarrow \mathbb {R}^n\) such that
$$\begin{aligned} x'(t) = -\nabla f(x(t)), ~~~ \forall t \in (0,T), \end{aligned}$$there exists \(c>0\) such that \(\Vert x(t)\Vert \leqslant c\) for all \(t\in [0,T)\).
-
3.
For any bounded subset \(X_0\) of \(\mathbb {R}^n\), there exist \(\bar{\alpha }>0\) and \(c>0\) such that, for all \(\alpha _0,\alpha _1,\alpha _2,\ldots \in (0,\bar{\alpha }]\) and \(x_0 \in X_0\), the sequence \(x_0,x_1,x_2,\ldots \in \mathbb {R}^n\) defined by (1) obeys
$$\begin{aligned} \sum _{k=0}^{\infty } \Vert x_{k+1}-x_k\Vert \leqslant c. \end{aligned}$$
The bound on the length implies that the iterates converge to a critical point of f (i.e., a point \(x^* \in \mathbb {R}^n\) such that \(\nabla f(x^*)=0\)) if the step sizes are not summable. If in particular there exists \(\underline{\alpha }>0\) such that \(\alpha _0,\alpha _1,\alpha _2,\ldots \geqslant \underline{\alpha }\), then
where \(\lfloor \cdot \rfloor \) stands for floor.Footnote 1 The previously known global convergence rate is \(o(1/\sqrt{k})\) for lower bounded differentiable functions with Lipschitz continuous gradients [67, Equation (1.2.22)], [53, Lemma 1], which improves to o(1/k) if additionally the function is convex and attains its infimum [66, Equation (2)], [53, Theorem 3]. Corollary 1 gives sufficient conditions for the critical point to be a local minimum.
Corollary 1
Let \(f:\mathbb {R}^n \rightarrow \mathbb {R}\) be a definable twice continuously differentiable function with bounded continuous gradient trajectories. If the Hessian of f has a negative eigenvalue at all saddle points of f, then for any bounded subset \(X_0\) of \(\mathbb {R}^n\), there exists \(\bar{\alpha }>0\) such that for all \(\alpha \in (0,\bar{\alpha }]\) and for almost every \(x_0 \in X_0\), the sequence \(x_0,x_1,x_2,\ldots \in \mathbb {R}^n\) defined by \(x_{k+1} = x_k - \alpha \nabla f(x_k)\) for all \(k \in \mathbb {N}\) converges to a local minimum of f.
Corollary 1 immediately follows from Theorem 1 and [70, Theorem 3] via the center and stable manifolds theorem [81, Theorem III.7]. In the o-minimal setting, no assumption on the Hessian is required at local maxima, unlike in existing work [54, 55, 71]. Indeed, local maxima that are not local minima lie on the boundary of the set of critical points, which has measure zero by [89, (1.10) Corollary p. 68]. In the spirit of [41, 55], we use the shorthand strict saddle to denote a saddle point where the Hessian has a negative eigenvalue (originally referred to as linearly unstable by Pemantle [73, Theorem 1]). We next illustrate Corollary 1 using principal component analysis.
Example 1
Let \(M \in \mathbb {R}^{m\times n}\) and consider the function
where \(m,n,r\in \mathbb {N}^*:=\{1,2,\ldots \}\). In this example, \(\Vert \cdot \Vert =\sqrt{ \langle \cdot ,\cdot \rangle }\) is the Frobenius norm and \(\Vert \cdot \Vert _2\) is the spectral norm. The function is not coercive and its gradient is not Lipschitz continuous. Thus none of the convergence theorems in the optimization literature apply, to the best of our knowledge. There only exist results tailored to low-rank matrix factorization [35, Theorem 3.1], [95, Theorem 1.1]. They require initialization near the origin and \(\text {rank}(M) = r\), and only guarantee convergence with high probability. Fortunately, the function is semi-algebraic, hence definable in the real field with constants, and its saddle points are strict [12, 85, 86, Theorem 3.3]. It also has bounded continuous gradient trajectories. Indeed, let \(X:[0,T)\rightarrow \mathbb {R}^{m\times r}\) and \(Y:[0,T)\rightarrow \mathbb {R}^{n\times r}\) where \(0<T\leqslant \infty \) be differentiable functions such that
On the one hand,
and thus \(X^\top X-Y^\top Y\) is constant (property known as balance [4, 5, 35]). On the other hand,
Hence X and Y are bounded. By Corollary 1, the gradient method with constant step size initialized in any bounded set converges almost surely to a local minimum. In fact, since f has no spurious local minima, as was discovered in 1989 [12], we have established convergence to a global minimum almost surely.
Boundedness of continuous subgradient trajectories, which holds for lower semicontinuous convex functions that admit a minimum [24, Theorem 4], is a property shared by several other applications. Indeed, it can be shown that linear neural networks [27, Proposition 1], [10, Theorem 3.2], [46, Proposition 4.1] and some nonlinear neural networks with the sigmoid activation function have bounded continuous gradient trajectories [46, Proposition 4.2] (see [36] for recent work using the ReLU activation). Theorem 1 implies convergence to a critical point, which may not be a local minimum since not all saddle points are strict [48]. Matrix sensing also has bounded continuous gradient trajectories [46, Proposition 4.4] under the restricted isometry property (RIP) due to Candès and Tao [25]. In addition, all critical points are either global minima or strict saddles [58, Theorem III.1] provided that the RIP constant is less that 1/5. Corollary 1 again implies convergence to a global minimum almost surely.
In order to prove Theorem 1, we propose the following result regarding real-valued multivariate functions.
Lemma 1
If a locally Lipschitz definable function has bounded continuous subgradient trajectories, then continuous subgradient trajectories initialized in a bounded set have uniformly bounded lengths.
Figuratively, Lemma 1 says that lava flowing from the vent of a volcano always stays in a bounded region. A key idea in the proofs of Lemma 1 and Theorem 1 is to consider the supremum of the lengths of subgradient trajectories over all possible initial points in a bounded set, as well as over all possible step sizes in the discrete case (see (15) and (21)). We then construct a sequence of bounded sets that iteratively exclude critical values of the objective function until none remain. In order to do so, we rely on the Kurdyka–Łojasiewicz inequality [49, Theorem 1], the Morse-Sard theorem [65, 79], and the monotonicity theorem [89, (1.2) p. 43], [74].
We in fact propose a uniform Kurdyka–Łojasiewicz inequality (see Proposition 5) better suited for our purposes. It should not to be confused with the uniformized KL property [21, Lemma 6] which extends a pointwise version of the Kurdyka–Łojasiewicz inequality to compact sets. The Kurdyka–Łojasiewicz inequality guarantees the existence of a desingularizing function around each critical value of a locally Lipschitz definable function. By extending the inequality to hold across multiple critical values, we refine an important result of Kurdyka [49, Theorem 2] regarding the length of gradient trajectories (see Proposition 7). Our proof is also new because we integrate the Kurdyka–Łojasiewicz inequality along a subgradient trajectory (see (10a)) and we use Jensen’s inequality [45].
Kurdyka’s aforementioned result states that continuous gradient trajectories of a continuously differentiable definable function that lie in a bounded set have uniformly bounded lengths, generalizing Łojasiewicz’ discovery for real analytic functions [62, 60, Theorème 5]. We make explicit the link between the length and the function variation using the desinguralizing function and the number of critical values, in both continuous (Proposition 7) and discrete cases (Proposition 8).
This link, refined in the continuous case, new in the discrete case, enables us to determine how subgradient trajectories behave in the vicinity of saddle points. Either they stay above the corresponding critical value, or they admit a uniform decrease below it (see Example 2). By the definable Morse–Sard theorem [18, Corollary 9], lower semicontinuous definable functions have finitely many critical values. In order to navigate from one to the next in the proofs of Lemma 1 and Theorem 1, we reason by induction in a way that is reminiscent of Bellman’s principle of optimality [14, p. 83].
This paper is organized as follows. Section 2 contains a literature review. Section 3 contains some definitions and basic properties of subgradient trajectories. Section 4 contains the uniform Kurdyka–Łojasiewicz inequality and some consequences. Section 5 contains the proof of Lemma 1. We then prove Theorem 1 in a cyclic manner in Sect. 6.
2 Literature review
The gradient method was proposed by Cauchy [26] for minimizing a nonnegative continuous multivariate function. In Lemaréchal’s words [56], “convergence is just sloppily mentioned” in [26] and “we are now aware that some form of uniformity is required from the objective’s continuity”. According to Theorem 1, no such assumption is required in the o-minimal setting.
The first convergence proof is due to Temple [84]. It deals with the case where the objective function is quadratic with a positive definite Hessian. He showed that the gradient converges to zero if the step size is chosen so as to minimize the function along the negative gradient (known as exact line search). Curry [30] generalized this result to any function with continuous partial derivatives by taking the step size to correspond to the first stationary point along the negative gradient (known as Curry step). This stationary point is assumed to exist. It is also assumed that the iterates admit a converging subsequence. Interestingly, both assumptions hold if the objective is coercive.
Subsequently, Kantorovich [47] proposed his eponymous inequality which established a linear convergence rate for quadratic objective functions with positive definite Hessians. Akaike [2] then argued that for ill-conditioned Hessians, the rate is generally close to its worst possible value, as observed by Forsythe and Motkzin [38]. Goldstein [43], Armijo [3], and Wolfe [94] later proposed inexact line search methods for differentiable functions that guarantee a linear decrease along the negative gradient. All their convergence theorems require some form of uniformity from the objective’s continuity. These can be proven using Zoutendijk’s condition [96] and assuming Lipschitz continuity of the gradient on a sublevel set (see [69, Theorem 3.2] and [42, Propositions 6.10\(-\)6.12]). The latter assumption is also used in the convex setting [67, 76].
The assumption of Lipschitz continuity of the gradient seems to be omnipresent in the more general context of first-order methods. For the proximal gradient method, Bauschke et al. [13] recently proposed to exchange it with a Lipschitz-like/convexity condition when minimizing convex composite functions. This idea was generalized to nonconvex composite functions for a Bregman-based proximal gradient method [22], where the new assumption is named smooth adaptable. The gradient method with constant step size is a special case of this algorithm, but in that case being smooth adaptable means having a Lipschitz continuous gradient. Note that the convergence theorem of the Bregman-based proximal gradient method [22, Theorem 4.1] also requires the iterates to be bounded. A notion of stopping time [72, Equation (3.1)] was recently proposed in order to analyze the gradient method with diminishing step sizes without assuming Lipschitz continuity of the gradient. Several results are derived regarding the stopping time [72, Theorems 3.3 and 4.1], but the results devoid of it again require the iterates to be bounded.
Once the iterates are assumed to be bounded, then a lot can be said about the gradient method. Absil et al. [1, Theorem 4.1] showed that bounded iterates of the gradient method with Wolfe’s line search converge to a critical point if the objective function is analytic [1, Theorem 4.1]. The proof relies on the Łojasiewicz gradient inequality [61, Proposition 1 p. 67] and implies that the iterates have finite length, albeit not uniformly as in Theorem 1. Note that without uniformity, Corollary 1 cannot be deduced. The exponent in the Łojasiewicz gradient inequality also informs the convergence rate [57, 75]. A result of Attouch et al. [7, Theorem 3.2] implies that bounded iterates of the gradient method with sufficiently small constant step sizes converge to a critical point if the objective function is differentiable with a Lipschitz continuous gradient and it satisfies the Kurdyka–Łojasiewicz inequality at every point. If additionally the function is twice continuously differentiable and its Hessian has a negative eigenvalue at all saddle points and local maxima, then the limiting critical point must be a local minimum for almost every initial point, as shown by Lee et al. [55, Proposition 14] and Panageas and Piliouras [70, Theorem 3] using the center and stable manifolds theorem. This convergence result was generalized to other first-order methods in [54, Assumption 7]. Although not explicitly stated, the boundedness assumption is implicit in [70, Theorem 3] since the forward invariant domain needs to be bounded in order to guarantee convergence to a local minimum, as stated in the title of that paper.
In the main result of this paper, we establish an equivalence between boundedness of the iterates of the gradient method and boundedness of their continuous counterpart. The closest result in the literature seems to be [19, Theorem 39]. It considers a coercive differentiable convex objective function which satisfies the Kurdyka–Łojasiewicz inequality and which has a Lipschitz continuous gradient. It shows that piecewise gradient iterates have uniformly bounded lengths if and only if piecewise gradient curves have uniformly bounded lengths, under the assumption that the iterates satisfy a strong descent assumption [19, Equation (53)] [1, Definiton 3.1]. The notions of piecewise gradient iterates and curves [19, Definiton 15] do not seem to inform the behavior of discrete and continuous gradient trajectories considered in this paper (see Definition 5).
In order to establish global convergence of the gradient method, we propose Lemma 1 as mentioned in the introduction. The length of subgradient trajectories has been of significant interest in the last decades. Łojasiewicz [62] proved in the early eighties that bounded continuous gradient trajectories of analytic functions have finite length. This result has since been generalized to continuously differentiable definable functions by Kurdyka [49, Theorem 2], and later extended to nonsmooth settings by Bolte et al. [17, Theorem 3.1], [18, Theorem 14]. Manselli and Pucci [63, IX], [31, Corollary 2.4] showed that continuous subgradient trajectories of multivariate convex functions that admit a minimum have finite length. This is false in infinite dimension due to a counterexample of Baillon [11]. These results relating to convexity solved an open problem posed by Brézis [23, Problem 13 p. 167]. Discrete gradient trajectories of convex differentiable functions with Lipschitz continuous gradients also have finite length if the step size is constant and sufficiently small [15, Corollary 3.9] [44, Theorem 15].
It is conjectured that continuous subgradient trajectories of locally Lipschitz definable functions are nonoscillatory [49, Conjecture F], that is, the intersection of their orbit and any definable set has finitely many connected components. This would immediately imply Thom’s gradient conjecture, which was shown to be true for analytic functions [50], and more generally for continuously differentiable functions definable in polynomially bounded o-minimal structures [51]. In fact, it was shown that the radial projection of the difference between the trajectory and its limit has finite length.
Finally, let us discuss two relevant works [37, 44] published in 2021. The former bounds the lengths of continuous gradient trajectories that lie in a bounded set for families of definable functions and for polynomial functions, in which case the bound is explicit. The latter bounds the lengths of continuous and discrete gradient trajectories of differentiable functions with Lipschitz continuous gradients under the assumption of linear convergence to the set of global minimizers.
3 Subgradient trajectories
We begin by stating some standard definitions. Let B(a, r) and S(a, r) respectively denote the closed ball and the sphere of center \(a\in \mathbb {R}^n\) and radius \(r \geqslant 0\).
Definition 1
A function \(f:\mathbb {R}^n\rightarrow \mathbb {R}^m\) is locally Lipschitz if for all \(a \in \mathbb {R}^n\), there exist \(r>0\) and \(L>0\) such that
Definition 2
[28, Chapter 2] Let \(f:\mathbb {R}^n \rightarrow \mathbb {R}\) be a locally Lipschitz function. The Clarke subdifferential is the set-valued mapping \(\partial f:\mathbb {R}^n\rightrightarrows \mathbb {R}^n\) defined for all \(x \in \mathbb {R}^n\) by \(\partial f(x):= \{ s \in \mathbb {R}^n: f^\circ (x,h) \geqslant \langle s, h \rangle , ~ \forall h\in \mathbb {R}^n \}\) where
We say that \(x \in \mathbb {R}^n\) is critical if \(0 \in \partial f(x)\). If f is continuously differentiable in a neighborhood of \(x \in \mathbb {R}^n\), then \(\partial f(x) = \{\nabla f(x)\}\) [28, 2.2.4 Proposition p. 33].
Definition 3
A point \(x^* \in \mathbb {R}^n\) is a local minimum (respectively global minimum) of a function \(f:\mathbb {R}^n\rightarrow \mathbb {R}\) if there exists \(\epsilon >0\) such that \(f(x^*) \leqslant f(x)\) for all \(x \in B(x^*,\epsilon )\) (respectively for all \(x\in \mathbb {R}^n\)). A local minimum \(x^* \in \mathbb {R}^n\) is spurious if \(f(x^*) > \inf \{ f(x): x \in \mathbb {R}^n\}\). A point \(x^* \in \mathbb {R}^n\) is a saddle point if it is critical and it is neither a local minimum of f nor \(-f\).
In order to define continuous subgradient trajectories, we recall the notion of absolute continuity.
Definition 4
[9, Definition 1 p. 12] Given some real numbers \(a\leqslant b\), a function \(x:[a,b]\rightarrow \mathbb {R}^n\) is absolutely continuous if for all \(\epsilon >0\), there exists \(\delta >0\) such that, for any finite collection of disjoint subintervals \([a_1,b_1],\ldots ,[a_m,b_m]\) of [a, b] such that \(\sum _{i=1}^m b_i-a_i \leqslant \delta \), we have \(\sum _{i=1}^m \Vert x(b_i) - x(a_i)\Vert \leqslant \epsilon \).
By virtue of [68, Theorem 20.8], \(x:[a,b]\rightarrow \mathbb {R}^n\) is absolutely continuous if and only if it is differentiable almost everywhere on (a, b), its derivative \(x'(\cdot )\) is Lebesgue integrable, and \(x(t) - x(a) = \int _a^t x'(\tau )d\tau \) for all \(t\in [a,b]\). Given a noncompact interval I of \(\mathbb {R}\), \(x:I\rightarrow \mathbb {R}^n\) is absolutely continuous if it is absolutely continuous on all compact subintervals of I. Given an interval I of \(\mathbb {R}\), let \(\mathcal {A}(I,\mathbb {R}^n)\) be the set of absolutely continuous functions defined from I to \(\mathbb {R}^n\).
Definition 5
Let \(f:\mathbb {R}^n \rightarrow \mathbb {R}\) be a locally Lipschitz function. Let \((S,\leqslant )\) be the set of absolutely continuous functions \(x:[0,T)\rightarrow \mathbb {R}^n\) where \(0<T\leqslant \infty \) such that
equipped with the partial order \(\leqslant \) defined by \(x_1:[0,T_1)\rightarrow \mathbb {R}^n\) is less than or equal to \(x_2:[0,T_2)\rightarrow \mathbb {R}^n\) if and only if \(T_1\leqslant T_2\) and \(x_1(t) = x_2(t)\) for all \(t\in [0,T_1)\). We refer to maximal elements of \((S,\leqslant )\) as continuous subgradient trajectories.
We say that a continuous subgradient trajectory is globally defined if it is of the form \(x:[0,T)\rightarrow \mathbb {R}^n\) where \(T=\infty \). We refer to discrete subgradient trajectories as sequences \((x_k)_{k\in \mathbb {N}}\) in \(\mathbb {R}^n\) such that \(x_{k+1} \in x_k -\alpha _k \partial f(x_k)\) for all \(k\in \mathbb {N}\) for some \(\alpha _0,\alpha _1,\alpha _2,\ldots >0\). When f is continuously differentiable, we refer to subgradient trajectories as gradient trajectories.
Definition 6
A continuous subgradient trajectory \(x: [0,T) \rightarrow \mathbb {R}^n\) where \(0< T\leqslant \infty \) is bounded if there exists \(c>0\) such that \(\Vert x(t)\Vert \leqslant c\) for all \(t\in [0,T)\).
In the rest of the section, we list basic properties of continuous subgradient trajectories that will be needed later. For other treatments of subgradient trajectories, see [8, Chapter 17], [40].
Proposition 1
Locally Lipschitz functions have at least one continuous subgradient trajectory for every initial point.
Proof
Let \(f:\mathbb {R}^n \rightarrow \mathbb {R}\) be a locally Lipschitz function and let \(x_0\in \mathbb {R}^n\). Since f is locally Lipschitz, the set-valued function \(-\partial f\) is upper semicontinuous [28, 2.1.5 Proposition (d) p. 29] with nonempty, compact and convex values [28, 2.1.2 Proposition (a) p. 27]. By virtue of [9, Theorem 3 p. 98], there exist \(\epsilon >0\) and an absolutely continuous function \(x:[0,\epsilon )\rightarrow \mathbb {R}^n\) such that
Let \(S_{x_0}\) be the set of functions in S from Definition 5 such that \(x(0) = x_0\). Then \(S_{x_0} \ne \emptyset \). Let P be a nonempty totally ordered subset of \(S_{x_0}\). Let \(0<T \leqslant \infty \) be the supremum of the endpoints of the domains of all functions in P. Consider the function \(x:[0,T)\rightarrow \mathbb {R}^n\) such that for all \(\bar{x}:[0,\overline{T})\rightarrow \mathbb {R}^n\) in P we have \(x(t):= \bar{x}(t)\) for all \(t\in [0,\overline{T})\). It is well defined and it is an upper bound of P in \(S_{x_0}\). By virtue of Zorn’s lemma [52, Corollary 2.5 p. 884], \(S_{x_0}\) contains a maximal element. \(\square \)
Proposition 2
Bounded continuous subgradient trajectories are globally defined.
Proof
Let \(x:[0,T)\rightarrow \mathbb {R}^n\) be a bounded continuous subgradient trajectory of f where \(0<T \leqslant \infty \). We reason by contradiction and assume that \(T<\infty \). By Definition 6, there exists \(c>0\) such that \(\Vert x(t)\Vert \leqslant c\) for all \(t\in [0,T)\). Consider a sequence \(t_0,t_1,t_2,\ldots \in [0,T)\) converging to T. For all \(k\in \mathbb {N}\), let \(x_k:[0,T]\rightarrow \mathbb {R}^n\) be defined by \(x_k(t):= x(t)\) for all \(t\in [0,t_k]\) and \(x_k(t) = 0\) for all \(t\in (t_k,T]\). By construction, \(x_k\) converges pointwise almost everywhere to x on (0, T). Let \(L>0\) be a Lipschitz constant of f on B(0, c). By [28, 2.1.2 Proposition (a) p. 27], for all \(x\in B(0,c)\) and \(s\in \partial f(x)\), we have \(\Vert s\Vert _* \leqslant L\) where \(\Vert \cdot \Vert _*\) is the dual norm of \(\Vert \cdot \Vert \) with respect to the Euclidean inner product. For almost every \(t\in (0,T)\), we thus have \(\Vert x_k'(t)\Vert _* \leqslant \Vert x'(t)\Vert _* \leqslant L\). By Lebesgue’s dominated convergence theorem, \(x(\cdot )\) is Lebesgue integrable on (0, T) and \(\int _0^{t_k} x'(t)dt = \int _0^T x'_k(t)dt \rightarrow \int _0^T x'(t)dt\). Since \(x(\cdot )\) is absolutely continuous on \([0,t_k]\), we have \(x(t_k) - x(0) = \int _0^{t_k} x'(t)dt\). Thus \(x(\cdot )\) can be extended to an absolutely continuous function on [0, T] where \(x(T):= x(0) + \int _0^T x'(t)dt\). According to Proposition 1, \(x(\cdot )\) can further be extended to an absolutely continuous function on \([0,T+\epsilon )\) for some \(\epsilon >0\) while satisfying the differential inclusion. This contradicts the maximality of \(x(\cdot )\). \(\square \)
Proposition 3 shows that the second statement in Theorem 1 is equivalent to requiring that all the continuous gradient trajectories are bounded, as stated in the abstract and Corollary 1.
Proposition 3
Let \(f:\mathbb {R}^n \rightarrow \mathbb {R}\) be a locally Lipschitz function and \(x_0\in \mathbb {R}^n\). The following statements are equivalent:
-
1.
For all \(0< T \leqslant \infty \) and any absolutely continuous function \(x:[0,T)\rightarrow \mathbb {R}^n\) such that
$$\begin{aligned} x'(t) \in -\partial f(x(t)), ~~~ \mathrm {for~a.e.}~ t \in (0,T), ~~~ x(0) = x_0, \end{aligned}$$(2)there exists \(c>0\) such that \(\Vert x(t)\Vert \leqslant c\) for all \(t\in [0,T)\).
-
2.
All the continuous subgradient trajectories of f initialized at \(x_0\) are bounded.
Proof
(\(1\Longrightarrow 2\)) Let \(x:[0,T)\rightarrow \mathbb {R}^n\) be a continuous subgradient trajectory of f where \(x(0)=x_0\) and \(0<T\leqslant \infty \). Since it is absolutely continuous and satisfies (2), there exists \(c>0\) such that \(\Vert x(t)\Vert \leqslant c\) for all \(t\in [0,T)\). Thus the subgradient trajectory is bounded by Definition 6. (\(2\Longrightarrow 1\)) Let \(x:[0,T)\rightarrow \mathbb {R}^n\) be an absolutely continuous function where \(x(0) = x_0\) and \(0<T\leqslant \infty \) such that (2) holds. Since the continuous subgradient trajectories initialized at \(x_0\) are bounded, by Proposition 2 they are globally defined. Thus \(x(\cdot )\) can be extended to an absolutely continuous function on \(\mathbb {R}_+:= [0,\infty )\) while satisfying the differential inclusion. Again because the continuous subgradient trajectories are bounded, by Definition 6 there exists \(c>0\) such that \(\Vert x(t)\Vert \leqslant c\) for all \(t\in \mathbb {R}_+\). \(\square \)
Remark 1
It may be tempting to only require \(T=\infty \) in first statement of Proposition 3 and the second statement of Theorem 1, but a counterexample is given by \(f(x)=-x^4/4\). Indeed, the only differentiable function \(x:[0,T)\rightarrow \mathbb {R}\) such that (2) holds with \(T=\infty \) is the constant function equal to zero (when \(x_0=0\)), which is trivially bounded. The other gradient trajectories are neither bounded nor globally defined (they are of the form \(x:[0,x_0^{-2}/2) \rightarrow \mathbb {R}\) with \(x(t) := \textrm{sign}(x_0)(x_0^{-2} -2t)^{-1/2}\) when \(x_0\ne 0\)).
Proposition 4 guarantees that discrete trajectories track continuous trajectories up to a certain time in a uniform way with respect to the initial point. A key idea for proving Lemma 1 and Theorem 1 alluded to in the introduction is also used to prove Proposition 4 (see (4)).
Proposition 4
Let \(f:\mathbb {R}^n \rightarrow \mathbb {R}\) be a lower bounded differentiable function with a locally Lipschitz gradient. Let \(X_0\) be a bounded subset of \(\mathbb {R}^n\) and let \(T>0\). For all \(\epsilon >0\), there exists \(\bar{\alpha }>0\) such that for all \(\alpha _0,\alpha _1,\alpha _2,\ldots \in (0,\bar{\alpha }]\) and for all sequence \(x_0,x_1,x_2,\ldots \in \mathbb {R}^n\) such that \(x_0 \in X_0\) and \(x_{k+1} = x_k - \alpha _k \nabla f(x_k)\) for all \(k \in \mathbb {N}\), the continuous gradient trajectory \(x:\mathbb {R}_+\rightarrow \mathbb {R}^n\) of f initialized at \(x_0\) satisfies
Proof
Let \(L>0\) and \(M>0\) respectively denote Lipschitz constants of f and \(\nabla f\) with respect to \(\Vert \cdot \Vert \) on the convex hull of \(B(X_0,\sigma _T(X_0)+1):= X_0 + B(0,\sigma _T(X_0)+1)\) where
Above, \(\mathcal {C}^1(\mathbb {R}_+,\mathbb {R}^n)\) is the set of continuous functions on \([0,\infty )\) that are continuously differentiable on \((0,\infty )\). Note that \(\sigma _T(X_0)<\infty \) since for any feasible point \(x(\cdot )\) of (4), we have
Indeed, (5a) is due to the Cauchy–Schwarz inequality. (5e) holds because \(X_0\) is bounded and f is lower bounded.
It is easy to check that L and ML are respectively Lipschitz and gradient Lipschitz constants on [0, T] of all continuous gradient trajectories of f initialized in \(X_0\). Indeed, let \(x:\mathbb {R}_+\rightarrow \mathbb {R}^n\) be a continuous gradient trajectory initialized in \(X_0\). Since \(x(t) \in B(X_0,\sigma _T(X_0))\) for all \(t\in [0,T]\), we have \(\Vert x'(t)\Vert _* = \Vert \nabla f(x(t))\Vert _* \leqslant L\). By the mean value theorem [78, 5.19 Theorem], for all \(s,t \in [0,T]\) we have \(\Vert x'(t)-x'(s)\Vert = \Vert \nabla f(x(t)) - \nabla f(x(s))\Vert \leqslant M \Vert x(t)-x(s)\Vert \leqslant M L |t-s |\). As a byproduct, we get the Taylor bound
Let \(\epsilon \in (0,1)\) and let \(\bar{\alpha }:= 2\epsilon e^{-MT}/(LMT)\). Consider \(\alpha _0,\alpha _1,\alpha _2,\ldots \in (0,\bar{\alpha }]\) and a sequence \(x_0,x_1,x_2,\ldots \in \mathbb {R}^n\) such that \(x_{k+1} = x_k - \alpha _k \nabla f(x_k)\) for all \(k \in \mathbb {N}\) and \(x_0 \in X_0\). Since f is lower bounded and differentiable with a Lipschitz continuous gradient, by [8, Theorem 17.1.1] there exists a unique continuous gradient trajectory \(x:\mathbb {R}_+\rightarrow \mathbb {R}^n\) of f initialized at \(x_0\). Let \(t_0:=0\) and \(t_k := \alpha _0+\cdots +\alpha _{k-1}\) when \(k\in \mathbb {N}^*\) so that \(\Vert x_0 - x(t_0)\Vert = 0 \leqslant \epsilon \). Assume that (3) holds up to some index K. For \(k=0,\ldots ,K\), we have
The term in (7c) is equal to the local truncation error \(\Vert x(t_{k+1}) - x(t_k) - x'(t_k)(t_{k+1}-t_k) \Vert \), and can hence be bounded above using (6d). In the second term of (7d), we invoke a Lipschitz constant of \(\nabla f\) on the convex hull of \(B(X_0,\sigma _T(X_0)+1)\). Indeed, by the induction hypothesis and \(\epsilon < 1\), \(x_k\) and \(x(t_k)\) belong to \(B(X_0,\sigma _T(X_0)+\epsilon )\). Hence
The term in (8a) is equal to zero because \(x_0 = x(t_0)\). By convention, we set the product in (8b) to be equal to one if the index set for l is empty. We bound the partial products ranging from \(k+1\) to K inside the summation of (8b) by the full product ranging from 0 to K in order to obtain (8c). We then use the inequality of arithmetic and geometric means and \(\alpha _k\leqslant \bar{\alpha }\) in order to obtain (8d). In order to prove the induction step, we assume that \(\alpha _0+\cdots +\alpha _K \leqslant T\), hence (8e). (8f) follows from \(\ln (1+x) \leqslant x\) for all \(x>0\). Finally, (8g) holds because \(\bar{\alpha } = 2\epsilon e^{-MT}/(LMT)\). \(\square \)
Remark 2
If \(X_0\) is a singleton \(\{x_0\}\) and \(x:[0,\hat{T})\rightarrow \mathbb {R}^n\) is a gradient trajectory initialized at \(x_0\), then one may remove the assumption that f is lower bounded in Proposition 4 and instead require that \(T \in (0,\hat{T})\). In that case, \(\sigma _T(X_0)=\int _0^T \Vert x'(t)\Vert dt < \infty \) since \(\nabla f\) is Lipschitz continuous on the bounded set x([0, T]).
4 Uniform Kurdyka–Łojasiewicz inequality
The Kurdyka–Łojasiewicz inequality generalizes the Łojasiewicz gradient inequality [61, Proposition 1 p. 67] from lower semicontinuous functions definable in polynomially bounded o-minimal structures [59] to lower semicontinuous functions definable in arbitrary o-minimal structures [18, Theorem 14].
O-minimal structures (short for order-minimal) were originally considered in [74, 87]. They are founded on the observation that many properties of semi-algebraic sets can be deduced from a few simple axioms [89]. Recall that a subset A of \(\mathbb {R}^n\) is semi-algebraic [16] if it is a finite union of basic semi-algebraic sets, which are of the form \(\{ x \in \mathbb {R}^n: p_i(x) = 0, ~ i = 1,\ldots ,k; ~ p_i(x) > 0, ~ i = k+1,\ldots ,m \}\) where \(p_1,\ldots ,p_m \in \mathbb {R}[X_1,\ldots ,X_n]\) (i.e., polynomials with real coefficients).
Definition 7
[91, Definition pp. 503–506] An o-minimal structure on the real field is a sequence \(S = (S_k)_{k \in \mathbb {N}}\) such that for all \(k \in \mathbb {N}\):
-
1.
\(S_k\) is a boolean algebra of subsets of \(\mathbb {R}^k\), with \(\mathbb {R}^k \in S_k\);
-
2.
\(S_k\) contains the diagonal \(\{(x_1,\ldots ,x_k) \in \mathbb {R}^k: x_i = x_j\}\) for \(1\leqslant i<j \leqslant k\);
-
3.
If \(A\in S_k\), then \(A\times \mathbb {R}\) and \(\mathbb {R}\times A\) belong to \(S_{k+1}\);
-
4.
If \(A \in S_{k+1}\) and \(\pi :\mathbb {R}^{k+1}\rightarrow \mathbb {R}^k\) is the projection onto the first k coordinates, then \(\pi (A) \in S_k\);
-
5.
\(S_3\) contains the graphs of addition and multiplication;
-
6.
\(S_1\) consists exactly of the finite unions of open intervals and singletons.
A subset A of \(\mathbb {R}^n\) is definable in an o-minimal structure \((S_k)_{k\in \mathbb {N}}\) if \(A \in S_k\). A function \(f:\mathbb {R}^n\rightarrow \mathbb {R}\) is definable in an o-minimal structure if its graph, that is to say \(\{ (x,t) \in \mathbb {R}^{n+1}: f(x)=t \}\), is definable in that structure. Examples of o-minimal structures include the real field with constants, whose definable sets are the semi-algebraic sets (by Tarski–Seidenberg [80, 83]), the real field with restricted analytic functions, whose definable sets are the globally subanalytic sets (by Gabrielov [39, 88]). the real field with the exponential function (by Wilkie [93]), the real field with the exponential and restricted analytic functions (by van den Dries, Macintyre, and Marker [90]), the real field with restricted analytic and real power functions (by Miller [64]), and the real field with convergent generalized power series (by van den Dries and Speissegger [92]). Note that there is no largest o-minimal structure [77]. Recall that throughout this paper, we fix an arbitrary o-minimal structure \((S_k)_{k\in \mathbb {N}}\).
We next state the uniform Kurdyka–Łojasiewicz inequality. Given a subset of S of \(\mathbb {R}^n\), let \(\mathring{S}\) and \(\overline{S}\) denote the interior and closure of S in \(\mathbb {R}^n\) respectively. A function \(\psi :S \rightarrow S\) is a homeomorphism if it is a continuous bijection and the inverse function \(\psi ^{-1}\) is continuous. \(\psi :S \rightarrow S\) is a diffeomorphism if \(\mathring{S} \ne \emptyset \), \(\psi \) is a homeomorphism, and both \(\psi \) and \(\psi ^{-1}\) are continuously differentiable on \(\mathring{S}\). Given \(x\in \mathbb {R}^n\), consider the distance of x to S defined by \(d(x,S):= \inf \{ \Vert x-y\Vert : y \in S \}\). Given a locally Lipschitz function \(f:\mathbb {R}^n\rightarrow \mathbb {R}\), a real number v is critical value of f in S if there exists \(x \in S\) such that \(v = f(x)\) and \(0\in \partial f(x)\). Given a set-valued mapping \(F:\mathbb {R}^n\rightrightarrows \mathbb {R}^m\) and \(y \in \mathbb {R}^m\), let \(F^{-1}(y):= \{ x \in \mathbb {R}^n: F(x) \ni y \}\).
Proposition 5
Let \(f:\mathbb {R}^n \rightarrow \mathbb {R}\) be a locally Lipschitz definable function and let X be a bounded subset of \(\mathbb {R}^n\). Let V be the set of critical values of f in \(\overline{X}\) if it is nonempty, otherwise let \(V:=\{0\}\). There exists a concave definable diffeomorphism \(\psi :[0,\infty )\rightarrow [0,\infty )\) such that
where \(\tilde{f}(x):= d(f(x),V)\) for all \(x\in \mathbb {R}^n\).
Proof
By the definable Morse–Sard theorem [18, Corollary 9], the set V is finite. In addition, by the Kurdyka–Łojasiewicz inequality [18, Corollary 15], there exist \(\epsilon >0\) and a strictly increasing concave continuous definable function \(\psi :[0,\epsilon )\rightarrow \mathbb {R}\) that is continuously differentiable on \((0,\epsilon )\) with \(\psi (0) = 0\) such that, for all \(x \in X\) and \(v \in V\) satisfying \(0< \vert f(x)-v \vert < \epsilon \), we have \(d(0,\partial (\psi \circ \vert f-v\vert )(x)) \geqslant 1\). The fact that \(\psi \) can be assumed to be concave is due to the monotonicity theorem [89, (1.2) p. 43], [49, Lemma 2] by following the argument in [6, Theorem 4.1]. Let \(\rho := \inf \{(v-v')/2: v,v' \in V, v> v'\}>0\) and \(\rho ': = \min \{ \rho , \epsilon \}\). Observe that \(c>0\) where
Indeed, assume that there exist sequences \((s_k)_{k\in \mathbb {N}}\) and \((x_k)_{k\in \mathbb {N}}\) such that \(\Vert s_k\Vert \) converges to zero and \(s_k \in \partial f(x_k)\), \(x_k\in X\), and \(\vert f(x_k) - v \vert \geqslant \rho '\) for all \(v\in V\). Since X is bounded, there exist subsequences (again denoted \(s_k\) and \(x_k\)) such that \(x_k\) has a limit \(x^*\) in \(\overline{X}\). Since f is continuous, \(\vert f(x^*) - v \vert \geqslant \rho '>0\) for all \(v \in V\). Also, since \(s_k\) converges to zero, by [28, 2.1.5 Proposition (b) p. 29], we have \(0\in \partial f(x^*)\). This yields a contradiction.
After possibly reducing \(\epsilon \), we may assume that \(\lim _{t\nearrow \rho '} \psi '(t)>0\). If \(\lim _{t\nearrow \rho '} \psi '(t) \geqslant 1/c\), then we may extend \(\psi \) to an affine function on \([\rho ',\infty )\) with slope equal to \(\lim _{t\nearrow \rho '} \psi '(t)\). Otherwise, we can multiply \(\psi \) by \(1/(c\lim _{t\nearrow \rho '} \psi '(t))\) before taking the affine extension. Now let \(x \in X\) be such that \(0 \notin \partial \tilde{f}(x)\). If f(x) is strictly within \(\rho '\) distance of some \(v \in V\), then from \(\rho ' \leqslant \rho \) it follows that \(\tilde{f}(\tilde{x}) = d(f(\tilde{x}),V) = \vert f(\tilde{x})-v\vert \) for all \(\tilde{x}\) in a neighborhood of x in \(\mathbb {R}^n\), and thus \(d(0,\partial ( \psi \circ \tilde{f})(x)) = d(0,\partial (\psi \circ \vert f-v\vert )(x)) \geqslant 1\). The inequality is due to \(\rho ' \leqslant \epsilon \). Otherwise, by [28, 2.3.9 Theorem (Chain Rule I) (ii) p. 42] we have \(d(0,\partial ( \psi \circ \tilde{f})(x)) = \psi '(\tilde{f}(x)) d(0,\partial \tilde{f} (x)) = \psi '(\tilde{f}(x)) d(0,\partial f(x)) \geqslant \psi '(\tilde{f}(x)) c \geqslant 1\). \(\square \)
We say that \(\psi \) in Proposition 5 is a desingularizing function of f on X. In order to prove Proposition 7, we recall the following result.
Proposition 6
Let \(f:\mathbb {R}^n \rightarrow \mathbb {R}\) be a definable function and let \(x:(0,T)\rightarrow \mathbb {R}^n\) with \(0 < T \leqslant \infty \) be an absolutely continuous function. If f is locally Lipschitz at x(t) for all \(t \in (0,T)\) and \(x'(t) \in -\partial f(x(t))\) for almost every \(t\in (0,T)\), then
Proof
Since f is definable and locally Lipschitz at x(t) for all \(t\in (0,T)\), it satisfies the chain rule [20, Proposition 2 (iv)] (see also [32, Theorem 5.8] and [33, Lemma 2.10]), that is to say \((f \circ x)'(t) = \langle s , x'(t) \rangle \) for all \(s\in \partial f(x(t))\) and almost every \(t\in (0,T)\). In particular, we may take \(s := - x'(t) \in \partial f(x(t))\). Finally, by [32, Lemma 5.2] (see also [34, Proposition 4.10]) it holds that \(\Vert x'(t)\Vert = d(0,\partial f(x(t)))\) for almost every \(t\in (0,T)\). \(\square \)
The following proposition is a refinement of [49, Theorem 2], as discussed in the introduction.
Proposition 7
Let \(f:\mathbb {R}^n \rightarrow \mathbb {R}\) be a locally Lipschitz definable function and let X be a bounded subset of \(\mathbb {R}^n\). Assume that f has at most \(m\in \mathbb {N}^*\) critical values in \(\overline{X}\). Let \(\psi \) be a desingularizing function of f on X. If \(x:[0,T]\rightarrow X\) with \(T \geqslant 0\) is an absolutely continuous function such that \(x'(t) \in -\partial f(x(t))\) for almost every \(t\in (0,T)\), then
Proof
We first consider the special case where \(0 \notin \partial \tilde{f}(x(t))\) for all \(t\in (0,T)\) where \(\tilde{f}\) is defined as in Proposition 5. Consider the change of variables \(\bar{x} = x \circ \varphi \) where \(\bar{t}=\varphi ^{-1}(t) = \int _0^{t} ds /(\psi ' \circ \tilde{f} \circ x)(s)\) and \(t=\varphi (\bar{t}) = \int _0^{\bar{t}} (\psi ' \circ \tilde{f} \circ \bar{x})(\bar{s}) d\bar{s}\) by the inverse function theorem [82, Theorem 17.7.2]. We have \(\bar{x}'(\bar{t}) = \varphi '(\bar{t})x'(t) \in -(\psi ' \circ \tilde{f} \circ \bar{x})(\bar{t}) \partial f(\bar{x}(\bar{t})) = \pm \partial (\psi \circ \tilde{f})(\bar{x}(\bar{t}))\) for almost every \(\bar{t}\in (0,\overline{T})\), where \(\overline{T} = \varphi ^{-1}(T)\) and the sign is constant. By Proposition 6 and the Cauchy–Schwarz inequality, we thus have
Hence \(\overline{T} \leqslant \vert (\psi \circ \tilde{f}\circ \bar{x})(0)-(\psi \circ \tilde{f}\circ \bar{x})(\overline{T})\vert \) and, since \(\psi \) is concave, we have
We next consider the general case where there may exist \(t\in (0,T)\) such that \(0 \in \partial \tilde{f}(x(t))\), namely \(0< t_1< \cdots< t_{k} < T\), and potentially \((t_k,T)\). For notational convenience, let \(t_0 := 0\) and \(t_{k+1}:=T\) where k is possibly equal to zero. Since \(k \leqslant 2m-1\) and \(\psi \) is concave, we have
\(\square \)
We next propose a discrete version of Proposition 7.
Proposition 8
Let \(f:\mathbb {R}^n \rightarrow \mathbb {R}\) be a definable differentiable function with a locally Lipschitz gradient and let X be a bounded open subset of \(\mathbb {R}^n\). Assume that f has at most \(m\in \mathbb {N}^*\) critical values in \(\overline{X}\) and that \(L>0\) is a Lipschitz constant of f on the convex hull of X. Let \(\psi \) be a desingularizing function of f on X and \(\epsilon >0\). There exists \(\bar{\alpha }>0\) such that, for all \(K \in \mathbb {N}\), \(\alpha _0,\ldots ,\alpha _K \in (0,\bar{\alpha }]\), and \((x_0,\ldots ,x_{K+1}) \in X \times \cdots \times X \times \mathbb {R}^n\) such that \(x_{k+1} = x_k - \alpha _k \nabla f(x_k)\) for \(k = 0,\ldots ,K\), we have
and \(f(x_0)\geqslant \cdots \geqslant f(x_{K+1})\).
Proof
Let \(M>0\) be a Lipschitz constant of \(\nabla f\) with respect to \(\Vert \cdot \Vert \) on the convex hull of \(B(X,1):=X+B(0,1)\) and let \(\bar{\alpha } := \min \{L^{-1},2\epsilon (6+\epsilon )^{-1}M^{-1}\}\). Let \(K \in \mathbb {N}\), \(\alpha _0,\ldots ,\alpha _K \in (0,\bar{\alpha }]\), and \((x_0,\ldots ,x_{K+1}) \in X \times \cdots \times X \times \mathbb {R}^n\) be such that \(x_{k+1} = x_k - \alpha _k \nabla f(x_k)\) for \(k=0,\ldots ,K\). It holds that \(\Vert x_{K+1}-x_K\Vert = \alpha _K\Vert \nabla f(x_K)\Vert \leqslant \bar{\alpha }L \leqslant 1\) and thus \(x_0,\ldots ,x_{K+1} \in B(X,1)\). A bound on the Taylor expansion of f yields
for \(k=0,\ldots ,K\), and thus
We also have
and thus
Note that
Let \(\tilde{f}\) and V be defined as in Proposition 5. Assume that \([f(x_K),f(x_0)]\) excludes the elements of V and the averages of any two consecutive elements of V. Then \(0\notin \partial \tilde{f}(x_k)\) and \(1 \leqslant \Vert \nabla (\psi \circ \tilde{f})(x_k)\Vert = \psi '(\tilde{f}(x_k)) \Vert \nabla \tilde{f}(x_k)\Vert \) for \(k=0,\ldots ,K\). Let \(k \in \{0,\ldots ,K-1\}\). If \(\tilde{f}(x_k) \geqslant \tilde{f}(x_{k+1})\), then multiplying (12) by \(\psi '(\tilde{f}(x_k))\) and using the concavity of \(\psi \), we find that
If \(\tilde{f}(x_k) \leqslant \tilde{f}(x_{k+1})\), then multiplying (13) by \(\psi '(\tilde{f}(x_{k+1}))\) and using the concavity of \(\psi \), we find that
As a result,
We obtain the telescoping sum
Assume that \([f(x_K),f(x_0))\) excludes the elements of V and the averages of any two consecutive elements of V. Since we are excluding a finite number of elements, there exists \(\epsilon >0\) such that \([f(x_K)- \epsilon ,f(x_0))\) satisfies the same property. If \(x_0\) is a local minimum of f on the open set X, then \(\nabla f(x_0) = 0\) by Fermat’s rule. The length of \(x_0,\ldots ,x_{K+1}\) is then equal to zero and the formula obtained in (14) trivially holds. Otherwise, there exists a sequence \((x_0^l)_{l\in \mathbb {N}}\) in \(\mathbb {R}^n\) such that \(f(x_0^l) < f(x_0)\) and \(x_0^l\) converges to \(x_0\). For every \(l \in \mathbb {N}\), consider the sequence \((x^l_k)_{k\in \mathbb {N}}\) such that \(x^l_{k+1} = x^l_k - \alpha _k \nabla f(x_k^l)\) for all \(k \in \mathbb {N}\). Since \(\nabla f\) is continuous, for any fixed \(k \in \{0,\ldots ,K\}\), \(x_k^l\) converges to \(x_k \in X\) and eventually belongs to the open set X. Thus \([f(x^l_K),f(x^l_0)] \subset [f(x_K)-\epsilon ,f(x_0))\) eventually excludes the elements of V and the averages of any two consecutive elements of V. We can apply the formula obtained in (14), namely
Passing to the limit yields
We next consider the general case where
excludes the elements of V and the averages of any two consecutive elements of V. For notational convenience, let \(K_0 := -1\) and \(K_{p+1} := K\). Since \(p \leqslant 2m-1\), we have
An immediate consequence of Propositions 7 and 8 is that bounded continuous subgradient trajectories and bounded discrete gradient trajectories have finite length, as is well known. An easy fact that we will not prove here is that continuous subgradient trajectories of finite length converge to critical points of the objective function under the sole assumption that it is locally Lipschitz. The same holds for discrete subgradient trajectories if the step sizes are not summable.
Propositions 7 and 8 shed light on a seemingly unexplored consequence of the Kurdyka-Łojasiewicz inequality. When considering subgradient trajectories in a bounded region, length, not time nor the number of iterations, guarantees a uniform decrease of the objective function. Indeed, since \(\psi \) is bijective and strictly increasing, one can compose with \(\psi ^{-1}\) while preserving the order of the inequalities in (11) and (13). This is illustrated in Example 2.
Example 2
The function \(f(x_1,x_2) := x_1^3 - x_1^2x_2\) in Figure 1, whose critical points are denoted in black, admits the desingularizing function \(\psi (t) := 3t^{1/3}\) on \(\mathbb {R}^2\). Hence for all sufficiently small step sizes, discrete gradient trajectories initialized in B(0, 0.3) below the critical value decrease by at least \(2\psi ^{-1}(1/9) \geqslant 0.0001\) by the time they exit B(0, 0.8). \(\psi \) is a desingularizing function of f on \(\mathbb {R}^2\) because \(\Vert \nabla (\psi \circ | f| )(x)\Vert \geqslant 1\) for all \((x_1,x_2)\in \mathbb {R}^2\) such that \(f(x_1,x_2)\ne 0\), i.e., \(x_1 \ne 0\) and \(x_1 \ne x_2\). The inequality follows from \(\Vert \nabla f(x_1,x_2)\Vert = ((3x_1^2 - 2x_1x_2)^2 + x_1^4)^{1/2} \geqslant | x_1^3 - x_1^2x_2|^{2/3}\). Indeed, \(((3x_1^2 - 2x_1x_2)^2 + x_1^4)^3 - (x_1^3 - x_1^2x_2)^4 = x_1^6 [((3x_1 - 2x_2)^2 + x_1^2)^3 - x_1^2(x_1 - x_2)^4] = x_1^6 [((x_1 +2x_3)^2 + x_1^2)^3 - x_1^2x_3^4]\) where \(x_3 := x_1-x_2\). By the inequality of arithmetic and geometric means, for any \(c \in (\sqrt{2}/2,1)\) we have
Thus \(((x_1 +2x_3)^2 + x_1^2)^3 \geqslant 54(1-c^2)(2-1/c^2)^2 x_1^2x_3^4 = 9x_1^2x_3^4/2 \geqslant x_1^2x_3^4\) by taking \(c = \sqrt{2/3}\) in order to obtain the equality.
5 Proof of Lemma 1
Let \(f:\mathbb {R}^n \rightarrow \mathbb {R}\) be a locally Lipschitz definable function with bounded continuous subgradient trajectories. Let \(X_0\) be a bounded subset of \(\mathbb {R}^n\). We will show that \(\sigma (X_0) < \infty \) where
We first consider the case with finite time horizon \(T\geqslant 0\). By the definable Morse–Sard theorem [18, Corollary 9], f has finitely many critical values. Notice that \(\sigma _T(X_0) \leqslant \sqrt{T(\sup _{X_0} f - m(f))}\) where m(f) is the smallest critical value of f and
Indeed, by the Cauchy–Schwarz inequality and Propositions 6 and 7, for any feasible point \(x(\cdot )\) of (16) we have
We next treat the case with infinite time horizon. Consider a sequence of feasible points \(x_0(\cdot ), x_1(\cdot ), x_2(\cdot ), \ldots \) of (15) such that \(\int _0^{\infty } \Vert x_k'(t)\Vert dt\) converges to \(\sigma (X_0)\). We proceed to show that the sequence is equicontinuous. Let \(\epsilon >0\) and \(t\geqslant 0\). Consider problem (16) with finite time horizon \(T:=t+\epsilon \). Since \(x_0(\cdot ),x_1(\cdot ),x_2(\cdot ),\ldots \) are feasible points of (16), for all \(s \in [0,T]\) and \(k=0,1,2,\ldots \) we have
All the trajectories \(x_0(\cdot ),x_1(\cdot ),x_2(\cdot ),\ldots \) hence belong to a common ball centered at the origin up to time T. Let \(L>0\) be a Lipschitz constant of f on that ball. As a result, for all \(s \in [t-\delta ,t+\delta ]\) with \(\delta :=\epsilon /(2L)\) and for all \(k\in \mathbb {N}\), we have
where we remind the reader that \(\Vert \cdot \Vert _*\) is the dual norm of \(\Vert \cdot \Vert \). It follows that \(x_0(\cdot ),x_1(\cdot ),x_2(\cdot ),\ldots \) is equicontinuous on \(\mathbb {R}_+\). In addition, (18a)–(18c) imply that, for all \(t\geqslant 0\), the sequence \(x_0(t),x_1(t),x_2(t),\ldots \) is bounded. The Arzelà-Ascoli theorem [9, Theorem 1 p. 13] implies that there exists a subsequence (again denoted \(x_k(\cdot )\)) converging uniformly over compact intervals to a continuous function \(x:\mathbb {R}_+\rightarrow \mathbb {R}^n\).
We next show that \(x(\cdot )\) is a continuous subgradient trajectory of f. Let \(T\geqslant 0\). By virtue of (18a)–(18c) and local Lipschitz continuity of f, the restrictions of \(x'_0(\cdot ),x'_1(\cdot ),x'_2(\cdot ),\ldots \) to [0, T] lie in a ball of the dual space of \(L^1([0,T],\mathbb {R}^n)\), namely \(L^{\infty }([0,T],\mathbb {R}^n)\). By the Banach-Alaoglu theorem [9, Theorem 3 p. 13], there exists a subsequence (again denoted \(x_k'(\cdot )\)) that converges weakly\(^{*}\) to a function \(y(\cdot )\) in \(L^{\infty }([0,T],\mathbb {R}^n)\). Together with \(L^{\infty }([0,T],\mathbb {R}^n)\subset L^1([0,T],\mathbb {R}^n)\), we find that \(x_k'(\cdot )\) converges weakly to \(y(\cdot )\) in \(L^1([0,T],\mathbb {R}^n)\). Since \(x_k(t)-x_k(s) = \int _s^t x_k'(\tau )d\tau \) for all \(0\leqslant s \leqslant t \leqslant T\), we have \(x(t)-x(s) = \int _s^t y(\tau )d\tau \). As a result, \(x'(t) = y(t)\) for almost every \(t\in (0,T)\). According to [9, Convergence Theorem p. 60], it follows that \(x'(t) \in -\partial f(x(t))\) for almost every \(t\in (0,T)\). As \(T \geqslant 0\) was arbitrary, we have \(x'(t) \in -\partial f(x(t))\) for almost every \(t>0\).
Since f is definable and has bounded continuous subgradient trajectories, by Proposition 7\(x(\cdot )\) has finite length and converges to a critical point \(x^*\) of f. Let \(\epsilon >0\) and let \(m \in \mathbb {N}^*\) be the number of critical values of f in \(B(\overline{x(\mathbb {R}_+)},\epsilon )\). Let \(\psi \) be a desingularizing function of f on \(B(\overline{x(\mathbb {R}_+)},\epsilon )\). Since f is continuous, there exists \(\delta \in (0,\epsilon /2)\) such that
Let \(t^*\geqslant 0\) be such that \(\Vert x(t)-x^*\Vert \leqslant \delta /2\) for all \(t\geqslant t^*\). By the uniform convergence of \(x_k(\cdot )\), we have that \(\Vert x_k(t)-x(t)\Vert \leqslant \delta /2\) for all \(t\in [0,t^*]\) for all k large enough. Hence \(\Vert x_k(t^*) - x^*\Vert \leqslant \Vert x_k(t^*)-x(t^*)\Vert +\Vert x(t^*)-x^*\Vert \leqslant \delta /2 + \delta /2 = \delta \). If \(T_k:= \inf \{ t \geqslant t^*: x_k(t) \notin \mathring{B}(x^*,\epsilon )\}<\infty \), then
Above, (20a) through (20d) rely on the fact that \(\psi ^{-1}\) is increasing. (20a) is due to \(\delta < \epsilon /2\). (20b) holds because \(\Vert x_k(T_k)-x^*\Vert \geqslant \epsilon \) by continuity of \(x_k(\cdot )\) and \(x_k(t^*) \in B(x^*,\delta )\). (20c) is a consequence of the triangular inequality. (20d) holds because \(x_k(\cdot )\) is absolutely continuous. (20e) is due to Proposition 7 and the fact that \(x_k(t) \in B(x^*,\epsilon )\) for all \(t \in [t^*,T_k]\) by continuity of \(x_k(\cdot )\). Finally, (20f) is due to \(x_k(t^*)\in B(x^*,\delta )\) and (19). Since \(x_k(t) \in B(\overline{x(\mathbb {R}_+)},\epsilon )\) for all \(t\in [0,T_k]\) and \(x_k(T_k)\) belongs to
by Proposition 7 and the definition of \(\sigma (\cdot )\) in (15) we have
Note that the inequality still holds if \(T_k = \infty \). By taking the limit, we get
It now suffices to replace \(X_0\) by \(X_1\) and repeat the proof starting below (17d). A maximizing sequence \(\bar{x}_k(\cdot )\) corresponding to \(\sigma (X_1)\) converges to a continuous subgradient trajectory \(\bar{x}(\cdot )\) whose initial point lies in the compact set \(X_1\). If \(X_1 \ne \emptyset \), then the critical value \(f(\lim _{t\rightarrow \infty } \bar{x}(t))\) is less than or equal to \(f(x^*) - m\psi ^{-1}(\epsilon /(4m)) < f(x^*)\). By the definable Morse–Sard theorem [18, Corollary 9], f has finitely many critical values. Thus, it is eventually the case that one of the sets \(X_0,X_1,\ldots \) is empty. We conclude that \(\sigma (X_0)<\infty \) by the above recursive formula.
6 Proof of Theorem 1
(\(1\Longrightarrow 2\)) We prove the contrapositive. Assume that there exists \(0< T \leqslant \infty \) and a differentiable function \(x:[0,T)\rightarrow \mathbb {R}^n\) such that
for which, for all \(c>0\), there exists \(t\in [0,T)\) such that \(\Vert x(t)\Vert > c\). Let \(x_0:= x(0)\). Let \(\bar{\alpha }\) and c be some positive constants. Let \(\tilde{t} \geqslant 0\) be such that \(\Vert x(\tilde{t})\Vert \geqslant c+2\). By Proposition 4 and Remark 2, there exists \(\tilde{\alpha }\in (0,\bar{\alpha }]\) such that for all \(\alpha \in (0,\tilde{\alpha }]\), the sequence \(x_0,x_1,x_2,\ldots \in \mathbb {R}^n\) defined by \(x_{k+1} = x_k -\alpha \nabla f(x_k)\) for all \(k \in \mathbb {N}\) satisfies \(\Vert x_k-x(k\alpha )\Vert \leqslant 1/2\) for all \(k\in \{0,\ldots , \lfloor \tilde{t}/\alpha \rfloor \}\). We use the notation \(\lfloor t \rfloor \) to denote the floor of a real number t which is the unique integer such that \(\lfloor t \rfloor \leqslant t < \lfloor t \rfloor + 1\). If \(\tilde{k} = \lfloor \tilde{t}/\alpha \rfloor \), then \(\Vert x_{\tilde{k}} - x(\tilde{t})\Vert \leqslant \Vert x_{\tilde{k}}-x(\tilde{k}\alpha )\Vert +\Vert x(\tilde{k}\alpha )-x(\tilde{t})\Vert \leqslant 1/2 + \tilde{L}\vert \tilde{k}\alpha -\tilde{t}\vert \leqslant 1/2 + \tilde{L}\alpha \) where \(\tilde{L}>0\) is a Lipschitz constant of f on the convex hull of \(x([\tilde{t}-\tilde{\alpha },\tilde{t}])\). Let \(\alpha _0,\alpha _1,\alpha _2,\ldots \in (0,\bar{\alpha }]\) be the constant sequence equal to \(\min \{\tilde{\alpha }, 1/(2\tilde{L})\}\) and consider the sequence \(x_0,x_1,x_2,\ldots \in \mathbb {R}^n\) defined by \(x_{k+1} = x_k -\alpha _k \nabla f(x_k)\) for all \(k \in \mathbb {N}\). By the triangular inequality, we have \(\Vert x_{\tilde{k}}\Vert \geqslant \Vert x(\tilde{t})\Vert - \Vert x_{\tilde{k}}-x(\tilde{t})\Vert \geqslant c+2 - 1/2 - 1/2>c\) where \(\tilde{k}:= \lfloor \tilde{t}/\alpha \rfloor \).
(\(2 \Longrightarrow 3\)) Let \(X_0\) be a bounded subset of \(\mathbb {R}^n\). We will show that there exists \(\bar{\alpha }>0\) such that \(\sigma (X_0,\bar{\alpha })<\infty \) where
Let \(\Phi :\mathbb {R}_+ \times \mathbb {R}^n \rightarrow \mathbb {R}^n\) be the gradient flow of f defined for all \((t,x_0) \in \mathbb {R}_+ \times \mathbb {R}^n\) by \(\Phi (t,x_0) := x(t)\) where \(x(\cdot )\) is the unique continuous gradient trajectory of f initialized at \(x_0\). Uniqueness follows from the Picard-Lindelöf theorem [29, Theorem 3.1 p. 12]. Let C be the set of critical points of f in \(\overline{\Phi (\mathbb {R}_+,X_0)}\). If \(X_0 \subset C\), then we have \(\sigma (X_0,\bar{\alpha }) \leqslant 0\) for all \(\bar{\alpha }>0\) and there is nothing left to prove. Otherwise, since C is closed by [28, 2.1.5 Proposition p. 29], there exists \(\epsilon >0\) be such that \(X_0{\setminus } \mathring{B}(C,\epsilon /6) \ne \emptyset \) where \(\mathring{B}(C,\epsilon /6):= C + \mathring{B}(0,\epsilon /6)\). It is safe to assume this from now on.
Let \(\psi \) be a desingularizing function of f on \(\mathring{B}(\overline{\Phi }_0,\epsilon )\), where we use the shorthand \(\Phi _0:= \Phi (\mathbb {R}_+,X_0)\). By the definable Morse–Sard theorem [18, Corollary 9], f has finitely many critical values. Let \(m \in \mathbb {N}\) be the number of critical values of f in \(B(\overline{\Phi }_0,\epsilon )\). Note that \(m \geqslant 1\) due to Proposition 7 and the fact that \(X_0 \ne \emptyset \). Since f is continuous and C is compact by Lemma 1, there exists \(\delta \in (0,\epsilon /2)\) such that
Note that \(\mathring{B}(\overline{\Phi }_0,\epsilon )\) is bounded due to Lemma 1. Thus, by Proposition 8, there exists \(\alpha _\delta \in (0,\delta /(5mL)]\) such that, for all \(K \in \mathbb {N}^*\), \(\alpha _0,\ldots ,\alpha _{K-1} \in (0,\alpha _\delta ]\), and \((x_0,\ldots ,x_K) \in \mathring{B}(\overline{\Phi }_0,\epsilon ) \times \cdots \times \mathring{B}(\overline{\Phi }_0,\epsilon ) \times \mathbb {R}^n\) such that \(x_{k+1} = x_k - \alpha _k \nabla f(x_k)\) for \(k = 0,\ldots ,K-1\), we have
Since \(\nabla f\) is continuous, its norm attains its infimum \(\nu \) on the nonempty compact set \(\overline{\Phi }_0 {\setminus } \mathring{B}(C,\delta /3)\). It is nonempty because \(\overline{\Phi }_0 {\setminus } \mathring{B}(C,\delta /3) \supset X_0{\setminus } \mathring{B}(C,\epsilon /6) \ne \emptyset \) and \(\delta < \epsilon /2\). If \(\nu =0\), then there exists \(x^* \in \overline{\Phi }_0 {\setminus } \mathring{B}(C,\delta /3)\) such that \(\Vert \nabla f(x^*)\Vert = 0\). Then \(x^*\in C {\setminus } \mathring{B}(C,\delta /3)\), which is a contradiction. We thus have \(\nu >0\). Hence we may define \(T:= 2\sigma (X_0)/\nu \) where \(\sigma (X_0)\) is defined in (15) and is finite by Lemma 1. Note that \(\sigma (X_0)>0\) and thus \(T>0\) because \(X_0\not \subset C\). By Proposition 4, there exists \(\bar{\alpha } \in (0,\alpha _\delta ]\) such that for any feasible point \(((x_k)_{k\in \mathbb {N}}, (\alpha _k)_{k\in \mathbb {N}})\) of (21), the continuous gradient trajectory \(x:\mathbb {R}_+\rightarrow \mathbb {R}^n\) of f initialized at \(x_0\) satisfies
Now suppose that \(\Vert x'(t)\Vert \geqslant 2\sigma (X_0)/T\) for all \(t\in (0,T)\). Then we obtain the following contradiction
Hence, there exists \(t^* \in (0,T)\) such that \(\Vert x'(t^*)\Vert = \Vert \nabla f(x(t^*))\Vert < 2\sigma (X_0)/T = 2\sigma (X_0)/(2\sigma (X_0)/\nu ) = \nu \). Since \(x(t^*) \in \Phi (\mathbb {R}_+,X_0) \subset \overline{\Phi }_0\) and the infimum of the norm of \(\nabla f\) on \(\overline{\Phi }_0 {\setminus } \mathring{B}(C,\delta /3)\) is equal to \(\nu \), it must be that \(x(t^*) \in \mathring{B}(C,\delta /3)\). Hence there exists \(x^* \in C\) such that \(\Vert x(t^*)-x^*\Vert \leqslant \delta /3\).
If \(\sum _{k=0}^{\infty } \alpha _k \leqslant T\), then by (24) we have \(x_k \in B(\overline{\Phi }_0,\delta /3)\) for all \(k \in \mathbb {N}\). Otherwise, since \(\alpha _k \leqslant \bar{\alpha } \leqslant \alpha _\delta \leqslant \delta /(5\,mL) \leqslant \delta /(3\,L)\) for all \(k \in \mathbb {N}\), there exists \(k^* \in \mathbb {N}\) such that \(t_{k^*}:= \sum _{k=0}^{k^*-1} \alpha _k \in [ t^* - \delta /(3\,L), t^*]\), where \(\sum _{k=0}^{k^*-1} \alpha _k = 0\) if \(k^* = 0\). Thus \(\Vert x_{k^*}-x^*\Vert \leqslant \Vert x_{k^*}-x(t_{k^*})\Vert + \Vert x(t_{k^*}) - x(t^*)\Vert + \Vert x(t^*)-x^*\Vert \leqslant \delta /3 + L |t_{k^*}-t^* |+ \delta /3 \leqslant \delta /3+\delta /3+\delta /3 = \delta \). If \(K:= \inf \{ k \geqslant k^*: x_k \notin \mathring{B}(C,\epsilon )\}<\infty \), then
Above, the arguments of \(\psi ^{-1}\) in (25a) are equal. (25b) through (25e) rely on the fact that \(\psi ^{-1}\) is an increasing function. (25b) is due to \(\delta <\epsilon /2\). (25c) holds because \(x_K \notin \mathring{B}(C,\epsilon )\), \(x^* \in C\), and \(x_{k^*} \in B(x^*,\delta )\). (25d) and (25e) are consequences of the triangular inequality. (25f) is due to the length formula (23) and the fact that \(x_{k^*},\ldots ,x_{K-1} \in \mathring{B}(C,\epsilon ) \subset \mathring{B}(\overline{\Phi }_0,\epsilon )\). Finally, (25g) is due to \(x_{k^*}\in B(C,\delta )\) and (22). We remark that \(K\geqslant k^*+2\) since \(\Vert x_{k^*+1}-x^*\Vert \leqslant \Vert x_{k^*+1}-x_{k^*}\Vert +\Vert x_{k^*}-x^*\Vert \leqslant \alpha _{k^*}\Vert \nabla f(x_{k^*})\Vert +\delta \leqslant (\delta /(5\,mL))L+\delta < \epsilon \). Since \(x_0,\ldots ,x_{K-2} \in \mathring{B}(\overline{\Phi }_0,\epsilon )\) and \(x_{K-1}\) belongs to
by the length formula (23) and the definition of \(\sigma (\cdot ,\cdot )\) in (21) we have
Note that the inequality still holds if \(K = \infty \) or \(\sum _{k=0}^{\infty } \alpha _k \leqslant T\). Hence
It now suffices to replace \(X_0\) by \(X_1\) and repeat the proof starting below (21). Since \(f(\Phi (t,x_1)) \leqslant f(\Phi (0,x_1)) \leqslant \max _{C} f - m\psi ^{-1}(\epsilon /(40\,m))< \max _{C} f\) for all \(t\geqslant 0\) and \(x_1\in X_1\), the maximal critical value of f in \(\overline{\Phi (\mathbb {R}_+,X_1)}\) is less than the maximal critical value of f in \(\overline{\Phi (\mathbb {R}_+,X_0)}\). By the definable Morse–Sard theorem [18, Corollary 9], f has finitely many critical values. Thus, it is eventually the case that one of the sets \(X_0,X_1,\ldots \) is empty. In order to conclude, one simply needs to choose an upper bound on the step sizes \(\hat{\alpha }\) corresponding to \(X_1\) that is less than or equal to the upper bound \(\bar{\alpha }\) used for \(X_0\). \(\sigma (X_0,\cdot )\) is finite when evaluated at the last upper bound thus obtained. Indeed, the above recursive formula still holds if we replace \(\bar{\alpha }\) by any \(\alpha \in (0,\bar{\alpha }]\). In particular, we may take \(\alpha := \hat{\alpha }\).
(\(3 \Longrightarrow 1\)) Obvious.
Change history
12 June 2023
A Correction to this paper has been published: https://doi.org/10.1007/s10107-023-01972-2
Notes
Any nonnegative decreasing sequence \(u_0,u_1,u_2,\ldots \), and in particular the minimum gradient norm, satisfies \((k/2+1)u_k \leqslant (k -\lfloor k/2 \rfloor +1)u_k \leqslant \sum _{i=\lfloor k/2\rfloor }^k u_i \leqslant \sum _{i=\lfloor k/2\rfloor }^\infty u_i\) for all \(k\in \mathbb {N}\).
References
Absil, P.A., Mahony, R., Andrews, B.: Convergence of the iterates of descent methods for analytic cost functions. SIAM J. Optim. 16(2), 531–547 (2005)
Akaike, H.: On a successive transformation of probability distribution and its application to the analysis of the optimum gradient method. Ann. Inst. Stat. Math. 11(1), 1–16 (1959)
Armijo, L.: Minimization of functions having Lipschitz continuous first partial derivatives. Pac. J. Math. 16(1), 1–3 (1966)
Arora, S., Cohen, N., Hazan, E.: On the optimization of deep networks: implicit acceleration by overparameterization. In: ICML, pp. 244–253. PMLR (2018)
Arora, S., Cohen, N., Hu, W., Luo, Y.: Implicit regularization in deep matrix factorization. In: NeurIPS, pp. 7413–7424 (2019)
Attouch, H., Bolte, J., Redont, P., Soubeyran, A.: Proximal alternating minimization and projection methods for nonconvex problems: an approach based on the kurdyka-łojasiewicz inequality. Math. Oper. Res. 35(2), 438–457 (2010)
Attouch, H., Bolte, J., Svaiter, B.F.: Convergence of descent methods for semi-algebraic and tame problems: proximal algorithms, forward–backward splitting, and regularized Gauss–Seidel methods. Math. Program. 137(1), 91–129 (2013)
Attouch, H., Buttazzo, G., Michaille, G.: Variational analysis in Sobolev and BV spaces: applications to PDEs and optimization. SIAM (2014)
Aubin, J.P., Cellina, A.: Differential inclusions: set-valued maps and viability theory, vol. 264. Springer, Berlin (1984)
Bah, B., Rauhut, H., Terstiege, U., Westdickenberg, M.: Learning deep linear neural networks: Riemannian gradient flows and convergence to global minimizers. Inf. Inference J. IMA 11(1), 307–353 (2022)
Baillon, J.: Un exemple concernant le comportement asymptotique de la solution du problème \(du/dt + \partial \varphi (u) \ni 0\). J. Funct. Anal. 28(3), 369–376 (1978)
Baldi, P., Hornik, K.: Neural networks and principal component analysis: learning from examples without local minima. Neural Netw. 2(1), 53–58 (1989)
Bauschke, H.H., Bolte, J., Teboulle, M.: A descent lemma beyond Lipschitz gradient continuity: first-order methods revisited and applications. Math. Oper. Res. 42(2), 330–348 (2017)
Bellman, R.E.: Dynamic Programming. Princeton University Press, Princeton (1957)
Böhm, A., Daniilidis, A.: Ubiquitous algorithms in convex optimization generate self-contracted sequences. J. Conv. Anal. 29, 119–128 (2022)
Bochnak, J., Coste, M., Roy, M.F.: Real Algebraic Geometry, vol. 36. Springer, Berlin (2013)
Bolte, J., Daniilidis, A., Lewis, A.: The Łojasiewicz inequality for nonsmooth subanalytic functions with applications to subgradient dynamical systems. SIAM J. Optim. 17(4), 1205–1223 (2007)
Bolte, J., Daniilidis, A., Lewis, A., Shiota, M.: Clarke subgradients of stratifiable functions. SIAM J. Optim. 18(2), 556–572 (2007)
Bolte, J., Daniilidis, A., Ley, O., Mazet, L.: Characterizations of Łojasiewicz inequalities: subgradient flows, talweg, convexity. Trans. Am. Math. Soc. 362(6), 3319–3363 (2010)
Bolte, J., Pauwels, E.: Conservative set valued fields, automatic differentiation, stochastic gradient methods and deep learning. Math. Program. pp. 1–33 (2020)
Bolte, J., Sabach, S., Teboulle, M.: Proximal alternating linearized minimization for nonconvex and nonsmooth problems. Math. Program. 146(1), 459–494 (2014)
Bolte, J., Sabach, S., Teboulle, M., Vaisbourd, Y.: First order methods beyond convexity and Lipschitz gradient continuity with applications to quadratic inverse problems. SIAM J. Optim. 28(3), 2131–2151 (2018)
Brezis, H.: Opérateurs maximaux monotones et semi-groupes de contractions dans les espaces de Hilbert. Elsevier, New York (1973)
Bruck, R.E., Jr.: Asymptotic convergence of nonlinear contraction semigroups in Hilbert space. J. Funct. Anal. 18(1), 15–26 (1975)
Candes, E.J., Tao, T.: Decoding by linear programming. IEEE Trans. Inf. Theory 51(12), 4203–4215 (2005)
Cauchy, A.: Méthode générale pour la résolution des systemes d’équations simultanées. C. R. Sci. Paris 25(1847), 536–538 (1847)
Chitour, Y., Liao, Z., Couillet, R.: A geometric approach of gradient descent algorithms in linear neural networks. Mathematical Control and Related Fields (2022)
Clarke, F.H.: Optimization and nonsmooth analysis. SIAM Classics in Applied Mathematics (1990)
Coddington, E.A., Levinson, N.: Theory of Ordinary Differential Equations. Tata McGraw-Hill Education, New York (1955)
Curry, H.B.: The method of steepest descent for non-linear minimization problems. Q. Appl. Math. 2(3), 258–261 (1944)
Daniilidis, A., David, G., Durand-Cartagena, E., Lemenant, A.: Rectifiability of self-contracted curves in the Euclidean space and applications. J. Geom. Anal. 25(2), 1211–1239 (2015)
Davis, D., Drusvyatskiy, D., Kakade, S., Lee, J.D.: Stochastic subgradient method converges on tame functions. Found. Comput. Math. 20(1), 119–154 (2020)
Drusvyatskiy, D., Ioffe, A.D.: Quadratic growth and critical point stability of semi-algebraic functions. Math. Program. 153(2), 635–653 (2015)
Drusvyatskiy, D., Ioffe, A.D., Lewis, A.S.: Curves of descent. SIAM J. Control Optim. 53(1), 114–138 (2015)
Du, S.S., Hu, W., Lee, J.D.: Algorithmic regularization in learning deep homogeneous models: layers are automatically balanced. NeurIPS (2018)
Du, S.S., Zhai, X., Poczos, B., Singh, A.: Gradient descent provably optimizes over-parameterized neural networks. ICLR (2019)
D’Acunto, D., Kurdyka, K.: Bounding the length of gradient trajectories. In: Annales Polonici Mathematici, vol. 127, pp. 13–50. Instytut Matematyczny Polskiej Akademii Nauk (2021)
Forsythe, G.E., Motzkin, T.S.: Asymptotic properties of the optimum gradient method. Bull. Am. Math. Soc. 57, 183 (1951)
Gabrielov, A.M.: Projections of semi-analytic sets. Funct. Anal. Appl. 2(4), 282–291 (1968)
Garrigos, G.: Descent dynamical systems and algorithms for tame optimization, and multi-objective problems. Ph.D. thesis, Université Montpellier; Universidad técnica Federico Santa María (Valparaiso) (2015)
Ge, R., Huang, F., Jin, C., Yuan, Y.: Escaping from saddle points—online stochastic gradient for tensor decomposition. In: Conference on Learning Theory, pp. 797–842. PMLR (2015)
Gilbert, J.C.: Fragments d’optimisation différentiable – théories et algorithmes (2021)
Goldstein, A.A.: On steepest descent. J. Soc. Ind. Appl. Math. Ser. A Control 3(1), 147–151 (1965)
Gupta, C., Balakrishnan, S., Ramdas, A.: Path length bounds for gradient descent and flow. J. Mach. Learn. Res. 22(68), 1–63 (2021)
Jensen, J.L.W.V.: Sur les fonctions convexes et les inégalités entre les valeurs moyennes. Acta mathematica 30(1), 175–193 (1906)
Josz, C., Li, X.: Certifying the absence of spurious local minima at infinity. Submitted (2022)
Kantorovich, L.V.: Functional analysis and applied mathematics. Uspekhi Matematicheskikh Nauk 3(6), 89–185 (1948)
Kawaguchi, K.: Deep learning without poor local minima. NeurIPS (2016)
Kurdyka, K.: On gradients of functions definable in o-minimal structures. In: Annales de l’institut Fourier, vol. 48, pp. 769–783 (1998)
Kurdyka, K., Mostowski, T., Parusinski, A.: Proof of the gradient conjecture of R. Thom. Annals of Mathematics pp. 763–792 (2000)
Kurdyka, K., Parusiski, A.: Quasi-convex decomposition in o-minimal structures. Application to the gradient conjecture. Singularity theory and its applications, 137177. Adv. Stud. Pure Math 43 (2006)
Lang, S.: Algebra, vol. 211. Springer, Berlin (2012)
Lee, C.P., Wright, S.: First-order algorithms converge faster than \( o (1/k) \) on convex problems. In: ICML, pp. 3754–3762. PMLR (2019)
Lee, J.D., Panageas, I., Piliouras, G., Simchowitz, M., Jordan, M.I., Recht, B.: First-order methods almost always avoid strict saddle points. Math. Program. pp. 311–337 (2020)
Lee, J.D., Simchowitz, M., Jordan, M.I., Recht, B.: Gradient descent only converges to minimizers. In: Conference on Learning Theory (2016)
Lemaréchal, C.: Cauchy and the gradient method. Doc. Math. Extra 251(254), 10 (2012)
Li, G., Pong, T.K.: Calculus of the exponent of Kurdyka–Łojasiewicz inequality and its applications to linear convergence of first-order methods. Found. Comput. Math. 18(5), 1199–1232 (2018)
Li, S., Li, Q., Zhu, Z., Tang, G., Wakin, M.B.: The global geometry of centralized and distributed low-rank matrix recovery without regularization. IEEE Signal Process. Lett. 27, 1400–1404 (2020)
Loi, T.L.: Łojasiewicz inequalities in o-minimal structures. Manuscr. Math. 150(1), 59–72 (2016)
Łojasiewicz, S.: Une propriété topologique des sous-ensembles analytiques réels. Les Équations aux Dérivées Partielles (1963)
Łojasiewicz, S.: Ensembles semi-analytiques. IHES notes (1965)
Łojasiewicz, S.: Sur les trajectoires du gradient d’une fonction analytique. Seminari di geometria 1982–1983, 115–117 (1984)
Manselli, P., Pucci, C.: Maximum length of steepest descent curves for quasi-convex functions. Geometriae Dedicata 38(2), 211–227 (1991)
Miller, C.: Expansions of the real field with power functions. Ann. Pure Appl. Log. 68(1), 79–94 (1994)
Morse, A.P.: The behavior of a function on its critical set. Ann. Math. pp. 62–70 (1939)
Nesterov, Y.: How to make the gradients small. Optim. Math. Optim. Soc. Newsl. 88, 10–11 (2012)
Nesterov, Y.: Lectures on Convex Optimization, vol. 137. Springer, Berlin (2018)
Nielsen, O.A.: An Introduction to Integration and Measure Theory, vol. 17. Wiley-Interscience, Hoboken (1997)
Nocedal, J., Wright, S.: Numerical Optimization. Springer, Berlin (2006)
Panageas, I., Piliouras, G.: Gradient descent only converges to minimizers: non-isolated critical points and invariant regions. ITCS (2017)
Panageas, I., Piliouras, G., Wang, X.: First-order methods almost always avoid saddle points: the case of vanishing step-sizes. NeurIPS (2019)
Patel, V., Berahas, A.S.: Gradient descent in the absence of global Lipschitz continuity of the gradients: convergence, divergence and limitations of its continuous approximation. arXiv preprint arXiv:2210.02418 (2022)
Pemantle, R.: Nonconvergence to unstable points in urn models and stochastic approximations. Ann. Probab. 18(2), 698–712 (1990)
Pillay, A., Steinhorn, C.: Definable sets in ordered structures. I. Trans. Am. Math. Soc. 295(2), 565–592 (1986)
Polyak, B.T.: Gradient methods for the minimisation of functionals. USSR Comput. Math. Math. Phys. 3(4), 864–878 (1963)
Polyak, B.T.: Introduction to Optimization, vol. 1. Optimization Software. Inc., Publications Division, New York (1987)
Rolin, J.P., Speissegger, P., Wilkie, A.: Quasianalytic Denjoy–Carleman classes and o-minimality. J. Am. Math. Soc. 16(4), 751–777 (2003)
Rudin, W., et al.: Principles of Mathematical Analysis, vol. 3. McGraw-hill, New York (1964)
Sard, A.: The measure of the critical values of differentiable maps. Bull. Am. Math. Soc. 48(12), 883–890 (1942)
Seidenberg, A.: A new decision method for elementary algebra. Ann. Math. pp. 365–374 (1954)
Shub, M.: Global Stability of Dynamical Systems. Springer, Berlin (2013)
Tao, T.: Analysis II. Texts and Readings in Mathematics, vol. 38. Hindustan Book Agency, New Delhi (2006)
Tarski, A.: A decision method for elementary algebra and geometry: prepared for publication with the assistance of JCC McKinsey (1951)
Temple, G.: The general theory of relaxation methods applied to linear systems. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 169(939), 476–500 (1939)
Valavi, H., Liu, S., Ramadge, P.: Revisiting the landscape of matrix factorization. In: International Conference on Artificial Intelligence and Statistics, pp. 1629–1638. PMLR (2020)
Valavi, H., Liu, S., Ramadge, P.J.: The landscape of matrix factorization revisited. arXiv preprint arXiv:2002.12795 (2020)
van den Dries, L.: Remarks on Tarski’s problem concerning (\(\mathbb{R}\),+,\(\cdot \), exp). In: Studies in Logic and the Foundations of Mathematics, vol. 112, pp. 97–121. Elsevier (1984)
van den Dries, L.: A generalization of the Tarski-Seidenberg theorem, and some nondefinability results. Bullet. AMS 15(2), 189–193 (1986)
van den Dries, L.: Tame Topology and o-Minimal Structures, vol. 248. Cambridge University Press, Cambridge (1998)
van den Dries, L., Macintyre, A., Marker, D.: The elementary theory of restricted analytic fields with exponentiation. Ann. Math. 140(1), 183–205 (1994)
van den Dries, L., Miller, C.: Geometric categories and o-minimal structures. Duke Math. J. 84(2), 497–540 (1996)
van Den Dries, L., Speissegger, P.: The real field with convergent generalized power series. Trans. Am. Math. Soc. 350(11), 4377–4421 (1998)
Wilkie, A.J.: Model completeness results for expansions of the ordered field of real numbers by restricted Pfaffian functions and the exponential function. J. Am. Math. Soc. 9(4), 1051–1094 (1996)
Wolfe, P.: Convergence conditions for ascent methods. SIAM Rev. 11(2), 226–235 (1969)
Ye, T., Du, S.S.: Global convergence of gradient descent for asymmetric low-rank matrix factorization. NeurIPS 34, 1429–1439 (2018)
Zoutendijk, G.: Nonlinear programming, computational methods. Integer and nonlinear programming pp. 37–86 (1970)
Acknowledgements
I am grateful to the reviewers and editors for their precious time and valuable feedback. Many thanks to Lexiao Lai and Xiaopeng Li for fruitful discussions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work was supported by NSF EPCN grant 2023032 and ONR grant N00014-21-1-2282.
The original online version of this article was revised: Due to various inaccuracies were corrected, including typographical mistakes, missing or incorrect references, hyperlinks, and inconsistent notations in the proofs.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Josz, C. Global convergence of the gradient method for functions definable in o-minimal structures. Math. Program. 202, 355–383 (2023). https://doi.org/10.1007/s10107-023-01937-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10107-023-01937-5