Abstract
We consider the sum-of-squares hierarchy of approximations for the problem of minimizing a polynomial f over the boolean hypercube \({{\mathbb {B}}^{n}=\{0,1\}^n}\). This hierarchy provides for each integer \(r \in {\mathbb {N}}\) a lower bound \(\smash {f_{({r})}}\) on the minimum \(f_{\min }\) of f, given by the largest scalar \(\lambda \) for which the polynomial \(f - \lambda \) is a sum-of-squares on \({\mathbb {B}}^{n}\) with degree at most 2r. We analyze the quality of these bounds by estimating the worst-case error \(f_{\min }- \smash {f_{({r})}}\) in terms of the least roots of the Krawtchouk polynomials. As a consequence, for fixed \(t \in [0, 1/2]\), we can show that this worst-case error in the regime \(r \approx t \cdot n\) is of the order \(1/2 - \sqrt{t(1-t)}\) as n tends to \(\infty \). Our proof combines classical Fourier analysis on \({\mathbb {B}}^{n}\) with the polynomial kernel technique and existing results on the extremal roots of Krawtchouk polynomials. This link to roots of orthogonal polynomials relies on a connection between the hierarchy of lower bounds \(\smash {f_{({r})}}\) and another hierarchy of upper bounds \(\smash {f^{({r})}}\), for which we are also able to establish the same error analysis. Our analysis extends to the minimization of a polynomial over the q-ary cube \(\mathbb ({\mathbb {Z}}/ q{\mathbb {Z}})^{n}\). Furthermore, our results apply to the setting of matrix-valued polynomials.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
We consider the problem of minimizing a polynomial \(f \in {\mathbb {R}}[x]\) of degree \(d \le n\) over the n-dimensional boolean hypercube \({\mathbb {B}}^{n} = \{0, 1\}^n\), i.e., of computing
This optimization problem is NP-hard in general. Indeed, as is well-known, one can model an instance of max-cut on the complete graph \(K_n\) with edge weights \(w=(w_{ij})\) as a problem of the form (1) by setting:
As another example one can compute the stability number \(\alpha (G)\) of a graph \(G=(V,E)\) via the program
One may replace the boolean cube \({\mathbb {B}}^{n}=\{0,1\}^n\) by the discrete cube \(\{\pm 1\}^n\), in which case maximizing a quadratic polynomial \(x^\top Ax\) has many other applications, e.g., to max-cut [13], to the cut norm [1], or to correlation clustering [4]. Approximation algorithms are known depending on the structure of the matrix A (see [1, 6, 13]), but the problem is known to be NP-hard to approximate within any factor less than 13/11 [2].
Problem (1) also permits to capture polynomial optimization over a general region of the form \({\mathbb {B}}^{n}\cap P\) where P is a polyhedron [17] and thus a broad range of combinatorial optimization problems. The general intractability of problem (1) motivates the search for tractable bounds on the minimum value in (1). In particular, several lift-and-project methods have been proposed, based on lifting the problem to higher dimension by introducing new variables modelling higher degree monomials. Such methods also apply to constrained problems on \({\mathbb {B}}^{n}\) where the constraints can be linear or polynomial; see, e.g., [3, 18, 27, 35, 39, 44]. In [21] it is shown that the sums-of-squares hierarchy of Lasserre [18] in fact refines the other proposed hierarchies. As a consequence the sum-of-squares approach for polynomial optimization over \({\mathbb {B}}^{n}\) has received a great deal of attention in the recent years and there is a vast literature on this topic. Among many other results, let us just mention its use to show lower bounds on the size of semidefinite programming relaxations for combinatorial problems such as max-cut, maximum stable sets and TSP in [25], and the links to the Unique Game Conjecture in [5]. For background about the sum-of-squares hierarchy applied to polynomial optimization over general semialgebraic sets we refer to [16, 19, 24, 32] and further references therein.
This motivates the interest in gaining a better understanding of the quality of the bounds produced by the sum-of-squares hierarchy. Our objective in this paper is to investigate such an error analysis for this hierarchy applied to binary polynomial optimization as in (1).
1.1 The sum-of-squares hierarchy on the boolean cube
The sum-of-squares hierarchy was introduced by Lasserre [16, 18] and Parrilo [32] as a tool to produce tractable lower bounds for polynomial optimization problems. When applied to problem (1) it provides for any integer \(r\in {\mathbb {N}}\) a lower bound \(\smash {f_{({r})}} \le f_{\min }\) on \(f_{\min }\), given by:
The condition ‘\(f(x)-\lambda \) is a sum-of-squares of degree at most 2r on \({\mathbb {B}}^{n}\)’ means that there exists a sum-of-squares polynomial \(s \in \varSigma _r\) such that \(f(x) - \lambda = s(x)\) for all \(x \in {\mathbb {B}}^{n}\), or, equivalently, the polynomial \(f-\lambda -s\) belongs to the ideal generated by the polynomials \(x_1-x_1^2,\ldots ,x_n-x_n^2\). Throughout, \(\varSigma _r\) denotes the set of sum-of-squares polynomials with degree at most 2r, i.e., of the form \(\sum _i p_i^2\) with \(p_i\in {\mathbb {R}}[x]_r\).
As sums of squares of polynomials can be modelled using semidefinite programming, problem (2) can be reformulated as a semidefinite program of size polynomial in n for fixed r [16, 32], see also [23]. In the case of unconstrained boolean optimization, the resulting semidefinite program is known to have an optimum solution with small coefficients (see [31, 33]). For fixed r, the parameter \(\smash {f_{({r})}}\) may therefore be computed efficiently (up to any precision).
The bounds \(\smash {f_{({r})}}\) have finite convergence: \(\smash {f_{({r})}}=f_{\min }\) for \(r\ge n\) [18, 21]. In fact, it has been shown in [36] that the bound \(\smash {f_{({r})}}\) is exact already for \(2r \ge n+d-1\). That is,
In addition, it is shown in [36] that the bound \(\smash {f_{({r})}}\) is exact for \({2r\ge n+d-2}\) when the polynomial f has only monomials of even degree. This extends an earlier result of [12] shown for quadratic forms (\(d=2\)), which applies in particular to the case of max-cut. Furthermore, this result is tight for max-cut, since one needs to go up to order \(2r\ge n\) in order to reach finite convergence (in the cardinality case when all edge weights are 1) [22]. Similarly, the result (3) is tight when d is even and n is odd [15].
The main contribution of this work is an analysis of the quality of the bounds \(\smash {f_{({r})}}\) for parameters \(r, n \in {\mathbb {N}}\) which fall outside of this regime, i.e., \(2r<n+d-1\). The following is our main result, which expresses the error of the bound \(\smash {f_{({r})}}\) in terms of the roots of Krawtchouk polynomials, which are classical univariate orthogonal polynomials with respect to a discrete measure on the set \(\{0, 1, \ldots , n\}\) (see Sect. 2 for details).
Theorem 1
Fix \(d \le n\) and let \(f \in {\mathbb {R}}[x]\) be a polynomial of degree d. For \(r, n \in {\mathbb {N}}\), let \(\xi ^n_{r}\) be the least root of the degree r Krawtchouk polynomial (19) with parameter n. Then, if \((r+1)/n \le 1/2\) and \({d(d+1) \cdot \xi _{r+1}^n / n \le 1/2}\), we have:
Here \(C_d > 0\) is an absolute constant depending only on d and we set \(\Vert f\Vert _\infty := \max _{x \in {\mathbb {B}}^{n}} | f(x) |.\)
The extremal roots of Krawtchouk polynomials are well-studied in the literature. The following result of Levenshtein [26] shows their asymptotic behaviour.
Theorem 2
([26], Section 5) For \(t \in [0, 1/2]\), define the function
Then the least root \(\xi _r^n\) of the degree r Krawtchouk polynomial with parameter n satisfies
for some universal constant \(c > 0\).
Applying (6) to (4), we find that the relative error of the bound \(\smash {f_{({r})}}\) in the regime \(r \approx t \cdot n\) behaves as the function \(\varphi (t) = 1/2 - \sqrt{t(1-t)}\), up to a term in \(O(1/n^{2/3})\), which vanishes as n tends to \(\infty \). As an illustration, Fig. 1 in Appendix A shows the function \(\varphi (t)\).
1.2 A second hierarchy of bounds
In addition to the lower bound \(\smash {f_{({r})}}\), Lasserre [20] also defines an upper bound \(\smash {f^{({r})}} \ge f_{\min }\) on \(f_{\min }\) as follows:
where \(\mu \) is the uniform probability measure on \({\mathbb {B}}^{n}\). For fixed r, similarly to \(\smash {f_{({r})}}\), one may compute \(\smash {f^{({r})}}\) (up to any precision) efficiently by reformulating problem (7) as a semidefinite program [20]. Furthermore, as shown in [20] the bound is exact for some order r, and it is not difficult to see that the bound \(\smash {f^{({r})}}\) is exact at order \(r = n\) and that this is tight (see Sect. 5).
Essentially as a side result in the proof of Theorem 1, we can show the following analog for the upper bounds \(\smash {f^{({r})}}\), which we believe to be of independent interest.
Theorem 3
Fix \(d \le n\) and let \(f \in {\mathbb {R}}[x]\) be a polynomial of degree d. Then, for any \(r, n \in {\mathbb {N}}\) with \((r+1)/n \le 1/2\), we have:
where \(C_d > 0\) is the constant mentioned in Theorem 1.
So we have the same estimate of the relative error for the upper bounds \(\smash {f^{({r})}}\) as for the lower bounds \(\smash {f_{({r})}}\) (up to a constant factor 2) and indeed we will see that our proof relies on an intimate connection between both hierarchies. Note that the above analysis of \(\smash {f^{({r})}}\) does not require any condition on the size of \(\xi _{r+1}^n\) as was necessary for the analysis of \(\smash {f_{({r})}}\) in Theorem 1. Indeed, as will become clear later, the condition put on \(\xi _{r+1}^n\) follows from a technical argument (see Lemma 6), which is not required in the proof of Theorem 3.
1.3 Asymptotic analysis for both hierarchies
The results above show that the relative error of both hierarchies is bounded asymptotically by the function \(\varphi (t)\) from (5) in the regime \(r\approx t\cdot n\). This is summarized in the following corollary, which can be seen as an asymptotic version of Theorem 1 and Theorem 3.
Corollary 1
Fix \(d\le n\) and for \(n,r\in {\mathbb {N}}\) write
Let \(C_d\) be the constant of Theorem 1 and let \(\varphi (t)\) be the function from (5). Then, for any \(t\in [0,1/2]\), we have:
and, if \(d(d+1)\cdot \varphi (t) \le 1/2\), we also have:
Here, the limit notation \(r/n\rightarrow t\) means that the claimed convergence holds for all sequences \((n_j)_j\) and \((r_j)_j\) of integers such that \(\lim _{j\rightarrow \infty } n_j=\infty \) and \(\lim _{j\rightarrow \infty }r_j/n_j=t\).
We close with some remarks. First, note that \(\varphi (1/2) = 0\). Hence Corollary 1 tells us that the relative error of both hierarchies tends to 0 as \(r / n \rightarrow 1/2\). We thus ‘asymptotically’ recover the exactness result (3) of [36].
Our results in Theorems 1 and 3 and Corollary 1 extend directly to the case of polynomial optimization over the discrete cube \(\{\pm 1\}^n\) instead of the boolean cube \({\mathbb {B}}^{n}=\{0,1\}^n\), as can easily be seen by applying a change of variables \(x\in \{0,1\}\mapsto 2x-1\in \{\pm 1\}\). In addition, as we show in Appendix A, our results extend to the case of polynomial optimization over the q-ary cube \(\{0,1,\ldots ,q-1\}^n\) for \(q > 2\).
After replacing f by its negation \(-f\), one may use the lower bound \(\smash {f_{({r})}}\) on \(f_{\min }\) in order to obtain an upper bound on the maximum \(f_{\max }\) of f over \({\mathbb {B}}^{n}\). Similarly, one may obtain a lower bound on \(f_{\max }\) using the upper bound \(\smash {f^{({r})}}\) on \(f_{\min }\). To avoid possible confusion, we will also refer to \(\smash {f_{({r})}}\) as the outer Lasserre hierarchy (or simply the sum-of-squares hierarchy), whereas we will refer to \(\smash {f^{({r})}}\) as the inner Lasserre hierarchy. This terminology (borrowed from [7]) is motivated by the following observations. As is well-known (and easy to see) the parameter \(f_{\min }\) can be reformulated as an optimization problem over the set \({\mathcal {M}}\) of Borel measures on \({\mathbb {B}}^{n}\):
If we replace the set \({\mathcal {M}}\) by its inner approximation consisting of all measures \(\nu (x)=s(x)d\mu (x)\) with polynomial density \(s\in \varSigma _r\) with respect to a given fixed measure \(\mu \), then we obtain the bound \(f^{(r)}\). On the other hand, any \(\nu \in {\mathcal {M}}\) corresponds to a linear functional \(L_\nu :p\in {\mathbb {R}}[x]_{2r}\mapsto \int _{{\mathbb {B}}^{n}}p(x)d\nu (x)\) which is nonnegative on sums-of-squares on \({\mathbb {B}}^{n}\). These linear functionals thus provide an outer approximation for \(\mathcal M\) and maximizing \(L_\nu (p)\) over it gives the bound \(f_{(r)}\) (in dual formulation).
1.4 Related work
As mentioned above, the bounds \(\smash {f_{({r})}}\) defined in (2) are known to be exact when \(2r \ge n+d -1\). The case \(d=2\) (which includes max-cut) was treated in [12], positively answering a question posed in [22]. Extending the strategy of [12], the general case was settled in [36]. These exactness results are best possible when d is even and n is odd [15].
In [14], the sum-of-squares hierarchy is considered for approximating instances of knapsack. This can be seen as a variation on the problem (1), restricting to a linear polynomial objective with positive coefficients, but introducing a single, linear constraint, of the form \(a_1x_1+\cdots +a_nx_n\le b\) with \(a_i>0\). There, the authors show that the outer hierarchy has relative error at most \(1 / (r - 1)\) for any integer \(r\ge 2\). To the best of our knowledge this is the only known case where one can analyze the quality of the outer bounds for all orders \(r\le n\).
For optimization over sets other than the boolean cube, the following results on the quality of the outer hierarchy \(\smash {f_{({r})}}\) are available. When considering general semi-algebraic sets (satisfying a compactness condition), it has been shown in [30] that there exists a constant \(c>0\) (depending on the semi-algebraic set) such that \(\smash {f_{({r})}}\) converges to \(f_{\min }\) at a rate in \(O(1 / \log (r/c)^{1/c})\) as r tends to \(\infty \). This rate can be improved to \(O(1 / r^{1/c})\) if one considers a variation of the sum-of-squares hierarchy which is stronger (based on the preordering instead of the quadratic module), but much more computationally intensive [38]. Specializing to the hypersphere \(S^{n-1}\), better rates in O(1/r) were shown in [10, 34], and recently improved to \(O(1/r^2)\) in [11]. Similar improved results exist also for the case of polynomial optimization on the simplex and the continuous hypercube \([-1,1]^n\); we refer, e.g., to [7] for an overview.
The results for semi-algebraic sets other than \({\mathbb {B}}^{n}\) mentioned above all apply in the asymptotic regime where the dimension n is fixed and \(r \rightarrow \infty \). This makes it difficult to compare them directly to our new results. Indeed, we have to consider a different regime in the case of the boolean cube \({\mathbb {B}}^{n}\), as the hierarchy always converges in at most n steps. The regime where we are able to provide an analysis in this paper is when \(r \approx t\cdot n\) with \(0<t\le 1/2\).
Turning now to the inner hierarchy (7), as far as we are aware, nothing is known about the behaviour of the bounds \(\smash {f^{({r})}}\) on \({\mathbb {B}}^{n}\). For full-dimensional compact sets, however, results are available. It has been shown that, on the hypersphere [8], the unit ball and the simplex [40], and the unit box [9], the bound \(\smash {f^{({r})}}\) converges at a rate in \(O(1/r^2)\). A slightly weaker convergence rate in \(O(\log ^2 r / r^2)\) is known for general (full-dimensional) semi-algebraic sets [40, 42]. Again, these results are all asymptotic in r, and thus hard to compare directly to our analysis on \({\mathbb {B}}^{n}\).
1.5 Overview of the proof
Here, we give an overview of the main ideas that we use to show our results. Our broad strategy follows the one employed in [11] to obtain information on the sum-of-squares hierarchy on the hypersphere. The following four ingredients will play a key role in our proof:
-
1.
we use the polynomial kernel technique in order to produce low-degree sum-of-squares representations of polynomials that are positive over \({\mathbb {B}}^{n}\), thus allowing an analysis of \(f_{\min }- \smash {f_{({r})}}\);
-
2.
using classical Fourier analysis on the boolean cube \({\mathbb {B}}^{n}\) we are able to exploit symmetry and reduce the search for a multivariate kernel to a univariate sum-of-squares polynomial on the discrete set \([0:n] := \{0,1,\ldots ,n\}\);
-
3.
we find this univariate sum-of-squares by applying the inner Lasserre hierarchy to an appropriate univariate optimization problem on [0 : n];
-
4.
finally, we exploit a known connection between the inner hierarchy and the extremal roots of corresponding orthogonal polynomials (in our case, the Krawtchouk polynomials).
Following these steps we are able to analyze the sum-of-squares hierarchy \(\smash {f_{({r})}}\) as well as the inner hierarchy \(\smash {f^{({r})}}\). We now sketch how our proof articulates along these four main steps.
Let \(f\in {\mathbb {R}}[x]_d\) be the polynomial with degree d for which we wish to analyze the bounds \(f_{(r)}\) and \(f^{(r)}\). After rescaling, and up to a change of coordinates, we may assume w.l.o.g. that f attains its minimum over \({\mathbb {B}}^{n}\) at \(0 \in {\mathbb {B}}^{n}\) and that \(f_{\min }=0\) and \(f_{\max } = 1\). So we have \(\Vert f\Vert _\infty =1\). To simplify notation, we will make these assumptions throughout.
The first key idea is to consider a polynomial kernel \(K\) on \({\mathbb {B}}^{n}\) of the form:
where \(u \in {\mathbb {R}}[t]_r\) is a univariate polynomial of degree at most r and d(x, y) is the Hamming distance between x and y. Such a kernel K induces an operator \({\mathbf {K}}\), which acts linearly on the space of polynomials on \({\mathbb {B}}^{n}\) by:
Recall that \(\mu \) is the uniform probability distribution on \({\mathbb {B}}^{n}\). An easy but important observation is that, if p is nonnegative on \({\mathbb {B}}^{n}\), then \({\mathbf {K}}p\) is a sum-of-squares (on \({\mathbb {B}}^{n}\)) of degree at most 2r. We use this fact as follows.
Given a scalar \(\delta \ge 0\), define the polynomial \({\tilde{f}} := f + \delta \). Assuming that the operator \({\mathbf {K}}\) is non-singular, we can express \({\tilde{f}}\) as \({\tilde{f}} = {\mathbf {K}}({\mathbf {K}}^{-1} {\tilde{f}})\). Therefore, if \({\mathbf {K}}^{-1} {\tilde{f}}\) is nonnegative on \({\mathbb {B}}^{n}\), then we find that \({\tilde{f}}\) is a sum-of-squares on \({\mathbb {B}}^{n}\) with degree at most 2r, which implies \(f_{\min }- \smash {f_{({r})}} \le \delta \).
One way to guarantee that \({\mathbf {K}}^{-1} {\tilde{f}}\) is indeed nonnegative on \({\mathbb {B}}^{n}\) is to select the operator \({\mathbf {K}}\) in such a way that \({\mathbf {K}}(1)=1\) and
We collect this as a lemma for further reference.
Lemma 1
If the kernel operator \({\mathbf {K}}\) associated to \(u \in {\mathbb {R}}[t]_r\) via relation (8) satisfies \({\mathbf {K}}(1)=1\) and \(\Vert {\mathbf {K}}^{-1}-I\Vert \le \delta \), then we have \(f_{\min }-f_{(r)}\le \delta \).
Proof
With \({\tilde{f}}=f+\delta \), we have: \(\Vert {\mathbf {K}}^{-1}{\tilde{f}}-\tilde{f}\Vert _\infty =\Vert {\mathbf {K}}^{-1}f -f\Vert _\infty \le \delta \Vert f\Vert _\infty =\delta \), where we use the fact that \({\mathbf {K}}(1) = 1 = {\mathbf {K}}^{-1} (1)\) and thus \({\mathbf {K}}^{-1}\tilde{f}-{\tilde{f}} ={\mathbf {K}}^{-1}f -f\) for the first equality and (9) for the inequality. The inequality \(\Vert {\mathbf {K}}^{-1}{\tilde{f}}-{\tilde{f}}\Vert _\infty \le \delta \) then implies \({\mathbf {K}}^{-1}{\tilde{f}}(x)\ge {\tilde{f}}(x)-\delta =f(x)\ge f_{\min }=0\) on \({\mathbb {B}}^{n}\). \(\square \)
In other words, we want the operator \({\mathbf {K}}^{-1}\) (and thus \({\mathbf {K}}\)) to be ‘close to the identity operator’ in a certain sense. As kernels of the form (8) are invariant under the symmetries of \({\mathbb {B}}^{n}\), we are able to use classical Fourier analysis on the boolean cube to express the eigenvalues \(\lambda _i\) of \({\mathbf {K}}\) in terms of the polynomial u. More precisely, it turns out that these eigenvalues are given by the coefficients of the expansion of \(u^2\) in the basis of Krawtchouk polynomials. As we show later (see (33)), inequality (9) then holds for \(\delta \approx \sum _{i} |\lambda _i^{-1} - 1|\).
It therefore remains to find a univariate polynomial \(u \in {\mathbb {R}}[t]_r\) for which these coefficients, and thus the eigenvalues of \({\mathbf {K}}\), are sufficiently close to 1. Interestingly, this problem boils down to analyzing the quality of the inner bound \(g^{(r)}\) (see 7) for a particular univariate polynomial g (given in (35)).
In order to perform this analysis and conclude the proof of Theorem 1, we make use of a connection between the inner Lasserre hierarchy and the least roots of orthogonal polynomials (in this case the Krawtchouk polynomials).
Finally, we generalize our analysis of the inner hierarchy (for the special case of the selected polynomial g in Step 3 to arbitrary polynomials) to obtain Theorem 3.
1.6 Matrix-valued polynomials
As we explain in this section the results of Theorems 1 and 3 may be extended to the setting of matrix-valued polynomials.
For fixed \(k \in {\mathbb {N}}\), let \({\mathcal {S}}^k\subseteq {\mathbb {R}}^{k \times k}\) be the space of \(k \times k\) real symmetric matrices. We write \({\mathcal {S}}^k[x] \subseteq {\mathbb {R}}^{k \times k}[x]\) for the space of n-variate polynomials whose coefficients lie in \({\mathcal {S}}^k\), i.e., the set of \(k\times k\) symmetric polynomial matrices. The polynomial optimization problem (1) may be generalized to polynomials \(F \in {\mathcal {S}}^k[x]\) as:
where \(F\in {\mathcal {S}}^k[x]\) is a polynomial matrix and \(\lambda _{\min }(F(x))\) denotes the smallest eigenvalue of F(x). That is, \(F_{\min }\) is the largest value for which \(F(x) - F_{\min } I~{ \succeq 0}\) for all \(x \in {\mathbb {B}}^{n}\), where \(\succeq \) is the positive semidefinite Löwner order.
The Lasserre hierarchies (2) and (7) may also be defined in this setting. A polynomial matrix \(S \in {\mathcal {S}}^k[x]\) is called a sum-of-squares polynomial of degree 2r if it can be written as:
We write \(\varSigma ^{k \times k}_r\) for the set of all such polynomials. See, e.g., [37] for background and results on sum-of-squares polynomial matrices. Note that a sum-of-squares polynomial matrix \(S \in \varSigma ^{k \times k}_r\) satisfies \(S(x) \succeq 0\) for all \(x \in {\mathbb {B}}^{n}\). For a matrix \(A \in {\mathcal {S}}^k\), \(\Vert A\Vert \) denotes its spectral (or operator) norm, defined as the largest absolute value of an eigenvalue of A. Then, for \(F\in {\mathcal {S}}^k[x]\), we set
The outer hierarchy \(F_{(r)}\) for the polynomial F is then given by:
Similarly, the inner hierarchy \(F^{(r)}\) is defined as:
Indeed, (2) and (7) are the special cases of the above programs when \(k=1\). As before, the parameters \(F_{(r)}\) and \(F^{(r)}\) may be computed efficiently for fixed r (and fixed k) using semidefinite programming, and they satisfy
As was already noted in [11] (in the context of optimization over the unit sphere), the proof strategy outlined in Sect. 1.5 naturally extends to the setting of polynomial matrices. This yields the following generalizations of our main theorems.
Theorem 4
Fix \(d \le n\) and let \(F \in {\mathcal {S}}^k[x]\) (\(k\ge 1\)) be a polynomial matrix of degree d. For \(r, n \in {\mathbb {N}}\), let \(\xi ^n_{r}\) be the least root of the degree r Krawtchouk polynomial (19) with parameter n. Then, if \((r+1)/n \le 1/2\) and \({d(d+1) \cdot \xi _{r+1}^n / n \le 1/2}\), we have:
where \(C_d > 0\) is the absolute constant depending only on d from Theorem 1.
Theorem 5
Fix \(d \le n\) and let \(F \in {\mathcal {S}}^k[x]\) be a matrix-valued polynomial of degree d. Then, for any \(r, n \in {\mathbb {N}}\) with \((r+1)/n \le 1/2\), we have:
where \(C_d > 0\) is the constant of Theorem 1.
1.7 Organization
The rest of the paper is structured as follows. We review the necessary background on Fourier analysis on the boolean cube in Sect. 2. In Sect. 3, we recall a connection between the inner Lasserre hierarchy and the roots of orthogonal polynomials. Then, in Sect. 4, we give a proof of Theorem 1. In Sect. 5, we discuss how to generalize the proofs of Sect. 4 to obtain Theorem 3. We group the proofs of some technical results needed to prove Lemma 5 in Sect. 6. In Appendix A, we indicate how our arguments extend to the case of polynomial optimization over the q-ary hypercube \(\{0,1,\ldots ,q-1\}^n\) for \(q>2\). Finally, we give the proofs of our results in the matrix-valued setting (Theorems 4 and 5) in Appendix B.
2 Fourier analysis on the Boolean cube
In this section, we cover some standard Fourier analysis on the boolean cube. For a general reference on Fourier analysis on (finite, abelian) groups, see e.g. [43]. See also Section 4 of [45] for the boolean case.
Some notation For \(n \in {\mathbb {N}}\), we write \({\mathbb {B}}^{n} = \{0, 1\}^n\) for the boolean hypercube of dimension n. We let \(\mu \) denote the uniform probability measure on \({\mathbb {B}}^{n}\), given by \(\mu = \frac{1}{2^n} \sum _{x \in {\mathbb {B}}^{n}}\delta _x\), where \(\delta _x\) is the Dirac measure at x. Further, we write \(|x| = \sum _{i}x_i = |\{i\in [n]: x_i = 1 \}|\) for the Hamming weight of \(x \in {\mathbb {B}}^{n}\), and \(d(x,y) = |\{i\in [n]: x_i \ne y_i\}|\) for the Hamming distance between \(x, y \in {\mathbb {B}}^{n}\). We let \(\text {Sym}(n)\) denote the set of permutations of the set \([n]=\{1,\ldots ,n\}\).
We consider polynomials \(p : {\mathbb {B}}^{n} \rightarrow {\mathbb {R}}\) on \({\mathbb {B}}^{n}\). The space \({\mathcal {R}}[{x}]\) of such polynomials is given by the quotient ring of \({\mathbb {R}}[x]\) over the equivalence relation \(p \sim q\) if \( p(x) = q(x)\) on \({\mathbb {B}}^{n}\). In other words, \({\mathcal {R}}[{x}]= \mathbb R[x]/{\mathcal {I}}\), where \({\mathcal {I}}\) is the ideal generated by the polynomials \(x_i-x_i^2\) for \(i\in [n]\), which can also be seen as the vector space spanned by the (multilinear) polynomials \(\prod _{i\in I}x_i\) for \(I\subseteq [n].\)
For \(a\le b \in {\mathbb {N}}\), we let [a : b] denote the set of integers \(a, a + 1, \dots , b\).
The character basis Let \(\langle \cdot , \cdot \rangle _\mu \) be the inner product on \({\mathcal {R}}[{x}]\) given by:
The space \({\mathcal {R}}[{x}]\) has an orthonormal basis w.r.t. \(\langle \cdot , \cdot \rangle _{\mu }\) given by the characters:
In other words, the set \(\{ \chi _a : a \in {\mathbb {B}}^{n} \}\) of all characters on \({\mathbb {B}}^{n}\) forms a basis for \({\mathcal {R}}[{x}]\) and
Then any polynomial \(p \in {\mathcal {R}}[{x}]\) can be expressed in the basis of characters, known as its Fourier expansion:
with Fourier coefficients \(\widehat{p}(a) := \langle p, \chi _a \rangle _{\mu } \in {\mathbb {R}}\).
The group \({{\,\mathrm{Aut}\,}}({\mathbb {B}}^{n})\) of automorphisms of \({\mathbb {B}}^{n}\) is generated by the coordinate permutations, of the form \(x\mapsto \sigma (x):=(x_{\sigma (1)},\ldots ,x_{\sigma (n)})\) for \(\sigma \in \text {Sym}(n)\), and the automorphisms corresponding to bit-flips, of the form \(x\in {\mathbb {B}}^{n}\mapsto x\oplus a\in {\mathbb {B}}^{n}\) for \(a\in {\mathbb {B}}^{n}\). If we set
then each \(H_k\) is an irreducible, \({{\,\mathrm{Aut}\,}}({\mathbb {B}}^{n})\)-invariant subspace of \({\mathcal {R}}[{x}]\) of dimension \({n \atopwithdelims ()k}\). Using (16), we may then decompose \({\mathcal {R}}[{x}]\) as the direct sum
where the subspaces \(H_k\) are pairwise orthogonal w.r.t. \(\langle \cdot , \cdot \rangle _\mu \). In fact, we have that \({\mathcal {R}}[{x}]_d = H_0 \perp H_1 \perp \dots \perp H_d\) for all \(d \le n\), and we may thus write any \(p \in {\mathcal {R}}[{x}]_d\) (in a unique way) as
The polynomials \(p_k\in H_k\) (\(k=0,\ldots ,d\)) are known as the harmonic components of p and the decomposition (17) as the harmonic decomposition of p. We will make extensive use of this decomposition throughout.
Let \({\mathrm{St}}(0) \subseteq {{\,\mathrm{Aut}\,}}({\mathbb {B}}^{n})\) be the set of automorphisms fixing \(0 \in {\mathbb {B}}^{n}\), which consists of the coordinate permutations \(x\mapsto \sigma (x) =(x_{\sigma (1)},\ldots ,x_{\sigma (n)})\) for \(\sigma \in \text {Sym}(n)\). The subspace of functions in \(H_k\) that are invariant under \({\mathrm{St}}(0)\) is one-dimensional and it is spanned by the function
These functions \(X_k\) are known as the zonal spherical functions with pole \({0 \in {\mathbb {B}}^{n}}\).
Krawtchouk polynomials For \(k \in {\mathbb {N}}\), the Krawtchouk polynomial of degree k (and with parameter n) is the univariate polynomial in t given by:
(see, e.g. [41]). The Krawtchouk polynomials form an orthogonal basis for \({\mathbb {R}}[t]\) with respect to the inner product given by the following discrete probability measure on the set \([0:n]=\{0,1,\ldots ,n\}\):
Indeed, for all \(k, k' \in {\mathbb {N}}\) we have:
The following (well-known) lemma explains the connection between the Krawtchouk polynomials and the character basis on \({\mathcal {R}}[{x}]\).
Lemma 2
Let \(t \in [0:n]\) and choose \(x, y \in {\mathbb {B}}^{n}\) so that \(d(x, y) = t\). Then for any \(0\le k \le n\) we have:
In particular, we have:
where \(1^t 0^{n-t} \in {\mathbb {B}}^{n}\) is given by \((1^t 0^{n-t})_i = 1\) if \(1\le i \le t\) and \((1^t 0^{n-t})_i = 0\) if \(t+1\le i\le n\).
Proof
Noting that \(\chi _a(x) \chi _a(y) = \chi _a(x+y)\) and \(|x + y| = d(x,y) = t\), we have:
\(\square \)
From this, we see that any polynomial \(p\in {\mathbb {R}}[x]_d\) that is invariant under the action of \({\mathrm{St}}(0)\) is of the form \(\sum _{i=1}^d \lambda _i {\mathcal {K}}^n_i(|x|)\) for some scalars \(\lambda _i\), and thus \(p(x)=u(|x|)\) for some univariate polynomial \(u \in {\mathbb {R}}[t]_d\).
It will sometimes be convenient to work with a different normalization of the Krawtchouk polynomials, given by:
So \(\widehat{{\mathcal {K}}}^n_k(0)=1\). Note that for any \(k \in {\mathbb {N}}\), we have
meaning that \(\widehat{{\mathcal {K}}}^n_k(t) = {\mathcal {K}}^n_k(t) / \Vert {\mathcal {K}}^n_k\Vert ^2_\omega \).
Finally we give a short proof of two basic facts on Krawtchouk polynomials that will be used below.
Lemma 3
We have:
for all \(0\le k \le n\) and \(t \in [0 : n]\).
Proof
Given \(t \in [0:n]\) consider an element \(x \in {\mathbb {B}}^{n}\) with Hamming weight t, for instance the element \(1^t 0^{n-t}\) from Lemma 2. By (22) we have
making use of the fact that \(|\chi _a(x)| = 1\) for all \(a \in {\mathbb {B}}^{n}\). \(\square \)
Lemma 4
We have:
for all \(0\le k \le n\).
Proof
Let \(t\in [0:n-1]\) and \(0 < k \le d\). Consider the elements \(1^t 0^{n-t}\) and \(1^{t+1} 0^{n-t-1}\) of \({\mathbb {B}}^{n}\) from Lemma 2. We have:
where for the inequality we note that \(\chi _a(1^t 0^{n-t}) = \chi _a(1^{t+1} 0^{n-t-1})\) if \(a_{t+1} = 0\). As \({\mathcal {K}}^n_k(0) = {n \atopwithdelims ()k}\), this implies that:
This shows the first inequality of (24). The second inequality follows using the triangle inequality, a telescope summation argument and the fact that \(\widehat{{\mathcal {K}}}^n_k(0)=1\). \(\square \)
Invariant kernels and the Funk–Hecke formula Given a univariate polynomial \(u \in {\mathbb {R}}[t]\) of degree r with \(2r \ge d\), consider the kernel \({K: {\mathbb {B}}^{n} \times {\mathbb {B}}^{n} \rightarrow {\mathbb {R}}}\) defined by
A kernel of the form (25) coincides with a polynomial of degree \(2\mathrm {deg}(u)\) in x on the binary cube \({\mathbb {B}}^{n}\), as \(d(x,y) = \sum _i (x_i + y_i - 2x_iy_i)\) for \(x, y \in {\mathbb {B}}^{n}\). Furthermore, it is invariant under \({{\,\mathrm{Aut}\,}}({\mathbb {B}}^{n})\), in the sense that:
The kernel \(K\) acts as a linear operator \({\mathbf {K}}: {\mathcal {R}}[{x}] \rightarrow {\mathcal {R}}[{x}]\) by:
We may expand the univariate polynomial \(u^2 \in {\mathbb {R}}[t]_{2r}\) in the basis of Krawtchouk polynomials as:
As we show now, the eigenvalues of the operator \({\mathbf {K}}\) are given precisely by the coefficients \(\lambda _i\) occurring in this expansion. This relation is analogous to the classical Funk–Hecke formula for spherical harmonics (see, e.g., [11]).
Theorem 6
(Funk–Hecke) Let \(p \in {\mathcal {R}}[{x}]_d\) with harmonic decomposition \(p= p_0 + p_1 + \dots + p_d\). Then we have:
Proof
It suffices to show that \( {\mathbf {K}}\chi _z = \lambda _{|z|} \chi _z \) for all \(z \in {\mathbb {B}}^{n}\). So we compute for \(x \in {\mathbb {B}}^{n}\):
\(\square \)
Finally, we note that since the Krawtchouk polynomials form an orthogonal basis for \({\mathbb {R}}[t]\), we may express the coefficients \(\lambda _i\) in the decomposition (27) of \(u^2\) in the following way:
In addition, since in view of Lemma 3 we have \(\widehat{{\mathcal {K}}}^n_i(t)\le \widehat{{\mathcal {K}}}^n_0(t)\) for all \(t\in [0:n]\), it folllows that
3 The inner Lasserre hierachy and orthogonal polynomials
The inner Lasserre hierachy, which we have defined for the boolean cube in (7), may be defined more generally for the minimization of a polynomial g over a compact set \(M \subseteq {\mathbb {R}}^n\) equipped with a measure \(\nu \) with support M, by setting:
for any integer \(r\in {\mathbb {N}}\). So we have: \(g^{(r)}\ge g_{\min }:=\min _{x\in M}g(x).\) A crucial ingredient of the proof of our main theorem below is an analysis of the error \(g^{(r)} - g_{\min }\) in this hierarchy for a special choice of \(M \subseteq {\mathbb {R}}\), g and \(\nu \).
Here, we recall a technique which may be used to perform such an analysis in the univariate case, which was developed in [9] and further employed for this purpose, e.g., in [8, 40].
First, we observe that we may always replace g by a suitable upper estimator \({\widehat{g}}\) which satisfies \(\widehat{g}_{\min } = g_{\min }\) and \({\widehat{g}}(x) \ge g(x)\) for all \(x \in M\). Indeed, it is clear that for such \({\widehat{g}}\) we have:
Next, we consider the special case when \(M\subseteq {\mathbb {R}}\) and \(g(t) = t\). Here, the bound \(g^{(r)}\) may be expressed in terms of the orthogonal polynomials on M w.r.t. the measure \(\nu \), i.e., the polynomials \(p_i \in {\mathbb {R}}[t]_i\) determined by the relation:
Theorem 7
([9]) Let \(M \subseteq {\mathbb {R}}\) be an interval and let \(\nu \) be a measure supported on M with corresponding orthogonal polynomials \(p_i\in {\mathbb {R}}[t]_i\) (\(i \in {\mathbb {N}}\)). Then the Lasserre inner bound \(g^{(r)}\) (from 31) of order r for the polynomial \(g(t) = t\) equals
where \(\xi _{r+1}\) is the smallest root of the polynomial \(p_{r+1}\).
Remark 1
The upshot of the above result is that, for any polynomial \(g : {\mathbb {R}}\rightarrow {\mathbb {R}}\) which is upper bounded on an interval \(M\subseteq {\mathbb {R}}\) by a linear polynomial \({\widehat{g}}(t) = ct\) for some \(c > 0\), we have:
where \(\xi _{r+1}\) is the smallest root of the corresponding orthogonal polynomial of degree \(r+1\).
4 Proof of Theorem 1
Throughout, \(d\le n\) is a fixed integer (the degree of the polynomial f to be minimized over \({\mathbb {B}}^{n}\)). Recall \(u \in {\mathbb {R}}[t]\) is a univariate polynomial with degree r (that we need to select) with \(2r\ge d\). Consider the associated kernel \(K\) defined in (25) and the corresponding linear operator \({\mathbf {K}}\) from (26). Recall from (9) that we are interested in bounding the quantity:
Our proof consists of two parts. First, we relate the coefficients \(\lambda _i\), that appear in the decomposition (27) of \(u^2(t) = \sum _{i = 0}^{2r} \lambda _i {\mathcal {K}}^n_i(t)\) into the basis of Krawtchouk polynomials, to the quantity \(\Vert {\mathbf {K}}^{-1} - I\Vert \).
Then, using this relation and the connection between the inner Lasserre hierarchy and extremal roots of orthogonal polynomials outlined in Sect. 3, we show that u may be chosen such that \(\Vert {\mathbf {K}}^{-1}-I\Vert \) is of the order \(\xi ^n_{r+1} / n\), with \(\xi ^n_{r+1}\) the smallest root of the degree \(r+1\) Krawtchouk polynomial (with parameter n).
Bounding \(\Vert {\mathbf {K}}^{-1}-I\Vert \) in terms of the \(\lambda _i\) We need the following technical lemma, which bounds the sup-norm \(\Vert p_k\Vert _\infty \) of the harmonic components \(p_k\) of a polynomial \(p \in {\mathcal {R}}[{x}]\) in terms of \(\Vert p\Vert _\infty \), the sup-norm of p itself. The key point is that this bound is independent of the dimension n. We delay the proof which is rather technical to Sect. 6.
Lemma 5
There exists a constant \(\gamma _d > 0\), depending only on d, such that for any \(p = p_0 + p_1 + \ldots + p_d \in {\mathcal {R}}[{x}]_d\), we have:
Corollary 2
Assume that \(\lambda _0 = 1\) and \(\lambda _k \ne 0\) for \(1\le k\le d\). Then we have:
Proof
By assumption, the operator \({\mathbf {K}}\) is invertible and, in view of Funk–Hecke relation (28), its inverse is given by \({\mathbf {K}}^{-1}p =\sum _{i=0}^d \lambda _i^{-1}p_k\) for any \(p = p_0 + p_1 + \ldots + p_d \in {\mathcal {R}}[{x}]_d\). Then we have:
where we use Lemma 5 for the last inequality. \(\square \)
The expression \(\varLambda \) in (33) is difficult to analyze. Therefore, following [11], we consider instead the simpler expression:
which is linear in the \(\lambda _i\). Under the assumption that \(\lambda _0 = 1\), we have \({\lambda _i \le \lambda _0 = 1}\) for all i (recall relation (30)). Thus, \(\varLambda \) and \({\tilde{\varLambda }}\) are both minimized when the \(\lambda _i\) are close to 1. The following lemma makes this precise.
Lemma 6
Assume that \(\lambda _0 = 1\) and that \({\tilde{\varLambda }}\le 1/2\). Then we have \(\varLambda \le 2 {\tilde{\varLambda }}\), and thus
Proof
As we assume \({\tilde{\varLambda }}\le 1/2\), we must have \(1/2 \le \lambda _i \le 1\) for all i. Therefore, we may write:
\(\square \)
Optimizing the choice of the univariate polynomial u In light of Lemma 6, and recalling (29), we wish to find a univariate polynomial \(u \in {\mathbb {R}}[t]_r\) for which
Unpacking the definition of \(\langle \cdot , \cdot \rangle _{\omega }\), we thus need to solve the following optimization problem:
(Indeed \(\int gu^2d\omega =\langle g,u^2\rangle _\omega = {\tilde{\varLambda }}\) and \(\int u^2d\omega = \langle 1,u^2\rangle _\omega \).) We recognize this program to be the same as the program (31) defining the inner Lasserre boundFootnote 1 of order r for the minimum \(g_{\min } = g(0) = 0\) of the polynomial g over [0 : n], computed with respect to the measure \(d\omega (t) = 2^{-n}{n \atopwithdelims ()t}\). Hence the optimal value of (35) is equal to \(g^{(r)}\) and, using Lemma 6, we may conclude the following.
Theorem 8
Let g be as in (35). Assume that \(g^{(r)} - g_{\min } \le 1/2\). Then there exists a polynomial \(u \in {\mathbb {R}}[t]_r\) such that \(\lambda _0 = 1\) and
Here, \(g^{(r)}\) is the inner Lasserre bound on \(g_{\min }\) of order r, computed on [0, n] w.r.t. \(\omega \), via the program (35), and \(\gamma _d\) is the constant of Lemma 5.
It remains, then, to analyze the range \(g^{(r)} - g_{\min }\). For this purpose, we follow the technique outlined in Sect. 3. We first show that g can be upper bounded by its linear approximation at \(t = 0\).
Lemma 7
We have:
Furthermore, the minimum \({\hat{g}}_{\min }\) of \({\hat{g}}\) on [0 : n] clearly satisfies \({\widehat{g}}_{\min } = {\widehat{g}}(0) = g(0) = g_{\min }\).
Proof
Using (24), we find for each \(k \le n\) that:
Therefore, we have:
\(\square \)
Lemma 8
We have:
where \(\xi _{r + 1}^n\) is the smallest root of the Krawtchouk polynomial \({\mathcal {K}}^n_{r+1}(t)\).
Proof
This follows immediately from Lemma 7 and Remark 1 at the end of Sect. 3, noting that the Krawtchouk polynomials are indeed orthogonal w.r.t. the measure \(\omega \) on [0 : n] (cf. 20). \(\square \)
Putting things together, we may prove our main result, Theorem 1.
Proof of Theorem 1
Assume that r is large enough so that \({d(d+1)\cdot (\xi ^n_{r+1}/n) \le 1/2}\). By Lemma 8, we then have
By Theorem 8 we are thus able to choose a polynomial \(u \in {\mathbb {R}}[t]_r\) whose associated operator \({\mathbf {K}}\) satisfies \({\mathbf {K}}(1)=1\) and
We may then use Lemma 1 to obtain Theorem 1 with constant \({C_d := \gamma _d \cdot d(d+1)}\). \(\square \)
5 Proof of Theorem 3
We turn now to analyzing the inner hierarchy \(\smash {f^{({r})}}\) defined in (7) for a polynomial \(f\in {\mathbb {R}}[x]_d\) on the boolean cube, whose definition is repeated for convenience:
As before, we may assume w.l.o.g. that \(f_{\min } = f(0) = 0\) and that \(f_{\max } = 1\). To facilitate the analysis of the bounds \(f^{(r)}\), the idea is to restrict in (37) to polynomials s(x) that are invariant under the action of \({\mathrm{St}}(0) \subseteq {{\,\mathrm{Aut}\,}}({\mathbb {B}}^{n})\), i.e., depending only on the Hamming weight |x|. Such polynomials are of the form \(s(x)=u(|x|)\) for some univariate polynomial \(u\in {\mathbb {R}}[t]\). Hence this leads to the following, weaker hierarchy, where we now optimize over univariate sums-of-squares:
By definition, we must have \(\smash {f_{\mathrm{sym}}^{({r})}} \ge \smash {f^{({r})}} \ge f_{\min }\), and so an analysis of \(\smash {f_{\mathrm{sym}}^{({r})}}\) extends immediately to \(\smash {f^{({r})}}\).
The main advantage of working with the hierarchy \(\smash {f_{\mathrm{sym}}^{({r})}}\) is that we may now assume that f is itself invariant under \({\mathrm{St}}(0)\), after replacing f by its symmetrization:
Indeed, for any \(u \in \varSigma [t]_r\), we have that:
So we now assume that f is \({\mathrm{St}}(0)\)-invariant, and thus we may write:
By the definitions of the measures \(\mu \) on \({\mathbb {B}}^{n}\) and \(\omega \) on [0 : n] we have the identities:
Hence we get
In other words, the behaviour of the symmetrized inner hierarchy \(\smash {f_{\mathrm{sym}}^{({r})}}\) over the boolean cube w.r.t. the uniform measure \(\mu \) is captured by the behaviour of the univariate inner hierarchy \(F_{[0: n], \omega }^{(r)}\) over [0 : n] w.r.t. the discrete measure \(\omega \).
Now, we are in a position to make use again of the technique outlined in Sect. 3. First we find a linear upper estimator \({\widehat{F}}\) for F on [0 : n].
Lemma 9
We have
where \(\gamma _d\) is the same constant as in Lemma 5.
Proof
Write \(F(t)= \sum _{i=0}^d \lambda _i \widehat{{\mathcal {K}}}^n_i(t) \) for some scalars \(\lambda _i\). By assumption, \({F(0)=0}\) and thus \(\sum _{i=0}^d\lambda _i=0\). We now use an analogous argument as for Lemma 7:
As \(\Vert f\Vert _\infty =1\), using Lemma 5, we can conclude that:
which gives the desired result. \(\square \)
In light of Remark 1 in Sect. 3, we may now conclude that
As \(\smash {f^{({r})}} \le \smash {f_{\mathrm{sym}}^{({r})}} = F_{[0: n], \omega }^{(r)}\), we have thus shown Theorem 3 with constant \({C_d = d(d+1) \gamma _d}\). Note that in comparison to Lemma 8, we only have the additional constant factor \(\gamma _d\).
Exactness of the inner hierarchy As is the case for the outer hierarchy, the inner hierarchy is exact when r is large enough. Whereas the outer hierarchy, however, is exact for \(r \ge (n+d-1)/2\), the inner hierarchy is exact in general if and only if \(r \ge n\). We give a short proof of this fact below, for reference.
Lemma 10
Let f be a polynomial on \({\mathbb {B}}^{n}\). Then \(\smash {f^{({r})}} = f_{\min }~\) for all \(r \ge n\).
Proof
We may assume w.l.o.g. that \(f(0) = f_{\min }\). Consider the interpolation polynomial:
which satisfies \(s^2(0) = 2^n\) and \(s^2(x) = 0\) for all \(0 \ne x \in {\mathbb {B}}^{n}\). Clearly, we have:
and so \(\smash {f^{({n})}} = f_{\min }\). \(\square \)
The next lemma shows that this result is tight, by giving an example of polynomial f for which the bound \(\smash {f^{({r})}}\) is exact only at order \(r=n\).
Lemma 11
Let \(f(x) = |x|=x_1+\cdots +x_n\). Then \(\smash {f^{({r})}} - f_{\min }> 0\) for all \(r < n\).
Proof
Suppose not. That is, \(f^{(r)}= f_{\min }=0\) for some \(r\le n-1\). As \({f(x) > 0 = f_{\min }}\) for all \(0 \ne x \in {\mathbb {B}}^{n}\), this implies that there exists a polynomial \(s \in {\mathbb {R}}[x]_r\) such that \(s^2\) is interpolating at 0, i.e. such that \(s^2(0) = 1\) and \(s^2(x) = 0\) for all \(0 \ne x \in {\mathbb {B}}^{n}\). But then s is itself interpolating at 0 and has degree \(r < n\), a contradiction. \(\square \)
6 Proof of Lemma 5
In this section we give a proof of Lemma 5, where we bound the sup-norm \(\Vert p_k \Vert _{\infty }\) of the harmonic components \(p_k\) of a polynomial p by \(\gamma _d \Vert p\Vert _\infty \) for some constant \(\gamma _d\) depending only on the degree d of p. The following definitions will be convenient.
Definition 1
For \(n \ge d \ge k \ge 0\) integers, we write:
We are thus interested in finding a bound \(\gamma _d\) depending only on d such that:
We will now show that in the computation of the parameter \(\rho (n,d,k)\) we may restrict to feasible solutions p having strong structural properties. First, we show that we may assume that the sup-norm of the harmonic component \(p_k\) of p is attained at \(0 \in {\mathbb {B}}^{n}\).
Lemma 12
We have
Proof
Let p be a feasible solution for \(\rho (n, d, k)\) and let \(x \in {\mathbb {B}}^{n}\) for which \(p_k(x) = \Vert p_k\Vert _\infty \) (after possibly replacing p by \(-p\)). Now choose \(\sigma \in {{\,\mathrm{Aut}\,}}({\mathbb {B}}^{n})\) such that \(\sigma (0) = x\) and set \({\widehat{p}} = p \circ \sigma \). Clearly, \({\widehat{p}}\) is again a feasible solution for \(\rho (n, d, k)\). Moreover, as \(H_k\) is invariant under \({{\,\mathrm{Aut}\,}}({\mathbb {B}}^{n})\), we have:
which shows the lemma. \(\square \)
Next we show that we may in addition restrict to polynomials that are highly symmetric.
Lemma 13
In the program (40) we may restrict the optimization to polynomials of the form
Proof
Let p be a feasible solution to (40). Consider the following polynomial \({\widehat{p}}\) obtained as symmetrization of p under action of \({\mathrm{St}}(0)\), the set of automorphism of \({\mathbb {B}}^{n}\) corresponding to the coordinate permutations:
Then \(\Vert {\widehat{p}}\Vert _\infty \le 1\) and \({\widehat{p}}_k(0) = p_k(0)\), so \({\widehat{p}}\) is still feasible for (40) and has the same objective value as p. Furthermore, for each i, \({\widehat{p}}_i\) is invariant under \({\mathrm{St}}(0)\), which implies that \({\widehat{p}}_i(x) = \lambda _i X_i(x) = \lambda _i \sum _{|a| = i} \chi _a(x)=\lambda _i {\mathcal {K}}^n_i(|x|)\) for some \(\lambda _i \in {\mathbb {R}}\) (see 18). \(\square \)
A simple rescaling \(\lambda _i \leftarrow \lambda _i \cdot {n \atopwithdelims ()i}\) allows us to switch from \({\mathcal {K}}^n_i\) to \(\widehat{{\mathcal {K}}}^n_i={\mathcal {K}}^n_i/{n\atopwithdelims ()i}\) and to obtain the following reformulation of \(\rho (n, d, k)\) as a linear program.
Lemma 14
For any \(n\ge d\ge k\) we have:
Limit functions The idea now is to prove a bound on \(\rho (n, d, d)\) which holds for fixed d and is independent of n. We will do this by considering ‘the limit’ of problem (41) as \(n \rightarrow \infty \). For each \(k \in {\mathbb {N}}\), we define the limit function:
which, as shown in Lemma 15 below, is in fact a polynomial. We first present the polynomial \(\widehat{{\mathcal {K}}}^\infty _k(t)\) for small k as an illustration.
Example 1
We have:
Lemma 15
We have: \(\widehat{{\mathcal {K}}}^\infty _k(t) = (1 - 2t)^k\) for all \(k \in {\mathbb {N}}\).
Proof
The Krawtchouk polynomials satisfy the following three-term recurrence relation (see, e.g., [28]):
for \(1\le k\le n-1\). By evaluating the polynomials at nt we obtain:
As \(\widehat{{\mathcal {K}}}^\infty _{0}(t) = 1\) and \(\widehat{{\mathcal {K}}}^\infty _{1}(t) = 1 - 2t\) we can conclude that indeed \({\widehat{{\mathcal {K}}}^\infty _k(t) = (1 - 2t)^k}\) for all \(k \in {\mathbb {N}}\). \(\square \)
Next, we show that solutions to (41) remain feasible after increasing the dimension n.
Lemma 16
Let \(\lambda = (\lambda _0, \lambda _1, \dots , \lambda _d)\) be a feasible solution to (41) for a certain \(n \in {\mathbb {N}}\). Then it is also feasible to (41) for \(n+1\) (and thus for any \(n'\ge n+1\)). Therefore, \(\rho (n+1,d,k) \ge \rho (n,d,k)\) for all \(n\ge d\ge k\) and thus \(\rho (n+1,d)\ge \rho (n,d)\) for all \(n\ge d\).
Proof
We may view \({\mathbb {B}}^{n}\) as a subset of \({\mathbb {B}}^{n+1}\) via the map \(a \mapsto (a,0)\), and analogously \({\mathcal {R}}[{x_1,\ldots ,x_n}]\) as a subset of \( {\mathcal {R}}[{x_1,\ldots ,x_n,x_{n+1}}]\) via \(\chi _a \mapsto \chi _{(a,0)}\). Now for \(m, i \in {\mathbb {N}}\) we consider again the zonal spherical harmonic (18):
Consider the set \({\mathrm{St}}(0) \subseteq {{\,\mathrm{Aut}\,}}({\mathbb {B}}^{n+1})\) of automorphisms fixing \(0 \in {\mathbb {B}}^{n+1}\), i.e., the coordinate permutations arising from \(\sigma \in \text {Sym}(n+1)\). We will use the following identity:
To see that (42) holds note that its left hand side is equal to
where \(N_b\) denotes the number of pairs \((\sigma ,a)\) with \(\sigma \in \text {Sym}(n+1)\), \(a\in {\mathbb {B}}^{n}\), \(|a|=i\) such that \(b=\sigma (a,0)\). As there are \(n\atopwithdelims ()i\) choices for a and \(i!(n + 1 - i)!\) choices for \(\sigma \) we have \(N_b= {n\atopwithdelims ()i}i!(n + 1 - i)!\) and thus (42) holds.
Assume \(\lambda \) is a feasible solution of (41) for a given value of n. Then, in view of (21), this means
Using (42) we obtain:
for all \(x\in {\mathbb {B}}^{n+1}\). Using (21) again, this shows that \(\lambda \) is a feasible solution of program (41) for \(n+1\). \(\square \)
Example 2
To illustrate the identity (42), we give a small example with \(n=i=2\). Consider:
The automorphisms in \({\mathrm{St}}(0) \subseteq {{\,\mathrm{Aut}\,}}({\mathbb {B}}^{3})\) fixing \(0 \in {\mathbb {B}}^{3}\) are the permutations of \(x_1, x_2, x_3\). So we get:
and indeed \({2 \atopwithdelims ()2} / {3 \atopwithdelims ()2} = 1/3\).
Lemma 17
For \(d\ge k \in {\mathbb {N}}\), define the program:
Then, for any \(n\ge d\), we have: \(\rho (n, d, k) \le \rho (\infty , d, k)\).
Proof
Let \(\lambda \) be a feasible solution to (41) for (n, d, k). We show that \(\lambda \) is feasible for (43). For this fix \(t \in [0, 1] \cap {\mathbb {Q}}\). Then there exists a sequence of integers \((n_j)_j \rightarrow \infty \) such that \(n_j \ge n\) and \(tn_j \in [0, n_j]\) is integer for each \(j \in {\mathbb {N}}\). As \(n_j\ge n\), we know from Lemma 16 that \(\lambda \) is also a feasible solution of program (41) for \((n_j,d,k)\). Hence, since \(n_jt\in [0:n_j]\) we obtain
But this immediately gives:
As \([0, 1] \cap {\mathbb {Q}}\) lies dense in [0, 1] (and the \(\widehat{{\mathcal {K}}}^\infty _i\)’s are continuous) we may conclude that (44) holds for all \(t \in [0, 1]\). This shows that \(\lambda \) is feasible for (43) and we thus have \(\rho (n, d, k) \le \rho (\infty , d, k)\), as desired. \(\square \)
It remains now to compute the optimum solution to the program (43). In light of Lemma 15, and after a change of variables \(x = 1 - 2t\), this program may be reformulated as:
In other words, we are tasked with finding a polynomial p(x) of degree d satisfying \(|p(x)| \le 1\) for all \(x \in [-1, 1]\), whose k-th coefficient is as large as possible in absolute value. This is a classical extremal problem solved by V. Markov.
Theorem 9
(see, e.g., Theorem 7, pp. 53 in [29]) For \(m \in {\mathbb {N}}\), let \(T_m(x) = \sum _{i=0}^m t_{m, i} x^i\) be the Chebyshev polynomial of degree m. Then the optimum solution \(\lambda \) to (45) is given by:
In particular, \(\rho (\infty , d, k)\) is equal to \(|t_{d, k}|\) (resp. \(|t_{d-1, k}|\)).
As the coefficients of the Chebyshev polynomials are known explicitely, Theorem 9 allows us to give exact values of the constant \(\gamma _d\) appearing in our main results (see Table 1). Using the following identity:
we are also able to concretely estimate:
7 Concluding remarks
Summary We have shown a theoretical guarantee on the quality of the sum-of-squares hierarchy \(\smash {f_{({r})}} \le f_{\min }\) for approximating the minimum of a polynomial f of degree d over the boolean cube \({\mathbb {B}}^{n}\). As far as we are aware, this is the first such analysis that applies to values of r smaller than \((n+d) / 2\), i.e., when the hierarchy is not exact. Additionally, our guarantee applies to a second, measure-based hierarchy of bounds \(\smash {f^{({r})}} \ge f_{\min }\). Our result may therefore also be interpreted as bounding the range \(\smash {f^{({r})}} - \smash {f_{({r})}}\). Our analysis also applies to polynomial optimization over the cube \(\{\pm 1\}^n\) (by a simple change of variables), over the q-ary cube (see Appendix A) and in the setting of matrix-valued polynomials (see Appendix B).
Analysis for small values of r A limitation of Theorem 1 is that the analyis of \(\smash {f_{({r})}}\) applies only for choices of d, r, n satisfying \(d(d+1) \xi ^n_{r+1} \le 1/2\). One may partially avoid this limitation by proving a slightly sharper version of Lemma 6, showing instead that \( \varLambda \le {\tilde{\varLambda }}/(1 - {\tilde{\varLambda }}), \) assuming now only that \({\tilde{\varLambda }}\le 1\). Indeed, Lemma 6 is a special case of this result, assuming that \({\tilde{\varLambda }}\le 1/2\) to obtain \(\varLambda \le 2 {\tilde{\varLambda }}\). Nevertheless, our methods exclude values of r outside of the regime \(r = \varOmega (n)\).
The constant \(\gamma _d\) The strength of our results depends in large part on the size of the constant \(C_d\) appearing in Theorem 1 and Theorem 3, where we may set \(C_d=d(d+1)\gamma _d\). Recall that \(\gamma _d\) is defined in Lemma 5 as a constant for which \(\Vert p_k\Vert _{\infty } \le \gamma _d \Vert p\Vert _{\infty }\) for any polynomial \({p = p_0 + p_1 + \ldots + p_d}\) of degree d and \(k \le d\) on \({\mathbb {B}}^{n}\), independently of the dimension n. In Sect. 6 we have shown the existence of such a constant. Furthermore, we have shown there that we may choose \(\gamma _d \le (1 + \sqrt{2})^d\), and have given an explicit expression for the smallest possible value of \(\gamma _d\) in terms of the coefficients of Chebyshev polynomials. Table 1 lists these values for small d.
Computing extremal roots of Krawtchouk polynomials Although Theorem 2 provides only an asymptotic bound on the least root \(\xi _{r}^n\) of \({\mathcal {K}}^n_r\), it should be noted that \(\xi _{r}^n\) can be computed explicitely for small values of r, n, thus allowing for a concrete estimate of the error of both Lasserre hierarchies via Theorems 1 and 3, respectively. Indeed, as is well-known, the root \(\xi _{r+1}^n\) is equal to the smallest eigenvalue of the \((r+1)\times (r+1)\) matrix A (aka Jacobi matrix), whose entries are given by \(A_{i,j} = \langle t\widehat{{\mathcal {K}}}^n_i(t), \widehat{{\mathcal {K}}}^n_j(t) \rangle _\omega \) for \(i,j\in \{0,1,\ldots , r\}\). See, e.g., [41] for more details.
Connecting the hierarchies Our analysis of the outer hierarchy \(\smash {f_{({r})}}\) on \({\mathbb {B}}^{n}\) relies essentially on knowledge of the the inner hierarchy \(\smash {f^{({r})}}\). Although not explicitely mentioned there, this is the case for the analysis on \(S^{n-1}\) in [11] as well. As the behaviour of \(\smash {f^{({r})}}\) is generally quite well understood, this suggests a potential avenue for proving further results on \(\smash {f_{({r})}}\) in other settings.
For instance, the inner hierarchy \(\smash {f^{({r})}}\) is known to converge at a rate in \(O(1/r^2)\) on the unit ball \(B^n\) or the unit box \([-1, 1]^n\), but matching results on the outer hierarchy \(\smash {f_{({r})}}\) are not available. The question is thus whether the strategy used for the hypersphere \(S^{n-1}\) in [11] and for the boolean cube \({\mathbb {B}}^{n}\) here might be extended to these cases as well.
A difficulty is that the sets \(B^n\) and \([-1, 1]^n\) have a more complicated symmetric structure than \(S^{n-1}\) and \({\mathbb {B}}^{n}\), respectively. In particular, the group actions have uncountably many orbits in these cases, and a direct analog of the Funk–Hecke formula (28) is not available. New ideas are therefore needed to define the kernel \(K(x,y)\) (cf. 8) and analyze its eigenvalues.
Notes
Technically, the program (31) allows for the density to be a sum of squares, whereas the program (35) requires the density to be an actual square. This is no true restriction, though, since, as a straightforward convexity argument shows, the optimum solution to (31) can in fact always be chosen to be a square [20].
Note that as p is assumed to be real-valued, the coefficients \(\lambda _i\) must be real. Indeed, for each \(a \in \mathbb ({\mathbb {Z}}/ q{\mathbb {Z}})^{n}\), we have \(\langle p, \chi _a \rangle _{\mu } = \lambda _{|a|} \Vert \chi _a\Vert ^2 = \lambda _{|a|} \Vert \chi ^{-1}_{a}\Vert ^2 = \langle p, \overline{\chi _a} \rangle _{\mu } = \overline{\langle p, \chi _a \rangle _{\mu }}\).
References
Alon, N., Naor, A.: Approximating the cut-norm via Grothendieck’s inequality. In: 36th Annual ACM Symposium on Theory of Computing, pp. 72–80 (2004)
Arora, S., Berger, E., Hazan, E., Kindler, G., Safra, M.: On non-approximability for quadratic programs. In: Proceedings of the 46th Annual IEEE Symposium on Foundations of Computer Science, pp. 206–215 (2005)
Balas, E., Ceria, S., Cornuéjols, G.: A lift-and-project cutting plane algorithm for mixed 0–1 programs. Math. Program. 58, 295–324 (1993)
Bansal, N., Blum, A., Chawla, S.: Correlation clustering. Mach. Learn. 46(1–3), 89–113 (2004)
Barak, B., Steurer, D.: Sum-of-squares proofs and the quest toward optimal algorithms. In Proceedings of International Congress of Mathematicians (ICM) (2014)
Charikar, M., Wirth, A.: Maximizing quadratic programs: Extending Grothendieck’s inequality. In: Proceedings of the 45th Annual IEEE Symposium on Foundations of Computer Science, pp. 54–60 (2004)
de Klerk, E., Laurent, M.: A survey of semidefinite programming approaches to the generalized problem of moments and their error analysis. In: Araujo C., Benkart G., Praeger C., Tanbay B. (eds), World Women in Mathematics 2018. Association for Women in Mathematics Series, vol. 20, pp. 17–56. Springer, Cham (2019)
de Klerk, E., Laurent, M.: Convergence analysis of a Lasserre hierarchy of upper bounds for polynomial minimization on the sphere. Math. Program. (2020). https://doi.org/10.1007/s10107-019-01465-1
de Klerk, E., Laurent, M.: Worst-case examples for Lasserre’s measure based hierarchy for polynomial optimization on the hypercube. Math. Oper. Res. 45(1), 86–98 (2020)
Doherty, A.C., Wehner, S.: Convergence of SDP hierarchies for polynomial optimization on the hypersphere (2012). arXiv:1210.5048
Fang, K., Fawzi, H.: The sum-of-squares hierarchy on the sphere, and applications in quantum information theory. Math. Program. (2020). https://doi.org/10.1007/s10107-020-01537-7
Fawzi, H., Saunderson, J., Parrilo, P.A.: Sparse sums of squares on finite abelian groups and improved semidefinite lifts. Math. Program. 160(1–2), 149–191 (2016)
Goemans, M., Williamson, D.: Improved approximation algorithms for maximum cut and satisfiability problems using semidefinite programming. J. Assoc. Comput. Mach. 42(6), 1115–1145 (1995)
Karlin, A.R., Mathieu, C., Nguyen, C.T.: Integrality gaps of linear and semi-definite programming relaxations for knapsack. In: Günlük, O., Woeginger, G.J. (eds.) Integer Programming and Combinatoral Optimization, pp. 301–314. Springer, Berlin, Heidelberg (2011)
Kurpisz, A., Leppänen, S., Mastrolilli, M.: Tight Sum-of-Squares lower bounds for binary polynomial optimization problems. In: Chatzigiannakis, I., et al. (eds) 43rd International Colloquium on Automata, Languages, and Programming (ICALP 2016) vol. 78, pp. 1–14 (2016)
Lasserre, J.B.: Global optimization with polynomials and the problem of moments. SIAM J. Optim. 11(3), 796–817 (2001)
Lasserre, J.B.: A max-cut formulation of \(0/1\) programs. Oper. Res. Lett. 44, 158–164 (2016)
Lasserre, J.B.: An explicit exact sdp relaxation for nonlinear 0–1 programs. In: Aardal, K., Gerards, B. (eds.) Integer Programming and Combinatorial Optimization, pp. 293–303, Springer, Berlin, Heidelberg (2001)
Lasserre, J.B.: Moments. Positive Polynomials and Their Applications. Imperial College Press, London (2009)
Lasserre, J.B.: A new look at nonnegativity on closed sets and polynomial optimization. SIAM J. Optim. 21(3), 864–885 (2010)
Laurent, M.: A comparison of the Sherali–Adams, Lovász-Schrijver and Lasserre relaxations for 0-1 programming. Math. Oper. Res., 28(3):470–496 (2003)
Laurent, M.: Lower bound for the number of iterations in semidefinite hierarchies for the cut polytope. Math. Oper. Res. 28(4), 871–883 (2003)
Laurent, M.: Semidefinite representations for finite varieties. Math. Program. 109, 1–26 (2007)
Laurent, M.: Sums of squares, moment matrices and optimization over polynomials. In: Putinar, M., Sullivant, S. (eds.) Emerging Applications of Algebraic Geometry, Vol. 149 of IMA Volumes in Mathematics and its Applications, pp. 157–270. Springer (2009)
Lee, J.R., Raghavendra, P., Steurer, D.: Lower bounds on the size of semidefinite programming relaxations. In: STOC ’15: Proceedings of the Forty-Seventh Annual ACM Symposium on Theory of Computing, pp. 567–576 (2015)
Levenshtein, V.I.: Universal bounds for codes and designs. In: Handbook of Coding Theory, vol. 9, pp. 499–648. North-Holland, Amsterdam (1998)
Lovász, L., Schrijver, A.: Cones of matrices and set-functions and 0–1 optimization. SIAM J. Optim. 1, 166–190 (1991)
Macwilliams, F., Sloane, N.: The Theory of Error Correcting Codes, volume 16 of North-Holland Mathematical Library. Elsevier (1983)
Natanson, I.P.: Constructive Function Theory, Vol. I Uniform Approximation (1964)
Nie, J., Schweighofer, M.: On the complexity of Putinar’s positivstellensatz. J. Complex. 23(1), 135–150 (2007)
O’Donnell, R.: SOS is not obviously automatizable, even approximately. In: 8th Innovations in Theoretical Computer Science Conference vol. 59, pp. 1–10 (2017)
Parrilo, P.A.: Structured semidefinite programs and semialgebraic geometry methods in robustness and optimization. Ph.D thesis, California Institure of Technology (2000)
Raghavendra, P., Weitz, B.: On the bit complexity of sum-of-squares proofs. In: 44th International Colloquium on Automata, Languages, and Programming, vol. 80, pp. 1–13 (2017)
Reznick, B.: Uniform denominators in Hilbert’s seventeenth problem. Math. Z. 220(1), 75–97 (1995)
Rothvoss, T.: The Lasserre hierarchy in approximation algorithms. Lecture Notes for the MAPSP 2013 Tutorial (2013)
Sakaue, S., Takeda, A., Kim, S., Ito, N.: Exact semidefinite programming relaxations with truncated moment matrix for binary polynomial optimization problems. SIAM J. Optim. 27(1), 565–582 (2017)
Scherer, C.W., Hol, C.W.J.: Matrix sum-of-squares relaxations for robust semi-definite programs. Math. Program. 107, 189–211 (2006)
Schweighofer, M.: On the complexity of Schmüdgen’s positivstellensatz. J. Complex. 20(4), 529–543 (2004)
Sherali, H.D., Adams, W.P.: A hierarchy of relaxations between the continuous and convex hull representations for zero-one programming problems. SIAM J. Discret. Math. 3, 411–430 (1990)
Slot, L., Laurent, M.: Improved convergence analysis of Lasserre’s measure-based upper bounds for polynomial minimization on compact sets. Math. Program. (2020). https://doi.org/10.1007/s10107-020-01468-3
Szegö, G.: Orthogonal Polynomials. vol. 23 in American Mathematical Society colloquium publications. American Mathematical Society (1959)
Slot, L., Laurent, M.: Near-optimal analysis of of Lasserre’s univariate measure-based bounds for multivariate polynomial optimization. Math. Program. (2020). https://doi.org/10.1007/s10107-020-01586-y
Terras, A.: Fourier Analysis on Finite Groups and Applications. London Mathematical Society Student Texts, Cambridge University Press, Cambridge (1999)
Tunçel, L.: Polyhedral and Semidefinite Programming Methods in Combinatorial Optimization. Fields Institute Monograph (2010)
Vallentin, F.: Semidefinite programs and harmonic analysis. arXiv:0809.2017 (2008)
Acknowledgements
We wish to thank Sven Polak and Pepijn Roos Hoefgeest for several useful discussions. We also thank the anonymous referees for their helpful comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work is supported by the European Union’s Framework Programme for Research and Innovation Horizon 2020 under the Marie Skłodowska-Curie Actions Grant Agreement No. 764759 (MINOA)
Appendices
The q-ary cube
In this section, we indicate how our results for the boolean cube \({\mathbb {B}}^{n}\) may be extended to the q-ary cube \(\mathbb ({\mathbb {Z}}/ q{\mathbb {Z}})^{n} = \{0, 1, \dots , q-1\}^n\) when \(q > 2\) is a fixed integer. Here \({\mathbb {Z}}/ q{\mathbb {Z}}\) denotes the cyclic group of order q, so that \(\mathbb ({\mathbb {Z}}/ q{\mathbb {Z}})^{n}={\mathbb {B}}^{n}\) when \(q=2\). The lower bound \(\smash {f_{({r})}}\) for the minimum of a polynomial f over \(\mathbb ({\mathbb {Z}}/ q{\mathbb {Z}})^{n}\) is defined analogously to the case \(q=2\); namely we set
where the condition means that \(f(x) - \lambda \) agrees with a sum of squares \(s \in \varSigma [x]_{2r}\) for all \(x \in \mathbb ({\mathbb {Z}}/ q{\mathbb {Z}})^{n}\) or, alternatively, that \(f - \lambda - s\) belongs to the ideal generated by the polynomials \(x_i(x_i -1)\ldots (x_i - q + 1)\) for \(i \in [n]\). Similarly, the upper bound \(\smash {f^{({r})}}\) is defined as in (7) after equipping \(\mathbb ({\mathbb {Z}}/ q{\mathbb {Z}})^{n}\) with the uniform measure \(\mu \). The parameters \(\smash {f_{({r})}}\) and \(\smash {f^{({r})}}\) may again be computed by solving a semidefinite program of size polynomial in n for fixed \(r, q \in {\mathbb {N}}\), see [23].
As before d(x, y) denotes the Hamming distance and |x| denotes the Hamming weight (number of nonzero components). Note that, for \(x,y\in \mathbb ({\mathbb {Z}}/ q{\mathbb {Z}})^{n}\), d(x, y) can again be expressed as a polynomial in x, y, with degree \(q-1\) in each of x and y.
We will prove Theorem 11 below, which can be seen as an analog of Corollary 1 for \(\mathbb ({\mathbb {Z}}/ q{\mathbb {Z}})^{n}\). The general structure of the proof is identical to that of the case \(q=2\). We therefore only give generalizations of arguments as necessary. For reasons that will become clear later, it is most convenient to consider the sum-of-squares bound \(\smash {f_{({r})}}\) on the minimum \(f_{\min }\) of a polynomial f with degree at most \((q-1)d\) over \(\mathbb ({\mathbb {Z}}/ q{\mathbb {Z}})^{n}\), where \(d\le n\) is fixed.
Fourier analysis on \(\mathbb ({\mathbb {Z}}/ q{\mathbb {Z}})^{n}\) and Krawtchouk polynomials Consider the space
consisting of the polynomials on \(\mathbb ({\mathbb {Z}}/ q{\mathbb {Z}})^{n}\) with complex coefficients. We equip \({\mathcal {R}}[{x}]\) with its natural inner product
where \(\mu \) is the uniform measure on \(\mathbb ({\mathbb {Z}}/ q{\mathbb {Z}})^{n}\). The space \({\mathcal {R}}[{x}]\) has dimension \(|\mathbb ({\mathbb {Z}}/ q{\mathbb {Z}})^{n}| = q^n\) over \({\mathbb {C}}\) and it is spanned by the polynomials of degree up to \((q-1)n\). The reason we now need to work with polynomials with complex coefficients is that the characters have complex coefficients when \(q>2\).
Let \(\psi = e^{2\pi i / q}\) be a primitive q-th root of unity. For \(a \in \mathbb ({\mathbb {Z}}/ q{\mathbb {Z}})^{n}\), the associated character \(\chi _a \in {\mathcal {R}}[{x}]\) is defined by:
So (14) is indeed the special case of this definition when \(q=2\). The set of all characters \(\{ \chi _a : a \in \mathbb ({\mathbb {Z}}/ q{\mathbb {Z}})^{n} \}\) forms an orthogonal basis for \({\mathcal {R}}[{x}]\) w.r.t. the above inner product \(\langle \cdot , \cdot \rangle _{\mu }\). A character \(\chi _a\) can be written as a polynomial of degree \((q-1) \cdot |a|\) on \(\mathbb ({\mathbb {Z}}/ q{\mathbb {Z}})^{n}\), i.e., we have \(\chi _a \in {\mathcal {R}}[{x}]_{(q-1)|a|}\) for all \(a \in \mathbb ({\mathbb {Z}}/ q{\mathbb {Z}})^{n}\).
As before, we have the direct sum decomposition into pairwise orthogonal subspaces:
where \(H_i\) is spanned by the set \(\{ \chi _a : |a| = i \}\) and \(H_i\subseteq {\mathbb {R}}[x]_{(q-1)i}\). The components \(H_i\) are invariant and irreducible under the action of \({{\,\mathrm{Aut}\,}}(\mathbb ({\mathbb {Z}}/ q{\mathbb {Z}})^{n})\), which is generated by the coordinate permutations and the action of \(\text {Sym}(q)\) on individual coordinates. Hence any \(p \in {\mathcal {R}}[{x}]\) of degree at most \((q-1)d\) can be (uniquely) decomposed as:
As before \({\mathrm{St}}(0) \subseteq {{\,\mathrm{Aut}\,}}(\mathbb ({\mathbb {Z}}/ q{\mathbb {Z}})^{n})\) denotes the stabilizer of \(0 \in \mathbb ({\mathbb {Z}}/ q{\mathbb {Z}})^{n}\), which is generated by the coordinate permutations and the permutations in \(\text {Sym}(q)\) fixing 0 in \(\{0,1,\ldots ,q-1\}\) at any individual coordinate. We note for later reference that the subspace of \(H_i\) invariant under action of \({\mathrm{St}}(0)\) is of dimension one, and is spanned by the zonal spherical function:
The Krawtchouk polynomials introduced in Sect. 2 have the following generalization in the q-ary setting:
Analogously to relation (20), the Krawtchouk polynomials \({\mathcal {K}}^n_k\) (\(0\le k\le n\)) are pairwise orthogonal w.r.t. the discrete measure \(\omega \) on [0 : n] given by:
To be precise, we have:
As \({\mathcal {K}}^n_k(0) = (q-1)^k {n \atopwithdelims ()k} = \Vert {\mathcal {K}}^n_k \Vert ^2_{\omega }\), we may normalize \({\mathcal {K}}^n_k\) by setting:
so that \(\widehat{{\mathcal {K}}}^n_k\) satisfies \(\max _{t=0}^n \widehat{{\mathcal {K}}}^n_k(t) = \widehat{{\mathcal {K}}}^n_k(0) = 1\) (cf. 23).
We have the following connection (cf. 22) between the characters and the Krawtchouk polynomials:
Note that for all \(a, x, y \in \mathbb ({\mathbb {Z}}/ q{\mathbb {Z}})^{n}\), we have:
Hence, for any \(x,y\in \mathbb ({\mathbb {Z}}/ q{\mathbb {Z}})^{n}\), we also have (cf. 21):
Invariant kernels In analogy to the binary case \(q=2\), for a degree r univariate polynomial \(u\in {\mathbb {R}}[t]_r\) we define the associated polynomial kernel \(K(x,y) := u^2(d(x,y))\) (\(x,y\in \mathbb ({\mathbb {Z}}/ q{\mathbb {Z}})^{n}\)) and the associated kernel operator:
Note that K(x, y) is a polynomial on \(\mathbb ({\mathbb {Z}}/ q{\mathbb {Z}})^{n}\) with degree \(2r(q-1)\) in each of x and y. Let us decompose the univariate polynomial \(u(t)^2\) in the Krawtchouk basis as
Then the kernel operator \({\mathbf {K}}\) acts as follows on characters: for \(z \in \mathbb ({\mathbb {Z}}/ q{\mathbb {Z}})^{n}\),
which can be seen by retracing the proof of Theorem 6, and we obtain the Funk–Hecke formula (recall (28)): for any polynomial \(p \in {\mathcal {R}}[{x}]_{(q-1)d}\) with Harmonic decomposition \(p=p_0+\cdots +p_d\),
Performing the analysis It remains to find a univariate polynomial \(u \in {\mathbb {R}}[t]\) of degree r with \(u^2(t) = \sum _{i=0}^{2r}\lambda _i {\mathcal {K}}^n_i(t)\) for which \(\lambda _0 = 1\) and the other scalars \(\lambda _i\) are close to 1. As before (cf. 29), we have:
So we would like to minimize \(\sum _{i=1}^{2r} (1-\lambda _i)\). We are therefore interested in the inner Lasserre hierarchy applied to the minimization of the function \(g(t) = d - \sum _{i = 0}^d \widehat{{\mathcal {K}}}^n_i(t)\) on the set [0 : n] (equipped with the measure \(\omega \) from (47)). We show first that this function g again has a nice linear upper estimator.
Lemma 18
We have:
for all \(k \le n\).
Proof
The proof is almost identical to that of Lemma 4. Let \(t\in [0:n-1]\) and \(0 < k \le d\). Consider the elements \(1^t 0^{n-t}, 1^{t+1} 0^{n-t-1} \in \mathbb ({\mathbb {Z}}/ q{\mathbb {Z}})^{n}\) from Lemma 2. Then we have:
where for the inequality we note that \(\chi _a(1^{t} 0^{n-t}) = \chi _a(1^{t+1} 0^{n-t-1})\) if \(a_{t+1} = 0\). As \({\mathcal {K}}^n_k(0) = (q-1)^k {n \atopwithdelims ()k}\), this implies that:
This shows the first inequality of (49). The second inequality follows using the triangle inequality, a telescope summation argument and the fact that \(\widehat{{\mathcal {K}}}^n_k(0)=1\). \(\square \)
From Lemma 18 we obtain that the function \(g(t)= d - \sum _{i = 0}^d \widehat{{\mathcal {K}}}^n_i(t) \) admits the following linear upper estimator: \(g(t) \le d(d+1) \cdot (t/n)\) for \(t \in [0:n]\). Now the same arguments as used for the case \(q=2\) enable us to conclude:
and, when \(d(d+1) \xi _{r+1,q}^n / n \le 1/2\),
Here \(C_d\) is a constant depending only on d and \(\xi _{r+1,q}^n\) is the least root of the Krawtchouk polynomial \({\mathcal {K}}^n_{r+1, q}\). Note that as the kernel \(K(x,y) = u^2(d(x,y))\) is of degree \(2(q-1)r\) in x (and y), we are only able to analyze the corresponding levels \((q-1)r\) of the hierarchies. We come back below to the question on how to show the existence of the above constant \(C_d\).
But first we finish the analysis. Having shown analogs of Theorem 1 and Theorem 3 in this setting, it remains to state the following more general version of Theorem 2, giving information about the smallest roots of the q-ary Krawtchouk polynomials.
Theorem 10
([26], Section 5) Fix \(t\in [0,{q-1\over q}]\). Then the smallest roots \(\xi ^n_{r,q}\) of the q-ary Krawtchouk polynomials \({\mathcal {K}}^n_{r, q}\) satisfy:
Here the above limit means that, for any sequences \((n_j)_j\) and \((r_j)_j\) of integers such that \(\lim _{j\rightarrow \infty } n_j=\infty \) and \(\lim _{j\rightarrow \infty }r_j/n_j=t\), we have \(\lim _{j\rightarrow \infty } \xi _{r_j,q}^{n_j}/n_j =\varphi _q(t)\).
Note that for \(q=2\) we have \(\varphi _q(t) ={1\over 2} -\sqrt{t(1-t)}\), which is the function \(\varphi (t)\) from (5). To avoid technical details we only quote in Theorem 10 the asymptotic analog of Theorem 2 (and not the exact bound on the root \(\xi ^n_{r,q}\) for any n). Therefore we have shown the following q-analog of Corollary 1.
Theorem 11
Fix \(d\le n\) and for \(n,r\in {\mathbb {N}}\) write
There exists a constant \(C_d>0\) (depending also on q) such that, for any \(t\in [0,{q-1\over q}]\), we have:
and, if \(d(d+1)\cdot \varphi _q(t) \le 1/2\), then we also have:
Here \(\varphi _q(t)\) is the function defined in (50). Recall that the limit notation \(r/n\rightarrow t\) means that the claimed convergence holds for any sequences \((n_j)_j\) and \((r_j)_j\) of integers such that \(\lim _{j\rightarrow \infty } n_j=\infty \) and \(\lim _{j\rightarrow \infty }r_j/n_j=t\).
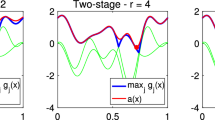
For reference, the function \(\varphi _q(t)\) is shown for several values of q in Fig. 1.
The function \(\varphi _q(t)\) for several values of q. Note that the case \(q=2\) corresponds to the function \(\varphi (t)\) of (5)
A generalization of Lemma 5 The arguments above omit a generalization of Lemma 5, which is instrumental to show the existence of the constant \(C_d\) claimed above. In other words, we still need to show that if \(p : \mathbb ({\mathbb {Z}}/ q{\mathbb {Z}})^{n} \rightarrow {\mathbb {R}}\) is a polynomial of degree \((q-1)d\) on \(\mathbb ({\mathbb {Z}}/ q{\mathbb {Z}})^{n}\) with harmonic decomposition \(p=p_0+\ldots +p_d\), there then exists a constant \(\gamma _d > 0\) (independent of n) such that:
Then, as in the binary case, we may set \(C_d=d(d+1)\gamma _d\). The proof given in Sect. 6 for the case \(q=2\) applies almost directly to the general case, and we only generalize certain steps as required. So consider again the parameters:
Lemmas 12 and 13, which show that the optimum solution p to \(\rho (n, d, k)\) may be assumed to be invariant under \({\mathrm{St}}(0) \subseteq {{\,\mathrm{Aut}\,}}(\mathbb ({\mathbb {Z}}/ q{\mathbb {Z}})^{n})\), clearly apply to the case \(q > 2\) as well. That is to say, we may assume p is of the form:Footnote 2
where \(X_i = \sum _{|a| = i}\chi _a \in H_i\) is the zonal spherical function of degree \((q-1)i\) (cf. 46 and 18). Using (48), we obtain a reformulation of \(\rho (n, d, k)\) as an LP (cf. 41):
For \(k \in {\mathbb {N}}\), let \(\widehat{{\mathcal {K}}}^\infty _k(t) := \lim _{n \rightarrow \infty } \widehat{{\mathcal {K}}}^n_k(nt) = \Big (1 - \frac{q}{q-1}t\Big )^k\) and consider the program (cf. 43):
As before, we have \(\rho (n, d, k) \le \rho (\infty , d, k)\), noting that (the proofs of) Lemmas 16 and 17 may be applied directly to the case \(q>2\). From there, it suffices to show \(\rho (\infty , d, k) < \infty \), which can be argued in an analogous way to the case \(q=2\).
Matrix-valued polynomials
In this section, we show how the arguments used for the proofs of our main results in Theorems 1 and 3 may be applied in the setting of matrix-valued polynomials, thereby proving Theorems 4 and 5.
Recall that \({\mathcal {S}}^k\) is the space of \(k\times k\) real symmetric matrices and \({\mathcal {S}}^k[x] \subseteq {\mathbb {R}}^{k \times k}[x]={\mathbb {R}}[x]^{k\times k}\) is the space of n-variate polynomials whose coefficients lie in \({\mathcal {S}}^k\). Given a polynomial matrix \(F\in {\mathcal {S}}^k[x]\) we consider the matrix-valued polynomial optimization problem:
for which we have the outer Lasserre hierarchy:
and the inner Lasserre hierarchy:
Here, the set \(\varSigma ^{k \times k}_r\) consists of all sum-of-squares polynomial matrices \(S \in {\mathcal {S}}^k[x]\), of the form:
The outer hierarchy (proof of Theorem4) We generalize the outline of Sect. 1.5 to the matrix-valued setting. Let \(F\in {\mathcal {S}}^k[x]\) be the polynomial matrix of degree d to be optimized, and assume w.l.o.g. that \(0 \le \Vert F\Vert _\infty \le 1\). Here, and throughout this section, \(\Vert F\Vert _\infty := \max _{x \in {\mathbb {B}}^{n}} \Vert F(x) \Vert \) is the largest absolute value of an eigenvalue of F(x) over \({\mathbb {B}}^{n}\). A kernel \(K\) of the form \(K(x, y) = u^2(d(x,y))\) with \(u \in {\mathbb {R}}[t]_r\) (cf. 8) induces a linear operator \({\mathbf {K}}\) on \({\mathcal {S}}^k[x]\) by:
If \(P(x) \succeq 0\) for all \(x \in {\mathbb {B}}^{n}\), then the polynomial \({\mathbf {K}}P\) is a sum-of-squares polynomial matrix of degree at most 2r on \({\mathbb {B}}^{n}\). Indeed, we then have:
Given \(\delta > 0\) to be determined later, set \({\tilde{F}} = F + \delta I\). Assuming that \({\mathbf {K}}\) is non-singular, we can write \(F = {\mathbf {K}}({\mathbf {K}}^{-1} {\tilde{F}})\). Therefore, assuming that \({\mathbf {K}}^{-1} {\tilde{F}}\) is positive semidefinite over \({\mathbb {B}}^{n}\), we find that \(F + \delta I\) is a sum-of-squares polynomial matrix of degree 2r on \({\mathbb {B}}^{n}\), and thus that \(F_{\min } - F_{(r)} \le \delta \).
To guarantee positive semidefiniteness of \({\tilde{F}}\), it suffices to ensure that (cf. 9):
Indeed, as the smallest eigenvalue of \({\tilde{F}}(x)\) is at least \(\delta \) for each \(x \in {\mathbb {B}}^{n}\), the smallest eigenvalue of \({\mathbf {K}}^{-1}F(x)\) must then be at least zero.
As in the case of scalar-valued polynomials, the eigenvalues of \({\mathbf {K}}\) are given by the coefficients \(\lambda _i\) in the expansion \({u^2(t) = \sum _{i = 0}^{2r} \lambda _i {\mathcal {K}}^n_i(t)}\). Indeed, if \(P \in {\mathcal {S}}^k[x]\) is a polynomial matrix of degree d then we may decompose it into harmonic components entry-wise to obtain \({P(x) = \sum _{i=0}^d P_i(x)}\) and (cf. Theorem 6):
It remains to express the quantity \(\Vert {\mathbf {K}}^{-1} - I\Vert \) in terms of the eigenvalues \(\lambda _i\) of \({\mathbf {K}}\), after which the proof proceeds as in the case of scalar polynomials. For this, note that:
where \(\gamma _d\) is the constant of Lemma 5 (cf. 34). The last inequality relies on the following generalization of Lemma 5, whose proof here is essentially as given in [11].
Lemma 19
Let \(P(x) = \sum _{i=0}^d P_i(x)\) be a polynomial matrix of degree d, decomposed into harmonic components. If \(\gamma _d\) is the constant of Lemma 5, we then have:
Proof
For any matrix \(M \in {\mathcal {S}}^k\), its spectral norm is \(\Vert M \Vert _{} = \max _{y \in {\mathbb {R}}^k} \{ |y^\top M y| : \Vert y\Vert = 1\}\). Therefore, we have:
For fixed y, the function \(p^y : x \mapsto y^\top P(x) y\) is a (scalar) polynomial on \({\mathbb {B}}^{n}\) of degree d, whose harmonic components are given by \(p^y_i : x \mapsto y^\top P_i(x) y\). Therefore, we may invoke Lemma 5 to bound:
and conclude that \(\Vert P_i\Vert _\infty \le \gamma _d \Vert P\Vert _\infty \). \(\square \)
The inner hierarchy (proof of Theorem5) We generalize the arguments of Sect. 5 to the matrix-valued setting. Let F again be the polynomial matrix of degree d to be optimized, and assume w.l.o.g. that \(0 \le \Vert F\Vert _\infty \le 1\) and that the minimum in the optimization problem (53) is attained at 0, i.e., that \(F_{\min } = \lambda _{\min } \big (F(0)\big )\).
As in the scalar case, we work to reduce problem (55) to a (now matrix-valued) instance of the inner hierachy in one variable. Note first that \(F^{(r)} \le F_\mathrm{sym}^{(r)}\) for each \(r \in {\mathbb {N}}\), where \(F_\mathrm{sym}^{(r)}\) is obtained by restricting the optimization in (55) to polynomial matrices S(x) of the form \(S(x) = U(|x|)\). Writing \({\widehat{F}}\) for the univariate polynomial matrix satisfying
we find (cf. 38):
It remains to analyze the program (56). We first give a linear upper estimator for \({\widehat{F}}\) (cf. Lemma 9).
Lemma 20
For all \(t \in [0:n]\), we have:
where \(C={\widehat{F}}(0)\) is a constant matrix with \(\lambda _{\min }(C) = 0\).
Proof
We may write \({\widehat{F}}(t) = \sum _{i=0}^d \varLambda _i \widehat{{\mathcal {K}}}^n_i(t)\) for certain \(\varLambda _i \in {\mathcal {S}}^k\). We then have:
making use of Lemma 19 and (24) for the final inequality. It remains to note that \(\sum _{i=0}^d \varLambda _i = {\widehat{F}}(0)\), and that \(\lambda _{\min } ({\widehat{F}}(0)) = 0\) by assumption. \(\square \)
As \({\widehat{F}}(t) \preceq {\widehat{G}}(t)\) for all \(t \in [0:n]\), we have \(F_\mathrm{sym}^{(r)} \le {\widehat{G}}^{(r)}_{[0:n], \omega }\), where:
is the inner Lasserre hierarchy for G computed on [0 : n] w.r.t. the measure \(\omega \). To conclude the argument, we prove the following generalization of Theorem 7 (see also Remark 1).
Corollary 3
Let \(G(t) = ct \cdot I + C\) be a linear matrix-valued polynomial with \(c>0\) and \(\lambda _{\min }(C) = 0\). Then we have:
where \(\xi ^n_{r+1}\) is the least root of the degree \(r+1\) Krawtchouk polynomial.
Proof
Let u be a unit eigenvector for C corresponding to (one of its) zero eigenvalues. Then for any univariate sum-of-squares polynomial \(s \in \varSigma _r\), the matrix-valued polynomial \(U(t) = s(t) u u^\top \) is a sum-of-squares polynomial matrix of degree 2r. Furthermore, for such a U we have:
and
Therefore, writing \(g(t) = ct\), and making use of Theorem 7 and Remark 1, we have:
This concludes the proof. \(\square \)
Rights and permissions
About this article
Cite this article
Slot, L., Laurent, M. Sum-of-squares hierarchies for binary polynomial optimization. Math. Program. 197, 621–660 (2023). https://doi.org/10.1007/s10107-021-01745-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10107-021-01745-9