Introduction

The determination of tissue optical properties is an important issue in laser medical applications such as in photodynamic therapy and diagnostic techniques. The knowledge of tissue optical properties is of great importance for the interpretation and quantification of the diagnostic data and for the prediction of light distribution and absorbed energy for therapeutic and surgical use [1, 2]. Different theoretical models and experimental techniques are used to determine the optical properties of tissue. However, for a complete evaluation of the optical properties of tissue, an integrating-sphere method was usually used where diffused, collimated, transmittance, and reflectance have to be measured to obtain tissue optical properties. The investigation of optical study in modern biological tissue in the areas of diagnostics, therapy, and surgery has stimulated the study of optical properties of various biological tissues. Typically, optical properties are obtained using solutions of the radiative transport equation that express the optical properties in terms of readily measurable quantities [3]. These solutions are either exact or approximate and corresponded to the direct or indirect methods as described by Wilson et al. [4]. The theory used in indirect methods usually falls into one of three categories: Beer’s law, Kubelka-Munk, or the diffusion approximation. Methods based on the diffusion approximation or a similar approximation (e.g., uniform radiances over the forward and backward hemispheres) seem to be more accurate than the Kubelka-Munk method [5, 6]. The diffusion approximation assumed that the internal radiance is nearly isotropic, and consequently, it is inaccurate when scattering is comparable with absorption. [7]. The adding-doubling method is a general, numerical solution of the radiative transport equation [8].

In this work, a new methodology has been proposed to determine tissue optical properties using a laser to induce heat in tissue, such induced heat results in temperature increase, which is detected by a thermocouple inserted in the middle of a tissue sample where the temperature history is used in an inverse heat transfer technique to determine optical properties.

Theory

Due to its advantages, inverse heat transfer problem (IHTP) occupies more interest in both theory and application. It has been used in every branch of science wherever special phenomenon could not be detected directly but its effects could be measured [9]. Laser was used to induce heat to a tissue of known thermal properties and water content. The induced heat results in an increase in the temperature of the tissue. These temperature distributions are recorded and used in an inverse heat transfer technique to detect absorption and reduced scattering coefficients of a homogeneous tissue of known thermal properties.

Monte Carlo simulation

Biological tissue is treated as a linear isotropic homogeneous medium. While a photon enters the tissue, the Monte Carlo method introduces random propagation variables from a well-defined probability distribution. The step size of the photon traveling inside the tissue between two interaction sites is based on the photon’s mean free path. Also, by multiplying the absorption photon probability density by the desired laser power, the total power absorbed in the region is obtained. The absorbed power at each location can be used as a heat source for the thermal diffusion process. The heat generation rate is calculated as

$$ q=\mathrm{photon}\ \mathrm{absorption}\ \mathrm{probability}\times \mathrm{laser}\ \mathrm{power}, $$

where the photon absorption probability is the portion of photon energy deposited in a unit volume, obtained by the Monte Carlo simulation [10].

Heat transfer equation

The determination of optical properties of a sample needs an accurate determination of temperature distribution which can be obtained using the heat equation [11].

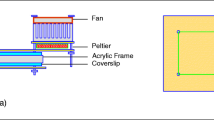
$$ k{\nabla}^2T\left(r,z,t\right)+\dot{Q}=\rho c\frac{\partial T}{\partial t} $$
(1)

where \( \dot{Q} \) is the heat generation inside the tissue, T is the temperature, k is the thermal conductivity of the tissue, ρ is the density, and c is the specific heat. For tissue thermal properties, the relation between them and water content are used here, see ref. [12]. Constant thermal properties are assumed, because in most cases, the temperature increase is not significant enough to change the tissue properties. The possible boundary conditions are that laser will hit one face of the sample where the sample faces are assumed to be subjected to convection natural convection heat transfer (i.e., h=10 W/m2 K), assume the tissue sample has a dimension of 20 × 20 × 1 mm where the edges of the sample are far from the center of the sample where the laser hits the tissue and the assumption of insulated boundary conditions seems to be reasonable, see Fig. 1 which shows the experimental set up. The mathematical formulation of boundary conditions can be written as shown below. The heat generation can be obtained from the Monte Carlo simulation if the scattering coefficient is much larger than the absorption coefficient otherwise the modified Beer-Lambert law can be used [13, 14]:

$$ \overset{\cdot }{Q}={\mu}_a\kern0.5em {I}_o{e}^{-\left({\mu}_a+{\mu}_s^{\hbox{'}}\right)x} $$
(2a)
$$ -k\frac{dT}{dx}=\dot{Q}\ at\ any\ x $$
(2b)
$$ k\partial T/\partial x=h\left(T-{T}_{\infty}\right)\kern0.5em \mathrm{at}\ \mathrm{x}=0,\mathrm{L} $$
(2c)
Fig. 1
figure 1

a Experimental setup. b The sample and its boundary conditions and thermocouple location

Full size image
$$ T\left(x,t\right)={T}_{\infty }={22}^{{}^{\circ}}C\kern0.5em \mathrm{at}\ \mathrm{t}=0 $$
(2d)

Finite element formulation

The discretization of the Fourier equation subjected to the above boundary conditions can be accomplished using the Galerkin method. The region of interest Ω is divided into a number of elements, Ωe, with a usual shape function Ni associated with each node. The unknown function T is approximated through the solution domain at any time by

$$ T=\sum {N}_i\left(x,t\right)\;{T}_i(t) $$
(3)

where Ti(t) are the nodal parameters. Substitution of the above equation into eq. (1) and the application of the Galerkin method result in a system of ordinary differential equations of the form [15]

$$ \left[C\right]\overrightarrow{T}+\left[K\right]T+\left[F\right]=0 $$
(4)

where

$$ \overset{\dot \rightharpoonup }{T}=\left\{\begin{array}{c}\frac{\partial {T}_1}{\partial t}\\ {}\frac{\partial {T}_2}{\partial t}\\ {}\\ {}\\ {}\frac{\partial {T}_p}{\partial t}\end{array}\right\},\kern0.5em \overset{\rightharpoonup }{T}=\left\{\begin{array}{c}{T}_1\\ {}{T}_2\\ {}..\\ {}..\\ {}{T}_p\end{array}\right\}\kern0.5em \mathrm{and}\kern0.5em \left[F\right]=\left\{\begin{array}{c}{F}_1\\ {}{F}_2\\ {}..\\ {}{F}_p\end{array}\right\}\mathrm{where}\ p\ \mathrm{is}\ \mathrm{the}\ \mathrm{total}\ \mathrm{no}.\mathrm{of}\ \mathrm{node} $$
(5)

And the typical matrix elements are

$$ {K}_{ij}=\sum {\int}_{\varOmega^e}k\left(\frac{\partial {N}_i}{\partial x}\frac{\partial {N}_j}{\partial x}\right)\ d\varOmega +\sum {\int}_{\varGamma^e}{N}_ih\ d\varGamma $$
(6)
$$ {C}_{ij}=\sum \underset{\varOmega^e}{\int}\rho\;C{N}_i{N}_j d\varOmega $$
(7)
$$ {F}_i=\sum \underset{\varGamma^e}{\int }{N}_i\left(q-h{T}_{\infty}\right) d\varGamma -\sum \underset{\varOmega^e}{\int }{N}_i\dot{Q} d\varOmega $$
(8)

In the above, the summations are taken over the contribution of each element,Ωe, in the element region and Γe refers only to the element with an external boundary on which surface condition is applied. Using the linear shape function, which normalizes to the time interval Δt, the result is in a standard linear shape function, then the application of weighted residual theory to eq.4 with the linear shape function result in a matrix form of

$$ \left(\frac{\left[C\right]}{\varDelta t}+\varTheta \left[K\right]\right)\;{\overset{\rightharpoonup }{T}}_{n+1}+\left(\frac{-\left[C\right]}{\varDelta t}+\left(1-\varTheta \right)\left[K\right]\right)\;{\overset{\rightharpoonup }{T}}_n+\overset{\rightharpoonup }{F}=0 $$
(9)

where

$$ \overset{\rightharpoonup }{F}={\overset{\rightharpoonup }{F}}_{n+1}\varTheta +{\overset{\rightharpoonup }{F}}_n\left(1-\varTheta \right) $$
(9a)

Θ can have different values. In this solution, a forward difference has been chosen due to its simplicity (i.e., Θ = 0) and an iteration solution has been used at each time step to insure an accurate result.

Levenberg-Marquardt iteration

The Levenberg-Marquardt iteration, which started with any initial value of optical properties, has been used in this work since it has an advantage of convergence even at initial guess parameters. The steps are as follows [9, 16,17,18]:

  1. 1.

    Solve the heat transfer equation (eq. 1) using the finite element method to obtain the temperature distribution T(Pk) with the assumed initial values of Pk (i.e., \( {\mu}_a,{\mu}_s^{\prime } \))

  2. 2.

    Compute S(P) where

$$ S(P)={\left[Y-T(P)\right]}^T\left[Y-T(P)\right] $$

the superscript T refers to the transpose matrix and [Y − T(P)]T refers to[Y1-T1,Y2-T2, … …… ..,YI-TI]where I is the total number of measurements which must be greater or at least equal to the total number of unknown (N), Y refers to the measured temperature, and T refers to the estimated temperature.

  1. 3.

    Using the current values of Pk, calculate the sensitivity matrix J(Pk) which can be written as

$$ \left[\begin{array}{ccccc}\frac{\partial {T}_1}{\partial {P}_1}& \frac{\partial {T}_1}{\partial {P}_2}& \frac{\partial {T}_1}{\partial {P}_3}& \cdots & \frac{\partial {T}_1}{\partial {P}_N}\\ {}\frac{\partial {T}_2}{\partial {P}_1}& \frac{\partial {T}_2}{\partial {P}_2}& \frac{\partial {T}_2}{\partial {P}_3}& \cdots & \frac{\partial {T}_2}{\partial {P}_N}\\ {}\vdots & \vdots & \vdots & & \vdots \\ {}\frac{\partial {T}_1}{\partial {P}_1}& \frac{\partial {T}_1}{\partial {P}_2}& \frac{\partial {T}_1}{\partial {P}_3}& \cdots & \frac{\partial {T}_1}{\partial {P}_N}\end{array}\right] $$
  1. 4.

    Solve the following linear equation:

$$ {P}^{k+1}={P}^k+{\left[{\left({J}^k\right)}^T{J}^k+{\mu}^k{\varOmega}^k\right]}^{-1}{\left({J}^k\right)}^T\left[Y-T\left({P}^k\right)\right] $$

where μk is the damping parameter, and

$$ {\varOmega}^k=\operatorname{diag}\left[{\left({J}^k\right)}^T{J}^k\right] $$
  1. 5.

    by the finite element method using Pk+1 to obtain the new value of T(Pk+1) then, compute S(Pk+1).

  2. 6.

    If S(Pk+1) ≥ S(Pk), replace μk by 10 μk, go back to step 4.

  3. 7.

    If S(Pk+1) < S(Pk), replace μk by 0.10 μ,k, accept the new estimated Pk+1

  4. 8.

    If any of the stopping criteria is satisfied which are

    1. (i)

      Sk+1 < ε1

    2. (ii)

      \( \frac{\left|{S}^{k+1}-{S}^k\right|}{S^{k+1}}<{\varepsilon}_2 \)

    3. (iii)

      |Sk + 1 − SK| < ε3,

calculation usually preformed with ε1=ε2 = ε3 = 10−5Then, stop the iteration, if not replace k by k + 1 and return to step 3.

Optical properties determination

After the determination of the absorbed heat, absorption and reduced scattering coefficients for any single tissue type could be obtained. The procedure is to bring the thermocouple to perfect contact with the tissue where the transient temperature measurements are recorded for 180 reading with a 5 s time interval, carrying the Levenberg-Marquardt iteration where the unknowns are absorption and reduced scattering coefficient which could be found with high accuracy. Assuming any initial value of the absorption and reduced scattering coefficient, then, FEM has been used to determine the temperature distribution through the sample. Transient temperatures are saved to be compared later and to determine the sum of square error (i.e., S1). Calculating sensitivity matrix J(P1), determining its transpose, and using the equations mentioned in step 4, then, a new enhanced values of the unknowns could be obtained where a new value of sum of error could be obtained S2, comparing the two differences between the obtained values; then, the direct of the iteration could determine the satisfied values of the unknowns.

Result and discussion

The aim of the work is to determine the absorption and reduced scattering coefficient of a homogeneous tissue by measuring the temperature at the center of the tissue sample subjected to laser radiation. The accuracy of the temperature readings has a major effect on the correctness of the obtained values. The total number of temperature readings during the test from t = 0 to 900 s is 180 reading. In order to evaluate the accuracy and the uniqueness of the analysis, the inverse procedure has been tested with noisy measurements ω =  ± 2.576., zero mean and unitary standard deviation. For the 99% confidence level, we have − 2.576 < w < 2.576. In order to minimize measurement errors, a random error noise ω was added to the exact temperature that is a random variable with normal distribution:

$$ {T}_{\mathrm{measured}}={T}_{\mathrm{exact}}+\sigma \omega $$

σ is the standard deviation of the measurement errors, which may take the value of 2% or 4% of the maximum temperature measured by the sensor. These values are referred to the accuracy of thermocouple and are taken from their manufacturing manual. In special thermocouple, this value may reach less than 0.7% of the max. temperature.

Temperature measurement

A thermocouple type k is used where the reading started from an initial temperature of the environment of 22 °C and the reading was recorded for 5 s each after subjecting the tissue of 1 mm thick to an Nd, YAG laser of 30 mW with top hat beam of 1 mm in radius. It was also assumed that the optical properties are constant through the used temperature range.

Figures 2 and 3 show the exact temperature history at the center of the sample (smoothed line) with 2% Tmax. and 4% Tmax. random error associated with a 99% confidence level (Corrugated line). These readings could be used later as input data to predict tissue optical properties following the Levenberg-Marquardt iteration, see Tables 1 and 2. These tables show an error in the output result as a result of error in input data for Bovine muscle and retina where good nearby results are obtained in detecting tissue optical properties (i.e., the error is no more than 6.4% for Bovine muscle and 3.6% for Bovine retina) even with maximum error in temperature reading of 4% Tmax.

Fig. 2
figure 2

Exact solution indicates smoothed line and Tmeasured that associated with probability of 99% for 4% Tmax. (Corrugated line)

Full size image
Fig. 3
figure 3

Exact solution indicates smoothed line and Tmeasured that is associated with probability of 99% for 2% Tmax. (Corrugated line)

Full size image
Table 1 Error in output result as a result of error in input data for Bovine retina
Full size table
Table 2 Error in output result as a result of error in input data for Bovine Muscle
Full size table

To study the effect of sensor position, the error in the obtained results (i.e., absorption coefficient for solid line and dashed line for scattering coefficient, see Fig. 3) at a different position of the sensor was studied with a random error in temperature reading of 2% Tmax in the input data. It is found that the minimum error could happen nearly at the mid of the sample, see Fig. 4. This may be helpful in designing the setup where the position of the sensor may be located in the middle of the sample to minimize the error in determining optical properties.

Fig. 4
figure 4

Error in output result (i.e., absorption coefficient, solid line; scattering coefficient, dashed line) at different locations of the temperature sensor

Full size image

Finally, the work is extended to determine the three optical properties (absorption coefficient, scattering coefficient, and anisotropy). The same procedure above is followed with the three unknown. The initial values of the properties can be used to predict the temperature distributions at the center of the sample of 1 mm thickness. The obtained temperature distributions were compared with those measured practically, and the difference was minimized so that the results are as nearly as possible to the measured value to detect the optical properties. The only limitation is that a more accurate temperature measurement sensor is needed to obtain acceptable accuracy in detecting optical properties, see Fig. 5. It means that for the accuracy of 10% in the value of optical properties, accuracy in the temperature reading of less than 0.4% Tmax is needed.

Fig. 5
figure 5

Random error in input data and the corresponding error in optical properties (small-dashed line for scattering coefficient, solid line for absorption coefficient, large-dashed line for anisotropy)

Full size image

Conclusions

An inverse heat transfer analysis was used to detect absorption and reduced scattering coefficients of a homogeneous tissue. The proposed method could simply be used to detect any optical property of a homogeneous tissue subjected to a laser that induces heat to the tissue. The generated heat could be used by either the Monte Carlo method or the modified Beer-Lambert law to obtain the temperature distribution through a tissue from which an inverse solution could obtain the optical properties. The influence of error in temperature reading and its effect on the obtained optical properties were studied, and it was found that the minimization error in temperature reading could obtain an accurate result. In addition, the location of the sensor that measured the temperature was studied and it was found that by locating the sensor at the center of the tissue, an optimum accuracy could be obtained. Finally, the work was extended to detect absorption coefficient, scattering coefficient, and anisotropy of a tissue with good accuracy and the only limitation was that high accuracy in temperature sensor (i.e., less than 0.4% Tmax) was needed.