Introduction

The mechanical behavior and the failure process of a jointed rock mass is important research for mining and civil engineering (Ranjith et al. 2017). High rock slopes are typical of open pits and tunnels with surrounding rock excavation; their design often requires the evaluation of rock mass strength along failure surfaces, partly along existing joints. The estimation of the strength and deformation of a rock mass is complex in nature because the nonpersistent jointed rock mass will lead to the interaction of rock bridges (Cai et al. 2004; Prudencio and Jan 2007; Li et al. 2019). For the nonpersistent joint, understanding the whole process of microcrack initiation, development, coalescence, and model failure during rock loading is important (Wong and Einstein 2009a, b; Chen et al. 2013; Zhang and Wong 2013). The mechanical behavior of a rock mass with nonpersistent joints is controlled by the complex interactions of joints and intact rock bridges.

Many studies have been performed to investigate the mechanical behavior of a jointed rock mass (such as Amadei and Goodman 1981; Hoek and Brown 1997; Yang et al. 1998; Kulatilake et al. 2015), whereas studies of randomly distributed nonpersistent joints are limited. Studies have calculated the empirical estimation of rock mass strength and modulus (Jennings 1970; Hoek and Diederichs 2006; Brown 2008), though they lack the role of nonpersistent joints on the mechanical properties of a jointed rock mass. Some analytical studies, such as damage mechanics, deal with the problems of rock mass cut by many small joints (Pietruszczak et al. 2002; Kawamoto et al. 2010; Liu and Yuan 2015; Zhao et al. 2016). Many experimental tests have been performed on offset joints containing one or more set flaws in natural (Wong and Einstein 2009c; Yang et al. 2009; Yang 2011) or rock-like materials (Bobet and Einstein 1998; Zhang and Wong 2012; Afolagboye et al. 2017; Peng et al. 2018). Some numerical simulations have been undertaken to estimate the strength and failure mode of nonpersistent jointed rock masses, such as particle flow code (PFC) (Bahaaddini et al. 2013; Yang et al. 2014; Bahaaddini et al. 2016), rock failure process analysis (FRFA) (Tang and Zhao 1997; Wasantha et al. 2014), universal distinct element code (UDEC), and 3 dimension distinct element code (3DEC) (Vergara et al. 2016; Li et al. 2019).

A limited number of studies on the effect of joint geometrical parameters for nonpersistent jointed rock mass have been performed (Prudencio and Jan 2007; Wong 2008; Prudencio 2009), and the effect of joint mechanical parameters have been determined (Huang et al. 2015; Hu et al. 2017). Bahaaddini et al. (2016) ran a numerical simulation to investigate the mechanical behavior of nonpersistent jointed rock masses using PFC. However, for the rock mass with a random distribution of joint sets, the strength, deformation, and failure processes of the model are very difficult to evaluate. The DFN is an effective technology that represents the joint system with random distribution and has been widely used in the field of joint description and simulation (Grenon and Hadjigeorgiou 2008). The SRM approach is an effective tool based on the idea that discrete element method (DEM) can be utilized to characterize the mechanical behavior of a nonpersistent jointed rock mass (Mas Ivars et al. 2011). The rock is represented by the bonded particle model (BPM) (Potyondy and Cundall 2004) for the simulation of intact rock behavior (Cho et al. 2007), and the joint is presented by the smooth joint model (SJM) for constructing the DFN.

This paper presents a numerical simulation of the effect of joint geometrical parameters for a random distribution nonpersistent rock mass on the uniaxial compressive strength (UCS) σ1 and the deformation modulus E* using the PFC in two dimensions. Additionally, the process of crack initiation, propagation, and coalescence are tested under different loading regimes, and the failure mode is determined. Furthermore, the relationships between the damage variable and joint geometrical parameters and between the initial damage variable and peak strength of jointed rock mass are discussed. In this article, “joint” represents a preexisting flaw in the rock masses, “microcracks” represent the micro cracks that appear during the loading process, and the joint geometrical parameters considered are the joint dip angle α, joint length L, and joint density ρ.

Damage constitutive model of a jointed rock mass

In damage mechanics, the damage variable is a basic concept that represents the damage degree of materials. The test results of joints and a jointed rock mass show that the strength and deformation characteristics of a rock mass are most affected by the joint orientation, length, density, and distribution (Yaméogo et al. 2013; Müller et al. 2018).

For the jointed rock mass, using the elastic modulus can define the initial damage variables from the macroscopic mechanics (D0) of the rock mass directly:

$${\text{D}}_{0} = 1 - \frac{{E^{*} }}{{E_{0} }}$$
(1)

where E* is the deformation modulus of the jointed rock mass, and E0 is the deformation modulus of the intact rock.

Under an external load, randomly distributed mesoscopic damage began to occur in the rock mass. We can study this load damage through statistics. Based on the assumption of rock mass strain equivalence, according to the Weibull distribution damage model, the probability density function (P) of the rock mass micro-element strength is

$$P(\varepsilon ) = \frac{m}{{\varepsilon_{0} }}(\frac{\varepsilon }{{\varepsilon_{0} }})^{m - 1} e^{{ - (\frac{\varepsilon }{{\varepsilon_{0} }})^{m} }}$$
(2)

where \(\varepsilon\) is the rock mass strain and m and \(\varepsilon_{0}\) are the parameters of the rock mass materials.

When the rock mass strain reaches strain \(\varepsilon\) under loading, the damage variable (Ds) can be expressed as

$$D_{{\text{s}}} = 1 - e^{{ - (\frac{\varepsilon }{{\varepsilon_{0} }})^{m} }}$$
(3)

For the intact rock, according to the strain equivalence principle (Zhang et al. 2002), the constitutive relationship (σ1) is

$$\sigma_{1} = (1 - D_{{\text{s}}} )E_{0} \varepsilon$$
(4)

where \(D_{{\text{s}}}\) is the loading damage variable.

For the jointed rock mass, the damage containing initial damage, and loading damage, the constitutive relationship is

$$\sigma_{1} = (1 - D_{0} )(1 - D_{{\text{s}}} )E_{0} \varepsilon$$
(5)

The damage variable D in the coupling state of the two damages can be expressed as

$$D = D_{0} + D_{{\text{s}}} - D_{0} D_{{\text{s}}}$$
(6)
$$D = 1 - \frac{{E^{*} }}{{E_{0} }}e^{{ - (\frac{\varepsilon }{{\varepsilon_{0} }})^{m} }}$$
(7)

Thus, the constitutive relationship of a jointed rock mass can be written as

$$\sigma_{1} = E^{*} e^{{ - (\frac{\varepsilon }{{\varepsilon_{0} }})^{m} }} \varepsilon$$
(8)

Then, if we take the partial derivative of both sides of Formula (8), we find

$$\frac{{\partial \sigma_{1} }}{\partial \varepsilon } = E^{*} e^{{ - (\frac{\varepsilon }{{\varepsilon_{0} }})^{m} }} [1 - m(\frac{\varepsilon }{{\varepsilon_{0} }})^{m} ]$$
(9)

When the strength of a jointed rock mass reaches peak stress \(\sigma_{f}\), the strain is \(\varepsilon_{f}\), and \(\frac{{\partial \sigma_{1} }}{\partial \varepsilon } = 0\). The distribution parameters can be obtained:

$$m = \frac{1}{{\ln \frac{{E^{*} \varepsilon_{f} }}{{\sigma_{f} }}}}$$
(10)
$$\varepsilon_{0} = \varepsilon_{f} m^{\frac{1}{m}}$$
(11)

Synthetic rock mass methodology

Bonded particle model

The PFC (Itasca Consulting Group 2014) is a discontinued code that represents a rock mass as an assemblage of circular or spherical particles connected by planar walls. Rocks can be represented by the BPM, where they are joined together by parallel bonds with certain normal and shear strength values. The BPM can reproduce many rock behavior characteristics, including elasticity, rupture, hysteresis, swelling, post-peak softening, and intensity, with increasing constraints (Hazzard et al. 2000; Park and Song 2009).

The rock core model was at the same scale as the experimental marble specimen. The construction and calibration of the BPM test the marble samples extracted from the Jinping II Hydropower Station (Chu 2009). The macroscopic mechanical properties of rocks under 2D and 3D model characterization methods are relatively close. And their failure modes are similar; the 2D model can represent the main fracture form of rock. In this paper, a rock model with multiple discrete cracks was constructed to analyze its failure characteristics. Considering the efficiency of calculation and the intuitiveness of crack analysis, the 2D model has certain advantages.

Calibration is the process of trial-and-error adjustment to match the measured response of the marble samples. To ensure that the sample remained quasi-statically balanced throughout the test, the load was added at a rate of 0.08 m/s (the model time step was approximately 4.24 × 10−8 s). The boundary conditions of the model include loading in the Y direction and a free boundary for the X direction of the model. The macro-shear strength and normal strength of the rock are not exactly equal to the micro-parameters of shear and normal bond strength in the model. In order to simplify the calculation, Potyondy and Cundall (2004) set the same values for the micro-parameters of shear and normal bond strength. The particle and bond micro-parameters are constantly checked, and the final particle and bond micro-parameters of the rock core and rock block models are presented in Table 1.

Table 1 Micro-parameters of the BPM numerical model
Full size table

A rock core model of size 50 mm × 100 mm and a rock block model of size 1 m × 2 m were constructed by the BPM. Keep the ratio of the model width and the particle average diameter the same for different models, as shown in Table 2. Macro-properties of the laboratory core, rock core model, and rock block model of uniaxial compressive tests are shown in Table 3. The rock core model and rock block model predictions agree with the laboratory core, and the macro-properties of the rock core model and rock block model are consistent.

Table 2 Particle size of different models
Full size table
Table 3 Laboratory measurements and model predictions of the macro properties for the Jinping marble
Full size table

Smooth joint model

The SJM was proposed to simulate the behavior of a smooth interface created by a rock joint in a BPM material. SJM changes the motion of the balls, which are along the joint plane and do not rotate with the contact point of the particle, as shown in Fig. 1. A comprehensive study on the SJM was performed, and the unconfined compressive strength is very sensitive to the change of the relationship between the geometric micro-parameters and the mechanical micro-parameters. Therefore, the mechanical micro-parameters of the SJM remain the same, as listed in Table 4.

Fig. 1
figure 1

a Motions of the balls for the BPM, b the trends of the ball motions, and c the motions of the balls under SJM

Full size image
Table 4 The mechanical micro-parameters of SJM
Full size table

Discrete fracture network (DFN)

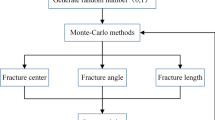
The DFN model is generated by the statistical distribution of joint length, dip angle, and position distribution. With the DFN module, the joint embedded into a rock mass is considered a set of discrete, planar, and finite-sized flaws. In three dimensions, the discrete joints are disk-shaped, and in two dimensions, the discrete joints are linear. A sketch of a rock containing one set of joints is illustrated in Fig. 2, DFN models with one set of joints at different dip angles are shown in Fig. 2a, and SRM models with one set of joints at different dip angles are shown in Fig. 2b. The model is a 1 m × 2 m rectangular numerical model with a single preexisting joint represented by the dip angle α, and the joint length L and the joint density ρ are listed in Table 5.

Fig. 2
figure 2

a DFN models with one set of joints at different dip angles; b SRM models with one set of joints at different dip angles

Full size image
Table 5 The micro-parameters of the smooth joint model
Full size table

Strength and mechanics analysis

Strength and deformation of jointed rock mass under uniaxial compression

Compared with the rock block model (peak strength σ = 128.26 MPa; elasticity modulus E = 39.22 GPa), the relationship between the strength ratio σ1/σ and dip angle \(\alpha\) is presented in Fig. 3. Figure 3a shows the model at different joint lengths; Fig. 3b shows the model for respective joint densities. As shown in Fig. 3a, regardless of length L, the largest peak strength is found when \(\alpha\) is 90°, and the smallest peak strength is found when \(\alpha\) is 0°. For the same \(\alpha\), the largest peak strength is found when L is 0.1 m, and the smallest peak strength is found when L is 0.2 m, and peak strength is almost the same when \(\alpha\) is 90°. This shows that the parameters \(\rho\) and \(L\) have a coupled effect on the strength of the rock mass. As shown in Fig. 3b, for the same \(\alpha\), the largest peak strength is found when \(\rho\) is 0.5, and the smallest peak strength is found when \(\rho\) is 4.0. For the same \(\rho\), the largest peak strength is found when \(\mathrm{\alpha }\) is 90°, and the smallest peak strength is found when \(\alpha\) is 0°. Despite the random distribution of joints, there is also a regular influence on joint geometrical parameters for the rock mass strength, and the parameters \(\rho\) and \(\alpha\) have a monotonic effect on the strength of the rock mass.

Fig. 3
figure 3

The relationship between σ1/σ and \(\alpha\) for a different L; b different \(\rho\)

Full size image

The relationship between elastic modulus ratio E*/E and dip angle \(\alpha\) is shown in Fig. 4. From Fig. 4a, we observe that for the same L value, at a smaller dip angle, the values of E* are smaller in general. For dip angle α = 90°, the changes in flaw length have little impact on the values of E*. For dip angle α = 60°, the values of E* are practically the same for L = 0.2, 0.3, and 0.4 m. From Fig. 4b, we find that for the same α value, when the density is lower, the values of E* are larger in general. For the same ρ value, the smaller the dip angle is, the smaller the values of E* are in general. When ρ = 4.0, the change in joint density has little influence on the values of E*. Despite the random distribution of joints, there is still a regular influence on the joint geometrical parameters of the elastic modulus, and the parameter \(\rho\) has a monotonic effect on the elastic modulus of the rock mass.

Fig. 4
figure 4

The relationship between E*/E and \(\alpha\) for a different L; b different \(\rho\)

Full size image

Stress redistribution analysis

To determine the rock stress distribution status in the loading process, we must understand the relationship between stress redistribution and microcracks. The model with coplanar joints (\(\alpha =45^\circ\), L = 0.1 m, and \(\rho =2\)) is used as an example. Figure 5 shows the microcrack distribution and axial stress contours at different stages, and the stress values \(\sigma\), strain value \(\varepsilon\), and number of microcracks (\({N}_{\mathrm{mc}}\)) are listed below the picture.

Fig. 5
figure 5

Microcrack distributions and axial stress contours at different stages

Full size image

When the strain value \(\varepsilon\) is 1e − 3, the stress value \(\sigma\) is 33.31 MPa, and there are 21 microcracks. The microcracks are displayed on the tips of the joints, and the region with the fewest microcracks has the largest stress. When the strain value \(\varepsilon\) is 1.5e − 3, the stress value \(\sigma\) is 48.93 MPa, which is near the peak strength, and the microcracks total 75. The microcracks also appear at the tips of the joints, and the stress distribution rule is similar to before. When the strain value \(\varepsilon\) is 2e − 3, the stress value \(\sigma\) is 41.93 MPa, which is after the peak strength, and there are 875 microcracks. Some of the joints have coalesced, and stress is released in the area where the microcracks appear. When the strain value \(\varepsilon\) reaches 2.5e − 3, the stress value \(\sigma\) is 39.34 MPa. Furthermore, after peak strength, the number of microcracks is 1420. The microcracks appeared on the coalescence part of the joints, and the stress concentration area did not change. When the strain value \(\varepsilon\) reaches 3e − 3, the stress value \(\sigma\) is 26.81 MPa, and the number of microcracks is 2023. Each microcrack grows along the nearest joint, and the stress concentrations are reduced. When the strain value \(\varepsilon\) reaches 3.5e − 3, the stress value \(\sigma\) is 6.75 MPa, and the number of microcracks is 2563. The microcracks grow throughout the entire model, dividing it, and the stress concentration and residual strength exist in a very small area. In the stress redistribution process, the microcrack development can be easily determined. The microcracks first appear in the area where microcracks are already clustered; they grow along the nearest joints and finally penetrate the area where microcracks are less developed.

Comparison with experiment and model

The failure modes for a jointed rock mass with nonpersistent joints have been previously studied and summarized. Prudencio and Jan (2007) observed three failure modes in the test program: failure through a plane, stepped failure, and rotation of new blocks. Bahaaddini et al. (2013) summarized five failure modes: planar failure, block rotation failure, step-path failure, and semi-block (initial) failure; semi-block (peak) failure is observed by the discrete element method. Chen et al. (2013) summarized seven failure modes, including axial cleavage, crushing, crushing and rotation of new blocks, stepped failure, stepped failure and rotation of new blocks, shear failure along a single plane, and shear failure along multiple planes. Cording and Jamil (1997) identified four failure modes: planar failure, step-path failure, multi-plane stepping failure, and intact rock failure. According to the microcrack distribution, we summarized the six failure modes: through a plane, stepped, rotation of new blocks, mixed, multiplane stepped, and shearing through intact rock. Overall, the cracking process and failure modes are more strongly affected by joint orientation than by joint length and joint density.

For the model with discretely distributed joints, there is a lack of the exact corresponding experiments. We compare the failure modes for the qualitative analysis, as seen in Fig. 6. We compare the lab test from Prudencio and Jan (2007) and the contrasting model from the numerical test. The failure mode of model a is through a plane. Compared with the experiment, the failure patterns are similar. The failure mode of model b is stepped, and we see from the test and simulation that the microcrack appears in the rock bridge, forming the step failure. The failure mode of model c is rotation. Compared with the experiment, the failure patterns are similar, and the model fractures into a series of blocks that can rotate. The failure mode of model d is mixed, including both stepped and rotation.

Fig. 6
figure 6

Comparison between the experiment and simulation of similar models

Full size image

Failure modes of jointed rock mass model

The failure mode of models with different joint lengths are shown in Fig. 7. At L = 0.1 m, there is a large number of microcracks, tensile wing cracks are common, and the model failure modes are rotation, mixed, and shear. At L = 0.2 m, there are fewer microcracks, tensile wing cracks initiate from the joint tips and coalesce at the rock bridge, and the failure modes include multi-stepped, step, mixed, and rotation. At L = 0.3 m, there are fewer microcracks, the rock bridge has become shorter with an increase in joint length, and the failure modes are rotation, plane, mixed, and shear. At L = 0.4 m, there are fewer microcracks, one flaw may play a major role during failure, and the failure modes are rotation, mixed, and shear. The dip angle also has an effect on the failure mode. For example, when the dip angle was 90°, the failure mode was almost shearing through intact rock. There are couple effects of the joint length and joint dip angle for the failure mode.

Fig. 7
figure 7

Effect of the dip length L on failure mode

Full size image

The failure modes of models with different joint densities are shown in Fig. 8. At \(\rho\) = 0.5, the distribution of microcracks is relatively concentrated, and the model failure modes are rotation and shear. At \(\rho\) = 1.0, tensile wing cracks initiate from the joint tips and coalesce at the rock bridge, and the failure modes are rotation, mixed, and shear. At \(\rho\) = 2.0, more microcracks appear in the rock bridge, and the failure modes are step, mixed, and rotation. At \(\rho\) = 3.0, the failure modes are multi-planed, mixed, and shear. At \(\rho\) = 4.0, the failure modes are step, mixed, rotation, and shear. As the joint density increases, the number of microcracks increases, and the randomness of microcrack development becomes stronger. The dip angle also has an effect on the failure mode. For example, when the dip angle was 90°, the failure mode almost shears through intact rock. There is a coupling effect of the joint density and joint dip angle for the failure mode.

Fig. 8
figure 8

Effect of the dip density ρ on the failure mode

Full size image

Damage evolution and failure process analysis

In the numerical simulation test, the value of peak strength σf, the strain at peak strength εf and the deformation modulus of the jointed rock mass E* were obtained. The calculated values of m and ε0 in the model set with different joint dip angles, joint lengths, and joint densities are shown in Table 6.

Table 6 The mechanical parameters of the jointed rock mass
Full size table

According to damage variable formula of jointed rock mass, damage varies with the strain under different joint dip angles, joint lengths, and different joint densities, as shown in Fig. 9. The damage variable value increases slowly under loading, and inflection point of the damage variable occurs near the peak strength. The damage variable value is near 1 at the failure stage. The growth rate of the damage variable is related to the failure mode. The growth rate is bigger for brittle failure and smaller for plastic or ductile failure.

Fig. 9
figure 9

Changes in damage variable with strain for a different joint dip angles; b different joint lengths; c different joint densities

Full size image

The initial damage variable is related to the geometry of the joints. The larger the dip angle is, the smaller the initial damage variable will be; the smaller the dip length is, the smaller the initial damage variable; and the smaller the dip density is, the smaller the initial damage variable. Therefore, the initial damage variable D0 is defined as a function between dip angle \(\alpha\), flaw length L, and flaw density ρ:

$${D}_{0}=0.1479-0.0049\mathrm{\alpha }+0.9412\mathrm{L}+0.0814\uprho$$
(12)

Once the geometry of flaws was determined, the initial damage variable value was calculated. The relationship between initial damage variable and peak strength of the jointed rock mass is shown in Fig. 10. Therefore, we can roughly find the strength of the jointed rock mass based on the geometry of flaws.

Fig. 10
figure 10

Relationship between the initial damage variable and peak strength of the jointed rock mass

Full size image

Take the model (α = 0–90°, L = 0.1 m, and ρ = 2.0) for example, the curve comparison between the DEM simulation and damage constitutive model is shown in Fig. 11. The numerical simulation curve and constitutive calculation curve are matched well before the peak strength. For the brittle failure of the model, the numerical simulation curve and constitutive calculation curve are also matched well, such as when the dip angle was 60 or 90°. For the ductile failure of the model, the numerical simulation curve and constitutive calculation curve are matched well at the first stage, such as the dip angle was 0°, 30°, or 45°. Overall, this damage constitutive model is more suitable for brittle failure of the jointed rock mass than ductile and plastic failure.

Fig. 11
figure 11

Comparison between numerical simulation and constitutive calculation stress–strain curve of the jointed rock mass for different dip angles: a α = 0°, b α = 30°, c α = 45°, d α = 60°, and e α = 90°

Full size image

Conclusions

SRM modeling with one set of randomly distributed nonpersistent joints is used to explore the effect of joint geometry parameters on the mechanical behavior of a rock mass under uniaxial compression. We draw the following conclusions from this study:

  1. 1.

    Three geometry parameters α, L, and ρ are used to investigate the strength and deformation of jointed rock masses. In general, the bigger the α values are, the bigger the ρ values, and the bigger the values of the strength and deformation values. The parameters \(\rho\) and \(L\) have a coupled effect on the strength and deformation of the rock mass.

  2. 2.

    The stress redistribution is used to analyze the stress change during the loading process. The crack development can be roughly determined. The microcracks first appear in the area where microcracks are previously concentrated, then grow along the nearest joint, and finally penetrate the area where microcracks are less developed.

  3. 3.

    We summarize six failure modes in the model of a randomly distributed set of joints: through a plane, stepped, rotation of new blocks, mixed, multiplane stepped, and shearing through intact rock. Three geometry parameters α, L, and ρ all affect the failure mode of the model, and there is a coupled effect of the joint length and joint dip angle for the failure mode. The ability to forecast the failure mode has a significant economical factor on the stability of open pits: rotational failure would lead to a regressive slope failure, while a planar failure, although associated with a possibly steeper pit, would lead to brittle slope behavior.

  4. 4.

    The damage variable D contains the initial damage variable D0 and the loading damage variable Ds. The initial damage variable D0 is related to dip angle \(\alpha\), flaw length L, and flaw density ρ. Once the geometry of the flaws is determined, the initial damage variable value is calculated. The damage constitutive model and stress-stain curve of the SRM model are compared in the article. The numerical simulation curve and constitutive calculation curve are matched well before the peak strength. A damage variable is an effective tool for quantifying the failure process and benefits surrounding rock classification and tunnel support design.